Light-Weighted Decision Support Framework for Selecting Cloud Service Providers

1  Introduction

Cloud computing is a concept based on information technology that meets the needs of users based on their requests and needs. Consumers are supplied with completed prepared hardware and software in a cloud environment through the use of a network in an autonomous self-serviced mechanism [1]. Due to cloud computing’s inherent benefits, several organizations, such as academic, governmental, and commercial ones, have transferred their business solutions to cloud infrastructures, in favour of making their business operations more nimble at a lower cost and with less effort [2]. Users’ growing adoption of the cloud computing paradigm has resulted in heightened benefits for cloud consumers as well cloud service providers (CSPs). As a result of this expansion, the resource management process has become more complicated, so that it requires more resource provisioning and scheduling. Cloud consumers seek for service providers who can deliver high-quality services at a low cost, since many cloud service providers adopt a pay-as-you-use strategy. Various criteria determine the cost of these services, such as throughput, response time, size of the task, and resource cost [3]. Thus, it is important that cloud consumers have an opportunity to select the most suitable CSP from among several alternatives. Since making the right decision when choosing a CSP is crucial to enhance the level of reliability between consumers and providers, the marvelous innovations and growing use of cloud computing make it necessary to have an approach to cloud service selection that is accurate and effective [4]. Moreover, the similarities between the services offered by different service providers increases the complexity of the selection problem. Deciding the appropriate CSP requires thoughtful consideration due to the variety of available providers. Therefore, consumers require cloud service selection frameworks to assist them in figuring out which service providers will work best for them.

Cloud consumers share their resources outside of the organization’s environment and become more reliant on networks when they use cloud services. This leads consumers to encounter various risks, such as service interruptions due to possible network disruptions and information leakage due to malicious conduct in shared environments. Moreover, cloud service consumers are affected by a growing number of laws and regulations that require consumers to address further requirements, like data security [5].

Several technical and management quality-of-service (QoS) criteria must be evaluated when choosing the best CSP, like performance and reliability. For example, to identify CSP characteristics, technical QoS criteria, such as performance and reliability, are essential to consider. However, cloud consumers appreciate the security and privacy attributes of services. The process of selecting the best CSP depends on the matching of consumer needs with the available cloud service features offered by different CSPs. Furthermore, several of these attributes, such as performance and cost, may involve trade-offs between each other. A wide range of diverse evaluation criteria concerning cloud services provided by several CSPs must be addressed in order to select the most appropriate CSPs that perfectly match consumer preferences. Thus, it is evident that the problem of selecting the best service provider is a multi-criteria decision making (MCDM) problem, where multiple criteria need to be weighted in order to achieve the best solution (i.e., choice).

Optimum decisions regarding the selection, ranking, and prioritizing of various alternatives can be achieved by adopting MCDM approaches based on the decision maker’s evaluation of pre-defined criteria. Several studies included in the literature examine the effectiveness of MCDM approaches for constructing task-scheduling problems, where task fea-tures represent as pre-defined criteria and tasks represent as alternatives. The analytical hierarchy process (AHP) is a type of MCDM that has been used in cloud computing to prioritize tasks.

This paper introduces a model that considers consumer preferences (e.g., price, quality, time, etc.) and service provider preferences (e.g., price, speed, quality, time, etc.). The model illustrates various components where the scope in this paper is the broker architecture which mainly seeks for satisfying consumers requirements by discovering the most suitable CSP. The BWM is applied in the presented model to obtain and manipulate preferences in order to prioritize tasks. The prioritized tasks for each consumer are evaluated against all service providers in order to determine the best solution (i.e., the best service provider), as well as to ensure fairness in assigning the best service provider to later consumers in subsequent iterations. To demonstrate the efficacy of the provided algorithms in the model, the proposed model was validated on various sets of consumers, service providers, and tasks. The model was able to effectively assign a large number of consumers with a diversity of preferences to the best service providers. Service providers, on the other hand, were equally evaluated against each request while maintaining their competency priority. Thus, this paper aims to evaluate the preferences of both consumers and CSPs to come up with an optimal solution by adopting the BWM. This research also aims to highlight and prioritize the most influential factors that affect cloud tasks. The contribution of this research can be described as follow:

1)   Acquiring the preferences of all parties, consumers and CSPs, and prioritizing criteria and tasks.

2)   Determining the similarities among all tasks and CSPs to facilitate the assigning process.

3)   Assuring the utilization of all available CSPs with respect to their importance.

2  Related Work

Resource management is the broad concept that covers both resource provisioning and resource scheduling. Consumers’ requests provide the main QoS requirements to complete both the provisioning and scheduling processes based on different algorithms and techniques. Mainly, a broker provides the suitable resources based on these requirements; then, the broker send the request for scheduling [6]. Many challenges have been identified regarding the provisioning of resources and scheduling of tasks within a cloud environment. First, consumers and service providers have different requirements to be met, which raises the need to implement the best technique to assure optimal performance. Singh et al. [7] have investigated the resource scheduling algorithms and its implications for providers and consumer profits by conducting a methodical survey and compared the scheduling algorithms with respect to important resource scheduling criteria. Due to the increasing capabilities and speed of computing systems, there is a need for modern computing features, such as optimal task scheduling and enhanced security [8–10]. Several Internet of things (IoT) protocols have been investigated by Farahmandpour et al. [11] to determine the primary technological obstacles that must be overcome to implement services virtualization in cloud environments. An obvious solution for distributed cloud infrastructure is proposed, while considering various features of CSPs, like scalability and on-demand usage [12]. Liu et al. [13] addressed how conflicts of interest among cloud service stakeholders (i.e., consumers, providers, and operators) are a major challenge, where each individual has their own preferences and objectives. To overcome the aforementioned challenges, different algorithms and techniques have been proposed and discussed. The proposed algorithms can be categorized based on various themes, such as the technique used in task allocation (e.g., optimization techniques), the proposed algorithm’s scheduling type (e.g., static or dynamic), and the objective of the algorithm (e.g., energy aware or network aware).

Shyam et al. have provided the benefits of applying various optimization techniques [14]. These techniques have been proven to enhance efficient task scheduling in cloud environments. Successfully adopted optimization techniques include genetic algorithms (GA) [15], particle swarm optimization (PSO) [16], game theory [17], and ant colony optimization algorithms (ACO) [18]. However, there is a persistent lack of studies that identify the influence of these techniques on workload and resources [14]. Regarding the objective of the proposed technique, the GA algorithm, for example, was proposed to achieve QoS based on consumer requirements within a given budget [19], while a proposed algorithm has used the PSO algorithm for efficient energy consumption [20].

The problem of choosing a CSP is not new. One of the primary objectives for improving the efficiency of an organization is to select the best provider, which impacts the organization’s growth and effectiveness. Various studies have investigated this problem in order to provide possible solutions. For example, Do Chung et al. [21] introduced a cloud service selection model based on the analytic network process (ANP) to select the best CSP. Based on the ANP model, the authors defined several criteria, such as provider point of view, service point of view, and support point of view, and also each criterion contains various sub-criteria, such as service brand name and price, service availability and performance, service scalability and security, and service level agreement. These various criteria and sub-criteria were evaluated by 7 domain experts by entering their judgements into pairwise comparisons in order to derive the weight for each element in the model.

A number of proposed algorithms have adopted one or more of the MCDM methods. These algorithms have investigated the applicability of the MCDM to rank resources based on their QoS [22] and the feasibility of prioritizing tasks based on different criteria [23,24]. Godse et al. [25] defined the selection of a cloud service as an MCDM challenge and proposed a case study involving a sales force automation service in order to better understand the empirical method’s importance in tackling the problem of software as a service (SaaS) selection. The proposed framework uses several parameters to select cloud services based on the user’s needs. According to Krishankumar et al. [26] the AHP, the preferences ranking organization method for enrichment evaluation (PROMETHEE), and the technique for order of preference by similarity to ideal solution (TOPSIS) are the most used MCDMs for CSP selection. The BWM was integrated with TOPSIS by Youssef [27] in order to specify the appropriate CSP. The author evaluates several service providers based on various criteria, such as cost, sustainability, response time, inter-operability, reliability, maintainability, scalability, usability, and security. Moreover, in mobile cloud computing, MCDM approaches are being used to enhance the efficiency and efficacy of job offloading [28,29].

A hybrid MCDM framework, called SELCLOUD, was introduced by Jatoth et al. [30] to select cloud services based on the integration of extended Grey TOPSIS with AHP. Garg et al. [31] proposed the SMICloud model to rank cloud services based on the service measurement index (SMI) cloud. Using the AHP method, the authors obtained the weight of each criterion in the model, and they considered the interdependence among them in order to achieve accurate results. The proposed model includes attributes such as agility, cost, security, performance, and accountability. A combination of AHP and the TOPSIS framework was introduced by Kumar et al. [32] for selecting the most appropriate cloud service. Using the AHP importance scale, pairwise comparisons were made in order to specify the importance of each cloud service over the other ones with respect to several criteria, such as assurance, reliability, stability, auditability, accuracy, data integrity, and data privacy. Then, using the TOPSIS method, the final prioritizing of cloud services was obtained. Alashaikh et al. presented a framework to select the best service based on the adoption of conditional preference networks (CP-nets) with respect to a set of criteria with complicated inter-dependencies [33]. Sun et al. [34] proposed a cloud service selection with criteria interactions (CSSCI) model to evaluate criteria inter-dependencies based on a fuzzy measure and Choquet integral. The authors determined the significance weight for each criterion using pairwise comparisons to determine the degree of interaction between each pair of criteria. Garg [35] investigated the problem of cloud deployment model selection in the educational institute based on Fuzzy-euclidean-Taxicab distance-based approach (Fuzzy-ETDBA). Four cloud deployment models have been evaluated with respect to 17 criteria using Fuzzy-ETDBA. The author addressed that the presented study can be enhanced by identifying more decision criteria and implementing advanced fuzzy sets.

In general, the work is based on extraction of the relationships between several entities. The recent work for extraction of knowledge from the relationships of entities has been representation to shift the focus from supervised learning to active learning [36,37] to save the requirement of substantial amount of training data and time. The authors in [36] have presented a lexicalized dependency paths (LDPs) between entities in a dependency tree for fast, efficient and transparent representation of relationships between entities. The method used entity types and subtypes to counter the effect of data sparsity. In [37] they have proposed a new representation that combined LDPs with an active learner for LDPs.

Most of the abovementioned methods are associated with several drawbacks; for example, in [33] the CP-nets was successfully adopted to choose the best CSP regarding a group of attributes with complex inter-dependencies; however, while CP-nets is a compact model, its application on the cloud is still being researched. The task of determining which solution dominates the other ceteris paribus is computationally challenging [38] and, thus, only the weaker version of dominance is computationally attractive. The TOPSIS and PROMETHEE techniques, on the other hand, also offer several disadvantages. One of the issues associated with these techniques is that they can result in a situation known as rank reversal, which might occur when an alternative is added or eliminated from the alternatives list, as the order of priorities of the alternatives changes. This might result in what is known as total rank reversal, where the order of priorities is completely reversed [39].

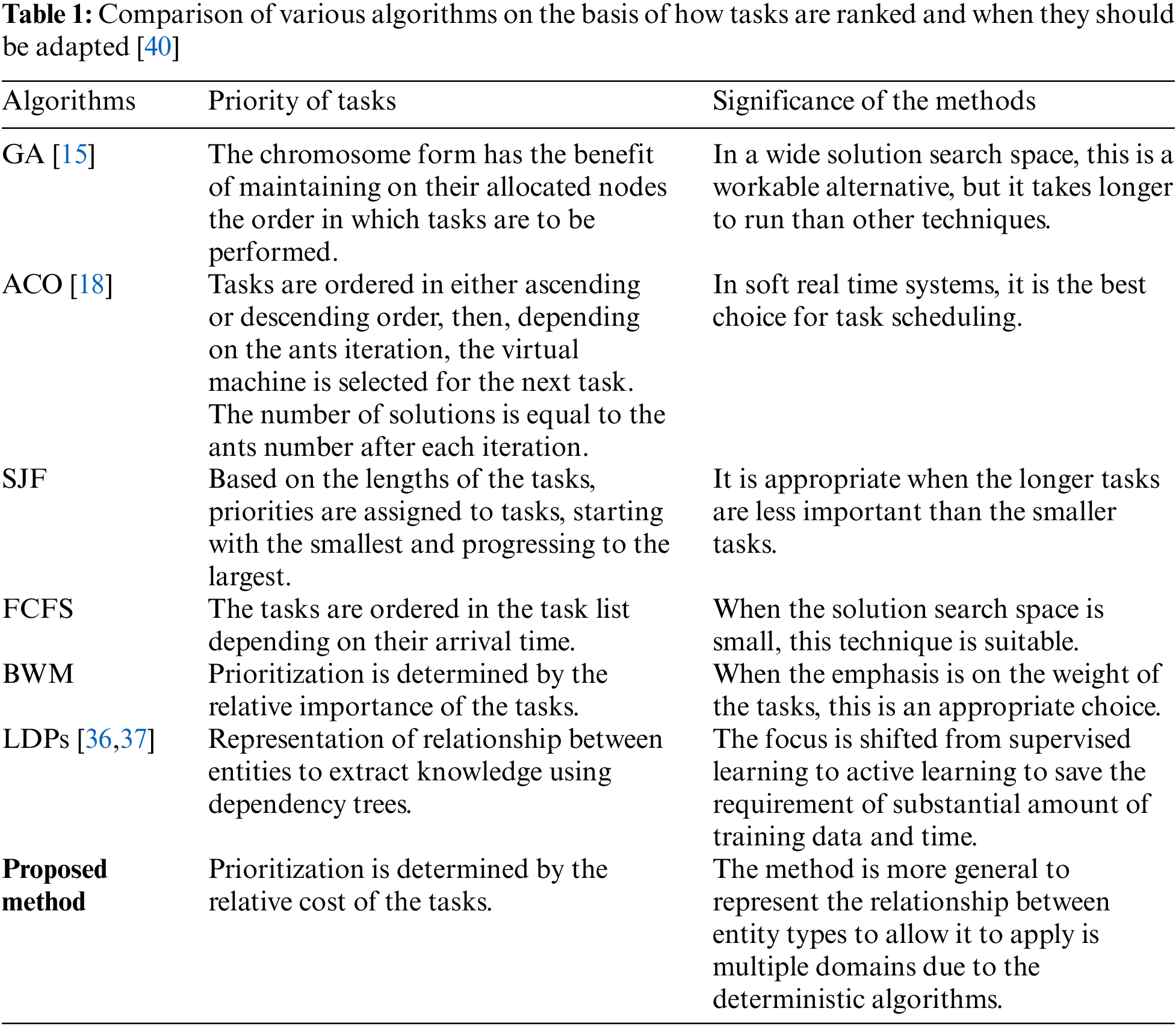
Thus, each optimization technique has a suitable situation that can be used in task scheduling. Table 1 compares and contrasts the various algorithms, such as GA, ACO, first come first Service (FCFS), short job first scheduling (SJF), and BWM on the basis of how tasks are ranked and when they should be adopted.

3  Framework

The first component in our proposed framework is the task repository. This repository should contains all available tasks (i.e., tasks that can be accomplished by one or more service providers). The goal in creating the list of tasks is to enable consumers to specify the required tasks for later ranking. Furthermore, service providers can access the repository and add, remove, change, or update the pool of tasks.

Regardless of the available service providers, consumers are asked to provide their preferences based on a predefined set of criteria, such as price, quality, and completion time. The evaluation process compares all criteria in order to develop weighted and ranked criteria for each consumer; then, prioritized tasks are determined later in the process.

Similarly, service providers evaluate sets of criteria that ultimately increase service provider’ benefits. Each service provider seeks benefits with different priorities, such as building trust, establishing reputation, increasing profit, and so on. Furthermore, each service provider provides services with different capabilities, such as accountability, agility, cost, and performance. The service provider is asked to evaluate all specified criteria in order for the model to rank the criteria and reflect the results on the tasks accordingly.

Having a pool of available service providers with associated resources allows the model to enrich the evaluation of the service providers for each resource by evaluating the historical data. The cloud service-level agreement (SLA) contains a list of minimum criteria, such as availability and reliability, that service providers agree to provide. However, it has been found that not all service providers strictly adhere to the SLA; therefore, evaluating the services and resources based on historical data can make the model more efficient. However, for new services and resources, the model can only rank available tasks based on providers’ preferences.

The successful application of MCDM methods has facilitated the representation of the problem of evaluating criteria and prioritize tasks as a hierarchical problem that can be mathematically dealt with using various inputs from decision makers (i.e., consumers and service providers). The model should take all tasks and calculate the weight of each criterion based on all provided evaluations. To enhance the performance of the proposed model, we propose the adoption of the BWM, as we explain in the next section.

The ultimate results of executing the BWM steps are two sets of prioritized tasks along with a subset of prioritized tasks for each consumer and each service provider. When there is a small number of tasks or service providers, the matching process can be easy, and the assignment of each available task to the best corresponding provider occurs. When a large number of tasks and/or service providers is available, we offer a matching process that ensures the best results for task allocation among all service providers.

The final component of the model is the matcher that connects each consumer to a service provider. Two main issues arise when designing an algorithm for the matching problem. First, the algorithm should distribute the set of consumers’ tasks among the set of service providers in a way that maximizes profits for both parties. Second, this algorithm should somehow ensure a balanced distribution of tasks among all service providers. Suppose that a service provider (SP), named SP1, provides a high speed of service with a low cost, while another service provider, named SP2, provides a medium speed of service with a low cost. Also, suppose ten consumers (Cs) look for quick service and a low price at the same time. If the proposed algorithm assigned all ten consumers’ tasks to SP1, perhaps the last consumer’s tasks on the queue will take a longer time than if two-thirds of consumers were assigned to SP1 and one-third to SP2. Assigning all ten consumers to SP1 also creates an issue in terms of not utilizing the resources of SP2, thus minimizing SP2’s profits. In Section 5, we explain our algorithm that represents how the matching process should occur. The proposed model and its components are shown in Fig. 1.

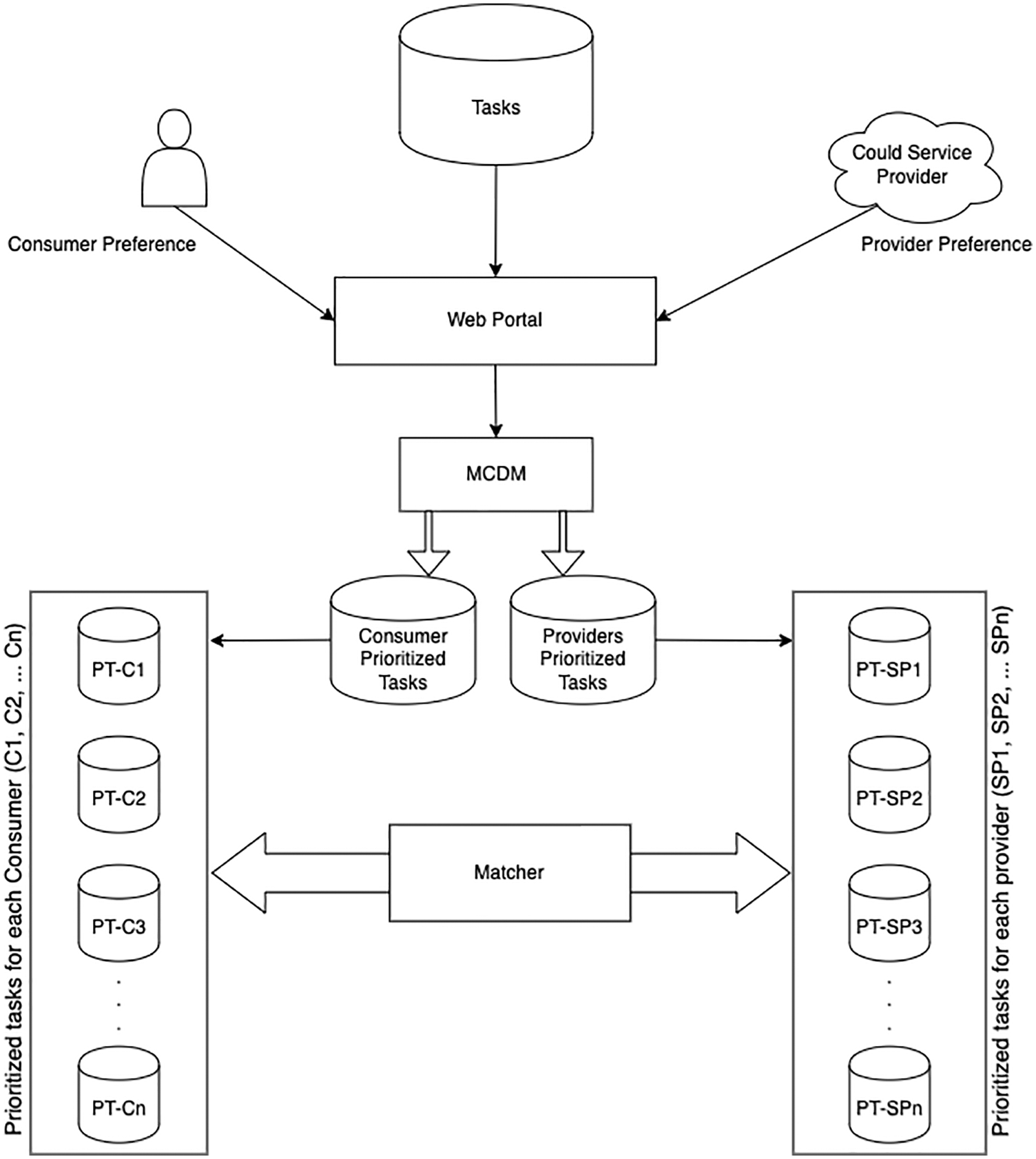
Figure 1: Framework for selecting the best cloud service provider

4  BWM for Weighting Criteria and Prioritizing Tasks

The BWM is a MCDM approach that numerous leaders approve of for organizing choice issues and making ideal decisions dependent on light pairwise examinations among various options [41]. The BWM provides reliable results and overcomes the consistency and time-utilization issues that are the drawbacks of most popular MCDM methods, such as the AHP. The BWM simply compares the best criterion to all other criteria, as well as comparing the worst criterion to all other criteria.

The best and worst criteria are identified by decision makers to help them identify the most important and least important factors that the evaluation process must consider.

The steps (1 to 7) illustrate the evaluation of cloud criteria and tasks in order to calculate the optimal weight of each criteria. Steps 8 and 9 deal with calculating the similarities between the two Cs and SPs in order to find the best match with respect to the priority, as explained in Section 5.

1)   The decision maker selects the most important criterion (CB) for the cloud task.

2)   The decision maker selects the least important criterion (CW) for the cloud task.

3)   The decision maker determines the preference of CB over all other criteria

(Best-to-Others), which results the following vector:

Best-to-Others = [PCB1, PCB2, PCB3, PCBn]; where PCBj indicates the preference of CB over Cj.

4)   The decision maker determines the preference of all criteria over CW (Others-to-Worst), which results in the following vector:

Others-to-Worst = [PC1W, PC2W, PC3W, PCnW]; where PCjW indicates the preference of Cj overCW.

5)   For each decision maker’s evaluation, calculate the optimal weight of all Criteria (WC1, WC2, … WCn) including WCB and WCW.

6)   Aggregate optimal weights from all decision makers and calculate the average weights.

7)   Prioritize all criteria based on the resulting average weights.

8)   Calculate the similarities between all Cs’ preferences and SPs’ preferences.

9)   With respect to priority, find the best match between each C’s task and each SP’s task based on the similarity index.

Before the start of the evaluation process, the set of criteria should be presented to the decision-makers. Various cloud criteria influence the ranking and optimization process. Substantial work has been done to identify and provide a measurement of the CSPs. Cloud Services Measurement Initiative Consortium (CSMIC) has proposed a hierarchical standard measurement framework (SMI) to solve the problem of measuring cloud-based service [42]. The framework divides the measurement space into seven categories: namely, financial, Agility, Assurance, Accountability, Security and Privacy, Usability, and Performance. Each category contains three or more criteria/attributes. For example, Performance is further refined by four criteria: namely, accuracy, functionality, interoperability, and service response time.

Step 1 presents several criteria/attributes to the decision-makers to start the evaluation process. It is important to mention that there is a trade-off between presenting some or all criteria to the decision-making. More number of criteria will increase the computational complexity of the process for prioritizing the criteria whereas presenting a small number of criteria can influence the quality of prioritization. Selecting the best criteria to present to the decision-maker can be affected by various factors such as domain-based services. Therefore, our framework delegates the selection of cloud criteria/attributes to the application phase. In steps 2 and 3, the most significant as well as the least important task-based criterion will be determined by the consumer. For example, if the consumer is primarily concerned with the service re-sponse time, this would be the best criterion. If the consumer is unconcerned about the on-going cost of the service, this would be the worst criterion. In step 3, the decision-maker will prefer the best criterion over all other criteria. In our example, the preference to the service response time is given over all other criteria by the consumer which results in the Best-to-Others vector [PCB1, PCB2, PCB3, PCBn]. In step 4, the preference to all criteria is given over the worst criteria. In our example, the on-going cost which results in the Other-to-Worst vector [PC1W, PC2W, PC3W, PCnW]. To execute steps 5 to 7, the following equations, from [41,43], are used that are introduced into the problem of selecting a CSP in order to weigh all criteria based on a decision maker’s preferences.

To determine the optimal weight (WC1, WC2, … WCn) of all C1, C2, … Cn, the maximum absolute differences |WCBWCn−aCBn| and |WCnWCw−aCnw| for all n are minimized. Thus, the following minmax model obtains an optimized solution with unique weights by extracting the maximum among the absolute difference values which must be minimized.

minmax n{|WCBWCn−aCBn|,|WCnWCw−aCnw|}(1)

where aCBn is the preference of CB over Cn, and aCnw is the preference of Cn over CW. Such that:

∑nWCn=1

WCn ≥ 0 for all n

A complete step-by-step guideline on how to adopt the BWM for structuring task-scheduling problems, accommodating consumer preferences, and prioritizing tasks in the cloud can be found in [24]. The authors of [44] have proposed a model based on BWM method to accomplish prioritization of many significant barriers using big data analytic framework for smart cities.

The decision maker, in the BWM, provides only 2n − 3 pairwise comparisons, which is significantly less than the AHP, for instance, where decision makers need to provide n(n − 1)/2 pairwise comparisons. Assume that we have 18 criteria that the service providers want to weight; for example, reputation of organization, increasing profit, utilizing resources, etc. Adopting the BWM, each service provider provides 33 pairwise comparisons to facilitate the process of calculating the weight of all 18 criteria. When the AHP is adopted instead, the service provider will be required to provide 153 pairwise comparisons to weight the 18 criteria. When compared to AHP and ANP, BWM produces more consistent results and requires fewer pairwise comparisons, making it better suited to situations involving a large number of criteria [45,46]. Table 2 shows the detailed structures of both AHP and BWM.

The proposed model adopts the BWM for the aforementioned advantages. All steps to weight tasks are depicted in Fig. 2. There are two main runs for the BWM process, one for weighting the tasks based on consumers’ preferences and the other for weighting the tasks based on providers’ preferences.

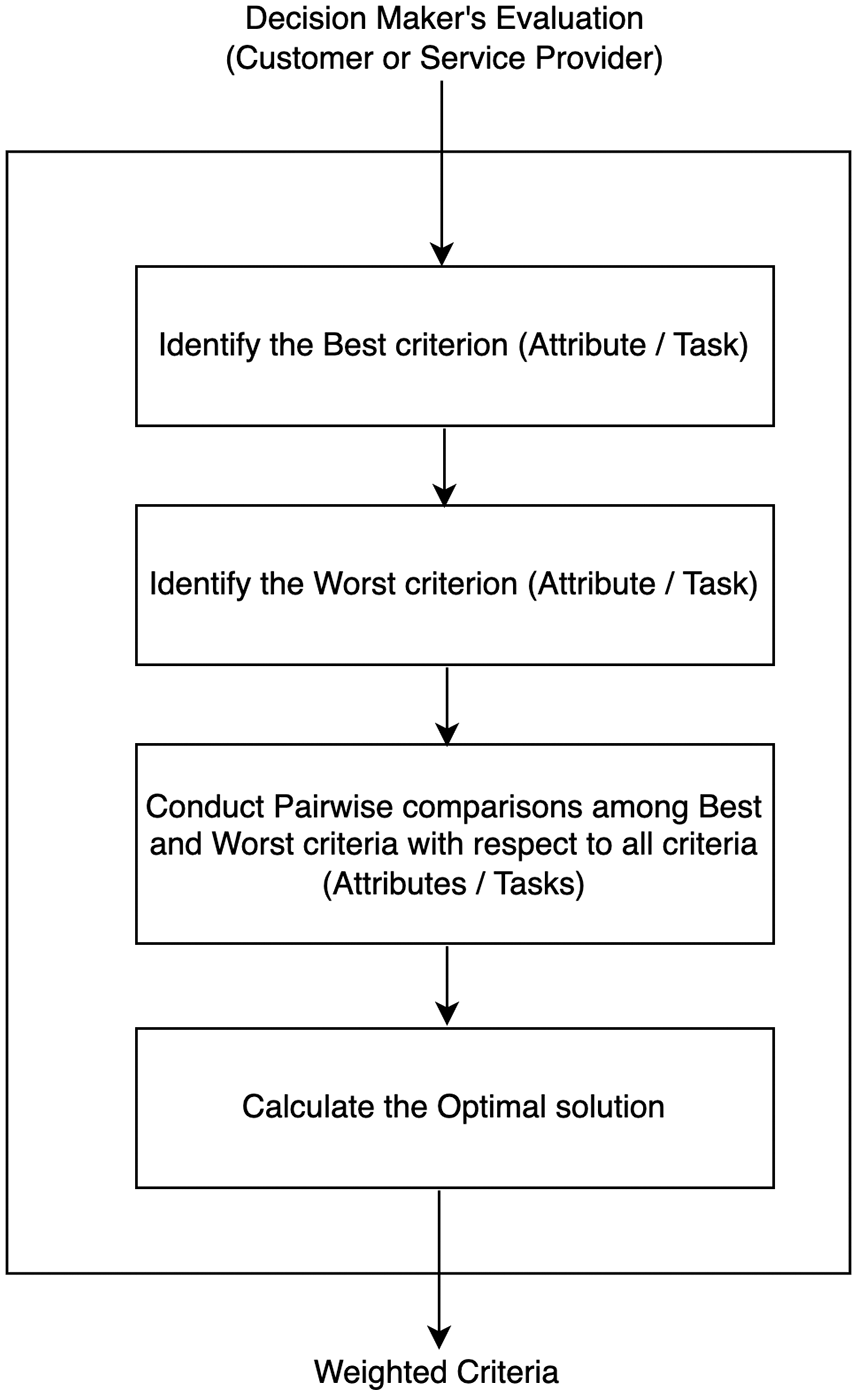
Figure 2: The BWM steps for prioritizing cloud tasks

The model proposes to calculate a set of weighted tasks for all consumers and providers and subsets of weighted criteria for each consumer and provider. The reason for providing one pool of criteria is to enhance the performance of the model in case there is a small number of consumers, tasks, or providers.

5  Matching Technique for Linking Consumer with the Best Service Provider

In this section, we describe, in detail, the two algorithms suggested for matching each consumer’s task priorities to each service providers’ task priority. The overall procedure of the two algorithms is to 1) calculate the similarities between consumers’ preferences and CSPs’ preferences, and 2) match the tasks to the best available CSP by considering the preferences of both parties. The output of Algorithm 1 (the similarity table) is passed to Algorithm 2, which, in turn, searches for the best match for each task. Initially, suppose we have two sets. The consumer set, which is denoted as C = {c1, c2, c3, …, cn}, and the service provider set denoted as SP = {sp1, sp2, sp3, …, spm}. Each SP provides a set of priority tasks (e.g., quality, capacity, price, etc.), based on their perspective, where sp1 = {t1, t2, t3, …, tk}. Therefore, a two-dimensional matrix is presented as PT-SP = {sp1 = {t1, t2, …, tk}, sp2 = {t2, t1, …, tk},…, spm = {tk, t2, …, t1}}, where the task is the most important, as explained in Table 3. Similarly, each consumer in C has a preferable set of tasks as well, where c1 = {t1, t2, t3, …, tk}. As illustrated in Algorithms 1, two main parameters were passed, which are the consumer priority tasks array (CParray[ ]), and the service providers’ priority tasks array (PT-SParray[ ][ ]). After passing the two parameters, the find_C_Matches func-tion traverses (CParray[ ]) and compares it to each (PT-SParray[ ][ ]) to return the number of matched tasks between each consumer and each service provider (see Algorithms 1: Step 9). Note that we assume a large number of consumers applied at different times and can be assigned to different SPs as their priorities changed, so we pass each individual C# in a one-dimensional array. As depicted in Fig. 3, the function returns a consumer ID with service provider ID and the number of matches between them. The output of Algorithm 1 is passed to Algorithm 2 (see step 5), which returns the number of matches between the new C priority and each (PT-SParray[ ][ ]). The primary advantage of this approach is fairly matching new consumers (C) with the best service provider (SP). Also, if we have more than one best match SP, then we assign the first one to the consumer and the rest of them will be given high priority for future consumers’ matches.

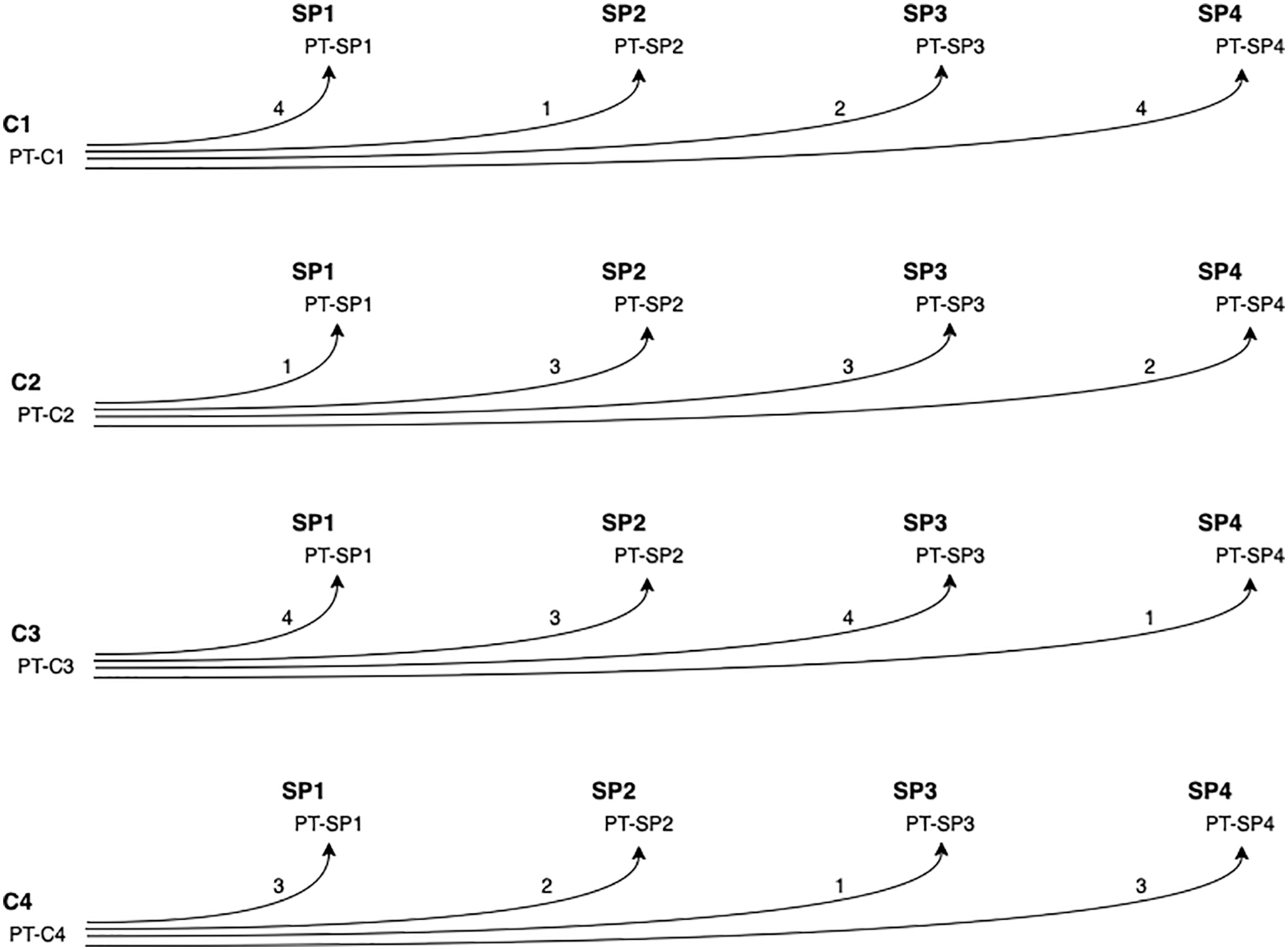
Figure 3: Matches between consumers and providers’ prioritized tasks

5.1 Analysis of Algorithm 1

The three for loops, in Algorithm 1 are used to find the number of matches between a new consumer C# and all of the PT-SP. A number of iterations of for loop in step 1 are carried out n times, where n is the number of tasks that are prioritized by the C#. Each iteration brings a new task specified by the consumer and compares it with the tasks order for each service provider. A number of iterations of for loop in step 2 are carried out m times, where m is the number of service providers (SPs). Similarly, a number of iterations of for loop in step 4 are carried out t times, where t is the number of tasks. The condition of if structure in step 5 is evaluated n × m × t times. Now, the individual operations in various steps of the Algorithm 1 will contribute to the overall time complexity of the algorithm as described below:

1)   All operations inside the body of step 1 for loop will be computed (n) times.

2)   All operations inside the body of step 2 for loop will be computed (n × m) times.

3)   All operations inside the body of step 4 for loop will be computed (n × m × t) times.

4)   The increment operation in step 6 takes (n × m × t) times in the worst case. Therefore, the overall time complexity of Algorithm 1 in the worst case is O(n × m × t).

5.2 Time Complexity Measurement of Algorithm 1

In the Algorithm 1, the computational work is performed inside three for loops, where the first for loop nests inside the second one and the second one nests inside the third one.

Now, the individual operations in various steps of the Algorithm 1 will contribute to its overall time complexity, as described below:

1)   The loop variable initialization takes 1 operation, the test condition in for loop of step 1 is evaluated n times as true for its successful iterations and 1 more time when it is evaluated to be false for termination of the loop. So, operations inside the body of this loop will be computed n times. The increment of loop variable takes 2 operations. Therefore, the number of operations in step 1 is 3n + 2.

2)   Step 2 for loop is nested inside step 1 for loop. So, all operations inside the body of this loop will be computed n × m times. The number of operations in step 2 is 3 nm + 2n.

3)   The operation, MT-CSP[i][j] ← 0 in step 3 will need 1 operation and will be repeated n × m times. Therefore, the number of operations in step 3 is nm.

4)   The step 4 for loop is nested inside the step 2 for loop. So, all operations inside the body of this loop will be computed n × m × t times. The number of operations in step 4 is 3 nmt + 2 nm.

5)   The condition inside the if structure in step 5 requires 1 operation, and it is evaluated n × m × t times. Therefore, the number of operations in step 5 is nmt.

6)   The operation MT-CSP[i][j] + + in step 6 will be performed not more than nmt times. Therefore, the overall time complexity of Algorithm 1 is: = (3n + 2) + (3 nm + 2n) + nm + (3 nmt + 2 nm) + nmt + nmt = 5 nmt + 6 nm + 5n + 2. Hence, by ignoring the lower order terms and the coefficient of the highest order term, we get the worst case time complexity of the Algorithm 1 as O(n × m × t) ≃ O(n3).

5.3 Analysis of Algorithm 2

Algorithm 2 has been developed to overcome two problems. The first challenge is to assign the most suitable SP to the new C request. Secondly, there is the problem of guaranteeing honest competition between the different service providers. The suggested procedural instructions to solve the first problem involve requesting that new consumers set their task priorities. The 2D array, MT-CSP[ ][ ] is taken as input. For every matched task between the consumer and a service provider, the matched variable is incremented by one. Once we get the number of matches between the C and all SPs, we sort them in descending order and copy them in 1D array SP[ ], where the highest match is at the beginning of the array. In case there is more than one best match, then the first best match is assigned to the C and the rest of them are inserted into a queue. There are many scenarios taken under consideration before assigning the best match to the C, which include:

1)   If there is no best match in the queue, then the best match given by 1D array SP[ ] is assigned to C.

2)   If there is no best match in the queue, and 1D array SP[ ] is empty, then the first SP in the queue is assigned to C.

3)   If there is a best match in the queue, and 1D array SP[ ] returns a best match as well, then we compare the two matches, and we choose the highest match between them.

    a)   If the highest match is in the queue, then assign the SP in the queue to the C, remove the SP from the queue, and add the new SPs returned in the 1D array SP[ ] to the queue for later comparison, as depicted in Fig. 4.

    b)   If the SP returned by 1D array SP[] was higher, then we assign it to the C.

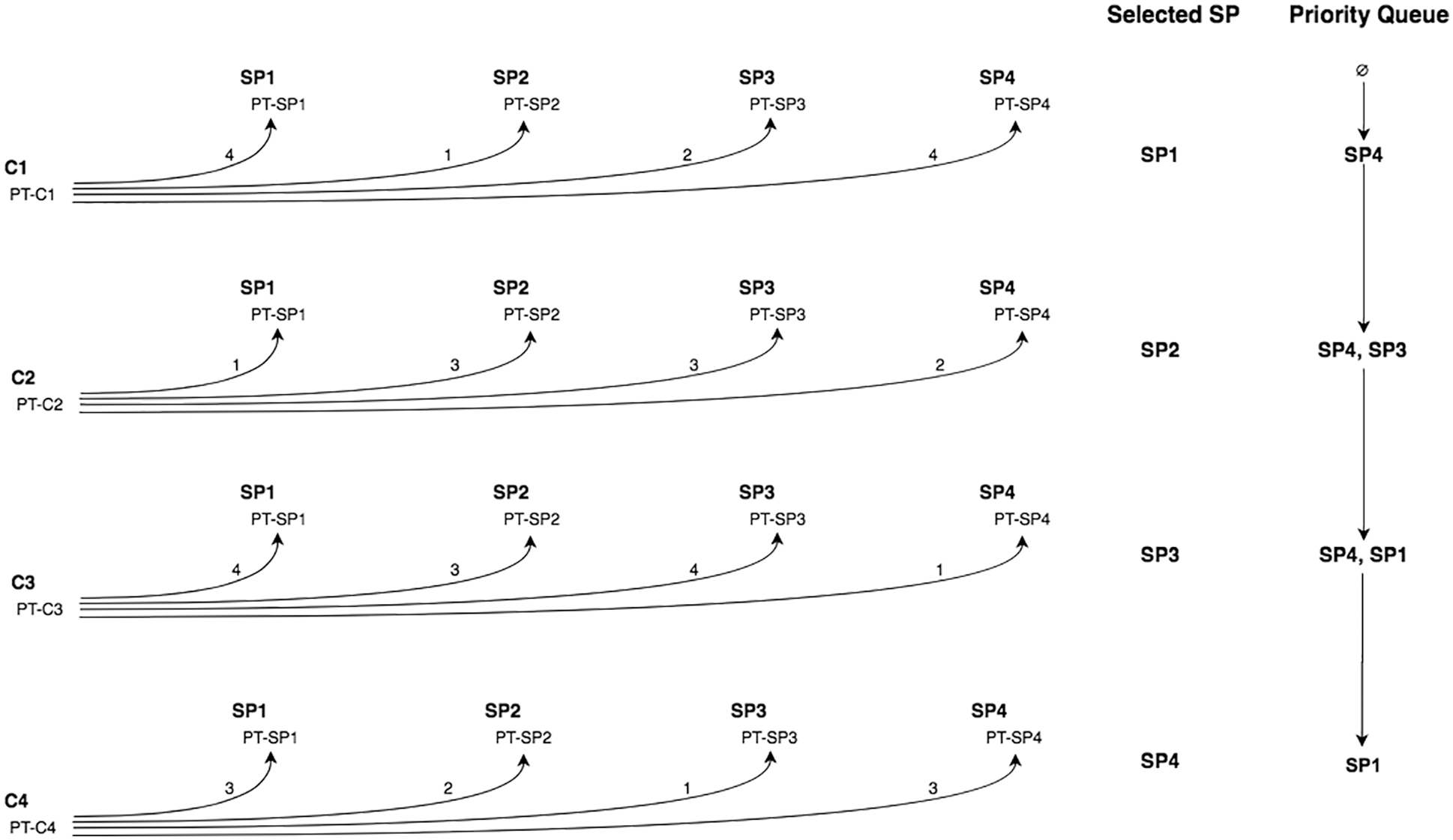
Figure 4: The assigning of service provider for each consumer

In Algorithm 2, we use a one-dimensional array to hold all possible matches for the new C# called SP[], a queue called L to preserve the previously prioritised SPs, and a Boolean variable priorityCheck to determine if the queue is empty or has no matched SPs. Next, copying only the matched SPs into SP[] in descending order, we see the best match at the first index of the array.

The if condition in the step 30 is applied to check the L. If L is not empty, then we check all the items in the L to see if there is a SP that has a greater or equal number of matches to that SP. If so, then we assign the SP found in the L to the C#, remove it from the L, add the highest matches SPs in SP[] to the L, clear SP[], and, finally, set priorityCheck to false (see steps 29–35).

If L is empty, then priorityCheck remains true. Thus, the second if condition block will be executed as shown in steps 46–47. Therefore, the returned best match stored in SP[ ] is assigned to C#. The SP in SP[] will be removed, and we add the rest of the highest matches in SP[] to L.

Generally, the worst-case time complexity for Algorithm 2 is O(n3), where the cubic function is given from step 1–49 and 31–39.

5.4 Illustrative Examples of the Algorithms

Suppose there are four consumers (C1, C2, C3, and C4), four service providers (SP1, SP2, SP3, SP4), and six tasks. The proposed Algorithm 1 will run as illustrated in Fig. 3 to find the matches between each consumer’s prioritized tasks (PT-C) and each service provider’s prioritized tasks (PT-SP). For example, there are four matches between the two sets of PT-C1 and PT-SP1, while there is only one match between the two sets of PT-C1 and PT-SP2, and so on.

Simply put, a SP will be selected for each consumer based on the highest match between the task priorities of the two. When more than one SP has similar highest matches, the non-selected SPs are added to a priority queue to reserve their place for subsequent selections. Fig. 4 shows the selected SP for each C and the priority queue content after each selection. For C1, both SP1 and SP4 have higher matches; therefore, SP1 is selected and SP4 is added to the priority queue. Similarly, both SP2 and SP3 have higher matches for C2; therefore, SP2 is selected and SP3 is added to the priority queue. For C3, both SP1 and SP3 have higher matches, so SP3 is selected because it has precedence as the priority queue indicates. Note that SP1 is added to the queue. We allow multiple occurrences of a certain SP. For example, if a SP is not selected three times although it had a similar higher match as other SPs, the SP must be added three times to the priority queue. For the last run of algorithm 2, both SP1 and SP4 compete for C4; therefore, SP4 is selected and SP1 is added to the priority queue.

Any selected SP from the priority queue must be removed, and the queue should be updated by removing the SP. Finally, if two SPs have higher matches for a certain C and both SPs are in the priority queue, the first-in first-out (FIFO) algorithm is adopted.

5.5 Time Complexity Measurement of Algorithm 1

In the Algorithm 2, the for loops and if structures will contribute time complexities similar to the case of Algorithm 1. In the Algorithm 2, the major computational works are performed inside three for loops, where the first for loop (for each Cs) nests inside the second one (for each SPs in L) and the second one nests inside the third one (for each SPs in SP[ ]).

Now, the individual operations in various steps of the Algorithm 2 will contribute to its overall time complexity similar to the case of Algorithm 1. Therefore, the worst case time complexity of Algorithm 2 is O(n3).

6  Experimental Results and Discussions

To validate the correctness and effectiveness of the proposed algorithms, we have implemented the algorithms and verified that they work on a number of occasions. On every occasion, the algorithms were found to be correct. In this section, we describe the experimental setup, the data set, and the results obtained.

6.1 Experimental Environment

The two algorithms, Algorithm 1 and Algorithm 2, were designed to support the research. They have been implemented in Java due to Java language’s elegance and efficiency, apart from its well-known platform independence feature. For developing the code and testing its correctness, IntelliJ IDEA Community Edition 2019.2.3 x64 was used on a PC with processor Intel(R) Core(TM) i7-4600U CPU @ 2.10 GHz 2.70 GHz, installed RAM 8.00 GB, Windows 10 64-bit operating system, and x64-based processor.

6.2 Dataset

The data sets for the research were randomly created with four different cases, as shown in Table 4. The data sets were created so that they are realistic-looking in every aspect as far as the experimental study is concerned.

6.3 Results and Discussion

In this section, the first working of the algorithms, Algorithm 1 and Algorithm 2 is illustrated. The two algorithms are deterministic and sequential in nature, and they were found to be correct on all occasions. We have shown the results of the first two data sets in the manuscript. The results show that the proposed model is correct and effective.

Moreover, we have described the working of the algorithms for the case I data set as supported by the implemented program. At the end of the section, another sample’s results have been tabulated for the case II data set.

Algorithm 1 takes as input the two matrices illustrated in Tables 5 and 6. Table 5 represents the matrix for each consumer’s prioritized tasks and Table 6 represents each service provider’s prioritized tasks. The Algorithm 1 gives as output the number of matching tasks between each pair of a consumer and a service provider, which is represented in a matrix form, as depicted in Table 7 and also illustrated in the bar chart shown in Fig. 5. The actual assignment of a service provider to each consumer has been illustrated in Fig. 6.

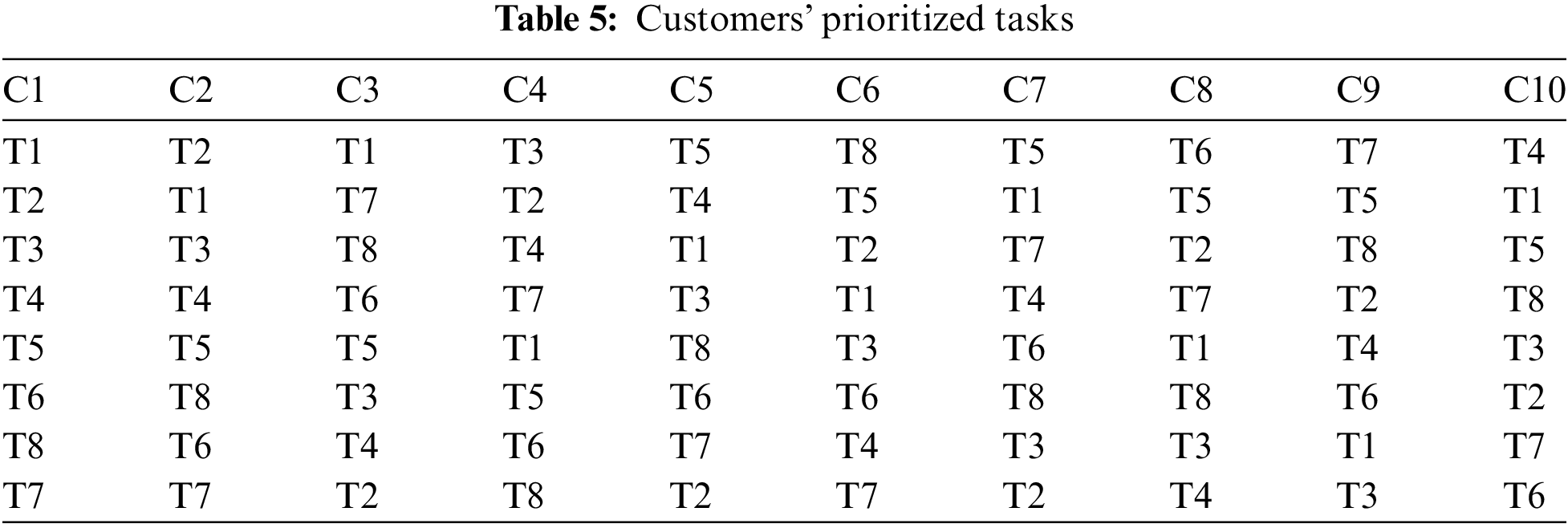
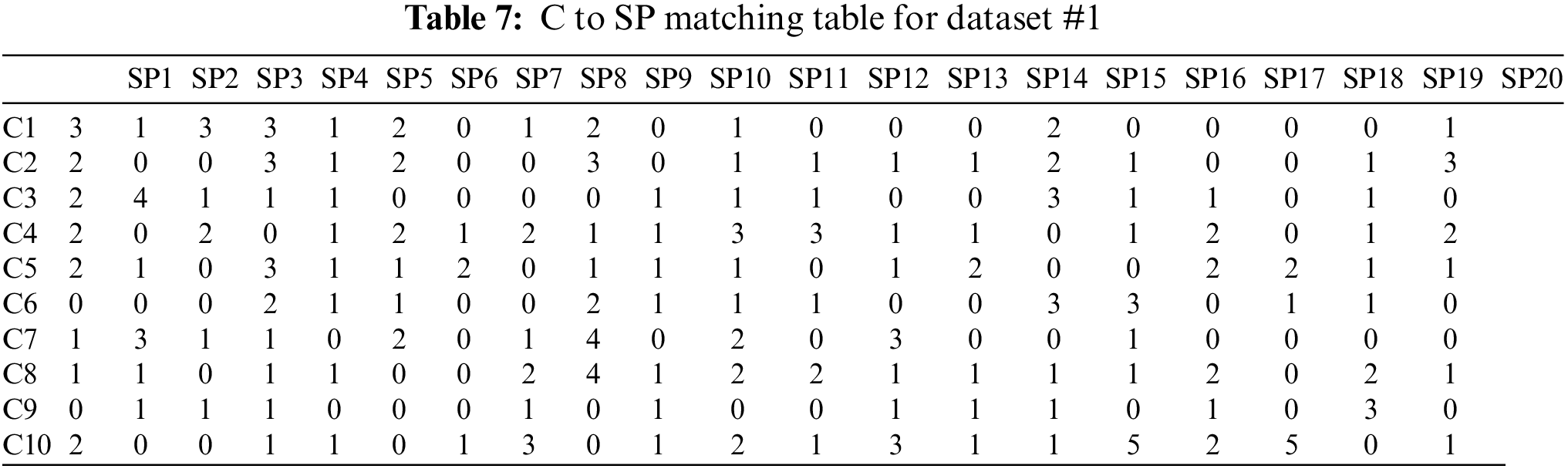
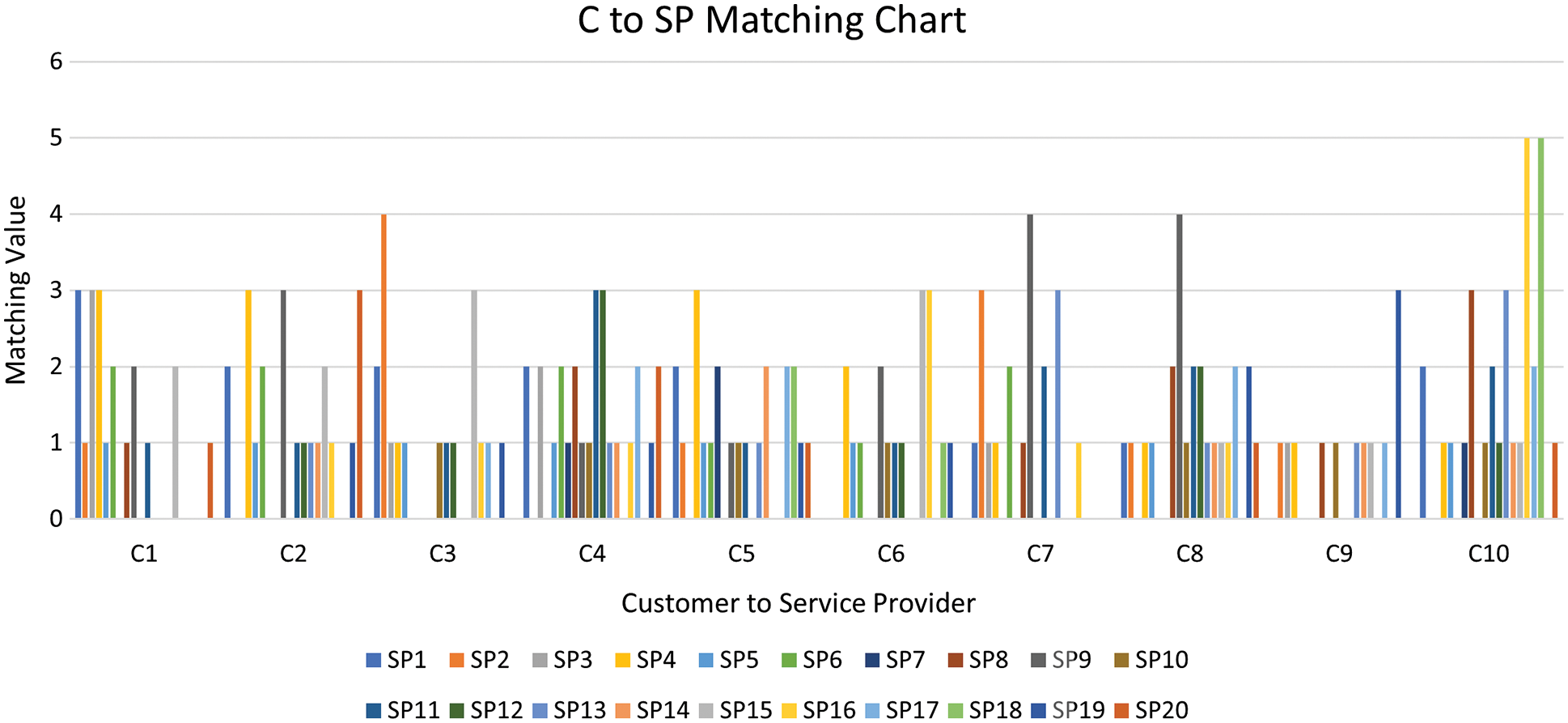
Figure 5: The suggesting service provider for each consumer for dataset #1

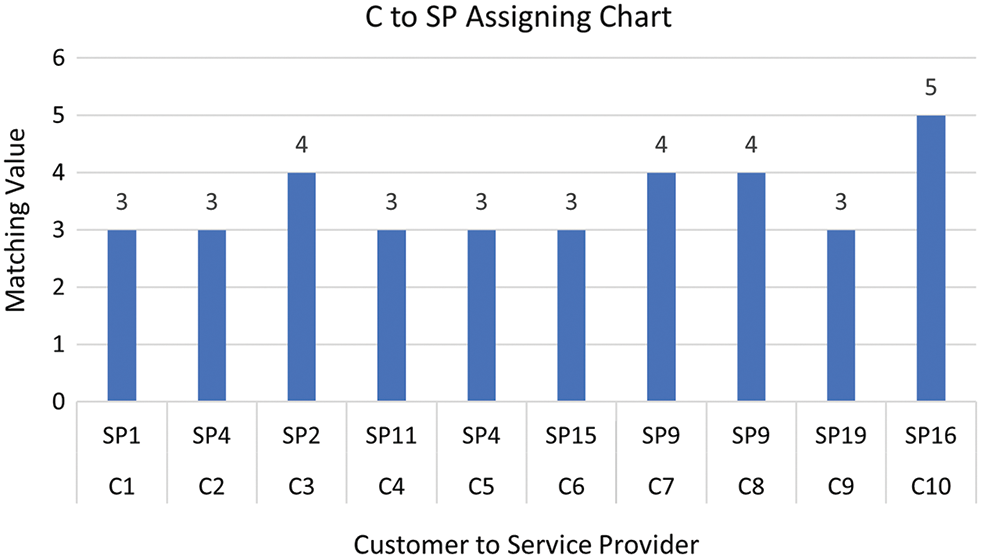
Figure 6: Assigning the best service provider for each consumer for dataset #1

Algorithm 2 takes as input the output matrix given by the Algorithm 1 that is shown in Table 7. Finally, the Algorithm 2 gives the assigned service provider for each consumer, as depicted in Table 8.

Now, we present the results of the case II data set. Algorithm 1 takes as input the two matrices illustrated in Tables 9 and 10. Table 9 represents the matrix for each customer’s prioritized tasks, and Table 10 represents each service provider’s prioritized tasks. Algorithm 1 gives as output the number of matching tasks between each pair of a customer and a service provider, which is represented in matrix form as depicted in Table 11 and also illustrated in the bar chart shown in Fig. 7.

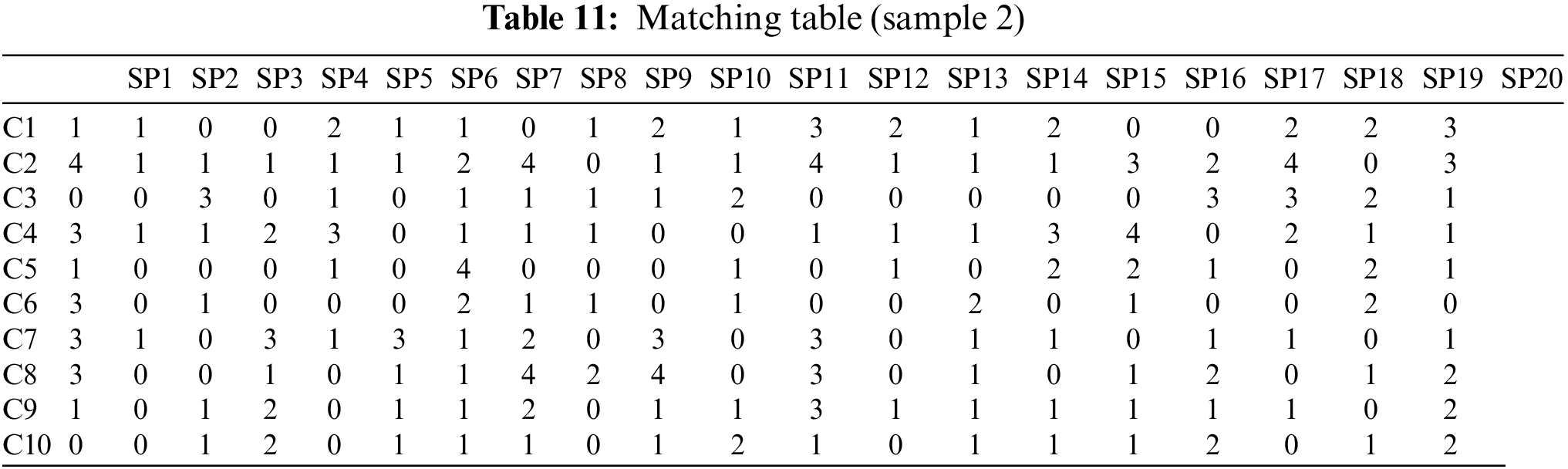
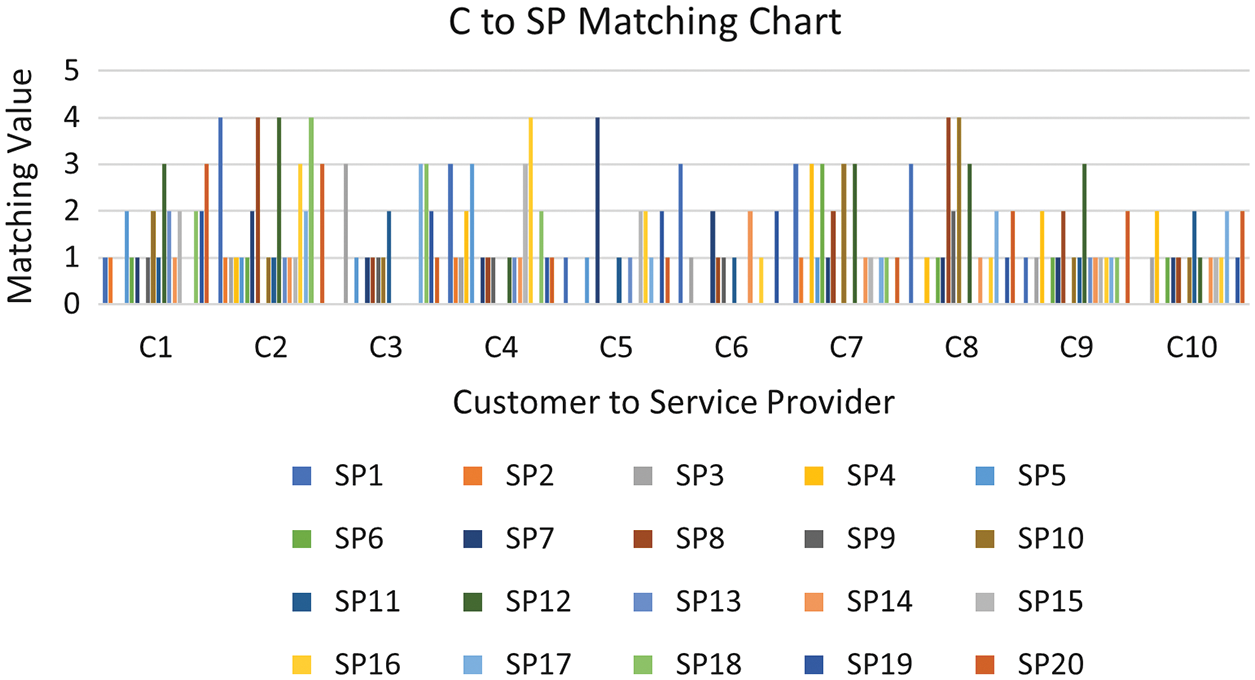
Figure 7: The suggesting service provider for each consumer for data set #2

The output of Algorithm 1 is a matrix presenting the number of tasks matching for every pair of a customer and a service provider, which is depicted in Table 11. This matrix is given to Algorithm 2 as input. The actual assignment of a service provider to each customer has been illustrated in the Fig. 8 and Table 12.

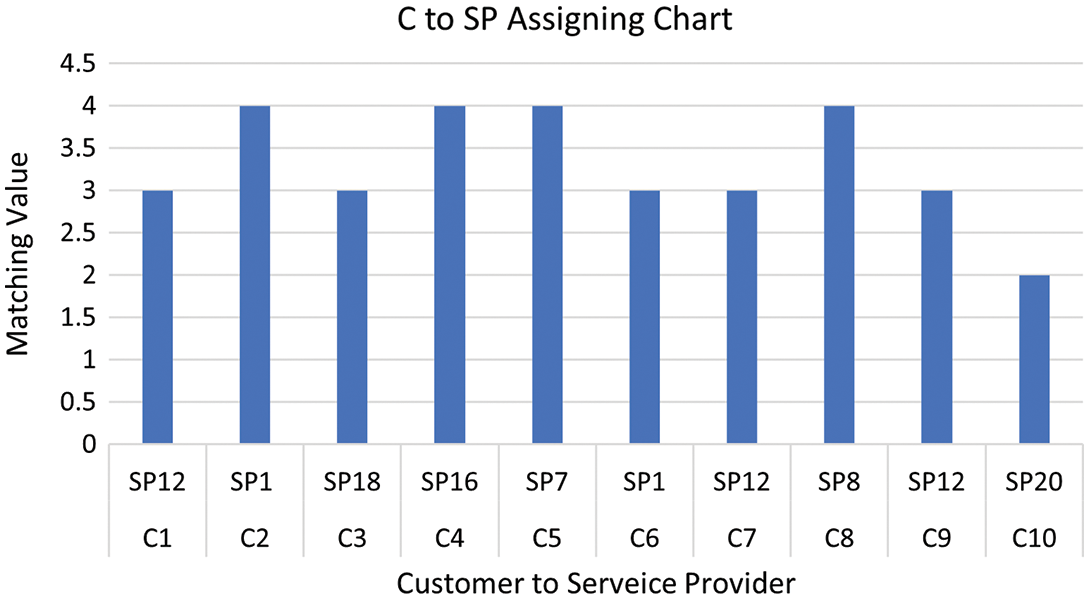
Figure 8: Assigning the best service provider for each consumer for data set #2

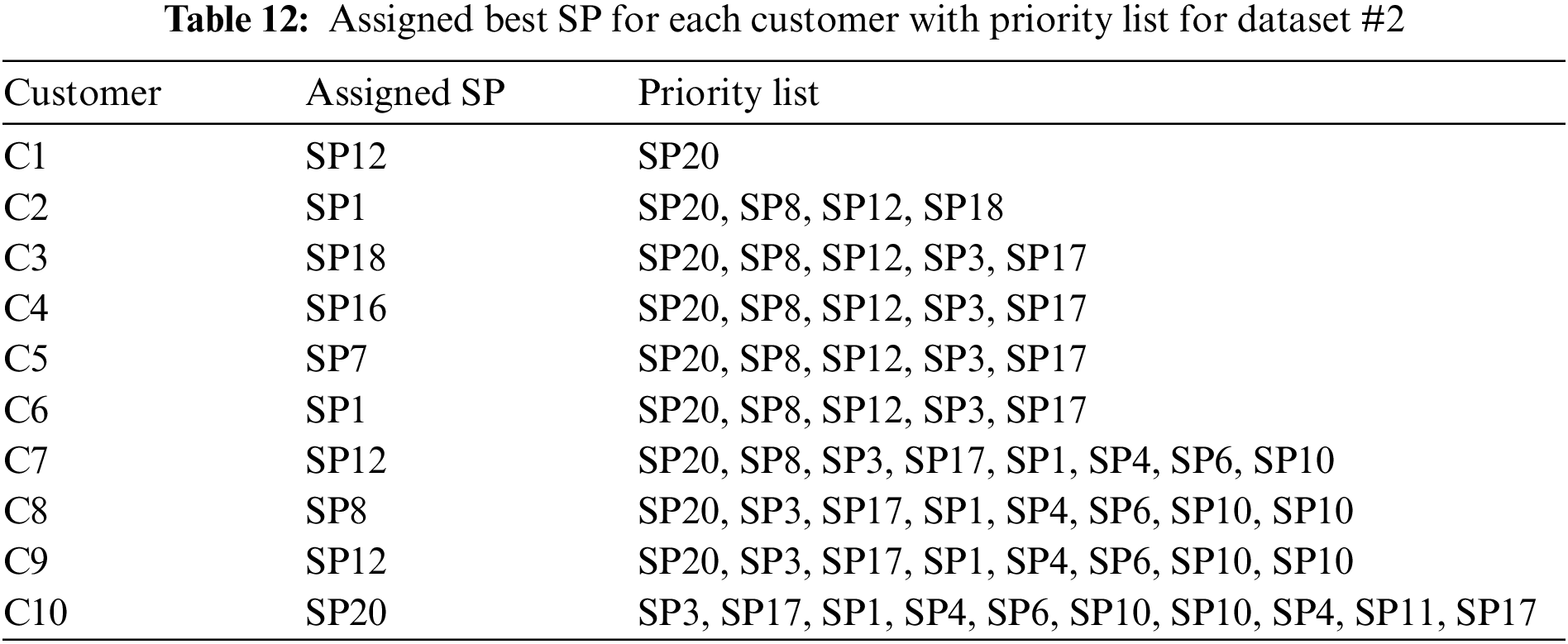
Therefore, from the two sample outputs of the algorithms, it is evident that the algorithms are correct and able to effectively assign the best SP for each C, giving preference to a SP if it is in the priority list with the same matching value.

7  Conclusion

As cloud services become increasingly dominant and important to consumers who seek quality services while minimizing expense. The increasing number of CSPs and the variety of services and tasks that providers offer consumers creates a problem in terms of choosing the best service provider for consumers’ preferred tasks. The paper provides a model to consider consumers’ preferences (price, quality, time, etc.) and service providers’ preferences (price, speed, quality, etc.), adopting the BWM to acquire and manipulate the preferences to prioritize tasks. The prioritized tasks for each consumer are evaluated against all service providers to find the optimal solution (i.e., best service provider) while ensuring fairness in terms of assigning the best service provider in subsequent iterations of assigning service providers to later consumers.

The main importance of conducting the experiments is to provide a proof that the proposed model can accommodate preferences of various customers and service providers and match their preferences effectively and efficiently. Further, various experiments were conducted to cover various cases where customers’ and service providers’ preferences varies in each case. Therefore, the proposed model was tested on different sets of consumers and service providers (along with their tasks) to show the effectiveness of the two proposed algorithms in the model.

Results show that the model is able to effectively assign a high number of consumers with a variety of preferences to the best service providers. On the other hand, service providers were fairly evaluated against each request, preserving their precedence in terms of competence.

The model works effectively with the random set of data. It is based on two deterministic algorithms. The correctness of the algorithms has been verified. Therefore, the model will perform its task on real data as well, while also providing indepth definitions of all criteria that influence the selection of a service provider.

In the future, the model can be employed to acquire historical data and a set of consumers’ evaluation criteria for selecting of the best service provider for each customer. This can overcome a limitation of the proposed model which does not automatically extract useful knowledge about priorities for the service providers from the historical data. The proposed model can also be extended to a mechanism that will allow for the evaluation and prioritizing of tasks for service providers, which will be achieved by automating the process of creating the priorities of each service provider based on the extracted knowledge from the historical data. Moreover, the proposed method can be generalized to represent the relationship between several entity types for extraction of knowledge out of the relationships between those entity types.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Liu, F. T. Chan and W. Ran, “Decision making for the selection of cloud vendor: An improved approach under group decision-making with integrated weights and objective/subjective attributes,” Expert Systems with Applications, vol. 55, no. C, pp. 37–47, 2016. [Google Scholar]

 2.  O. Gireesha, N. Somu, K. Krithivasan and S. S. Vs, “Iivifs-waspas: An integrated multi-criteria decision-making perspective for cloud service provider selection,” Future Generation Computer Systems, vol. 103, pp. 91–110, 2020. [Google Scholar]

 3.  R. R. Kumar, S. Mishra and C. Kumar, “A novel framework for cloud service evaluation and selection using hybrid mcdm methods,” Arabian Journal for Science and Engineering, vol. 43, no. 12, pp. 7015–7030, 2018. [Google Scholar]

 4.  R. R. Kumar, S. Mishra and C. Kumar, “Prioritizing the solution of cloud service selection using integrated mcdm methods under fuzzy environment,” The Journal of Supercomputing, vol. 73, no. 11, pp. 4652–4682, 2017. [Google Scholar]

 5.  S. Schneider and A. Sunyaev, “Determinant factors of cloud-sourcing decisions: Reflecting on the it outsourcing literature in the era of cloud computing,” Journal of Information Technology, vol. 31, no. 1, pp. 1–31, 2016. [Google Scholar]

 6.  S. Singh and I. Chana, “Q-Aware: Quality of service based cloud resource provisioning,” Computers & Electrical Engineering, vol. 47, no. C, pp. 138–160, 2015. [Google Scholar]

 7.  S. Singh and I. Chana, “A survey on resource scheduling in cloud computing: Issues and challenges,” Journal of Grid Computing, vol. 14, no. 2, pp. 217–264, 2016. [Google Scholar]

 8.  S. H. H. Madni, M. S. AbdLatiff, M. Abdullahi, S. M. Abdulhamid and M. J. Usman, “Performance comparison of heuristic algorithms for task scheduling in iaas cloud computing environment,” PloS One, vol. 12, no. 5, pp. e0176321, 2017. [Google Scholar]

 9.  N. H. AbRahman and K. -K. R. Choo, “A survey of information security incident handling in the cloud,” Computers & Security, vol. 49, no. C, pp. 45–69, 2015. [Google Scholar]

10. S. Iqbal, M. L. M. Kiah, B. Dhaghighi, M. Hussain, S. Khan et al., “On cloud security attacks: A taxonomy and intrusion detection and prevention as a service,” Journal of Network and Computer Applications, vol. 74, no. C, pp. 98–120, 2016. [Google Scholar]

11. Z. Farahmandpour, S. Versteeg, J. Han and A. Kameswaran, “Service virtualisation of internet-of-things devices: Techniques and challenges,” in Proc. of IEEE/ACM 3rd Int. Workshop on Rapid Continuous Software Engineering (RCoSE), Buenos Aires, pp. 32–35, 2017. [Google Scholar]

12. M. Z. Hasan and H. Al-Rizzo, “Task scheduling in internet of things cloud environment using a robust particle swarm optimization,” Concurrency and Computation: Practice and Experience, vol. 32, no. 2, pp. e5442, 2020. [Google Scholar]

13. Y. Liu, L. Wang, X. V. Wang, X. Xu and L. Zhang, “Scheduling in cloud manufacturing: State-of-the-art and research challenges,” International Journal of Production Research, vol. 57, no. 15–16, pp. 4854–4879, 2019. [Google Scholar]

14. G. K. Shyam and I. Chandrakar, “Resource allocation in cloud computing using optimization techniques,” Cloud Computing for Optimization: Foundations, Applications, and Challenges, vol. 39, pp. 27–50, 2018. [Google Scholar]

15. S. H. Jang, T. Y. Kim, J. K. Kim and J. S. Lee, “The study of genetic algorithm-based task scheduling for cloud computing,” International Journal of Control and Automation, vol. 5, no. 4, pp. 157–162, 2012. [Google Scholar]

16. A. Awad, N. El-Hefnawy and H. Abdel_kader, “Enhanced particle swarm optimization for task scheduling in cloud computing environments,” Procedia Computer Science, vol. 100, no. 65, pp. 920–929, 2015. [Google Scholar]

17. J. Yang, B. Jiang, Z. Lv and K. -K. R. Choo, “A task scheduling algorithm considering game theory designed for energy management in cloud computing,” Future Generation Computer Systems, vol. 105, pp. 985–992, 2020. [Google Scholar]

18. K. Li, G. Xu, G. Zhao, Y. Dong and D. Wang, “Cloud task scheduling based on load balancing ant colony optimization,” in 2011 Sixth Annual China Grid Conf., Dalian, China, IEEE, pp. 3–9, 2011. [Google Scholar]

19. P. Devarasetty and S. Reddy, “Genetic algorithm for quality of service based resource allocation in cloud computing,” Evolutionary Intelligence, vol. 14, no. 2, pp. 381–387, 2021. [Google Scholar]

20. A. -P. Xiong and C. -X. Xu, “Energy efficient multiresource allocation of virtual machine based on pso in cloud data center,” Mathematical Problems in Engineering, vol. 2014, pp. 1–8, 2014. [Google Scholar]

21. B. Do Chung and K. -K. Seo, “A cloud service selection model based on analytic network process,” Indian Journal of Science and Technology, vol. 8, no. 18, pp. 1–5, 2015. [Google Scholar]

22. A. Singh and K. Dutta, “Apply ahp for resource allocation problem in cloud,” Journal of Computer and Communications, vol. 3, no. 10, pp. p13–21, 2015. [Google Scholar]

23. D. Ergu, G. Kou, Y. Peng, Y. Shi and Y. Shi, “The analytic hierarchy process: Task scheduling and resource allocation in cloud computing environment,” The Journal of Supercomputing, vol. 64, no. 3, pp. 835–848, 2013. [Google Scholar]

24. A. Alhubaishy and A. Aljuhani, “The best-worst method for resource allocation and task scheduling in cloud computing,” in 2020 3rd Int. Conf. on Computer Applications & Information Security(ICCAIS), Riyadh, KSA, IEEE, pp. 1–6, 2020. [Google Scholar]

25. M. Godse and S. Mulik, “An approach for selecting software-as-a-service (saas) product,” in 2009 IEEE Int. Conf. on Cloud Computing, Bangalore, India, vol. 1, pp. 155–158, 2009. [Google Scholar]

26. R. Krishankumar, K. S. Ravichandran and S. K. Tyagi, “Solving cloud vendor selection problem using intuitionistic fuzzy decision framework,” Neural Computing and Applications, vol. 32, no. 2, pp. 589–602, 2020. [Google Scholar]

27. A. E. Youssef, “An integrated mcdm approach for cloud service selection based on topsis and bwm,” IEEE Access, vol. 8, pp. 71851–71865, 2020. [Google Scholar]

28. H. Wu, “Multi-objective decision-making for mobile cloud offloading: A survey,” IEEE Access, vol. 6, pp. 3962–3976, 2018. [Google Scholar]

29. H. Bangui, M. Ge, B. Buhnova, S. Rakrak, S. Raghay et al., “Multi-criteria decision analysis methods in the mobile cloud offloading paradigm,” Journal of Sensor and Actuator Networks, vol. 6, no. 4, pp. 25, 2017. [Google Scholar]

30. C. Jatoth, G. Gangadharan, U. Fiore and R. Buyya, “Selcloud: A hybrid multi-criteria decision-making model for selection of cloud services,” Soft Computing, vol. 23, no. 13, pp. 4701–4715, 2019. [Google Scholar]

31. S. K. Garg, S. Versteeg and R. Buyya, “A framework for ranking of cloud computing services,” Future Generation Computer Systems, vol. 29, no. 4, pp. 1012–1023, 2013. [Google Scholar]

32. R. R. Kumar and C. Kumar, “A multi criteria decision making method for cloud service selection and ranking,” International Journal of Ambient Computing and Intelligence (IJACI), vol. 9, no. 3, pp. 1–14, 2018. [Google Scholar]

33. A. Alashaikh and E. Alanazi, “Conditional preference networks for cloud service selection and ranking with many irrelevant attributes,” IEEE Access, vol. 9, pp. 131214–131222, 2021. [Google Scholar]

34. L. Sun, H. Dong, O. K. Hussain, F. K. Hussain and A. X. Liu, “A framework of cloud service selection with criteria interactions,” Future Generation Computer Systems, vol. 94, pp. 749–764, 2019. [Google Scholar]

35. R. Garg, “MCDM-based parametric selection of cloud deployment models for an academic organization,” IEEE Transections on Cloud Computing, vol. 10, no. 2, pp. 863–871, 2022. [Google Scholar]

36. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

37. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

38. C. Boutilier, R. I. Brafman, C. Domshlak, H. H. Hoos and D. Poole, “Cp-nets: A tool for representing and reasoning with conditional ceteris paribus preference statements,” Journal of Artificial Intelligence Research, vol. 21, pp. 135–191, 2004. [Google Scholar]

39. C. Z. Rădulescu and I. C. Rădulescu, “An extended topsis approach for ranking cloud service providers,” Studies in Informatics and Control, vol. 26, no. 2, pp. 183–192, 2017. [Google Scholar]

40. T. Aladwani, “Improving tasks scheduling performance in cloud computing environment by using analytic hierarchy process model,” in 2017 Int. Conf. on Green Informatics (ICGI), Fuzhou, China, pp. 98–104, 2017. [Google Scholar]

41. J. Rezaei, “Best-worst multi-criteria decision-making method,” Omega, vol. 53, pp. 49–57, 2015. [Google Scholar]

42. J. Siegel and J. Perdue, “Cloud services measures for global use: The service measurement index (smi),” in 2012 Annual SRII Global Conf., California, USA, IEEE, pp. 411–415, 2012. [Google Scholar]

43. J. Rezaei, “Best-worst multi-criteria decision-making method: Some properties and a linear model,” Omega, vol. 64, pp. 126–130, 2016. [Google Scholar]

44. M. A. Khan, M. S. Siddiqui, M. K. I. Rahmani and S. Husain, “Investigation of big data analytics for sustainable smart city development: An emerging country,” IEEE Acess, vol. 10, pp. 16028–16036, 2022. [Google Scholar]

45. M. J. Pour, J. Mesrabadi and M. Hosseinzadeh, “A comprehensive framework to rank cloud-based e-learning providers using best-worst method (bwmA multidimensional perspective,” Online Information Review, vol. 44, no. 1, pp. 114–138, 2019. [Google Scholar]

46. A. M. Mostafa, “An mcdm approach for cloud computing service selection based on best-only method,” IEEE Access, vol. 9, pp. 155072–155086, 2021. [Google Scholar]

47. M. Singh and M. Pant, “A review of selected weighing methods in mcdm with a case study,” International Journal of System Assurance Engineering and Management, vol. 12, no. 1, pp. 126–144, 2021. [Google Scholar]