Proposed Biometric Security System Based on Deep Learning and Chaos Algorithms

1  Introduction

Cancelable biometrics schemes are being significantly used nowadays. In general, a cancelable biometric scheme depends on extracting various facial, iris, and fingerprint features in order to authenticate individuals in a real-time manner [1]. These extracted features of the obtained biometrics structure the cancelable biometric templates. A cancelable biometric scheme mainly consists of two core stages, enrolment and authentication. In the enrolment stage, the obtained biometrics from the sensors for specific users are stored in a database. However, during the authentication stage, a query template is generated to be compared with the biometrics that is stored in the database [2]. The user is authenticated if both the stored biometrics and the provided query templates match. A cancelable biometric scheme can be either uni-biometric-based or multi-biometric-based [3]. The uni-biometric-based schemes deploy a single input such as the face, iris, or fingerprint to authenticate the individuals. Whereas, the multi-biometric-based scheme exploits two or more inputs. However, multi-biometric-based schemes are considered more secure since it is hard to hack a set of biometrics simultaneously.

Usually, the obtained biometrics are stored in the database during the enrollment stage. Even in the case of deploying encryption techniques on the stored biometrics, this requires implementing decryption during the authentication stage. Thus, the original biometrics might be exposed. Consequently, an ideal cancelable biometric scheme should take into consideration preventing unauthorized access to the original biometric templates while maintaining the biometric scheme’s high performance. Furthermore, the cancelable biometric scheme should guarantee that authorized users can easily access the system with high recognition performance. Besides assuring high recognition, the cancelable biometric scheme should attain the International Organization for Standardization/International Electrotechnical Commission (ISO/IEC) 24745:2022 requirements [4]. The first requirement is to assure preventing the cross-matching of the biometric templates whether the templates have been obtained from the same or different biometrics. In other words, the correlation of various templates across different databases should be infeasible. The second requirement is to assure irreversibility in which infeasible to retrieve the original biometrics given the cancelable biometric template. A further condition restricts generating new cancelable templates before abolishing the old versions in order to protect the database if it has been compromised.

The aforementioned conditions arose the need to develop a cancelable biometric scheme to protect the original biometric by applying some encryption or transformation techniques. For instance, feature domain transformation can be deployed utilizing non-invertible transformation techniques such as polar and Cartesian transformations [5]. A further non-invertible transformation is the random projection technique [6], in which the extracted biometric feature is transformed by projecting it to a random space. Deep learning (DL) algorithms have recently proven noticeable results in supervised learning [7–9]. Since the cancelable biometrics scheme authorizes individuals based on their biometric features, it mainly includes supervised learning. Thus, deep learning techniques can achieve great success in this domain. Furthermore, deep learning uses multiple layers to abstract features the deeper the network gets. Its core use is Convolutional Neural Networks (CNN), in which features are extracted by applying a series of filters to the biometric input [10]. Subsequently, the resulted images are reduced in size by utilizing a pooling layer.

A further protection level can be applied by implementing encryption methods before storing the cancelable biometrics in the database. One of the most efficient techniques is the utilization of chaotic encryption techniques [11]. Chaotic encryption has various characteristics such as non-periodicity, independency on initial conditions, and divergence. Thus, a small deviation in the biometric input results in a huge change in the whole generated cancelable template. These characteristics match the standards of securing the cancelable biometric sensors. In this work, both deep learning algorithms and chaos encryption techniques have been adopted.

The significant contributions of the proposed work are:

•   Summarizing the recent related BSS frameworks utilized in biometric authentication and cybersecurity applications.

•   Hybridizing of DL and chaos algorithms for implementing an efficient and robust cancelable BSS model to secure private user biometric information.

•   Generating highly robust permutation and confusion matrices that are used as sensitive secret keys to produce the cancelable and ciphered biometric patterns.

•   Testing different standardized color and grayscale biometric images for evaluating the proposed cancelable BSS model.

•   Examining different security and recognition evaluation metrics to comprehensively assess the performance of the proposed cancelable BSS model.

•   Performing deep comparisons to prove the superiority of the proposed cancelable BSS model compared to other related cancelable BSS models.

The remainder of this paper is organized as follows. Section 2 summarizes the recent security algorithms used in cancelable biometric applications. Section 3 introduces the proposed biometric security system. Section 4 discusses the security analysis and obtained results of the proposed BSS model. Finally, Section 5 presents the concluding remarks and some suggestions for future work.

2  Literature Review

Various approaches have been proposed in the literature for implementing biometric recognition schemes, as shown in Tab. 1. The authors of [12] deploy Discrete Cosine Transform (DCT) compression on four biometric images of the same person. Subsequently, the resulting image is encrypted using the Double Random Phase Encoding (DRPE) algorithm. At the receiver, the counter approach is implemented to decrypt the biometric. However, for the identity verification, the recognition method deploys a cepstral approach. Other research works deployed only one biometric sensor, such as the face or iris features, for implementing the security solution. For example, Sudhakar et al. extracted the iris features by combining random projection and deep learning algorithms to generate revocable biometrics [13].

On the other side, some existing solutions utilized the cloud as a platform to provide the biometric system as a cloud service enabling fast response, intensive computing, and high accuracy. In [14], the authors developed a CNN-based biometric system on the Amazon Web Services (AWS) cloud platform. By implementing cross folding algorithms and quick response (QR) code steganography technique, the CNN-based system on the cloud outperformed the standalone systems. Another CNN-based solution was proposed by [15] in which the facial features were extracted from different face regions to create the cancelable biometric.

In general, different transformation algorithms can be applied to biometrics such as DCT, Discrete Fourier Transform (DFT), Discrete Wavelet Transform (DWT), and Fractional Fourier Transform (FrFT) to generate cancelable biometric templates. In [16], several discrete transformations such as DFT, FrFT, DCT, and DWT have been employed to generate the cancelable face and fingerprint templates. Furthermore, multiple rotations have been applied to ensure the irreversibility of the process. The authors of [17] developed a cancelable face and iris system by extracting features using scale-invariant feature transform. Subsequently, the extracted features were encrypted using the optical DRPE method.

In [18], the authors have applied sequential steps to generate non-invertible cancelable face templates. Initially, the grayscale pixels were transformed from the spatial domain into the fuzzy domain. As a pre-processing phase, the Intuitionistic Fuzzy Logic (IFL) was applied. Then, a further distortion was implemented via the Random Projection (RP). The authors of [19] developed a cancelable biometric recognition cryptosystem based on the optical Phase Truncated Fourier Transform (PTFT) asymmetric encryption by employing public keys. Consequently, the user can retrieve the original biometric by using two different private truncated keys. Ibrahim et al. applied more permutation and diffusion to create robust cancelable biometrics using a hybrid optical encryption algorithm resulting in more secure templates against attacks [20]. Mainly, the proposed hybrid system deployed the 3D jigsaw transform and FrFT to generate cancelable face and fingerprint templates.

Another implemented technique along with encryption is chaos-based ciphering to achieve better the loss of randomness. In [21], several cancelable templates were generated from the same biometric by applying different chaotic maps. El-Shafai et al. proposed a cancelable biometric scheme that hides all discriminative features of biometrics by employing a Genetic algorithm (GA) [22]. Initially, the GA scans a set of biometric templates. Subsequently, successive sample sets were generated by applying some statistical operators to the original set of biometric templates. The final cancelable biometric templates were generated by performing crossover and mutation techniques.

An efficient solution proposed by [23] utilized the greatest common divisor (GCD) algorithm. To blur the biometric with two prime operators and retrieve it by calculating the GCD of the two generated cancelable biometrics. Thus, eliminating the need for extra data or images to generate the cancelable biometric. Due to some of the limitations in the related biometric security systems concerning lower robustness and security accomplishments, in this work, we proposed an efficient BSS model. This model is based on hybridizing AE-based DL and 2D CLM-based ciphering algorithms to secure and cipher the stored biometric patterns. The foremost merit of integrating DL and chaotic-based security algorithms for biometric authentication is accomplishing better-ciphering efficiency. The first step in the proposed BSS model is the generation of two chaotically and random security keys using an AE network with only three layers. Then, these two random security keys are used together for permutation and confusion purposes to completely cipher the user’s biometric details. The first chaotic key is the utilized shuffling matrix used to permutate and shuffle the biometric image pixels. The second chaotic key is the employed confusion matrix used to distort the correlation between the permuted biometric pixels. The examined security and biometric recognition analyses prove the authentication and robustness superiority of the proposed BSS compared to other related BSS models.

3  Proposed Biometric Security System (BSS)

This section discusses the proposed BSS model based on the hybridization of deep learning and chaotic map algorithms in detail. Fig. 1 presents the primary steps of the proposed BSS model. It consists of two separate stages: the enrollment and authentication stages.

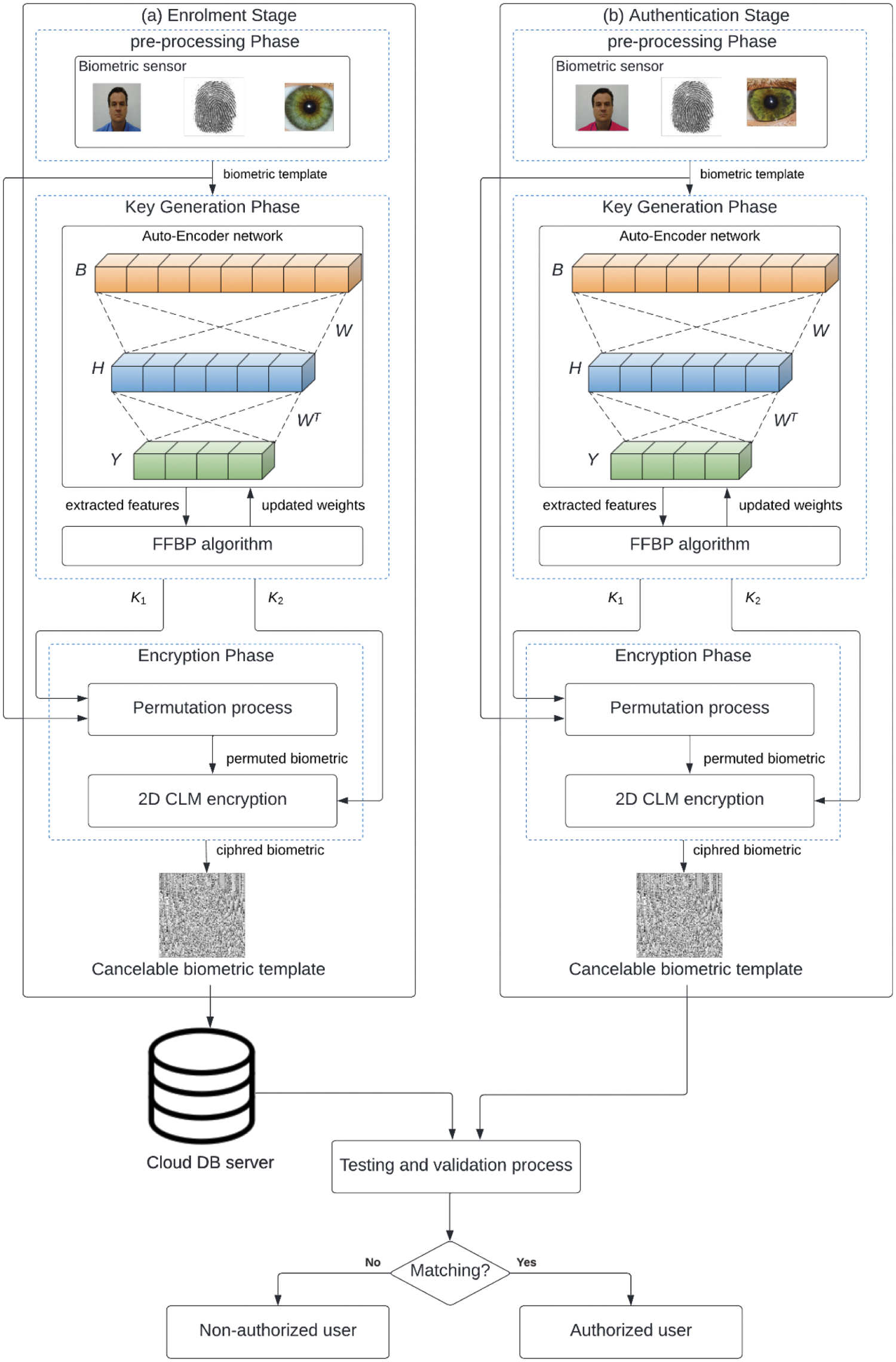
Figure 1: Proposed DL-chaos-based biometric security system

Although the chaos-based ciphering algorithms introduced high security & efficiency for encrypting the color & grayscale visual images, they still have some demerits regarding the ciphering key sensitivity. So, the hybridization of deep learning algorithms with chaos-based ciphering algorithms can improve image security performance. Thus, this inspired us to exploit both DL and chaos algorithms for securing the biometric images for implementing a more secure cancelable BSS model. Therefore, the proposed hybrid DL-chaos map ciphering technique is introduced to achieve better optimization performance towards improving the ciphering efficiency of biometric templates. Furthermore, the hybrid ciphering approach in the proposed BSS model performs extensive optimization and learning processes to generate sensitive and robust secret keys against various multimedia assaults and attacks.

The employed deep learning algorithm in the proposed BSS model uses an Auto-Encoder (AE) network as a pre-processing step prior to the chaos-based ciphering step to enhance and optimize the security efficiency by obtaining the main features and details in biometric images. These extracted features from the biometric templates are exploited to generate two different security keys (random chaos matrices). The first security key is exploited to produce a permutation matrix that is applied to scramble the pixels of biometric images. The second security key is used to generate a non-correlated random sequence (confusion matrix) that is exploited to further encrypt the permuted biometric images. Therefore, both permutation and confusion processes are utilized to cipher the biometric images sufficiently to hide all visual biometric details. The confusion process is performed using the 2D CLM algorithm [24].

The utilized AE network in the proposed BSS model is an unsupervised network used for biometric feature extraction. So, the employed deep neural AE network is working based on the Feed-Forward Back-Propagation (FFBP) algorithm [25] in the generation process of the secret keys. Thus, the proposed BSS model can efficiently resist the possible attacks on the encrypted biometric templates. Besides, the main benefit of using the AE network in the proposed BSS model is its parallelization in processing and computation, thus decreasing the complexity and runtime of the proposed BSS model. In addition, because the utilized AE network is an unsupervised algorithm, there is no mandatory prerequisite for labeled and identified biometric data in the learning process.

As shown in Fig. 1, firstly, the user biometric images are captured using the biometric sensors, and then they are forwarded to the proposed structure of the AE network for training purposes. This is to generate new random matrices with similar dimensions to those of the input biometric images. Then, the FFBP algorithm is employed to efficiently generate the best possible randomness keys (K1 and K2).

The first key (K1) is the random permutation key, while the second key (K2) is the random confusion key. Therefore, the key, K1, is used to permutate the pixels’ positions of biometric images. After that, the resulting permutated biometric images are further ciphered using the second key, K2, by applying the 2D CLM algorithm. This algorithm performs the bit eXclusive OR (XOR) process between the permuted biometric image and the key, K2, to produce the final ciphered biometric image that is stored in the cloud server instead of keeping the original biometric templates. Thus, the 2D CLM algorithm exploits the generated keys to further improve biometric image security and ciphering quality.

So, as shown in Fig. 1, the utilized hybrid DL-chaos-based ciphering algorithm in the proposed BSS model incorporates two sequential stages, which are (1) key generation stage and (2) encryption stage. The stacked AE network with only two stacks based on utilizing the FFBP algorithm is used in the key generation stage. In the encryption stage, both permutation and confusion mechanisms are performed using the generated secret keys from the first stage and the 2D CLM algorithm.

The stacked AE network used in the generation process of secret keys is considered the backbone stage of the biometric ciphering operation. It is an unsupervised deep neural structure with three consecutive layers stages (input, hidden, and output). First, the input layer collects the input biometric images and transfers their representation to another vector representation. Then, the single hidden layer takes a weighted version of the output vectors resulting from the preceding input layer. Finally, the hidden layer forwards the weighted decoding reconstruction vectors to the output layer. So, the input layer represents the encoder part of the utilized stacked AE network, while the output layer represents the decoder part. The values of weights and biases are initiated arbitrarily, and after that, they are updated iteratively during the back-propagation mechanism in the training process. The input and output parameters of the utilized stacked AE network are (1) encoder input (biometric vectors) Bi = (B1, B2, …., Bn), (2) hidden layer (H), (3) weighted matrix (W), (4) tied weighted matrix (WT), (5) decoder output (reconstructed biometric vectors) Yo = (Y1, Y2, …., Yn), and (6) generated random keys (K1 and K2)

Through the operation of the FFBP algorithm, deep fine-tuning and optimization processes are performed to achieve better backward and forward secrecy during the key generation stage. In addition, the main benefit of using the FFBP algorithm in the training process of the proposed stacked AE structure is minimizing or removing the noise that can reduce the performance of the training efficiency of the AE network. This is to produce and generate the most effective randomization and robust secret keys. Therefore, integrating the DL-based AE network with the 2D CLM-based ciphering algorithm reduces the number of iterations and achieves better ciphering and security of biometric images.

To generate efficient random and robust secret keys from the employed stacked AE network, different cost (error) and activation functions are utilized during the training process. So, in the operation of the FFBP algorithm, the softmax activation function [26] and cross-entropy error function [27] are used. This softmax activation function is based on a sigmoid function [28]. In addition, the stochastic gradient optimization algorithm [29] is applied in the training process of the utilized stacked AE network to minimize the training loss.

The best-generated secret keys are the ones that achieve the best uniform pixels distribution of the ciphered biometric images. So, in the training process of the stacked AE network, the minimization of the uniform distribution error is one of our main targets in the key generation process to produce the best efficient random secret keys. Thus, to obtain ciphered biometric images with a uniform pixels distribution, an error function is incorporated in the training stages of the stacked AE structure. This error function is calculated based on estimating the minimal value of the mean square error (MSE) between the ciphered biometric image and an image with pixel values of l (that has uniform distribution). The expression of the MSE function [30] utilized in the training process is given as follows:

MSE=∑i=1M∑j=1N(Bc(i,j)−l)2(1)

where Bc(i,j) is the ciphered biometric image and M & N are the dimension of the input image.

The authentication step in the proposed BSS model is the testing and evaluation process between the stored ciphered biometric templates and new input ciphered biometric images. This validation step is a mandatory process to check if the input user biometric image is a licensed template or an unlicensed template.

4  Results and Security Analysis

This section discusses and explains the obtained results and security analysis of the proposed BSS model. To comprehensively assess the proposed cancelable BSS model’s efficiency, different security and recognition evaluation metrics [20–23] are examined. The objective evaluation parameters that are used to evaluate the proposed BSS model are (1) correlation scores, (2) SSIM, (3) EER, (4) false positive rate (FPR), (5) true positive rate (TPR), (6) AROC, (7) FRR, (8) FAR, (9) mean and variance of authorized and unauthorized patterns, and (10) computational time.

The ciphering process for biometric patterns was developed using Python programming and run on a Windows 10 machine with an Intel Core i7 processor and 8 Giga-Byte memory. Also, different standardized color and grayscale images from six various datasets [31–36] of faces, fingerprint, and iris biometrics were also tested in the evaluation analysis of the proposed cancelable BSS model. Fig. 2 shows the original image samples from the examined biometric datasets.

Figure 2: Original image samples from the examined biometric datasets

As shown in the following subsections, the security efficiency assessment of the proposed BSS model is investigated in terms of (1) visual ciphering analysis, (2) histogram analysis, (3) ROC and PDF analysis, (4) correlation and SSIM analysis, (5) recognition, security, and computational analysis, (6) noise analysis, (6) comparative analysis with other related and recent BSS models. For a simple presentation of all obtained simulation outcomes, we selected the objective and subjective results of only 15 sample images from each tested biometric dataset to be presented.

4.1 Visual Ciphering Analysis

This section presents the visual ciphering results of the proposed hybrid AE-based DL and chaos-based encryption algorithms used in the proposed BSS model. Fig. 3 introduces the encrypted biometrics of the examined users’ samples for the six analyzed datasets. These ciphered biometric images prove the cancelability efficiency and security capability of the proposed BSS model in encrypting all details of recognized data within the biometric patterns. Also, the obtained results confirm that the proposed BSS model performed well for different modalities of user biometrics. Thus, the proposed BSS model can be implemented and utilized efficiently in biometric authentication and cybersecurity applications.

Figure 3: Encrypted biometrics of the examined user samples

4.2 Histogram Analysis

This section presents the visual histogram analysis of the proposed BSS model for the examined biometric samples. The histogram distribution is considered a subjective evaluation metric that is used to clarify the power density of the distributed pixels within biometric images. It is well known that the most efficient and secure ciphering algorithm in terms of mitigating statistical and intrusion attacks is the one that can generate uniform histogram representation for the ciphered biometrics [37]. Also, it is the one that can produce entirely different histograms for the ciphered biometrics compared to those of their original biometrics.

Fig. 4 demonstrates the visual representation of the histograms of the original image samples from the analyzed biometric datasets presented in Fig. 2, while Fig. 5 offers the obtained visual histograms of the examined users’ encrypted biometrics samples. It is observed that the histogram representations of the obtained ciphered biometric samples are totally different from those of the original ones. In addition, all histograms of encrypted biometrics have uniform distributions compared to those of the original ones. Thus, this proves the high security & efficiency of the proposed hybrid cryptography algorithm used in the proposed BSS model.

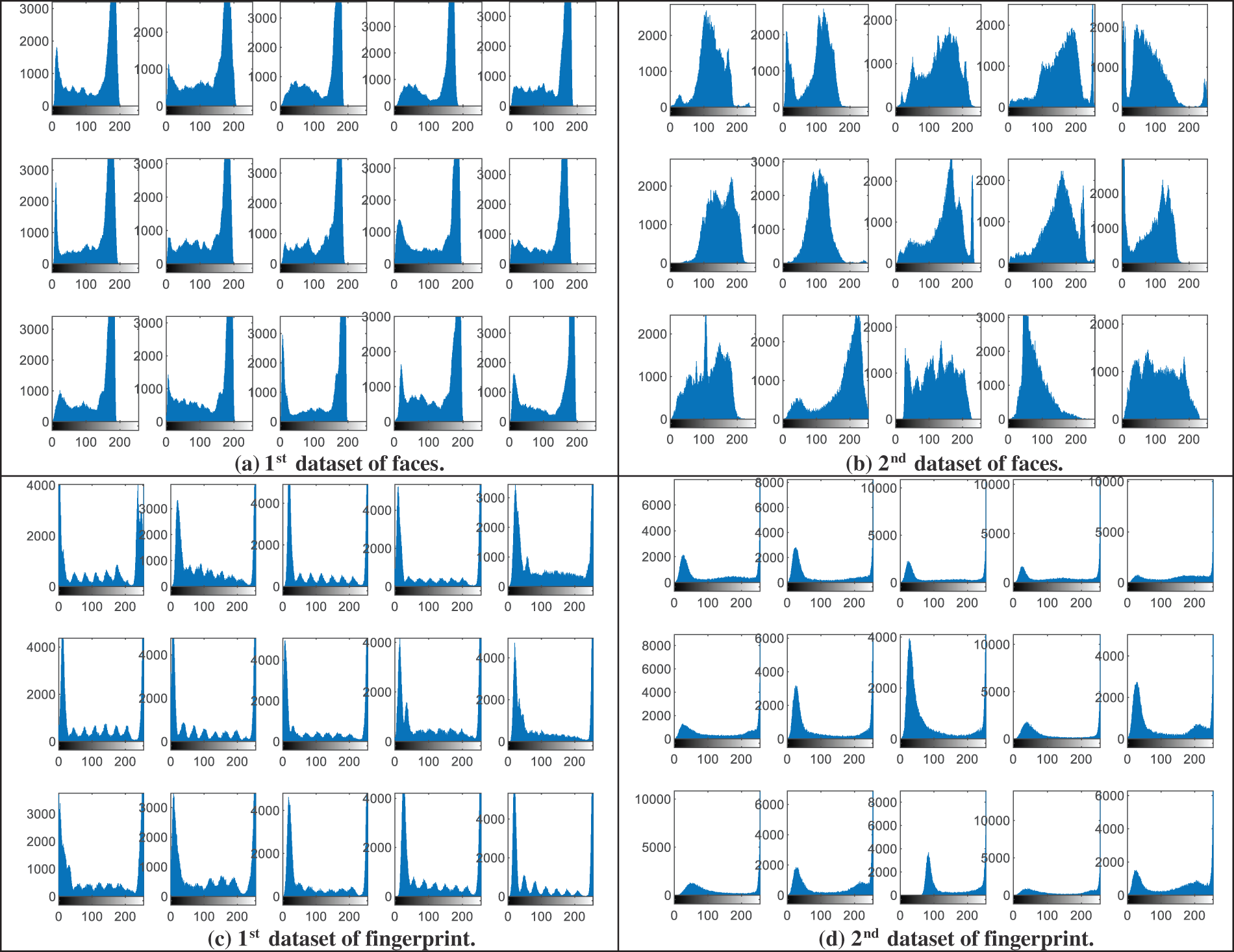
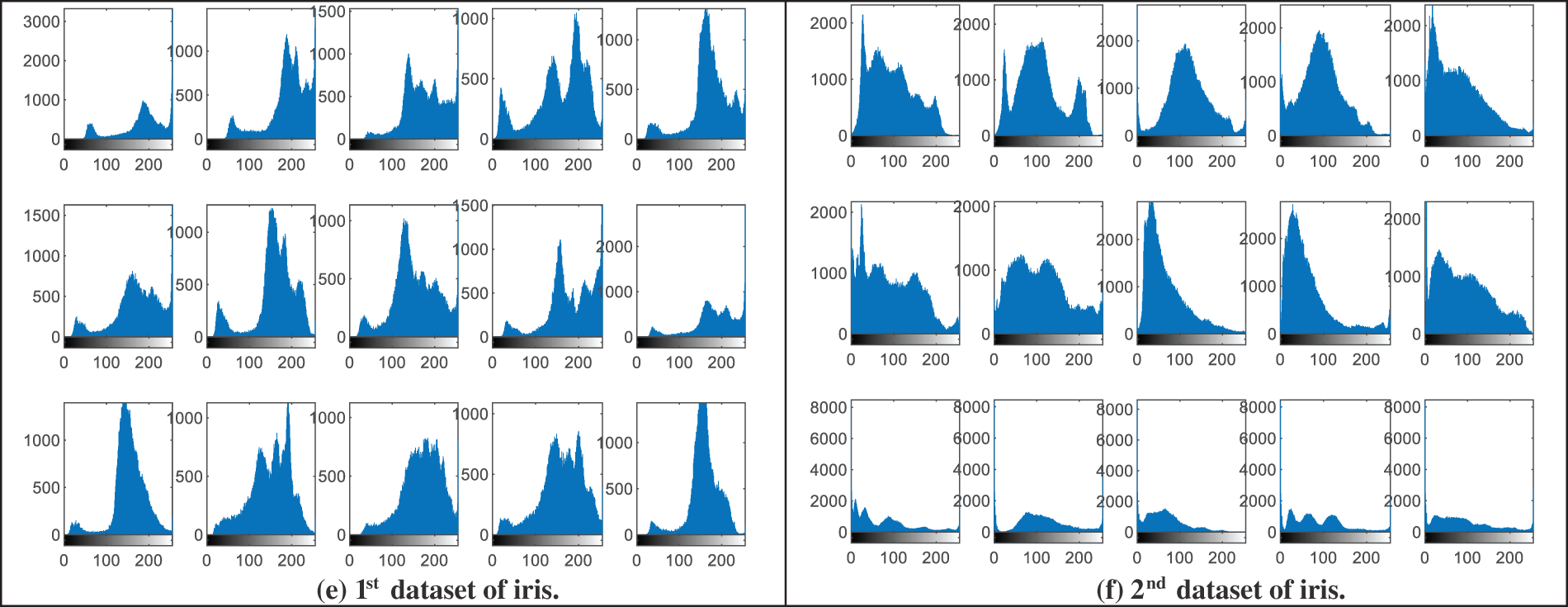
Figure 4: Histograms of the original image samples from the examined biometric datasets

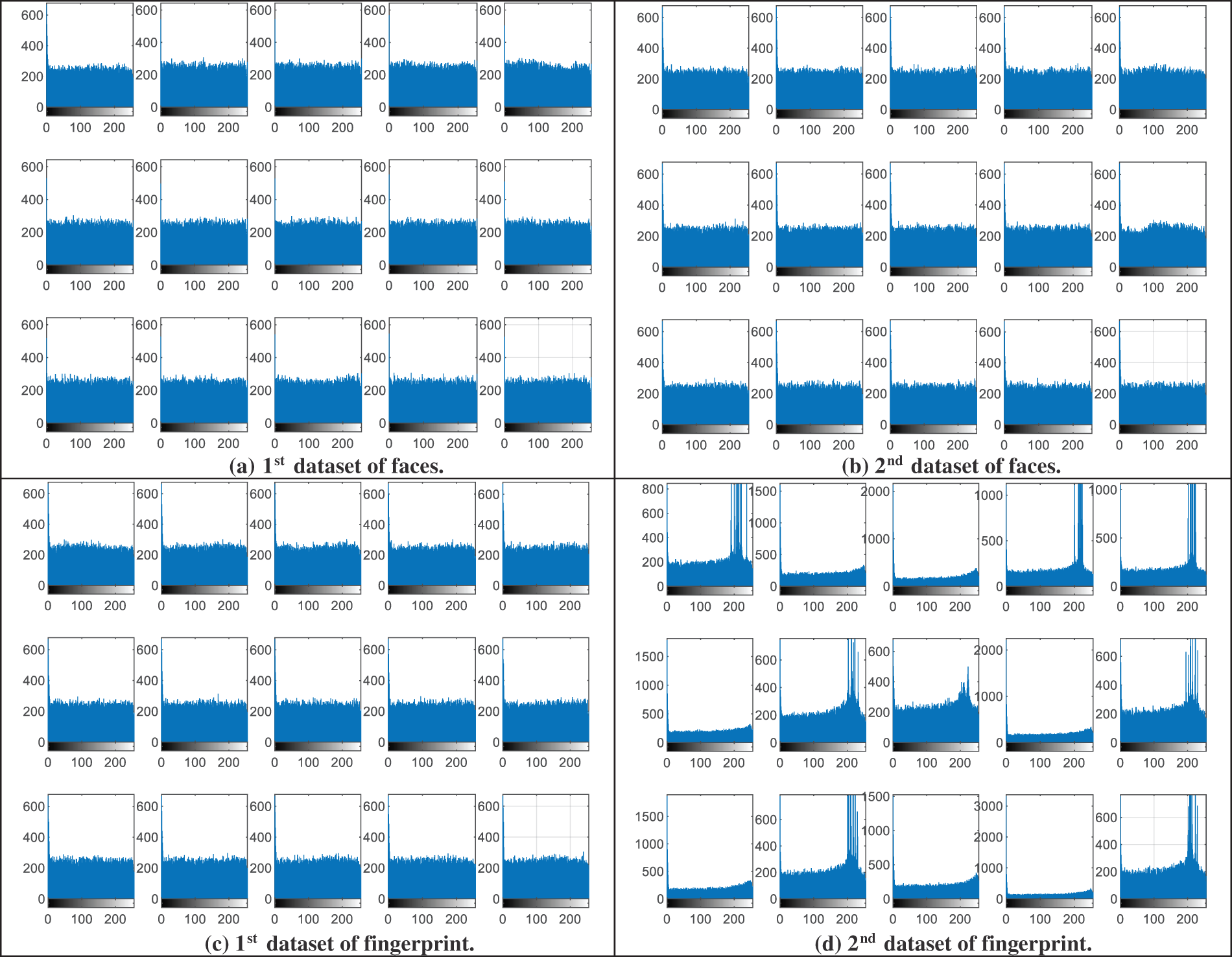
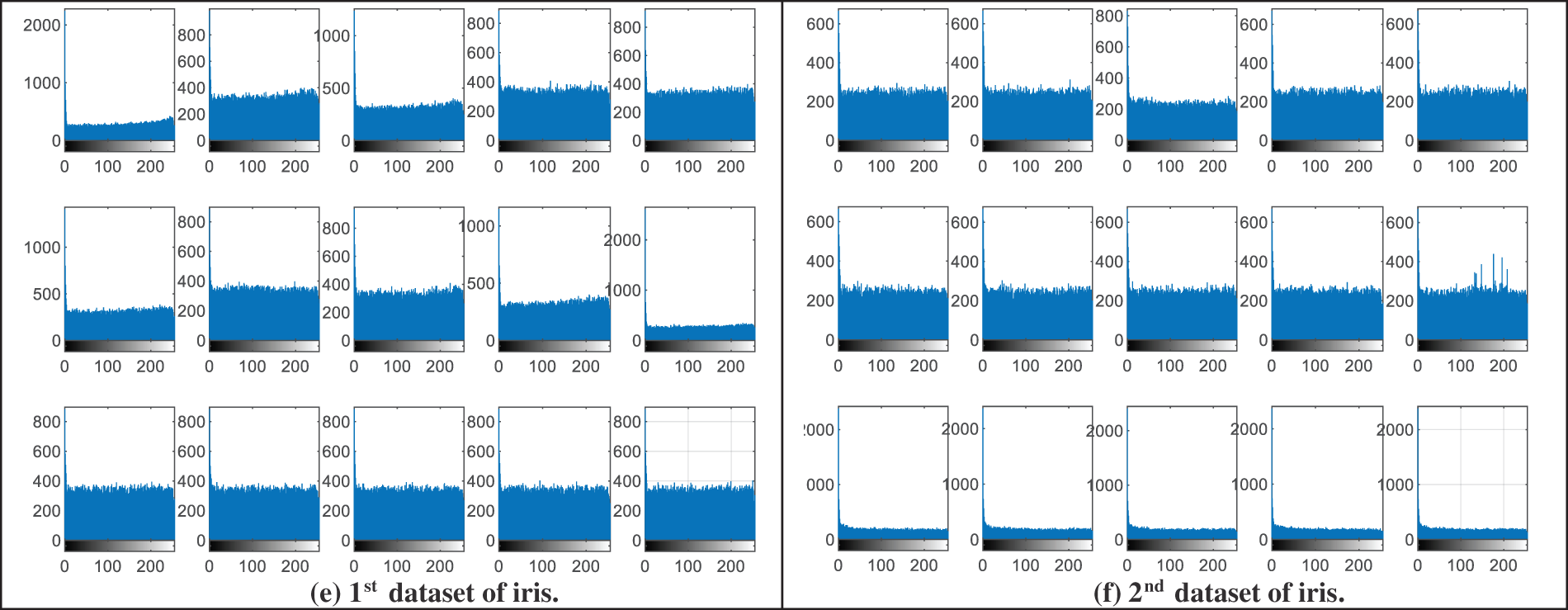
Figure 5: Histograms of encrypted biometrics of the examined users samples

4.3 ROC and PDF Analysis

This section discusses the ROC and PDF analysis of the proposed BSS model. The ROC distribution shows the percentage and relation between FPR and TPR values of the biometric authentication system. The PDF distribution offers the representation of the density function of the correlation scores for license and unlicensed patterns. Fig. 6 displays the ROC and correlation score distributions of the stored encrypted biometrics of the examined user samples for the six analyzed datasets. The obtained ROC distributions confirm that the proposed BSS model achieves high TPR values that near to be ideal for all analyzed biometric samples. In addition, the attained PDF distributions prove that they achieved high correlation scores for the biometric patterns of the licensed users and low correlation scores for the biometric patterns of the unlicensed users. Moreover, it is demonstrated that there are no intersections between the PDF of the licensed patterns and unlicensed patterns; thus, the proposed BSS model achieves low ERR percentages. Therefore, all these ROC and PDF results verify the high performance of the proposed biometric security system’s authentication, robustness, and recognition.

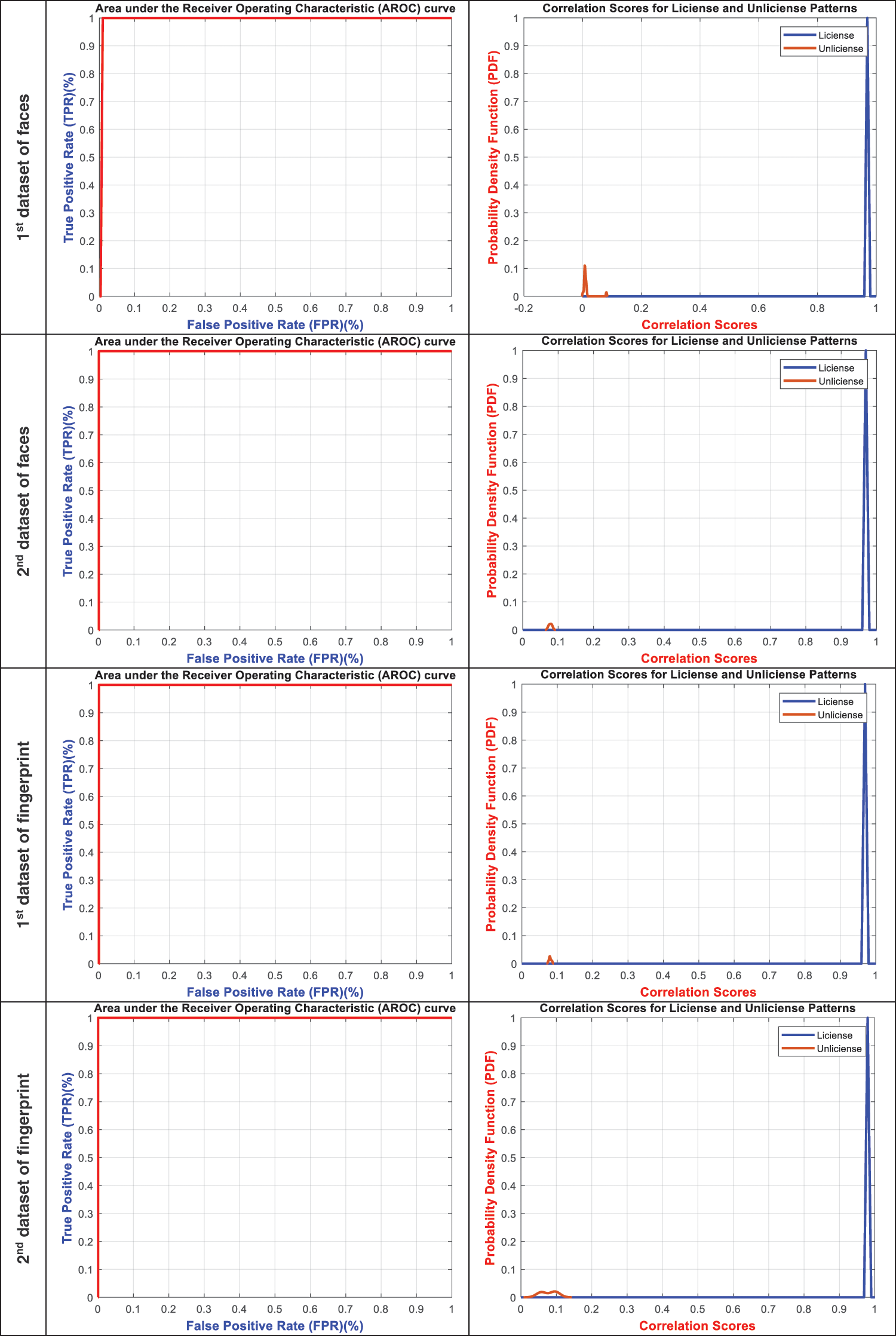
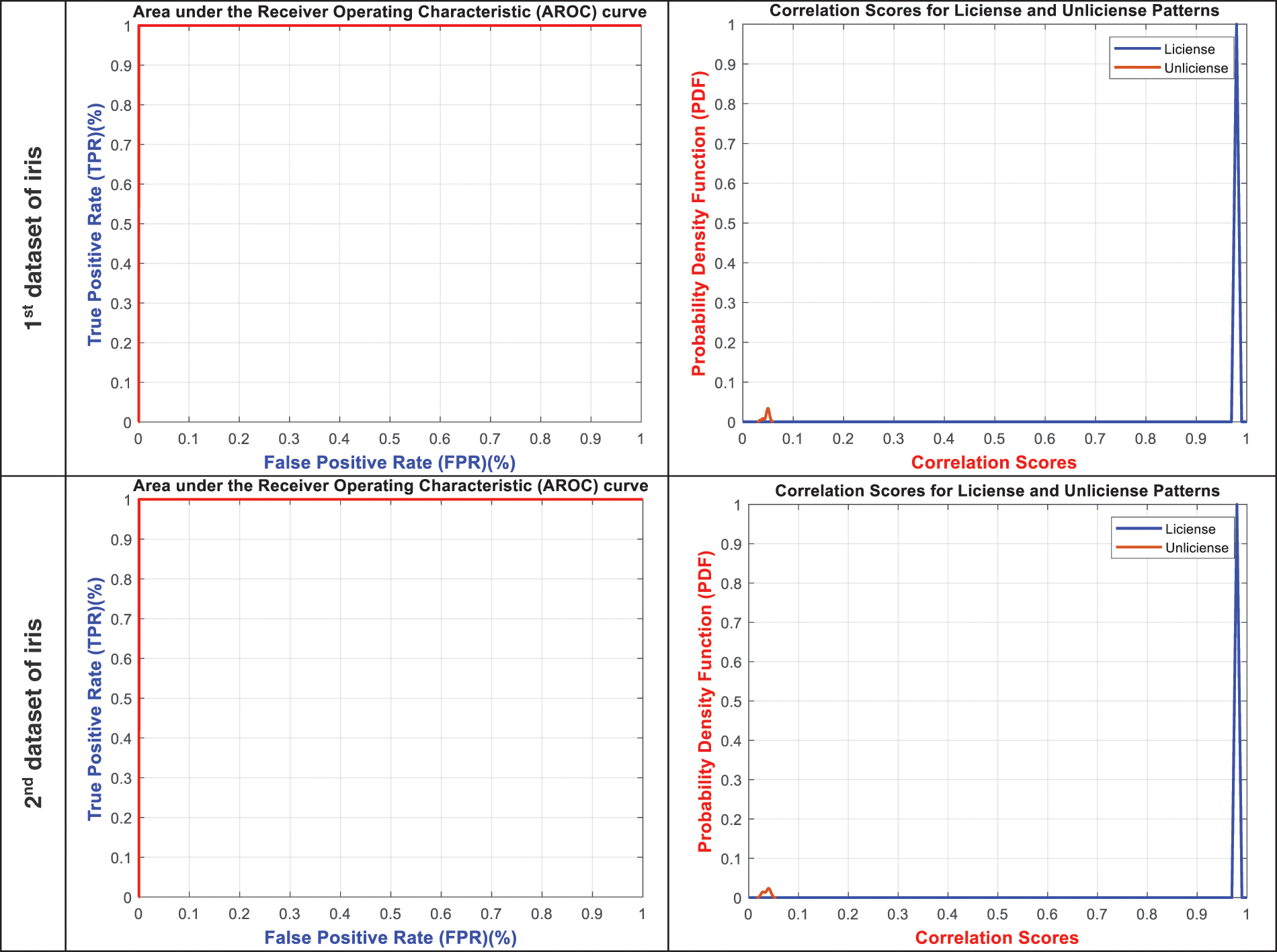
Figure 6: ROC and correlation score distributions of the stored encrypted biometrics

4.4 SSIM and Correlation Analysis

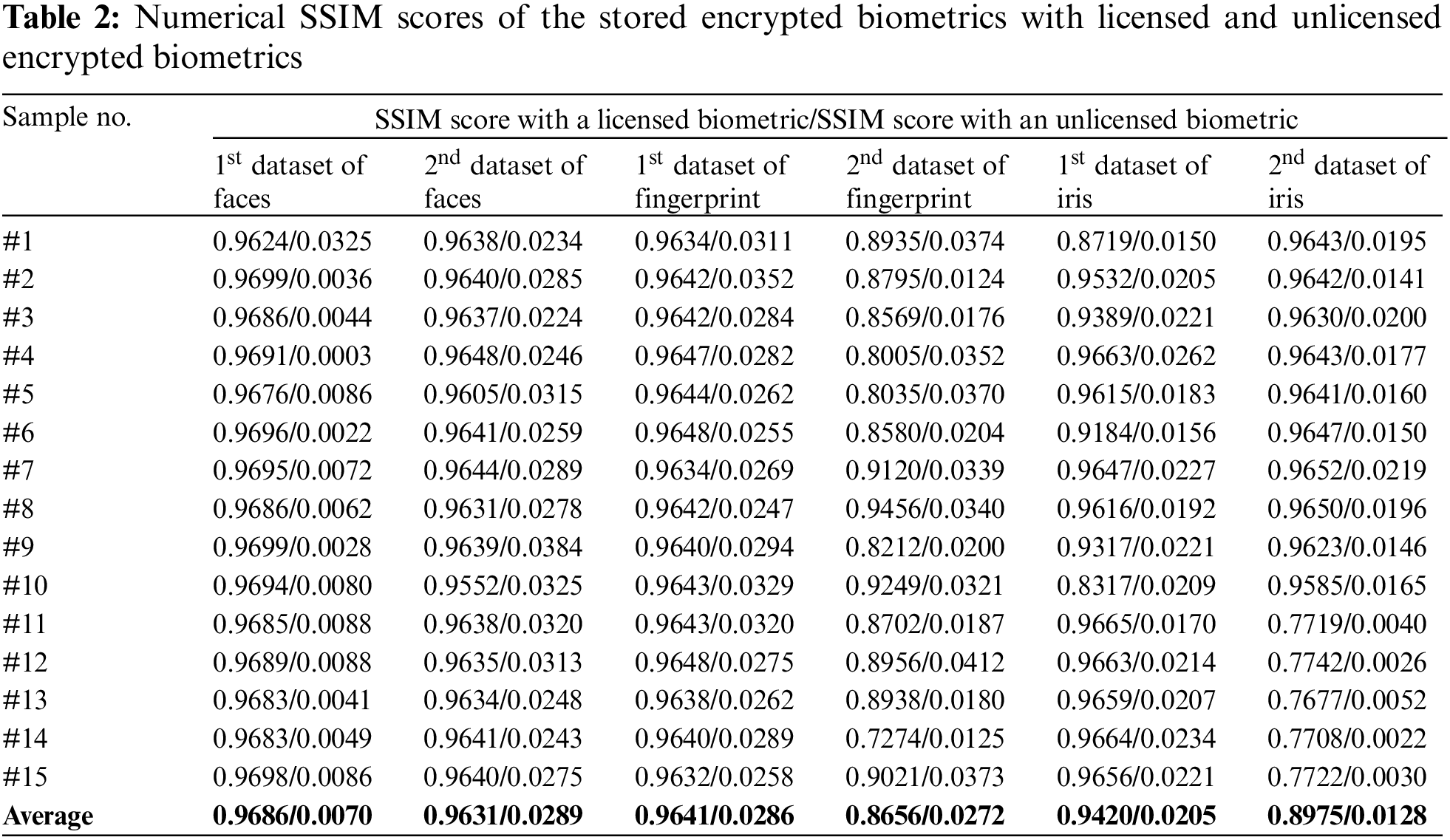
To further confirm the achieved security and recognition results in Section 4.3, the numerical analysis of the SSIM and correlation scores for the proposed BSS model is presented in this section. In the experimental study, we investigated the authentication performance of two recognition cases. The first case compares the encrypted biometrics of licensed users with the stored encrypted biometrics, while the second case compares the encrypted biometrics of unlicensed users with the stored encrypted biometrics. These recognition comparisons and authentication tests are examined using two standard statistical objective evaluation metrics: SSIM and correlation coefficients [37].

Tabs. 2 and 3 offer the numerical SSIM and correlation scores of the stored encrypted biometrics with licensed and unlicensed encrypted biometrics. These numerical results show that the proposed BSS model attains high SSIM and correlation scores for the encrypted biometrics of licensed users. On the other hand, it achieves low SSIM and correlation scores for the encrypted biometrics of unlicensed users for all tested biometric datasets. Thus, the proposed BSS model can efficiently differentiate between licensed and unlicensed patterns when they are compared to the stored encrypted patterns, and therefore, it can mitigate the possible trials of intrusion attacks.

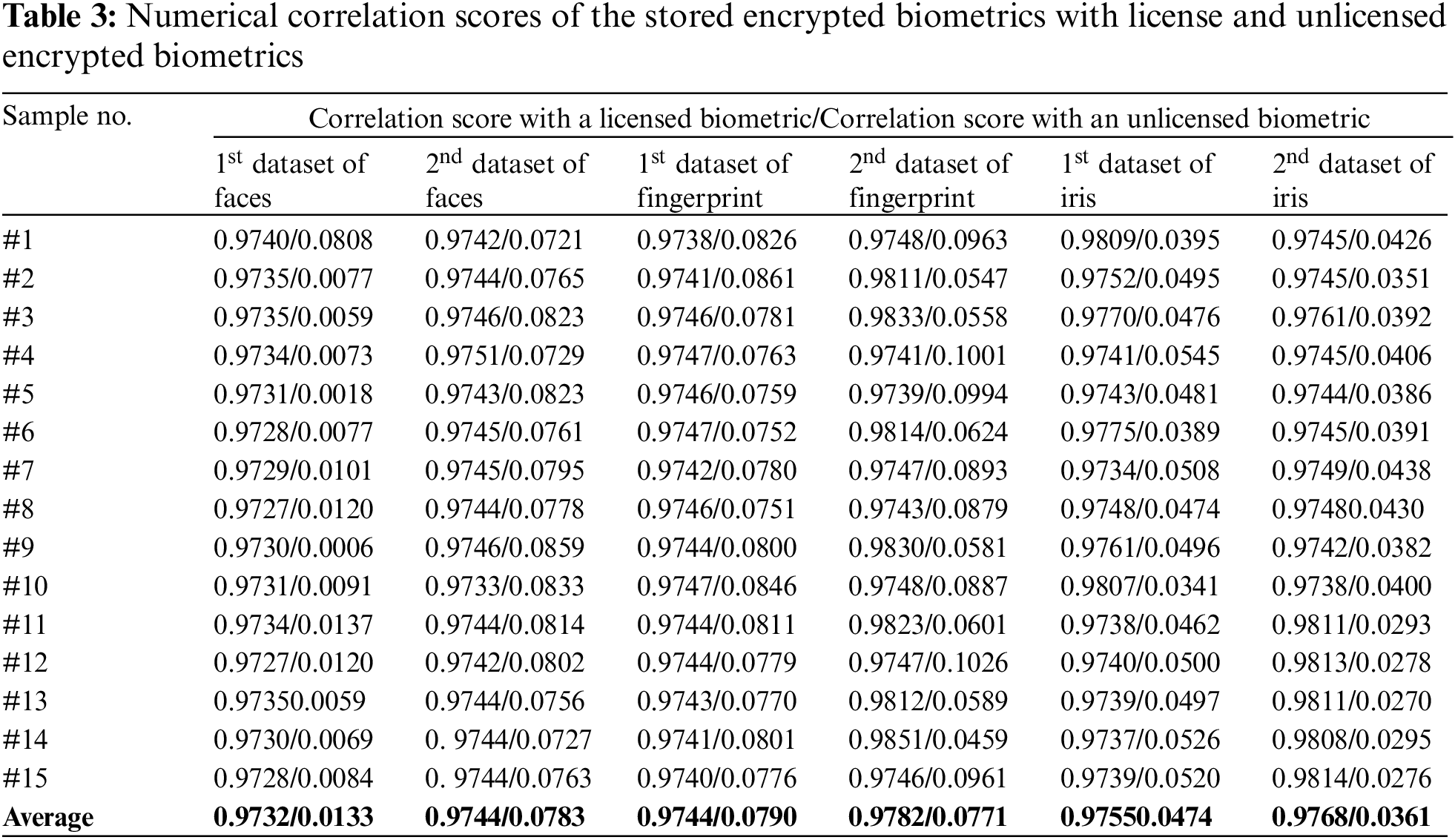
4.5 Recognition, Security, and Computational Analysis

The recognition and authentication efficiency of the proposed BSS model can be evaluated by different quantitative assessment recognition, security, and computational parameters such as AROC, FAR, the mean & variance of licensed and unlicensed patterns, FRR, EER, and computational processing time. Tab. 4 presents the obtained numerical values of the average recognition, security, and computational metrics of the examined biometric datasets. These results confirm the authentication and recognition efficacy of the proposed BSS model in identifying and recognizing the biometric input patterns. Furthermore, it is demonstrated that the proposed biometric security system achieves high values for AROC and mean of licensed patterns, which indicates higher recognition efficiency for the proposed system. On the other hand, the proposed security system achieves low values for EER, FRR, FAR, mean of unlicensed patterns, and variance of licensed and unlicensed patterns, proving that the proposed BSS model has a low false detection rate.

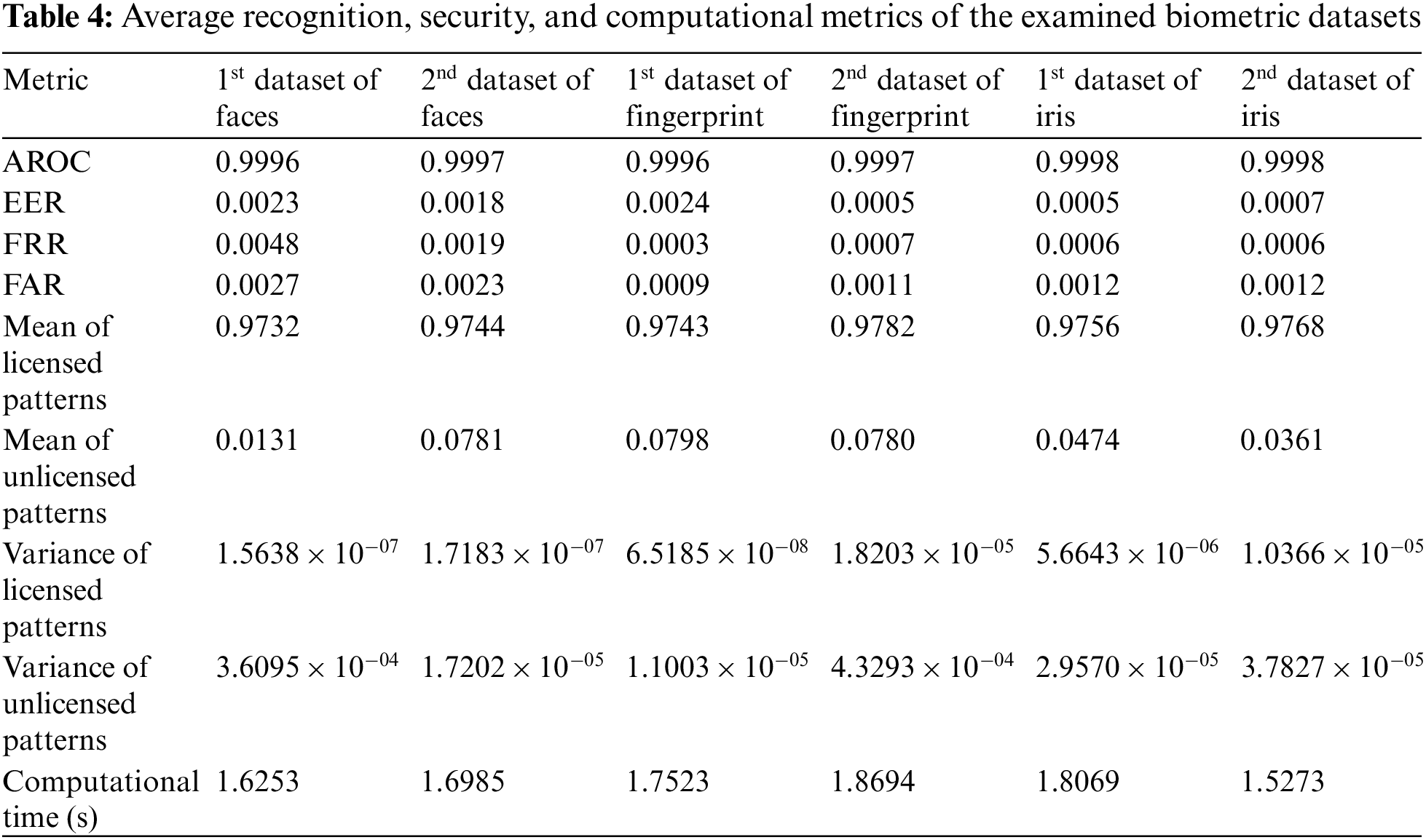
In addition, it is clarified that the proposed hybrid ciphering algorithm used in the proposed security model introduces low computational time in encrypting the biometric patterns before storing in cloud servers. Thus, the proposed BSS model is recommended to be implemented efficiently in real-time biometric authentication and cybersecurity applications.

4.6 Noise Analysis

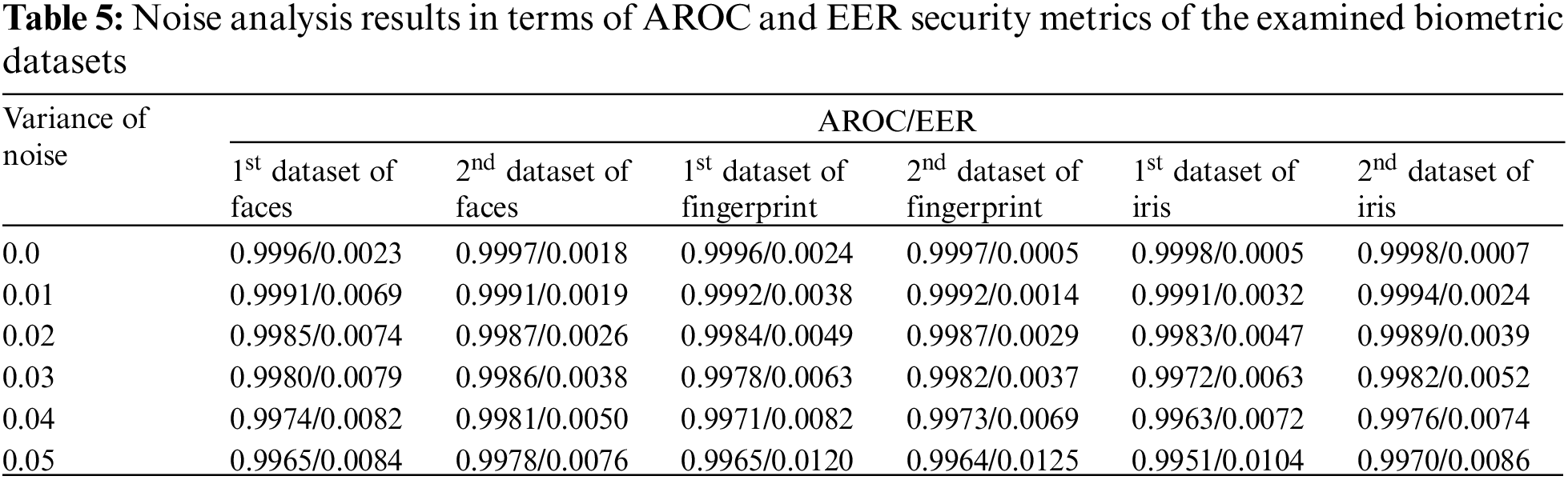
To further approve the authentication efficacy of the proposed BSS model, it is important to study its sensitivity and recognition performance in the case of existing possible noise attacks on the collected biometric patterns. For testing the sensitivity efficiency of the proposed security model against noise attacks, we examined the recognition performance in terms of AROC and EER parameters at different values of Gaussian noise variances. Tab. 5 demonstrates the noise analysis results of the AROC and EER security metrics of all examined biometric datasets. It is observed that the proposed BSS model has low sensitivity against noise attacks as it still achieves high AROC and low ERR values at high noise variance. Thus, the proposed BSS model can recognize the input biometrics proficiently with and without noise.

4.7 Comparative Analysis

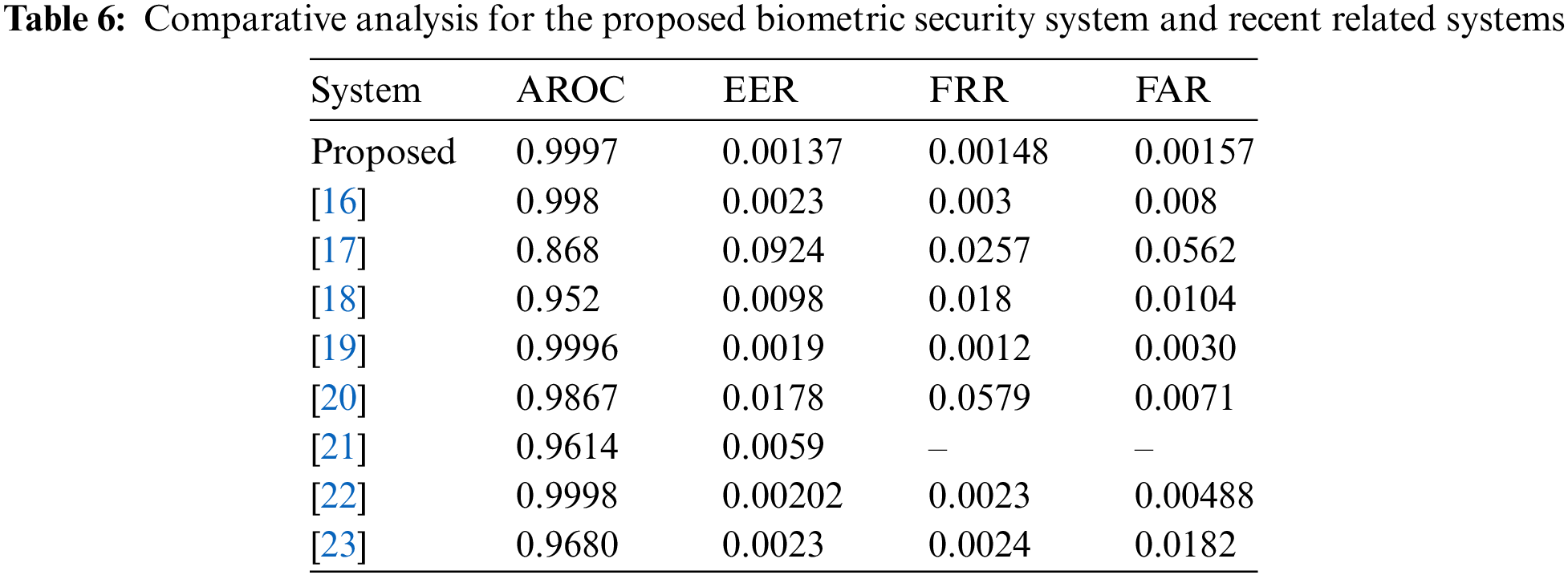
To ensure that the proposed BSS model is highly efficient in differentiating between the licensed and unlicensed patterns, we carried out further experiments to compare the proposed model’s efficiency with the authentication performance of the preceding and recent BSS models [16–23] in terms of calculating the AROC, FAR, ERR, and FRR recognition parameters. Tab. 6 offers the comparative analysis results for the proposed biometric security system and recent related systems. The obtained values of all examined security parameters for the proposed BSS model confirm its authentication and recognition superiority compared to other related BSS models.

5  Conclusion and Future Works

Authenticating users to control their access to different buildings, systems or services has become essential these days. Biometric-based authentication approaches, including faces, iris, and fingerprints, are heavily used in such contexts. However, ensuring the confidentiality of these biometrics is important to guarantee the efficiency of the provided authentication services. Many existing systems try to store these biometrics encrypted to avoid any unattended disclosure that might cause misuse of these biometrics and allow intruders to gain illegal access to systems and resources. However, the existing approaches vary in their efficiency in terms of security and complexity. Therefore, this paper competes with related work by integrating the unsupervised auto-encoder (AE) network and chaos-based ciphering algorithm to secure and cipher the details of the stored biometric patterns to build an efficient biometric security system (BSS). The proposed BSS was heavily assessed through different evaluation metrics and compared with recent related work. The experiments’ results revealed the outperformance of the proposed BSS from security and recognition capabilities compared to exiting biometric-based authentication systems.

In future work, we plan to fuse different biometrics to authenticate the users. Moreover, different deep learning would be investigated with the aim of enhancing the biometrics-based authentication system. Additionally, other biometrics datasets could be collected and tested. Furthermore, we target to study other security parameters to test the recognition and security accomplishment of the proposed biometric system.

Acknowledgement: We would like to thank SAUDI ARAMCO Cybersecurity Chair for funding this project. In addition, the authors would like to acknowledge the support of Prince Sultan University, especially the Security Engineering Lab (SEL).

Funding Statement: We would like to thank SAUDI ARAMCO Cybersecurity Chair for funding this project.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Singh, C. Vashist, P. Gaurav and A. Nigam, “A generic framework for deep incremental cancelable template generation,” Neurocomputing, vol. 4, no. 6, pp. 83–98, 2022. [Google Scholar]

 2.  N. Kumar, “CBRW: A novel approach for cancelable biometric template generation based on 1-D random walk,” Applied Intelligence, vol. 6, pp. 1–19, 2022. [Google Scholar]

 3.  I. Badr, A. Radwan, E. EL-Rabaie, L. Said, G. El Banby et al., “Cancellable face recognition based on fractional-order lorenz chaotic system and haar wavelet fusion,” Digital Signal Processing, vol. 11, 3, no. 6, pp. 1–25, 2021. [Google Scholar]

 4.  A. Sarkar and B. Singh, “A review on performance, security and various biometric template protection schemes for biometric authentication systems,” Multimedia Tools and Applications, vol. 79, no. 37, pp. 27721–27776, 2020. [Google Scholar]

 5.  N. Kumar, “Cancelable biometrics: A comprehensive survey,” Artificial Intelligence Review, vol. 53, no. 5, pp. 3403–3446, 2020. [Google Scholar]

 6.  J. Peng, B. Yang, B. Gupta, A. El-Latif and A. Ahmed, “A biometric cryptosystem scheme based on random projection and neural network,” Soft Computing, vol. 25, no. 11, pp. 7657–7670, 2021. [Google Scholar]

 7.  K. Sundararajan and D. Woodard, “Deep learning for biometrics: A survey,” ACM Computing Surveys, vol. 51, no. 3, pp. 1–34, 2018. [Google Scholar]

 8.  H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

 9.  H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

10. A. AlDuwaile and M. Islam, “Using convolutional neural network and a single heartbeat for ECG biometric recognition,” Entropy, vol. 23, no. 6, pp. 73–83, 2021. [Google Scholar]

11. R. Sujarani, D. Manivannan, R. Manikandan and B. Vidhyacharan, “Lightweight bio-chaos crypt to enhance the security of biometric images in internet of things applications,” Wireless Personal Communications, vol. 9, no. 3, pp. 2517–2537, 2021. [Google Scholar]

12. Y. Zakaria, R. Nassar, O. Zahran, G. Hussein, E. El-Rabaie et al., “Cancelable multi-biometric security system based on double random phase encoding and cepstral analysis,” Multimedia Tools and Applications, vol. 78, no. 22, pp. 32333–32355, 2021. [Google Scholar]

13. T. Sudhakar and M. Gavrilova, “Multi-instance cancelable biometric system using convolutional neural network,” in Proc. of IEEE Int. Conf. on Cyberworlds (CW), Kyoto, Japan, pp. 287–294, 2019. [Google Scholar]

14. T. Sudhakar and M. Gavrilova, “Cancelable biometrics using deep learning as a cloud service,” IEEE Access, vol. 8, pp. 112932–112943, 2020. [Google Scholar]

15. E. Abdellatef, N. Ismail, S. Abd Elrahman, K. Ismail, M. Rihan et al., “Cancelable multi-biometric recognition system based on deep learning,” The Visual Computer, vol. 36, no. 6, pp. 1097–1109, 2020. [Google Scholar]

16. A. Algarni, G. El Banby, S. Ismail, W. El-Shafai, F. El-Samie et al., “Discrete transforms and matrix rotation based cancelable face and fingerprint recognition for biometric security applications,” Entropy, vol. 22, no. 12, pp. 13–27, 2020. [Google Scholar]

17. R. Soliman, G. El Banby, A. Algarni, M. Elsheikh, N. Soliman et al., “Double random phase encoding for cancelable face and iris recognition,” Applied Optics, vol. 57, no. 35, pp. 10305–10316, 2018. [Google Scholar]

18. A. Algarni, G. El Banby, N. Soliman, F. El-Samie and A. Iliyasu, “Efficient implementation of homomorphic and fuzzy transforms in random-projection encryption frameworks for cancellable face recognition,” Electronics, vol. 9, no. 6, pp. 10–36, 2020. [Google Scholar]

19. A. Alarifi, M. Amoon, M. Aly and W. El-Shafai, “Optical PTFT asymmetric cryptosystem-based secure and efficient cancelable biometric recognition system,” IEEE Access, vol. 8, pp. 221246–221268, 2020. [Google Scholar]

20. S. Ibrahim, M. Egila, H. Shawky, M. Elsaid, W. El-Shafai et al., “Cancelable face and fingerprint recognition based on the 3D jigsaw transform and optical encryption,” Multimedia Tools and Applications, vol. 79, no. 19, pp. 14053–14078, 2020. [Google Scholar]

21. I. Bendib, A. Meraoumia, M. Haouam and L. Laimeche, “A new cancelable deep biometric feature using chaotic maps,” Pattern Recognition and Image Analysis, vol. 32, no. 1, pp. 109–128, 2022. [Google Scholar]

22. W. El-Shafai, F. Mohamed, H. Elkamchouchi, M. Abd-Elnaby and A. Elshafee, “Efficient and secure cancelable biometric authentication framework based on genetic encryption algorithm,” IEEE Access, vol. 9, pp. 77675–77692, 2021. [Google Scholar]

23. N. Soliman, A. Algarni, W. El-Shafai, F. Abd El-Samie and G. El Banby, “An efficient GCD-based cancelable biometric algorithm for single and multiple biometrics,” CMC-Computers Materials & Continua, vol. 69, no. 2, pp. 1571–1595, 2021. [Google Scholar]

24. N. Pareek, V. Patidar and K. Sud, “Image encryption using chaotic logistic map,” Image and Vision Computing, vol. 24, no. 9, pp. 926–934, 2006. [Google Scholar]

25. S. Maniyath and V. Thanikaiselvan, “An efficient image encryption using deep neural network and chaotic map,” Microprocessors and Microsystems, vol. 77, no. 10, pp. 31–54, 2020. [Google Scholar]

26. S. Sharma and A. Athaiya, “Activation functions in neural networks,” Towards Data Science, vol. 6, no. 12, pp. 310–316, 2017. [Google Scholar]

27. Y. Aurelio, G. Almeida, C. Castro and A. Braga, “Learning from imbalanced data sets with weighted cross-entropy function,” Neural Processing Letters, vol. 50, no. 2, pp. 1937–1949, 2019. [Google Scholar]

28. J. Han and C. Moraga, “The influence of the sigmoid function parameters on the speed of backpropagation learning,” in Proc. of Int. Workshop on Artificial Neural Networks (IWANN), Berlin, Heidelberg, Springer, pp. 195–201, 1995. [Google Scholar]

29. R. Sweke, W. Frederik, M. Johannes, S. Maria, K. Paul et al., “Stochastic gradient descent for hybrid quantum-classical optimization,” Quantum Computing, vol. 4, no. 3, pp. 1–22, 2020. [Google Scholar]

30. D. Allen, “Mean square error of prediction as a criterion for selecting variables,” Technometrics, vol. 13, no. 3, pp. 469–475, 1971. [Google Scholar]

31. FEI Faces Dataset, [Online]. Available: https://fei.edu.br/~cet/facedatabase.html (Last Access on 23-3-2022). [Google Scholar]

32. UFI Faces Dataset, [Online]. Available: http://ufi.kiv.zcu.cz/ (Last Access on 23-3-2022). [Google Scholar]

33. FVC DB-A Fingerprint Dataset, [Online]. Available: http://bias.csr.unibo.it/fvc2002/databases.asp (Last Access on 23-3-2022). [Google Scholar]

34. CASIA Fingerprint Dataset, [Online]. Available: Http://www.biometrics.idealtest.org (Last Access on 23-3-2022). [Google Scholar]

35. CASIA-IntervalV3 Iris Dataset, [Online]. Available: http://www.cbsr.ia.ac.cn/english/IrisDatabase.asp (Last Access on 23-3-2022). [Google Scholar]

36. Libor Machala Iris Database, [Online]. Available: http://phoenix.inf.upol.cz/iris/ (Last Access on 23-3-2022). [Google Scholar]

37. K. Byeong-Ho, “A review on image and video processing,” International Journal of Multimedia and Ubiquitous Engineering, vol. 2, no. 2, pp. 25–49, 2007. [Google Scholar]