Double Update Intelligent Strategy for Permanent Magnet Synchronous Motor Parameter Identification

1  Introduction

For Field-oriented control (FOC), the parameters of the current control loop will directly affect the overall performance of the system, with the stator resistance and stator inductance directly influencing the current control loop controller. In addition, the parameters of the speed and position loop controllers are also influenced by the current loop control parameters. In direct torque control (DTC), the electromagnetic torque and flux linkage are used as control variables, and the torque and chain deviations are directly controlled by a hysteresis comparator [1–4]. Numerous control techniques have been proposed to present high performance control of servo systems, and the parameters of magneto-synchronous motors can be affected by temperature, stator winding current and flux saturation during operation [3–5]. In addition, changes in electrical parameters are considered as an indication of servo system state changes; a short circuit between turns can lead to sudden changes in d/q-axis inductance and stator winding resistance [6], and demagnetization of the rotor permanent magnet can lead to a sudden decrease in the amplitude of the flux linkage [7]. Therefore, whether controlling speed, position, or torque control, the realization of high dynamic response and high precision control requires the use of accurate motor parameters, and obtaining accurate motor parameter values helps to improve the control performance of the whole servo system.

In order to obtain reliable permanent magnet synchronous motor parameters, suitable parameter identification methods are required, and the main methods for permanent magnet synchronous motor parameter identification are: model reference adaptive algorithm [8,9], recursive least squares method [10], extended Kalman filter algorithm [11], artificial neural network algorithm [12], particle swarm optimization [13,14]. With the development of machine learning [15,16], deterministic learning is applied to parameter identification of permanent magnet synchronous motor [17].

The reference [8] used the model reference adaptive algorithm to establish an adaptive observer and analyzed the large-signal convergence of the parameters using the Lyapunov second method and singular regression theory, and the designed method can improve the convergence speed and overall stability of the system but the complexity of the method implementation is high. In [9], a parameter identification method was designed using Popov’s superstability theory, which can identify the stator resistance and flux linkage amplitude simultaneously with good identification accuracy, but the design of the adaptive observer and the selection of the adaptive law are more complicated. The standby algorithm is used to obtain the initial value of the inductor, and the running algorithm is used to continuously update the identification parameters. The reference [11] is based on the extended Kalman filter method for parameter identification, but the P and Q matrices are difficult to determine and are closely related to the system state. At the same time, the extended Kalman filter has some inherent drawbacks, such as susceptibility to noise, long running time, and difficulty in determining the algorithm design and objective function. In the reference [12], the stator resistance is first estimated offline, and the flux linkage and inductance are identified online using a neural network discriminator based on this estimation result, and then the obtained inductance and flux linkage values are used to further update the stator resistance value to realize the parameter identification decoupling, but this method requires a combination of offline identification and online identification, which is difficult to meet the high real-time requirements of the operating conditions; The reference [13,14] improved on the basis of the traditional particle swarm method and proposed a dynamic self-learning particle swarm optimization, which enhanced the ability of global search of the population and jumped out of the local optimum. Reference [18] proposed an improved differential evolution algorithm (DE), which introduced clonal selection and receptor editing mechanisms, to improve the population diversity and the global search ability of the algorithm. However, the algorithm was only applied to non-salient pole PMSM motor, and the parameter identification of salient pole PSMSM still needs further research.

Reference [19] proposed a parameter identification method based on Taylor series expansion of motor speed response under constant voltage input. The relationship between motor parameters and Taylor series coefficients is established by this method, but the method requires speed/position sensors and related calculation software to achieve.

In reference [20–22], particle swarm optimization algorithm, neural network algorithm and adaptive algorithm are combined for parameter identification. These methods combine the advantages of particle swarm optimization algorithm and other algorithms and have good identification accuracy in different parameter identification problems.

In reference [23–25], differential evolution algorithm and particle swarm optimization algorithm are combined and applied to parameter identification in different backgrounds. The hybrid algorithm avoids the shortcomings of the two algorithms and has good accuracy and speed in identifying various parameters.

It provides a new idea for scientific research to combine the two methods to solve engineering problems by making full use of their respective advantages. In this paper, particle swarm optimization algorithm and weighted difference algorithm are combined for parameter identification of permanent magnet synchronous motor.

The main work of this paper:

(1) The advantages of the particle swarm optimization and the weighted differential evolution algorithm are combined, and a permanent magnet synchronous motor parameter identification method that combines the use of both algorithms is proposed.

Particle swarm optimization (PSO) algorithm has a fast convergence speed in the initial stage of solving the optimization problem, but in the later stage, because all particles are close to the optimal particle, the whole population loses diversity, and particles are easy to fall into local optimal. The weighted differential evolution (WDE) algorithm has the ability to maintain population diversity and explore local search, but it has no mechanism to store previous processes and use global information about the search space, so it can easily lead to waste of computing power. Therefore, in this paper, the advantages of PSO and WDE are combined to realize the identification of PMSM parameters.

(2) An adaptive judgment factor is proposed to control the ratio between the particle swarm optimization and the weighted differential evolution algorithm.

Adaptive judgment factors are introduced to control the proportion of particle swarm optimization and weighted differential evolution algorithm in each iteration process. According to the probability law, PSO algorithm or WDE algorithm is used to update individuals. The individuals obtained by WDE operation are used to guide the evolution process of individuals in PSO operation through information exchange mechanism, so as to ensure that the greater the crossover probability, the more information the new individuals inherit from the mutant individuals, and the richer the population diversity, thus ensuring the global solution accuracy and efficiency of the algorithm.

2  Mathematical Model of Permanent Magnet Synchronous Motor in Servo System

The permanent magnet synchronous motor has multivariable, nonlinear, and strongly coupled characteristics, and the mathematical model of the permanent magnet synchronous motor in the synchronous rotating coordinate system (d/q-axis coordinate system) can be expressed as (1) [26–28], after neglecting disturbances such as core saturation, harmonics, eddy currents, and losses caused by hysteresis.

{ud=Rid+Lddiddt−ωeLqiquq=Riq+Lqdiqdt+ωe(Ldid+ψf)(1)

where ud is the stator straight-axis voltage, uq is the stator cross-axis voltage; R is the stator resistance; id is the stator straight-axis current, iq is the stator cross-axis current; Ld is the stator straight-axis inductance, Lq is the stator cross-axis inductance; ωe is the electric angular velocity; ψf is the flux linkage. When the servo system is in steady-state operation, the stator cross-axis and straight-axis currents and rotational speed of the permanent magnet synchronous motor vary very little, which is approximated as:

diddt=diqdt=0(2)

Eq. (1) changes to

{ud=Rid−ωeLqiquq=Riq+ωe(Ldid+ψf)(3)

The order of the Eq. (3) is two, and there are four motor parameters to be identified, so the Eq. (3) is of non-full-rank type. The variables such as stator resistance, rotor chain and winding inductance change with load and temperature during motor operation, which may lead to inaccurate identification of the parameters to be identified. Permanent magnet synchronous motors generally use id=0 control strategy to reduce motor losses and to improve the system power factor. To solve the problem of equation under-ranking in Eq. (3), a negative-sequence weak magnetic current strategy with id≠0 injected in the d-axis for a short time is usually used. A full-rank permanent magnet synchronous motor system model [12] can be obtained under both id=0 and id≠0 strategies in the discrete form:

{ud0(k)=−Lq0ωe0(k)iq0(k)uq0(k)=Riq0(k)+ψmωe0(k)ud1(k)=Rid1(k)−Lq1ωe1(k)iq1(k)uq1(k)=Riq1(k)−Ld1ωe1(k)id1(k)+ψmωe1(k)(4)

the variables and parameters subscripted as “0” in Eq. (4) represent the sampled values in the id=0 model, and the variables or parameters subscripted as “1” represent the sampled values in the id≠0 model.

3  Algorithm Design

3.1 Weighted Differential Evolutionary Algorithm

The differential evolution algorithm was proposed by Rainer Storn and Kenneth Price in 1995 while studying the Chebyshev polynomial fitting problem [29]. The differential evolution algorithm and process can be summarized as follows: population initialization, mutation operation, crossover operation, and selection operation. Assuming that the current population size is NP and the individual dimension is D the basic principle is as follows.

Step 1: population initialization. The current population can be described as follows:

Pt={Xi,t|Xi,t=(Xi,t1,Xi,t2,Xi,t3⋯,Xi,tD)T},i∈[1,NP](5)

where t denotes the current evolutionary generation and Xi,t denotes the i-th individual vector in the population.

Xi=(xt1,xt2⋯xtD)(6)

{xi,0j=xminj+rand(0,1)(xmaxj−xminj)i∈[1,NP],j∈[1,D](7)

where, rand(0,1) denotes a random small number that conforms to a uniform distribution in the range (0,1), and Xmaxj , Xminj denote the maximum and minimum bounds of the j-th dimension of the individual, respectively.

Step 2: variant operation. Eq. (8) gives a simpler variation strategy:

Vi,t=Xr1,t+F(Xr2,t−Xr3,t)(8)

where r1, r2 , r3 populations of three randomly selected individual numbers, and each of the three is not equal, F is the scaling factor, used to control the search step, and its value range (0,1).

Step 3: crossover operations. Eq. (9) gives a crossover operation to obtain variant individuals by comparing the crossover factor CR with a uniformly distributed random number in the range (0,1), the variable individual ui,tj is obtained, and the value of CR ranges from 0 to 1.

ui,tj={vi,tj,rand(0,1)<CRxi,tj,else(9)

Step 4: select operation. The differential evolution algorithm uses a greedy strategy to compare the fitness of offspring individuals over their parents, and the individuals with better fitness will be selected to enter the next generation population.

xik+1={uik+1,f(uik+1)<f(xik)xik,else(10)

where f is the fitness function.

The weighted differential evolution algorithm (WDE) [30] was proposed in 2018. WDE is based on a two-population variation strategy, and the weighting operation is introduced in the variation operator to achieve parameter-free adjustment of the optimization process. A better balance between local and global search is sought. The process of weighted difference evolution algorithm is as follows.

Step 1: population initialization. The initial WDE population contains 2NP individuals of D-dimensional variables, and the population Pi0,j0 is initialized as:

Pi0,j0∼U(minj0,mini0),i0∈[1,2NP],j0∈[1,D](11)

In Eq. (11), NP is the number of variable individuals in the population in run mode, D is the dimension of the individuals, U is the initial parameter range, and minj0,mini0 are the lower and upper limit values of the parameters, respectively.

Step 2: weighted operation. WDE algorithm randomly selects NP subpopulation Psub1 from 2NP individuals, and the remaining individuals form subpopulation Psub2. In the evolution process of each generation, each dimension of continuous variables in Psub1 is weighted to generate temporary population xi(temp)j according to Eq. (12).

xi(temp)j=∑i=1NPωixi(Psub1)j/∑i=1NPωi,i∈[1,NP],j∈[1,D](12)

where ωi is determined by Eq. (13).

ωi=[rand(0,1)]3(13)

Step 3: cross-mutation operation. The crossover factor Eij of individuals in subpopulation Psub2 is 0, and the crossover factor of D×[rand(0,1)]3 variables in randomly selected individuals is set to 1, indicating that the crossover variation operation generates trial solutions.

One of the following two strategies is selected according to the probability of each pair to perform the variation operation.

Strategy 1. The variation factor is defined according to Eq. (14), for different dimension variables xi(i=1,2,3⋯D) of the same individual, the variation factor CFj takes the same value, and the operation of cross variation is carried out according to Eq. (15).

CFj=[rand(0,1)]3(14)

vi(Psub2)j=xi(Psub2)j+CFjEij(xi(temp)j−xi(Psub2)j)(15)

Strategy 2. Generate different variation factors CFi for each dimension of individual variable xij(j=1,2,3⋯NP), respectively, by calling random numbers in Eq. (16), and then perform the cross-variation operation according to Eq. (17).

CFi=[rand(0,1)]3(16)

vi(Psub2)j=xi(Psub2)j+CFiEij(xi(temp)j−xi(Psub2)j)(17)

Step 4: select operation. The differential evolution algorithm uses a greedy strategy to calculate the fitness values of individuals before and after the mutation, and selects the better solution with smaller fitness values to update and replace the initial values.

xik+1={vik+1,f(vik+1)<f(xik)xik,else(18)

where f is the fitness function.

From the algorithm steps, it can be seen that the weighting operation is an important difference between WDE and DE. Through the weighting operation of Eq. (12), individuals will synchronize the information of other individuals in each round of mutation is and increase the information exchange between individuals.

3.2 Particle Swarm Optimization Algorithm

The particle swarm optimization is inspired by observing the foraging messaging of a flock of birds. In the algorithm, each individual is a particle representing a feasible solution. Let Zi be the position of the i-th particle, and the adaptation value of Zi is calculated according to the previously set adaptation function, which is used to measure the merit of this particle position. Vi is the flight speed of particle i, i.e., the distance travelled by the particle per unit time. Pi is the optimal position found by particle i, and Pg is the optimal position found by the whole particle swarm [31].

In each iteration of the particle, its update equation is:

{Vik+1=ωVik+c1rand()(Pi−Zik)+c2rand()(Pg−Zik)Zik+1=Zik+Vik+1(19)

where K is the number of iterations; ω, c1, c2 are the inertia weight coefficients and learning factors, respectively; rand() is a random number between 0 and 1. PSO has strong small data seeking ability and can solve more complex optimization problems, but with the increase of the number of iterations, it is easy to fall into local optimum.

3.3 WDEPSO Algorithm

The evolution criterion of the differential evolution algorithm is based on adaptive information and does not require additional conditions such as function derivability and continuity. In addition, differential evolution is inherently parallel and suitable for massively parallel distributed processing. However, differential evolution algorithms do not utilize individual prior knowledge, i.e., there is no mechanism to store prior processes and use global information about the search space. The particle swarm optimization algorithm, on the other hand, makes decisions based on its own and other particles’ experience, so it can effectively compensate for the deficiencies of the differential evolution algorithm. The WDE algorithm and PSO algorithm are fused, and an adaptive judgment factor is introduced to control the ratio between the use of particle swarm optimization and differential evolution algorithms in each iteration, and the PSO algorithm or WDE algorithm is considered to update individuals according to the law of probability, which ensures that the greater the crossover probability, the more information the new individuals inherit from the mutant individuals, and the richer the population diversity. Judgment factor is used to select the update method of individuals, it is calculated as:

λG=λ02πarccotGmax−G+1G2(20)

where Gmax is the total number of iterations; G is the current evolutionary generation and G∈[1,Gmax]; λ0 is a constant.

Then when the i-th individual generates a new individual, first a random number Si∈[0,1] is generated, and if Si is smaller than λG, the individual is updated using the WDE algorithm, otherwise the particle swarm optimization algorithm is used for updating.

According to Eq. (20), the judgment factor gradually increases with the number of iterations, so that the solution space is mainly searched by the PSO algorithm during the preliminary search, while the WDE algorithm is mainly used for fine search at the later stage of the search to find the non-inferior solution set with high accuracy. In addition, the WDE algorithm in the preliminary stage of Si search can perform variational operations on individuals to prevent the particle swarm optimization algorithm from falling into local optimal solutions when searching. Eq. (20) combined with the role of random numbers makes it possible to update individuals in a probabilistic way, ensuring that the ratio of the two algorithms used in each iteration better conforms to the statistical law, and giving full play to the role of the judgment factor in regulating the intelligent evolutionary algorithm of the population. Fig. 1a is the change curve of λG, Fig. 1b is Parameter identification block diagram of permanent magnet synchronous motor based on WDEPSO.

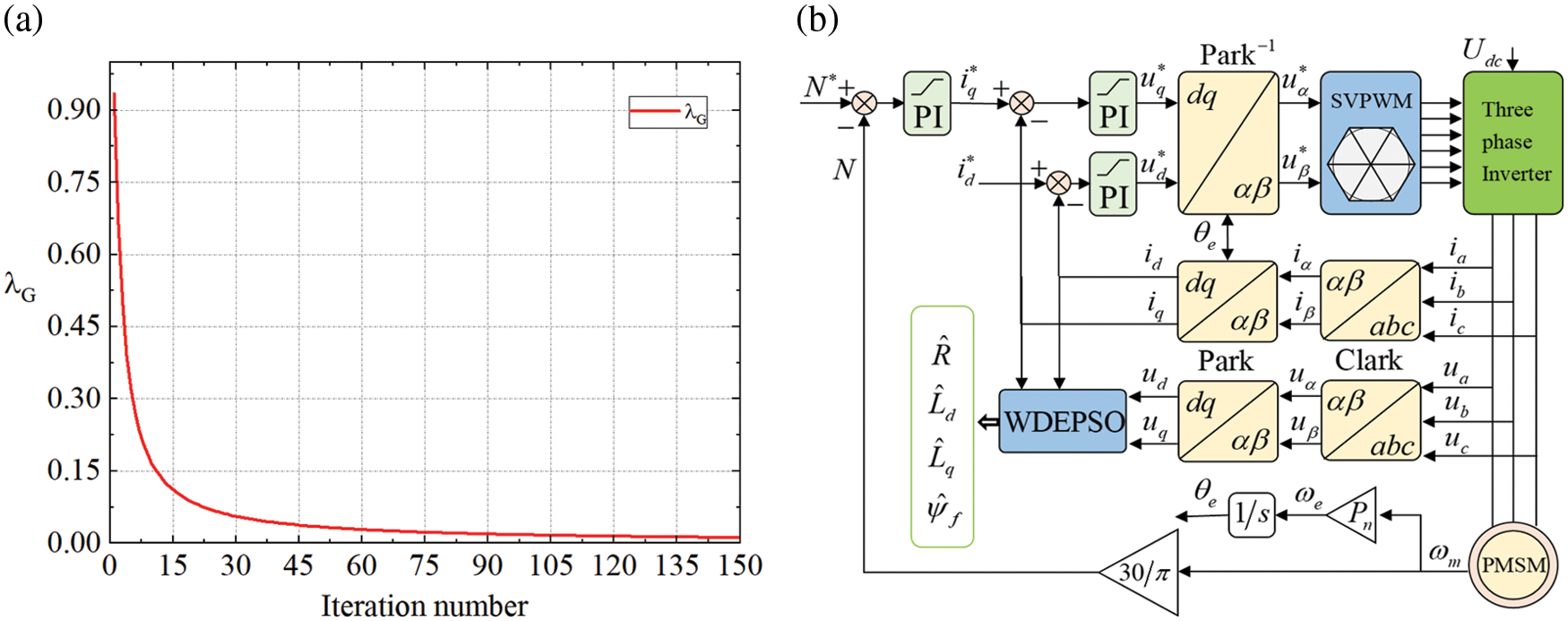
Figure 1: (a) curve of λG; (b) PMSM parameter identification based on WDEPSO

3.4 Fitness Function

The basic idea is that according to the difference between the actual output of the system and the output of the adjustable model, the parameters of the model to be identified are continuously adjusted by the identification algorithm to minimize the value of the error adaptation function between the actual output value and the adjustable model, the smaller the adaptation value, the closer the input of the identification model and the measured input, and the closer the parameters to be identified and the real value.

The fitness function is:

f=∑k=1n[a1(ud0(k)−u^d0(k))2+a2(ud1(k)−u^d1(k))2+a3(uq0(k)−u^q0(k))2+a4(uq1(k)−u^q1(k))2](21)

where a1, a2, a3, a4 are the weight coefficients; u^d0(k), u^d1(k) are the d-axis output voltage values of the stator of the identification model; u^q0(k), u^q1(k) are the q-axis output voltage values of the stator of the identification model. Under the same adaptation value, different weighting coefficients can change the accuracy of each parameter to be identified. Fig. 2a shows the identification principle of WDEPSO.

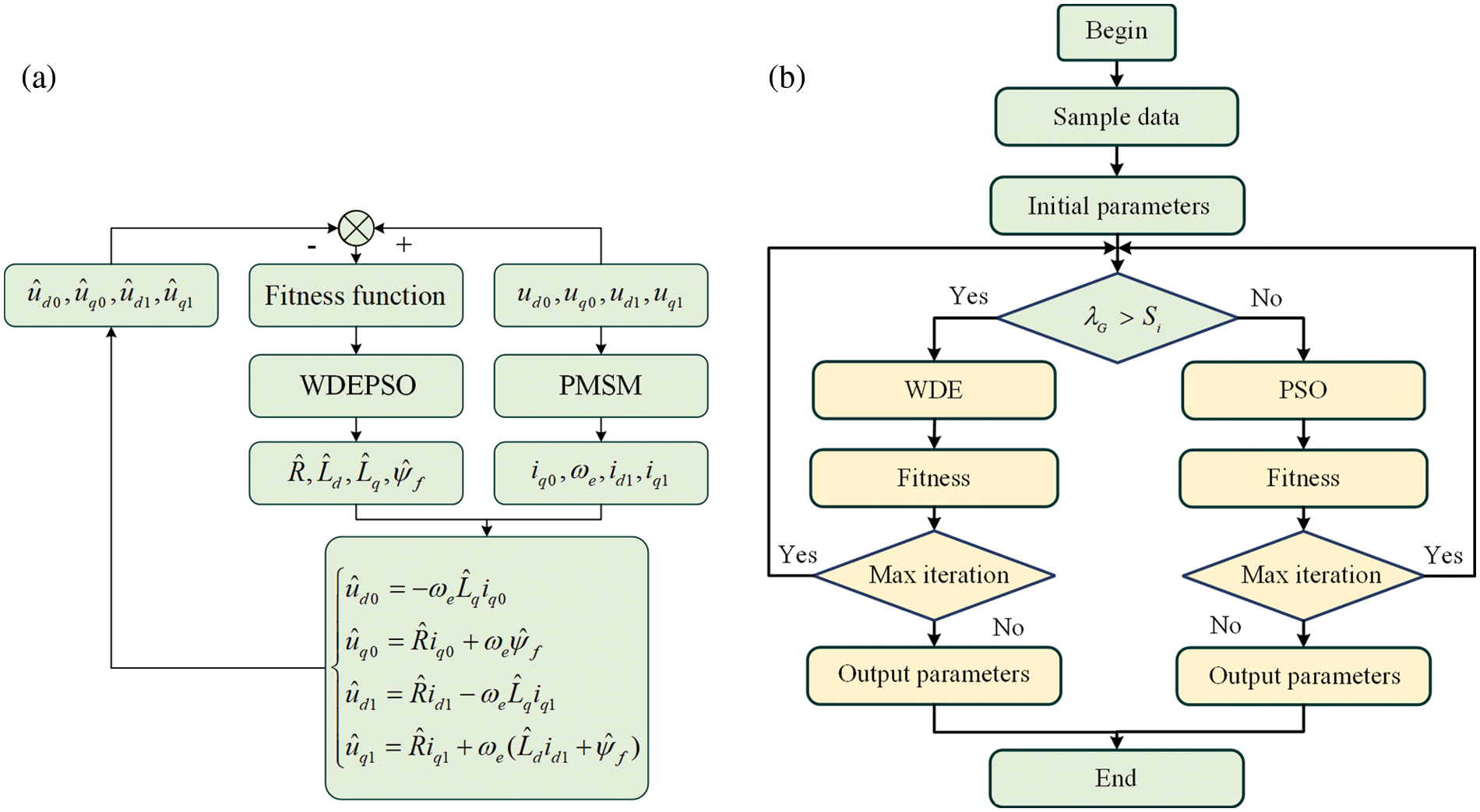
Figure 2: (a) Principle of WDEPSO; (b) Flow chart of the WDEPSO

3.5 PMSM Parameter Identification Based on WDEPSO

Parameter identification steps of permanent magnet synchronous motor based on WDEPSO:

Step 1: sampling current and angular velocity.

Step 2: initialize the two algorithms.

Step 3: judge the relationship between λG and Si.

Step 4: select one of the two algorithms for iteration according to the results of step 3.

Step 5: if the maximum number of iterations is not reached, re-enter step 3 for circulation.

Step 6: reach the maximum number of iterations and output identification parameters.

The algorithm flow is shown in Fig. 2b.

4  Simulation Results and Analysis

In this simulation, a simulation model based on the WDEPSO is built on the MATLAB/Simulink platform for the parameter identification of permanent magnet synchronous motor. The parameters of the simulation model are set as in Table 1.

To make the results comparable, the WDEPSO is compared with the WDE, DE, PSO, and particle swarm optimization with inertial weight variation (LPSO). To ensure the rationality of simulation, the WDEPSO, PSO, LPSO are set with the same parameters, and the WDE and DE algorithms are set with the same crossover factor and variation factor. In order to test the performance of the algorithms in global search, the initial domain of all parameters to be identified is set to (−2, 10), far from the real values set in the simulation. The simulations were run 50 times independently in order to reduce the testing error caused by the randomness of the single algorithm.

In order to fully verify the computational performance of various algorithms, the effectiveness of algorithm recognition is tested under changing working conditions. The algorithms are tested under two conditions: load change and speed change. The speed of the permanent magnet synchronous motor is designed to first accelerate to the rated speed, then run steadily, and finally decelerate to 20% of the rated speed until the end. Each speed change strategy accounts for one-third of the total sampling time, and the motor load increases from 0 to the rated value during stable operation, and decreases to 0 when the motor starts to decelerate.

The simulation data are presented in the following Table 2.

From the data in the Table 2, it can be seen that the WDEPSO has the highest recognition accuracy and the average value of the fitness function is smaller, and the algorithm performs better than several other algorithms.

The results of the five algorithms to identify each parameter of the permanent magnet synchronous motor are shown in Figs. 3~5.

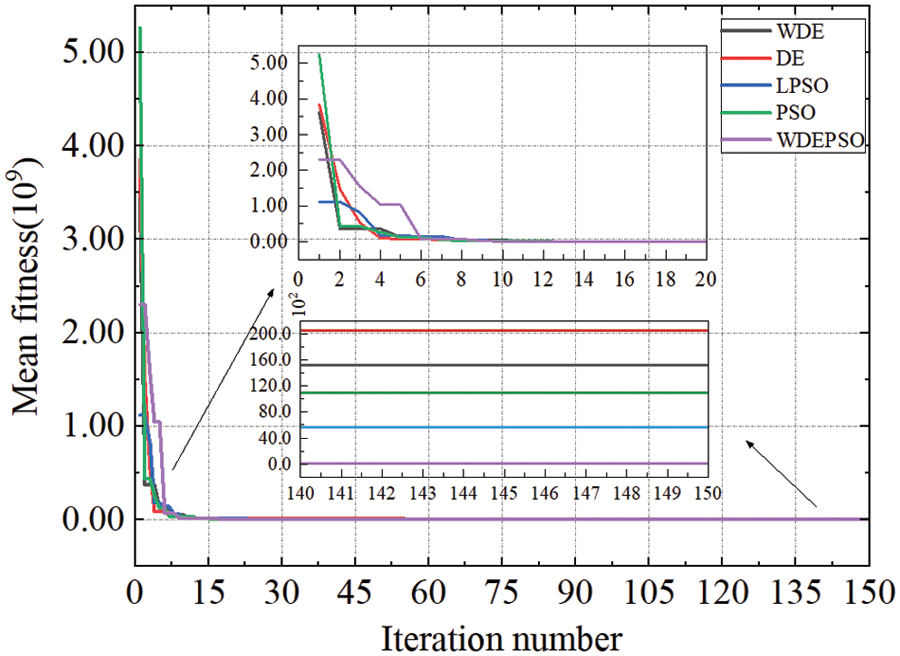
Figure 3: Plot of mean fitness

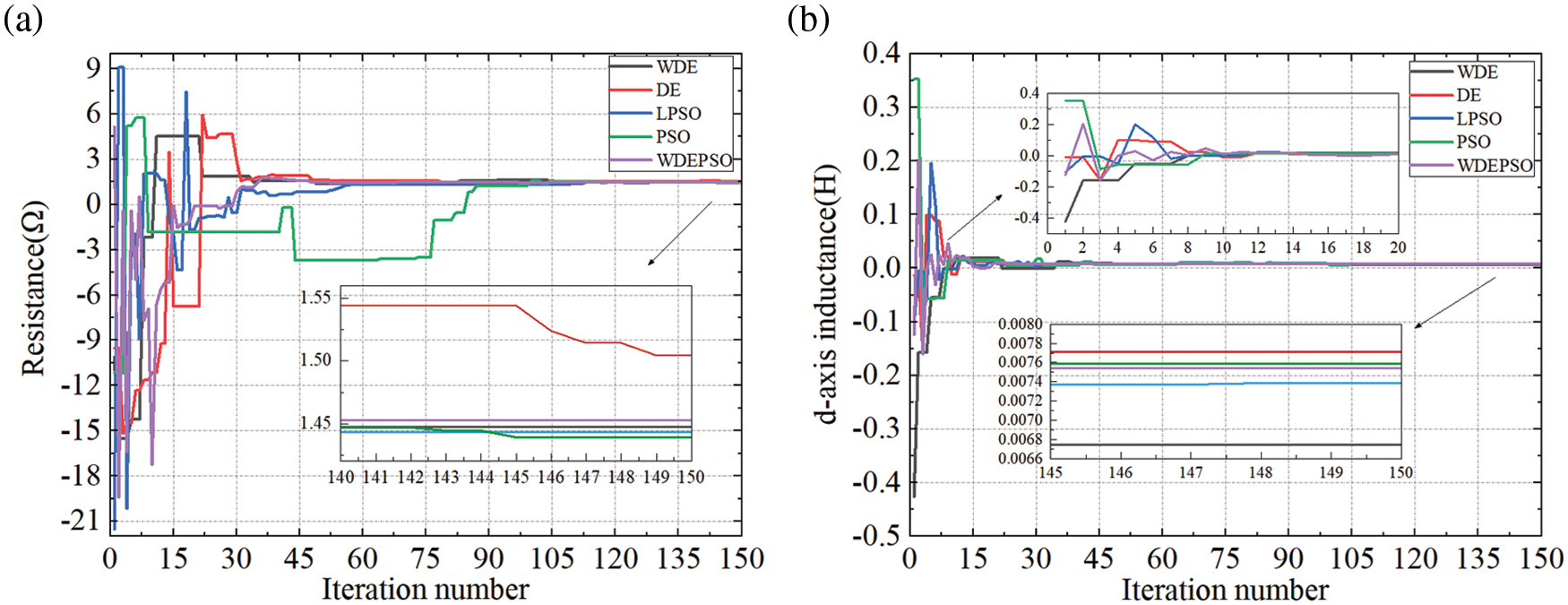
Figure 4: (a) Plot of stator resistance; (b) Plot of d-axis inductance

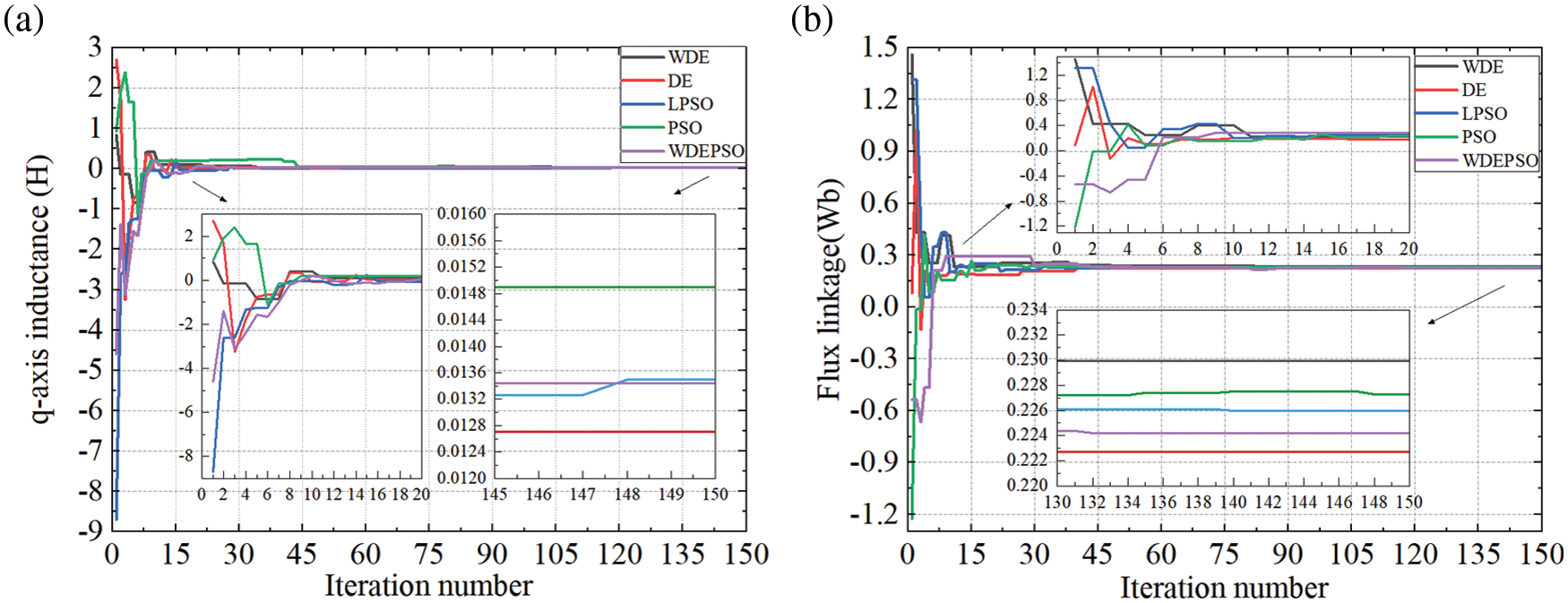
Figure 5: (a) Plot of q-axis inductance; (b) Plot of flux linkage

From Fig. 3, it can be seen that WDEPSO enters the local search around the 15th iteration, and the other four algorithms start to enter the local search around the 5th generation. From the convergence speed, the other four algorithms are faster, but from the data after the final iteration is completed, it can be seen that the other four algorithms converge faster, but the final error is larger, because the other four algorithms fall into the local search and cannot jump out. The slow convergence of the WDEPSO algorithm at the beginning of the iteration is to avoid getting into local optimum. This verifies the better global search performance of the WDEPSO algorithm and the ability to avoid getting into local optimal solutions.

Fig. 4a shows the identification curve of stator resistance. From the figure, it can be seen that the five algorithms fluctuate more at the beginning of the identification process, because the stator resistance is more affected after the motor operation, and the algorithm takes longer time to carry out the identification. Compared with the other four algorithms, WDEPSO converges faster and starts to converge at the 50th iteration, and the resistance identification value fluctuates less during the iteration, and the final identification result is closest to the set value, which verifies the ability of WDEPSO algorithm to find the optimal solution.

Fig. 4b shows the d-axis inductance identification curve. From the Fig. 4b, it can be seen that the five algorithms have less curve fluctuation and converge faster during the identification process, which indicates two things: firstly, the d-axis inductance is less affected when the motor is running, so it is easier for the five algorithms to find the optimal solution; secondly, the d-axis inductance is more affected by the operating conditions of the motor, but the algorithms have stronger identification ability and can accurately identify the inductance value. The WDEPSO does not converge faster than the other algorithms, but the final identification results show that the WDEPSO algorithm is closest to the set value. This confirms that WDEPSO has better solving ability.

Fig. 5a shows the identification curve of q-axis inductance values. From the Fig. 5a, it can be seen that the WDEPSO is gradually approaching the optimal solution from the beginning of the iteration to entering the local search process, and the identification results do not fluctuate significantly, while other algorithms fluctuate more in the beginning of the search process, which fully verifies the better global search capability of the WDEPSO.

Fig. 5b shows the flux linkage identification curve. From the Fig. 5b, it can be seen that the WDEPSO starts to converge at about the 40th iteration and then refines the search near the set value. Compared with several other algorithms, the convergence speed of WDEPSO has no obvious advantage in flux linkage identification, but the final identification result is closest to the set value, which verifies the stronger identification accuracy of the WDEPSO.

Parameter identification of PMSM is subject to large fluctuations or mis-convergence due to the high degree of nonlinearity of the PMSM model and the local extreme value points of the objective function, which makes it difficult to find the optimal solution for algorithms with low search degree, small solution space and poor stability. All five algorithms in this paper can converge quickly to near the true value, which indicates that all five algorithms have good global search performance. When the identified values of all five algorithms are close to the stable values, it can be seen that the WDEPSO converges faster than the other algorithms, and the identification accuracy is higher than the other algorithms, and it can be seen from the data in Table I that the identified values of the WDEPSO are closer to the design values, the average fitness value is smaller, and the WDEPSO can better track the motor in speed and load torque mutation. This shows that the WDEPSO has good robustness and convergence, which verifies the superiority of the algorithm.

5  Conclusion

In this paper, based on vector control, the motor electromechanical mathematical model is brought to full rank by injecting weak magnetic negative sequence current with id≠0. The double update strategy combining weighted differential evolution algorithm based on initial parameters and particle swarm optimization is used to accurately identify four parameters, namely, stator winding resistance, d-axis inductance, q-axis inductance and flux linkage, an adaptive judgment factor is introduced to control the ratio of WDE and PSO algorithms during each iteration. The adaptive judgment factor is introduced to control the proportion of WDE and PSO algorithm calls in each iteration, and the PSO algorithm or WDE algorithm is considered to update the individuals according to the probability law to ensure the diversity and effectiveness of the evolution of individuals in the population. By comparing the algorithm with other four algorithms under different operating conditions, it is proved that the algorithm has good robustness and high computational accuracy in the parameter identification of permanent magnet synchronous motor. When PMSM runs at high speed or low speed, the resistance identification results are affected by the voltage-source-inverter (VSI) nonlinearity, while the d-q axis inductance and flux linkage are affected when the motor runs at low speed. In the next step, the voltage-source-inverter (VSI) nonlinearity on PMSM parameter identification will be considered.

Funding Statement: This work was supported in part by the Natural Science Foundation of China under Grant 52077027, and in part by the Liaoning Province Science and Technology Major Project No.2020JH1/10100020.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

 1.  Z. Q. Zhu, D. Liang and K. Liu, “Online parameter estimation for permanent magnet synchronous machines: An overview,” IEEE Access, vol. 9, no. 8, pp. 59059–59084, 2021. [Google Scholar]

 2.  Z. Wang, J. Chai, X. Xiang, X. Sun and H. Lu, “A novel online parameter identification algorithm designed for deadbeat current control of the permanent-magnet synchronous motor,” IEEE Transactions on Industry Applications, vol. 58, no. 2, pp. 2029–2041, March--April 2022. [Google Scholar]

 3.  Y. Yu, X. Huang, Z. Li, M. Wu, T. Shi et al., “Full parameter estimation for permanent magnet synchronous motors,” IEEE Transactions on Industrial Electronics, vol. 69, no. 5, pp. 4376–4386, May 2022. [Google Scholar]

 4.  M. S. Rafaq and J. Jung, “A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnet synchronous motors in wide speed range,” IEEE Transactions on Industrial Informatics, vol. 16, no. 7, pp. 4747–4758, July 2020. [Google Scholar]

 5.  H. Ahn, H. Park, C. Kim and H. Lee, “A review of state-of-the-art techniques for PMSM parameter identification,” Journal of Electrical Engineering and Technology, vol. 15, no. 3, pp. 1177–1187, 2020. [Google Scholar]

 6.  Y. Xu, Z. Zhang, Y. Jiang, J. Huang and W. Jiang, “Numerical analysis of turn-to-turn short circuit current mitigation for concentrated winding permanent magnet machines with series and parallel connected windings,” IEEE Transactions on Industrial Electronics, vol. 67, no. 11, pp. 9101–9111, 2020. [Google Scholar]

 7.  K. C. Kim, K. Kim, H. J. Kim and J. Lee, “Demagnetization analysis of permanent magnets according to rotor types of interior permanent magnet synchronous motor,” IEEE Transactions on Magnetics, vol. 45, no. 6, pp. 2799–2802, Jun. 2009. [Google Scholar]

 8.  T. Boileau, N. Leboeuf, B. Nahid-Mobarakeh and F. Meibody-Tabar, “Online identification of PMSM parameters: Parameter identifiability and estimator comparative study,” IEEE Transactions on Industry Applications, vol. 47, no. 4, pp. 1944–1957, Jul. 2011. [Google Scholar]

 9.  K. H. Kim, S. K. Chung, G. W. Moon, I. C. Baik and M. -J. Youn, “Parameter estimation and control for permanent magnet synchronous motor drive using model reference adaptive technique,” in Proc. of IECON ’95-21st Annual Conf. on IEEE Industrial Electronics, Orlando, FL, USA, vol. 1, pp. 387–392, 1995. [Google Scholar]

10. S. Kallio, J. Karttunen, P. Peltoniemi, P. Silventoinen and O. Pyrhönen, “Online estimation of double-star IPM machine parameters using RLS algorithm,” IEEE Transactions on Industrial Electronics, vol. 61, no. 9, pp. 4519–4530, Sep. 2014. [Google Scholar]

11. Y. Shi, K. Sun, L. Huang and Y. Li, “Online identification of permanent magnet flux based on extended Kalman filter for IPMSM drive with position sensorless control,” IEEE Transactions on Industrial Electronics, vol. 59, no. 11, pp. 4169–4178, 2012. [Google Scholar]

12. K. Liu, Q. Zhang, J. Chen, Z. Q. Zhu and J. Zhang, “Online multiparameter estimation of nonsalient-pole PM synchronous machines with temperature variation tracking,” IEEE Transactions on Industrial Electronics, vol. 58, no. 5, pp. 1776–1788, 2011. [Google Scholar]

13. Z. H. Liu, H. L. Wei, Q. C. Zhong, K. Liu and X. -S. Xiao, “Parameter estimation for VSI-fed PMSM based on a dynamic PSO with learning strategies,” IEEE Transactions on Power Electronics, vol. 32, no. 4, pp. 3154–3165, Apr. 2017. [Google Scholar]

14. Z. H. Liu, H. L. Wei, X. H. Li, K. Liu and Q. C. Zhong, “Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO,” IEEE Transactions on Power Electronics, vol. 33, no. 12, pp. 10858–10871, 2018. [Google Scholar]

15. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

16. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

17. W. Yu, H. Liang, X. Dong and Y. Luo, “Modeling and identification of permanent magnet synchronous motor via deterministic learning,” IEEE Access, vol. 8, no. 6, pp. 168516–168525, 2020. [Google Scholar]

18. K. Lam, G. Feng and Y. Han, “Identification of PMSM parameters based on differential evolution algorithm with multiple evolutionary strategies,” in 2021 China Automation Congress (CAC), Beijing, China, pp. 4797–4802, 2021. [Google Scholar]

19. W. Wu, “DC motor identification using speed step responses,” in Proc. of the 2010 American Control Conf., Baltimore, MD, USA, pp. 1937–1941, 2010. [Google Scholar]

20. L. Nikakhtar, S. Zare, H. M. Nasirabad and B. Ferdosi, “Application of ANN-PSO algorithm based on FDM numerical modeling for back analysis of EPB TBM tunneling parameters,” European Journal of Environmental and Civil Engineering, vol. 26, no. 8, pp. 3169–3186, 2020. [Google Scholar]

21. F. Zha, W. Sheng, W. Guo, S. Qiu, J. Deng et al., “Dynamic parameter identification of a lower extremity exoskeleton using RLS-PSO,” Applied Sciences, vol. 9, no. 2, pp. 324–341, 2019. [Google Scholar]

22. J. Chrouta, A. Zaafouri and M. Jemli, “System identification using gray-based adaptive heterogeneous multi-swarm PSO algorithm: Application to an irrigation station,” Journal of Circuits, Systems and Computers, vol. 27, no. 4, pp. 1850059–1850086, 2017. [Google Scholar]

23. H. Yang, J. Li, B. Liu and L. Chen, “Identification of source information for sudden hazardous chemical leakage accidents in surface water on the basis of particle swarm optimisation, differential evolution and metropolis-hastings sampling,” Environmental Science and Pollution Research, vol. 28, no. 47, pp. 67292–67309, 2021. [Google Scholar]

24. S. Patel, T. Eldho and A. Rastogi, “Hybrid-metaheuristics based inverse groundwater modelling to estimate hydraulic conductivity in a nonlinear real-field large aquifer system,” Water Resources Management, vol. 34, no. 6, pp. 2011–2028, 2020. [Google Scholar]

25. B. Pourasghar, M. A. Ahandani and H. Kharrati, “Parameter identification of engineering problems using a differential shuffled complex evolution,” Artificial Intelligence Review, vol. 53, no. 4, pp. 2749–2782, 2020. [Google Scholar]

26. T. Sebastian, G. Slemon and M. Rahman, “Modelling of permanent magnet synchronous motors,” IEEE Transactions on Magnetics, vol. 22, no. 5, pp. 1069–1071, 2015. [Google Scholar]

27. J. Y. Lee, S. H. Lee, G. H. Lee, J. P. Hong and J. Hur, “Determination of parameters considering magnetic nonlinearity in an interior permanent magnet synchronous motor,” IEEE Transactions on Magnetics, vol. 42, no. 4, pp. 1303–1306, Apr. 2006. [Google Scholar]

28. F. Fernandez-Bernal, A. Garcia-Cerrada and R. Faure, “Determination of parameters in interior permanent-magnet synchronous motors with iron losses without torque measurement,” IEEE Transactions on Industry Applications, vol. 37, no. 5, pp. 1265–1272, Sep. 2001. [Google Scholar]

29. R. Storn and K. Price, “Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, no. 4, pp. 341–359, Dec. 1997. [Google Scholar]

30. P. Civicioglu, E. Besdok, M. A. Gunen and U. H. Atasever, “Weighted differential evolution algorithm for numerical function optimization: A comparative study with cuckoo search, artificial bee colony, adaptive differential evolution, and backtracking search optimization algorithms,” Neural Computing and Applications, vol. 32, no. 8, pp. 3923–3937, Apr. 2020. [Google Scholar]

31. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN’95-Int. Conf. on Neural Networks, Perth, WA, Australia, vol. 4, pp. 1942–1948, 1995. [Google Scholar]