Submit

Login Login

Register Register

Home/ Journals/ CMC/ Vol.74, No.2, 2023/ 10.32604/cmc.2023.033352

Table of Content

iconOpen Access

ARTICLE

crossmark

Stochastic Computational Heuristic for the Fractional Biological Model Based on Leptospirosis

Zulqurnain Sabir1, Sánchez-Chero Manuel2, Muhammad Asif Zahoor Raja3, Gilder-Cieza–Altamirano4, María-Verónica Seminario-Morales2, Fernández Vásquez José Arquímedes5, Purihuamán Leonardo Celso Nazario6, Thongchai Botmart7,*, Wajaree Weera7

1 Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
2 Universidad Nacional de Frontera, Sullana, Piura, Perú
3 Future Technology Research Center, National Yunlin University of Science and Technology, 123 University Road, Section 3, Douliou, 64002, Yunlin, Taiwan
4 Universidad Nacional Autónoma de Chota, Cajamarca, Perú
5 Universidad Cesar Vallejo, Trujillo, La Libertad, Perú
6 Universidad Señor de Sipán, Chiclayo, Perú
7 Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand

* Corresponding Author: Thongchai Botmart. Email: email

Computers, Materials & Continua 2023, 74(2), 3455-3470. https://doi.org/10.32604/cmc.2023.033352

Received 14 June 2022; Accepted 16 August 2022; Issue published 31 October 2022

Abstract

The purpose of these investigations is to find the numerical outcomes of the fractional kind of biological system based on Leptospirosis by exploiting the strength of artificial neural networks aided by scale conjugate gradient, called ANNs-SCG. The fractional derivatives have been applied to get more reliable performances of the system. The mathematical form of the biological Leptospirosis system is divided into five categories, and the numerical performances of each model class will be provided by using the ANNs-SCG. The exactness of the ANNs-SCG is performed using the comparison of the reference and obtained results. The reference solutions have been obtained by using the Adams numerical scheme. For these investigations, the data selection is performed at 82% for training, while the statics for both testing and authentication is selected as 9%. The procedures based on the recurrence, mean square error, error histograms, regression, state transitions, and correlation will be accomplished to validate the fitness, accuracy, and reliability of the ANNs-SCG scheme.

Keywords

1  Introduction

The spreading virus ratio creates several diseases in the population with high or low rates [1]. A few of the mentioned diseases in the world that have been created through the viruses are Dengue, Hantavirus and Leptospirosis. The transmittable viruses from one to individual another are known as infectious diseases, while those viruses generated due to the atmospheres are called noninfectious [2]. The famous Leptospirosis is a bacterial virus, mostly found in animals, but occasionally in humans [3]. Leptospirosis is a spreading virus that originated through the soil or water based on the urine of the host animal [4]. Leptospirosis affects humans with a low ratio by using dirty or muddy water, [5–7] and it affects a high ratio when an individual gets a cut in the water [8].

The mathematical modeling provides the basic operators using the good policies of minimizing or eliminating Leptospirosis and predicting its future occurrences [9,10]. There are various differential mathematical systems, that have been performed on population dynamics based on humans and rats. Kongnuy [11] proposed the spreading dynamics based on Leptospirosis using the mathematical formulation between the vector population and humans. Leptospirosis can be controlled by decreasing the transmission ratio (infected to susceptible) in humans. Khan et al. [12] proposed the performance of Leptospirosis from the drenched existence with the disposed population and condensed through the functioning conduct. The system simulations based on the infection ratio are 0.83 reducing Leptospirosis’s spreading ratio. Other severe and deathly transmittable viruses have been reported in [13–19].

Newton proposed fractional calculus many years ago, but it obtained enormous fame and significance in recent years. Over the last thirty years, fractional calculus has been widely used in industrial areas. The idea of the fractional order derivative has been modernized through the complexities connected to the typical inhomogeneity. The multilayered media construction based on the diffusion procedure is reported using the operators based on the fractional calculus. A significant apparatus presents the precise performance using the ordinary differential form of the systems. There is a wider range of complicated phenomena that have been proposed by many researchers based on the software models. There are various fractional/integer kinds of schemes reported in [20–26]. Fractional calculus has been studied by various researchers based on the integer kind of calculus using the mathematical form of real-world applications. A new perception of the fractional kind of derivative based on the control scheme of dengue infection has been emphasized efficiently in [27]. The simulations using the analytical/numerical schemes based on the mathematical systems indicate a significant character in describing the formulations of the systems [28–37].

These investigations aim to authenticate the numerical outcomes based on the fractional kind of biological system based on Leptospirosis by exploiting the strength of artificial neural networks (ANNs) aided by scale conjugate gradient (SCG), called ANNs-SCG. The derivatives based on the fractional order have been used to achieve precise mathematical performances. Moreover, the stochastic numerical computing performances based on the ANNs-SCG procedure for the mathematical form based on the biological Leptospirosis model have not been presented before in terms of the fractional form. The solution of this novel fraction order model will be presented first by using the stochastic ANNs-SCG scheme. The stochastic numerical performances have been applied to solve the corneal shape of model [38], human immunodeficiency virus (HIV) system [39], plant virus propagation model [40], coronavirus mathematical model [41], travelling wave solution-based new Riccati equation [42], solar energy model [43], Schrödinger equation [44], dusty plasma model [45] and relation extraction [46,47]. These applications enhance the motivations and inspirations for the authors to perform the exhaustive frameworks in the field of artificial intelligence (AI) through the stochastic computational structure to provide a substitute, stable, precise, robust, and accurate solutions to the mathematical form of the biological Leptospirosis model.

The remaining structure of the paper is given as follows: Section 2 presents the formulation of the fractional Leptospirosis system, Section shows the methodology of the stochastic ANNs-SCG scheme, Section 4 describes the simulations together with some important findings, while the last Section 5 presents the concluding remarks.

2  Fractional Kind of Leptospirosis System

The mathematical kind of the biological Leptospirosis system is divided into five categories (Human and vector). The Susceptible-Infected-Recovered (SIR) population dynamics based on the vector (rat) and human population are shown as [48]:

{dSh(τ)dτ=A−μhSh(τ)+θhRh(τ)−βhSh(τ)Ir(τ),(Sh)0=a1,dIh(τ)dτ=βhSh(τ)Ir(τ)−(δh+rh+μh)Ih(τ),(Ih)0=a2,dRh(τ)dτ=rhIh(τ)−(μh+θh)Rh(τ),(Rh)0=a3,dSr(τ)dτ=−βrSr(τ)Ih(τ)−rrSr(τ)+B,(Sr)0=a4,dIr(τ)dτ=−(δr+rr)Ir(τ)+βrSr(τ)Ih(τ),(Ir)0=a5,(1)

The integer kind of differential Leptospirosis system is presented in Eq. (1). The comprehensive details of the biological model based on Leptospirosis are given in Tab. 1.

images

The current work provides the numerical representations of the mathematical model based on Leptospirosis using artificial intelligence (AI) together through the artificial neural networks (ANNs) along with the scale conjugate gradient (SCG), i.e., ANNs-SCG. As a result, the mathematical model based on Leptospirosis is presented as follows:

{dυSh(τ)dτυ=A−μhSh(τ)+θhRh(τ)−βhSh(τ)Ir(τ),(Sh)0=a1,dυIh(τ)dτυ=βhSh(τ)Ir(τ)−(δh+rh+μh)Ih(τ),(Ih)0=a2,dυRh(τ)dτυ=rhIh(τ)−(μh+θh)Rh(τ),(Rh)0=a3,dυSr(τ)dτυ=−βrSr(τ)Ih(τ)−rrSr(τ)+B,(Sr)0=a4,dυIr(τ)dτυ=−(δr+rr)Ir(τ)+βrSr(τ)Ih(τ),(Ir)0=a5,(2)

where υ represents the fractional kind of Caputo derivative mathematical form of Leptospirosis, and the fraction order values have been chosen between [0, 1]. The fractional kinds of the derivatives in the mathematical form of the Leptospirosis shown in Eq. (2) to perform the minute’s specifications, i.e., superslow growth as well as superfast performances, which is hard to estimate from the integer kind provided in Eq. (1). Few novels feature to solve the fractional kind of mathematical model based on the Leptospirosis system are presented as:

•   The fractional derivatives provide more reliable performances of the mathematical Leptospirosis system.

•   The design of the stochastic ANNs-SCG is provided for the numerical investigations of the fractional kind of mathematical model based on Leptospirosis.

•   Three different variants of the fraction order have been used to perform the numerical simulations of the fractional kind of mathematical model based on Leptospirosis.

•   The correctness of the stochastic ANNs-SCG scheme is performed to compare the obtained results based on the ANNs-SCG and the reference solutions.

•   The excellence of the stochastic ANNs-SCG scheme is approved through the obtained negligible absolute error magnitude based fractional kind of mathematical Leptospirosis system.

•   The recurrence, mean square error, error histograms, regression, state transitions, and correlation supports the reliability of the ANNs-SCG scheme using the fractional kind of mathematical model based on Leptospirosis.

3  Proposed ANNs-SCG Scheme

The current section provides the stochastic artificial neural networks (ANNs) along with the scale conjugate gradient (SCG), i.e., ANNs-SCG scheme, along with the numerical results procedures to achieve the fractional kind of mathematical model based on the Leptospirosis as shown in Eq. (1). Fig. 1 represents the workflow depictions of the fractional kind of mathematical model based on the Leptospirosis using the ANNs-SCG based three blocks, methodology and obtained solutions.

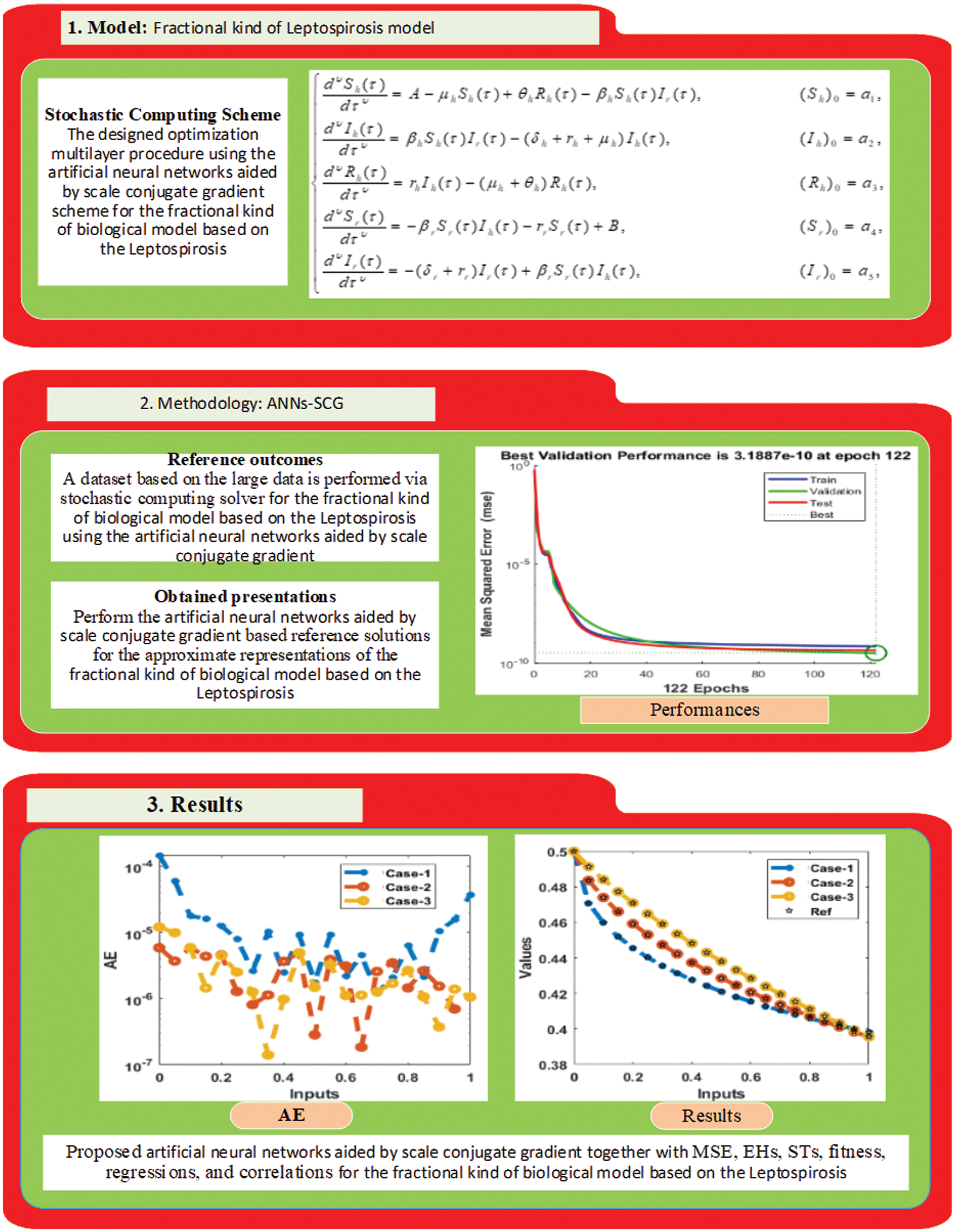
images

Figure 1: Workflow depictions of the stochastic scheme for the fractional kind of mathematical model based on the Leptospirosis

The computational ANNs-SCG scheme is provided in two steps: the system dataset is generated using the generalized Adams scheme and the significant operators to execute the estimated results of the fractional kind of mathematical model based on the Leptospirosis using the ANNs-SCG. The essential information based on the generalized Adam method can be observed in the reported investigation [48], whereas these numerical performances with default conditions perform the system dataset for different disparities. The statics performances are provided by taking 14 numbers of neurons together with the data is selected as 82% for training and the statics for both testing, and authentication is selected as 9% for the fractional kind of mathematical model based on the Leptospirosis using the ANNs-SCG.

The approximate numerical performances of the mathematical model of Leptospirosis with the artificial intelligence abilities based on the computing framework using the supervised neural networks trained with the scaled conjugate gradient in terms of best negotiation between the measures, including the complexity, premature convergence, underfitting, and overfitting situations.

Moreover, all the network parameters are adjusted after comprehensive simulation investigations, knowledge, care, experience, and minor dissimilarities in these situations to degrade the network’s performance.

4  Analysis and Simulations of Results

This section provides three cases-based fraction Leptospirosis systems through the artificial neural networks (ANNs) along with the scale conjugate gradient (SCG), i.e., ANNs-SCG. The mathematical representation of each case (C) is provided as:

C-1: Suppose the mathematical form of the fractional Leptospirosis model is written as:

{d0.6Sh(τ)dτ0.6=0.0067Rh(τ)+1.6−0.0098Ir(τ)Sh(τ)−0.03Sh(τ),(Sh)0=0.05,d0.6Ih(τ)dτ0.6=0.0098Ir(τ)Sh(τ)−0.0411Ih(τ),(Ih)0=0.1,d0.6Rh(τ)dτ0.6=0.007Ih(τ)−0.0407Rh(τ),(Rh)0=0.15,d0.6Sr(τ)dτ0.6=−0.078Ih(τ)Sr(τ)+1.2−0.17Sr(τ),(Sr)0=0.2,d0.6Ir(τ)dτ0.6=0.078Ih(τ)Sr(τ)−0.264Ir(τ),(Ir)0=0.25.(3)

C-2: Suppose the mathematical form of the fractional Leptospirosis model is written as:

{d0.7Sh(τ)dτ0.7=0.0067Rh(τ)+1.6−0.0098Ir(τ)Sh(τ)−0.03Sh(τ),(Sh)0=0.05,d0.7Ih(τ)dτ0.7=0.0098Ir(τ)Sh(τ)−0.0411Ih(τ),(Ih)0=0.1,d0.7Rh(τ)dτ0.7=0.007Ih(τ)−0.0407Rh(τ),(Rh)0=0.15,d0.7Sr(τ)dτ0.7=−0.078Ih(τ)Sr(τ)+1.2−0.17Sr(τ),(Sr)0=0.2,d0.7Ir(τ)dτ0.7=0.078Ih(τ)Sr(τ)−0.264Ir(τ),(Ir)0=0.25.(4)

C-3: Suppose the mathematical form of the fractional Leptospirosis model is written as:

{d0.8Sh(τ)dτ0.8=0.0067Rh(τ)+1.6−0.0098Ir(τ)Sh(τ)−0.03Sh(τ),(Sh)0=0.05,d0.8Ih(τ)dτ0.8=0.0098Ir(τ)Sh(τ)−0.0411Ih(τ),(Ih)0=0.1,d0.8Rh(τ)dτ0.8=0.007Ih(τ)−0.0407Rh(τ),(Rh)0=0.15,d0.8Sr(τ)dτ0.8=−0.078Ih(τ)Sr(τ)+1.2−0.17Sr(τ),(Sr)0=0.2,d0.8Ir(τ)dτ0.8=0.078Ih(τ)Sr(τ)−0.264Ir(τ),(Ir)0=0.25.(5)

The simulations of the fractional kind of mathematical model based on Leptospirosis using the computational ANNs-SCG approach have been provided by taking 14 numbers of neurons. Fig. 2 shows the stochastic ANNs-SCG scheme of the fractional kind of mathematical model based on Leptospirosis.

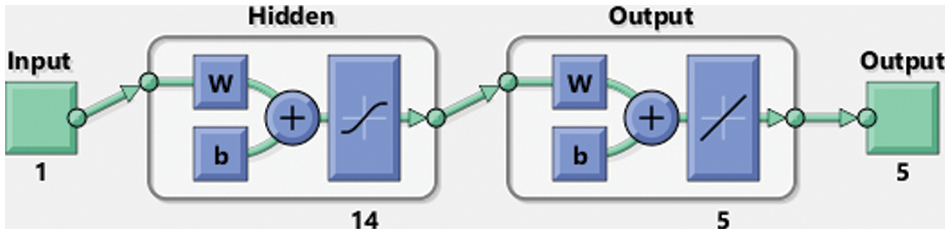
images

Figure 2: Stochastic ANNs-SCG scheme for the fractional Leptospirosis system

The fractional kind of mathematical Leptospirosis system simulations using the computational ANNs-SCG approach has been provided by taking 14 numbers of neurons together with data selection as 82% for training, and the statics for both testing and authentication is selected as 9%. Fig. 2 shows the stochastic ANNs-SCG scheme of the fractional kind of mathematical model based on Leptospirosis.

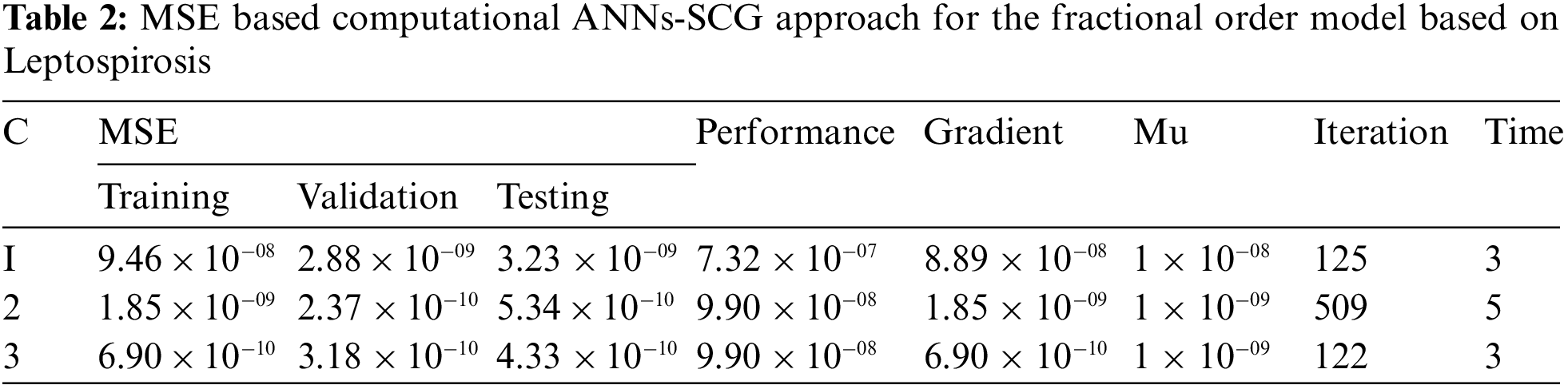
Figs. 3–5 represent the numerical outcomes of the fractional Leptospirosis system by using the stochastic ANNs-SCG scheme. Figs. 3 and 4 indicate the mean square error (MSE) values and state transitions (STs) measures based on the fractional kind of mathematical Leptospirosis system. The best calculations for the fractional kind of Leptospirosis model were performed at epochs 125, 509, and 122, which were performed as 9.46227 × 10−08, 1.85270 × 10−09, and 6.90443 × 10−10. The gradient representations are performed as 7.32 × 10−07, 9.90 × 10−08, and 9.92 × 10−08 for the respective cases of the fractional order model based on Leptospirosis. Fig. 4 presents the obtained results and the performances error histograms for solving the fractional mathematical model based on Leptospirosis using the stochastic ANNs-SCG scheme. The obtained best representations based on the training, authentication, and testing outcomes of the fractional order model based on Leptospirosis using the ANNs-SCG scheme have been provided. The EHs performances have also been provided in Fig. 4 which shows the values for C-1, 2 and 3 are 1.51 × 10−04, 9.33 × 10−06, and 3.09 × 10−06. Fig. 5 provides the values of the correlations by using the computational numerical ANNs-SCG approach-based fractional Leptospirosis system. It is depicted that the correlation values perform the perfect model due to 1 in the calculation for the fractional Leptospirosis system. The accuracy of the computational numerical ANNs-SCG approach for the fractional order model based on Leptospirosis is provided based on the substantiation, testing, and training measures. Tab. 2 shows the MSE values based on the fractional kind of model of Leptospirosis by using the computational ANNs-SCG approach.

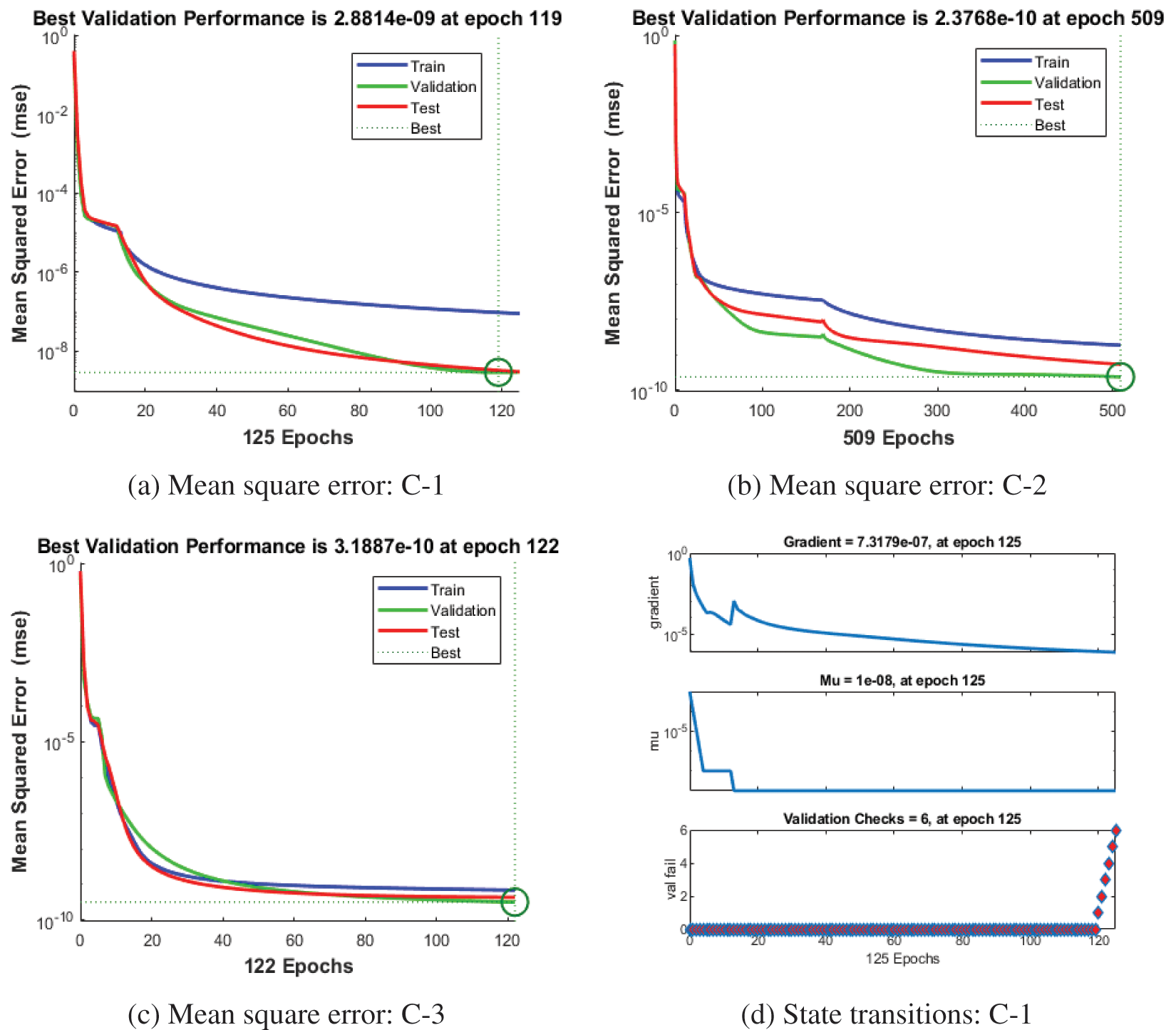
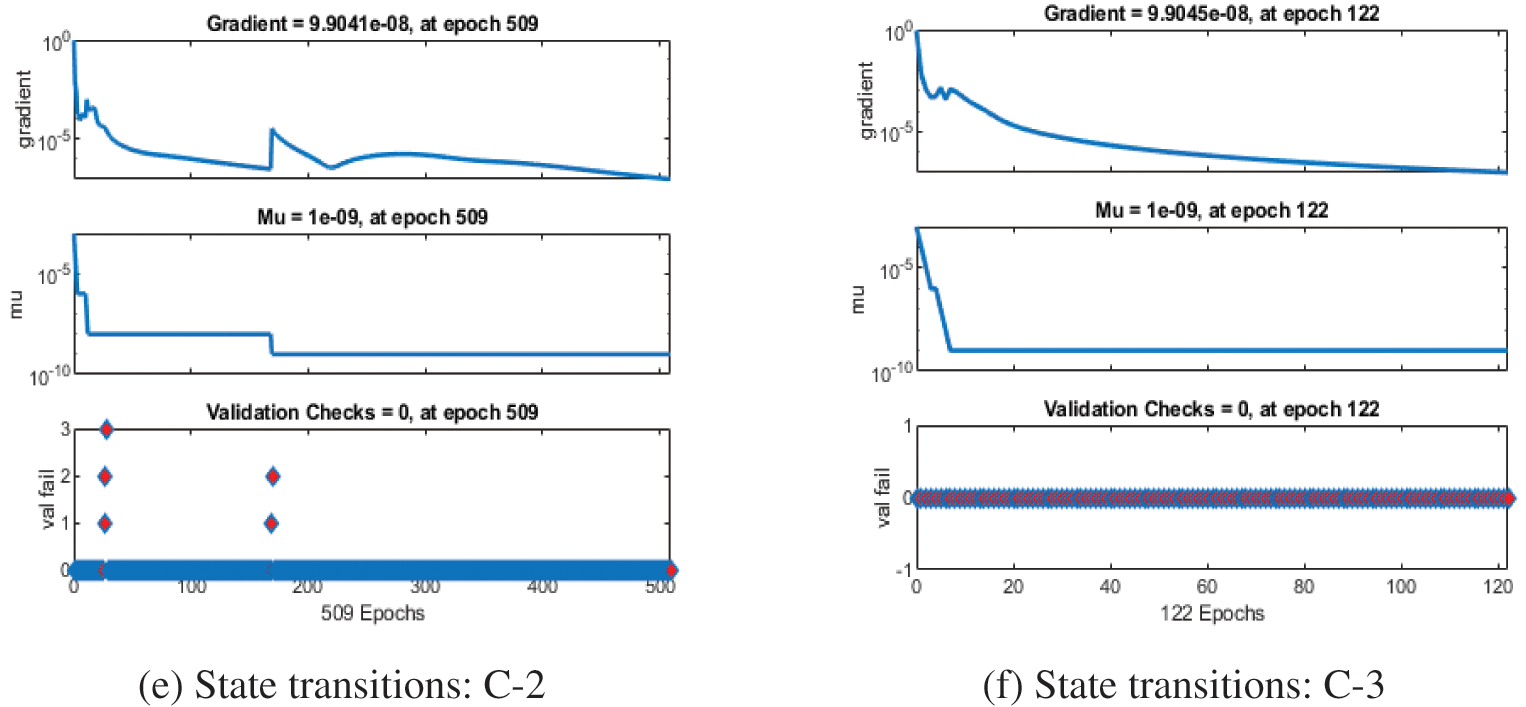
imagesimages

Figure 3: Mean square error measures and State transition performances values based on fractional kind of Leptospirosis system

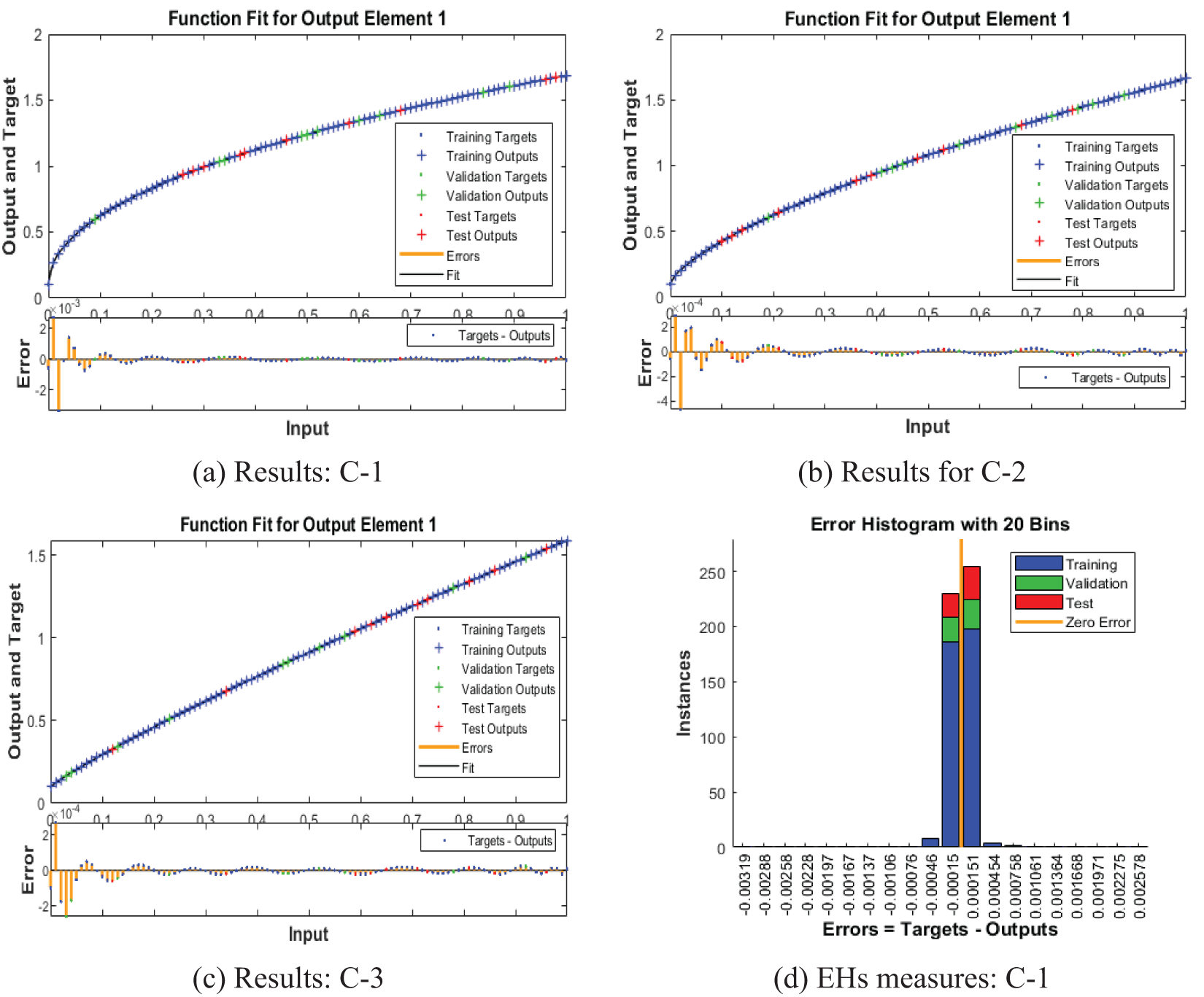
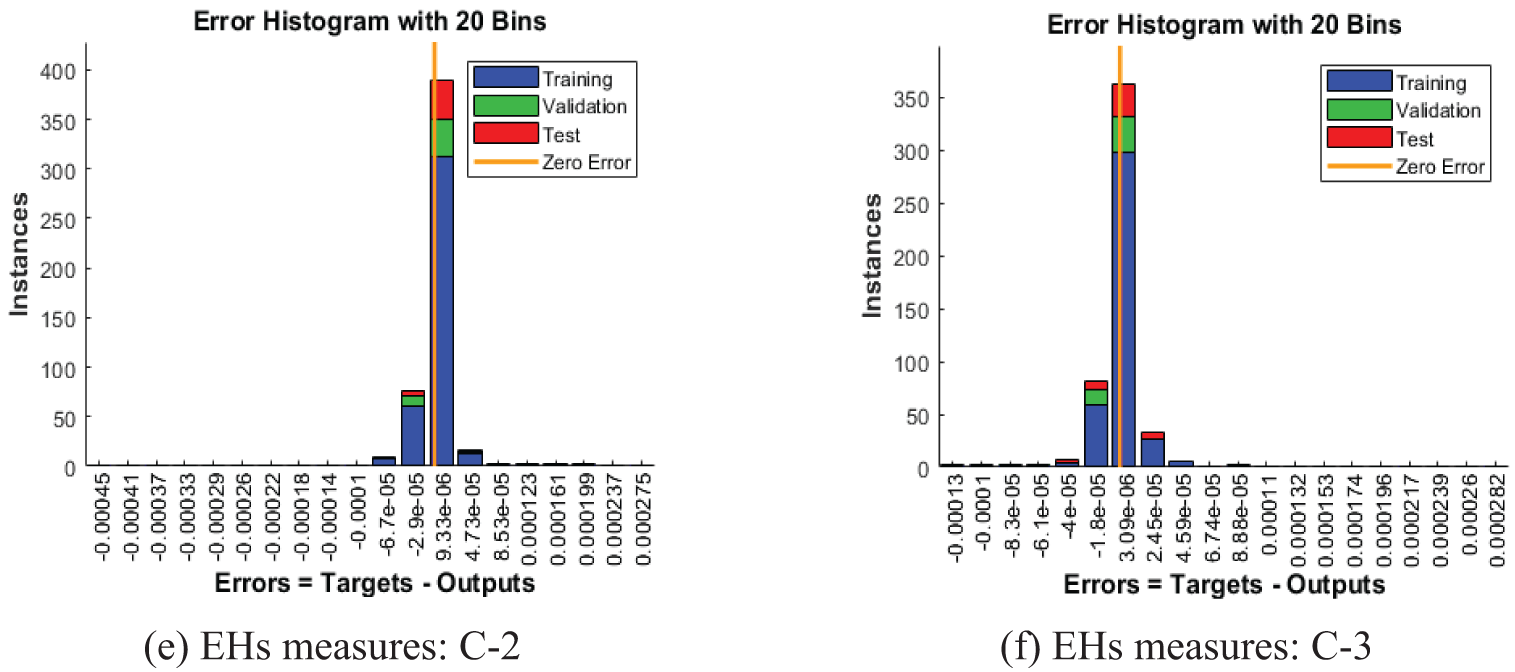
imagesimages

Figure 4: Assessments of the solutions and error histograms measures based on fractional kind of Leptospirosis system

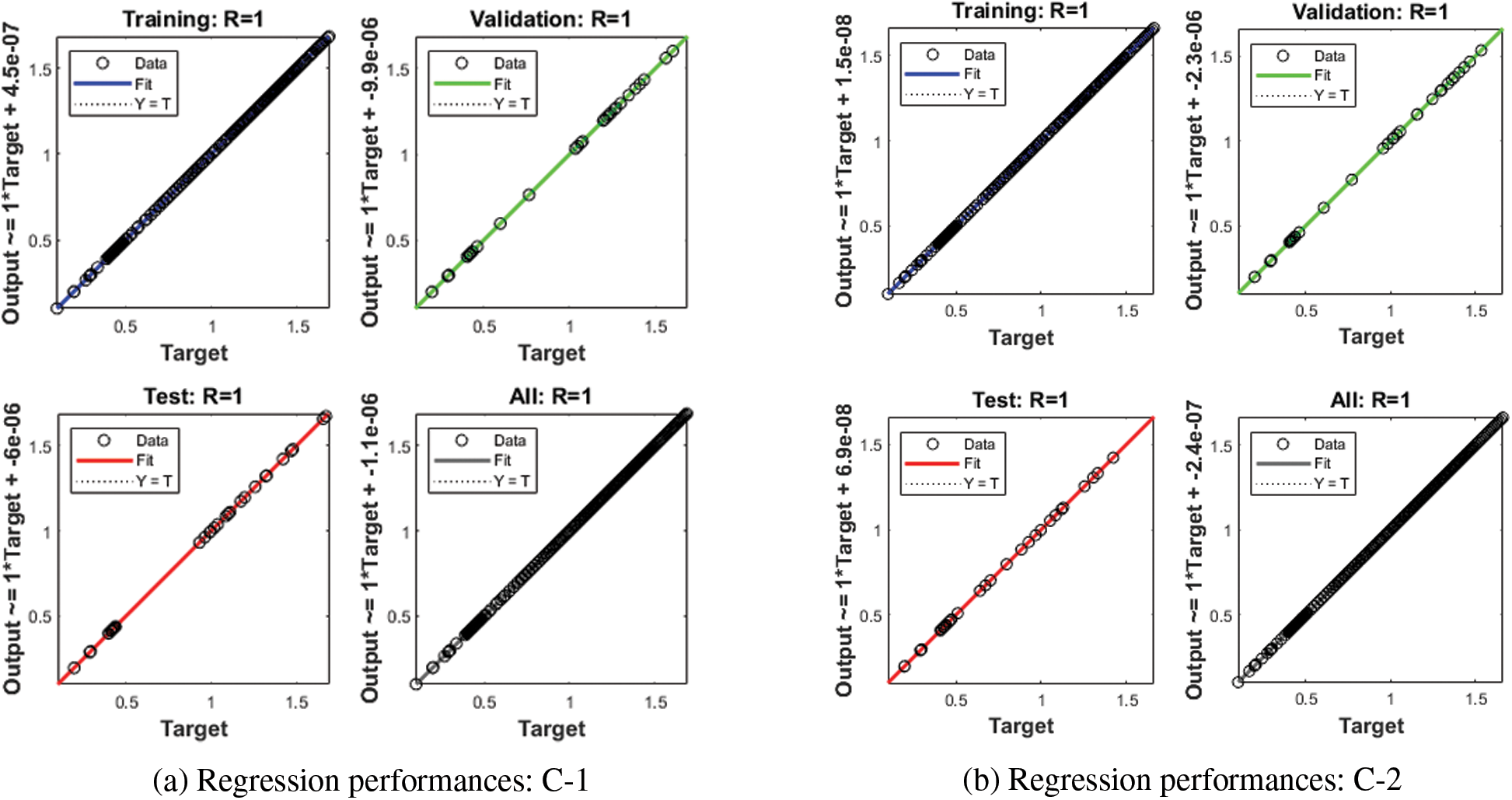
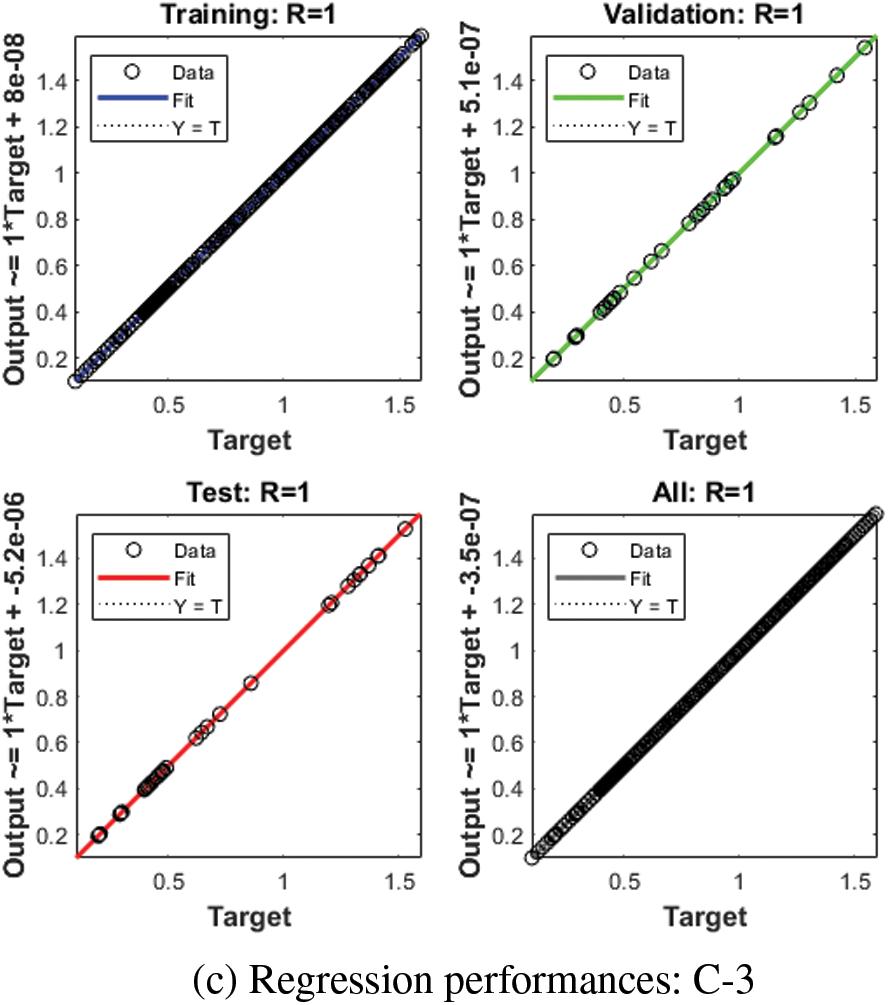
imagesimages

Figure 5: Regression performances based on fractional kind of Leptospirosis

images

The result comparisons and the values of the AE are performed in Figs. 6 and 7 using the artificial neural networks (ANNs) along with the scale conjugate gradient (SCG), i.e., ANNs-SCG algorithms for the fractional order model based on Leptospirosis. The achieved performances have been performed through the stochastic ANNs-SCG approach for the fractional order model based on Leptospirosis. Fig. 6 presents the results overlapping through the obtained performances based on the stochastic ANNs-SCG approach and reference solutions. These depictions perform the correctness and accuracy of the ANNs-SCG procedure for the fractional kind of system based on Leptospirosis. Fig. 7 depicts the AE descriptions for the fractional kind of model based on the Leptospirosis stochastic ANNs-SCG procedure. The AE measures for the category Sh(τ) have been performed around 10−03–10−05, 10−04–10−05 and 10−05–10−06. For Ih(τ), the AE values for C (1–3) have been performed as 10−04–10−06, 10−05–10−06 and 10−05–10−07. For Rh(τ), the AE measures have been reported as 10−04–10−05, 10−05–10−06 and 10−06–10−08 for C (1–3). For the fractional kind of system based on Leptospirosis, the AE for Sr(τ) is reported as 10−03–10−05, 10−04–10−06 and 10−05–10−06. For C (1–3), the AE for Ir(τ) is found as 10−04–10−06, 10−05–10−06 and 10−05–10−07. These best measures calculated through the AE perform the exactness of the stochastic ANNs-SCG procedure for the fractional kind of model based on Leptospirosis.

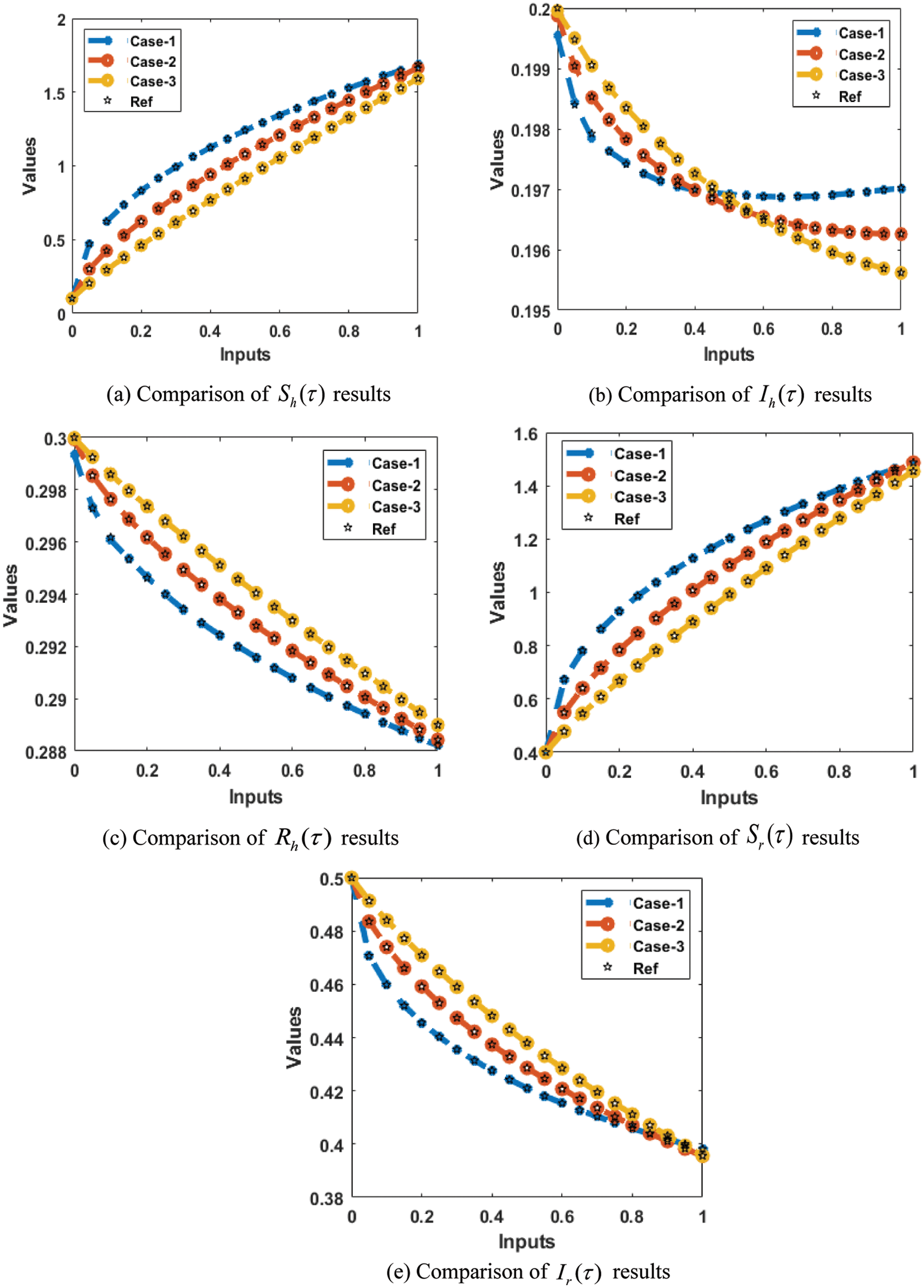
images

Figure 6: Comparison of the results using the stochastic procedure for the fractional kind of model based on Leptospirosis

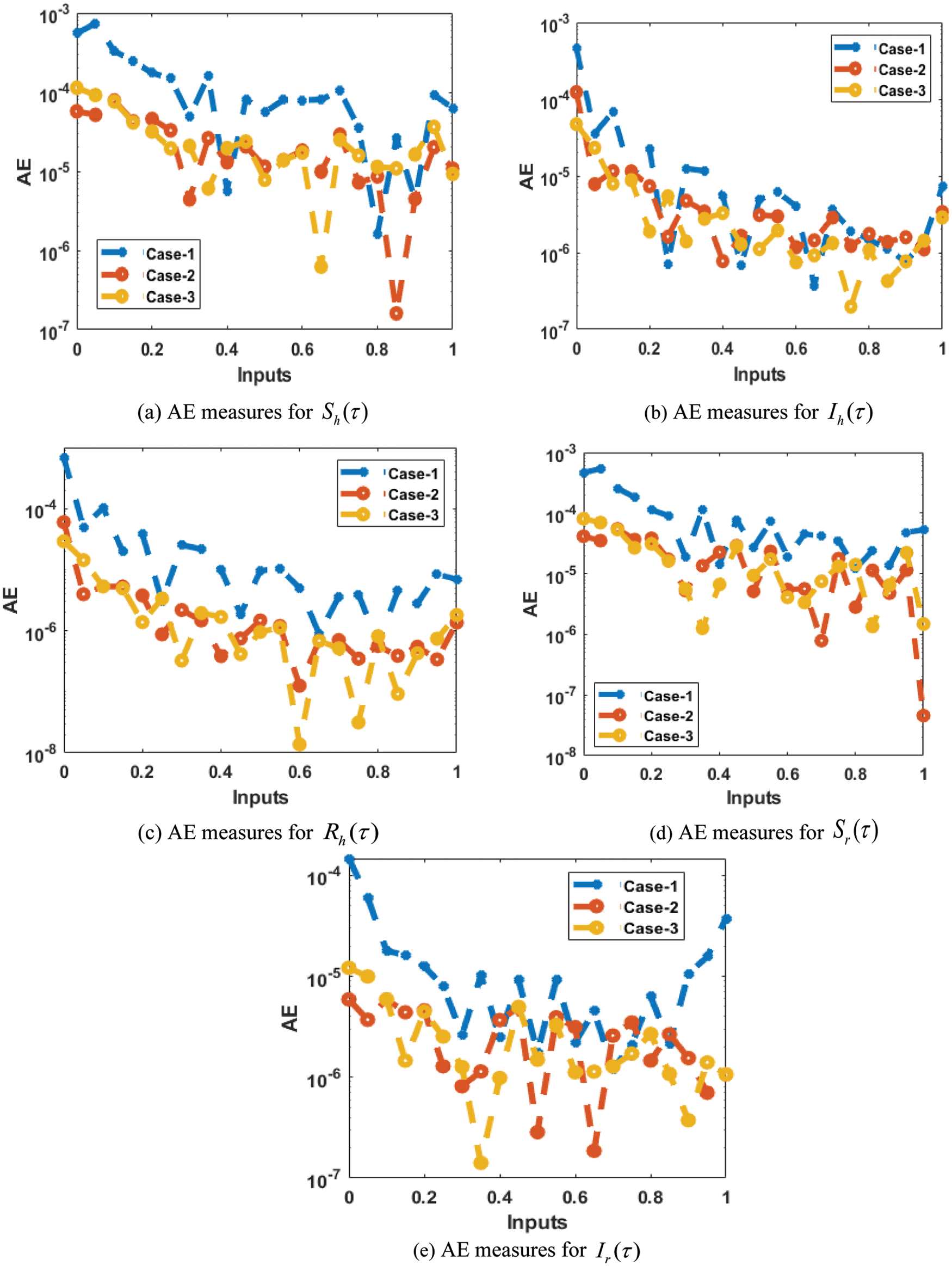
images

Figure 7: Values of the absolute error using the stochastic procedure for the fractional kind of model based on Leptospirosis

5  Conclusion

In this work, the solutions of the fractional kind of biological model based on Leptospirosis have been provided by exploiting the strength of artificial neural networks aided by the scaled conjugate gradient. The reliable and accurate results of the model have been achieved by using fractional kinds of derivatives. The biological Leptospirosis mathematical form is categorized into five classes. The numerical performances of each category of the biological Leptospirosis mathematical model have been presented through the stochastic artificial neural networks (ANNs) along with the scale conjugate gradient (SCG), i.e., the ANNs-SCG procedure. The correctness of the computing ANNs-SCG procedure is performed by comparing the achieved and reference solutions (Adam numerical method). The simulations of the fractional kind of mathematical model based on Leptospirosis using the computational ANNs-SCG approach have been provided by taking 14 numbers of neurons together with the selection of the data as 82% for training. At the same time the statics for both testing and authentication is selected as 9%. The AE has been calculated for the respective cases of the fractional kind of system are found as 10−06 to 10−08. The numerical procedures based on the recurrence, error histograms, regression, mean square error, state transitions, and correlation have been accomplished to validate the fitness, capability, accuracy, steadiness and reliability of the proposed ANNs-SCG method.

In upcoming work, the proposed ANNs-SCG numerical procedure can be implemented to solve different applications of extreme interest to researchers [49–52].

Funding Statement: This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. D. R. Bellwood, T. P. Hughes, C. Folke and M. Nyström, “Confronting the coral reef crisis,” Nature, vol. 429, pp. 827–833, 2004.
  2. J. O. Zavaleta and P. A. Rossignol, “Community-level analysis of risk of vector-borne disease,” Transactions of the Royal Society of Tropical Medicine and Hygiene, vol. 98, no. 10, pp. 610–618, 2004.
  3. S. Thayaparan, I. D. Robertson, A. Fairuz, L. Suut and M. T. Abdullah, “Leptospirosis, an emerging zoonotic disease in Malaysia,” Malaysian Journal of Pathology, vol. 35, no. 2, pp. 123–132, 201
  4. J. K. Lim, V. A. Murugaiyah, A. S. Ramli, H. A. Rahman, N. S. F. Mohamed et al., “A case study: Leptospirosis in Malaysia,” WebmedCentral Infectious Diseases, vol. 2, no. 12, pp. 2764, 2011.
  5. M. El-Shahed, “Fractional order model for the spread of leptospirosis,” International Journal of Mathematical Analysis, vol. 8, no. 54, pp. 2651–2667, 2014.
  6. W. Triampo, D. Baowan, I. M. Tang, N. Nuttavut, J. Wong-Ekkabut et al., “A simple deterministic model for the spread of leptospirosis in Thailand,” International Journal of Biological and Medical Sciences, vol. 2, pp. 22–26, 2007.
  7. S. H. Goh, R. Ismail, S. F. Lau, P. A. Megat Abdul Rani and T. B. Mohd Mohidin, “Risk factors and prediction of Leptospiral seropositivity among dogs and dog handlers in Malaysia,” International Journal of Environmental Research and Public Health, vol. 16, no. 9, pp. 1–11, 2019.
  8. A. Bhalraj and A. Azmi, “Mathematical modelling of the spread of Leptospirosis,” AIP Conference Proceedings, vol. 2184, no. 1, pp. 1–10, 2019.
  9. N. Sweilam, O. M. Saad and D. Mohamed, “Fractional optimal control in transmission dynamics of West Nile virus model with state and control time delay: A numerical approach,” Advances in Difference Equations, vol. 2019, no. 1, pp. 1–25, 201
  10. M. F. Khan, H. Alrabaiah, S. Ullah, M. A. Khan, M. Farooq et al., “A new fractional model for vector-host disease with saturated treatment function via singular and non-singular operators,” Alexandria Engineering Journal, vol. 60, no. 1, pp. 629–645, 2021.
  11. R. Kongnuy, “Local stability of equilibria: Leptospirosis,” International Journal of Mathematical and Computational Sciences, vol. 6, no. 6, pp. 625–629, 2012.
  12. M. A. Khan, S. F. Saddiq, S. Islam, I. Khan and S. Shafie, “Dynamic behavior of leptospirosis disease with saturated incidence rate,” International Journal of Applied and Computational Mathematics, vol. 2, no. 4, pp. 435–452, 2016.
  13. S. Luemsai and T. Botmart, “Improved extended dissipativity results for T-S fuzzy generalized neural networks with mixed interval time-varying delays,” IEEE Access, vol. 10, pp. 2480–2496, 2022.
  14. H. W. Berhe, S. Qureshi and A. A. Shaikh, “Deterministic modelling of dysentery diarrhea epidemic under fractional caputo differential operator via real statistical analysis,” Chaos, Solitons & Fractals, vol. 131, pp. 109536, 2020.
  15. Y. G. Sánchez, Z. Sabir and J. L. Guirao, “Design of a nonlinear SITR fractal model based on the dynamics of a novel coronavirus (COVID-19),” Fractals, vol. 28, no. 8, pp. 1–6, 2020.
  16. M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, pp. 1–9, 2020.
  17. W. Gao and H. M. Baskonus, “Deeper investigation of modified epidemiological computer virus model containing the caputo operator,” Chaos, Solitons & Fractals, vol. 158, pp. 112050, 2022.
  18. H. M. Baskonus and W. Gao, “Investigation of optical solitons to the nonlinear complex Kundu–Eckhaus and Zakharov–Kuznetsov–Benjamin–Bona–Mahony equations in conformable,” Optical and Quantum Electronics, vol. 54, no. 6, pp. 1–23, 2022.
  19. M. A. Khan, O. Kolebaje, A. Yildirim, S. Ullah, P. Kumam et al., “Fractional investigations of zoonotic visceral leishmaniasis disease with singular and non-singular kernel,” The European Physical Journal Plus, vol. 134, no. 10, pp. 1–29, 20
  20. B. Riemann, “Versuch einer allgemeinen Auffassung der integration und differentiation,” in Bernard Riemann’s Gesammelte Mathematische Werke und Wissenschaftlicher Nachlass, 1st ed., Cambridge, UK: Cambridge University Press, pp. 331–334, 1847.
  21. J. Liouville, “Memoire surquelques questions de geometrieet de mecanique, et sur un nouveau genre de calcul pour resoudreces questions,” Journal de L’école Polytechnique, vol. 13, pp. 1–69, 1832.
  22. M. Caputo, Elasticita e Dissipazione. 1st ed., Bologna, Italy: Zanichelli, pp. 1–300, 1969.
  23. K. S. Miller and B. Ross, An Introduction to Fractional Calculus and Fractional Differential Equations. 1st ed., New York, USA: A Wiley-Interscience, pp. 1–376, 1993.
  24. A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations. 1st ed., vol. 204. Amsterdam, Netherlands: Elsevier, pp. 1–540, 2006.
  25. I. Podlubny, Fractional Differential Equations. 1st ed., New York, USA: Academic Press, pp. 1–366, 1999.
  26. E. Ilhan, P. Veeresha and H. M. Baskonus, “Fractional approach for a mathematical model of atmospheric dynamics of CO2 gas with an efficient method,” Chaos, Solitons & Fractals, vol. 152, pp. 111347, 2021.
  27. A. Jajarmi, B. Ghanbari and D. Baleanu, “A new and efficient numerical method for the fractional modeling and optimal control of diabetes and tuberculosis co-existence,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 29, no. 9, pp. 1–15, 2019.
  28. R. F. Dashen, B. Hasslacher and A. Neveu, “Particle spectrum in model field theories from semiclassical functional integral techniques,” Physical Review D, vol. 11, no. 12, pp. 3424–3450, 1975.
  29. T. A. Sulaiman, H. Bulut and H. M. Baskonus, “Optical solitons to the fractional perturbed NLSE in nano-fibers,” Discrete & Continuous Dynamical Systems-S, vol. 13, no. 3, pp. 925–936, 2020.
  30. G. Yel, C. Cattani, H. M. Baskonus and W. Gao, “On the complex simulations with dark–bright to the Hirota–Maccari system,” Journal of Computational and Nonlinear Dynamics, vol. 16, no. 6, pp. 1–9, 2021.
  31. J. Singh, D. Kumar and R. Swroop, “Numerical solution of time-and space-fractional coupled Burgers’ equations via homotopy algorithm,” Alexandria Engineering Journal, vol. 55, no. 2, pp. 1753–1763, 2016.
  32. H. M. Srivastava, D. Kumar and J. Singh, “An efficient analytical technique for fractional model of vibration equation,” Applied Mathematical Modelling, vol. 45, pp. 192–204, 2017.
  33. M. A. El-Tawil and S. N. Huseen, “The q-homotopy analysis method (q-HAM),” The International Journal of Applied Mathematics and Mechanics, vol. 8, no. 15, pp. 51–75, 2012.
  34. P. Veeresha, D. G. Prakasha and H. M. Baskonus, “Novel simulations to the time-fractional Fisher’s equation,” Mathematical Sciences, vol. 13, no. 1, pp. 33–42, 2019.
  35. M. Umar, F. Amin, Q. Al-Mdallal and M. R. Ali, “A stochastic computing procedure to solve the dynamics of prevention in HIV system,” Biomedical Signal Processing and Control, vol. 78, pp.103888, 2022.
  36. D. Rani and V. Mishra, “Solving linear fractional order differential equations by Chebyshev polynomials based numerical inverse Laplace transform,” Mathematics in Engineering, Science & Aerospace (MESA), vol. 10, no. 4, pp. 781–791, 2019.
  37. M. Hajipour, A. Jajarmi, A. Malek and D. Baleanu, “Positivity-preserving sixth-order implicit finitedifference weighted essentially non-oscillatory scheme for the nonlinear heat equation,” Applied Mathematics and Computation, vol. 325, pp. 146–158, 2018.
  38. M. Umar, F. Amin, H. A. Wahab and D. Baleanu, “Unsupervised constrained neural network modeling of boundary value corneal model for eye surgery,” Applied Soft Computing, vol. 85, pp. 1–16, 2019.
  39. Z. U. A. Zafar, N. Ali, S. Younas, S. F. Abdelwahab and K. S. Nisar, “Numerical investigations of stochastic HIV/AIDS infection model,” Alexandria Engineering Journal, vol. 60, no. 6, pp. 5341–5363, 2021.
  40. N. Anwar, I. Ahmad, M. A. Z. Raja, S. Naz, M. Shoaib et al., “Artificial intelligence knacks-based stochastic paradigm to study the dynamics of plant virus propagation model with impact of seasonality and delays,” The European Physical Journal Plus, vol. 137, no. 1, pp. 1–47, 2022.
  41. J. P. Hespanha, R. Chinchilla, R. R. Costa, M. K. Erdal and G. Yang, “Forecasting COVID-19 cases based on a parameter-varying stochastic SIR model,” Annual Reviews in Control, vol. 51, pp. 460–476, 2021.
  42. H. Rezazadeh, A. Korkmaz, A. E. Achab, W. Adel and A. Bekir, “New travelling wave solution-based new Riccati equation for solving KdV and modified KdV equations,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 447–458, 2021.
  43. S. E. Awan, M. A. Z. Raja, A. Mehmood, S. A. Niazi and S. Siddiqa, “Numerical treatments to analyze the nonlinear radiative heat transfer in MHD nanofluid flow with solar energy,” Arabian Journal for Science and Engineering, vol. 45, no. 6, pp. 4975–4994, 2020.
  44. P. D. Çankal and E. Yaşar, “Optical soliton solutions to a (2 + 1) dimensional Schrödinger equation using a couple of integration architectures,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 381–396, 2021.
  45. A. H. Bukhari, M. Sulaiman, M. A. Z. Raja, S. Islam, M. Shoaib et al., “Design of a hybrid NAR-RBFs neural network for nonlinear dusty plasma system,” Alexandria Engineering Journal, vol. 59, no. 5, pp. 3325–3345, 2020.
  46. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022.
  47. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022.
  48. A. Bhalraj, A. Azmi and M. H. Mohd, “Analytical and numerical solutions of Leptospirosis model,” Computer Science, vol. 16, no. 3, pp. 949–961, 2021.
  49. T. A. Sulaiman, H. Bulut and H. M. Baskonus, “On the exact solutions to some system of complex nonlinear models,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 29–42, 2021.
  50. A. Aghili, “Complete solution for the time fractional diffusion problem with mixed boundary conditions by operational method,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 9–20, 2021.
  51. H. M. Baskonus and H. Bulut, “On the numerical solutions of some fractional ordinary differential equations by fractional Adams-Bashforth-Moulton method,” Open Mathematics, vol. 13, no. 1, pp. 547–556, 2015.
  52. M. T. Gençoğlu and P. Agarwal, “Use of quantum differential equations in sonic processes,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 21–28, 2021.

Cite This Article

Z. Sabir, S. Manuel, M. A. Zahoor Raja, . Gilder-Cieza–Altamirano, M. Seminario-Morales et al., "Stochastic computational heuristic for the fractional biological model based on leptospirosis," Computers, Materials & Continua, vol. 74, no.2, pp. 3455–3470, 2023. https://doi.org/10.32604/cmc.2023.033352


cc This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 1129

    View

  • 387

    Download

  • 0

    Like

Related articles

Copyright© 2024 Tech Science Press
© 1997-2024 TSP (Henderson, USA) unless otherwise stated

Share Link