Pixel’s Quantum Image Enhancement Using Quantum Calculus

1  Introduction

The term quantum is usually associated with the smallest quantity of any measure or item. The quantum calculus provides better representation for images, depending on the fact that different areas of an image frequently seem same. Many researchers have newly become interested in quantum calculus, which ascends in the mathematical studies of combinatorics and special functions, as well as in a diversity of areas connecting the study of fractals and multi-fractal processes. The term quantum is commonly used to describe the smallest quantity of any measure or item [1]. The application of quantum calculus concepts has gained in popularity during the last two decades. Researchers have discovered and published a possible analytic effected tool in image processing using the notion of quantum calculus (the calculus without limits) [2]. Image enhancement is an important aspect of image processing. Noises can be recognized with images through realization on transmission. The presence of noise prevents these images from being used in a variety of applications. By utilizing the extended concept of quantum calculus, we present the quantum calculus-based medical image enhancement method to dynamically selects the spatial distribution of image pixel intensity values.

Today, image enhancement is widely utilized to increase the quality of existing images in practically every field. Low contrast in medical images make it difficult to make a precise diagnosis, hence these images must be enhanced to avoid misinterpretation of important clinical data [3].

Image enhancement is a form of image processing that is necessary for image analysis and feature extraction. Enhancing medical imagery is a difficult task due to the unpredictably changing quality of the acquired images. These findings led to the use of an automated quantum calculus-based approach is proposed for improving brain MRI scans. The study’s main contributions are as follows:

2  Related Works

Due to differences in contrast, light reflections, and patient movement throughout the capture procedure, most medical images contain noise. Such noise causes computational issues and affects the precision of brain cancer diagnosis. Image enhancement is a type of pre-processing that improves image quality for a specific use. To generate more relevant images than the input image, most image enhancement algorithms involve spatial operations on image pixels [4,5]. The topic of q-calculus has piqued the interest of various scholars in recent years, and a range of fresh findings may be found in the papers. Spatial domain algorithms-based image enhancement techniques have been reported in the literature. The quantum and fractional calculus are the most extensively used in image enhancement methods [6]. Quantum calculus (q-calculus) is a relatively recent field of mathematics that allows the fractional derivative of a real function to be calculated without bounds [7,8]. Several image enhancing approaches with various mathematical models have been developed in the literature. The concept of fractional-order-based image enhancement algorithms has recently been proposed in several studies focusing on improving image quality [6,9].

Al-Shamasneh et al. 2018 [10] proposed a “local fractional entropy” based image enhancement approach for MRI kidney images enhancement. Only the MRI kidney image enhancement yielded good results with this model.

Ibrahim et al. 2020 [3] recently published a fractional partial differential equations (FPDEs) based mathematical medical image enhancement model. The ability of the FPDE to improve low-contrast images is its main advantage. Similarly, a new fractional calculus-based medical image enhancement method was developed by [11]. This enhancement method improves image contrast while maintaining image features, but it fails to improve non-uniform illumination areas in input images.

Fractional calculus operators have lately shown to be an excellent new strategy in image improvement [4,6]. Regardless of the results of the fractional operators as an image enhancement, there is still room for development.

The study’s main contribution is a novel quantum calculus-based medical image enhancement technique to improve low contrast image intensity. The ability of proposed enhancing method is to increase low contrast image intensities via the adjusting the q parameter which is its key advantage.

3  Proposed Enhancement Algorithm

For increasing image quality perception, we proposed a new enhancement technique that is based on the concept of quantum calculus because quantum calculus comprises such a model. The entropy quantifies the variety or unpredictability of a scheme that is presented as follows in the context of multi-dimensional quantum measurement. The spatial distribution of image pixel intensity values, where each pixel is adjusted according to a specific formula, characterizes image enhancement. This motivates us to improve image enhancement by using quantum calculus (QC). The QC is a limitless version of conventional normal calculus. As mentioned in [12], Jackson was the first to employ the q-derivative:

for q∈(0,1), a real interval, where 0∈I, and a function φ:I→R, the quantum derivative is

Δq[φ](t)=φ(qt)−φ(t)t(q−1),t≠0,Δq[f](0)=φ′(0).(1)

While, the h−derivative is defined by

Δh[φ](t)=φ(t+h)−φ(t)h,t≠0,h>0.(2)

Hahn proposed the difference operator as a method for building orthogonal polynomial families. Jackson’s q-difference operator and the forward difference operator are combined in Hahn’s quantum difference operator (in the limit).

Δq,w[φ](t)=φ(qt+w)−φ(t)t(q−1)+w,t≠w0=w1−q.(3)

More generalizations of quantum calculus are given by Chakrabarti et al. [13].

Δq,w[φ](t)=φ(qt)−φ(wt)t(q−w),(4)

where

[n]q,w=qn−wnq−w,(q≠w).

Based on the last definition, Eq. can be modified as follows:

Bω(q,w)=qN−wNq−wlimω→0(log⁡(Υ(q,w,ω))log⁡(1/ω)),(5)

where

Υ(q,w,ω)=∑k=1N(ω)ϱkq−w,1>q>w>0.

where ϱkq−w is the probability of distribution of image pixel intensity values, q, and w are quantum parameters defined by 1 > q > w > 0. The enhanced image is given by:

E=I×Bω(q,w)(6)

The Eq. (5) defines the proposed image enhancement model, which is based on quantum calculus and the quantum parameters q and w. The proposed image enhancement model enhances images with minor gray-level changes based on pixel probability, which is the idea behind employing it for pixel type image improvement.

The steps of the algorithm are as follows:

1.    Take the input image (I) and select the value of the second parameter w=0.09.

2.    Determine the quantum parameter q by experimenting with the image enhancement value.

3.    Determine the probability value for each pixel.

4.    Use Eq. (6) to calculate the enhanced image.

The idea behind employing quantum calculus (QC) as an image enhancement model is to improve low contrast intensities by estimating enhanced each pixel values based on the probability details of image pixels. The mathematical model of applying QC for image enhancement, which may be used as a successful pre-processing step in any image processing technique, is the study’s uniqueness. The quantum parameter q is employed for fine detail enhancement, which is empirically determined by averaging the NIQE scores of all the images in the dataset as shown in Fig. 1. To achieve the optimum image enhancement quality, the second parameter’s (w) value of 0.09 is chosen.

Figure 1: The average NIQE measure for various values of q

4  Experimental Results

MATLAB 2021b was used to develop the code for the proposed image enhancement algorithm [14]. In this study, 154 MRI brain images from the “multimodal brain tumor image segmentation benchmark” (BRATS) were employed [15].

In Fig. 2, the proposed image enhancement techniques’ qualitative outcomes for MRI images are shown in which all the images exhibit various trends with dark and bright parts.

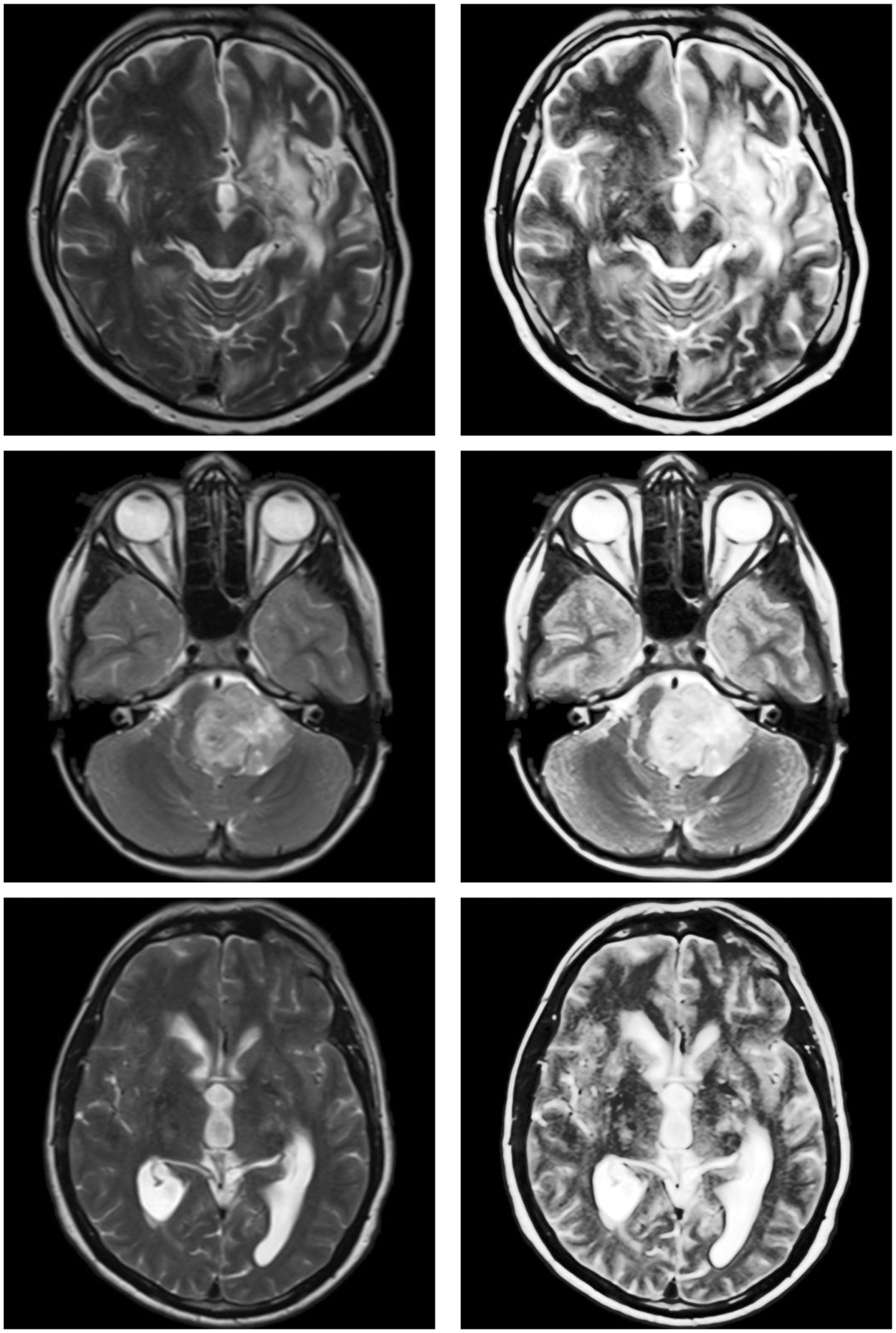
Figure 2: Sample inputs/outputs of the proposed algorithm

Overall, the proposed model’s produces the structures of medical images, which often depict edges, clearly specified. This is due to the model’s capacity to efficiently capture high frequency features. For images that are poorly lighted, the proposed approach produces reasonable visual results. This is the quantum calculus with q, and w parameters contribution to this study.

For the comparative analysis (Fig. 3), we used the following existing approaches to show that the proposed enhancement model is effective as a medical picture enhancing tool. Ibrahim et al. [3] developed an image enhancement approach for medical image improvement based on “fractional partial differential equations” (FPDEs). Aldawish et al. [6] proposed image enhancement model based on Mittag-Leffler sum convoluted with Chebyshev polynomial to improve images with low gray level changes by evaluating the probability of each pixel. Al-Shamasneh et al. [10] developed a fractional entropy-based approach for enhancing kidney images. Finally, a new fractional integral entropy based medical image enhancement approach that estimates the probabilities of imaging pixels was developed by [11]. In terms of image quality, the proposed method outperforms existing methods.

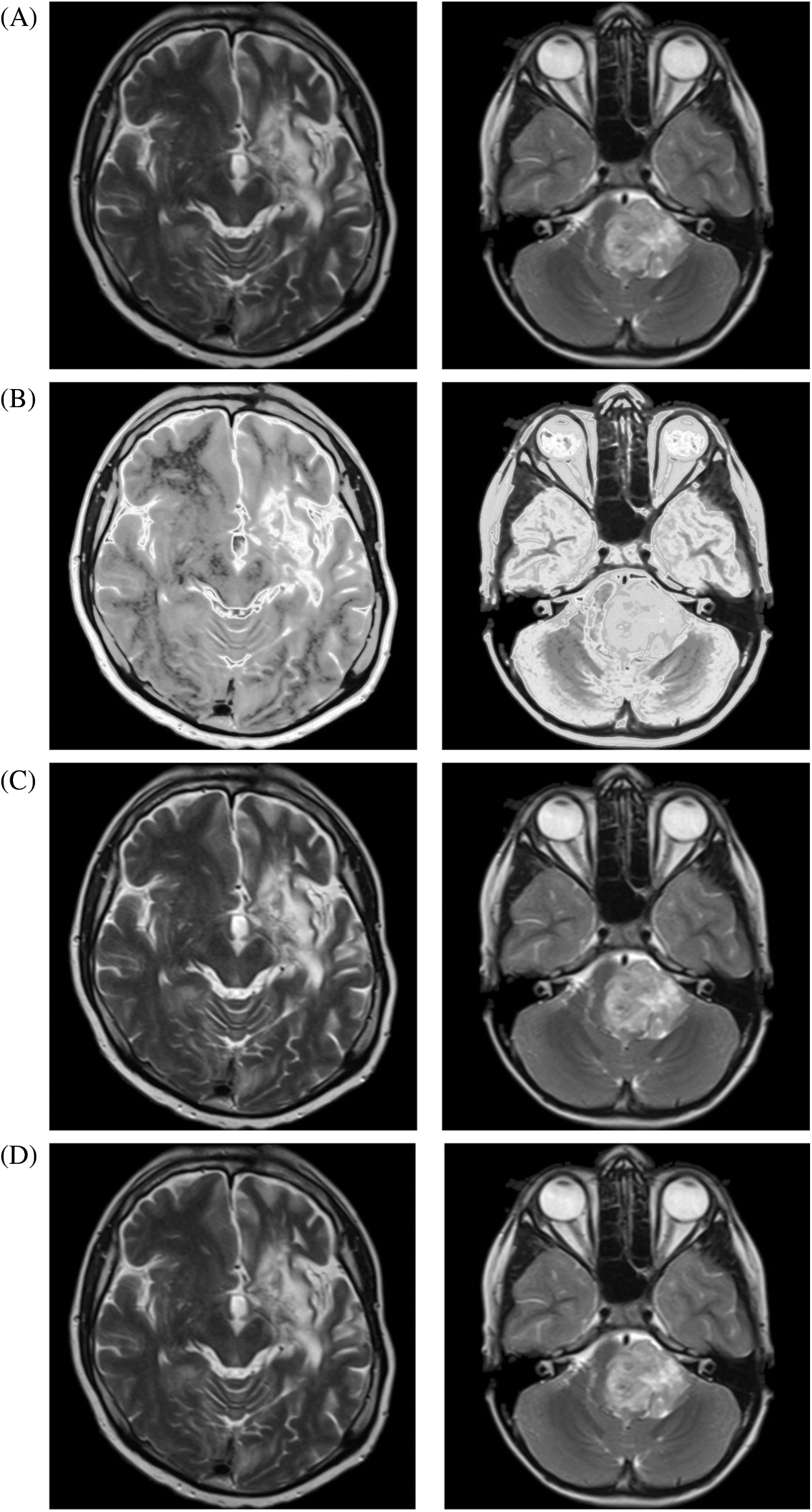
Figure 3: The proposed and existing enhancement models’ results on brain MRI. (A) Input image, (B) Ibrahim et al. [3], (C) Aldawish et al. [6], (D) Al-Shamasneh et al. [10], (E) Jalab et al. [11], (F) Proposed method

The blind image quality assessment BRISQUE and NIQE scores were employed for the quantitative comparisons, as shown in Tab. 1. The issue of assessing an image’s visual quality without any reference is known as blind image quality assessment. The blind image quality assessment focuses on the basic difference between fidelity and quality, which is usually not determined by a reference as in the human visual system when assessing a target image’s quality. The proposed image enhancement method outperforms the existing methods in terms of Brisque and Niqe scores. Regardless the degree of the gray level changes in MRI scans, the proposed method obtains the best of Brisque and Niqe scores (lower is preferable).

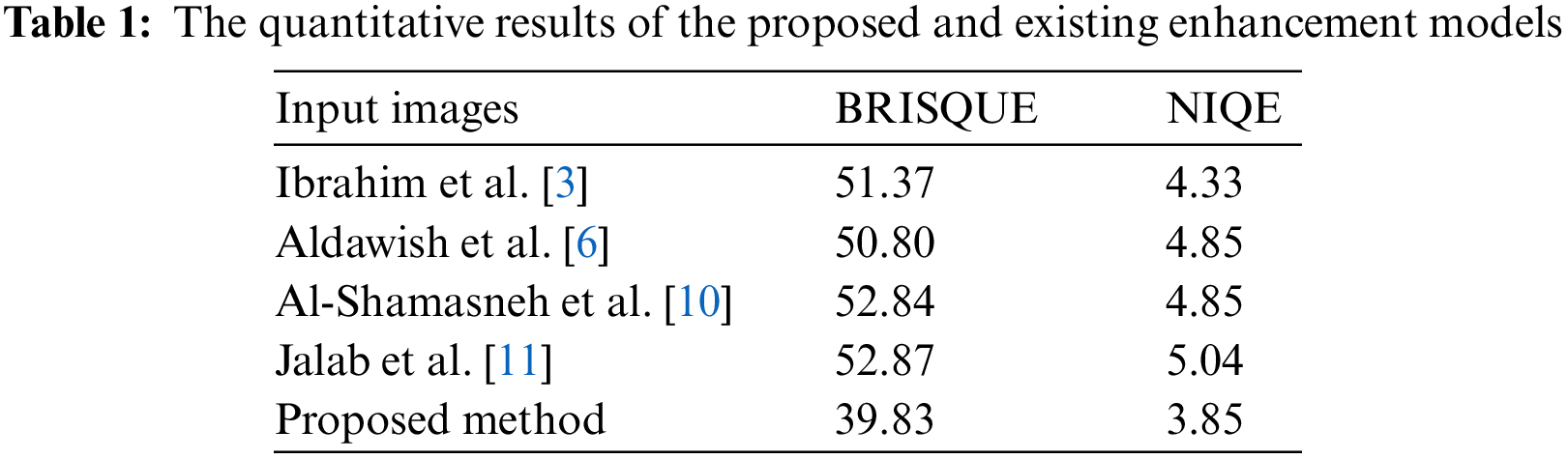
In conclusion, when compared to previous methods, the proposed method yields the best results for MRI scans of diverse visual impairments since its outcomes are reliable across varied datasets. However, because they were built with a specific application in mind, some existing procedures may give greater results when employed under specific conditions.

5  Conclusion

A new approach to image enhancing based on quantum calculus as a pre-processing step for low contrast images is proposed in this study. MRI images with low gray-level have been improved using the proposed image enhancement model, which estimates the likelihood of each image pixel. According to testing results on a variety of images, the proposed methodology outperforms existing methods in the broad application of image improvement. The main limitation of this study is that the performance of the proposed model drastically declines as the complexity of the input images rises. Future study may modify the existing model to specific applications in order to optimize the upgrade’s benefits.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  P. C. Victor Kac, Quantum calculus. New York: Springer, 2002. [Google Scholar]

 2.  R. J. Al-Azawi, N. M. Al-Saidi, H. A. Jalab, H. Kahtan and R. W. Ibrahim, “Efficient classification of COVID-19 CT scans by using q-transform model for feature extraction,” PeerJ Computer Science, vol. 7, no. 4, pp. 553–563, 2021. [Google Scholar]

 3.  R. W. Ibrahim, H. A. Jalab, F. K. Karim, E. Alabdulkreem and M. N. Ayub, “A medical image enhancement based on generalized class of fractional partial differential equations,” Quantitative Imaging in Medicine and Surgery, vol. 12, no. 1, pp. 172, 2022. [Google Scholar]

 4.  I. Aldawish and R. W. Ibrahim, “A new mathematical model of multi-faced COVID-19 formulated by fractional derivative chains,” Advances in Continuous and Discrete Models, vol. 2022, no. 1, pp. 1–10, 2022. [Google Scholar]

 5.  R. W. Ibrahim, “A new image denoising model utilizing the conformable fractional calculus for multiplicative noise,” SN Applied Sciences, vol. 2, no. 1, pp. 1–11, 2020. [Google Scholar]

 6.  I. Aldawish and H. A. Jalab, “A mathematical model for COVID-19 image enhancement based on Mittag-Leffler-Chebyshev shift,” Computers, Materials & Continua, vol. 73, no. 1, pp. 1307–1316, 2022. [Google Scholar]

 7.  R. W. Ibrahim, A. M. Ajaj, N. M. Al-Saidi and D. Balean, “Similarity analytic solutions of a 3D-fractal nanofluid uncoupled system optimized by a fractal symmetric tangent function,” CMES-Computer Modeling in Engineering & Sciences, vol. 130, no. 1, pp. 221–232, 2022. [Google Scholar]

 8.  S. S. Al-Bundi, K. Q. AL-Jubouri and N. M. Al-Saidi, “Modifying fractal image compression technique by hybridation of crowding genetic algorithm and scattered method,” in AIP Conf. Proc., Maltepe University, Istanbul-Turkey, AIP Publishing LLC, 2334, 2021. [Google Scholar]

 9.  S. Rashid, Z. Hammouch, R. Ashraf, D. Baleanu and K. S. Nisar, “New quantum estimates in the setting of fractional calculus theory,” Advances in Difference Equations, vol. 2020, no. 383, pp. 1–17, 2020. [Google Scholar]

10. A. R. Al-Shamasneh, H. A. Jalab, S. Palaiahnakote, U. H. Obaidellah, R. W. Ibrahim et al., “A new local fractional entropy-based model for kidney MRI image enhancement,” Entropy, vol. 20, no. 5, pp. 344, 2018. [Google Scholar]

11. H. A. Jalab, R. W. Ibrahim, A. M. Hasan, F. K. Karim, A. Al-Shamasneh et al., “A new medical image enhancement algorithm based on fractional calculus,” CMC-Computers Materials & Continua, vol. 68, no. 2, pp. 1467–1483, 2021. [Google Scholar]

12. F. H. Jackson, “On q-functions and a certain difference operator,” Earth and Environmental Science Transactions of the Royal Society of Edinburgh, vol. 46, no. 2, pp. 253–281, 1909. [Google Scholar]

13. R. Chakrabarti and R. Jagannathan, “A (p, q)-oscillator realization of two-parameter quantum algebras,” Journal of Physics A: Mathematical and General, vol. 24, no. 13, pp. L711, 1991. [Google Scholar]

14. MATLAB, MathWorks, Inc, Natick, Massachusetts, USA, 2022. [Google Scholar]

15. H. Bjoern, J. Andras, B. Stefan, K. Jayashree, F. Ketvan et al., “The multimodal brain tumor image segmentation benchmark (BRATS),” IEEE Transactions on Medical Imaging, vol. 34, no. 10, pp. 1993–2024, 2014. [Google Scholar]