Numerical Investigation of Malaria Disease Dynamics in Fuzzy Environment

1  Introduction

Malaria is a deadly infectious disease and occupies a special place in the earliest records of human history. It affects people from the Stone Age to ancient China. People living in tropical regions of sub-Saharan Africa, Asia, and the Amazon are the most affected by malaria. Forty percent of the population in these areas is still at risk of malaria. Malaria is caused by the plasmodium parasite and transmitted between humans through bites of Anopheles mosquitoes [1]. Although malaria has been studied for hundreds of years, it remains a significant public health problem in many countries. According to WHO, 241 million malaria cases and 0.62 million malaria-induced deaths worldwide were reported in 2020. These numbers show that 14 million more cases and 69000 more deaths in 2020 were reported compared to 2019. Mathematical modeling helps to get a comprehensive overview of these outbreaks. The construction of the model and its implementation make it possible to analyze the transmission and control of the malaria spread. Scientists have been ingenious through their efforts in developing different mechanisms and tools that have helped us apply the findings to control malaria transmission appropriately. A wide range of epidemiological models has been formulated, analyzed, and mathematically used to describe the spread and control of malaria. These models are examined from different angles. Otieno et al. proposed a model for the transmission of malaria control measures in Kenya [2]. Initially, constant control parameters were considered. Reproduction number, equilibrium, stability, and sensitivity analysis were also discussed. Then the time-dependent control parameters were considered, and Numerical simulations were performed. Rahman et al. presented SEIR and SEIR-SEI models for malaria transmission [3]. Reproduction number, equilibrium, and stability were also discussed. It was concluded that reducing the contact rate between humans and mosquitoes can control the spread of malaria. The use of active antimalarials is another factor in combating malaria. Treated insecticides and bed nets may help reduce mosquito populations and malaria transmission. Mandal et al. studied some models for malaria information, and their main features have been discussed [4]. Olaniyi developed a seven-dimensional model for malaria transmission [5]. Sensitivity analysis of a malaria transmission model was proposed by Chitnis et al. [6]. Smith et al. examined an individual-based stochastic malaria model [7]. Okosun et al. studied a malaria spread model to investigate the effectiveness and cost-effectiveness of using insecticide-treated mosquito nets, spraying insecticides, and a possible treatment of infected people that blocks transmission to mosquitoes [8]. A malaria transmission model was proposed by Kim et al. and concluded that the use of mosquito reduction strategies is, in some cases, but not always, more effective than personal protection [9]. Agusto et al. presented an SEIR-SEI malaria model by applying optimal control strategies [10]. Port et al. studied the prevention of malaria during pregnancy [11]. Chitnis et al. proposed a model for the malaria spread and discussed the studied model’s reproductive number and equilibrium analysis [12]. Niger and Gumel studied different aspects of a malaria model [13].

The fuzzy theory proposed by Zadeh [14] is extensively used in epidemiology. Verma et al. presented a model of Influenza spread in fuzzy senses [15]. Ortega et al. proposed a fuzzy epidemic model to study the rabies dynamics [16]. Das et al. studied a SIR model and introduced interval numbers as parametric functions [17]. Many other researchers used various approaches using fuzzy theory to prevent strategies to combat deadly diseases [18–22]. Allehiany et al. studied the SIR model in fuzzy senses and proposed different numerical and mathematical schemes to solve the model [23]. Mickens et al. constructed a SEIQR model with fuzzy parameters and developed a fuzzy NSFD method, an extension of the Mickens NSFD theory [24], to solve the studied model [25]. Dayan et al. proposed a fuzzy extension of the cyber consumerism epidemic model and developed an FNSFD scheme [26]. Many researchers studied fuzzy fractional-order dynamical systems [27–30], just to mention a few. SEIR mathematic model helps to understand malaria transmission dynamics, incorporating variables in human and mosquito populations.

Due to varying degrees of susceptibility, exposure, infectivity, and recovery among individuals, the concepts of ‘susceptible,’ ‘exposed,’ ‘infected,’ and ‘recovered’ are uncertain. Uncertainties may arise due to the different degrees of these parameters among population members. Other age groups of the considered population may have different customs, habits, and resistances due to their foreign origin, etc. It is challenging to collect numerical data as a fixed value in many real-life situations, while the date’s range can be decided quickly. Models capable of dealing with the above uncertainties are needed for these different levels of individuals. The fuzzy theory was developed to account for partial truth values ranging from totally true to false to provide robust and inexpensive solutions to real-world problems. It is one of the most powerful tools for dealing with inaccuracies, uncertainties, and partial truths. In this context, mathematical models with fuzziness are more meaningful and powerful. Keeping this in mind, we have extended a classical SEIR model by introducing fuzziness to the model. The malaria transmission rate and malaria-induced death rate of humans have been considered fuzzy numbers as these parameters are functions of the malaria-spreading virus. In the case of a classical system, these parameters are not direct functions of the virus. Therefore, the fuzzy model can be considered more balanced and flexible. Using fuzzy parameters helps us explain malaria transmission in more detail. A mathematical model with fuzziness is formulated and analyzed in this paper that illustrates the transmission dynamics of malaria disease. The novelty of our work is the development, execution, and mathematical investigation of a numerical scheme in fuzzy NSFD settings for a malaria model, particularly with fuzzy parameters.

2  SEIR Model with Fuzzy Parameters

2.1 Definition 1 [31]

A number A=(η1,η2,η3) is called a TFN if is of the form

μA(ω)={0,ω<η1ω−η1η2−η1,η1≤ω≤η2η3−ωη3−η2,η2≤ω≤η30,ω>η3

where η1≤η2≤η3.

2.2 Definition 2 [32]

The expected value of a TFN A=(η1,η2,η3) is

E[A]=η1+2η2+η34.

2.3 Definition 3 [32]

The fuzzy basic reproductive number Rmf is defined as

Rmf=E[Rm(ξ)].

We considered the SEIR mathematical model that has been talked about by Arfan et al. [29].

S′=Λ−βIS−μS,(1)

E′=βIS−α1E−μE,(2)

I′=α1E−(μ+α2+δ)I,(3)

R′=α2I−μR.(4)

The fuzzy SEIR model corresponding to the above model can be written as

S′=Λ−β(ξ)IS−μS,(5)

E′=β(ξ)IS−α1E−μE,(6)

I′=α1E−(μ+α2+δ(ξ))I,(7)

R′=α2I−μR.(8)

We suppose that the infectious rate of humans β(ξ) and malaria-induced death rate of humans δ(ξ) are fuzzy numbers depending on the virus load of an individual directly. Let β=β(ξ) be the chance of the transfer of the malaria virus when an infected Anopheles mosquito bites a susceptible person. It can be defined as

β(ξ)={0,ξ≤ξminξ−ξminξM−ξmin,ξmin<ξ≤ξM1,ξM<ξ.(9)

The death rate δ=δ(ξ) is also assumed to be a fuzzy number and can be defined as

δ(ξ)={(1−ζ)−ϵ0ξminξ+ϵ0,0≤ξ≤ξmin1−ζ,ξmin<ξ.(10)

2.4 The Fuzzy Basic Reproductive Number Rmf

We calculated the reproductive number, denoted by Rm, using the next-generation matrix method.

Rm=α1β(ξ)Λμ(μ+α1)(μ+α2+δ(ξ)).(11)

Rm being a function of the malaria virus load, can be analyzed for different amounts of the virus as

Case 1: If ξ<ξmin, then we have β(ξ)=0, and we obtain,

Rm(ξ)=0.(12)

Case 2: If ξmin<ξ≤ξM, then we have β(ξ)=ξ−ξminξM−ξmin and we obtain,

Rm(ξ)=α1Λβ(ξ)μ(μ+α1)(μ+α2+δ(ξ)).(13)

Case 3: If ξM<ξ<ξmax, then we have β(ξ)=1 and we obtain,

Rm(ξ)=α1Λμ(μ+α1)(μ+α2+δ(ξ)).(14)

The basic reproduction number Rm(ξ) can be written as a fuzzy number (triangular) as:

Rm(ξ)=(0,α1Λβ(ξ)μ(μ+α1)(μ+α2+δ(ξ)),α1Λμ(μ+α1)(μ+α2+δ(ξ))).(15)

Now by using definitions 3 and 4 we find Rmf as follows:

Rmf=E[Rm(ξ)],(16)

=α1Λ(2β(ξ)+1)4μ(μ+α1)(μ+α2+δ(ξ)).(17)

The effect of variation in β on Rm is shown in Fig. 1.

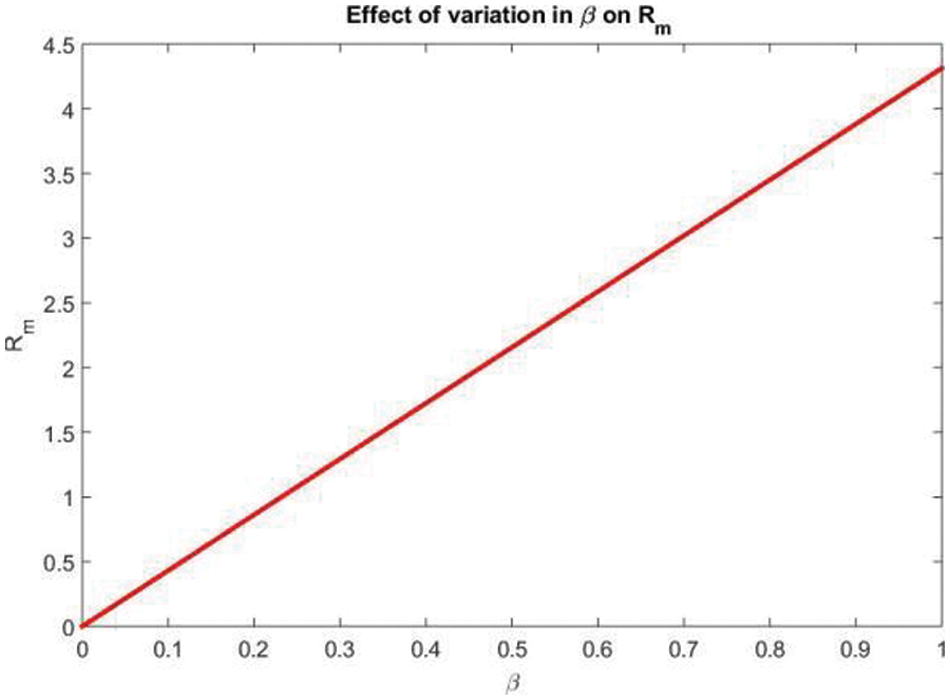
Figure 1: The effect of variation in β on Rm.

2.5 Equilibrium Analysis

Case 1: If ξ<ξmin, then we have β(ξ)=0, and we get the point

E0(S0,E0,I0,R0)=(Λμ,0,0,0),

where the human population has no malaria, which is called DFE (Disease Free Equilibrium). From a biological point of view, the malaria disease is eradicated when the concentration of the malaria virus is lesser than the least required concentration in the population for carrying the disease.

Case 2: If ξmin<ξ≤ξM, then we have β(ξ)=ξ−ξminξM−ξmin and we obtain E∗(S∗,E∗,I∗,R∗), where

S∗=(μ+α1)(μ+α2+δ(ξ))α1β(ξ),

E∗=α1Λ−μ(μ+α1)(μ+α2+δ(ξ))α1β(ξ)(μ+α1),

I∗=α1Λ−μ(μ+α1)(μ+α2+δ(ξ))β(ξ)(μ+α1)(μ+α2+δ(ξ)),

and R∗=α2μ[α1Λ−μ(μ+α1)(μ+α2+δ(ξ))β(ξ)(μ+α1)(μ+α2+δ(ξ))].

Case 3: If ξM<ξ<ξmax, then we have β(ξ)=1 and the point E∗∗(S∗∗,E∗∗,I∗∗,R∗∗) is obtained,

where S∗∗=(μ+α1)(μ+α2+δ(ξ))α1β(ξ),E∗∗=α1Λ−μ(μ+α1)(μ+α2+δ(ξ))α1β(ξ)(μ+α1),I∗∗=α1Λ−μ(μ+α1)(μ+α2+δ(ξ))β(ξ)(μ+α1)(μ+α2+δ(ξ)),andR∗∗=α2μ[α1Λ−μ(μ+α1)(μ+α2+δ(ξ))β(ξ)(μ+α1)(μ+α2+δ(ξ))].

Points E∗ and E∗∗ are the situations where the malaria virus is higher than the least required amount for malaria spread and the malaria virus persists in the human population.

3  Numerical Modeling

3.1 Non-Standard Finite Difference (NSFD) Scheme

NSFD scheme for the system (5)–(8) is

sn+1=sn+hΛ1+hβ(ξ)+hμ,(18)

en+1=en+hβ(ξ)sn+1in1+hα1+hμ,(19)

in+1=in+hα1en+11+h(μ+α2+δ(ξ)),(20)

rn+1=rn+hα2in+11+hμ.(21)

Case 1: If ξ<ξmin, then we have β(ξ)=0 and the above scheme becomes

sn+1=sn+hΛ1+hμ,(22)

en+1=en1+hα1+hμ,(23)

in+1=in+hα1en+11+h(μ+α2+δ(ξ)),(24)

rn+1=rn+hα2in+11+hμ.(25)

In Fig. 2, the graphical results of the susceptible compartment of the studied model are shown for different values of the step size h for case 1. The results show the convergence and non-negative behavior, which are the main features of the disease dynamic models, as the negativity of any compartment does not make any sense. Fig. 3 depicts the results of the exposed compartment at DFE, and one can see the converging and positive results. The critical feature of these graphs is their consistency at all step sizes. Many classical methods like Euler Maruyama, stochastic Euler, and stochastic RK-4 do not preserve this at large step sizes, as discussed by Rafiq et al. [33]. Figs. 4 and 5 show the compartments of the infected and recovered populations. Again, the results are positive and converging. From this, it can be concluded that the proposed method is reliable for investigating malaria transmission in the human population, even over a long period.

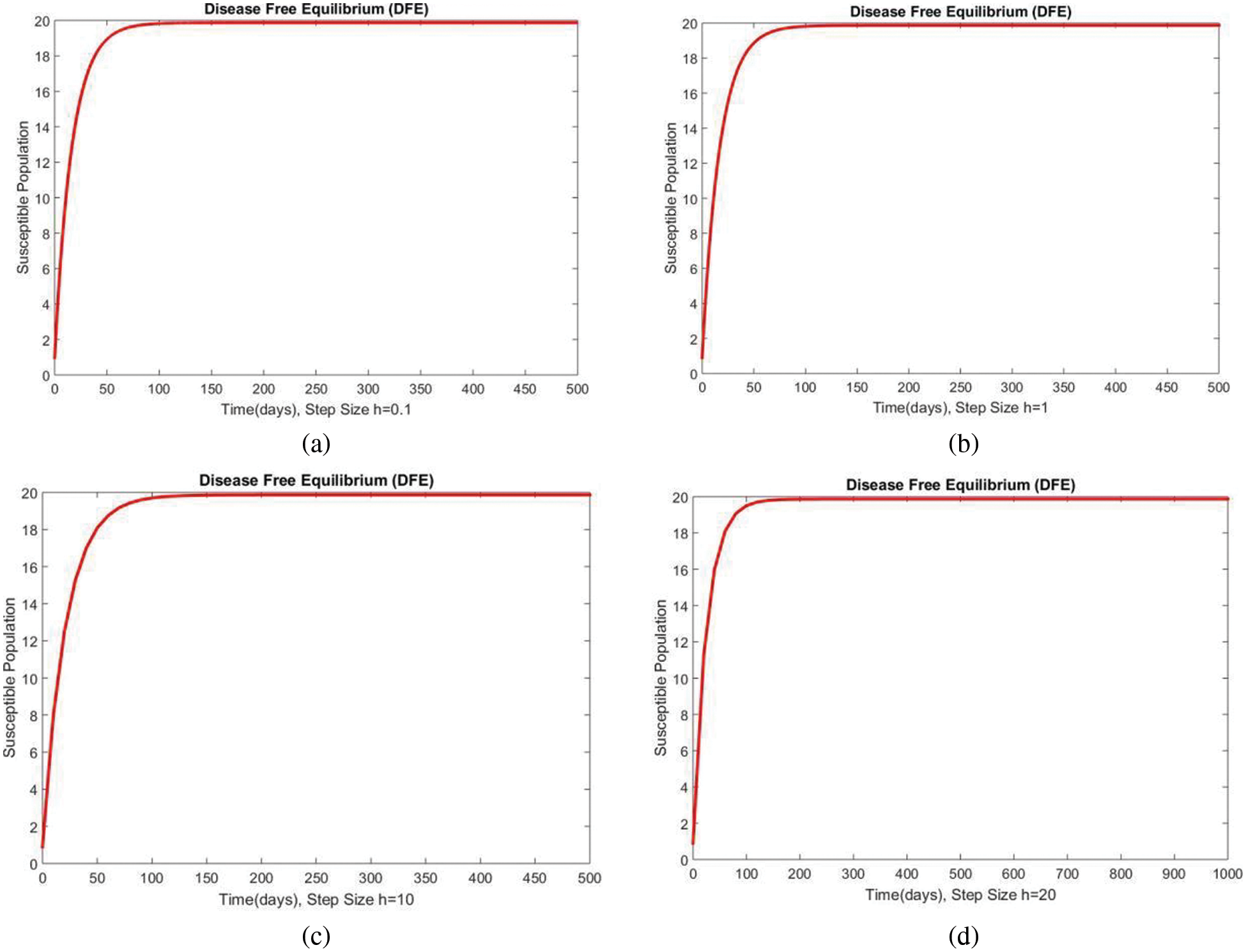
Figure 2: The portion of susceptible populations for case 1 at different step sizes

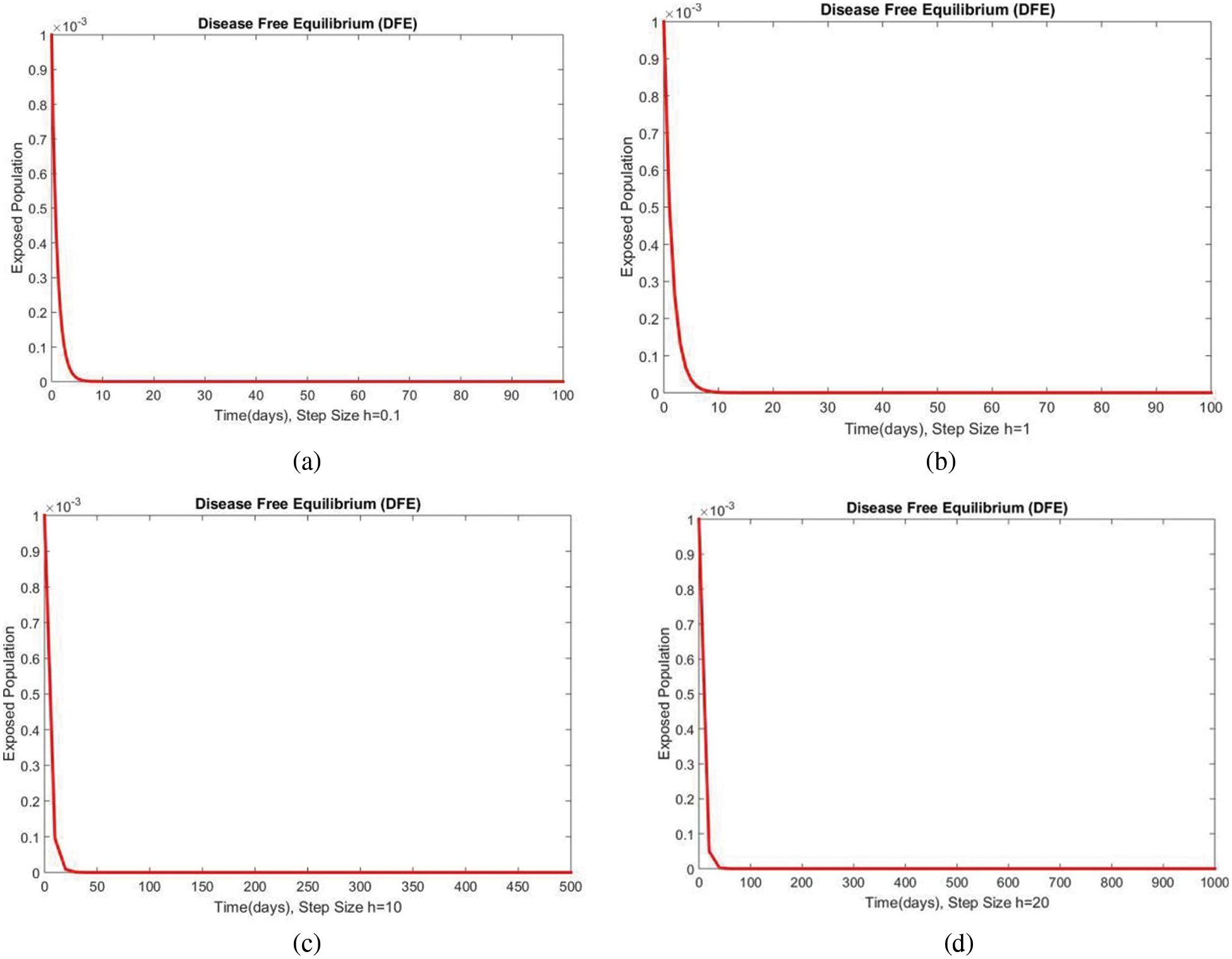
Figure 3: The portion of exposed populations for case 1 at different step sizes

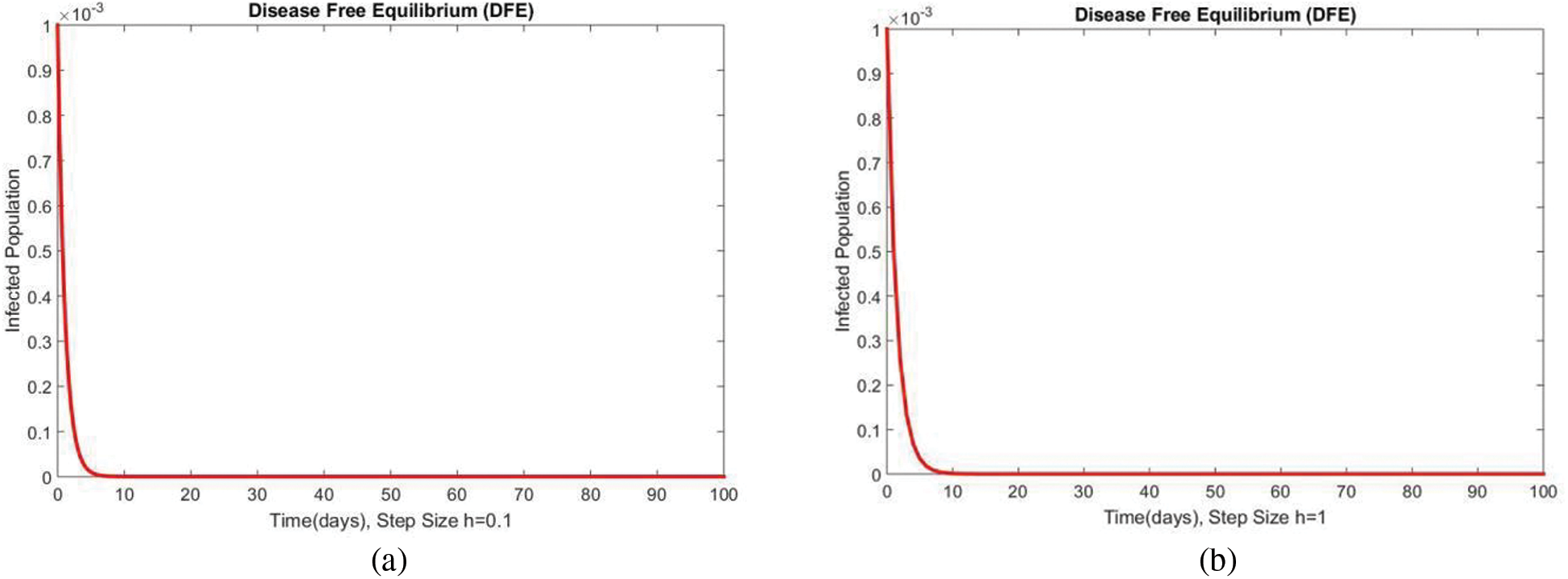
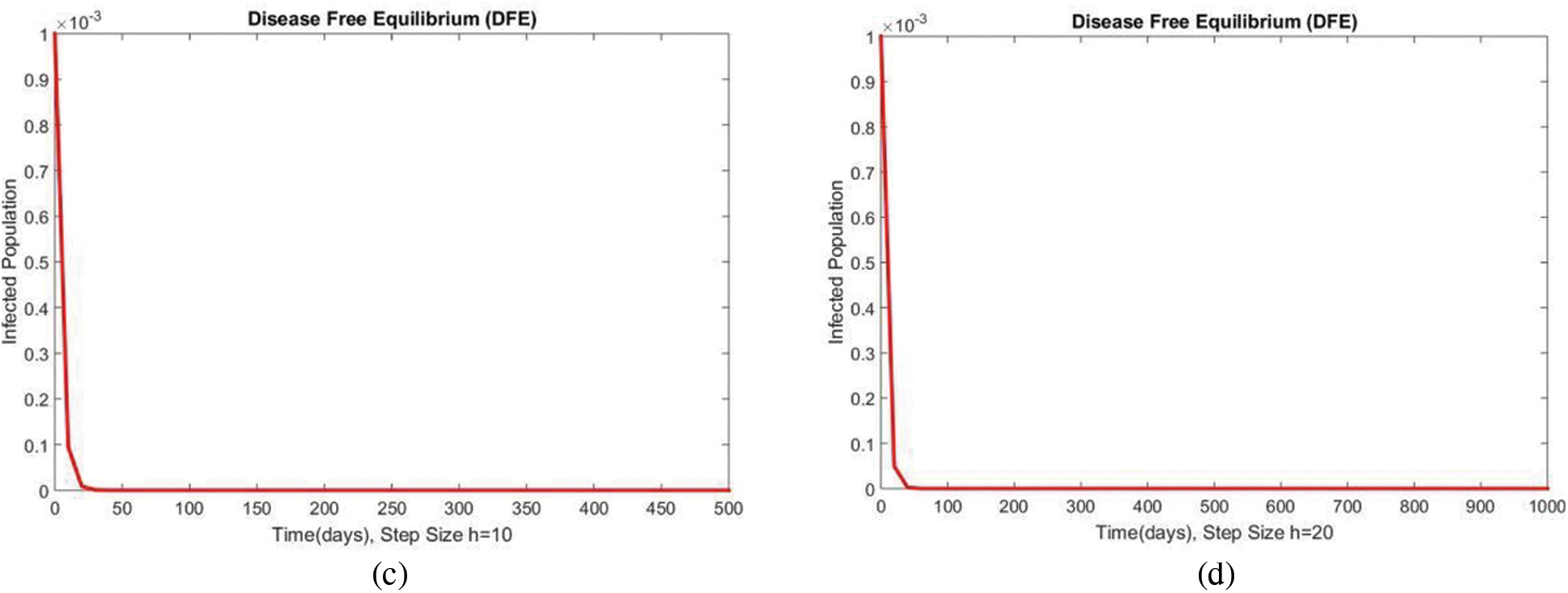
Figure 4: The portion of infected populations for case 1 at different step sizes

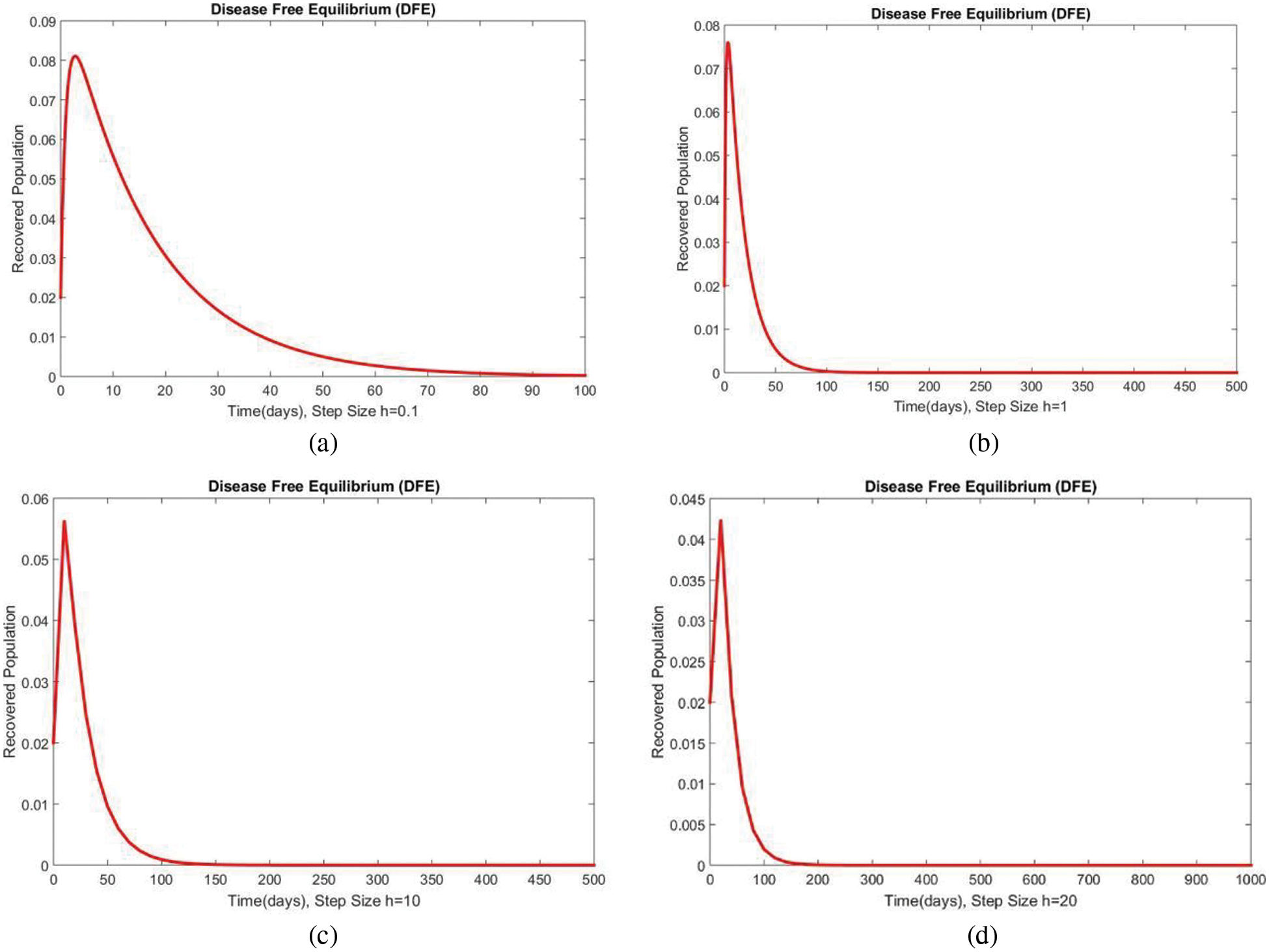
Figure 5: The portion of recovered populations for case 1 at different step sizes

Case 2: If ξmin<ξ≤ξM, then we have β(ξ)=ξ−ξminξM−ξmin and the above scheme becomes

sn+1=sn+hΛ1+hβ(ξ)+hμ,(26)

en+1=en+hβ(ξ)sn+1in1+hα1+hμ,(27)

in+1=in+hα1en+11+h(μ+α2+δ(ξ)),(28)

rn+1=rn+hα2in+11+hμ.(29)

In Figs. 6 and 7, the results of the susceptible and exposed compartments are shown at the first EE, which shows the convergence for all values of the time step size. We concluded that our proposed method is a reliable tool for studying malaria transmission in the human population.

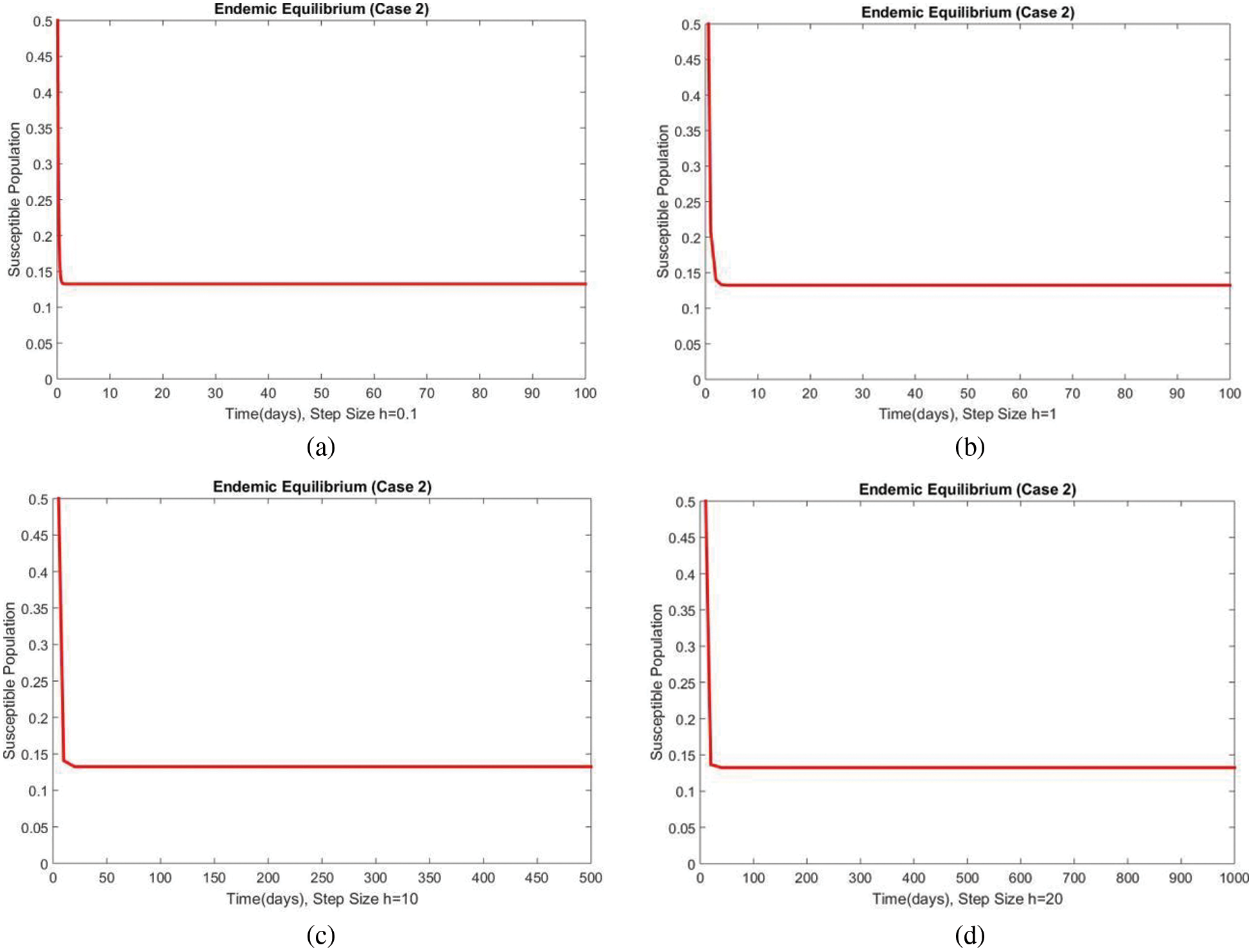
Figure 6: The portion of susceptible populations for case 2 at different step sizes

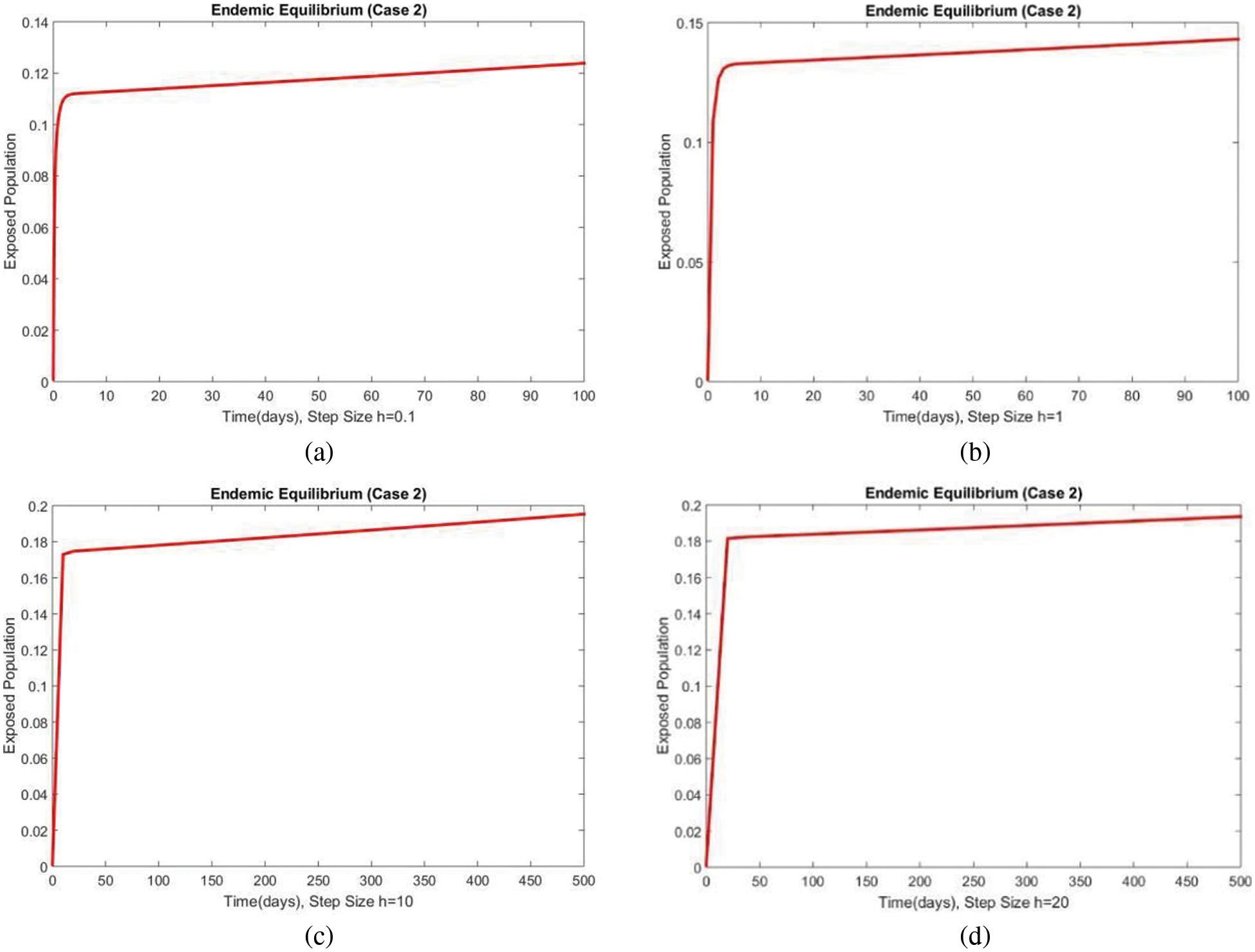
Figure 7: The portion of exposed populations for case 2 at different step sizes

Case 3: If ξM<ξ<ξmax, then we have β(ξ)=1 and the above scheme becomes

sn+1=sn+hΛ1+h+hμ,(30)

en+1=en+hsn+1in1+hα1+hμ,(31)

in+1=in+hα1en+11+h(μ+α2+δ(ξ)),(32)

rn+1=rn+hα2in+11+hμ.(33)

The susceptible and exposed human populations compartments at the second EE are presented in Figs. 8 and 9, respectively. At this stage, the resulting graphs of the NSFD method are not different from the previous cases. The classical standard difference schemes in the literature can cause chaos and misleading fluctuations for some passions of discretization constraints [34–49]. From all these results, we can conclude that the developed method can be considered an appropriate strategy to investigate the spread of malaria in the human population.

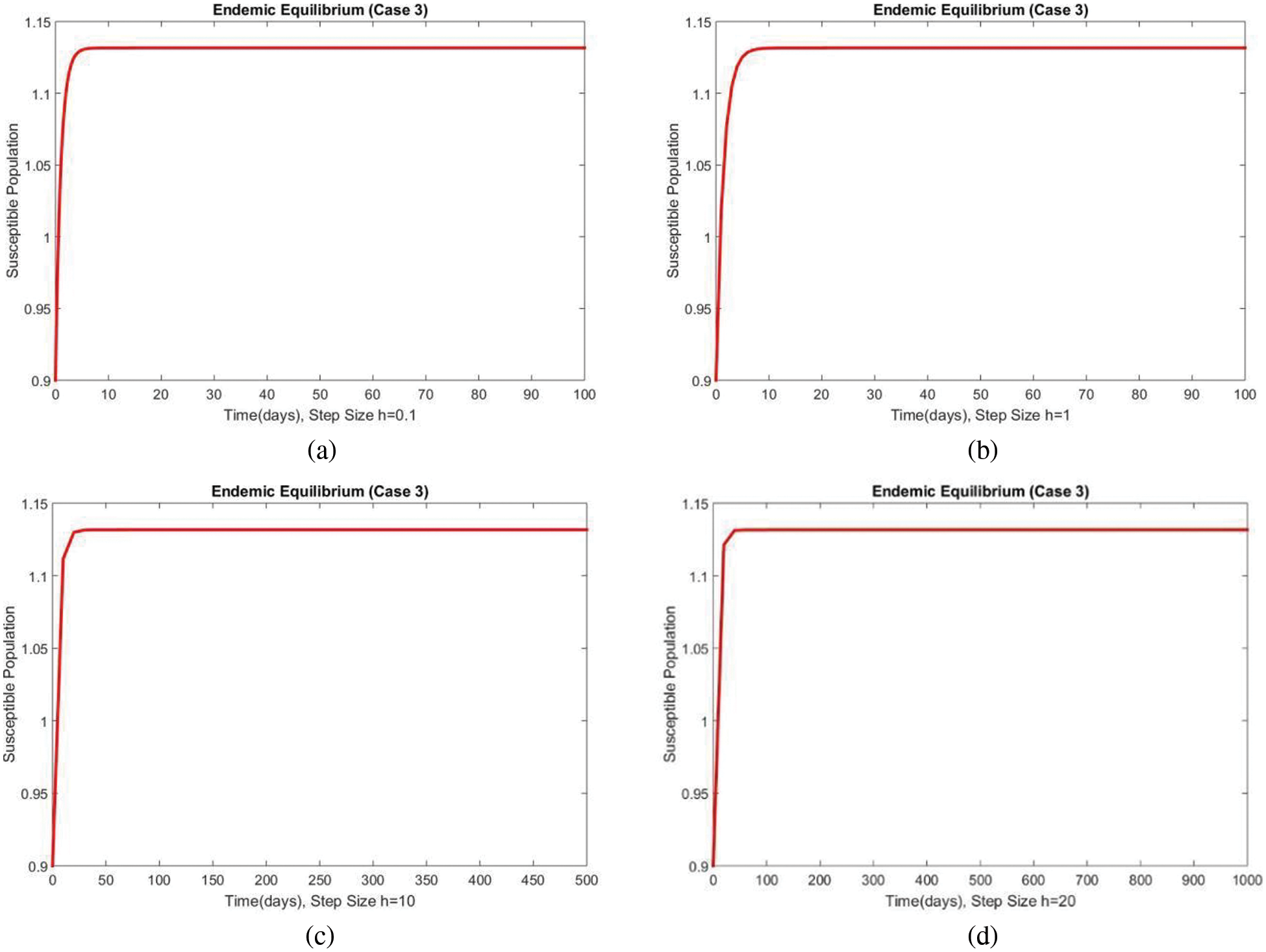
Figure 8: The portion of susceptible populations for case 3 at different step sizes

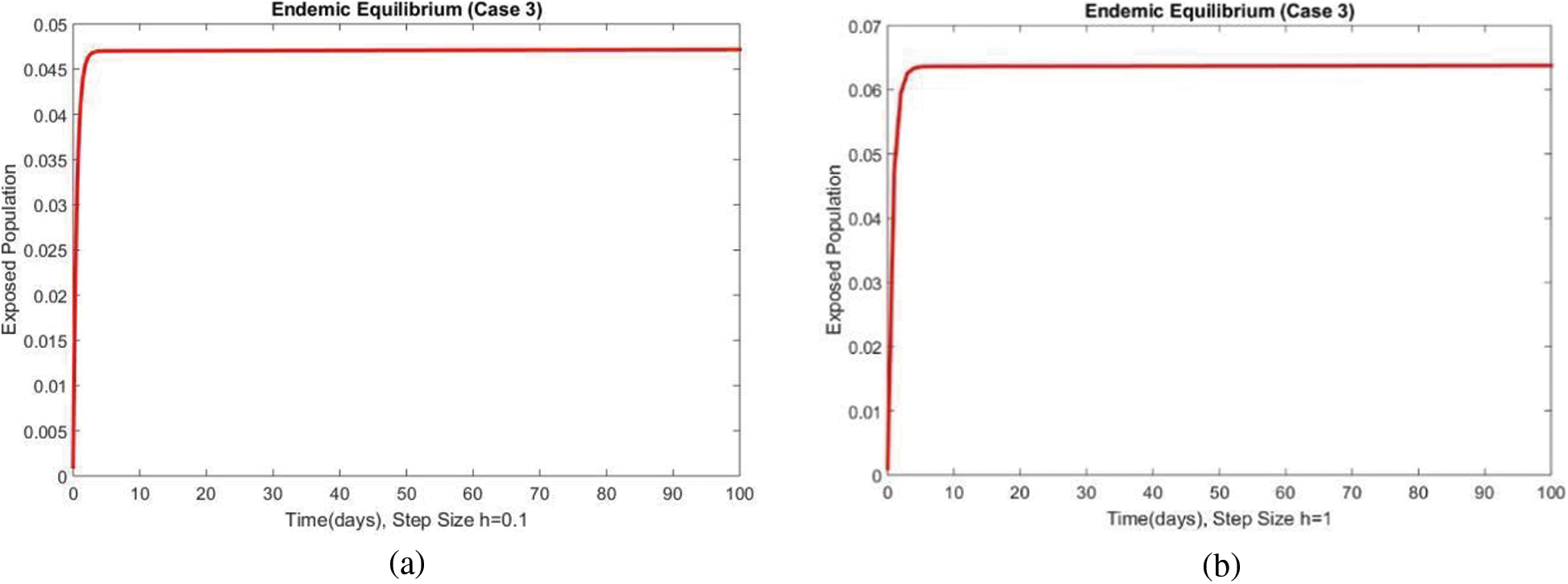
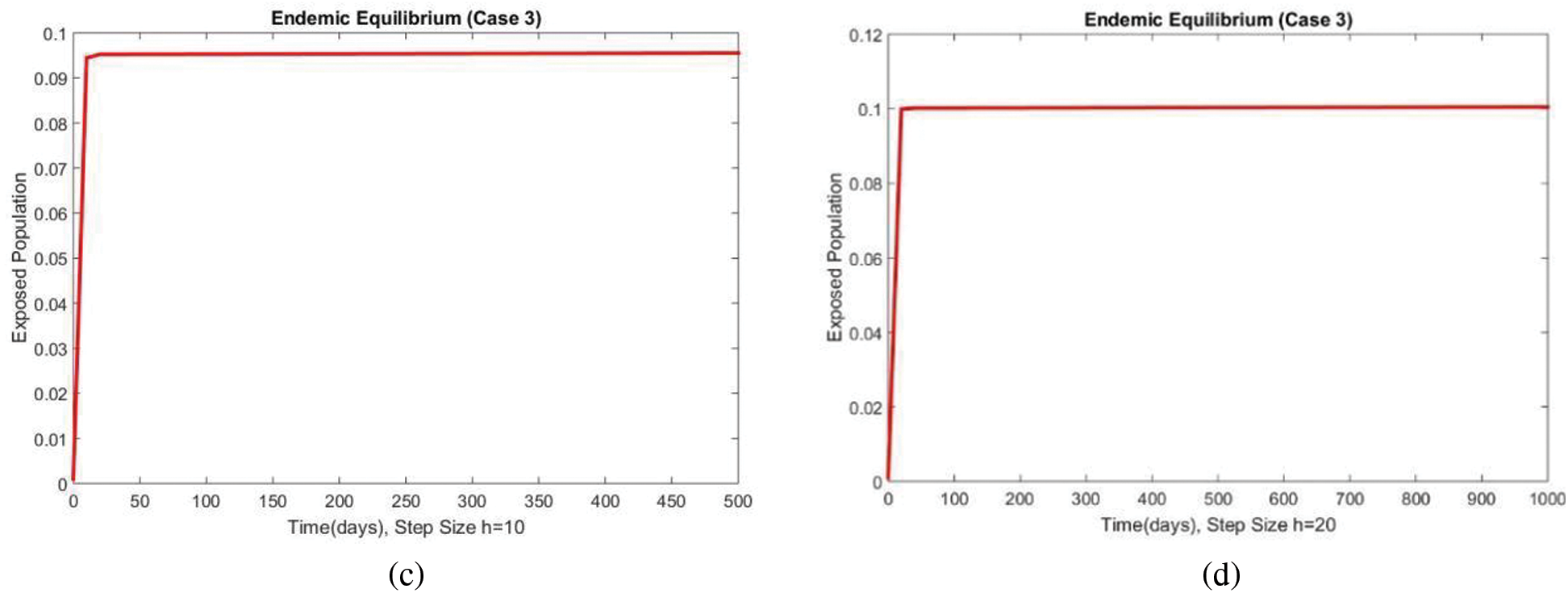
Figure 9: The portion of exposed populations for case 3 at different step sizes

3.2 Stability of the NSFD Scheme

Let

B1=s+hΛ1+hβ(ξ)+hμ,(34)

B2=en+hβ(ξ)si1+hα1+hμ,(35)

B3=i+hα1e1+h(μ+α2+δ(ξ)),(36)

B4=r+hα2i1+hμ.(37)

The Jacobian matrix corresponding to the system (34)–(37) is

J=[∂B1∂S∂B1∂I∂B1∂E∂B1∂R∂B2∂S∂B2∂I∂B2∂E∂B2∂R∂B3∂S∂B3∂I∂B3∂E∂B3∂R∂B4∂S∂B4∂I∂B4∂E∂B4∂R]

J=[11+hβ(ξ)+hμ000hβ(ξ)i1+hα1+hμ11+hα1+hμhβ(ξ)s1+hα1+hμ00hα11+h(μ+α2+δ(ξ))11+h(μ+α2+δ(ξ))000hα21+hμ11+hμ]

Jacobian at the DFE is

J=[11+hμ000011+hα1+hμ000hα11+h(μ+α2+δ(ξ))11+h(μ+α2+δ(ξ))000hα21+hμ11+hμ]

Eigenvalues of the above jacobian matrix are λ1=λ4=11+hμ<1, λ2=11+hα1+hμ<1 and λ3=11+h(μ+α2+δ(ξ))<1. Since all eigenvalues are less than one, it proves the desired result that the system (18)–(21) is convergent at DFE.

4  Conclusion

The core purpose of this study is to formulate a mathematical and numerical model for a better understanding of the dynamics of malaria diseases. In this work, we started from a classical SEIR malaria disease model and transformed it into a model with fuzzy parameters. The classical models fail when uncertainty in the parameters arises. More reliable models are needed when the problem of human health in the world is considered. The fuzzy theory is the best tool to solve problems containing uncertainty. The use of fuzzy theory makes this study more practical due to its ability to deal with uncertainty. The parameters β and δ are considered fuzzy numbers in this study due to their uncertain nature. The fuzzy variables being functions of malaria virus load, which depend directly on the amount of malaria virus, are analyzed for a different amount of the malaria virus. The R0 and three equilibrium points are analyzed in fuzzy senses. A reliable NSFD scheme in fuzzy settings is developed for the solution of the studied model, and its stability is analyzed. The proposed method holds the positivity of the numerical solutions at each time step, which is the main characteristic of this type of model. As a final remark, we would like to point out that the reliable solution of the studied model is a justification for this research. This study will open up some new avenues for researchers in this field. Delayed fuzzy model, stochastic fuzzy model, fractional fuzzy model, and many other directions can be considered as future directions. For instance, the proposed approach may also be extended to machine learning problems [50].

Acknowledgement: Thanks to our families and colleagues who supported us morally.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. A. Cobremeskel and H. E. Krogstad, “Mathematical modeling of endemic transmission,” American Journal of Applied Mathematics, vol. 3, no. 2, pp. 36–46, 2015. [Google Scholar]

 2.  G. Otieno, J. K. Koske and J. M. Mutiso, “Transmission dynamics and optimal control of malaria in Kenya,” Discrete Dynamics in Nature and Society, vol. 5, no. 1, pp. 01–27, 2016. [Google Scholar]

 3.  M. A. Rahman, E. N. Osman and I. K. Adu, “Simple mathematical model for malaria transmission,” Journal of Advances in Mathematics and Computer Science, vol. 25, no. 6, pp. 01–24, 2017. [Google Scholar]

 4.  S. Mandal, R. R. Sarkar and S. Sinha, “Mathematical models of malaria-a review,” Malaria Journal, vol. 10, no. 1, pp. 01–19, 2011. [Google Scholar]

 5.  S. Olaniyi and O. S. Obabiyi, “Mathematical model for malaria transmission dynamics on human and mosquito population with nonlinear forces of infectious disease,” International Journal of Pure and Applied Mathematics, vol. 88, no. 1, pp. 125–150, 2013. [Google Scholar]

 6.  N. Chitnis, J. M. Hyman and M. D. Cushing, “Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model,” Bulletin of Mathematical Biology, vol. 70, no. 5, pp. 1272–1296, 2008. [Google Scholar]

 7.  T. Smith, N. Maire, A. Ross, M. Penny, N. Chitnis et al., “Towards a comprehensive simulation model of malaria epidemiology and control,” Parasitology, vol. 135, no. 13, pp. 1507–1516, 2008. [Google Scholar]

 8.  K. O. Okosun, O. Rachid and N. Marcus, “Optimal control strategies and cost-effectiveness analysis of a malaria model,” Biosystems, vol. 111, no. 2, pp. 83–101, 2013. [Google Scholar]

 9.  B. N. Kim, K. Nah, C. Chu, S. U. Ryu, Y. H. Kang et al., “Optimal control strategy of plasmodium vivax malaria transmission in Korea,” Osong Public Health and Research Perspectives, vol. 3, no. 3, pp. 128–136, 2012. [Google Scholar]

10. F. B. Agusto, N. Marcus and K. O. Okosun, “Application of optimal control to the epidemiology of malaria,” Electronic Journal of Differential Equations, vol. 8, no. 1, pp. 01–22, 2012. [Google Scholar]

11. A. L. Port, G. Cottrell, C. Dechavanne, V. Briand, A. Bouraima et al., “Prevention of malaria during pregnancy: Assessing the effect of the distribution of IPTp through the national policy in Benin,” American Journal of Tropical Medicine and Hygiene, vol. 84, no. 2, pp. 270–275, 2011. [Google Scholar]

12. N. Chitnis, J. M. Cushing and J. M. Hyman, “Bifurcation analysis of a mathematical model for malaria transmission,” SIAM Journal on Applied Mathematics, vol. 67, no. 1, pp. 24–45, 2006. [Google Scholar]

13. A. M. Niger and A. B. Gumel, “Mathematical analysis of the role of repeated exposure on malaria transmission dynamics,” Differential Equations and Dynamical Systems, vol. 16, no. 3, pp. 251–287, 2008. [Google Scholar]

14. L. A. Zadeh, “Fuzzy sets,” Information Control, vol. 8, no. 1, pp. 338–353, 1965. [Google Scholar]

15. R. Verma, S. P. Tiwari and R. K. Upadhyay, “Fuzzy modeling for the spread of influenza virus and its possible control,” Computational Ecology and Software, vol. 8, no. 1, pp. 32–45, 2018. [Google Scholar]

16. N. R. S. Ortega, P. C. Sallum and E. Massad, “Fuzzy dynamical systems in epidemic modeling,” Kybernetes, vol. 29, no. 2, pp. 201–218, 2000. [Google Scholar]

17. A. Das and M. Pal, “A mathematical study of an imprecise SIR epidemic model with treatment control,” Journal of Applied Mathematics and Computing, vol. 56, no. 1, pp. 477–500, 2018. [Google Scholar]

18. R. Jafelice, L. C. Barros, R. C. Bassanezei and F. Gomide, “Fuzzy modeling in symptomatic HIV virus-infected population,” Bulletin of Mathematical Biology, vol. 66, no. 6, pp. 1597–1620, 2004. [Google Scholar]

19. P. Panja, S. K. Mondal and J. Chattopadhyay, “Dynamical study in fuzzy threshold dynamics of a cholera epidemic model,” Fuzzy Information and Engineering, vol. 9, no. 3, pp. 381–401, 2017. [Google Scholar]

20. A. Afzal, Z. Ansari, S. Alshahrani, A. K. Raj, M. S. Kuruniyan et al., “Clustering of COVID-19 data for knowledge discovery using c-means and fuzzy c-means,” Results in Physics, vol. 29, no. 1, pp. 01–18, 2021. [Google Scholar]

21. P. K. Mondal, S. Jana, P. Haldar and T. K. Kar, “Dynamical behavior of an epidemic model in a fuzzy transmission,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 23, no. 5, pp. 651–665, 2015. [Google Scholar]

22. R. Verma, S. P. Tiwari and R. K. Upadhyay, “Transmission dynamics of epidemic spread and outbreak of ebola in West Africa: Fuzzy modeling and simulation,” Journal of Applied Mathematics and Computing, vol. 60, no. 1, pp. 637–671, 2019. [Google Scholar]

23. F. M. Allehiany, F. Dayan, F. F. Al-Harbi, N. Althobaiti, N. Ahmed et al., “Bio-inspired numerical analysis of COVID-19 with fuzzy parameters,” Computers, Materials & Continua, vol. 72, no. 2, pp. 3213–3229, 2022. [Google Scholar]

24. R. E. Mickens, “A fundamental principle for constructing nonstandard finite difference schemes for differential equations,” Journal of Difference Equations and Applications, vol. 1, no. 1, pp. 645–653, 2005. [Google Scholar]

25. F. Dayan, N. Ahmed, M. Rafiq, A. Akgül, A. Raza et al., “Construction and numerical analysis of a fuzzy non-standard computational method for the solution of an SEIQR model of COVID-19 dynamics,” AIMS Mathematics, vol. 7, no. 5, pp. 8449–8470, 2022. [Google Scholar]

26. F. Dayan, M. Rafiq, N. Ahmed, D. Baleanu, A. Raza et al., “Design and numerical analysis of fuzzy nonstandard computational methods for the solution of rumor-base fuzzy epidemic model,” Physica A: Statistical Mechanics and Its Applications, vol. 600, no. 1, pp. 01–19, 2022. [Google Scholar]

27. M. Rahman, M. Arfan, K. Shah and J. F. Gómez-Aguilar, “Investigating a nonlinear dynamical model of COVID-19 disease under fuzzy caputo, random and ABC fractional-order derivative,” Chaos, Solitons & Fractals, vol. 140, no. 20, pp. 01–20, 2020. [Google Scholar]

28. K. Shah, A. R. Seadawy and M. Arfan, “Evaluation of one dimensional fuzzy fractional partial differential equations,” Alexandria Engineering Journal, vol. 59, no. 5, pp. 3347–3353, 2020. [Google Scholar]

29. M. Arfan, K. Shah, T. Abdeljawad and Z. Hammouch, “An efficient tool for solving two-dimensional fuzzy fractional-ordered heat equation,” Numerical Methods for Partial Differential Equations, vol. 37, no. 2, pp. 1407–1418, 2021. [Google Scholar]

30. M. Arfan, K. Shah, A. Ullah and T. Abdeljawad, “Study of fuzzy fractional order diffusion problem under the Mittag-Leffler Kernel Law,” Physica Scripta, vol. 96, no. 7, pp. 01–19, 2021. [Google Scholar]

31. L. C. Barros, R. C. Bassanezi and W. A. Lodwick, “The extension principle of Zadeh and fuzzy numbers,” in A First Course in Fuzzy Logic, Fuzzy Dynamical Systems, and Biomathematics, Berlin, Germany: Springer International Publishing, pp. 23–41, 2017. [Google Scholar]

32. Y. T. Mangongo, J. D. K. Bukweli and J. D. B. Kampempe, “Fuzzy global stability analysis of the dynamics of malaria with fuzzy transmission and recovery rates,” American Journal of Operations Research, vol. 11, no. 6, pp. 257–282, 2021. [Google Scholar]

33. M. Rafiq, A. Ahmadian, A. Raza, D. Baleanu, M. S. Ahsan et al., “Numerical control measures of stochastic malaria epidemic model,” Computers, Materials & Continua, vol. 65, no. 1, pp. 33–51, 2020. [Google Scholar]

34. M. S. Arif, A. Raza, W. Shatanawi, M. Rafiq and M. Bibi, “A stochastic numerical analysis for computer virus model with vertical transmission over the internet,” Computers, Materials Continua, vol. 61, no. 3, pp. 1025–1043, 2019. [Google Scholar]

35. A. Raza, A. Ahmadian, M. Rafiq, S. Salashour, M. Naveed et al., “Modeling the effect of delay strategy on transmission dynamics of HIV/AIDS disease,” Advances in Difference Equations, vol. 663, no. 1, pp. 01–19, 2020. [Google Scholar]

36. A. Raza, A. Ahmadian, M. Rafiq, S. Salahshour and I. R. Laganà, “An analysis of a nonlinear susceptible-exposed-infected-quarantine-recovered pandemic model of a novel coronavirus with delay effect,” Results in Physics, vol. 21, no. 1, pp. 01–07, 2021. [Google Scholar]

37. A. Raza, M. S. Arif, M. Rafiq, M. Bibi, M. Naveed et al., “Numerical treatment for stochastic computer virus model,” Computer Modeling in Engineering and Sciences, vol. 120, no. 2, pp. 445–465, 2019. [Google Scholar]

38. M. S. Arif, A. Raza, K. Abodayeh, M. Rafiq and A. Nazeer, “A numerical efficient technique for the solution of susceptible infected recovered epidemic model,” Computer Modeling in Engineering and Sciences, vol. 124, no. 2, pp. 477–491, 2020. [Google Scholar]

39. W. Shatanawi, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Essential features preserving dynamics of stochastic dengue model,” Computer Modeling in Engineering and Sciences, vol. 126, no. 1, pp. 201–215, 2021. [Google Scholar]

40. M. A. Noor, A. Raza, M. S. Arif, M. Rafiq, K. S. Nisar et al., “Non-standard computational analysis of the stochastic COVID-19 pandemic model: An application of computational biology,” Alexandria Engineering Journal, vol. 61, no. 1, pp. 619–630, 2021. [Google Scholar]

41. K. Abodayeh, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Numerical analysis of stochastic vector-borne plant disease model,” Computers, Materials and Continua, vol. 63, no. 1, pp. 65–83, 2020. [Google Scholar]

42. K. Abodayeh, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Stochastic numerical analysis for impact of heavy alcohol consumption on transmission dynamics of gonorrhoea epidemic,” Computers, Materials and Continua, vol. 62, no. 3, pp. 1125–1142, 2020. [Google Scholar]

43. A. Raza, J. Awrejcewicz, M. Rafiq, N. Ahmed, M. S. Ahsan et al., “Dynamical analysis and design of computational methods for nonlinear stochastic leprosy epidemic model,” Alexandria Engineering Journal, vol. 61, no. 10, pp. 1–15, 2022. [Google Scholar]

44. A. Raza, M. Rafiq, J. Awrejcewicz, N. Ahmed and M. Mohsin, “Stochastic analysis of nonlinear cancer disease model through virotherapy and computational methods,” Mathematics, vol. 10, no. 3, pp. 01–18, 2022. [Google Scholar]

45. A. Raza, “Mathematical modelling of rotavirus disease through efficient methods,” Computers, Materials and Continua, vol. 72, no. 3, pp. 4727–4740, 2022. [Google Scholar]

46. A. Raza, M. Rafiq, J. Awrejcewicz, N. Ahmed and M. Mohsin, “Dynamical analysis of Coronavirus disease with crowding effect, and vaccination: A study of third strain,” Nonlinear Dynamics, vol. 107, no. 4, pp. 3963–3982, 2022. [Google Scholar]

47. A. Raza, J. Awrejcewicz, M. Rafiq and M. Mohsin, “Breakdown of a nonlinear stochastic Nipah virus epidemic model through efficient numerical methods,” Entropy, vol. 23, no. 12, pp. 01–20, 2021. [Google Scholar]

48. M. Rafiq, M. Naveed, Z. Khan, A. Raza, J. Awrejcewicz et al., “Modeling the spread of leishmaniasis disease via delayed analysis,” Alexandria Engineering Journal, vol. 61, no. 12, pp. 11197–11209, 2022. [Google Scholar]

49. A. Raza, Y. M. Chu, M. Y. Bajuri, A. Ahmadian, N. Ahmed et al., “Dynamical and nonstandard computational analysis of heroin epidemic model,” Results in Physics, vol. 34, no. 1, pp. 01–10, 2022. [Google Scholar]

50. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]