A Neural Study of the Fractional Heroin Epidemic Model

1  Introduction

Heroin is a synthetic opioid from morphine, a natural chemical extracted from the seedlings of several opium poppy plants. These plants grow in Southeast and Southwest Asia, Mexico, and Colombia. Heroin produces in the form of a white or brown powder, and a black sticky material known as black tar heroin. People use heroin by injecting, sniffing, snorting, smoking, or speed-balling by mixing heroin and crack cocaine [1]. The growth of these opium poppies was discovered as evidence in ancient times. Opium poppies were first harvested and consumed around 6,000 years ago. Opium has been a popular narcotic for millennia. During the 1800 s, opium dens were prevalent, and the first drug, morphine, was derived from the opium poppy [2]. Later, heroin became an opiate substance derived from morphine [1–3]. Illicit drug exploitation is destructive to society. Drug users are often potential health extorts to others in order to assess the risk of acquiring and ingesting the drug. These individuals are more susceptible to infection, which can transmit to others due to their damaged immune system. Heroin is an illegal narcotic with major societal consequences. The number of heroin users is increasing every day. Heroin users are affected in many ways, especially physically, culturally, and financially. According to medical science, heroin enters the body, and targets the brain, heart rate, and other cell receptors [4]. Heroin addiction is an attractive trend to study from the perspective of infectious diseases because it is highly ubiquitous. Therefore, various approaches have been adopted to study the different aspects of heroin addiction through mathematical models. In 2007 [5], White and Comiskey constructed the mathematical model for infectious diseases and found through the threshold dynamics that prophylaxis is much better than treatment. After a couple of years, this model was modified by adding the eigenvalue equation, and the Poincare-Bendixson theory was used to obtain the stability of the equilibrium point [6]. Through the delay, global stability for the heroin model was studied by Huang et al. [7]. Wang et al. [8] added the bilinear law to analyze the dynamical behavior of the heroin model. Ma et al. [9] studied the interesting question on media coverage about the spreading of drug addiction. For this purpose, they studied the dynamical behavior based on the 3D drug model using the basic reproduction number. Age structure and nonlinear incidence phenomena were added to the heroin epidemic model using Yang et al. [10,11]. Time distributed delay and nonlinear incidence in the heroin epidemic model is discussed in [12]. The heroin epidemic model with treat age phenomena in mathematical epidemiology was introduced by Botmart et al. [13]. This mathematical model based on the relapse rate means how long time is required for the host in the treatment of heroin addiction. Other different epidemic models have been constructed and tested in various methods in order to capture the dynamics of opioid addiction [14–16]. Fractional calculus is used to model the physical and technical phenomena characterized by the fractional order system (the theory of real/complex order of integral/derivatives). The ideas of fractional calculus were proposed by well-known mathematicians, such as Leibniz, Abel, L’Hopital, Liouville, Riemann, and many others [17,18]. It is found that conventional nonlinear mathematical models, including derivatives integrations fail miserably in complicated situations. In recent years, fractional calculus has been more essential in numerous areas ranging from biomedical sciences to space sciences. Fractional differential system models play a vital role in electricity, chemistry, economics, control theory and automata, image processing, mechanics, chemistry, etc. Mostly, major topics of engineering include thermal diffusivity at semi-infinite, vibration, neutrons-point kinetic model, power-law, continuous-time random walk, die-electric polarization, colored and noise, electromagnetic waves robotics, chaos theory, and in biosciences especially in physiology can be better characterized through the fractional order system [19,20]. Recently, authors have been interested in developing the fractional differential system due to its wide use in almost all fields of engineering and biosciences. In [21–23], the kernel Hilbert space method has been adopted for first-order differential systems, BVPs with two points, integro-differential systems with two-points boundary value problems, and fractional diffusion Gorden Dirichlet time systems in the permeable source. The nonlinear homogenous time fractional gas dynamic system via fractional-order analytical technique is presented in [24]. In the biomedical field, the fractional system is used by Akinlar et al. [25] for the SIRE epidemic disease, Caputo-Fabrizio fractional Des for Rubella disease model [26], and Anthrax disease model in animals [27], for hepatitis B model [28], for the HBV infection model [29], world-known chickenpox disease [30], for infectious diseases [31], psoriasis diseases [32], for HIV/AIDS with treatment model [33] and SIR system of childhood disease [34,35].

An artificial neural network (ANN) is a major cognitive computing paradigm of artificial intelligence. ANNs are evolutionary adaptive in numerous cases based on the information through the network during the learning process, either internally or externally. The learning method entails constructing a set of links (weights) that give a representation compatible with the training set. Stochastic numerical solutions are created to model the ANNs and optimize them by combining of linear and non-linear search algorithms to solve differential problems. Sabir et al. [36] considered artificial neural networks essential for medical revolutions. Epidemic forecasting has been viewed in the light of artificial neural networks by Philemon et al. [37]. For the differentiation of infectious and non-infectious diseases, this paradigm has been used in [38].

The current study aims to solve the mathematical model by using the optimal approach to handle the drug and how a drug pandemic might take hold and spread over a population as well. First, the biological mathematical White and Comiskey model (WCM) involving the chemotaxes and nonlinear diffusion mechanism is discussed. This model is based on the fractional order differential equations, which explain the diffusion of heroin. Then the stochastics computing LMB-NNs technique was taken to solve the designed model. The purpose of introducing stochastic computing is to solve the nonlinear fractional derivative (NFD) WCM. The stochastic solvers have abundant applications to solve the diversity of applications, like food chain models [39,40], periodic differential models [41,42], thermal explosion theory [43,44], smoking differential models [45,46], corneal shape models [47,48], singular differential systems [49,50], Leptospirosis disease models [51,52] and prevention factor in the HIV systems [53,54]. In this paper, the simulations of the WCM are presented using stochastic procedures. The main procedure is given as follows:

•   The WCM describes the situation of heroin and non-heroin users but is expected to use it as this group is quite close to the heroin user group.

•   The mathematical model of WCM in the form of differential equations is solved through the LMB-NNs techniques.

•   A data set for training, testing, and validation based on the LMB-NNs for solving the NFD-WCM.

•   The fitness functions are taken in the NNs process, which converts many outputs to a single response.

•   Designed Backpropagation based neural networks by providing training and testing dataset LMB is adopted to faster the training.

•   The significance of the LMB-NNs technique is illustrated through statistical tool, such as mean square error, error histograms, correlation, regression, and fitting graphs.

The paper is planned to distribute in four sections: Section two delves into the (NFD-WCM) problem formulation and its equilibrium and stability conditions. Section third discusses the LMB for finding the answer to the problem. Section fourth contains the numerical and graphical results. The final portion contains the conclusions.

2  The White-Comiskey Model (WCM)

The WCM consists of three groups of individuals, which are described as:

(i)   Susceptible S: those who have never used a drug before.

(ii)   Drug user without treatment D1: those who take drugs without care.

(iii)   Drug user under-going treatment D2: those groups who go through medication to help them overcome their addiction.

The susceptible individual may either smarten up or die and depart or can shift to the drug addict. Drug users continue drug smarten-up or die or start treatment. Drug adductors may smarten up or return the drug. The comprehensive detail of each parameter of (WCM), used to observe the drug’ user group and their treatment process is dispatched in Table 1.

The mathematical model of (NFD-WCM) is constructed as follows,

{dS(τ)dτ=A−(β1ND1(τ)+μ)S(τ),dD1(τ)dτ=β1ND1(τ)S(τ)−(p+μ+δ1)D1(τ)+β3ND1(τ)D2(τ),dD2(τ)dτ=pD1(τ)−(δ2+μ)D2(τ)−β3ND1(τ)D2(τ),(1)

whereA=μS(η)+(δ1+μ)D1(η)+(δ2+μ)D2(η)(2)

Let N(τ)=S(τ)+D1(τ)+D2(τ); the total population size is the rate of susceptible inhabitants, and drug users without care and with care (treatment). A few basic assumptions of the WCM model are given:

•   N(η) is assumed to be a constant size within the specific period of the model.

•   Drug users can use the treatment during the period of model application.

•   Drug users under the treatment process are still using drugs.

•   Drug users without treatment group are infectious to adductors in susceptible and treatment.

•   Drug users do not infect the susceptible group under treatment.

•   Under going treatment can return to non-treatment drug users when contact with them.

•   In the population, everyone has the same chance of treatment as other individuals.

The updated form of Eq. (1) with the use of Eq. (1) is given as:

{dS(τ)dτ=−β1ND1(τ)S(τ)+(δ1+μ)D1(τ)+(δ2+μ)D2(τ),dD1(τ)dτ=β1ND1(τ)S(τ)−(p+μ+δ1)D1(τ)+β3ND1(τ)D2(τ),dD2(τ)dτ=pD1(τ)−(δ2+μ)D2(τ)−β3ND1(τ)D2(τ),(3)

where N(τ)=S(τ)+D1(τ)+D2(τ) is constant. To get the normalized form of the Eq. (3), the values are taken as

x~=S(τ)N(τ),y~=D1(τ)N(τ),z~=D2(τ)N(τ) with x~+y~+z~=1 in Eq. (3), which becomes as:

{dx~dτ=−β1x~y~+(δ1+μ)y~+(δ2+μ)z~,dy~dτ=β1x~y~−(p+μ+δ1)y~+β3z~y~,dz~dτ=py~−(δ2+μ)z~−β3z~y~,(4)

Reducing Eq. (4) in x~,y~ coordinates, let z~=1−x~−y~,

{dx~dτ=−β1x~y~+(δ2+μ)−(δ2+μ)x~+(δ1+δ2)y~,dy~dτ=(β1−β2)x~y~−(p−β3+μ+δ1)y~−β3y~2.(5)

The fractional order differential system of Eq. (5) can be represented as:

{dα1x~(τ)dτα1=−β1x~(τ)y~(τ)+(δ2+μ)−(δ2+μ)x~(τ)+(δ1−δ2)y~(τ),dα2y~(τ)dτα2=(β1−β3)x~(τ)y~(τ)−(p−β3+μ+δ1)y~(τ)−β3(y~(τ))2.(6)

The Caputo derivative is used in this study, and the fractional order derivative values have been taken between 0 and 1.

2.1 Free Equilibrium State of Drug

To get drug free equilibrium state, put Eq. (6) equal to zero, given as

−β1x~y~+(δ2+μ)−(δ2+μ)x~+(δ1−δ2)y~=0,(7)

(β1−β2)x~y~−(p−β3+μ+δ1)y~−β3y~2=0.(8)

From Eq. (7), the drug’s free equilibrium state conditions become as,(x~0,y~0)=(1,0). The Jacobian matrix of Eq. (6) is given as:

J(x~,y~)=(−β1y~−(δ2+μ)−β1x~+(δ1−δ2)(β1−β2)y~(β1−β2)x~−(p−β3+μ+δ1)−2β3y~).(9)

The disease free-state Jacobian matrix is provided as follows:

J(x~0,y~0)=(−(δ2+μ)(δ1−δ2)−β10β1−(p+μ+δ1)).(10)

The eigenvalues of the matrix (10) are λ1=−(δ2+μ), and λ2=β1−(p+μ+δ1). For stability of WCM, the λ1,λ2<1. Here λ1 is obviously less than 1. But for λ2<1, there must R0=β1(p+μ+δ1)<1. Otherwise, if β1>(p+μ+δ1), the model will be unstable.

2.2 Equilibrium of Endemic

For positive endemic equilibria, it is assumed that β1>(p+μ+δ1), the Eq. (8) for x~ takes the form as:

x~=(p−β3+μ+δ1)+β3y~(β1−β3),orx~=β1R0(β1−β3)−β3(1−y~)(β1−β3)(11)

The updated form of Eq. (7) by using the above equations becomes as follows:

β1β2y~2+((p+δ2+μ−β3)β1+β3(δ1+μ))y~+(p+δ1+μ−β1)(δ2+μ)=0.(12)

The Eq. (12) becomes as follows:

y~=−B±B2−4β1β2C2β1β2,(13)

where B=(p+δ2+μ−β3)β1+β3(δ1+μ), and C=(p+δ1+μ−β1)(δ2+μ). The value of y~ from Eq. (13) into Eq. (11) gives the positive endemic equilibrium results for y~>0, and x~>0.

3  Numerical Simulation

This part presents the numerical performances of the acquired results of three situations based on the nonlinear fractional differential system of the White-Comiskey heroin model is presented.

Case I: Consider a nonlinear fraction system of heroin model for simulation by taking the suitable values of relevant parameters and corresponding initial conditions.

Let p=0.04,δ1=0.05,μ=0.04,δ2=0.06,β1=0.008,β3=0.001 with ICs x~(0)=0.2,y~(0)=0.2 in Eq. (6) yields the following mathematical form,

{dα1x~(τ)dτα1=−0.008x~(τ)y~(τ)+0.1+0.11x~(τ)−0.01y~(τ),x~0=0.2,dα2y~(τ)dτα2=0.007x~(τ)y~(τ)+0.57y~(τ)−0.001(y~(τ))2,y~0=0.2.(14)

Case II: Consider p=0.03,δ1=0.05,μ=0.04,δ2=0.06,β1=0.007,β3=0.002 with ICs x~(0)=0.3,y~(0)=0.3 in Eq. (6) yield the following mathematical form:

{dα1x~(τ)dτα1=−0.007x~(τ)y~(τ)+0.1+0.1x~(τ)−0.01y~(τ),x~0=0.3,dα2y~(τ)dτα2=0.005x~(τ)y~(τ)+0.118y~(τ)−0.002(y~(τ))2,y~0=0.3.(15)

Case III: Consider the parameters p=0.02,δ1=0.04,μ=0.05,δ2=0.06,β1=0.006,β3=0.002 with ICs x~(0)=0.1,y~(0)=0.1 in Eq. (6) yield the following mathematical form:

{dα1x~(τ)dτα1=−0.006x~(τ)y~(τ)+0.11+0.11x~(τ)−0.02y~(τ),x~0=0.1,dα2y~(τ)dτα2=0.004x~(τ)y~(τ)+0.108y~(τ)−0.002(y~(τ))2,y~0=0.1.(16)

3.1 Design Methodology

The mathematical form in Eqs. (14)–(16) of the nonlinear fractional system of the White Chomiskey heroin model is investigated through the soft computing supervised LMB-NNs.

The emerging issue of artificial intelligence (AI) is considered a function optimization problem in which we look for the best network parameters to reduce neural network error. Levenberg-Marquardt’s approach easily implements network learning and intelligent computing. This is a method of supervised learning used to supervise the development of some prediction models, decrease notably nonlinear function problems over a few functional parameters, or precisely anticipate the outcomes by specifying a variety of distinct algorithms and patterns. LM technique is also the most prominent method for Feedforward neural networks.

Fig. 1 displays the standard procedure’s structure. First, the prepared LMBs-NNs algorithm is embedded for three cases of NFD-WCM, as illustrated in Table 1. By using 0.001 as the step size for each variable, the total data for LMBs-NNs is 1001 input points found between 0 and 1. Next, the data are randomly distributed for a set of validations, trained, and tested in various ratios to establish the percentage that provides a better grasp of stability and convergence analysis. Finally, the NFD-WCM model is interpreted for several cases using a data set for coupled non-linear higher order fractional differential equations. For LMBs-NNs, the “nftool” is sat, taking the data set for training, testing, and validation as along 7 neurons as, Data set obtained for training is 72%, Data set obtained for testing is 14%, Data set obtained for validation is 14%.

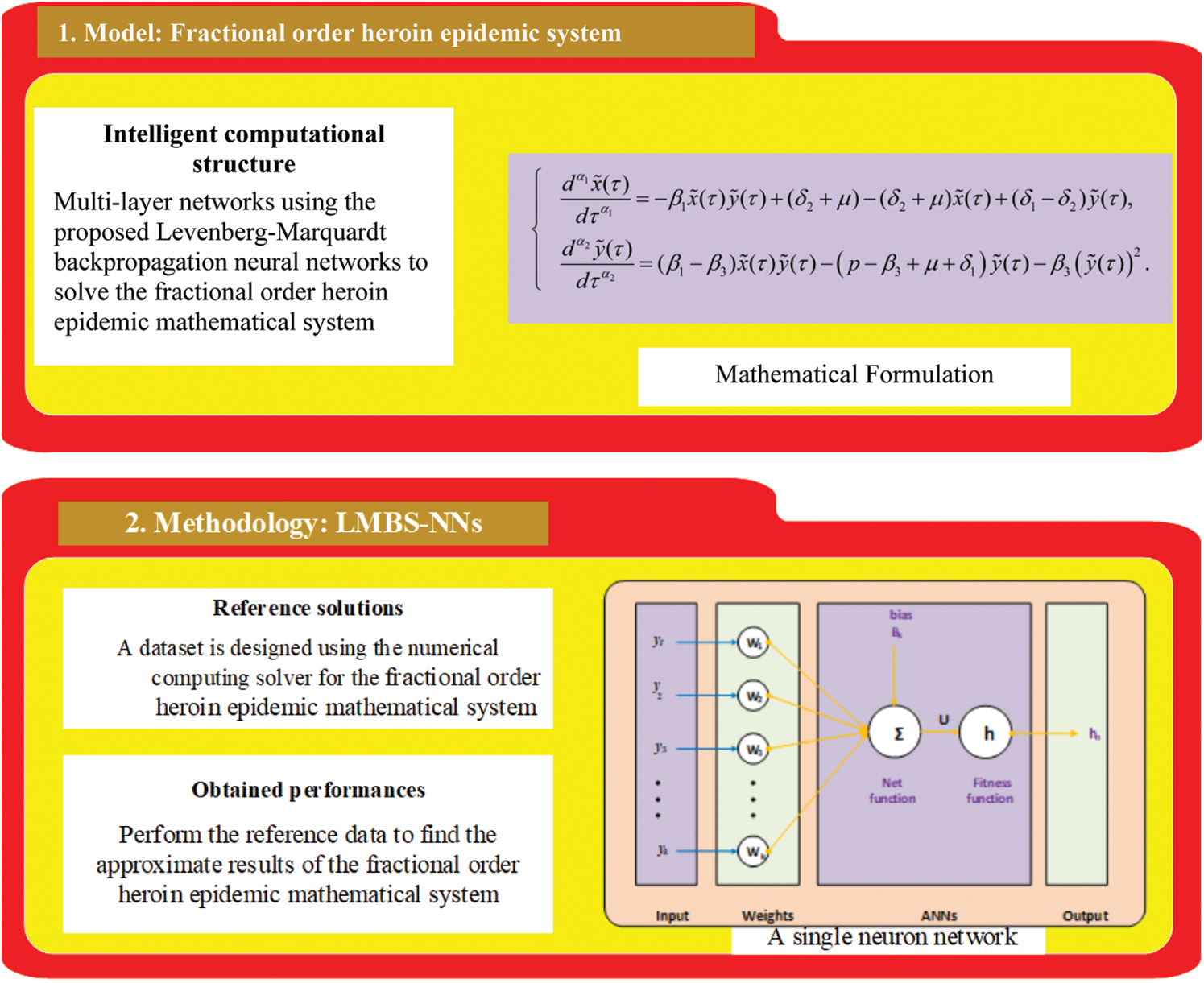
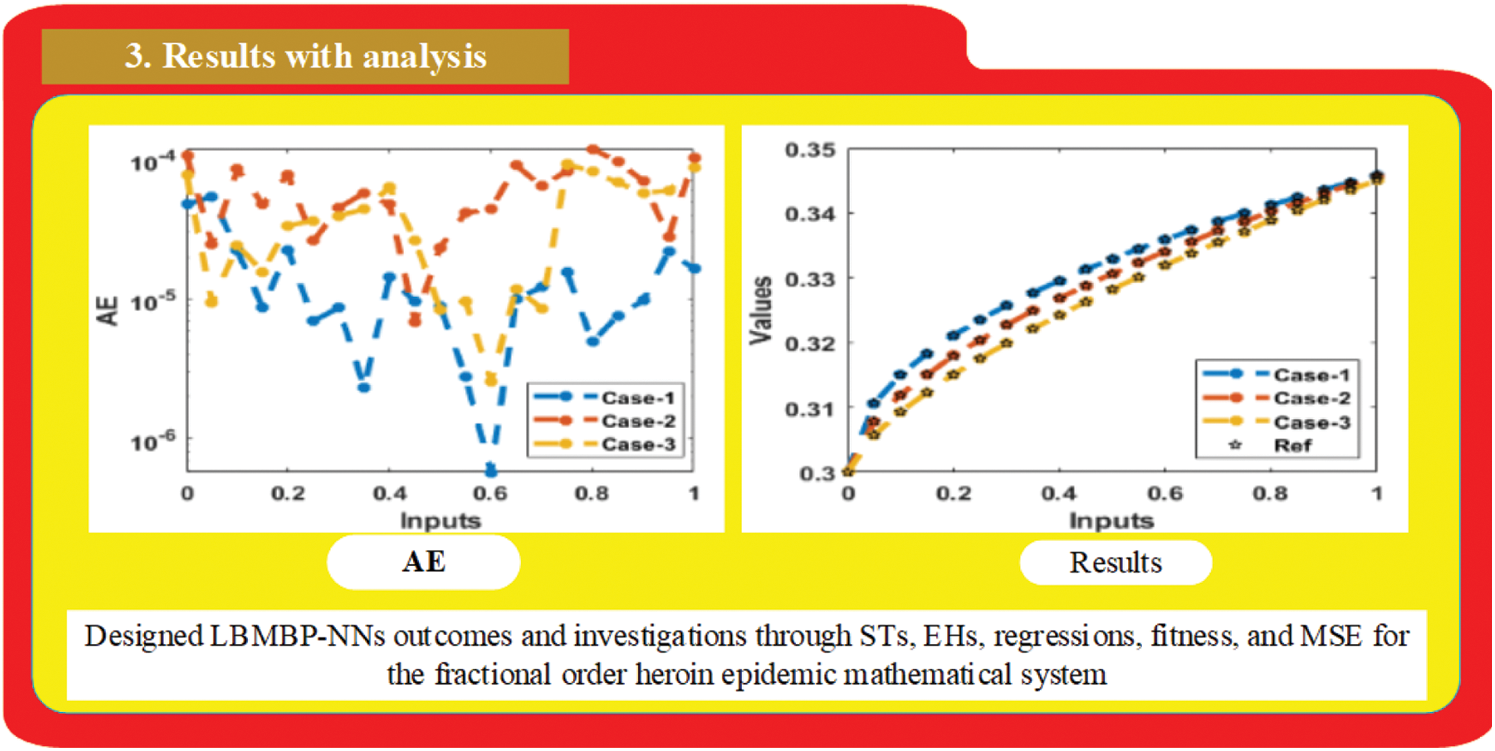
Figure 1: Stepwise frameworks of the nonlinear fractional system of WC heroin model via LMBs-NNs technique. a) mathematical system of heroin model, b) procedure of LMBs-NNs, c) simulation of the proposed model via LMBs-NNs

4  Numerical Results and Discussion

This part presents the numerical results of the proposed NFD-WC-based heroin model through the LMB-NNs algorithm. The fractional order derivatives have been used in many applications [55–61]. The Significant performance of LMBs-NNs has been checked through statistical tools. Comparing of the proposed technique proves the excellent agreement and precision of proposed technique with generated dataset. The structure to compute NFD-WCM is provided in Table 2.

Figs. 2–4 are drawn to show the analysis report of the designed LMBs-NNs technique for the NFD-WC heroin model. The mean square error is measured in Fig. 2 for training, testing, and authentication. The significant performance is found at the points 4.6637×10−10,1.28×10−10, and 4.64×10−9 at epochs 25, 28 and 16 respectively. Fig. 3 shows the state transition values that consist of gradient, Mu, and validation performance of the LMBs-NNs technique. The best gradient values for training, testing, and validation are 9.4085×10−8,9.704×10−8 and 7.8834×10−8 for three cases. Best Mu values are found in the range 1×10−10,1×10−11, and 1×10−10 for cases 1, 2 and 3. In general, the gradient is used for the neural networks’ weight. It ensures that the weight is in a suitable amount and correct direction. Mu tool controls the training algorithm within the domain, whereas the right tool checks the generalized standard of each process. The fitness function and error dynamic are plotted in Fig. 4 representing the precision, convergent, and accuracy of the proposed model solved by LMBs-NNs. The error dynamic is in the range 2×10−4,2×10−4, and 10×10−5. For training, the error between outputs and targeted values are found at points −2.2×10−6,3.1×10−6, and 4.8×10−6 for all three cases. For the testing procedure, the error between outputs and targeted values has been found at points −1.6×10−6,6.5×10−6, and −6.1×10−5. The validation accuracy between the outputs and targeted values are at points 1.5×10−5,1.3×10−5, and 8.8×10−6. The purpose of correlation is to check the validity of regression analysis. The correlation value reached to 1 indicates that the non-linear fractional order system executed the perfect result computed by LMBs-NNs. Figs. 5 and 6 display the results comparability of the function x~(τ) and y~(τ) from nonlinear fractional system of WC heroin model by LMBs-NNs and accomplished absolute errors of x~(τ) and y~(τ) for three different cases. Absolute error is considered the benchmark form of accuracy. The smallest AE values in the range 10−6−10−4, and 0−10−4 for the functions x~(τ) and y~(τ) respectively, indicates the performance of LMBs-NNs for NFD-WCM.

Figure 2: High Performance of LMBs-NNs for the nonlinear fractional system of WC heroin model using the mean square error tool at suitable epochs for three different cases

Figure 3: State transition for three cases using the nonlinear fractional system of WC heroin model by LMBs-NNs to compute the proposed model

Figure 4: Comparison of outputs using the LMBs-NNs for the nonlinear fractional system of WC heroin model

Figure 5: Results comparability of the function x~(τ) from the nonlinear fractional system of WC heroin model by LMBs-NNs and accomplished absolute error of x~(τ) for three different cases

Figure 6: Results comparability of the function y~(τ) from the nonlinear fractional system of WC heroin model by LMBs-NNs and accomplished absolute error of y~(τ) for three different cases

5  Conclusion

This study aims to construct the artificial neural networks in conjunction with Levenberg Marquardt backpropagation, i.e., LMBs-NNs, to solve the nonlinear fractional system of the White-Comiskey model of heroin (NFD-WCM). This model depends upon three compartments, susceptible, drug user without treatment, and drug’ user undergoing the treatment and cure. The significance of supervised LMBs-NNs can be described in the following steps of statistical tools:

•   The LMBs-NNs are implemented using authentication, testing, and training data samples.

•   For training, validation, and testing, the ratios for solving three cases of the NFD-WCM are chosen with samples of 72%, 14%, and 14%, respectively.

•   The nonlinear fractional order system of the heroin model is solved by observing the brilliance, quality, precision, and stability of the LMBs-NNs and matching/overlapping the findings.

•   The M.S.E convergence graphs are used to check the system’s testing, authentication, and security. M.S.E in the range 4.64×10−9 to 4.6637×10−10 show the efficacy of the method.

•   The correlation results are reliable enough to verify the regression processes. The gradient values for each case of the nonlinear fractional model of heroin are obtained using the step size.

Funding Statement: This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.