Optimization of Electrocardiogram Classification Using Dipper Throated Algorithm and Differential Evolution

1  Introduction

An Electrocardiogram (ECG) is a recording of the electrical activity of the heart. Different vital places have received these messages. Fig. 1 shows these sections, including P, QRS complex, and T [1]. The P wave occurs during the depolarization of the atria. A QRS wave that may be divided into two halves occurs [2]. Powerful and distinctive equipment in ECG applications has been developed to detect and classify the ECG signal [3]. In addition, the quick detection of heart illness is critical for people who have heart difficulties. Heart disease diagnosis relies heavily on electrocardiogram (ECG) analysis [4]. ECG categorization, in particular, has benefited from computer-aided techniques [5]. For many years, researchers have been working on ways to identify and distinguish between normal and abnormal cardiac records. The AdaBoost method [6], the Radial basis function [7], the Adaptive neuro-fuzzy [8], the Convolutional neural network (CNN) [9], and the Extreme Learning Machine (ELM) approach [10] are some examples of classification algorithms. As a result, computer-aided categorization of ECG and EEG has been used because of its capacity to quickly learn and generalize [11].

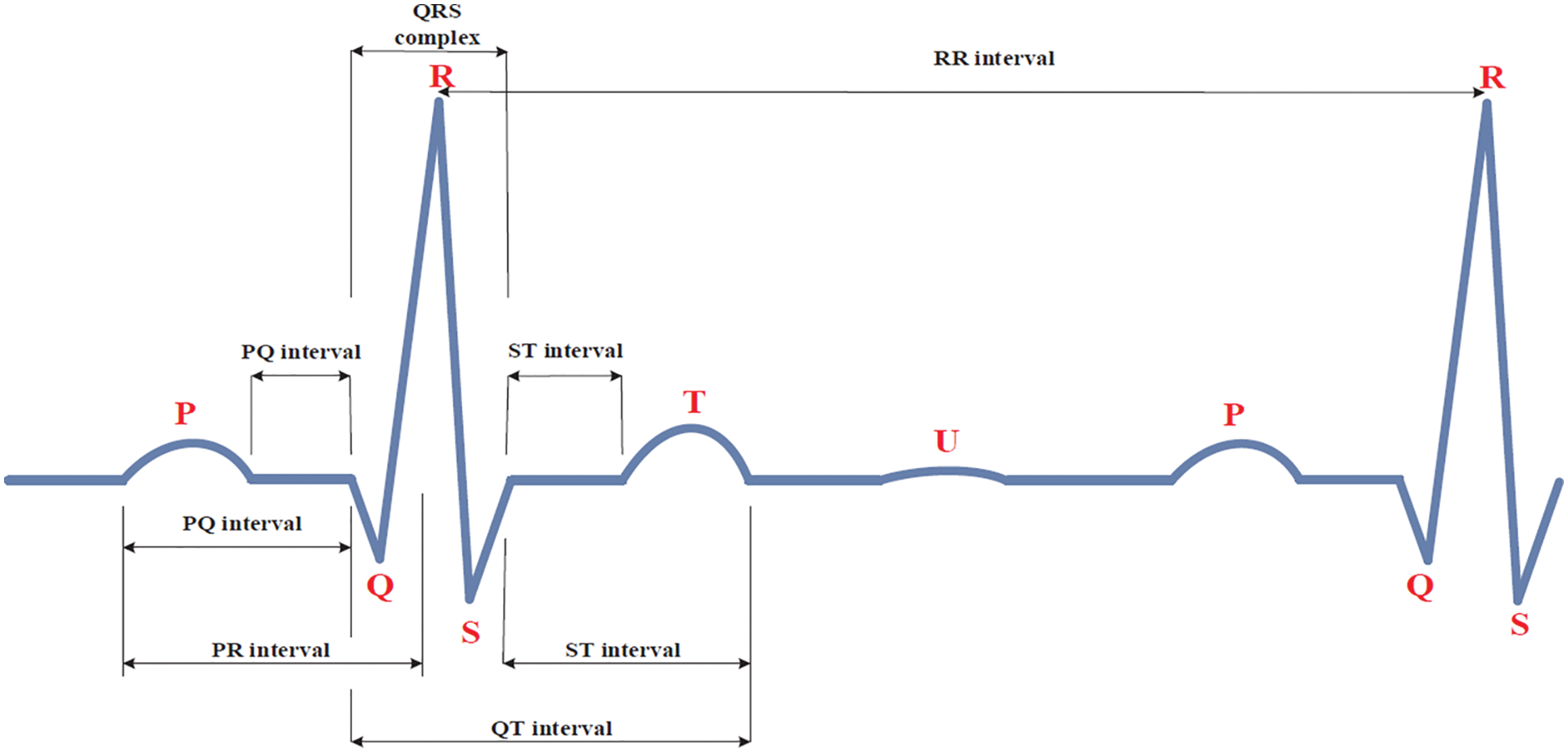
Figure 1: The waveform of the electrocardiogram signal

However, the lack of local minima, undetermined learning percentage, the selection of hidden neurons, and overfitting are some of the downsides. It may be possible to mitigate the drawbacks of the neural network (NN) by utilizing population-based methodologies inspired by nature and capable of global search, such as the dipper throated optimization (DTO), differential evolution (DE) approach, the particle swarm optimization (PSO) approach and the genetic algorithm (GA) approach [12]. ECG diagnostics, which are largely based on P, QRS, and T wave features, are used to assess the heart recordings. Professionals responsible for producing an accurate detection judgment must, in the meanwhile, precisely identify cardiac signals. Cardiovascular illness diagnosis relies heavily on machine learning algorithms that identify the heart’s electrical activity. This paper analyzes the influence of employing a new optimization algorithm to optimize the parameters of NN based on DTO and DE for the appropriate classification of heart activity.

2  Literature Review

In recent years, detecting CVD from ECG attracted a large number of researchers to present new algorithms aim at increasing the accuracy of detection. A proposed method that depends on measuring and analyzing the ECG measurements, which reflect the CVDs conditions, is presented in [13,14]. Machine learning algorithms based on ECG signals are also presented in [15]. A suggested three methods used convolutional neural networks (CNN) to classify atrial fibrillation; the first one achieves 89% accuracy [16], the second one achieves 86% accuracy [17], while the third one classifies ECG signals into three types and achieves 99% [18]. Another two methods depend on heart rate variability features and support vector machine to classify heart failure, and normal sinus rhythm is proposed. The first achieves 93.33% accuracy [19], while the second also depends on multifractal fluctuation analysis [20]. Extracting features from the interval between two successive peaks in the ECG and using a deep learning algorithm, which consists of CNN with a neural network, is presented and achieves 99% accuracy [21]. Another research that depends on the morphological conditions of ECG signal to detect heart failure used ECG heartbeats as an input of the CNN and achieved 100% accuracy [22]. Three classifier algorithms used k-mean clustering, k-nearest neighbor (K-NN), and multi-layer perception to achieve 88%, 99%, and 99%, respectively, presented in [23]. Another approach used a classifier with least-square, maximum likelihood, and support vector machine, and each approach achieved 84%, 88%, and 76% accuracy, respectively [24]. Numerous researchers used entropy-primarily based features to extract data from ECG signals. An entropy-based atrial fibrillation classifier and achieve an area under the curve score of 0.981 proposed in [25]. Another approach used entropy as a feature in classifying atrial fibrillation and achieving area under the curve score of 0.972 [26]. Area under curve score of 0.97 is also achieved when using entropy feature with support vector machine classifier [27]. Calculating Shannon entropy and sample entropy feature and proving that it represents atrial fibrillation and normal sinus rhythm is done with an accuracy of 91% [28]. Feature extraction is the difficult step in the process of ECG classification; the following research used a statistical method by applying the Hjorth descriptor algorithm for ECG feature extraction [29,30]. However, this method suffers from the noise that affects the value of variance. Therefore, the statistical method is limited and can not be used to extract ECG features effectively. Other approaches used Discrete wavelet transform (DWT) to extract ECG features in the time or frequency domain, which decomposes the signal into sub-bands containing low-frequency components and high-frequency components, giving more information for the feature selection. A suggested algorithm to classify arrhythmia depending on DWT achieves 99% accuracy is presented in [31].

3  Materials and Methods

The material and methods utilized in the proposed approach are presented and discussed in this section.

3.1 Differential Evolution Algorithm

Linear or non-linear optimization can be used for a wide range of scientific, social, and applied problems. Several of the application’s issues are non-linear in nature. There are several approaches to dealing with non-linear problems. Even additional variables and data kinds can enhance the difficulty of solving an issue even further if needed. Using deterministic methodologies, it is challenging to model and solve such problems. Heuristic techniques have been improved in order to address the issues outlined above. Fast results can be achieved by using multi-point search algorithms, which use heuristics depending on the population. Because of this, Price and Storm came up with the Differential Evolutionary Algorithm (DEA) in 1995. In situations where continuous data is complex, DEA can give successful results based on Genetic Algorithms (GA) for operations and operators [36–39]. Drug Enforcement Administration (DEA) research is ongoing at any given moment. There are several iterations in the process of solving problems with the help of operators. Additionally, the purpose of DEA is to enhance performance in real-valued coding-based problem-solving situations. Cross-breeding, mutation and selection operators are all used in the DEA, just as they are in the GA system. For example, in contrast with GA, no single operator can be applied to all of the population at once. The procedure of randomly choosing three chromosomes and processing them one at a time results in the birth of a new individual. Mutation and crossover processing are required for these processes.

To ensure the survival of future generations, the newly acquired youthful chromosome will be handed on to the next generation as a more physically fit individual. As a result, the selection operator is also employed. The quality of a solution is determined by its value to the target function, according to [40–42]. (fitness value). A number of advantages and crucial criteria are presented in Tab. 1 for the DEA algorithm. With a D vector, an optimization may be represented by the D parameter. Random NP population vector samples are generated using DEA. It is necessary to apply mutations, crossovers, and selection processes to generate this population [45]. Fig. 2 illustrates the DEA method’s fundamental structure. Some of the genes on the current chromosome will be altered by the mutation, which is meant to cause random changes. As a result of these many circumstances, the solution point denoted by its chromosome moves about inside the solution domain. Changes in direction and quantity of movement must be made in order for a mutation to occur. All of the DNA in the DEA is altered, yet there are three separate chromosomes. The difference between first two chromosomes selected is taken into consideration. Different chromosomes double the scaling factor parameter. This option commonly accepts values between 0 and 2. When the best match has been found, the weighted difference chromosome is combined with this chromosome. In other words, the crossover will benefit from the mutant chromosome’s abnormalities.

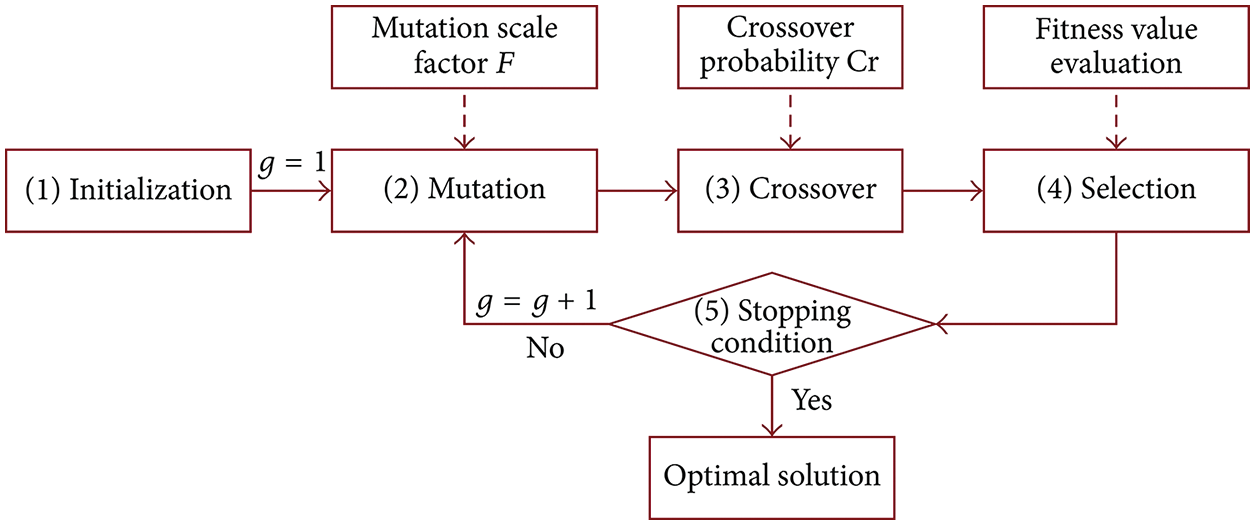
Figure 2: The differential evolution optimization algorithm

3.2 Dipper Throated Optimization

The optimization process of using throated dipper optimization (DTO) is based on measuring the locations and speed of swimming and flying birds in a simulation of the actual process of hunting their food. Fig. 3 shows the steps of the DTO process.

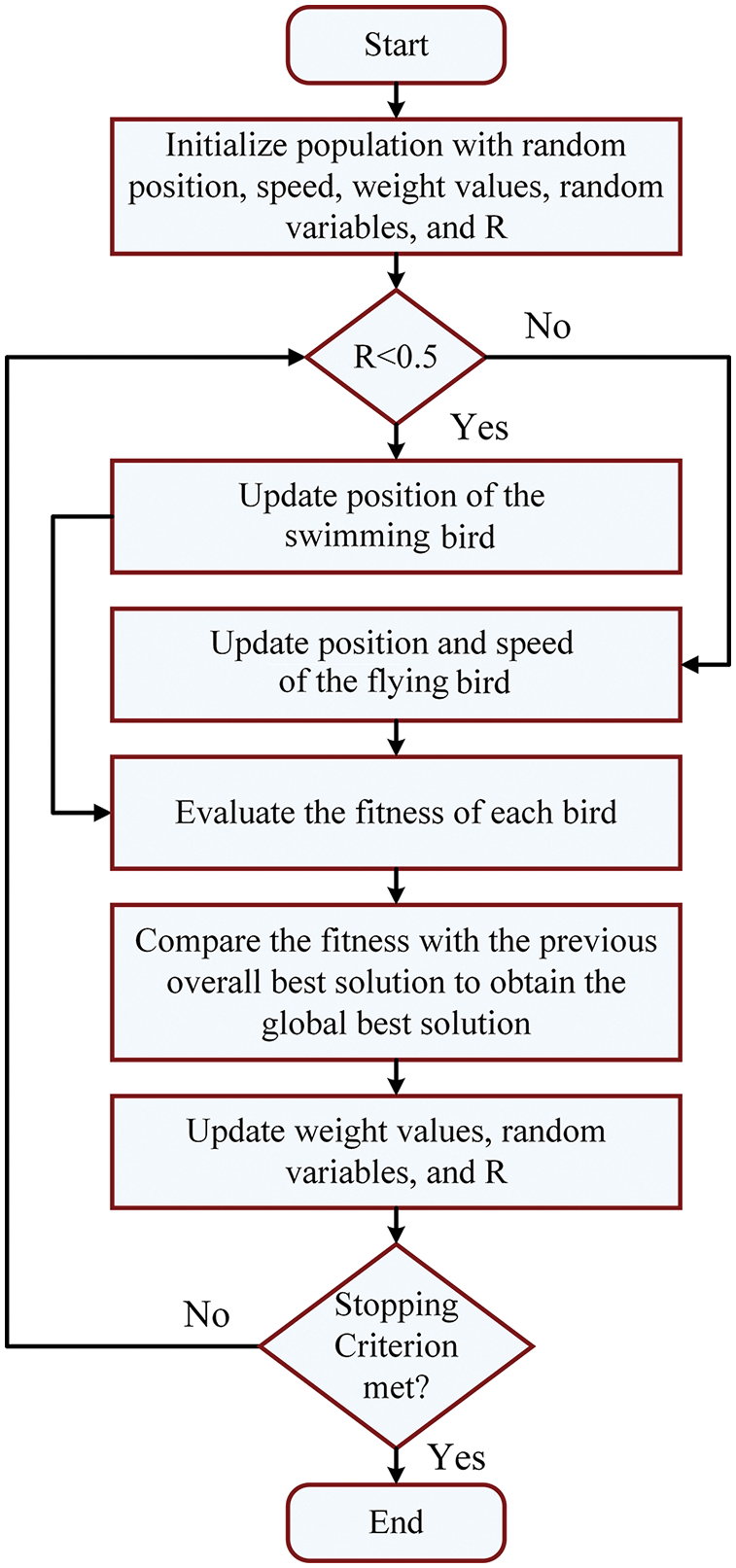
Figure 3: The steps of the dipper throated optimization process

The update of the locations and speed of the swimming birds is performed using the following equations.

BLnd(t+1)=BLbest(t)−C1.|C2.BLbest(t)−BLnd(t)|(1)

where t is the iteration number, and BLnd(t) and BLbest(t) are the normal location and best location of the bird, and C1 and C2 are adaptive values whose values are changed during the optimization process based on the iteration number and random values. On the other hand, the update of the flying bird’s location is performed using the following equation.

BLnd(t+1)=BLnd(t)+BS(t+1)(2)

BS(t+1)=C3BS(t)+C4r1(BLbest(t)−BLnd(t))+C5r1(BLGbest−BLnd(t))(3)

where BS(t+1) is the updated speed of each bird, r1 is a random number in [0; 1], BLGbest is the global best location, and C3 is a weight value, C4 and C5 are constants.

3.3 Multi-Layer Perceptron

For the processing of information and communication between a set of nodes, artificial neural networks (ANNs) follow the principles of the nervous system. Signals are sent from one neuron to another via the Synapse (the link between neurons). The most popular uses of ANN [46] are in speech recognition, regression, and learning algorithms. To get the most out of ANN, it is critical to focus on the learning process and parameter optimization. Multi-layer perceptron (MLP) is a popular ANN algorithm. Fig. 4 depicts the typical MLP structure.

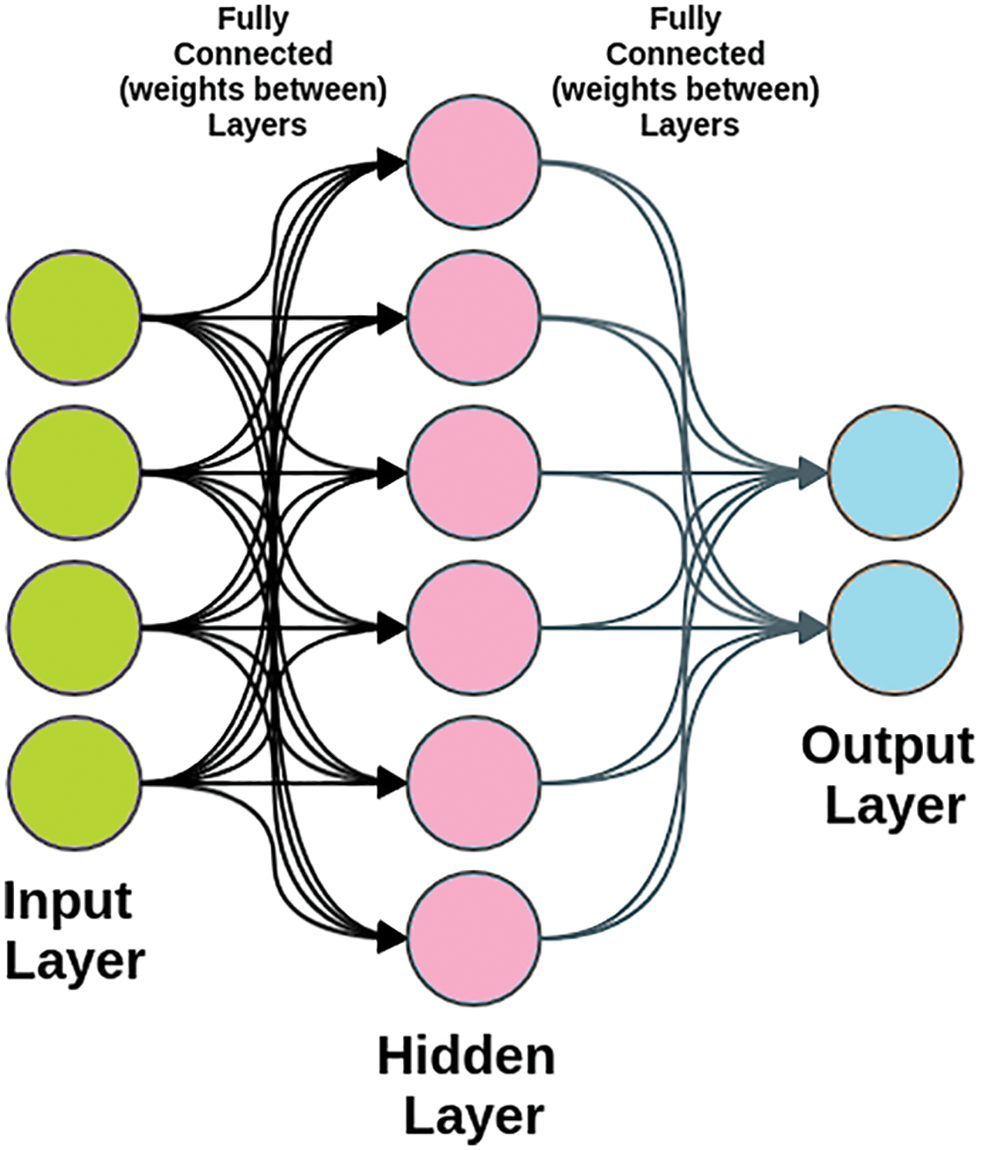
Figure 4: The structure of the multi-layer neural network

The output of a node in MLP is measured using the following equation.

Sj=∑i=1NwijIi+βj(4)

where Ii denotes the input i and wij stands for the weight of the connection between the input i and the neuron j. The value βj refers to the bias of layer j. The output of node j is determined using the most often suggested function, sigmoid activation, which is represented by the following equation.

fj(Sj)=11+exp−Sj(5)

4  Methodology

The block diagram of the proposed approach for classifying ECG signals is depicted in Fig. 5. This figure shows how the proposed approach is divided into four components. Preprocessing begins with ECG signals pulled from the PTBDB database. There are two parts to preprocessing: 60 Hz noise removal and baseline wandering. In addition, the block diagram shows how ECG signals is used to extract morphological and statistical features. Following the optimization and classification phase of the proposed model. The final step is to classify the signal into normal and abnormal categories.

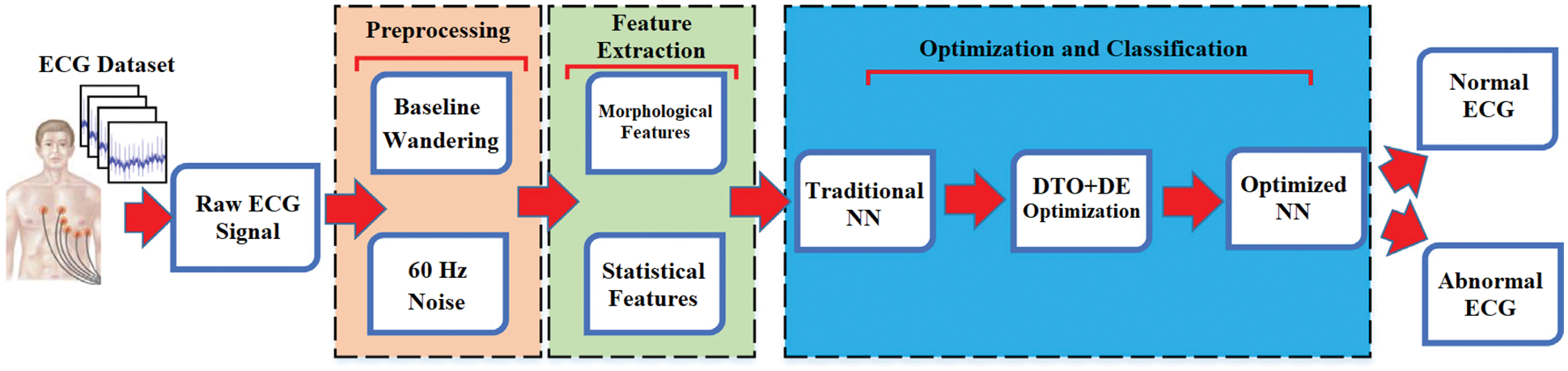
Figure 5: The block diagram of the proposed system of ECG signal classification

4.1 The Proposed DTO-DE Algorithm

As the classification of ECG signal is based on the NN classifier, in this section, we proposed a new optimization algorithm for optimizing the parameters of the NN to boost its performance. The proposed optimization algorithm is based on combining two powerful optimization algorithms in a unified algorithm. These two algorithms are the dipper throated algorithm and the differential evolution algorithm. Algorithm 1 presents the steps of the proposed algorithm. The main idea of the proposed algorithm is to move the birds more quickly towards the best solution. Therefore, the update of the bird locations is performed using the following equation.

BLnd(t+1)=r1+z∗r2+(1−z)∗r3+BS(t+1)(6)

where r1,r2,r3 are random variables, and z is a dynamic variable whose value is calculated as follows.

z=1−(titer_max)2(7)

4.2 Feature Selection

The feature selection process is performed by binary selection of the significant features. This process is realized by converting the resulting solution from the proposed optimization algorithm to binary. The conversion is performed in terms of the sigmoid function to get the binary values 0 or 1 corresponding to each feature. The following equation expresses the process of converting solution to binary, where BLbest denotes the bird’s best position at iteration t.

BinarySolution(t+1)={1,ifSigmoid(BLbest)≥0.50,otherwise(8)

Sigmoid(BLbest)=11+exp−10(BLbest−0.5)(9)

5  Experimental Results

The conducted experiments are split into two scenarios. The first scenario targets evaluating the proposed feature selection method, whereas the second scenario targets the evaluation of the proposed optimization approach. The following sections present the achieved results of each scenario, starting with presenting the dataset employed in the conducted experiments.

5.1 Dataset

Physionet’s PTBDB [47] was used to test the proposed approach. The total number of records in the PTB ECG diagnostic dataset is 549. A total of 294 people volunteered to donate their blood for the study. There are 15 simultaneously recorded signals in each of the samples. We were able to conduct experiments using data from healthy (52 cases) and abnormal patients (148 cases). Fig. 6 shows that all measurements in this investigation were taken from lead II on the PTB database.

Figure 6: Sample ECG in the PTB dataset with number s0001_re

5.2 Preprocessing

Signal processing experiences oscillations because of undesirable noise and interference. This stage is critical to the classification of ECGs since the ECG contains a large number of unsettling sounds. As a result, it is widely used in biomedical research to achieve robust and unambiguous results. Baseline system interactions and wandering are two examples of the types of abnormalities that may be detected in ECG recordings. These abnormalities are corrected using the symlet scaling filter and the denoising operations.

5.3 Feature Extraction

The biomedical signals can be classified by extracting the significant features from the input signal. Following the preprocessing stage, it is important to get the precise qualities that will be utilized in the last stage in the processing chain [48–54]. In this paper, we utilized 11 features, namely, mean, maximum, minimum, ST interval, QT interval, P-wave amplitude, PR interval, QRS complex amplitude, Kurtosis, Skewness, and Variance. The selection of the best features that can boost the classification accuracy of the ECG data can be achieved by means of the proposed feature selection method.

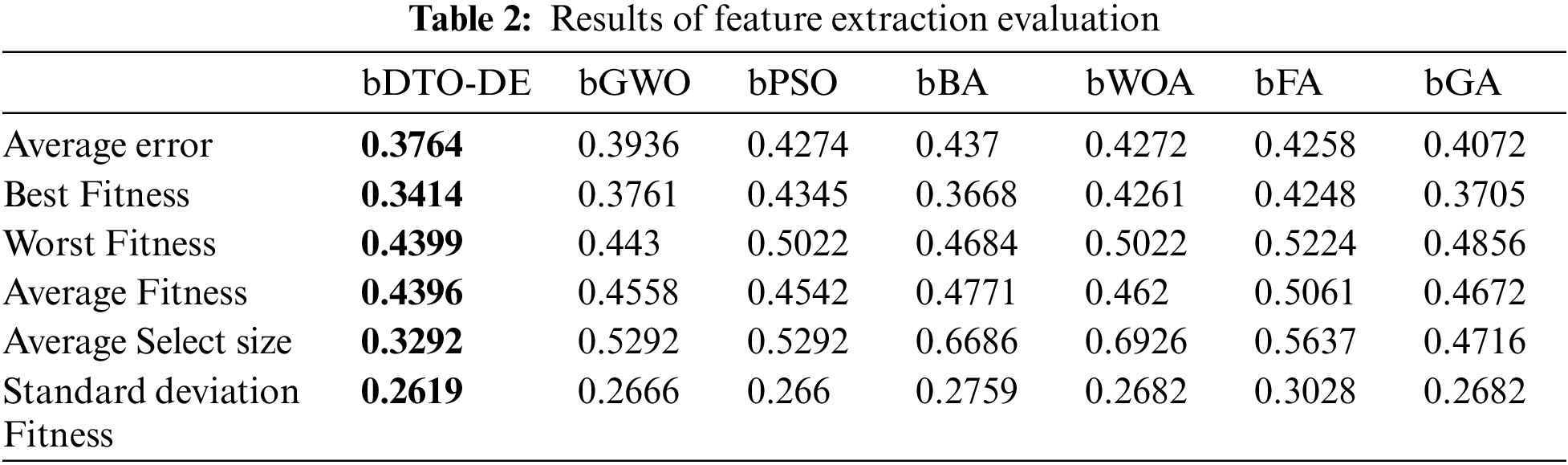
Tab. 2 presents the results of the feature selection using the proposed binary DTO-DE with comparison to other feature selection methods. In the table, six feature selection methods are included in the comparison results. These methods are binary grey wolf optimizer (bGWO), binary particle swarm optimization (bPSO), binary bat algorithm (bBA), binary whale optimization algorithm (bWOA), and binary firefly algorithm (bFA), and binary genetic algorithm (bGA). As shown in the table, the proposed feature selection algorithm achieved the best average error, best fitness, worst fitness, average select size, and standard deviation fitness. These results confirm the superiority of the proposed feature selection method.

5.4 Classification Results and Comparisons

On the other hand, to determine the best machine learning model to utilize for classifying the input ECG, an experiment is conducted to compare the performance of three classifiers, namely, neural network (NN), K-nearest neighbor (KNN), and support vector machine (SVM). The comparison results are presented in Tab. 3. From these results, it can be noted that the best classifier for this case is the neural network. Therefore, we adopted this classifier for optimization using the proposed optimization algorithm.

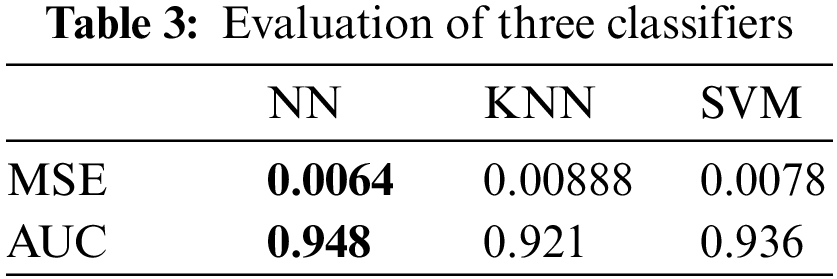
The adopted NN classifier is optimized using the proposed optimization algorithm and compared with four other optimization algorithms, namely WOA, GWO, GA, and PSO. Tab. 4 presents the evaluation of the results achieved by the optimized NN using the optimization methods. In this table, it can be noted that the optimization of NN using the proposed algorithm achieves the best results and outperforms the results achieved by NN when optimized using other optimization methods.

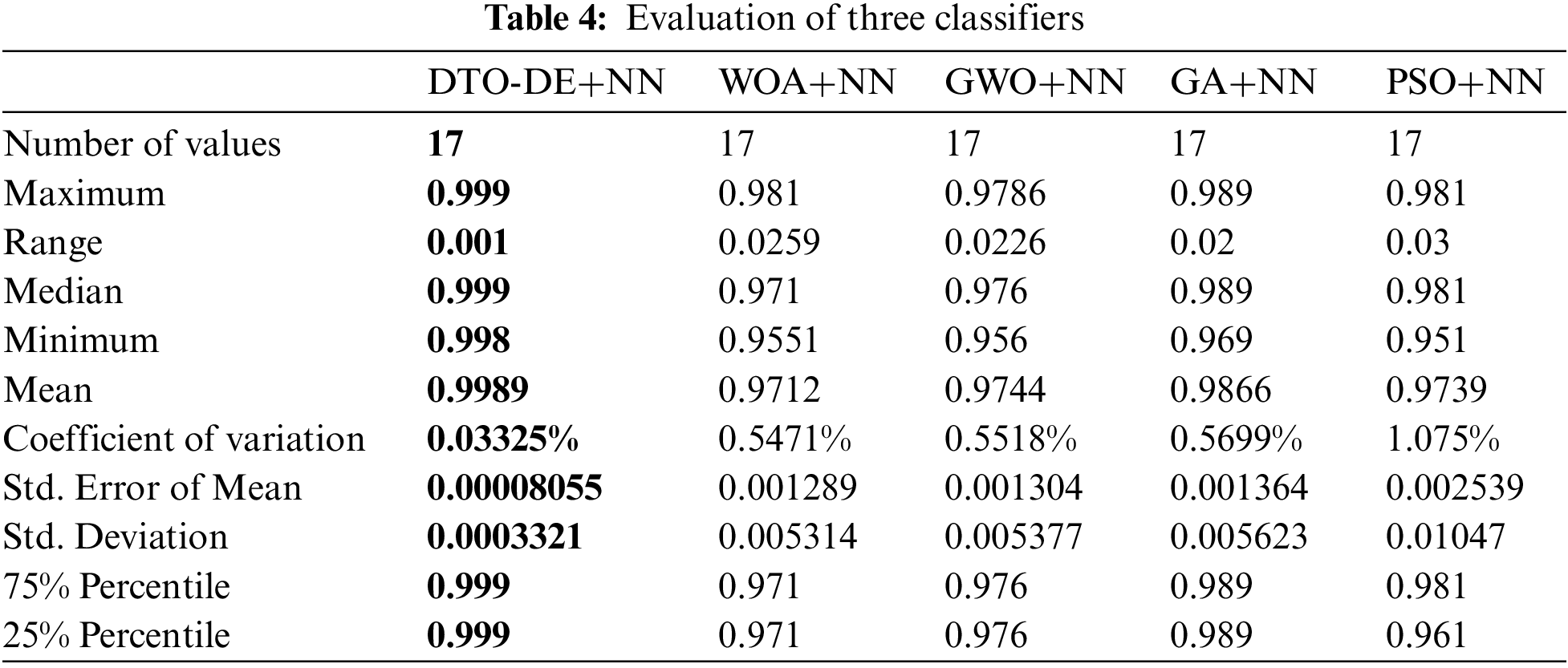
To further investigate the statistical significance and stability of the proposed approach, two statistical tests were performed, namely, Wilcoxon signed-rank test and the one-way analysis of variance (ANOVA) test. The results of the first test are presented in Tab. 5. In this table, the results show the significance of the proposed approach as well as the significance of the other methods. To show the effectiveness of the proposed approach, the ANOVA test results are presented in Tab. 6. These results emphasize the effectiveness of the proposed approach based on the test hypotheses.

In addition, a set of analysis plots are generated to study the results achieved by the proposed approach. These plots are shown in Fig. 7 as the residual, homoscedasticity, QQ, and heatmap plots. The residual and homoscedasticity represent the ranges of error in which the small range indicates the best performance. In these plots, the range of residual error in the prediction results is −0.03 to 0.01 and 0 to 0.025 for the residual and homoscedasticity plots, respectively. Moreover, the QQ plot shows a line fitting the achieved results with respect to the target values. In this plot, the results approximately fit a line which represents accurate results.

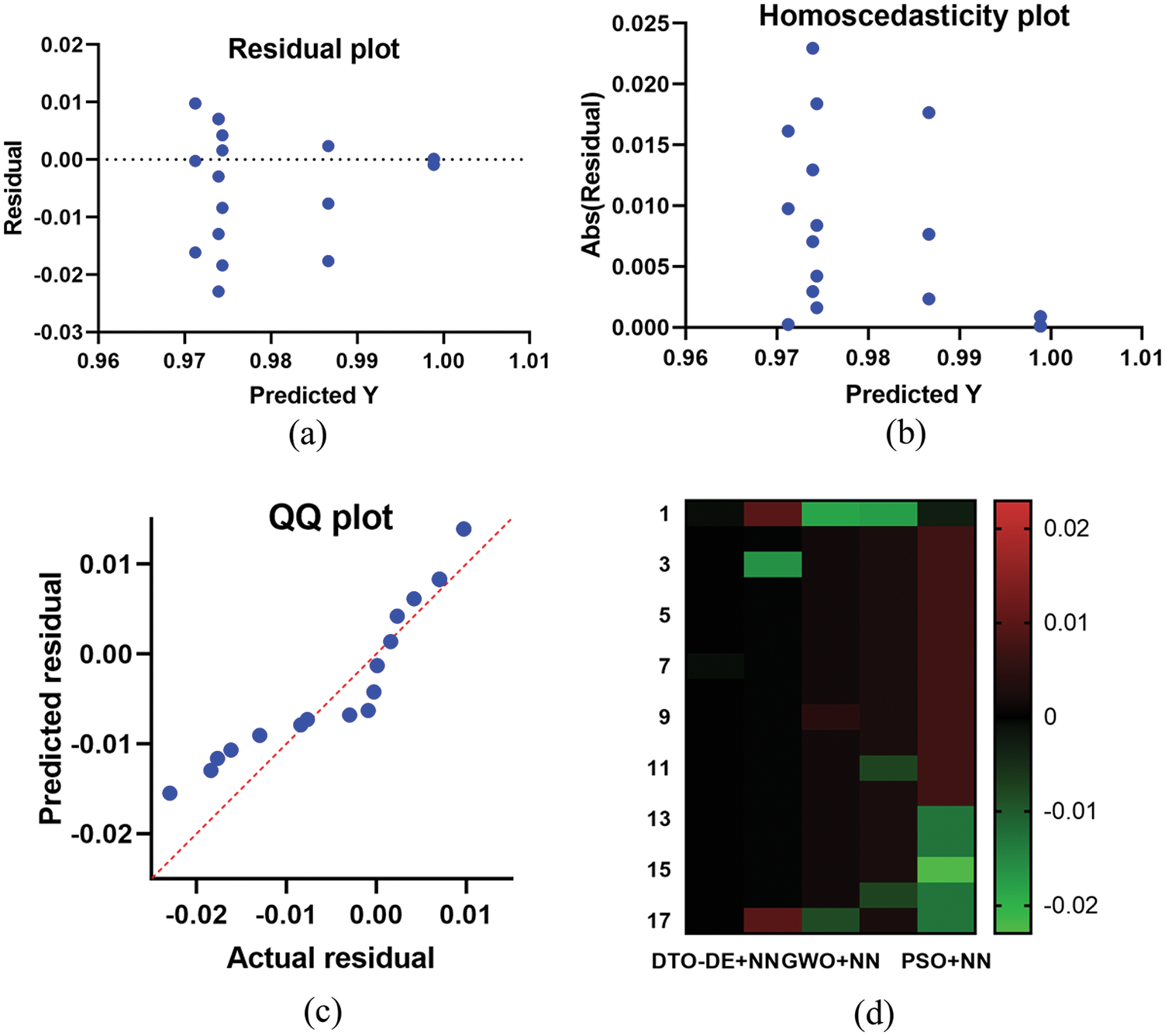
Figure 7: Analysis of the achieved results using the proposed approach

To emphasize the superiority of the proposed approach, two plots are generated based on the achieved results; the first plot is the accuracy plot, in which the range of accuracies achieved by each approach is drawn the figure. The accuracy ranges are plotted in Fig. 8. In this figure, it can be noted that the accuracy of the proposed approach is in the range of 0.998%–100%, which outperforms the accuracy range of the other methods. In addition, the histogram shown in Fig. 9 displays the number of achievements of certain accuracy. In this figure, the proposed approach has a significant number of results achieving an accuracy of 0.998%, which is superior to the other methods.

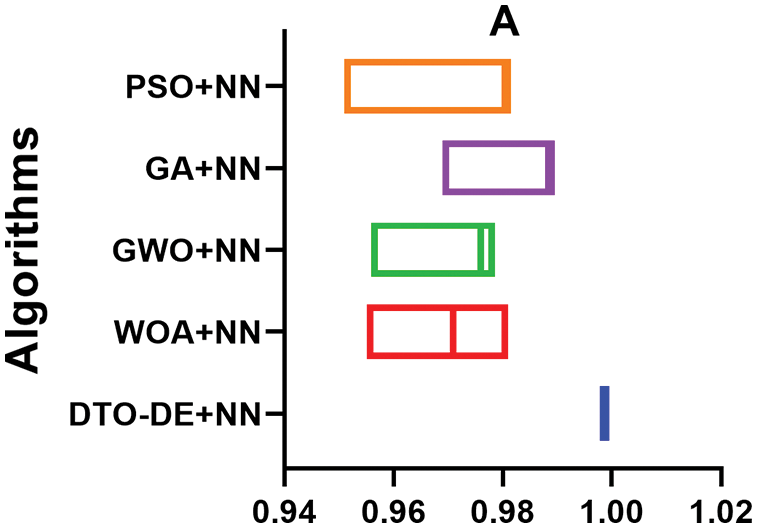
Figure 8: Range of accuracy achieved by the proposed approach and other approaches

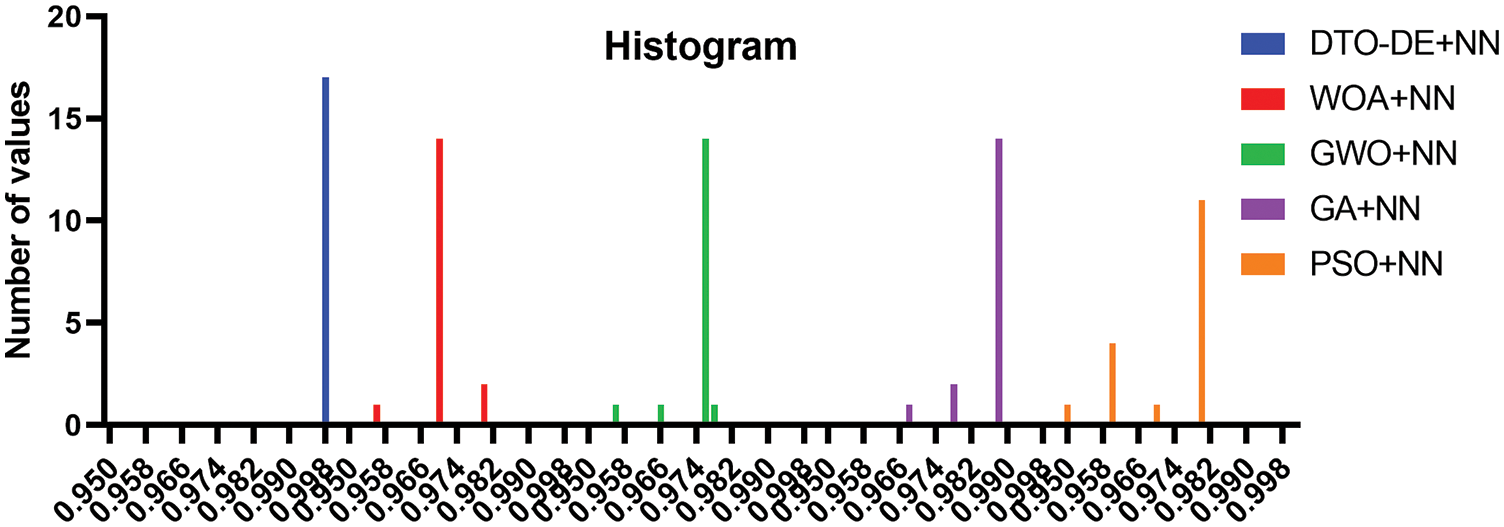
Figure 9: Histogram of the accuracy achieved by the proposed approach and other approaches

6  Conclusions

In this work, a novel approach for classifying the ECG signal is proposed. The proposed approach is based on optimizing the parameters of neural networks using a hybrid of dipper throated optimization and differential evolution optimization algorithms. The proposed model was evaluated using the freely available PTB Diagnostic ECG database. Taking into account important aspects of the automated ECG analysis, such as methodologies, databases, classes, feature types, and the accuracy, a comparison was carried out. The recorded results showed that the proposed approach could achieve the highest accuracy when compared to other non-optimized models. On the other hand, other optimization methods we applied to the same task to show the superiority of the proposed optimization approach. The comparison results confirmed the findings and emphasized the effectiveness of the proposed approach. In addition, a statistical analysis is performed to prove the stability and significance of the proposed approach. Moreover, a one-way analysis of variance and Wilcoxon signed-rank test were applied to get more insight into the significance of the proposed approach.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R300), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R300), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Diker, E. Avci and M. Gedikpinar, “Determination of R-peaks in ECG signal using hilbert transform and pan-tompkins algorithms,” in Signal Processing and Communications Applications Conf., Antalya, Turkey, pp. 1–4, 2017. [Google Scholar]

 2.  D. Ojha and M. Subashini, “Analysis of electrocardiograph (ECG) signal for the detection of abnormalities using MATLAB,” International Journal of Biomedical and Biological Engineering, vol. 8, no. 2, pp. 114–117, 2014. [Google Scholar]

 3.  S. Kulkarni, “DWT and ANN based heart arrhythmia disease diagnosis from MIT-BIH ECG signal data,” International Journal Recent Innovation Trends in Computation and Communication, vol. 3, no. 1, pp. 276–279, 2015. [Google Scholar]

 4.  J. Mannurmath and M. Raveendra, “MATLAB based ECG signal classification,” International Journal of Science Engineering Technology Research, vol. 3, no. 7, pp. 1946–1951, 2014. [Google Scholar]

 5.  E. Pasolli and F. Melgani, “Genetic algorithm-based method for mitigating label noise issue in ECG signal classification,” Biomedical Signal Process Control, vol. 19, no. 1, pp. 130–136, 2015. [Google Scholar]

 6.  Z. Yang and Z. Zhidong, “Fetal state assessment based on cardiotocography parameters using PCA and AdaBoost,” in Int. Congress on Image and Signal Proc cessing, BioMedical Engineering and Informatics, Shanghai, China, pp. 1–6, 2017. [Google Scholar]

 7.  M. Korurek and B. Dogan, “ECG beat classification using particle swarm optimization and radial basis function neural network,” Expert Systems Applications, vol. 37, no. 12, pp. 7563–7569, 2010. [Google Scholar]

 8.  A. Salamai, A. Ageeli and E. -S. M. El-kenawy, “Forecasting E-commerce adoption based on bidirectional recurrent neural networks,” Computers, Materials and Continua, vol. 70, no. 1, pp. 10.32604, 2021. [Google Scholar]

 9.  A. Ali Alhussan, E. M. El-kenawy, H. Nasser AlEisa, M. El-SAID, S. A. Ward et al., “Optimizationensemble weights model for wind forecasting system,” Computers, Materials & Continua, vol. 73, no. 2, pp. 2619–2635, 2022. [Google Scholar]

10. J. Tang, C. Deng and G. Huang, “Extreme learning machine for multi-layer perceptron,” IEEE Transactions on Neural Networks and Learning Systems, vol. 2015, no. 1, pp. 1–13, 2015. [Google Scholar]

11. G. Huang, H. Zhou, X. Ding and R. Zhang, “Extreme learning machine for regression and multiclass classification,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 42, no. 2, pp. 513–529, 2012. [Google Scholar]

12. H. Farahani and F. Rashidi, “Optimal allocation of plug-in electric vehicle capacity to produce active, reactive and distorted powers using differential evolution based artificial bee colony algorithm,” IET Science Measurement Technology, vol. 11, no. 8, no. 1, pp. 1058–1070, 2017. [Google Scholar]

13. C. Krittanawong, H. Virk, S. Bangalore, Z. Wang, K. Johnson et al., “Machine learning prediction in cardiovascular diseases: A meta-analysis,” Scientific Reports, vol. 10, no. 1, pp. 16057–16068, 2020. [Google Scholar]

14. G. Taye, H. Hwang and K. Lim, “Application of convolutional neural network for predicting the occurrence of ventricular tachyarrhythmia using heart rate variability features,” Scientific Reports, vol. 10, no. 1, pp. 6769–6776, 2020. [Google Scholar]

15. O. Faust, N. Lei, E. Chew, E. Ciaccio and U. Acharya, “A smart service platform for cost efficient cardiac health monitoring,” International Journal of Environment Resources and Public Health, vol. 17, no. 1, pp. 1–18, 2020. [Google Scholar]

16. Y. Ping and C. Chen, “Automatic detection of atrial fibrillation based on CNN-LSTM and shortcut connections,” Healthcare, vol. 8, no. 1, pp. 1–17, 2020. [Google Scholar]

17. L. Sidrah and K. Dashtipour, “Detection of atrial fibrillation using a machine learning approach,” Information, vol. 11, no. 1, pp. 1–15, 2020. [Google Scholar]

18. S. Nurmaini and A. Tondas, “Robust detection of atrial fibrillation from short-term electrocardiogram using convolutional neural networks,” Future Generation in Computer Systems, vol. 113, no. 1, pp. 304–317, 2020. [Google Scholar]

19. R. Sharma, A. Kumar, R. Pachori and U. Acharya, “Accurate automated detection of congestive heart failure using eigenvalue decomposition based features extracted from HRV signals,” Biocybernetics and Biomedical Engineering, vol. 39, no. 1, pp. 312–327, 2018. [Google Scholar]

20. S. Li, “Multifractal detrended fluctuation analysis of congestive heart failure disease based on constructed heartbeat sequence,” IEEE Access, vol. 8, no. 1, pp. 205244–205249, 2020. [Google Scholar]

21. W. Ning, S. Li, D. Wei, L. Guo and H. Chen, “Automatic detection of congestive heart failure based on a hybrid deep learning algorithm in the internet of medical things,” IEEE Internet Things, vol. 8, no. 1, pp. 12550–12558, 2021. [Google Scholar]

22. M. Porumb, E. Iadanza, S. Massaro and L. Pecchia, “A convolutional neural network approach to detect congestive heartfailure,” Biomedical Signal Processing Control, vol. 55, no. 1, pp. 101597–101610, 2020. [Google Scholar]

23. S. Hadiyoso and A. Rizal, “Electrocardiogram signal classification using higher-order complexity of hjorth descriptor,” Advanced Scientific Letters, vol. 23, no. 1, pp. 3972–3974, 2017. [Google Scholar]

24. T. Yingthawornsuk and P. Temsang, “Cardiac arrhythmia classification using hjorth descriptors,” Advances in Intelligent Informatics, vol. 807, no. 1, pp. 95–104, 2019. [Google Scholar]

25. L. Zhao, C. Liu, S. Wei, Q. Shen, F. Zhou et al., “A new entropy-based atrial fibrillation detection method for scanning wearable ECG recordings,” Entropy, vol. 20, no. 1, pp. 1–17, 2018. [Google Scholar]

26. S. Tang, P. Huang, C. Hung, S. Shan, Y. Lin et al., “Identification of atrial fibrillation by quantitative analyses of fingertip photoplethysmogram,” Scientific Reports, vol. 7, no. 1, pp. 1–7, 2017. [Google Scholar]

27. L. Hussain, W. Aziz, I. Rasool, M. Alkinani and J. Alowibdi, “Machine learning based congestive heart failure detection using feature importance ranking of multimodal features,” Journal of Mathematical Biosciences and Engineering, vol. 18, no. 1, pp. 69–91, 2021. [Google Scholar]

28. K. Yoon, Y. Nam, T. Thap, C. Jeong, N. Kim et al., “Automatic detection of congestive heart failure and atrial fibrillation with short RR interval time series,” Journal Electrical Engineering Technology, vol. 12,no. 1, pp. 346–355, 2017. [Google Scholar]

29. E. -S. M. El-kenawy, A. Ibrahim, N. Bailek, B. Kada, M. Hassan et al., “Sunshine duration measurements and predictions in saharan Algeria region: An improved ensemble learning approach,” Theoretical and Applied Climatology, vol. 147, no. 1, pp. 1015–1031, 2022. [Google Scholar]

30. A. Takieldeen, E., El-kenawy, E. Hadwan and M. Zaki, “Dipper throated optimization algorithm for unconstrained function and feature selection,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1465–1481, 2022. [Google Scholar]

31. S. S. M. Ghoneim, T. A. Farrag, A. A. Rashed, E. -S. M. El-Kenawy and A. Ibrahim, “Adaptive dynamic meta-heuristics for feature selection and classification in diagnostic accuracy of transformer faults,” IEEE Access, vol. 9, pp. 78324–78340, 2021. [Google Scholar]

32. E. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]

33. A. Ullah, S. Tu, R. Mehmood and M. Ehatisham-ul-haq, “Hybrid deep CNN model for abnormal arrhythmia detection based on cardiac ECG signal,” Sensors, vol. 21, no. 1, pp. 1–13, 2021. [Google Scholar]

34. E. S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, pp. 107635–107649, 2020. [Google Scholar]

35. A. Abdelhamid and S. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Computers, Materials & Continua, vol. 73, no. 1, pp. 917–933, 2022. [Google Scholar]

36. M. Le, V. Rathour, Q. Truong, Q. Mai, P. Brijesh et al., “Multi-module recurrent convolutional neural network with transformer encoder for ECG arrhythmia classification,” in Proc. of the 2021 IEEE EMBS Int. Conf. on Biomedical and Health Informatics (BHI), Athens, Greece, pp. 1–5, 2021. [Google Scholar]

37. Q. Li, C. Liu, Q. Li, S. Shashikumar, S. Nemati et al., “Ventricular ectopic beat detection using a wavelet transform and a convolutional neural network,” Physiology Measurements, vol. 40, no. 1, pp. 1–13, 2019. [Google Scholar]

38. C. Chen, Z. Hua, R. Zhang, G. Liu and W. Wen, “Automated arrhythmia classification based on a combination network of CNN and LSTM,” Biomedical Signal Processing Control, vol. 57, no. 1, pp. 101819–101825, 2020. [Google Scholar]

39. O. Yıldırım, P. Pławiak, R. Tan and U. Acharya, “Arrhythmia detection using deep convolutional neural network with long duration ECG signals,” Computer Biology and Medicine, vol. 102, no. 1, pp. 411–420, 2018. [Google Scholar]

40. R. He, Y. Liu, K. Wang, N. Zhao, Y. Yuan et al., “Automatic cardiac arrhythmia classification using combination of deep residual network and bidirectional LSTM,” IEEE Access, vol. 7, no. 1, pp. 102119–102135, 2019. [Google Scholar]

41. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. E. Takieldeen, T. M. Hassan et al., “Meta-heuristics for feature selection and classification in diagnostic breast cancer,” Computers, Materials & Continua, vol. 73, no. 1, pp. 749–765, 2022. [Google Scholar]

42. D. Sami Khafaga, A. Ali Alhussan, E. M. El-kenawy, A. Ibrahim, S. H. Abd Elkhalik et al., “Improved prediction of metamaterial antenna bandwidth using adaptive optimization of LSTM,” Computers, Materials & Continua, vol. 73, no. 1, pp. 865–881, 2022. [Google Scholar]

43. A. Abdelhamid and S. R. Alotaibi, “Robust prediction of the bandwidth of metamaterial antenna using deep learning,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2305–2321, 2022. [Google Scholar]

44. Z. Wang, H. Li, C. Han, S. Wang and L. Shi, “Arrhythmia classification based on multiple features fusion and random forest using ECG,” Journal of Medical Imaging and Health Information, vol. 9, no. 1, pp. 1645–1654, 2019. [Google Scholar]

45. A. Abdelhamid, E. -S. M. El-kenawy, B. Alotaibi, M. Abdelkader, A. Ibrahim et al., “Robust speech emotion recognition using CNN+LSTM based on stochastic fractal search optimization algorithm,” IEEE Access, vol. 10, pp. 49265–49284, 2022. [Google Scholar]

46. A. Khairuddin and K. Azir, “Using the HAAR wavelet transform and K-nearest neighbour algorithm to improve ECG detection and classification of arrhythmia,” in Proc. of the 34th Int. Conf. on Industrial, Engineering and other Applications of Applied Intelligent Systems, Kuala Lumpur, Malaysia, pp. 310–322, 2021. [Google Scholar]

47. A. Goldberger, L. Amaral, L. Glass, J. Hausdorff, P. Ivanov et al., “PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals,” Circulation, vol. 101, no. 23, pp. e215–e220, 2000. [Google Scholar]

48. H. Hassan, A. I. El-Desouky, A. Ibrahim, E. -S. M. El-Kenawy and R. Arnous, “Enhanced QoS-based model for trust assessment in cloud computing environment,” IEEE Access, vol. 8, no. 1, pp. 43752–43763, 2020. [Google Scholar]

49. M. M. Eid, E. -S. M. El-Kenawy and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 4th National Computing Colleges Conf. (NCCC 2021), Taif, Saudi Arabia, pp. 1–6, 2021. [Google Scholar]

50. E. -S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

51. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

52. A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 125787–125804, 2021. [Google Scholar]

53. N. Abdel Samee, E. M. El-Kenawy, G. Atteia, M. M. Jamjoom, A. Ibrahim et al., “Metaheuristic optimization through deep learning classification of COVID-19 in chest X-ray images,” Computers, Materials & Continua, vol. 73, no. 2, pp. 4193–4210, 2022. [Google Scholar]

54. H. Nasser AlEisa, E. M. El-kenawy, A. Ali Alhussan, M. Saber, A. A. Abdelhamid et al., “Transfer learning for chest X-rays diagnosis using dipper throated algorithm,” Computers, Materials & Continua, vol. 73, no. 2, pp. 2371–2387, 2022. [Google Scholar]