Modified 2 Satisfiability Reverse Analysis Method via Logical Permutation Operator

1  Introduction

Artificial Neural Network (ANN) is a subset of Artificial Intelligence that was inspired by artificial neurons. The primary aim of the ANN is to create black box model that can offer alternative explanation among the data. Using this explanation, one can use the output produced from ANN to solve various optimization problem. The main problem with conventional ANN is the lack of symbolic reasoning to govern the modelling of neurons. Reference [1] proposed logical rule in ANN by assigning each neuron to the variable of the logic. This leads to the introduction of Wan Abdullah method to find the optimal synaptic by comparing the cost function with the final energy function. Reference [2] proposed another variant of logic namely 2 Satisfiability (2SAT) in single layered ANN namely Discrete Hopfield Neural Network (DHNN). The proposed 2SAT was reported to obtain high global minima ratio if we optimize the learning phase of the DHNN. The discovery of this hybrid network inspires other study to implement 2SAT in ANN. Recently, [3] integrates 2SAT in Radial Basis Function Neural Network (RBFNN) by calculating the various parameters that leads to optimal output weight. The proposed work confirms the capability of the 2SAT in representing the modeling of the ANN. In another development, [4] proposed mutation DHNN by implementing estimated distribution algorithm (EDA) during retrieval phase of DHNN. This shows that the interpretation of the 2SAT logical rule in DHNN can be further optimized using optimization algorithm. The implementation of 2SAT in various network inspires the emergence of other useful logic such as [5–9] in doing DHNN. Various type of logical rule creates optimal modelling of DHNN that has wide range of behavior. Despite having various type of logical rule in this field, the exploration of different connectives among clauses is limited.

The most popular application of the logical rule in DHNN is logic mining. Reference [10] proposed the first logic mining namely Reverse Analysis (RA) method by implementing Horn Satisfiability in DHNN. The proposed logic mining managed to extract the logical relationship among the student datasets. One of the main issues of the proposed logic mining is the lack of focus of the obtained induced logic. In this context, more robust logic mining is required to extract single most optimal induced logic. Reference [11] proposed 2 Satisfiability Reverse Analysis Method (2SATRA) by introducing specific learning phase and retrieval phase that creates the most optimal induced logic. The proposed 2SATRA extracts the best induced logic for league of legends. The proposed logic mining was extended to various application such as Palm oil pricing [12,13] and football [14]. After the introduction of 2SATRA in the field of logic mining, [15] proposed the energy-based logic mining namely E2SATRA by considering only global neuron state during retrieval phase of DHNN. In this context, the proposed E2SATRA capitalize the dynamics of the Lyapunov energy function to arrive at the optimal final neuron state. Note that, the final global neuron state ensures the induced logic produced by E2SATRA is interpretable. One of the main issues with the conventional 2SATRA is the possible overfitting issue due to ineffective connection of attribute during pre-processing phase. In other word, the attribute might possess the optimal connection with other variable in 2SAT clause, but the other possible connection was disregarded. The optimal logical rule will be less flexible and fail to emphasize the appropriate non-contributing attributes of a particular data set.

In this paper, the modified 2SATRA integrated with permutation operator will enhance the capability of selecting the most optimal induced logic by considering other combination of variable in 2SAT logic. The proposed modified 2SATRA will extract the optimal logical rule for various real-life datasets. Therefore, Thus, the correct synaptic weight during learning phase will determine the capability of the logic mining model and the accuracy of the induced logic generated during testing phase. This work focused on the impact of the logical permutation mechanism in Hopfield Neural Network (HNN) towards the performance of 2SATRA in the tasks data mining and extraction. The contribution of this paper is as follows:

(a) To formulate 2 Satisfiability that incorporates permutation operators which consider various combination of variable in a clause.

(b) To implement permutation 2 Satisfiability in Discrete Hopfield Neural Network by minimizing the cost function during learning phase that leads to optimal final neuron state.

(c) To embed the proposed hybrid Discrete Hopfield Neural Network into logic mining where more diversified induced logic has been proposed.

(d) To evaluate the performance of the proposed permutation logic mining in doing real life datasets with other state of the art logic mining.

The organization of this paper is as follows. Section 2 encloses a bit of brief introduction of 2 Satisfiability logical representation including the conventional formulations and examples. Section 3 focuses on the formulations of logical permutation on 2 Satisfiability Based Reverse Analysis methods. Thus, Section 4 explains the experimental setup including benchmark dataset, performance metrics, baseline method and experimental design. Then, the results and discussions are covered briefly in Section 5. Definitively, the concluding remarks are included in the final section of this paper.

2  Satisfiability in Discrete Hopfield Neural Network

Satisfiability (SAT) is a class of problem of finding the feasible interpretation that satisfies a particular Boolean Formula based on the logical rule. Based on the literature in [16], SAT is recognized to be a variant of NP-complete problem and incorporated to generalize a plethora of constraint satisfaction problems. Thus, the breakthrough of SAT research contributes to the development of the systematic variant of SAT logical representation, for instance, the 2 Satisfiability (2SAT). Theoretically, the fundamental 2SAT logical representation composes of the following structural features [4]:

(a) Given a set of specified x variables, w1,w2,w3,…,wx where wi∈{−1,1} (bipolar states) that illustrate the False and True outcomes correspondingly.

(b) A set of logical literals comprising either the positive variable or the negation of variable in terms of wi∈{wi,¬wi}.

(c) Given a set of y definite clauses, C1,C2,C3,…,Cy in a set of logical rule. For every Ci is connected to logical operator AND (∧) consecutively. Additionally, the 2 literals structure as given in (b) are well-connected by logic operator OR (∨).

Based on the feature in (a) until (c), the precise definition of P2SAT with different clauces can be seen as follows

P2SAT=∧i=1yCi(1)

whereby Ci is a clause containing strictly 2 literals each

Ci=∨i=1x(mi,ni).(2)

Then, by governing the Eqs. (1) and (2) respectively, an illustration of P2SAT can be crafted as

P2SAT=(¬C∨D)∧(M∨N)∧(¬E∨¬G)(3)

whereby the logical clauses in Eq. (3) are divided into 3 clauses such as C1=(¬C∨D), C2=(M∨N) and C3=(¬E∨¬G). In particular, the aforementioned clauses must be satisfied with the appropriate bipolar interpretations with specific arrangements in align with the logical rule. Therefore, if the bipolar interpretation or assignment reads (C,D)=(1,−1), P2SAT yields the False outcome or −1. Due to the compatibility of P2SAT with the ample information storage mechanism, we implemented P2SAT into DHNN as a logical representation.

Specifically, the fundamental classification of DHNN with i-th activation is shown as follows

Si={1,if∑i=0NWijSj≥θ−1,otherwise(4)

where θ and Wij refer to the neuron threshold and second-order synaptic weight of the network correspondingly. In most of the DHNN research, θ=0 is chosen as a standard threshold parameter. Note that N denotes the total number of 2SAT literals in a logical representation. Then, Wij is defined as the connection between neuron Si and Sj. This paper utilizes DHNN to avoid any intervention of the hidden layer. Hidden layer requires additional optimized parameters that potentially disrupt the signal of the local field in (4). In other word, suboptimal signal will leads to suboptimal synaptic weight which cause the final state to be trapped in local minimum energy. The thought of employing P2SAT in DHNN (DHNN-2SAT) is due to the potential of the P2SAT logical rule that can govern the output of the network symbolically. Thus, P2SAT will take advantage of the DHNN content adressable memory as a remarkable storage especially to applied in logic mining.

3  Permutation in 2 Satisfiability Based Reverse Analysis Method

Logic mining is a paradigm that used logical rule to simplify the information of the data set. Based on the inspiration of a study by [11], they have successfully utilized logic mining by implemented reverse analysis method in inducing all possible logical rules that generalize the behavior of the data set. However, the main task in assessing the behavior of the data set with the pre-defined goal is the extraction of correct P2SAT logical rule so that it is efficiently evaluated the quality of data generalization. The structure of the optimum P2SAT must consist the possible tractable inference, and capable to categorize the outcome of the real datasets. The conventional paradigm is by formulating and proposing a data mining method that capitalizes learned P2SAT integrated with DHNN. 2 Satisfiability based Reverse Analysis Method (2SATRA) is a method that utilizes DHNN to learn and extract P2SAT from a particular dataset with different levels of instances and attributes.

Given a set of data, S1,S2,S3,S4,…,Sx where Si∈{−1,1} and x is the number of tested attributes. Note that, the number of tested attributes is randomly chosen from the factors that contribute to the outcome. Worth mentioning that, the role of 2SATRA is to find the final neuron state that maps from the learning neuron states. Throughout the learning phase, each dataset will be evaluated in order to find the synaptic weight by using Wan Abdullah Method [1]. Tab. 1 illustrated all the possible synaptic weight for P2SAT.

For instance, if the given dataset reads (S11,S21,S31,S41,S51,S61)=(1,−1,−1,1,1,1), 2SATRA will convert the logical assignments or interpretations into logical representation of P2SAT1=(S1∨¬S2)∧(¬S3∨S4)∧(S5∨S6). Based on Tab. 1, the acquired synaptic weight for P2SAT1 are C1, C2 and C3 correspondingly. In this work, we proposed the permutation of the attributes in order to find the best interpretation that will generalize the behaviour of the data set. Therefore, the implementation of several possible permutations for P2SAT1 such as in Eqs. (5) and (6).

P2SATmi=∧g=1nCgwhereCg=∨v=1k(xgva,ygvb),k=2(5)

Based on the Eq. (5), the possible permutation for P2SATmi is a as follows

P2SATm2=(S1∨¬S2)∧(¬S3∨¬S4)∧(¬S5∨S6)

P2SATm2=(¬S4∨S6)∧(¬S2∨¬S3)∧(S1∨¬S5)(6)

In this context, the P2SATmi embedded to DHNN exhibits more possible attribute arrangement and we only considered the structure of P2SATmi=1 in the learning phase of DHNN. Then, the P2SATmi will be selected as the Pbest if it comply the criteria as in Eq. (7).

n(P2SATki)≤Tol(7)

where n(P2SATki) is the number of logical rule and Tol is the acceptance tolerance range. The logical Pbest will determine the behaviour of the DHNN and the logical Pbest along with the acquired synaptic weight obtained will be stored in the content addressable memory for the retrieval phase purposes. The process of generating induced logical rules, PiB for this programme is follows exactly from the conventional 2SATRA. Note that, the implementation of permutation attribute arrangements with the 2SATRA is abbreviated as P2SATRA. To further test the performance of P2SATRA, the PiB obtained will be compared with the testing datasets, Ptest. Algorithm 1 illustrates the Pseudocode of the proposed P2SATRA while Fig. 1 shows the execution of the proposed P2SATRA.

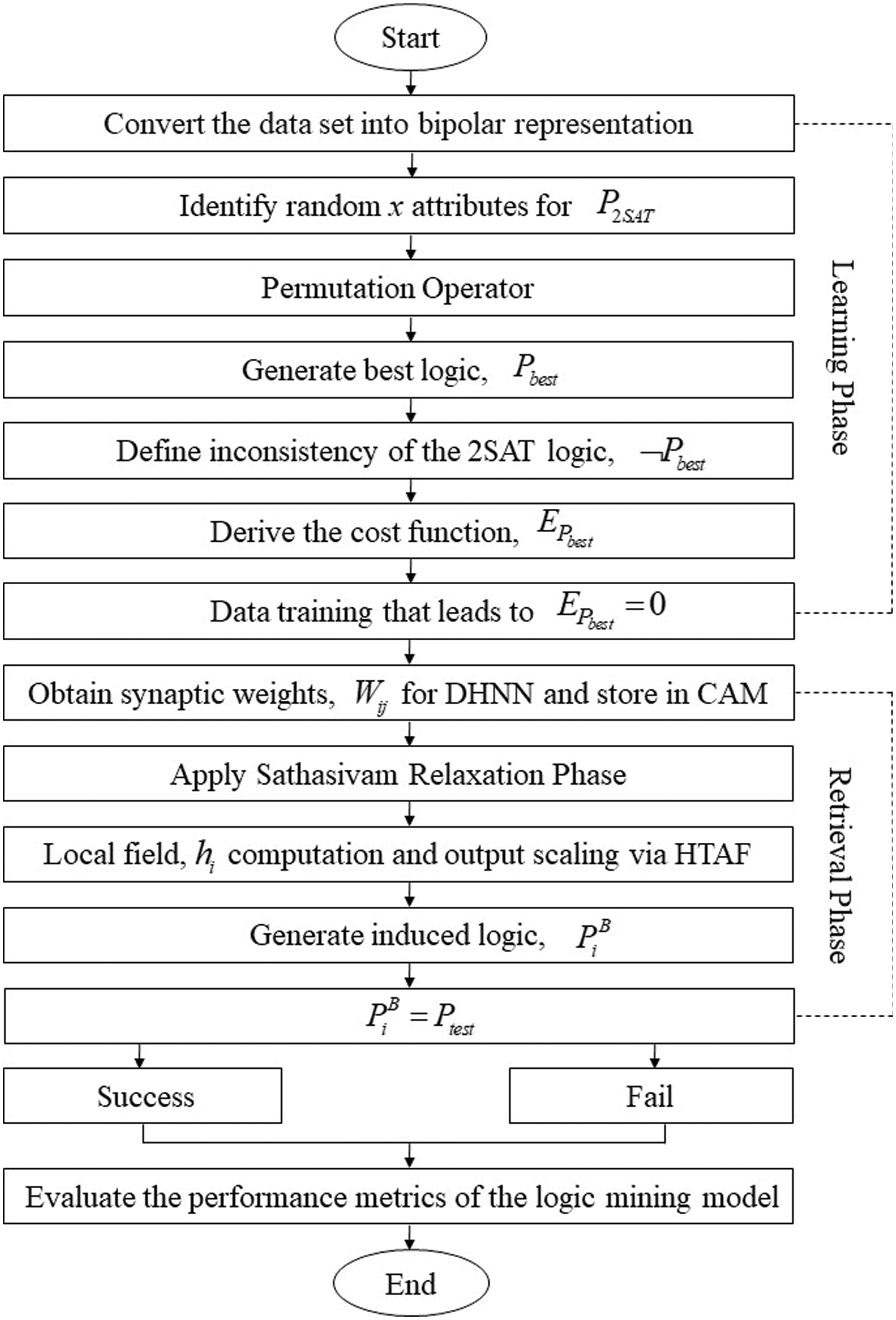
Figure 1: The execution of the proposed P2SATRA

Based on Fig. 1 and Algorithm 1, P2SATRA starts by identifying random logic Pbest which leads to P2SAT=1. In this context, P2SAT=−1 will be diregarded to ensure the Satisfiable property of the P2SAT. After obtaining the synaptic weight via [1], P2SATRA proceed with the retrieval phase of the DHNN. The main difference between conventional 2SATRA with P2SATRA is the position of the attributes in the P2SAT during learning phase and retrieval phase. In this context, the final neuron state of the proposed P2SATRA has bigger search space compared to conventional 2SATRA. Compared to other optimization method, permutation operator in Eq. (2) requires non-complex optimization problem to arrive to the optimal induced logic. Thus, P2SATRA only deals with permutation operatorto uncover possible combination of the connectives in P2SAT.

4  Experimental Setup

4.1 Benchmark Dataset

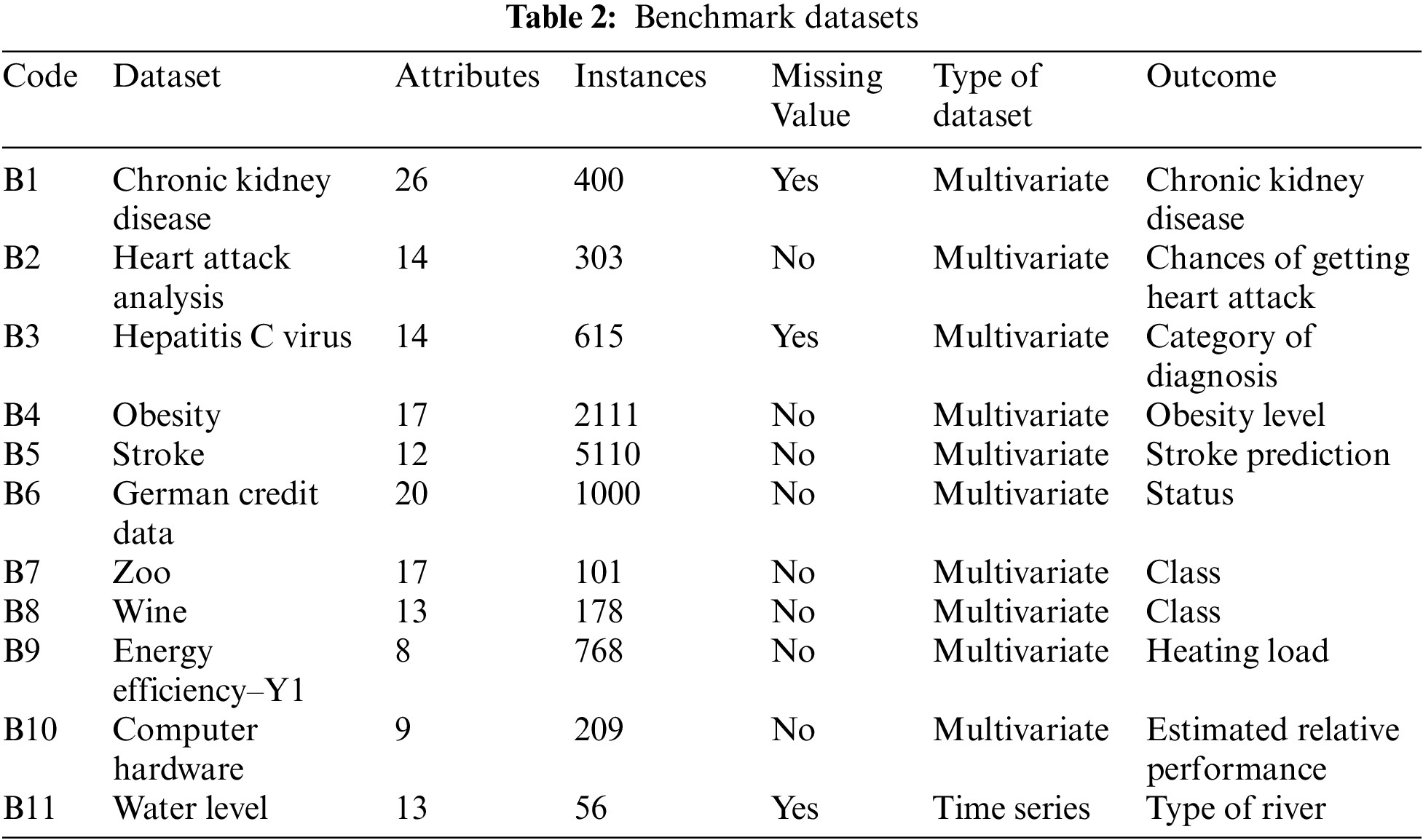
In this paper, the impact of logical permutation in attaining the optimum induced logic is examined. Thus, the first 10 publicly available datasets from repository (B1-B10) are acquired from the open source UCI repository databases via https://archive.ics.uci.edu/ml/datasets.php. Moreover, 1 real life dataset (B11) is taken from Department of Irrigation and Drainage, Malaysia. Tab. 2 encloses the lists of datasets being used in this experiment. Based on the analysis from several previous works, this study utilizes the standard train-test split method, via 60% set as a learning data and the remaining 40% as a testing data [17]. The data will be converted into bipolar representation (1 and −1) using k mean clustering as proposed by [18]. The conversion will be applied in both learning and retrieval phase. To guarantee reproducibility of the result, the implementation code of our proposed P2SATRA with the datasets can be retrieved from https://bit.ly/3nyUdm8.

4.2 Baselines Methods

As the primary impetus of this work is to evaluate the quality of the induced logical representation generated by P2SATRA, we restrict the baseline methods comparison to the standard method only with the capability in attaining the induced logic from the real datasets. Tabs. 3–6 show the list of important parameters for various logic mining approaches. The core concern of combining more attributes is the possible increment of the learning error as the results of non-effective learning phase of HNN [19]. Hence, the Hyperbolic activation function is applied to squash the final state of the neurons because of the capability and the behaviour of the functions such as the continuous, smooth, and non-linearity of the activation function. In retrieval phase of the logic mining method, the neuron initialization is set to be random in order to lessen the potential biasness of the network.

4.3 Performance Evaluation Metrics

Various performance evaluations such as the sensitivity, precision analysis, F-Score and Matthews Correlation Coefficient (MCC) are employed to analyze and assess the overall capability and the significant effect of logical permutation in P2SATRA. The performance of the P2SATRA is calculated based on the confusion matrix. Specifically, TP (true positive) refers to the number of positive instances that correctly classed, FN (false negative) denotes the number of positive instances that incorrectly classified, TN (true negative) is the number of negative instances that correctly classified, whereas FP (false positive) demarcates the number of positive instances that incorrectly classified by the model. In the context of logic mining, TP can be calculated if PiB=Ptest=1 and TN can be calculated if PiB=Ptest=−1. Sensitivity metric, (Se), examines the main positive result for an instance with respect to a particular condition.

Se=TPTP+FN(8)

Therefore, precision is employed to gauge the algorithm’s or model’s predictive capability. The computation and formulation for Precision (Pr) is defined as follows:

Pr=TPTP+FP(9)

Accuracy (Acc) refers to the ordinary indicator for verifying the performance of the classification processes. Thus, the accuracy determines the percentage of instances categorized correctly (emphasis given on the true outcomes in confusion matrix):

Acc=TP+TNTP+TN+FP+FN(10)

F-Score is a substantial indicator that indicates the maximum probability of optimal result, clearly demonstrating the capability of the computational model. Moreover, F-Score is depicted as the harmonic mean of the two-performance metrics, which are the precision and sensitivity analysis.

FScore=2TP2TP+FP+FN(11)

In addition, Matthews Correlation Coefficient (MCC) is utilized to quantify the execution of the entire logic mining approaches by taking into account the eight major derived ratios from the amalgamation of the entire elements of a confusion matrix. The MCC is given:

MCC=TP TN−FP FN(TP+FP)(TP+FN)(TN+FP)(TN+FN)(12)

4.4 Experimental Design

All simulations will be implemented and executed by employing the Dev C++ Version 5.11 software due to the versatility of the programming language and the user-friendly interface of the compiler. Hence, the simulations will be implemented in C++ language by using computer with Intel Core i7 2.5 GHz processor, 8GB RAM and Windows 8.1. Following that, the threshold CPU time for each execution was set 24 h and any possible outputs that go beyond the threshold time were omitted entirely from the analysis. The overall experiments were executed by using the similar device to prevent possible bad sector in the memory during the simulations.

5  Results and Discussions

This study created the 2SATRA integrated with HNN-2SAT to simulate and analyze the effect of logical permutation, forming P2SATRA. The composition of attributes will be randomly permuted as opposed to the previous 2SATRA models [11,12]. In this work, the comparison of our proposed P2SATRA will be examined with the conventional logic mining models such as RA, 2SATRA and E2SATRA methods.

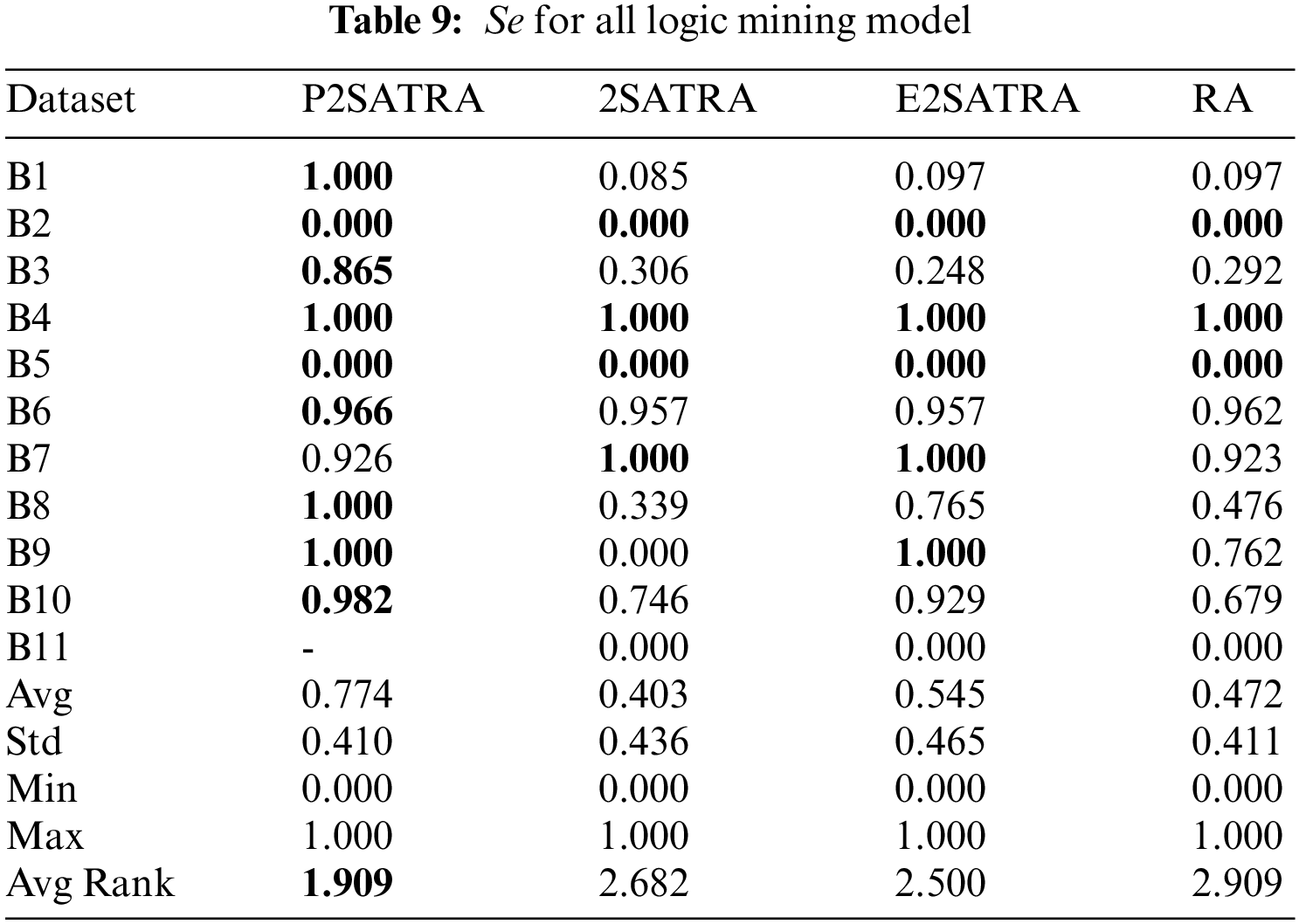
The results of Acc, Pr, Se, F-Score and MCC for four variants of logic mining apporaches can be viewed in Tab. 7 until Tabs. 8 and 11. Then, Tab. 12 encloses the induced logic of obtained for 11 real datasets. According to the results, there are several successful dominances and strength points for P2SATRA which are enclosed based on the analysis of the different performance metrics. Based on Acc analysis, P2SATRA achieve the maximum optimal Acc values for 11 real datasets, including the time-series dataset in B11. This manifests the capability of the logical permutation in P2SATRA in enhancing the accuracy of the logic mining for the entire datasets used in this work. According to the thorough observation, the next feasible models that compete in terms of Acc with P2SATRA are RA and E2SATRA. This implies that the proposed logic mining model has been enhanced by using permutation operator in diversifying the induced logics that lead to higher accuracy by tuning the high permutation parameter (maximum of 100 permutation/execution). Based on Tab. 1, all of the accuracy recorded by P2SATRA achieved Acc≥0.9 which confirms the capability to correctly differentiate TP and TN for all datasets in this study. Following that, there were three datasets (B4, B9, and B11) that attain Acc=1 which implies P2SATRA accurately predict all value of TP and TN. This shows that the capability of the proposed P2SATRA to work well with time-series datasets, which require proper enumerations in attaining the best induced logic as compared with the three counterparts. Interesting observation can be found where the 2SATRA and RA recorded the zero Acc during the execution with B11 dataset. The 100% differences in the Acc of P2SATRA as opposed to the standard logic mining approaches in B11 just confirmed the significant effect of logical permutation with the effective synaptic weight management during time-series data extraction. Statistically, P2SATRA has recorded an exceptional average rank of 1.045 for the accuracy, which 286% lower than RA and E2SATRA plus about 322.7% lower than 2SATRA.

   (a) For Pr, P2SATRA outperforms the other logic mining models in 7 out of 11 datasets. The higher Pr values of indicates the superiority of the proposed model to retrieve and generate more TP. Hence, the nearest model that strongly compares with P2SATRA is E2SATRA. However, no Pr values were reported in B2, B5 and B11 datasets indicating the failure to retrieve any value for Pr. This is occurring because P2SATRA and the other logic mining models fail to retrieve value of positive outcomes, consisting of TP and FP. The proposed P2SATRA has achieved Pr=1 value for 3 real datasets which entails P2SATRA correctly predict the tested data in evaluation with all the positive outcomes. One interesting result was recorded by 2SATRA for B9, where the Pr=0 implying the models fail to attain any TP values in the confusion matrix. This shows the major weakness of standard 2SATRA that requires reinforcement via the logical permutation approach. To support that, the 2SATRA has obtained Pr average rank of 3.1878 which approximately 230% higher than the Pr average rank for P2SATRA.

   (b) For result of Se, P2SATRA outperforms other logic mining model in 9 out of 11 datasets. In addition, according to the F-Score analysis, P2SATRA has recorded exceptional results in 10 out of 11 datasets as compared to 2SATRA, RA and E2SATRA. However, both results of Se and F-Score for B11 is not able to retrieve any value due to the failure to generate any positive and negative outcomes. This highlights the similar capability of P2SATRA with the other logic mining models when being assessed with Se and F-Score for B11, which a variant of time-series datasets. Overall, the nearest model that competes with P2SATRA is E2SATRA with the average rank of 2.500. Moreover, P2SATRA has an average rank of 1.909 which is the peak as compared to other conventional logic mining approaches based on the Se analysis. In addition, P2SATRA has recorded the superior average rank of F-Score with 1.545 with almost 99.5% lower than the worst 2SATRA with average rank of 3.000. Hence, both findings statistically authenticate the acceptable performance of P2SATRA for most of multivariate datasets as opposed to the conventional logic mining approach.

   (c) As well to MCC, logic mining model of P2SATRA shows the highest optimal MCC value among other model in 6 out of 11 datasets. In meantime, 5 datasets in MCC are not able to retrieve any value. No value of MCC reported in B2, B4, B5 and B11 for all logic mining methods due to the non-existence of positive outcomes for these datasets. In addition, no MCC value recorded for B7 data due to P2SATRA is not able to retrieve value of TP and FP. However, the performance of P2SATRA has been exceptional as recorded the best MCC for 55% of the datasets. The datasets that are equal to zero and approaching zero MCC are B10 and B9 dataset respectively. This demonstrates P2SATRA has excellent capability in distinguishing all outcome domains of the confusion matrix and a solid proof of powerful predictive capability.

   (d) According to the average rank for all the data sets in terms of Acc, Pr, Se, F-Score and MCC, it shows that P2SATRA has the highest average rank compared to other model. It has been statistically proven, where 2SATRA has been the weakest of the other conventional logic mining approaches, when being trained and tested with the real datasets in this study.

   (e) The further analysis via Friedman test rank has been performed for all 11 datasets with α=0.05 and degree of freedom, df=3. The p-value for Acc, Pr, Se, F-Score and MCC are 2.5×10−4(χ2=19.2), 0.032(χ2=8.813), 0.305(χ2=3.627), 0.038(χ2=8.455) and 0.209(χ2=4.53), respectively. In terms of Acc, Pr and F-Score, the null hypothesis of equal performance for all the logic mining models were rejected. P2SATRA recorded the average rank of 1.045, 1.375 and 1.545 in terms of Acc, Pr and F-Score, respectively, which highest compared to other existing models. As can be seen, E2SATRA is the nearest method that competes with P2SATRA with an average rank of 2.864, 2.688 and 2.818 for Acc, Pr and F-Score, respectively. Thus, it shows that the result for Acc, Pr and F-Score are statistically validating the dominance performance of P2SATRA. However, the null hypothesis of equal performance for all the logic mining models were accepted in terms of Se and MCC. It can be concluded that there no difference performance of P2SATRA with other models for Se and MCC.

6  Conclusion

In this work, a new alternative approach of attaining the optimal induced logic entrenched in any of multivariate or time-series datasets by introducing the logical permutations in 2SATRA has been successfully developed. The enhancements can be seen clearly in the substantial accuracy improvement of the proposed model as opposed to the existing approach, indicating the success in the generalization of the datasets. In this study, we have exploited the multi-connection between the attribute arrangements in generating the P2SATi with different accuracy values. Given the high expressibility and interpretibility of the proposed P2SATRA, the effects of the logical permutations have been very significant and substantial. By adapting various forms of 2SAT logical structure during the learning phase of HNN, P2SATRA outperfomed the 2SATRA, E2SATRA and RA approaches when being measured with the performance metrics such as the accuracy, precision, sensitivity, F-Score and MCC after the logic mining analysis with 11 different real datasets. For instance, it will be interesting to infuse different logical rule such as Maximum Satisfiability [20], Y-Type Random Satisfiability [8], G-Type Random Satisfiability [9] and Random k Satisfiability [5]. In terms of network architecture, it will be interesting if other learning mechanism such as in [21,22] were embeded into logic mining.

Acknowledgement: The authors would like to thank all AIRDG members and those who gave generously of their time, ideas and hospitality in the preparation of this manuscript.

Funding Statement: This research was supported by Universiti Sains Malaysia for Short Term Grant with Grant Number 304/PMATHS/6315390.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  W. A. T. W. Abdullah, “Logic programming on a neural network’,” International Journal of Intelligent Systems, vol. 7, no. 6, pp. 513–519, 1992. [Google Scholar]

 2.  M. S. M. Kasihmuddin, M. A. Mansor and S. Sathasivam, “Hybrid genetic algorithm in the hopfield network for logic satisfiability problem,” Pertanika Journal of Science & Technology, vol. 25, no. 1, pp. 227–243, 2017. [Google Scholar]

 3.  S. Alzaeemi, M. A. Mansor, M. S. M. Kasihmuddin, S. Sathasivam and M. Mamat, “Radial basis function neural network for 2 satisfiability programming,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 18, no. 1, pp. 459–469, 2020. [Google Scholar]

 4.  M. S. M. Kasihmuddin, M. A. Mansor, M. F. M. Basir and S. Sathasivam, “Discrete mutation hopfield neural network in propositional satisfiability,” Mathematics, vol. 7, no. 11, pp. 1133, 2019. [Google Scholar]

 5.  S. A. Karim, N. E. Zamri, A. Alway, M. S. M. Kasihmuddin, A. I. M. Ismail et al., “Random satisfiability: A higher-order logical approach in discrete hopfield neural network,” IEEE Access, vol. 9, pp. 50831–50845, 2021. [Google Scholar]

 6.  A. Alway, N. E. Zamri, S. A. Karim, M. A. Mansor, M. S. M. Kasihmuddin et al., “Major 2 satisfiability logic in discrete hopfield neural network,” International Journal of Computer Mathematics, vol. 99, no. 5, pp. 924–948, 2022. [Google Scholar]

 7.  S. S. M. Sidik, N. E. Zamri, M. S. M. Kasihmuddin, H. A. Wahab, Y. Guo et al., “Non-systematic weighted satisfiability in discrete hopfield neural network using binary artificial bee colony optimization,” Mathematics, vol. 10, no. 7, pp. 1129, 2022. [Google Scholar]

 8.  Y. Guo, M. S. M. Kasihmuddin, Y. Gao, M. A. Mansor, H. A. Wahab et al., “YRAN2SAT: A novel flexible random satisfiability logical rule in discrete hopfield neural network,” Advances in Engineering Software, vol. 171, pp. 103169, 2022. [Google Scholar]

 9.  Y. Gao, Y. Guo, N. A. Romli, M. S. M. Kasihmuddin, W. Chen et al., “GRAN3SAT: Creating flexible higher-order logic satisfiability in the discrete hopfield neural network,” Mathematics, vol. 10, no. 11, pp. 1899, 2022. [Google Scholar]

10. S. Sathasivam and W. A. T. W. Abdullah, “Logic mining in neural network: Reverse analysis method,” Computing, vol. 91, no. 2, pp. 119–133, 2011. [Google Scholar]

11. L. C. Kho, M. S. M. Kasihmuddin, M. A. Mansor and S. Sathasivam, “Logic mining in league of legends,” Pertanika Journal of Science & Technology, vol. 28, no. 1, pp. 211–255, 2020. [Google Scholar]

12. A. Alway, N. E. Zamri, M. S. M. Kasihmuddin, M. A. Mansor and S. Sathasivam, “Palm oil trend analysis via logic mining with discrete hopfield neural network,” Pertanika Journal of Science & Technology, vol. 28, no. 3, pp. 967–981, 2020. [Google Scholar]

13. S. A. S. Alzaeemi and S. Sathasivam, “Examining the forecasting movement of palm oil price using RBFNN-2SATRA metaheuristic algorithms for logic mining,” IEEE Access, vol. 9, pp. 22542–22557, 2021. [Google Scholar]

14. L. C. Kho, M. S. M. Kasihmuddin, M. A. Mansor and S. Sathasivam, “Logic mining in football matches,” Indones. J. Electr. Eng. Comput. Sci, vol. 17, pp. 1074–1083, 2020. [Google Scholar]

15. S. Z. M. Jamaludin, M. S. M. Kasihmuddin, A. I. M. Ismail, M. A. Mansor and M. F. M. Basir, “Energy based logic mining analysis with hopfield neural network for recruitment evaluation,” Entropy, vol. 23, no. 1, pp. 40, 2020. [Google Scholar]

16. S. A. Cook, “The complexity of theorem-proving procedures,” in Proc. Third Annual ACM Symp. on Theory of Computing-STOC ‘71, New York, NY, USA, pp. 151–158, 1971. [Google Scholar]

17. K. Jha and S. Saha, “Incorporation of multimodal multiobjective optimization in designing a filter based feature selection technique,” Applied Soft Computing, vol. 98, pp. 106823, 2021. [Google Scholar]

18. N. E. Zamri, M. A. Mansor, M. S. M. Kasihmuddin, A. Alway, S. Z. M. Jamaludin et al., “Amazon employees resources access data extraction via clonal selection algorithm and logic mining approach,” Entropy, vol. 22, no. 6, pp. 596, 2020. [Google Scholar]

19. D. L. Lee, “Pattern sequence recognition using a time-varying hopfield network,” IEEE Transactions on Neural Networks, vol. 13, no. 2, pp. 330–342, 2002. [Google Scholar]

20. M. S. M. Kasihmuddin, M. A. Mansor and S. Sathasivam, “Discrete hopfield neural network in restricted maximum k-satisfiability logic programming,” Sains Malaysiana, vol. 47, no. 6, pp. 1327–1335, 2018. [Google Scholar]

21. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

22. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]