SRResNet Performance Enhancement Using Patch Inputs and Partial Convolution-Based Padding

1  Introduction

Deep learning algorithms have the ability to learn hierarchical representation of the data and appeared to be a superior alternative to other machine learning algorithms. In image super-resolution problems, the major goal is to appropriately generate and estimate new adjacent pixels around given ones in a low resolution (LR) image in order to enhance the quality of the image by improving the image resolution. Single image super resolution (SISR) is a classical ill-posed problem of reconstructing a high-resolution image IHR from its low-resolution ILR counterpart. Contrary to multi-image super resolution (MISR) which is now merged into video super resolution task, SISR is more challenging task due to estimating single optimal solution image ISR from the wide range of possible target SR solutions.

SISR is particularly important in computer vision tasks. Many computer vision applications, ranging from advertisement to medical image processing can take benefit from image super resolution methods. SISR algorithms always strive for ISR outputs with better aesthetic quality. Interpolation-based methods are the simplest ones but results into visually poor ISR image. Deep learning methods are quality-wise more efficient but computationally expensive. With the advancements in computational resources more sophisticated deep learning algorithms are designed for SR tasks. One of the major issues with the deep learning algorithms is that, poorly modeled problem misleads the network which causes inefficiency. So, it is reasonable and efficient to develop a super-resolution algorithm using local patches of LR images focusing on local properties. Patch based approach is also advantageous in training of deep neural networks in many aspects.

Recently a lot of image super-resolution algorithms have been introduced based on well-known deep learning approaches [1–3] and convolutional neural network (CNN) based SR algorithms have shown excellent performance [4–6]. Deep neural network [7] is efficient to model the mappings of high complexity such as super-resolution function and it was shown that deeper networks have the potential to substantially increase the network accuracy even though it is not easy to train [8].

To train deep neural networks more efficiently, the concept of residual blocks [9] and skip-connections [10] has been introduced in deep neural networks such as SRResNet [11] which is considered in this paper. SRResNet, a customized ResNet [9], is a deep residual neural network specifically designed for super-resolution. The major strength of the SRResNet is the use of residual layers based on a technique of skip connections between two subsequent layers which can effectively manage vanishing gradient problem [10] encountered in deep neural networks. To implement skip connections in SRResNet, zeros should be padded to the inputs to generate outputs of the same size as the inputs which is called zero padding (ZP). In SRResNet, ZP is commonly used because of simplicity but padding algorithm should be carefully selected because ZP affects the network performance.

In this paper, patch image based SRResNet is considered to develop a super-resolution algorithm and PCP is adopted as a padding algorithm in SRResNet. Through the performance comparison between patch image based super-resolution and single image based one, it will be shown that patch image based SRResNet is more powerful both in performance and network efficiency and PCP is more effective than ZP as a padding scheme for patch based SRResNet.

Training of a deep neural network such as SRResNet requires a large amount of training data and powerful computational resources to implement. For example, in case of an SRResNet with four residual blocks and an image input of size 384 × 384 × 3 shown in Fig. 1, the network model utilizes 1,722,115 parameters to learn, which makes it unable to run on a 32 GB RAM of a CPU system. Particularly, it is not feasible to be implemented in widely used handheld devices. By the way, patch image based approach can facilitate to train complex networks more efficiently despite limited physical capability and provide comparably good performance. On the other hand, padding algorithms should be carefully selected in patch image based approach because it can affect the performance considerably by propagating padding noises through boundaries of many patches.

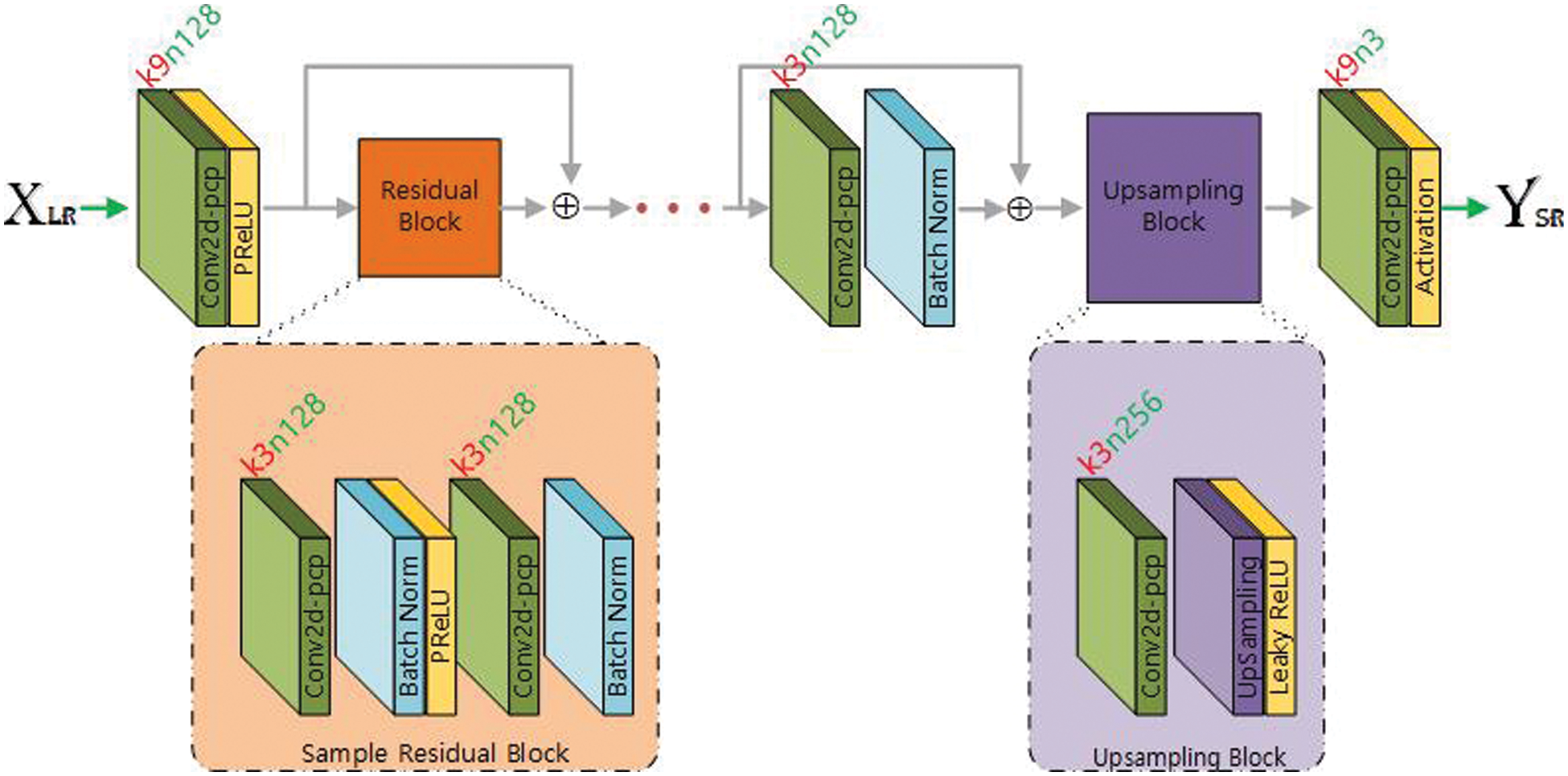
Figure 1: Network architecture of SRResNetp

Patch based deep learning algorithm for image super-resolution is considered to have many advantages in both performance and network efficiency. Nonetheless, there has been no report to investigate the performance with respect to input image size. Our contribution can be summarized as follows.

1.    In order to show the superior performance of patch input based SRResNet, performance comparison of SRResNet has been carried out with respect to input image size. It is shown that patch input based SRResNet performs better than single full image case.

2.    In order to improve the patch input based SRResNet, PCP is used as a padding algorithm instead of ZP, which is originally used in SRResNet. Performance analysis has been done depending on padding algorithms, which shows that PCP is more efficient than the simple ZP.

2  Related Work

2.1 Image Super-resolution

Deep learning methods for super-resolution are classified into nine categories: Linear, Residual, Multibranch, Recursive, Densely connected, Progressive, Attention based, Adversarial and Multiple degradation handling networks [12]. The pros and cons of each method are addressed in [12] regarding the issues of the ill-posed super-resolution problem. One of the first and simplest deep learning approach to super-resolution problem is Super-Resolution Convolutional Neural Network (SRCNN) [13]. SRCNN is a linear network consisting of only 3 layers. The first layer is focusing on feature extraction, the second layer is implementing a mapping between an LR input and a high resolution output, and finally the third layer is an output layer. The output functions of the first two layers are implemented using ReLU activation. SRCNN generates super-resolution images with better mean squared error (MSE)/peak signal-to-noise ratio (PSNR) than conventional machine learning methods, but the resultant images are visually less appealing as compared with other deep learning methods such as SRGAN [11]. Those methods which are based on residual networks can more efficiently manage the complexities of the super-resolution problem by extending depth level and overcoming vanishing gradients by introducing skip connections. Residual networks were originally designed for image classification [9]. Two types of residual networks are used for super-resolution tasks, which are single stage networks and multistage residual networks. Single stage residual networks have just a single network with residual blocks. Enhanced deep super-resolution (EDSR) [14] is a single stage residual network. EDSR modifies existing ResNet architecture and makes the network simpler by removing batch normalization layers from a residual block and bringing ReLU activation outside of a residual block. Removing batch normalization from the residual block is beneficial for better PSNR [15]. Major issue with EDSR is that it require mean of the three RGB channels from training dataset, which is later applied to the test images and there is a chance that the training set is not able to find the universal mean value from the limited training set. Cascading residual network (CARN) [16], another single stage residual network, adopts group convolution method by cascading intermediate layer features and converging on a 1 × 1 convolutional layer. The local and global cascading modules can efficiently learn multilevel information representation. Multistage residual networks are made up of multiple subnetworks. These networks learn different levels of abstractions and are usually trained one by one. FormResNet [17] composed of two subnetworks which are Formatting layer and DiffResNet and both are similar to DnCNN [18]. Formatting layer learns how to improve the uniform areas of the image, and DiffResNet enhances the structured regions of the image. Residual Encoder Decoder Network (REDNet) [19] is a UNet like architecture with convolutional layer which extracts feature maps but preserves image structures, and deconvolutional layer learns to estimate the missing information of an LR input image. Kernel-Oriented Adaptive Local Adjustment (KOALAnet) [20] is a blind super resolution method, which aim to recover the HR image from a LR input image, degraded with unknown kernel. SRGAN is a GAN based network with SRResNet as generator and a simple CNN network as discriminator [11]. In SRGAN, the authors used a multi-objective loss function which has three components: (a) an MSE loss, which represents the pixelwise differences, (b) high level feature’s space difference, which captures the perceptual loss of the generated image, and (c) a standard GAN loss (adversarial loss function) which works on balancing game concept of min-max between generator and discriminator. As our base deep learning model for SR, we adopt SRResNet which is used as a generator in SRGAN. In SRResNet, PixelShuffler is used as a kind of upsampler which needs to be trained with a big amount of data to ensure a good performance. By the way, UpSampling2D is a simple bicubic interpolation method with a consistent precision, so we replace PixelShuffler with it considering limited amount of data.

2.2 Padding Schemes

In deep learning networks, padding extra pixels to an input is required before convolution in order to obtain an output with the same size of an input, for example in modern networks for segmentation tasks [21–26] ZP is used at each convolution layer. Usually padding schemes are paid less attention and simple padding algorithms such as ZP and reflection padding are utilized for padding. In [27], a more systematic approach is considered to introduce 8 extra filters per each layer to learn padding pixels for the boundary of an input to the next convolutional layer, which loads additional burden to train extra filters for simple padding. Cube padding [28] is suggested based on image projection method to deal with boundaries, where the image is first projected on a cube and the cube faces are concatenated to construct a 2D image. Partial convolution based padding [29] can efficiently handle problems due to ZP by correcting convolution results. The correction can simply be implemented by multiplying a constant ratio matrix with the convolution results obtained using ZP.

3  Proposed Method

One of a major issue with SRResNet is the training of sizable networks. To overcome this issue, we consider patch inputs, which subsequently causes information loss due to ZP. In order to improve the performance of SRResNet, patch input based approach and PCP algorithm are considered.

Fig. 1 represents the overall network architecture of SRResNet [11] where the notation kx1nx2 has two parts, kx1 means kernel of size x1 and nx2 is x2 number of filters. According to Fig. 1, the input image is convolved with 64 filters of size 9 × 9 × 3 followed by Parametric Rectified Linear Unit (PReLU) [30], and then passed from B residual blocks. The output of each residual block is elementwise added with the block input to make a skip-connection. Each residual block has a convolutional layer with 3 × 3 filters followed by batch normalization [31] and PReLU and then passed from another convolutional layer with filter size 3 × 3 and batch normalization. A final skip connection is built by passing the residual block’s output from a convolution layer with filters of size 3 × 3 and batch normalization layer and the result is added with the input to the convolutional layer. Then the result is passed from UpSampling block. UpSampling block consists of convolutional layer followed by UpSampling Layer and then Leaky ReLU. Output of the upsampling block is passed from a final convolutional layer with 3 filters of size 9 × 9. The output of three filters corresponds to RGB color values. In the original SRResNet [11], the authors have used 64 filters in each layer, including input layer and within residual blocks, and 256 filters in the layer just before pixelshuffler, but here in this architecture we used 128 filters in each layer and 256 filters in the Upsampling block. The reason for spreading the layer is that the patches are more sensitive to ZP in the convection layer, so our aim is to reduce this negative effect by, using both the PCP and reduced exposure of the patch in ZP stages.

3.1 Patch Input Based Super-Resolution Deep Neural Network: SRResNetp

To estimate super-resolution images, additional pixels should be generated from LR images through proper algorithms. The values of additional generated pixels are dependent on the properties of neighboring ones. So, it is more efficient to use patch images to develop neural networks for super-resolution.

In this paper, SRResNet is considered to estimate super-resolution images and patch images obtained from a single image are provided to train SRResNet as input. The number of patches extracted from a single image can be calculated as:

TotalNumberofPatches=(x−x´)∗(y−y´)stridex∗stridey(1)

where, x´,y´ are the horizontal and vertical dimensions of a patch image, x,y are the horizontal and vertical dimensions of an image and stridex,stridey are the number of horizontal and vertical strides.

In this paper, we consider a target single image with the dimension of 640 × 640. To train SRResNet, the dimension of a target patch image is assumed to be 32 × 32 and patches are extracted from a single image with a stride of 5. So, the number of patches extracted from a single image is 13271. If the number of target single images for training is 36, the total number of patches generated from the training set is 13271*36 = 477,756 which is quite enough to train the network.

In this paper, 2× upscaling super-resolution is considered. To validate training results, patch outputs are assembled to reconstruct a single super-resolution image.

3.2 Partial Convolution Based Padding

Originally SRResNet utilizes ZP scheme to implement skip connections which can help to handle vanishing gradient issues in a deep neural network. ZP is a widely used padding scheme to generate an output of the same size with an input. Among padding schemes, ZP is the easiest way to implement but irrelevant zeros padded in the boundary of patches influence the performance of SRResNet.

Fig. 2 shows the image of the difference between a target image and a reconstructed one assembled from super-resolution output patches. Due to simple ZP on the boundary pixels, the boundary pixels in the super-resolution output patches are not properly generated and the boundaries are clearly observed in the image. So padding algorithm should be carefully chosen especially when patch inputs are applied to a deep learning model. In this paper, PCP algorithm proposed in [29] is adopted to improve the performance. PCP is described in:

x`(i,j)=WTX(i,j)P0r(i,j)+b(2)

where WT and b are a wight matrix and a bias respectively, X(i,j)P0 is a zero padded input and r(i,j) is a ratio value for position (i,j) which is less than one. The ratio r(i,j) is defined by

r(i,j)=||1(i,j)P1||1||1(i,j)P0||1(3)

where ||.||1 is a 1-norm of the window of similar size of the filter, and equal to ∑i,j=−f2+f21(i,j)Px where f is the size of the filter used for the current convolution, 1(i,j)P0 is a matrix of similar shape of input, with each element set to 1 and padded with zeros, 1(i,j)P1 is an input shaped matrix with each element set to 1 and padded with ones.

Figure 2: Difference image between reconstructed SR image and target HR image

4  Experimental Results

4.1 Experimental Setup

In order to analyze the performance of the SRResNet depending on input size, the amount of training data, network depth and padding schemes, a few of experiments have been carried out. In the experiments, NVIDIA GPU RTX2070 (8GB GDDR6) is utilized for GPU processing and deep learning software programs are implemented based on Keras-2.3.1 and tensorflow-1.14. In this paper, 2× upscaling case is considered for super-resolution. For single full image inputs, CPU is used instead of GPU.

We used 40 images of dimension 640 × 640 selected from ImageNet database [32] for the experiments. Among the selected 40 images, the number of images used for training is 36 and 4 images are used for validation.

The optimally trained model is selected based on the performance evaluation of super-resolution output image patches of size 32 × 32 considering target patch images extracted from the validation image data in each experiment. For the comparison between single image super-resolution and patch based one, LR single input images with the resolution of 192 × 192 are obtained through bicubic interpolation of HR images with the resolution of 384 × 384. We used 36 images for training and 4 images for testing.

In the training of SRResNet, the weighted combination of MSE and VGG-loss function which was introduced in [11] is considered as a performance measure. By assigning a bigger weight to VGG loss in the objective function, visual features in the images are concerned more than simple MSE [11]. In the experiments, the weights of MSE and VGG loss in the objective function are respectively assigned with 0.5 and 1.0.

The experimental results are evaluated using three well-known benchmark datasets of Set5 [33], Set14 [34], and BSD100 [35]. For better perspective comparison we use 6 different quality metrics i.e., Mean Squared Error (MSE), Signal to Reconstruction Error ratio (SRE) [36], Structural Similarity Index Measure (SSIM) [37], Feature based Similarity Index Measure (FSIM) [38], Information theoretic-based Statistic Similarity Measure (ISSM) [39] and Universal Image Quality index (UIQ) [40]. The details of the listed quality metrics can be found in [41,42].

4.2 Performance Analysis: Input Size

Input size is a major concern in many computer vision tasks. In hand-held devices a large sized network is less feasible and even if compressed, the network still requires lots of resources. Smaller input causes the network to focus more accurately on the SR function while regularizing the accompanying noise, and hence able to learn the said function from a smaller amount of training data. This technique works as a potential network regularizer. In super-resolution tasks, the major goal of the model is to learn the super-resolution function. In case of full image, the model learns the SR function along with other irrelevant latent features, like shapes, colors, or other global patterns. These features work like a noise, but in case of patches the model focuses on finer detail of the images and hence the latent noise eventually starts diluting along with the training, and hence the model is well generalized for the unseen data. Tab. 1 shows the comparison summary between the case of single full image input of 384 × 384 (SRResNet1) and that of patch input of 32 × 32 (SRResNet2) using networks with 4 residual layers and ZP scheme, incorporating total of 12 convolutional layers.

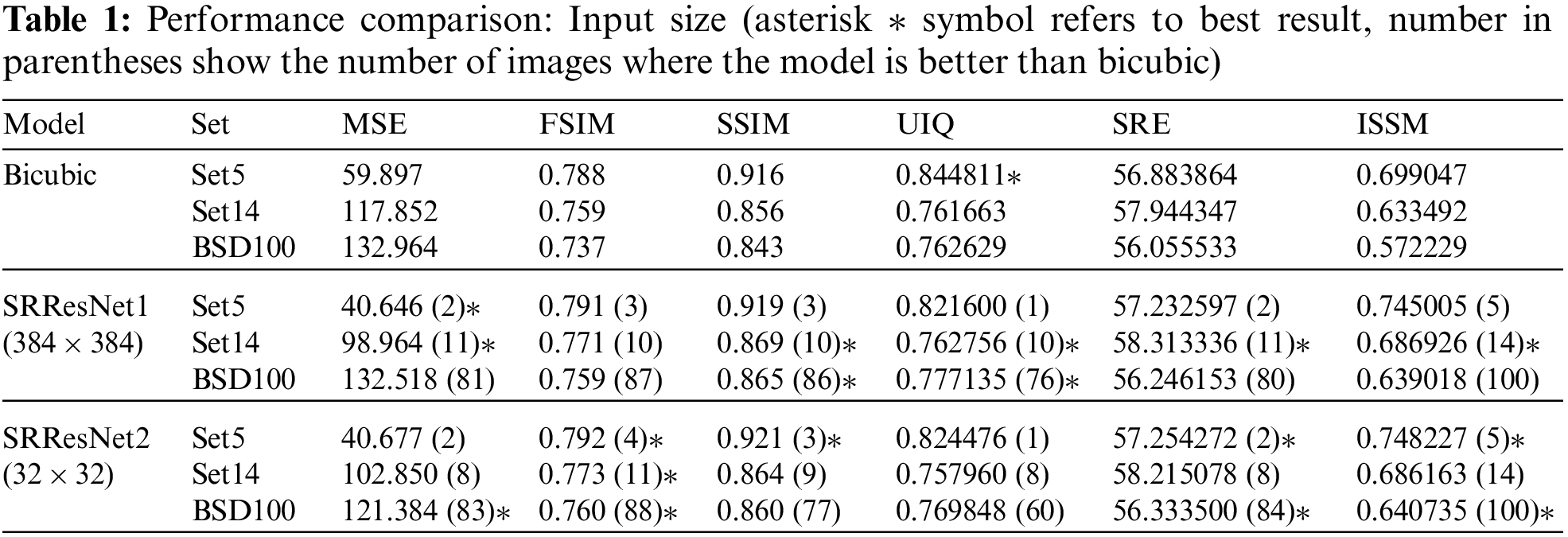
Tab. 1 summarizes the performance comparison depending on the input size. In Tab. 1, SRResNet1 is a ResNet model trained with input size 384 × 384, and SRResNet2 is a model trained with input size of 32 × 32.

Lower values for MSE mean better and higher values for FSIM, SSIM, UIQ, SRE and ISSM are better in the sense of performance in the table. The values in parenthesis present the number of cases that model shows better performance than bicubic interpolation.

As depicted in Tab. 1, the performance of both SRResNet1 and SRResNet2 show better performance than bicubic interpolation algorithm. Even though patch input based SRResNet2 has many advantages over single full image one (SRResNet1) and shows better performance in the average sense than SRResNet1, it is not always better than single full image case (SRResNet1) due to the effect of ZP.

4.3 Performance Analysis: Padding Scheme

In super-resolution problems, padding methods should be carefully considered especially in deep neural networks with patch inputs. The performance of deep neural networks depending on ZP and PCP is investigated in this section. The comparative results are summarized in Tab. 2 where SRResNetp has the same network structure with SRResNet2 but the ZP in SRResNet2 is replaced by PCP. In the simulations, both networks are trained using 32 × 32 patch images as inputs and SRResNetp shows better performance than SRResNet2. Considering the results in Tab. 1, it is also better than other models in almost all measures. The values in the parentheses represent the number of cases in which each model shows better performance than bicubic interpolation algorithm given in Tab. 1.

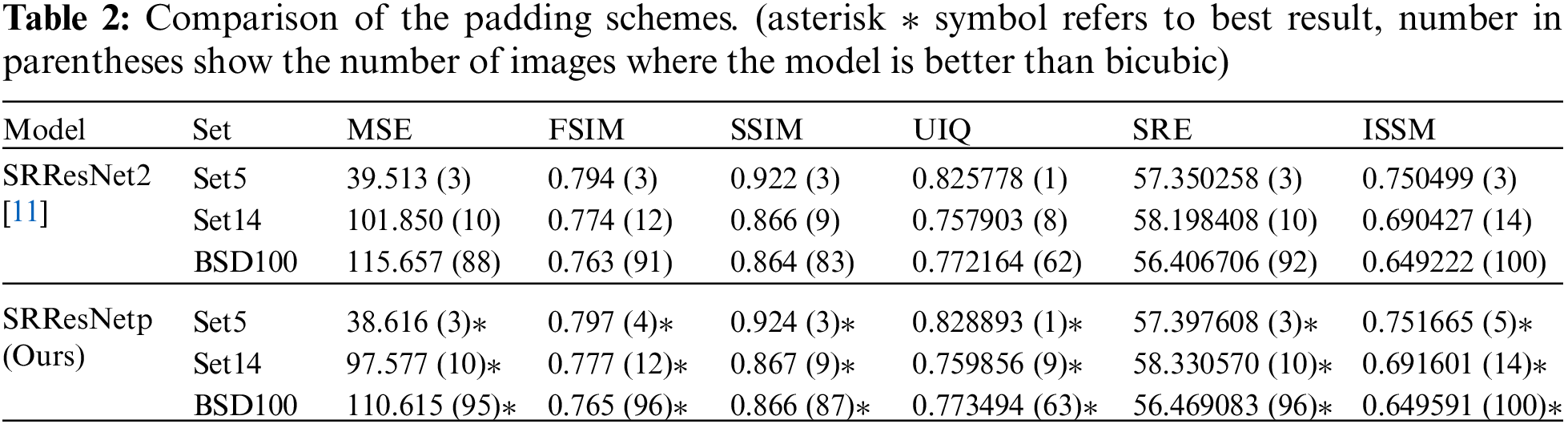
Fig. 3 is the graph of performance measure with respect to epoch number. Validation error is a cumulative error (MSE) over 1600 non-overlapping patches of 32 × 32 × 3 extracted from 4 validation images. Training error is calculated using MSE between super-resolution output patch and high-resolution target patch. SRResNetp shows more stable and consistent tendency than SRResNet2 during the training period.

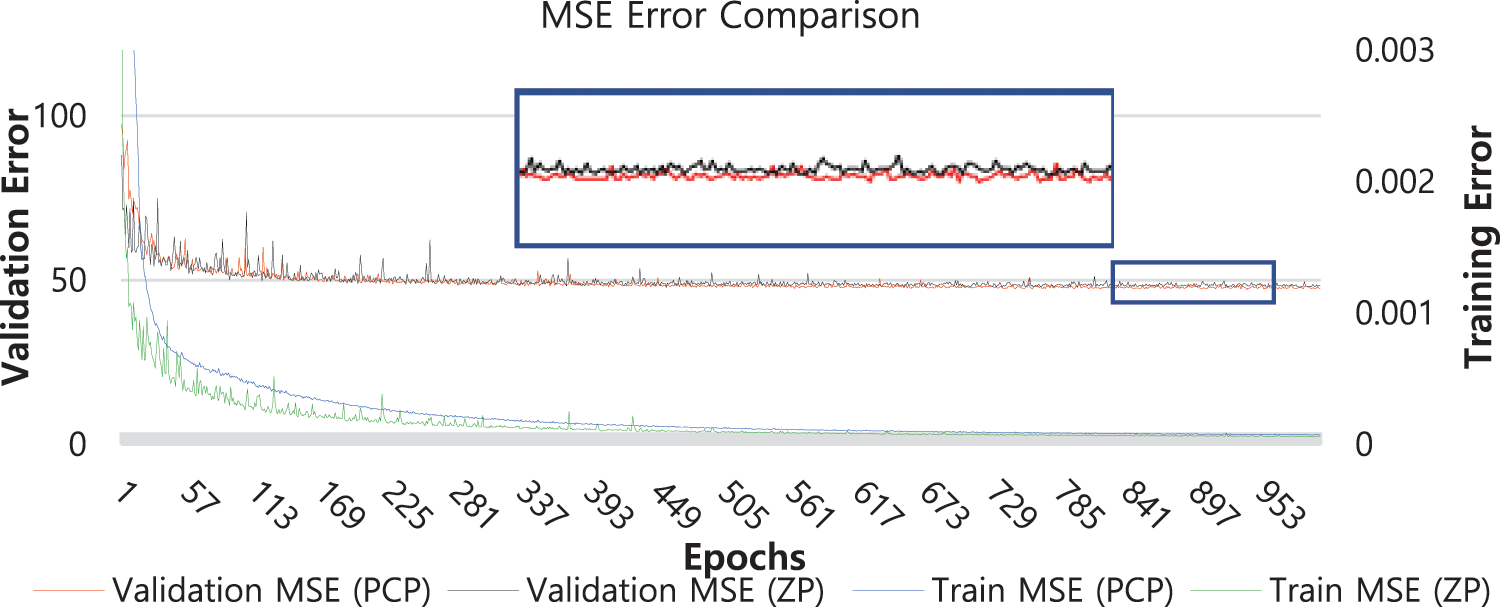
Figure 3: Training MSE and validation MSE of SRResNet with PCP and SRResNet with ZP

In order to check the effect of PCP more clearly, the difference of each pixel value between network output images and original target images is visualized in Fig. 4. The pixel values of the images in Fig. 4 are calculated using (4) which means the MSE value of each pixel considering 77 target images selected from the data set of BSD-100.

HMSRResNet(i,j)=∑k=0n(HRi,j−SRi,j)2n(4)

where HMSRResNet(i,j) is the heatmap index value for the difference image at position (i,j), HRi,j and SRi,j are the corresponding pixels of High Resolution and Super resolution images respectively. And the differences of similar corresponding pixels from n images are averaged.

Figure 4: Assembled images of pixel MSE of super-resolution and high-resolution images. (a) shows the image of MSE values between super-resolution image using ZP and HR image. (b) is image of MSE values between super-resolution image using PCP and HR image. (c) is the enlarged image of the area marked with a red square in (a). (d) is the enlarged image of the area marked with a yellow square in (b)

In Figs. 4a and 4b represent respectively the assembled images of pixel MSE values obtained from patch outputs of SRResNet2 and SRResNetp. The ZP case (a) shows more clear patch boundaries than PCP one (b). This phenomenon is more clearly observed as shown in the highlighted areas in both images depicted in (c) and (d). The PCP is shown to effectively compensate the drawbacks of ZP.

Tab. 3 summarizes the MSE values of both padding methods with respect to the areas. PCP algorithm shows better performance than ZP one in both areas and influences more on the boundary pixels than inner ones as expected.

4.4 Performance Analysis: Network Depth

Deep neural networks have capabilities to handle complicated problems efficiently but some issues such as vanishing gradient and ZP are inherently degrading the performance as network depth is increased. In SRResNet, the vanishing gradient issue is resolved by using skip connection structure. In this section, the performance of PCP algorithm is investigated depending on the depth of SRResNet.

The performance comparison between SRResNet2 and SRResNetp are depicted in Fig. 5 depending on the network depth. In the simulation, we considered four cases by choosing 4 residual blocks, 8 residual blocks, 16 residual blocks and 32 residual blocks in both networks. The numbers on the blue bar represent the MSE values and the ones on the yellow bar mean the percentage improvement of PCP with respect to ZP obtained by the formula (MSESRResNet2−MSESRResNetp)MSESRResNet2x100. As the network depth is increased, the super-resolution performance is shown to be improved in both networks as expected and the PCP shows superior performance to ZP. As observed in Fig. 5, the values of percentage improvement are decreasing as the network depth is increased because the performance degradation by ZP is overwhelmed by the super-resolution performance improvement as the depth is increased.

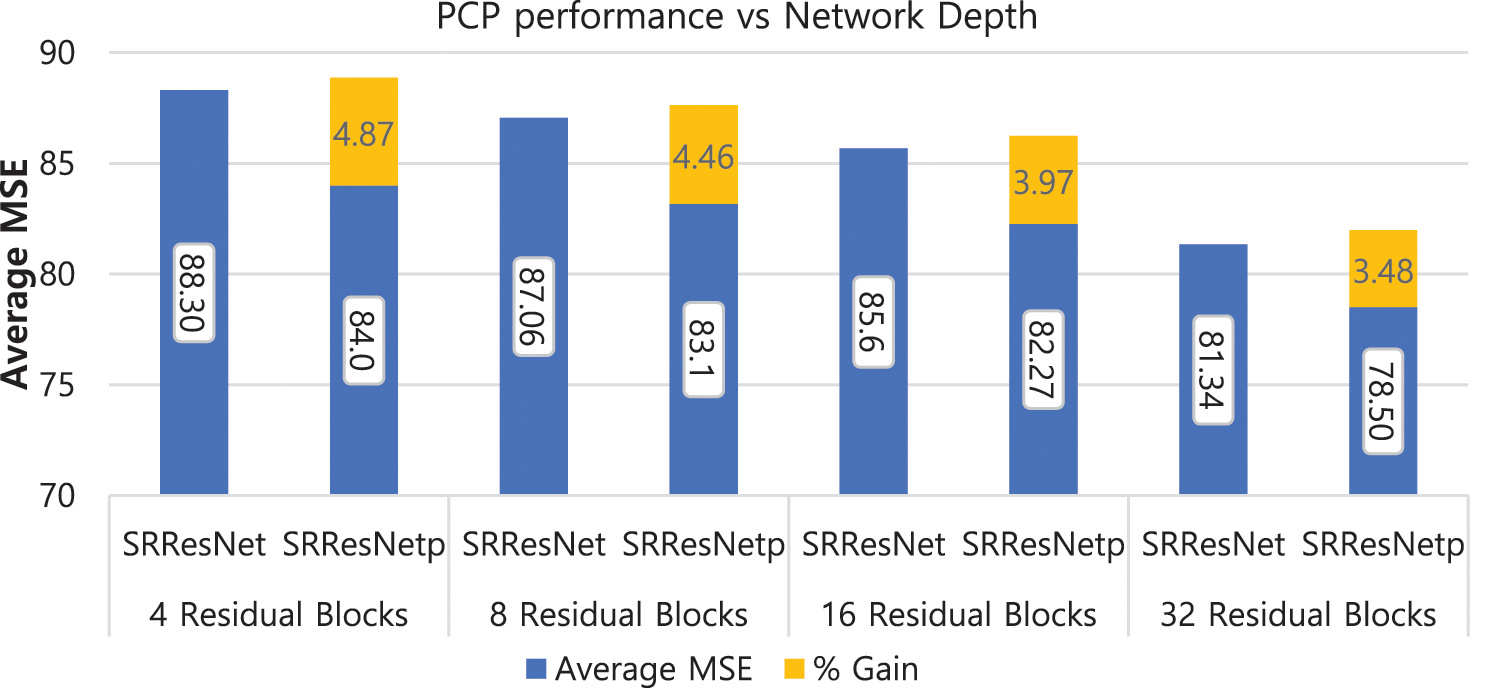
Figure 5: Average MSE of SRResNet and SRResNetp

4.5 Comparison with State-of-the-art Methods

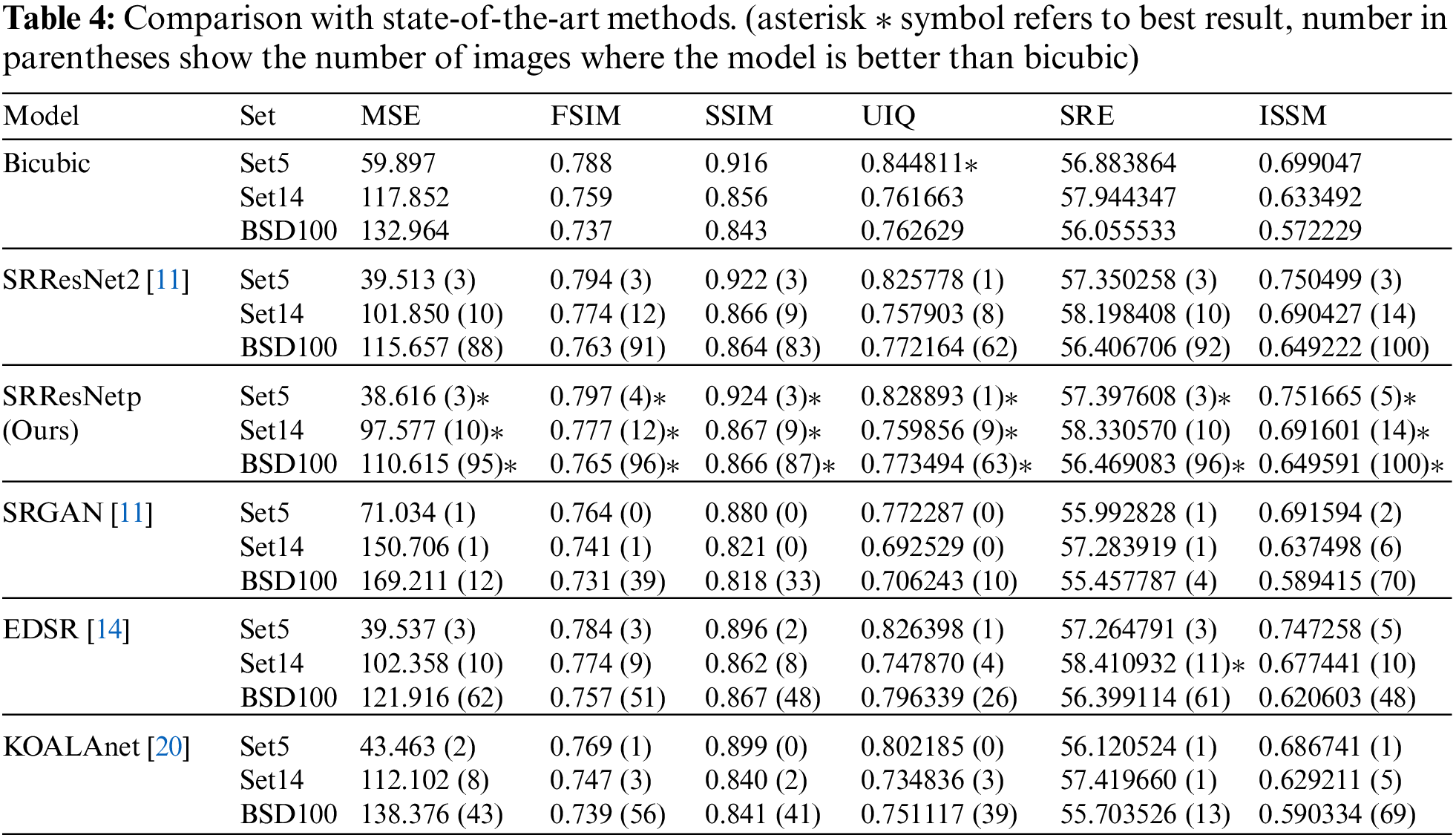
We compared our results with state-of-the-art methods, trained on a limited dataset of 36 training images and 4 validation images of size 640 × 640. The comparative results from Bicubic, SRResNet2 (with ZP), SRResNetp (ours, with PCP), EDSR [14], SRGAN [11], and KOALAnet [20] are summarized in Tab. 4 where SRResNetp has the same network structure with SRResNet2 but the ZP in SRResNet2 is replaced by PCP. The Networks SRResNet2, SRResNetp, and SRGAN are trained using 32 × 32 patch images as inputs and SRResNetp shows better performance than SRResNet2 and SRGAN. KOALAnet is trained in three phases and the third phase of upsampling network is used for inference. The results shows that SRResNetp has better results on all quality metrics. One of the possible reasons is that these networks are originally tunned according to a large training dataset and facing problem in learning the SR function from smaller training dataset (36 images). SRResNetp is able to learn the SR function effectively from a limited dataset of size 36 images. Other benefits of patch inputs is that the networks need less amount of computational resources, as shown in Tab. 5. Due to increased ratio of input data to the padded zeros in convolutional layers, the network must compromise on quality in case of patch inputs, but PCP can compensate the possible loss in quality. Hence patch inputs shall be used along with PCP or any other sophisticated padding scheme.

Visual comparison of various methods is shown in Fig. 6. One image is selected from each benchmark dataset. It can be seen from the visual results that SRResNet(PCP) can reconstruct finer details as compared to SRGAN, EDSR and KOALAnet. The result of KOALAnet is not good due to the fact that the network is too complex to learn from a limited dataset.

Figure 6: Visual comparison between (a) Original HR image, (b) SRGAN, (c) SRResNet-patch input, (d) SRResNet-PCP, (e) Bicubic interpolation, (f) EDSR, (g) KOALAnet

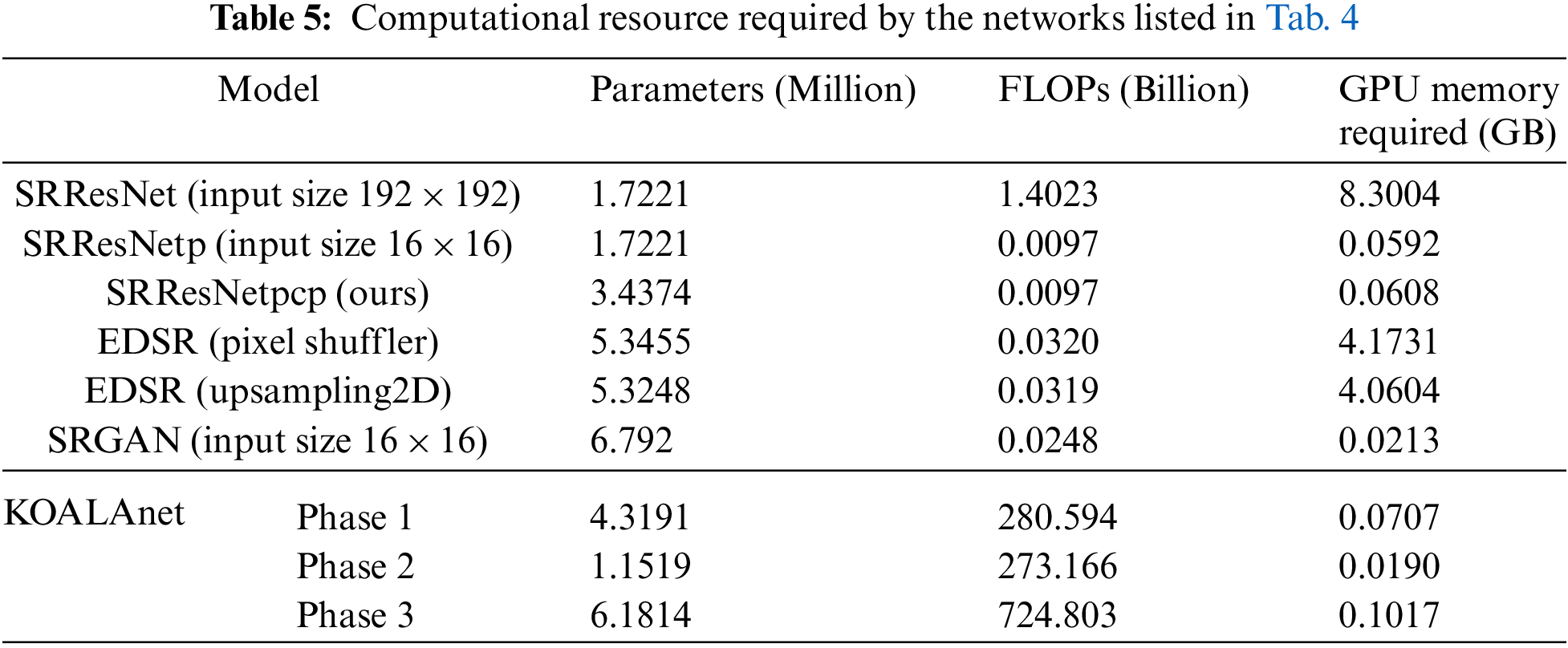
The total number of parameters in Tab. 5, includes both the trainable and non-trainable parameters. In terms of computational resources, the number of floating point operations (FLOPs) and the amount of GPU memory requirement by a method, are two main concerns during designing an algorithm or choosing among different alternatives. The need for GPU memory by an algorithm is directly related to the input image size and number of network parameters. The number of network parameters are usually kept constant, so the GPU memory required by the same method for two different inputs will be different, as shown in the case of SRResNet and SRResNetp. Both networks have same architecture and network parameters, but the memory requirement for the network with 384 × 384 input size and batch size of 1 causes the outburst of the available GPU memory with our NVIDIA GPU RTX2070 (8GB GDDR6). Here the SRGAN network is reduced to only 4 residual blocks (originally the network has 16 residual blocks) for the fair comparison.

5  Conclusion and Future Work

In this paper, it has been shown that the performance of SRResNet for single image super-resolution can be enhanced by considering patch images as input and replacing ZP with PCP. Even though patch input based super-resolution has lots of advantages including performance and network efficiency, there exists a limitation in performance enhancement of SRResNet due to ZP. We have shown that this limitation can be improved by introducing PCP as a padding algorithm instead of ZP. PCP is an efficient algorithm but still there is a possibility to improve the algorithm because it simply considers the number of pixels on the boundary overlapped with filters to be padded.

Funding Statement: This work was supported by Hallym University Research Fund HRF-202104-004.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Zhao, G. Li, W. Xie, W. Jia, H. Min et al., “GUN: Gradual upsampling network for single image super-resolution,” IEEE Access, vol. 6, pp. 39363–39374, 2018. [Google Scholar]

 2.  A. Sindal, K. Breininger, J. Käßer, A. Hess, A. Maier et al., “Learning from a handful volumes: MRI resolution enhancement with volumetric super-resolution forests,” in Proc. IEEE Int. Conf. on Image Processing (ICIP), Athens, Greece, pp. 1453–1457, 2018. [Google Scholar]

 3.  G. Song and K. M. Lee, “Depth estimation network for dual defocused images with different depth-of-field,” in Proc. IEEE Int. Conf. on Image Processing (ICIP), Athens, Greece, pp. 1563–1567, 2018. [Google Scholar]

 4.  J. Kim, J. Kwon Lee and K. Mu Lee, “Accurate image super-resolution using very deep convolutional networks,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 1646–1654, 2016. [Google Scholar]

 5.  J. Kim, J. Kwon Lee and K. Mu Lee, “Deeply-recursive convolutional network for image super-resolution,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 1637–1645, 2016. [Google Scholar]

 6.  Y. Tai, J. Yang and X. Liu, “Image super-resolution via deep recursive residual network,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, pp. 2790–2798, 2017. [Google Scholar]

 7.  P. P. Shinde and S. Shah, “A review of machine learning and deep learning applications,” in Proc. Int. Conf. on Computing Communication Control and Automation (ICCUBEA), Pune, Maharashtra, India, pp. 1–6, 2018. [Google Scholar]

 8.  K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Proc. 3rd Int. Conf. on Learning Representations (ICLR), San Diego, CA, USA, 2014. [Google Scholar]

 9.  K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

10. K. He, X. Zhang, S. Ren and J. Sun, “Identity mappings in deep residual networks,” in Proc. European Conf. on Computer Vision, Amsterdam, The Netherlands, pp. 630–645, October 2016. [Google Scholar]

11. C. Ledig, L. Theis, F. Huszar, J. Caballero, A. Cunningham et al., “Photo-realistic single image super-resolution using a generative adversarial network,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, pp. 105–114, 2017. [Google Scholar]

12. S. Anwar, S. Khan and N. Barnes, “A deep journey into super-resolution: A survey,” ACM Computing Survey, vol. 53, no. 3, pp. 1–34, 2021. [Google Scholar]

13. C. Dong, C. C. Loy, K. He and X. Tang, “Learning a deep convolutional network for image supar-resolution,” in Proc. European Conf. on Computer Vision, Zurich, Switzerland, pp. 184–199, 2014. [Google Scholar]

14. B. Lim, S. Son, H. Kim, S. Nah and K. M. Lee, “Enhanced deep residual networks for single image super-resolution,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, pp. 1132–1140, 2017. [Google Scholar]

15. R. Timofte, E. Agustsson, L. Van Gool, M. -H. Yang, L. Zhang et al., “NTIRE 2017 challenge on single image super-resolution: Methods and results,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, pp. 1110–1121, 2017. [Google Scholar]

16. N. Ahn, B. Kang and K. -A. Sohn, “Fast, accurate, and lightweight super-resolution with cascading residual network,” in Proc. European Conf. on Computer Vision (ECCV), Munich, Germany, pp. 256–272, 2018. [Google Scholar]

17. J. Jiao, W. -C. Tu, S. He and R. W. Lau, “Formresnet: Formatted residual learning for image restoration,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, pp. 1132–1140, 2017. [Google Scholar]

18. K. Zhang, W. Zuo, Y. Chen, D. Meng and L. Zhang, “Beyond a Gaussian denoiser: Residual learning of deep cnn for image denoising,” IEEE Transaction on Image Processing, vol. 26, no. 7, pp. 3142–3155, 2017. [Google Scholar]

19. X. Mao, C. Shen and Y. -B. Yang, “Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections,” in Proc. Int. Conf. on Neural Information Processing Systems (NIPS), Barcelona, Spain, pp. 2810–2818, 2016. [Google Scholar]

20. S. Y. Kim, H. Sim and M. Kim, “KOALAnet: Blind super-resolution using kernel-oriented adaptive local adjustment,” in Proc. Conf. on Computer Vision and Pattern Recognition (CVPR), Virtual Conference, pp. 10606–10615, 2021. https://cvpr2021.thecvf.com/. [Google Scholar]

21. R. A. Naqvi, D. Hussain and W. K. Loh, “Artificial intelligence-based semantic segmentation of ocular regions for biometrics and healthcare applications,” Computers Materials & Continua, vol. 66, pp. 715–732, 2020. [Google Scholar]

22. D. Hussain, R. A. Naqvi, W. K. Loh, J. Y. Lee, “Deep learning in DXA image segmentation,” Computers Materials & Continua, vol. 66, no. 3, pp. 2587–2598, 2021. [Google Scholar]

23. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

24. X. R. Zhang, J. Zhou, W. Sun and S. K. Jha, “A lightweight CNN based on transfer learning for COVID-19 diagnosis,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]

25. S. Albahli, T. Nazir, A. Mehmood, A. Irtaza, A. Alkhalifa et al., “AEI-DNET: A novel DenseNet model with an autoencoder for the stock market predictions using stock technical indicators,” Journal of Electronics, vol. 11, no. 4, pp. 611–636, 2022. [Google Scholar]

26. T. Mahmood, M. Owais, K. J. Noh, H. S. Yoon, J. H. Koo et al., “Accurate segmentation of nuclear regions with multi-organ histopathology images using artificial intelligence for cancer diagnosis in personalized medicine,” Journal of Personalized Medicine, vol. 11, no. 6, pp. 515–539, 2021. [Google Scholar]

27. C. Innamorati, T. Ritschel, T. Weyrich and N. J. Mitra, “Learning on the edge: Explicit boundary handling in CNNs,” in Proc. British Machine Vision Conf. (BMVC), Newcastle, UK, 2018. [Google Scholar]

28. H. Cheng, C. Chao, J. Dong, H. Wen, T. Liu et al., “Cube padding for weakly-supervised saliency prediction in 360° videos,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, Utah, pp. 1420–1429, 2018. [Google Scholar]

29. G. Liu, K. J. Shih, T. -C. Wang, F. A. Reda, K. Sapra et al., “Partial convolution based padding,” Technical report, NVIDIA Corporation, preprint arXiv:1811.11718, 2018. [Online] Available: http://arxiv.org/abs/1811.11718. [Google Scholar]

30. K. He, X. Zhang, S. Ren and J. Sun, “Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification,” in Proc. IEEE Int. Conf. on Computer Vision (ICCV), Santiago, Chile, pp. 1026–1034, 2015. [Google Scholar]

31. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. Int. Conf. on Machine Learning (ICML), Lille, France, pp. 448–456, 2015. [Google Scholar]

32. O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh et al., “ImageNet large scale visual recognition challenge,” International Journal of Computer Vision, vol. 3, pp. 1–42, 2014. [Google Scholar]

33. M. Bevilacqua, A. Roumy, C. Guillemot and M. L. Alberi-Morel, “Low-complexity single-image super-resolution based on nonnegative neighbor embedding,” in Proc. British Machine Vision Conf. (BMVC), Surrey, UK, pp. 1–10, 2012. [Google Scholar]

34. R. Zeyde, M. Elad and M. Protter, “On single image scale-up using sparse-representations,” in Curves and Surfaces, Lecture Notes in Computer Science, Berlin, Heidelberg: Springer, vol. 6920, pp. 711–730, 2010. [Google Scholar]

35. D. Martin, C. Fowlkes, D. Tal and J. Malik, “A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics,” in Proc. IEEE Int. Conf. on Computer Vision (ICCV), Vancouver, BC, Canada, vol. 2, pp. 416–423, 2001. [Google Scholar]

36. C. Lanaras, J. Bioucas-Dias, S. Galliani, E. Baltsavias and K. Schindler, “Super-resolution of sentinel-2 images: Learning a globally applicable deep neural network,” ISPRS Journal of Photogrammetry and Remote Sensing, vol 146, pp. 305–319, 2018. [Google Scholar]

37. Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, “Image quality assessment: From error measurement to structural similarity,” IEEE Transaction on Image Processing, vol. 13, no. 4, pp. 600–612, 2004. [Google Scholar]

38. L. Zhang, L. Zhang, X. Mou and D. Zhang, “FSIM: A feature similarity index for image quality assessment’, IEEE Transaction on Image Processing, vol. 20, no. 8, pp. 2378–2386, 2011. [Google Scholar]

39. M. A. Aljanabi, Z. M. Hussain, N. A. A. Shnain and S. F. Lu, “Design of a hybrid measure for image similarity: A statistical, algebraic and information-theoretic approach,” European Journal of Remote Sensing, vol. 52, no. Suppl. 4, pp. 2–15, 2019. [Google Scholar]

40. Z. Wang and A. C. Bovik, “A universal image quality index,” IEEE Signal Processing Letters, vol. 9, no. 3, pp. 81–84, 2002. [Google Scholar]

41. U. Sara, M. Akter and M. S. Uddin, “Image quality assessment through FSIM, SSIM, MSE and PSNR–a comparative study,”. Journal of Computer and Communication, vol. 7, no. 3, pp. 8–18, 2019. [Google Scholar]

42. R. R. Choudhary, V. Goel and G. Meena, “Survey paper: Image quality assessment,” in Int. Conf. on Sustainable Computing in Science, Technology and Management (SUSCOM), Jaipur, India, 2019. [Google Scholar]