Optimal Resource Allocation for NOMA Wireless Networks

1  Introduction

The rapid development of the mobile Internet and the Internet of Things will place more stringent requirements on future wireless communication systems [1]. Therefore, a Non-Orthogonal Multiple Access (NOMA) technique, also known as Layer Division Multiplexing (LDM), has recently been proposed as a promising technology for the next generation of digital terrestrial television (DTT), which provides a simultaneous transmission of fixed and mobile services on the same radio frequency (RF) channel. Non-orthogonal multiple access (NOMA) [2] has the advantages of low latency, high transmission rate, high connection density, etc. [3], and is considered to be one of the technologies to solve the massive user access in future communications. NOMA overcomes the shortcomings of low spectrum utilization in traditional orthogonal multiple access, and it will be more widely used in mobile communications.

The concept of the Internet of Everything has gained traction in the industry as a result of the advancement of Internet of Things technology. On the one hand, realizing vast connections with limited communication resources is a big issue in the Internet of Things’ information transmission; on the other hand, low-cost communication nodes account for a significant percentage. These communication nodes are difficult to execute sophisticated tasks due to equipment expense limitations. As a result, achieving dependable communication while keeping equipment costs low is a major difficulty. The core premise of NOMA technology is that the transmitter assigns different strengths to different users’ signals, while the receiver utilizes successive interference cancellation first when demodulating lower-power signals.

With the rapid growth of mobile communications, there is a growing demand for spectrum efficiency and system capacity [4]. Because the existing multiple access method can no longer meet development objectives, the industry has introduced NOMA, a new multiple access method. NOMA, as one of the fundamental technologies for 5G, enables multi-user power sharing by providing various powers to users on the same frequency at the same time, resulting in a 50 percent increase in overall wireless access [5–7]. Existing research shows that NOMA can obtain higher system capacity and higher spectrum efficiency than Orthogonal Multiple Access (OMA), so the power allocation problem in NOMA system has attracted widespread attention in the academic community in recent years. Strong signal interference is eliminated by the technology, and when demodulating a signal with a higher power, the signal with a lower power is directly recognized as interference. NOMA is recognized as one of the future network’s potential multiple access technologies, and it has gotten a lot of attention  [8].

The conjugate gradient approach is used in this research to provide a rapid power distribution strategy that is less difficult than FSPA. The performance is superior to FPA and FTPA, and it achieves a balance between system complexity and performance.

2  Literature Review

The evolutionary process of mobile networks has allowed the strong demands of users to use more efficient services with high data transmission speeds. However, the number of users and the required services are constantly increasing, which has led to a greater development of previous technologies that meet these requirements, being so, after the launch of the known generations, the deployment of the mobile network of fifth generation (5G).

For the research on the power allocation algorithm in the NOMA system, the objective function is mainly focused on minimizing the total transmit power [9–13], minimizing the probability of outage [14–17], and maximizing system throughput [18–20], etc. The main existing algorithms full search power allocation (FSPA) [21], fixed power allocation (FPA) [22], iterative water-filling power allocation (IWPA) [23], and fractional transmit power allocation (FTPA) [24]. Reference [21] pointed out in the study of power allocation and interference cancellation algorithms for non-orthogonal multiple access systems that FSPA can achieve the best performance of non-orthogonal multiple access systems by searching for all user-pair power allocation combinations, but FSPA has high complexity. The problem is that the system cost is relatively large, so it is generally not used in the actual system. Although FPA is relatively low in complexity, the system performance is greatly affected by the power allocation factor, and usually cannot achieve the best performance of the system. Reference [23] pointed out in the study of non-orthogonal multiple access systems that IWPA can achieve better power distribution performance, but it has problems with local optimization and high complexity. Reference [24] and others proposed the FTPA algorithm. FTPA balances the fairness of users with low signal-to-noise ratio and reduces the complexity of decoding at the receiving end. However, FTPA is a local optimization scheme, and system performance is also affected by the selected power allocation. The impact of factors, therefore, the FTPA program needs to be further improved.

Since the computational complexity of the conjugate gradient method is equivalent to that of the steepest descent method, but the convergence speed is better than that of the steepest descent method [25], this paper proposes a fast power distribution scheme based on the conjugate gradient method, which has a lower complexity than FSPA. The performance is better than FPA and FTPA, and it achieves a compromise between complexity and system performance.

3  System Model and Optimization Analysis

3.1 System Model

Assuming that the transmitting end of the system adopts the single-antenna transmission mode, and at the same time, on the same frequency resource block, the system schedules N users. After the base station allocates the power of the signals sent to the N users, the signals are linearly superimposed in the power domain, and the transmitted equivalent is complex. The baseband signal [26] can be expressed as:

x=β1s1+β2s2+⋯+βNsN(1)

Among them, s1,s2,…,andsN are the energy normalized signals sent to user 1, user 2, …, user N(Es1=1,Es2=1,…,EsN=1);β1,β2,…,andβN are power distribution factors, satisfying ∑n=1Nβn=1. Generally, users farther from the base station will be allocated more power.

After the wireless channel, the received signal [27] of user n(1≤n≤N) is:

yn=hnx+wn(2)

Among them, hn is the channel coefficient, and wn is the Gaussian white noise including cell interference, which obeys the complex Gaussian distribution with a mean value of 0 and a variance of  σw2.

At the receiving end of the NOMA downlink, users use interference cancellation receivers for detection. After other users decode, the interference of this user can be eliminated, so as to achieve correct decoding. Take two users as an example. Assuming that user 1 is far away from the base station, more power will be allocated to user 1. At the receiving end, user 1 can directly decode the desired signal x1. For user 2, the signal x1 of user 1 needs to be decoded first, and then the relevant component of x1 is subtracted from the received signal y2. Therefore, when user 2 decodes the signal x2, the interference of x1 has been removed, so that the signal can be decoded correctly.

Based on the above analysis, for the NOMA system based on the SIC receiver, it is assumed that there are N users. From user 1 to user N, the distance between the user and the base station gradually decreases.

Using Shannon’s formula, the reachable capacity of each user can be obtained separately. Assuming that the power allocation factor assigned to user n is βn, then the reachable capacity of user n is:

Rn(βn)=log2⁡(1+βn|hn|2∑j>nNβj|hn|2+1)(3)

In order to ensure the fairness of user scheduling, the weighted sum rate Rsum is used to maximize user power allocation criteria [26]:

Rsum=∑n=1N1log2⁡(1+|hn|2)Rn(4)

The above problems can be summarized as the following optimization function:

maxRsum=∑n=1N1log2⁡(1+|hn|2)Rn

s.t.0≤βN≤βN−1≤⋯≤β1≤1(5)

The optimal power allocation factor can be obtained by seeking the extreme value of the above formula. In order to solve this constrained optimization problem, this paper first uses the interior point penalty function method [27] to transform it into an unconstrained optimization problem, and then uses the conjugate gradient descent method to find the optimal solution. Let β=[β1β2…βN]T.

3.2 Objective Function for Unconstrained Optimization

The interior point penalty function method in the penalty function method is to define the new objective function in the feasible region, so that its initial point and the subsequent iteration point sequence must also be in the feasible region, and penalize points that may deviate from the feasible region, which is equivalent to an obstacle is set on the boundary of the feasible region to prevent the iteration point from crossing beyond the feasible region. Therefore, the interior point penalty function method is also called the obstacle function method. Rewrite Eq. (5) into the following form:

min−∑n=1N1log2⁡(1+|hn|2)Rn

s.t.βn−1≤0,n=1,…,N

βn+1−βn≤0,n=1,…,N−1

−βn≤0,n=1,…,N(6)

Then the following objective function can be constructed:

f=−∑n=1N1log2⁡(1+|hn|2)Rn−um{∑n=1N(1βn−1−1βn)+∑n=1N−11βn+1−βn}(7)

Among them, um is the penalty factor, which is a descending sequence of positive numbers, namely:

u0>u1>⋯um>um+1>⋯>0,limm→∞um=0(8)

Usually um = 1.0, 0.1, 0.01 and so on. The termination criterion for the convergence of the interior point penalty function method is as follows:

||βm∗(um)−βm+1∗(um+!)||≤ε1(9)

|f(βm∗(um))−f(βm+1∗(um+!))f(βm∗(um))|≤ε2(10)

Among them, βm∗(um) is the best advantage of unconstrained optimization when the penalty factor is um.

4  Conjugate Gradient Descent

The conjugate gradient method is an effective algorithm for solving optimization problems. Its iterative formula can be written as:

βk+1=βk+αkdk(11)

Among them, αk is determined by a certain linear search. Existing search algorithms include exact linear search and approximate linear search methods such as: Wolfe linear search, Armijo linear search and Goldstein linear search and so on [28]. The authors in [29] proved the global convergence of the (Polak–Ribière–Polyak) PRP algorithm [30] in the conjugate gradient method when Armijo linear search is used [31,32]. Therefore, this article uses the Armijo linear search algorithm to find the smallest non-negative integer h, so that the step factor αk=ρh satisfies the following conditions:

f(βk+αkdk)−f(βk)≤−δαk2||dk||2(12)

where ρ∈(0,1),δ>0. dk is the k-th search direction, which is obtained by the following calculation formula:

dk={−gk,k=0−gk+−γkdk−1,k>0(13)

where gk=∇f(βk) is the gradient of the function f at the point βk. The selection of the parameter γk satisfies the conjugacy, and the existing conjugate gradient methods include: Face recognition (FR) algorithm, PRP algorithm, Harmony search (HS) algorithm, collision detection (CD) and diffuse yield (DY) algorithms [33–41]. In this paper, the PRP algorithm is selected to calculate the value of γk, and its definition is as follows:

γkPRP=gkTzk−1||gk−1||2(14)

where zk−1=gk−gk−1, and ||⋅|| is the Euclidean norm.

In summary, the steps of the proposed unconstrained power allocation scheme are as follows in Algorithm 1.

After adding constraint conditions, the constraint function based on the conjugate gradient method.

The steps of the rate allocation plan are as follows:

(1)   Given the initial point β0 in the feasible region, as well as u0,c, and calculation accuracy ε1,ε2, set m=0.

(2)   Call the above unconstrained optimization method to find the optimal solution βm∗ and f(βm∗,um) of f.

(3)   Use the termination criterion to judge whether it has converged. If it converges, stop the iteration. The best advantage of the constrained power allocation scheme is β∗=βm∗. If it does not converge, set β0=βm∗(um), um+1=c.um, m=m+1 and transfer to step (2) to continue the calculation.

5  Simulation Results

Assuming that the channel obeys Rayleigh fading, the system performance of the two-user model is simulated. When the transmit power SNR1 of user 1 = 10 dB, and the signal-to-noise ratio difference SNR2-SNR1 of user 1 and 2 are 10, 20, 30 and 40 dB, respectively. The simulation parameters are shown in Tab. 1.

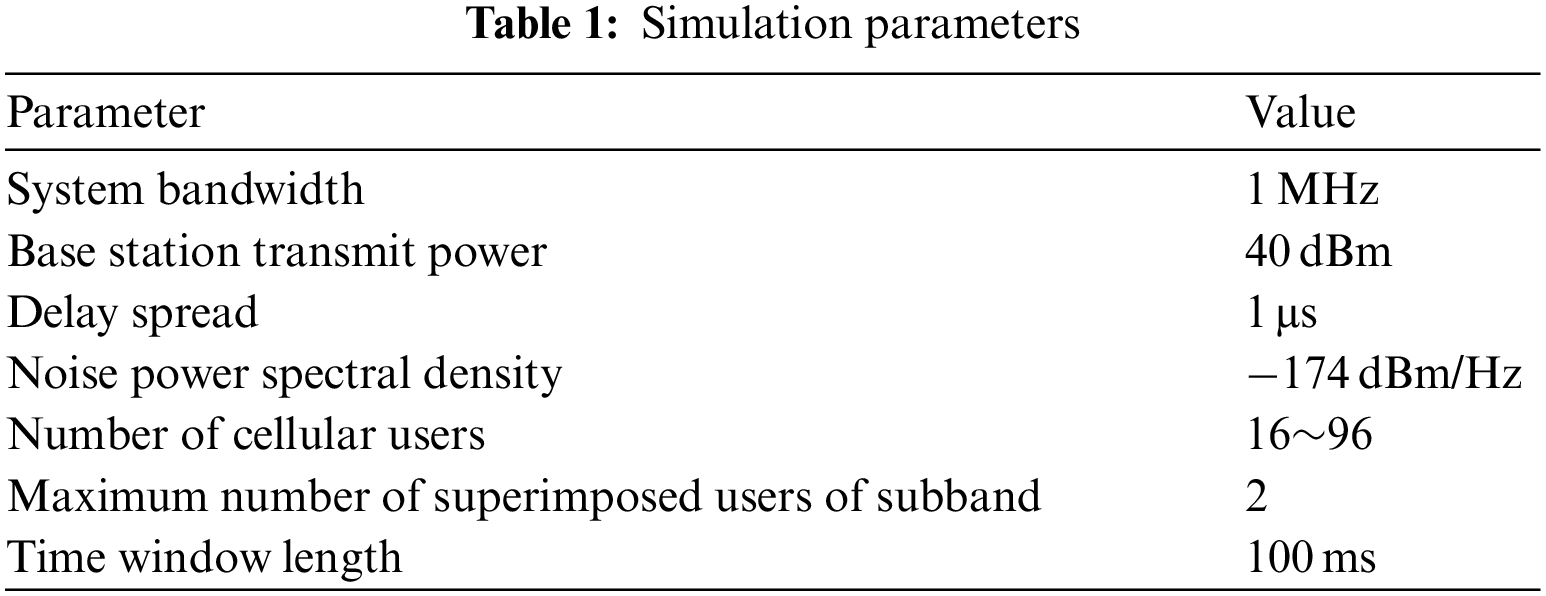
The change of the weight and rate Rsum of the proposed algorithm with the power allocation factor is shown in Fig. 1. It can be seen from Fig. 1 that:

(1)   The choice of power allocation factor directly affects the weighted sum rate;

(2)   When the signal-to-noise ratio of user 1 is fixed, as the difference between the two users’ signal-to-noise ratio increases, the optimal power allocation factor gradually decreases, which also indicates that the remote user will be allocated more power. It is because the criterion adopted in this article is the principle of fairness of user scheduling;

(3)   The greater the difference in signal-to-noise ratio between users, the greater the weighted sum rate of the system.

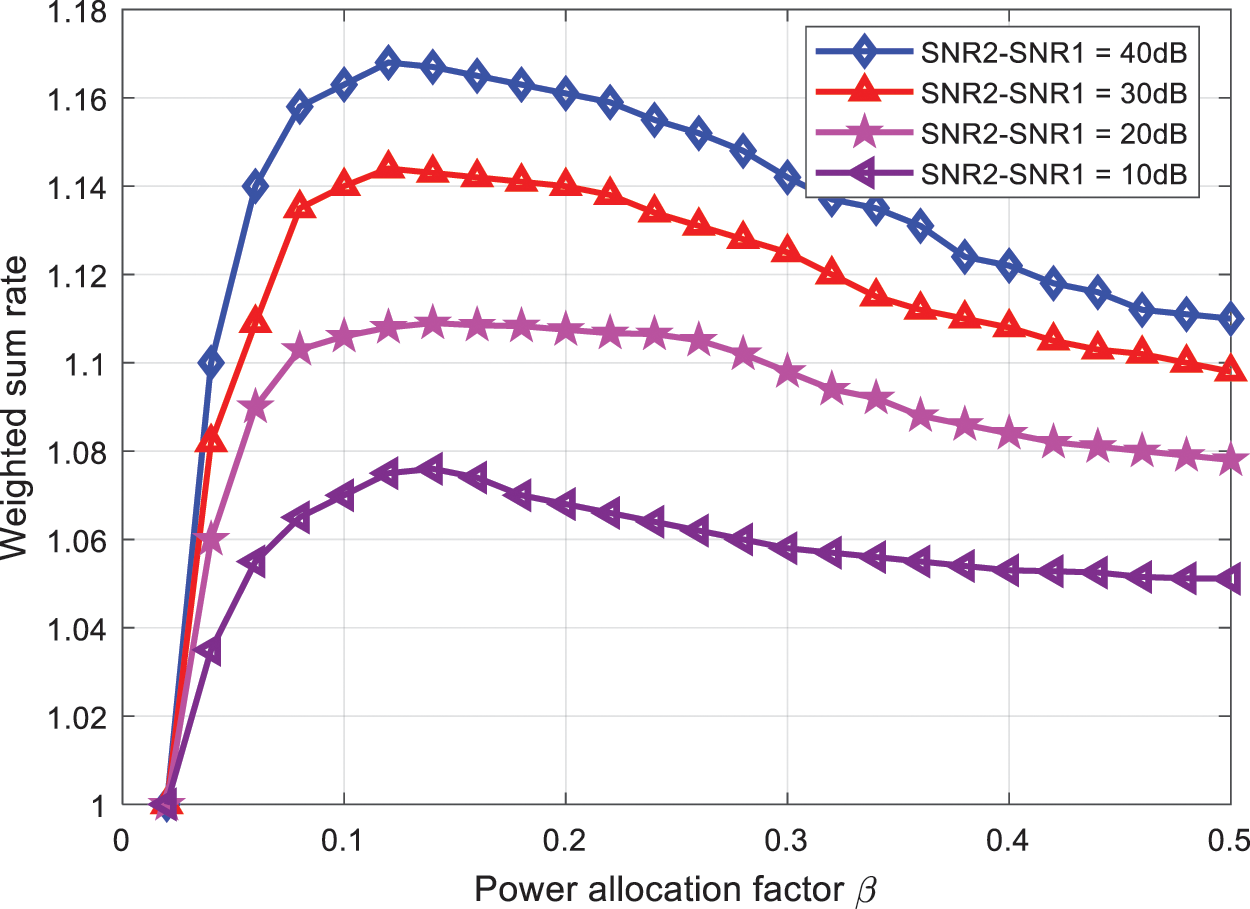
Figure 1: Comparison of the sum rate and power allocation factor of the proposed algorithm

When the difference in signal-to-noise ratio between users is fixed (SNR2-SNR1 = 20 dB) and the signal-to-noise ratio of user 1 is changed, when SNR1 is 2, 4, 6, 8 and 10 dB, the weight and rate of the algorithm in this paper vary with the power allocation factor. The curve is shown in Fig. 2. It can be seen from Fig. 2 that when the SNR difference between users is fixed, the weighted sum rate increases with the increase of user 1 SNR. This is because the difference in the signal-to-noise ratio between users is fixed. When the signal-to-noise ratio of user 1 increases, the corresponding signal-to-noise ratio of user 2 also increases, so the equivalent channel conditions of both users become better, so the weighted sum rate increases.

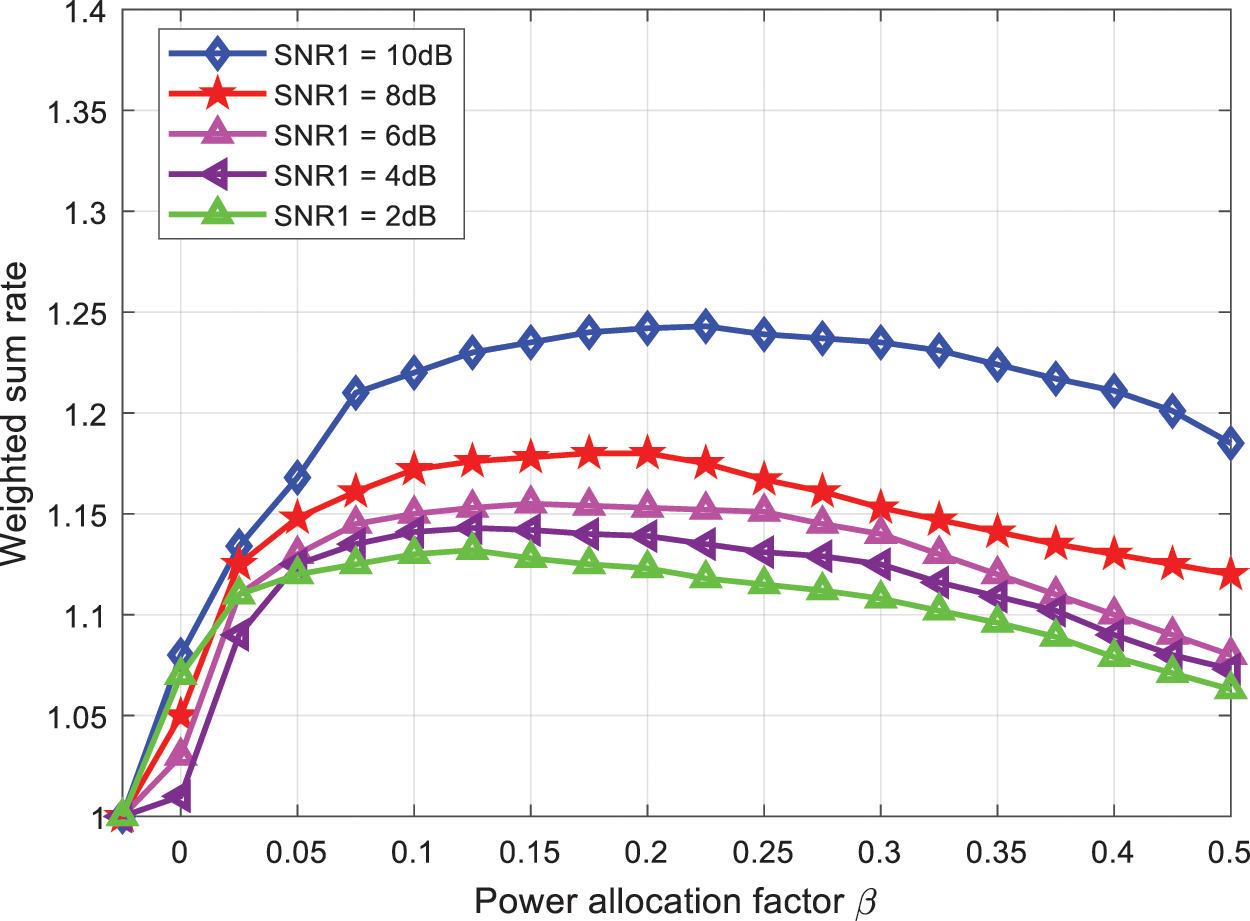
Figure 2: Comparison of the sum rate and power allocation factor of the proposed algorithm with 20 dB SNR difference

When the number of users is 2 and SNR1 = 5 dB, the change curve of the weighted sum rate of the NOMA system with SNR2 using the proposed algorithm, FPA algorithm and FTPA algorithm is shown in Fig. 3. The weighted and rate of the NOMA system utilizing the proposed algorithm, the FPA algorithm, and the FTPA method vary with the number of users when the number of users is 3, 4, 5, 6, and 7, as shown in Fig. 4. The system weights and rates of the three algorithms will increase if the signal-to-noise ratio of user 2 improves and the corresponding channel conditions improve, as shown in Figs. 3 and 4. Due to the stronger optimizing ability of the proposed algorithm, it shows significantly better performance than the FPA and FTPA algorithms, and with the increase of the number of users, the performance of the algorithm in this paper is slightly improved. The system weighting and rate will gradually decrease, so the advantages of the proposed algorithm will be more obvious.

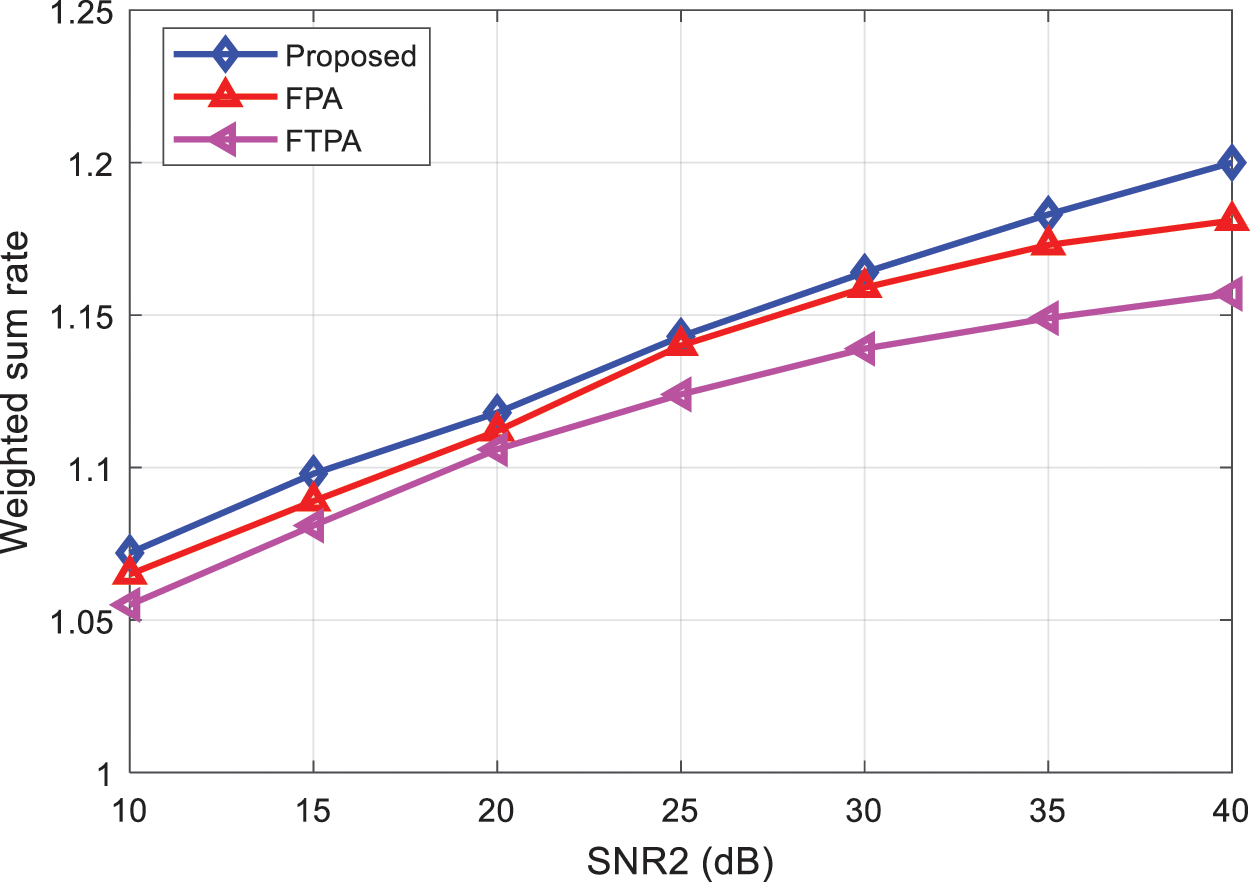
Figure 3: Comparison of the sum rate of the proposed and existing algorithms vs. SNR of user two

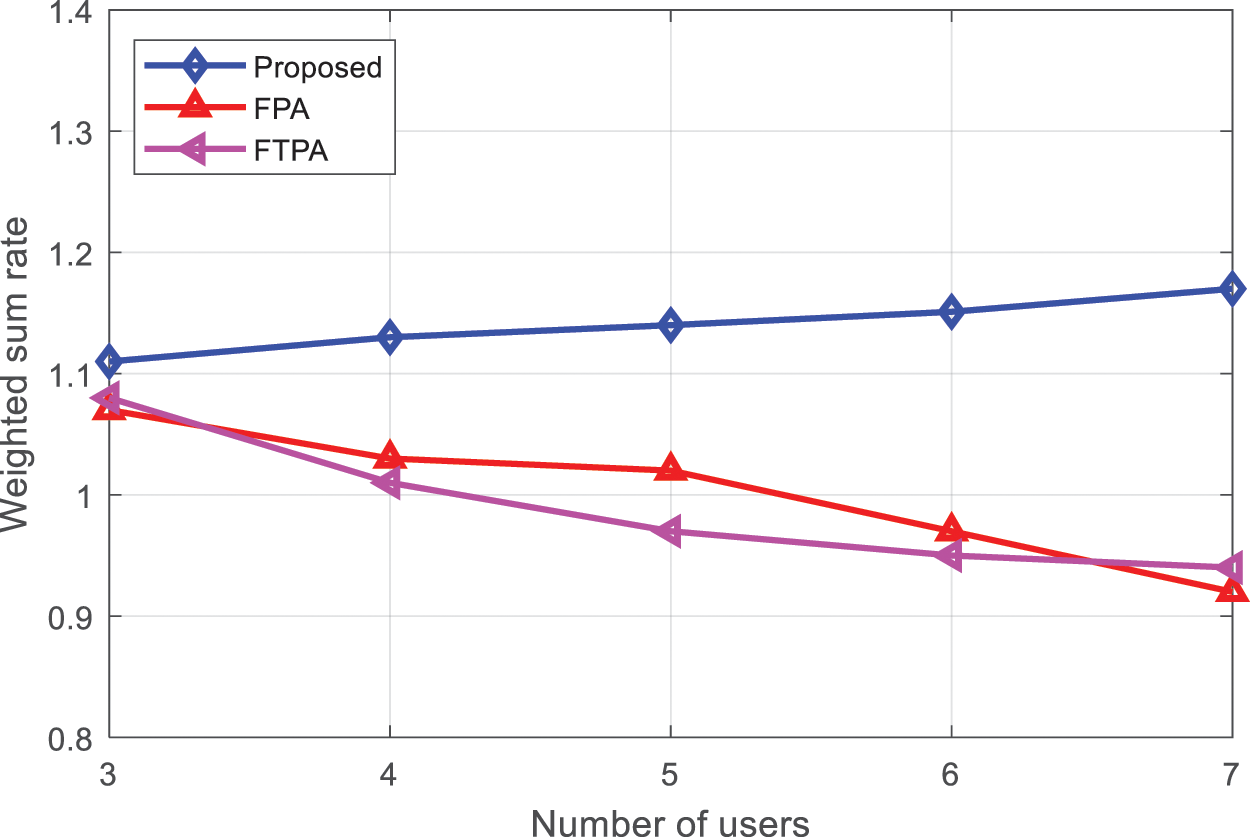
Figure 4: Comparison of the sum rate of the proposed and existing algorithms vs. the number of users

When the number of users is 2 and SNR1 = 5 dB, the sum rate of the NOMA system and the OMA system using the proposed algorithm varies with SNR2 as shown in Fig. 5. When the number of users is 3, 4, 5, 6, 7, and the sum rate of the NOMA system and the OMA system applying the proposed algorithm is shown in Fig. 6. From Figs. 5 and 6, it can be seen that the performance of the non-orthogonal multiple access system has been significantly improved compared to the orthogonal multiple access system.

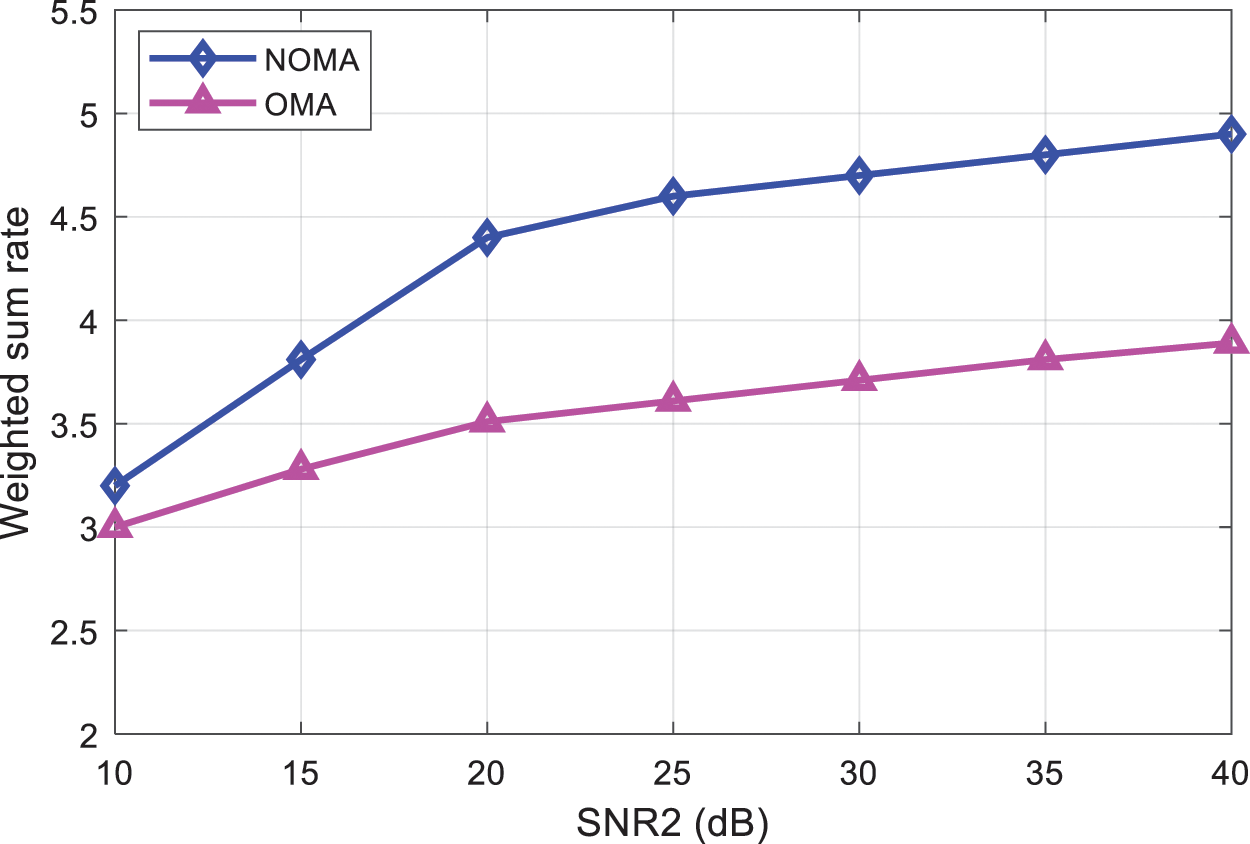
Figure 5: Comparison of the sum rate of the proposed algorithm under NOMA and OMA deployment under SNR variation

Figure 6: Comparison of the sum rate of the proposed algorithm under NOMA and OMA deployment under increasing number of users

Fig. 7 compared the complexities of the proposed and existing algorithms with increasing number of users. It can be seen from Fig. 7 that as the number of users increases, the computational complexities of all the algorithms increases. However, the complexity of the proposed algorithm is much lower and stable than existing algorithms which makes it suitable candidate in terms of hardware implementation with improved energy efficiency.

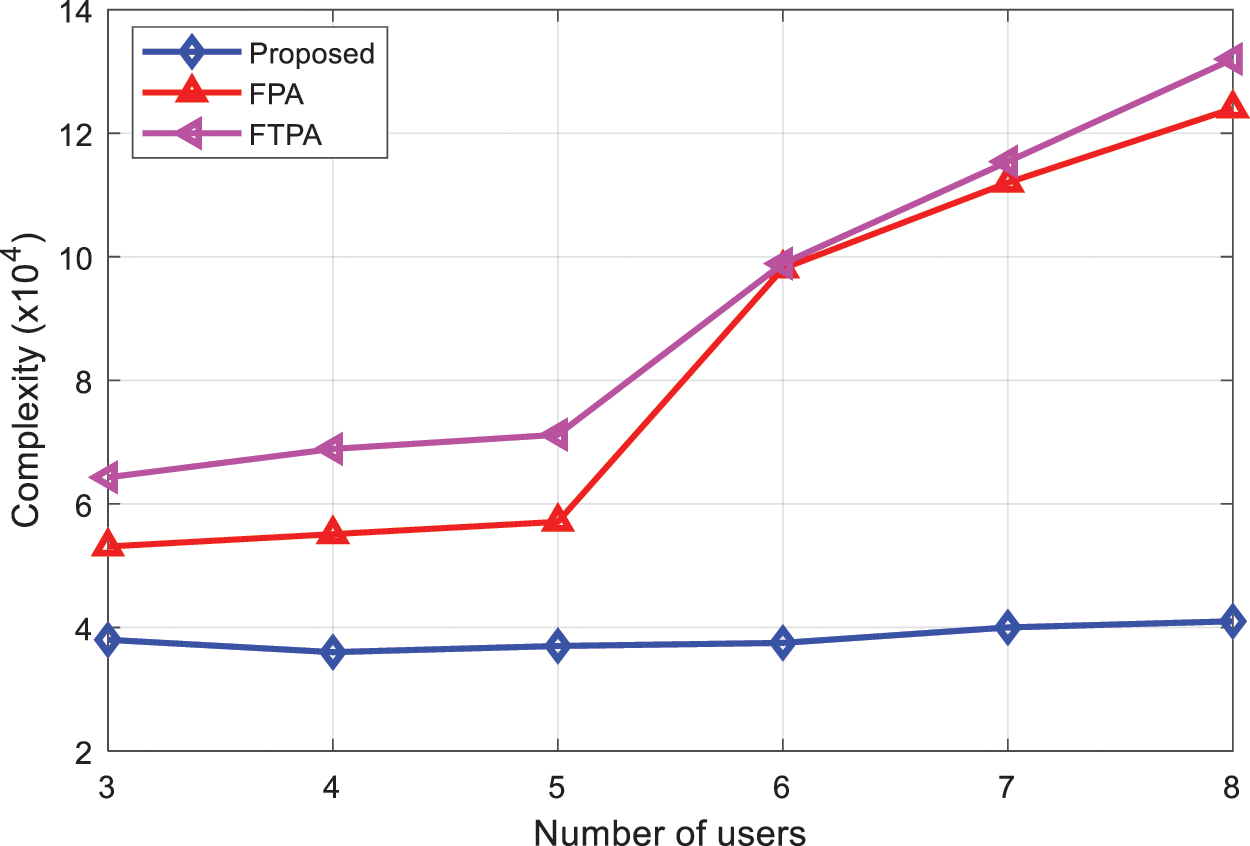
Figure 7: Complexity comparison of the proposed and existing algorithms

Fig. 8 compared the energy efficiency of the proposed algorithm and existing algorithms under increasing number of users per base station. As can be seen that the energy efficiency of all algorithms increases with increasing the number of users per base station. However, the proposed algorithm provides better energy efficiency than FTPA and FPA algorithms which makes it energy-efficient and computationally efficient.

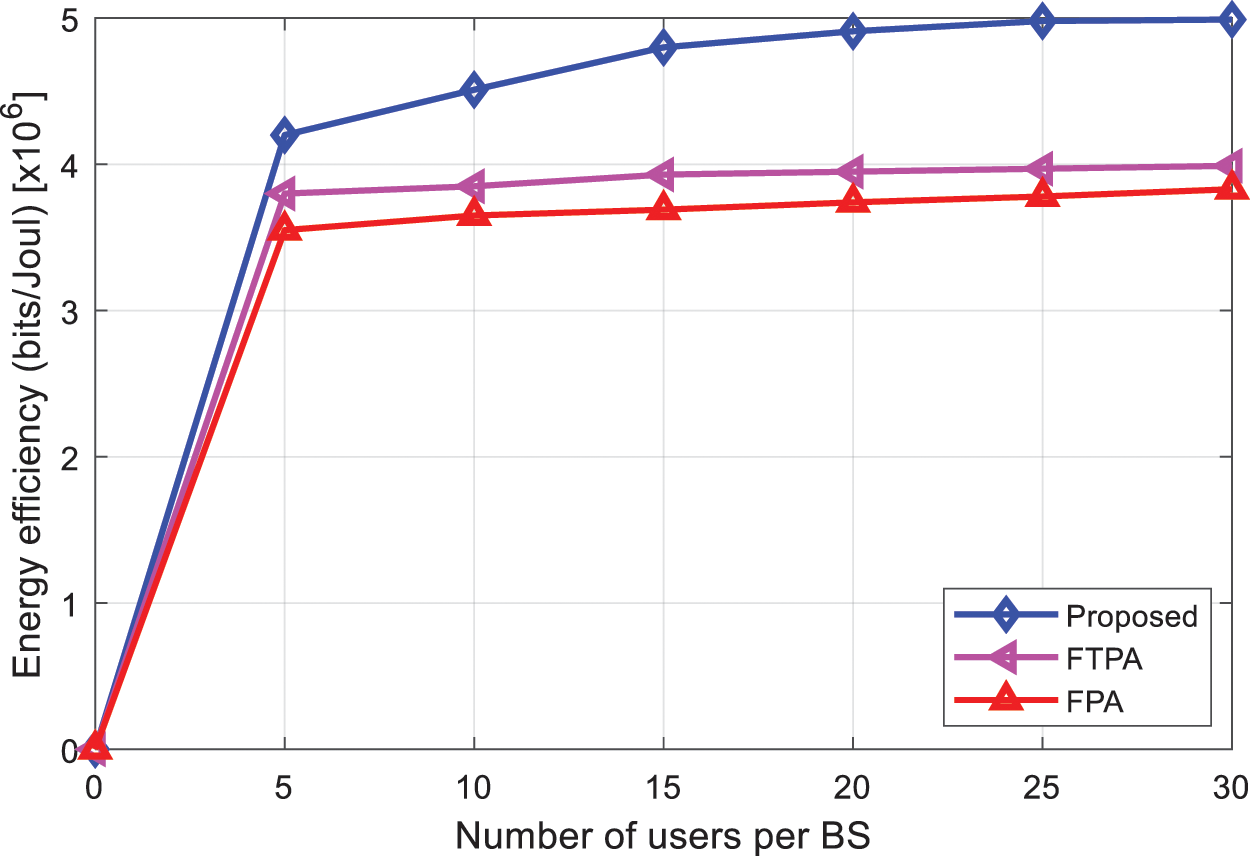
Figure 8: Energy efficiency analysis

6  Conclusion

In contrast to the prior OMA methods that characterized previous generation networks, NOMA is unique in its key design. It uses superposition coding (SC) to allow a transmitter to serve numerous customers at the same time while sharing the same resource blocks (RBs). It distinguishes them in the power domain by allocating various power levels to them, and it performs successive interference cancellation (SIC) at the receiver while allowing restricted multiple access interference (MAI). Aiming at the power allocation problem in the 5G NOMA system, this paper proposes a power allocation scheme based on the conjugate gradient method, which can maximize the weighted sum rate while ensuring the convergence speed. The simulation results prove the superiority of the performance of this method.

Acknowledgement: This work is supported by taif university, Saudi Arabia for the University Researchers Supporting Project Number (TURSP-2020/331), Taif University, Saudi Arabia.

Funding Statement: The authors would like to acknowledge the support from Taif University Researchers Supporting Project Number (TURSP-2020/331), Taif University, Taif, Saudi Arabia. This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the National Research Foundation (NRF), Korea (2022R1A2C4001270).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  O. Maraqa, A. S. Rajasekaran, S. A. Ahmadi, H. Yanikomeroglu and S. M. Sait, “A survey of rate-optimal power domain NOMA with enabling technologies of future wireless networks,” IEEE Communications Surveys & Tutorial, vol. 22, no. 4, pp. 2192–2235, 2020. [Google Scholar]

 2.  M. B. Shahab, R. Abbas, M. Shirvanimoghaddam and S. J. Johnson, “Grant-free non-orthogonal multiple access for IoT: A survey,” IEEE Communications Surveys & Tutorial, vol. 22, no. 3, pp. 1805–1838, 2020. [Google Scholar]

 3.  A. A. Bakar, R. Hamdan and N. S. Sani, “Ensemble learning for multidimensional poverty classification,” Sains Malaysiana, vol. 49, no. 2, pp. 447–459, 2020. [Google Scholar]

 4.  A. B. Abdulkareem, N. S. Sani, S. Sahran, Z. A. A. Alyessari, A. Adam et al., “Predicting COVID-19 based on environmental factors with machine learning,” Intelligent Automation & Soft Computing, vol. 28, no. 2, pp. 305–320, 2021. [Google Scholar]

 5.  Z. A. Othman, A. A. Bakar, N. S. Sani and J. Sallim, “Household overspending model amongst B40, M40 and T20 using classification algorithm,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 7, pp. 392–399, 2020. [Google Scholar]

 6.  D. Wan, M. Wen, X. Cheng, S. Mumtaz and M. Guizani, “A promising non-orthogonal multiple access based networking architecture: Motivation, conception, and evolution,” IEEE Wireless Communications, vol. 26, no. 5, pp. 152–159, 2019. [Google Scholar]

 7.  M. Vaezi, R. Schober, Z. Ding and H. V. Poor, “Non-orthogonal multiple access: Common myths and critical questions,” IEEE Wireless Communications, vol. 26, no. 5, pp. 174–180, 2019. [Google Scholar]

 8.  N. S. Sani, A. F. M. Nafuri, Z. A. Othman, M. Z. A. Nazri and K. N. Mohamad, “Drop-out prediction in higher education among B40 students,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 11, pp. 550–559, 2020. [Google Scholar]

 9.  M. Baghana, S. Parsaeefard, M. Derakhshani and W. Saad, “Dynamic non-orthogonal multiple access and orthogonal multiple access in 5G wireless networks,” IEEE Transactions on Communications, vol. 67, no. 9, pp. 6360–6373, 2019. [Google Scholar]

10. R. A. Stoica, G. T. Abreu, T. Hara and K. Ishibashi, “Massively concurrent non-orthogonal multiple access for 5G networks and beyond,” IEEE Access, vol. 7, pp. 82080–82100, 2019. [Google Scholar]

11. R. Dawadi, S. Parsaeefard, M. Derakhshani and T. Ngoc, “Power efficient resource allocation in NOMA virtualized wireless networks,” in IEEE Global Communications Conf., Washington DC, USA, pp. 1–6, 2016. [Google Scholar]

12. W. Zhiqiang, K. Ng and Y. Jinhong, “Power-efficient resource allocation for MC-NOMA with statistical channel state information,” in IEEE Global Communications Conf., Washington DC, USA, pp. 1–7, 2016. [Google Scholar]

13. M. Tareq, E. A. Sundararajan, M. Mohd and N. S. Sani, “Online clustering of evolving data streams using a density grid-based method,” IEEE Access, vol. 8, pp. 166472–166490, 2020. [Google Scholar]

14. C. Wenbo, C. Chen, B. Lin, Y. Jin and J. Choi, “User selection and power allocation schemes for downlink NOMA systems with imperfect CSI,” in IEEE 84th Vehicular Technology Conf., Montreal, Canada, pp. 1–5, 2016. [Google Scholar]

15. L. Xin, W. Xianbin and L. Yanan, “Power allocation and performance analysis of the collaborative NOMA assisted relaying systems in 5G,” China Communications, vol. 14, no. 1, pp. 50–60, 2017. [Google Scholar]

16. Y. Zheng, D. Zhiguo, F. Pingzhi and N. Dhahir, “A general power allocation scheme for guarantee quality of service in downlink and uplink NOMA systems,” IEEE Transactions on Wireless Communications, vol. 15, no. 11, pp. 7244–7257, 2016. [Google Scholar]

17. V. Nayak and K. Gurrala, “Power allocation-assisted secrecy analysis for NOMA enabled cooperative network under multiple eavesdroppers,” ETRI Journal, vol. 43, no. 4, pp. 758–768, 2021. [Google Scholar]

18. Y. Zhaohui, X. Wei, P. Cunhua, Y. Pan and M. Chen, “On the optimality of power allocation for NOMA downlinks with individual QoS constraints,” IEEE Communications Letters, vol. 21, no. 7, pp. 1649–1652, 2017. [Google Scholar]

19. S. Yan, K. Ng, Z. Ding and R. Schober, “Optimal joint power and subcarrier allocation for MC-NOMA systems,” in IEEE Global Communications Conf., Washington, DC, USA, pp. 1–6, 2016. [Google Scholar]

20. Z. Chen, Z. Ding, X. Dai and R. Zhang, “An optimization perspective of the superiority of NOMA compared to conventional OMA,” IEEE Transactions on Signal Processing, vol. 65, no. 19, pp. 5191–5202, 2017. [Google Scholar]

21. B. Chaoudhry, S. Hassan, J. speidel and H. Jung, “Energy efficiency of a decode-and-forward multiple relay network with rate adaptive LDPC codes,” Sensors Journal, vol. 19, no. 21, pp. 1–15, 2019. [Google Scholar]

22. J. Cheon and H. Cho, “Power allocation scheme for non-orthogonal multiple access in underwater acoustic communications,” Sensors Journal, vol. 17, no. 11, pp. 1–16, 2017. [Google Scholar]

23. S. Tao, H. Yu, Q. Li, X. Bai and Y. Tang, “Power allocation of non-orthogonal multiple access based on dynamic user priority for indoor QoS-guaranteed visible light communication networks,” Applied Sciences Journal, vol. 8, no. 8, pp. 1–14, 2018. [Google Scholar]

24. Y. Saito, A. Benjebbour, Y. Kishiyama and T. Nakamura, “System-level performance evaluation of downlink non-orthogonal multiple access (NOMA),” in IEEE Int. Symp. on Personal Indoor & Mobile Radio Communications, London, UK, pp. 611–615, 2015. [Google Scholar]

25. A. Assiri, “Efficient training of multi-layer neural networks to achieve faster validation,” Computer Systems Science and Engineering, vol. 36, no. 3, pp. 435–450, 2021. [Google Scholar]

26. J. Schaepperle and A. Ruegg, “Enhancement of throughput and fairness in 4G wireless access system by non-orthogonal signaling,” Bell Labs Technical Journal, vol. 13, no. 4, pp. 59–77, 2009. [Google Scholar]

27. Z. Zhu, “A feasible interior-point algorithm for non-convex nonlinear programming,” Applied Mathematics & Computation, vol. 163, no. 2, pp. 745–753, 2005. [Google Scholar]

28. J. Mendoza, I. Bandera, D. Palacios and R. Barco, “QoE optimization in a live cellular network through RLC parameter tuning,” Sensors Journal, vol. 21, no. 16, pp. 1–23, 2021. [Google Scholar]

29. L. Grippo and S. Lucidi, “A globally convergent version of the Polak-Ribiere conjugate gradient method,” Mathematical Programming, vol. 78, no. 3, pp. 375–391, 1997. [Google Scholar]

30. S. Hu, S. Xu, D. Wang and A. Zhang, “Optimization algorithm for Kalman filter exploiting the numerical characteristics of SINS/GPS integrated navigation systems,” Sensors Journal, vol. 15, no. 11, pp. 1–18, 2015. [Google Scholar]

31. M. Sinaie, D. Ng and E. Jorswieck, “Resource allocation in NOMA virtualized wireless networks under statistical delay constraints,” IEEE Wireless Communications Letters, vol. 7, no. 6, pp. 954–957, 2018. [Google Scholar]

32. A. Dey, S. Nandi and M. Sarkar, “Security measures in IoT based 5G networks,” in IEEE 3rd Int. Conf. on Inventive Computation Technologies (ICICT), Coimbatore, India, pp. 561–566, 2018. [Google Scholar]

33. B. Yin, S. W. Zhou, S. W. Zhang, K. Gu and F. Yu, “On efficient processing of continuous reverse skyline queries in wireless sensor networks,” KSII Transactions on Internet and Information Systems, vol. 11, no. 4, pp. 1931–1953, 2017. [Google Scholar]

34. J. M. Zhang, K. Yang, L. Y. Xiang, Y. S. Luo, B. Xiong et al., “A self-adaptive regression-based multivariate data compression scheme with error bound in wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 9, no. 3, pp. 913–924, 2013. [Google Scholar]

35. J. Wang, C. Ju, Y. Gao, A. K. Sangiah and G. J. Kim, “A PSO based energy efficient coverage control algorithm for wireless sensor networks,” Computers, Materials & Continua, vol. 56, no. 3, pp. 433–446, 2018. [Google Scholar]

36. J. Wang, X. J. Gu, W. Liu, A. K. Sangaiah and H. J. Kim, “An efficient harmilton loop based data collection algorithm with mobile agent for WSNs,” Human-Centric Computing and Information Sciences, vol. 9, no. 1, pp. 1–14, 2019. [Google Scholar]

37. J. Wang, Y. Gao, C. Zhou, S. Sherrat and L. Wang, “Optimal coverage multi-path scheduling scheme with multiple mobile sinks for WSNs,” Computers, Materials & Continua, vol. 62, no. 2, pp. 695–711, 2020. [Google Scholar]

38. J. Wang, Y. Gao, W. Liu and S. J. Lim, “An asynchronous clustering and mobile data gathering schema based on timer mechanism in wireless sensor networks,” Computers, Materials & Continua, vol. 58, no. 3, pp. 711–725, 2019. [Google Scholar]

39. J. Wang, Y. Gao, X. Yin, F. Li and H. J. Kim, “An enhanced PEGASIS algorithm with mobile sink support for wireless sensor networks,” Wireless Communications and Mobile Computing, vol. 75, no. 2, pp. 1–8, 2018. [Google Scholar]

40. Q. Tang, K. Yang, P. Li, J. M. Zhang, Y. S. Luo et al., “An energy efficient MCDS construction algorithm for wireless sensor networks,” EURASIP Journal on Wireless Communications and Networking, vol. 4, no. 1, pp. 1–18, 2012. [Google Scholar]

41. Z. Liao, J. Wang, S. Zhang, J. Cao and G. Min, “Minimizing movement for target coverage and network connectivity in mobile sensor networks,” IEEE Transactions on Parallel and Distributed Systems, vol. 26, no. 7, pp. 1971–1983, 2014. [Google Scholar]