GA-Stacking: A New Stacking-Based Ensemble Learning Method to Forecast the COVID-19 Outbreak

1  Introduction

In recent years, machine learning (ML) has been utilized as a method to forecast and predict COVID-19 cases [1–3]. It has been used in Polymerase Chain Reaction (PCR) tests to predict positive results for COVID-19 infections. Therefore, ML can reduce the strain on health care systems that are already overwhelmed by COVID-19 [1,4]. Ismail et al. [5] proposed a new model for positive COVID-19 prediction using binary features, including the patient’s profile, such as age and five clinical symptoms. Additionally, ML has been utilized to predict the severity of COVID-19 for a specific period. In [6], a model was built for ten Brazilian states to predict the number of COVID-19 infections between one and six days.

The field of ML has paid significant attention to Ensemble Machine Learning (EML) techniques, and these methods have shown significant predictive power and stability in numerous applications [1,2,7,8]. Unlike single ML models, EML involves multiple base learners that work individually in parallel or sequentially. An ensemble of classifiers can improve the performance of poorly performing classifiers, thus achieving a more robust and stable classification than any single ML model [9,10]. Three strategies are used for ensemble learning: boosting, in which homogeneous-base learners are trained sequentially; bagging, which uses homogeneous-base learners trained in parallel; and stacking, which utilizes heterogeneous-base learners trained in parallel and combined using a meta-model to find the final prediction results. The prediction accuracy and stability of the stacking strategy are often superior to those of any other strategy [11]. Therefore, the authors exploit its benefits to create a model for combatting the COVID-19 outbreak.

The stacking process involves different types of base learners and meta-learners; base learners are trained on all available data in the sample. However, a meta-learner is trained on the predictions made by base learners to produce the final prediction [12]. For each base learner, another machine learning model is used to determine how to best assemble the “out-of-fold” prediction results to maximize the final model classification accuracy. An analysis of the existing stacking-based EML studies reveals many determining factors concerning a stacking ensemble, including how to select the optimal combination of the base learners and the meta-learner and how to trust this combination [9–12]. Additionally, classifiers can be used as metaclassifiers to reduce the generalization error, and the selected classifier hyperparameters can be efficiently optimized to enhance the performance of the model [13,14]. In [15], a voting strategy is utilized to assemble the base-learner prediction results by assigning a certain weight to each learner (hard voting) or a variety of weights (soft voting). Ehwerhemuepha et al. [16] proposed a super learning model for predicting COVID-19 severity. Their model developed and combined 14 classifiers using multifold cross-validation to mathematically validate the super-learner model performance. A new ensemble strategy, the weighted strategy [17], is used to build a hybrid model for the detection of gang-related arson cases. Using the weighted strategy, the optimal combination of base learners is chosen. Cui et al. [18] developed a new earthquake casualty prediction framework using stack-based ensemble machine learning. A repetitive experiment is conducted to select the optimal combination of base and meta-learner. In this model, four base classifiers are used with a single gradient Decision Tree (DT)-based metaclassifier, and swarm intelligence is used for the hyperparameter optimization of base learners. The Genetic Algorithm (GA) is effectively used to optimize the parameters of classifiers. Due to their nonlinearity, global optimization, and combinatorial optimization, GAs are uniquely suited for solving complex problems compared with traditional soft computing methods [19]. The GA can effectively identify, select, and combine possible patterns in the defined problem space. Different applications of pattern recognition have used this approach effectively [20,21] as an evolutionary algorithm for model hyperparameter optimization, which is not tailored for performance prediction. This study proposes a novel stacking-based ensemble GA-Stacking technique in which ensemble learning and a GA are combined and used to identify a suitable structure for COVID-19 detection.

The proposed stacking ensemble-based model will utilize the ability of Genetic Programming (GP) to explore and exploit the classifier search space effectively. To the authors’ knowledge, this is the first study to determine the best way to select the optimal combination of base classifiers and meta-classifiers using genetic algorithms. The contribution can be summarized as follows. A hybrid stacking ensemble learning GA-Stacking model is proposed to predict the number of new COVID-19 cases. In this model, DT, Least Absolute Shrinkage and Selection Operator (LASSO), Random Forest (RF), RIGID regression and eXtreme Gradient Boosting (XGBoost) are used as the first-level base learners, and LR is used as a meta-learner (the second level). A new algorithm is developed that utilizes GA to obtain the best number and combination of base classifiers/learners for the ensemble prediction model. Furthermore, the model hyperparameters are optimized and the optimization process is verified through experiments to improve the model’s identification ability. Extensive numerical experiments are conducted on the collected data to assess the effectiveness of the proposed method. The results demonstrate that the proposed method outperforms popular traditional machine learning methods, including DT, RF, LASSO regression, RIGID regression, and XGBoost. Moreover, additional experiments are conducted to study the impact of vaccine indicators on the model performance for predicting new, positive COVID-19 cases. Unlike the state-of-the-art methods that fail to achieve a cross dataset generalization for a variety of countries with similar preventive and control measures (such as quarantine policies), the proposed adaptive model yields adequate performance under cross-dataset environments for different confirmed COVID-19 cases in different countries.

2  Related Work

To combat COVID-19, Deep Learning (DL), Artificial Intelligence (AI), and ML can be used for different applications, such as future likely case prediction, drug development, vaccines, and early disease monitoring and tracking [22–24]. In addition, identifying patients with COVID-19 that will progress to severe conditions during admission would be helpful for logistics and planning in the face of scarce clinical resources. Several ML studies have been developed to analyze all aspects of COVID-19 infection spread and transmission. The findings can be used by government and health service workers to make decisions and plans for future pandemics [25].

In [26], COVID-19 cases were predicted through Support Vector Regression (SVR) using different nonlinearity structures. Compared to SVR with other kernel functions, SVR with a Gaussian kernel displayed better prediction. A nonlinear ML approach combined with partially derivative regression is used in [25] to develop a method for predicting the COVID-19 global forecast. The authors in [27] proposed the SARIIqSq model to forecast COVID-19 transmission dynamics. Yang et al. [28] proposed a new approach using the XGBoost algorithm to predict critical patients using biomedical and epidemiological data. From a collection of 300 clinical features, the researchers identified three key features from the clinical data of 2799 patients collected from Tongji Hospital in Wuhan. In [29,30], XGBoost and the Gradient Boosting Decision Tree (GBDT) were used with proper adjustments to the parameter combinations to detect COVID-19 in a variety of countries. A model presented by Pourhomayoun et al. [31] allows for early detection of health risks and predicts mortality risks for COVID-19 patients. The researchers used a variety of ML algorithms to predict the mortality rate of patients, including Support Vector Machines (SVMs), neural networks, DTs, RF, logistic regression, and K-Nearest Neighbor (KNN). Accordingly, the tenfold cross-validated neural network executes the highest performance [1,27,32].

Despite the great ability of such single predictive models to mitigate some of the uncertainty associated with the progression of COVID-19, the ensemble models tend to outperform such models. Ensemble learning mainly involves training base classifiers and formulating combinations of base classifiers. The three most popular ensemble strategies are bagging, boosting, and stacking [8]. Therefore, in practical applications, both high-accuracy and diversified base classifiers are required for an effective ensemble model. As such, to create a good ensemble model, it is necessary to utilize both highly accurate and diverse base classifiers. The performance of the ensemble will decline if incorrect classifiers produce similar results [33]. Many factors affect how classifier diversity is expanded, including the base and hyper learners, their number, and the optimization of such a combination. For the classifier, different algorithms with base classifiers usually result in better performance. The study presented by Florez et al. [34] proposed a new enhanced bagging method to avoid random model training using an error-based bootstrapping mechanism that enhances the classification accuracy. In [32], the research improved the prediction performance of multiple classifiers (base or weak classifiers) by using ensembles of RF, naive Bayes, and SVM classifiers. A novel ensemble-based classifier was proposed in [35] for detecting COVID-19. The models are designed and developed with the three most common classifiers, namely, DTs, Iterative Dichotomies 3 (ID3), and SVM. In their model, the bootstrap sampling method was used to combine random subspaces, and bootstrap sampling was used to generate the most efficient set of trees possible. In another study, a stacking-ensemble learning method using machine learning regression and statistical models was proposed to forecast COVID-19 in ten Brazilian states. The Gaussian process is selected as the meta-learner, and the five learners (Auto-Regressive Integrated Moving Average (ARIMA), cubist regression, RF, RIGID regression, and SVR states) are selected as fixed base learners. The authors explained that stacking-ensemble learning and SVM regression exhibit better forecasting accuracy than other models. Malhorta et al. [36] achieved the diversity of the base classifier by initializing eight SVM classifiers.

In [37], hybrid features and SVM-based ensemble algorithms combining random sample subsets and random feature subspaces achieved high performance accuracy in many practical applications. A new model for forecasting the lockdown strategy for COVID-19 using time-series and machine learning models was proposed in Saba et al. (2016) [38]. Three countries undergoing three types of lockdowns were analyzed using RFs, KNN, SVM, DTs, polynomial regression, Holt winter, ARIMA, and Seasonal Auto-Regressive Integrated Moving Average (SARIMA). Predictions of confirmed infections and deaths were constructed using three of the top models, while outperforming models were adopted for out-of-sample prediction. Yahia [39] developed a stacked “Dot Net Nuke” (DNN) model to predict daily confirmed COVID-19 cases for three scenarios. In their model, first, the three learners, DNNs, Long Short-Term Memory (LSTM)s, and Convolutional Neural Network CNNs, are trained individually as base learners, and then a new dataset is generated from those learner prediction results. Subsequently, a meta-learner is designed and trained with the new dataset to generate outbreak predictions. Three different stacked models (stacked-DNN, stacked-LSTM, and stacked-CNN) are manually tested to select the one that will provide the best and most accurate prediction.

Three popular classifiers, extra trees, RF, and logistic regression, were used in [40]. These have different architectures and learning characteristics at the first level and are then combined with a second-level XGBoost classifier to predict the final model performance. To combine the strength of different individual ensemble models, in [16], the authors proposed a model of super learning ensembles to predict COVID-19 severity prior to hospital admission. Fourteen statistical and machine learning models were combined into a more powerful super learning model, which enhances the model performance compared with the base learners. However, there is no information available regarding the structure of the created model, and the accuracy is not satisfactory. With the help of the genetic algorithm, many models have been developed successfully in different application areas, including image segmentation, disease prediction and classification, and feature extraction and fusion [41–43].

Similarly, the authors in [41] proposed a novel classifier stacking-ensemble model called “Can–Evo–Ens” for predicting breast cancer amino acid sequences. The proposed model uses a stacking of four learners as base-level classifiers: naive Bayes, KNN, SVM, and RF. A second-level classifier (meta-learner) is then developed by combining the predictions of the base classifiers via GP. Meta-learners are designed to find the best way to combine the base-level classifier results. The GA was used for the final classifier prediction. According to the experimental results, the proposed approach performs better than the AdaBoostM1, bagging, GentleBoost, and random subspace approaches, as well as individual ML approaches.

Ensemble training based on genetic algorithms was utilized in [44] to accurately diagnose and predict the outcome of diabetes mellitus. Nine classifiers were utilized in classifying the data, including RF, SVM, Decision Trees, K-Nearest Neighbors, Gradient Boosting, Multilayer Perception, Extra Tree, AdaBoost classifier; basic Gaussian bays and the GA were used for the ensemble learning process. The accuracy of diabetes prediction using these ten algorithms rated on average at 98% accuracy.

In [42], a GA was developed for optimizing the prediction of COVID-19 deaths and confirmed cases with ensemble neural networks. This paper demonstrates the results of using a GA to optimize the number of neurons of an ensemble artificial neural network. In [45], the authors developed GA-optimized multivariate CNN-LSTM, which is a new deep learning-based ensemble model that incorporates CNN and LSTM for predicting human movement in future pandemics. In their study, the selected models were optimized using a GA, and their results outperformed stand-alone CNN and LSTM models.

Although recent research, including AI-based and ML-based models for COVID-19 predictions, has received more attention and promising initial results have been obtained, as shown in Tab. 1, there are some challenges as follows:

•   Some techniques need multiple steps to offer reliable model design, and the relative importance of the employed classifiers cannot be obtained directly by using most of the corresponding stand-alone approaches.

•   It may be difficult to attain an optimal structure for models when several features are present; developing models can require significant computational resources and expertise.

•   Hybrid ensemble-based models, which combine several predictive models, help improve the accuracy of predictions. However, building an ensemble often causes the performance of the model to decrease due to the increasing number of learners that are not being properly selected.

•   Most hybrid COVID-19 trend prediction models use the output of only one model as the input features for another model or use a voting mechanism. Predictive performance would be improved through the development of an automatic learning model from a multitude of different predictive models.

•   The deep learning-based COVID-19 prediction models are sensitive to the initial values of model parameters, such as the number of hidden layers, training features, and model hyperparameters. The determination of initial values of these parameters is usually based on domain knowledge, and any update for AI models to reflect the changing dynamics of the pandemic (such as an increasing number of confirmed new cases) is challenging because it requires more training time.

•   To perform early and targeted therapies for new COVID-19 cases, researchers have conducted studies combining statistical learning and artificial intelligence algorithms. It is not only the accuracy of the classifier that affects the performance of an ensemble but also the diversity of the classifiers used in the ensemble.

The objective of this research is to develop a novel stacking-based ensemble learning model based on genetic methods to aid country planners and government agencies in identifying and predicting pandemics more effectively and efficiently. This model addresses the following issues:

•   Developing a stacking ensemble strategy to mitigate high classification accuracy.

•   Identifying the best numbers of base classifiers.

•   Identifying the best combination of base classifiers that can further enhance the model performance.

•   Increasing the model generalization ability for the samples using unbalanced data.

•   Optimizing the model parameters to achieve the best performance.

3  Overall Research Framework

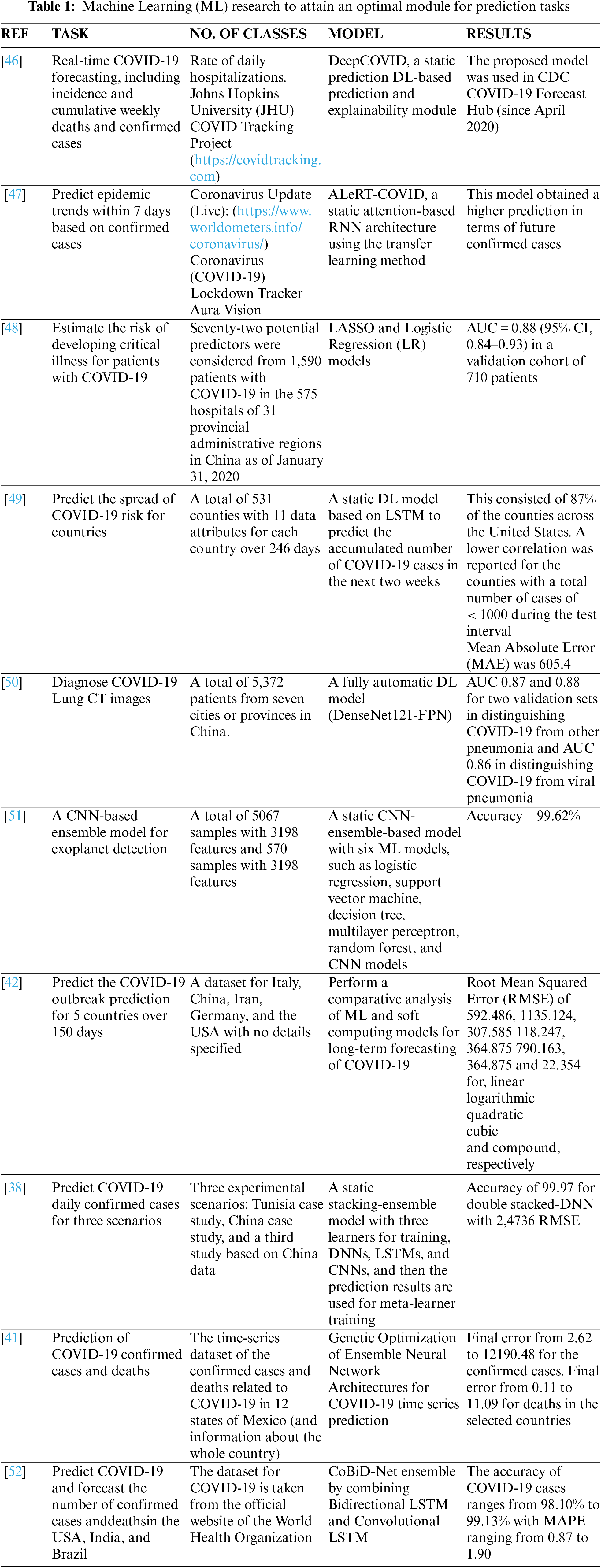
The proposed research framework is shown in Fig. 1. It consists of three parts: data preprocessing, model building, and model evaluation. The first part is data preprocessing and feature selection, in which the dataset is cleaned and converted into raw data. Afterward, feature selection is carried out for the different base-learners used in the GA-Stacking model. The main purpose of feature selection is to enable the model classifiers (base-learner) to test/train in the optimal feature space. The second part is the base-learner training and meta-learner optimization. For stacking-based ensemble learning modelling, the selection of the five base learners is determined through repeated experiments. Moreover, the GA is applied to the stacked learning process to optimize its performance. Each learner ultimately used in the GA-Stacking model is trained with the set of features selected in part one.

Figure 1: The proposed system methodology

Additionally, to enhance the model fitting ability, the prediction results of base learners will be integrated with Linear Regression (LR) as a meta-learner. An important aspect concerns how to select the optimal number and combination of the base learner to train the meta-classifier and trust the combination. Therefore, a genetic-based learner selection algorithm was developed to efficiently accelerate the selection of base learner combinations and enhance the fitting ability of the stacking-based ensemble learning model. Finally, all of the classification results obtained from the constructed model are combined and evaluated using different performance evaluation metrics. In the following subsections, the details related to each model part are represented. Five commonly used evaluation indicators were used to verify the generalizability of the proposed model (mean absolute error, mean square error, mean squared log error, r-squared value, and median absolute error).

4  Dataset and Methodology

4.1 Dataset Description and Preparation

COVID-19 dataset 1 was used to monitor the worldwide spread of the pandemic [42]. It contains 10,722 different medical records with 54 numerical attributes, including several variables, such as the country, the absolute and per-million numbers of new cases and total number of deaths, the number of tests performed, and the number of Intensive Care Unit admitted patients and vaccinated people. The machine learning model’s accuracy is heavily dependent on the quality of data used for training; therefore, it is crucial that the data is preprocessed before the final processing. First, to build the framework to combat the COVID-19 outbreak, a set of variables for three different countries was selected. The correlations between different features and the target value can serve as a powerful tool for understanding how they influence each other. Accordingly, before training the model, the heat-map of Pearson correlation is utilized to adjust the correlations between the dataset collection of different features and the target value according to Eq. (1):

p(x,y)=(xi−x)(yi−y)((xi−x)2(yi−y)2)12(1)

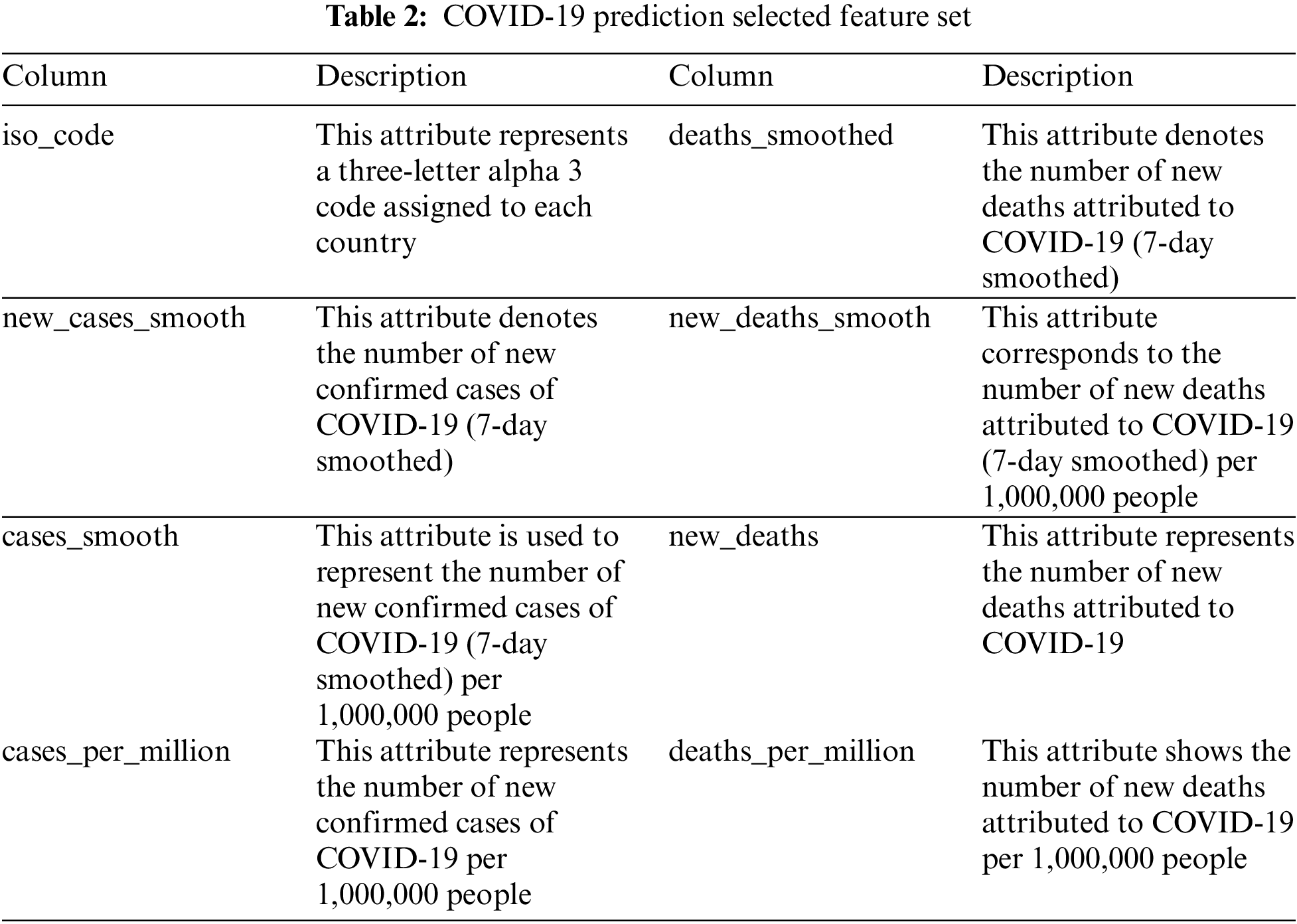
where X and Y are variables with measurements xi and yi and mean x and y. Nine (fixed) features in the dataset were identified (shown in Fig. 2); three are confirmed new COVID-19-positive cases, four are confirmed COVID-19-positive new deaths, and the other five features are confirmed new and total cases. The full list of features is presented in Tab. 2. Fig. 2 shows the heatmap of the selected features for GA-Stacking and the target variable (new_cases) for the model, revealing a strong positive correlation between new_cases and deaths features. Following this, to preserve the information embedded into the initial dataset, any incomplete or missing fields from those features are removed, and the data are then normalized via a min-max scaler. MinMaxScaler retains the original shape of the data distribution by placing all the data points between 0 and 1. Using MinMaxScaler, each data point is deducted from its smallest value and subsequently divided by the range between the original maximum and minimum values of the feature. Finally, the preprocessing procedure was completed by removing missing and incomplete values for some of their features.

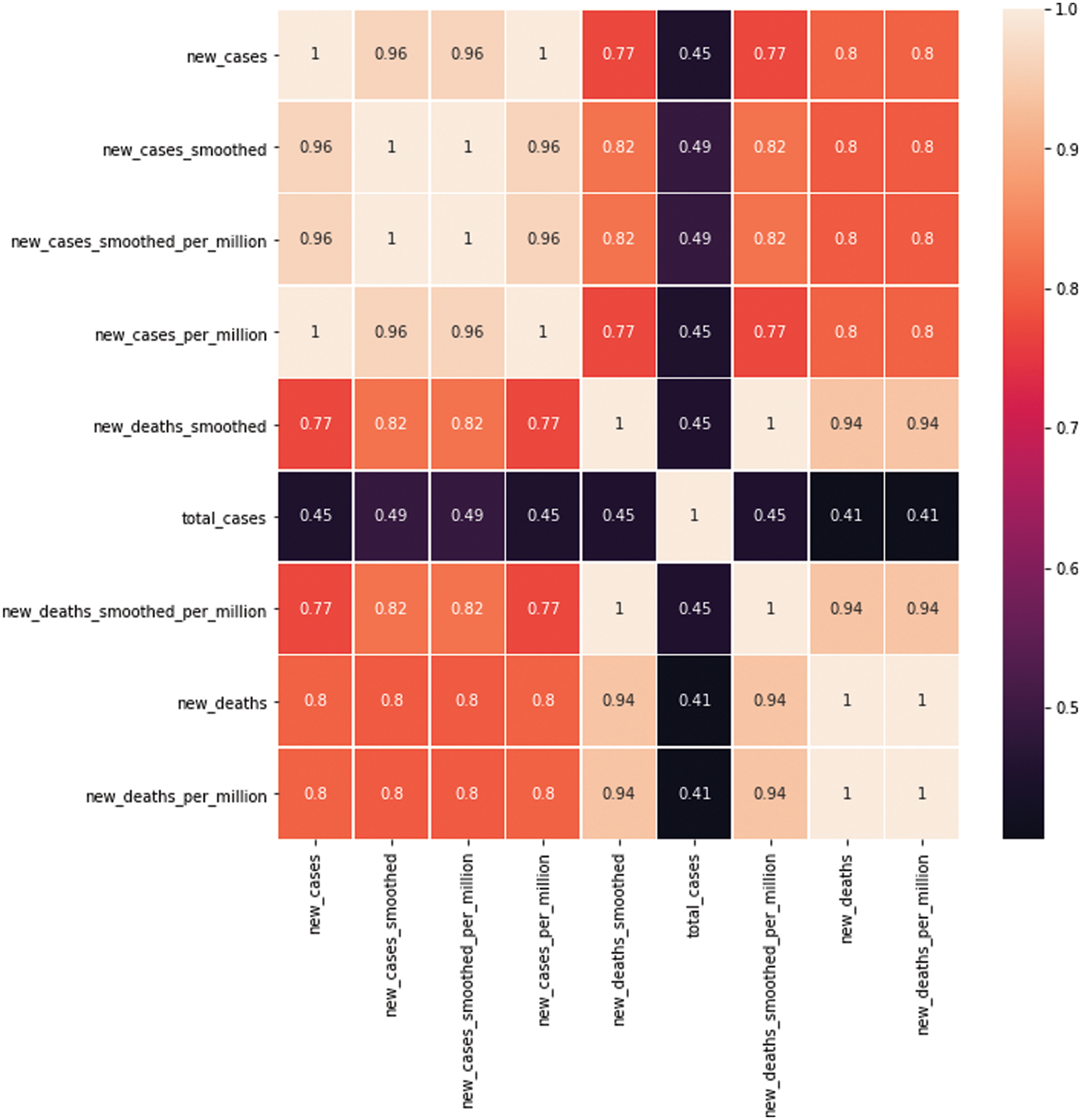
Figure 2: Correlation between the selected features

Selecting the most relevant features to the target variable (new_cases) that are used for the training step is essential for predicting problems. Feature Selection (FS) is a challenging task that aims to remove irrelevant and repetitive features from the original dataset and retain only important features. In this way, feature selection can be a beneficial step in terms of enhancing the performance of the model, reducing the dimension of the dataset in cases where there is a large number of features, and avoiding the overfitting problem. In this work, we utilized the Filter-based Feature Selection (FFS) method using the Top-K filter (the SelectKBest function) from sklearn.feature_selectionlibrary to select the top k features based on their relationship with target variable using a scoring function which is set to ‘F_Regression’.

4.2 Classification and Genetics-Based Stacking Ensemble (GA-Stacking) Approach

Stacking is a very effective ensemble learning method that is similar to bagging and boosting. The functionality of the stacking-based ensemble learning framework is explained by the following case study with ten hypothetical samples (N = 10). As shown in Tab. 3, a set of initial features [F1… F9] will be used to train the model, and one feature, F10, will be used to test the model classification performance. For the first-level training of the model, classifier X will be used to obtain the classification results of the first feature set [F1…, F3]. The X classifier will be trained with feature [F4… F9], and the classification results will be obtained as [X1… X9]. Additionally, Classifier Y and Classifier Z can be used to predict X10 as the final prediction result of sample, F10.

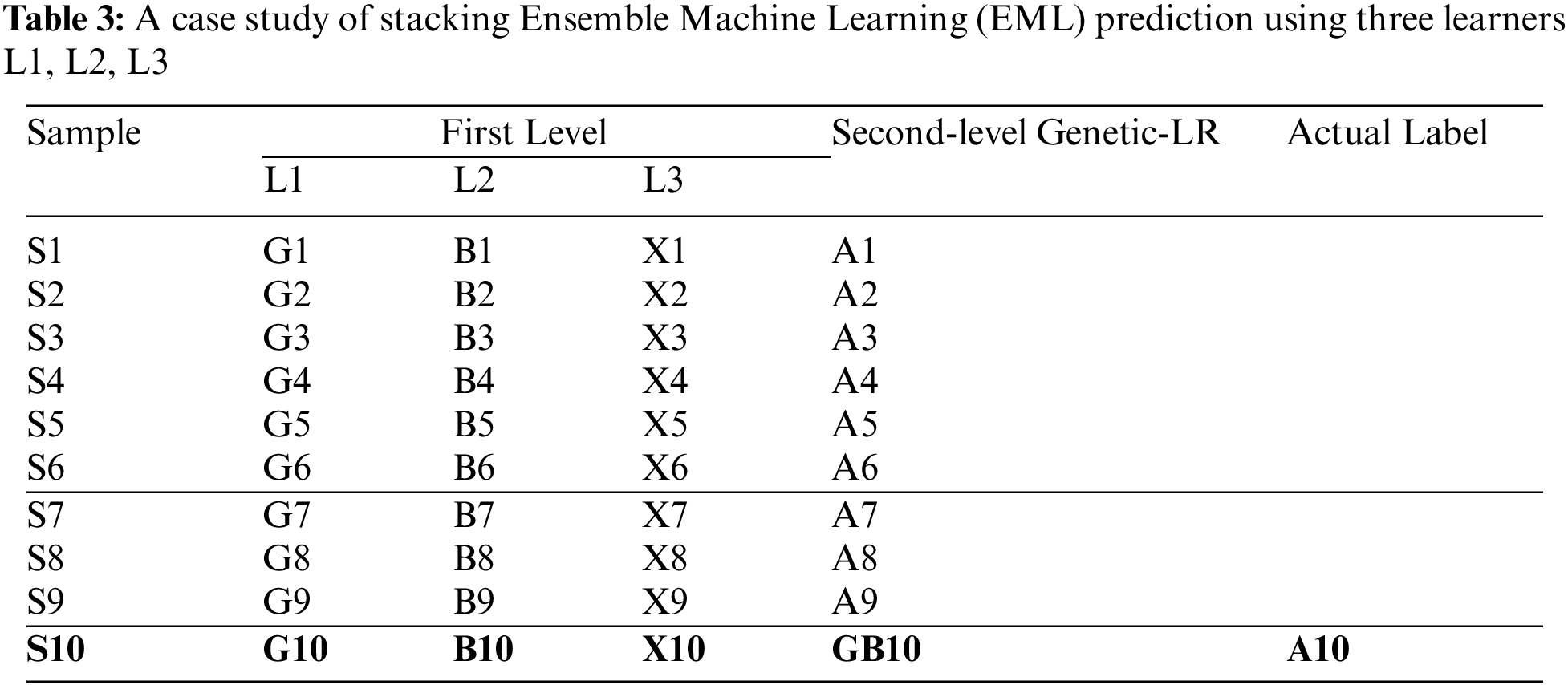
The second step in stack-based ensemble learning is to train the second-level model with the previous classification results [G1⋯X1⋮⋱⋮G9⋯X9]. Finally, a final prediction GB10 on the test set sample F10 will be obtained using all of the previously generated results [G10, B10, X10]. As illustrated by the example case, in the stacked ensemble learning method, the following advantages are observed:

1.    The stacking ensemble model fully utilized the training data, which increased the models’ capabilities to classify new samples.

2.    When training the first-level models, the stacking ensemble learning method used the cross-validation method, which made the trained model more robust.

3.    A mix of tree-based and regression classifiers can be selected for construction of the model base learner, which is consistent with the imbalanced sample modeling problem treated in this study.

4.    The auto-selection of the optimal combination of a heterogeneous base learner can improve the classification and generalization ability of the model.

In the proposed GA-Stacking model, the first level was formed by using different algorithms to generate N base learners. The GA, which is a type of soft computing, is a powerful evolutionary approach that has been applied in different applications. The GA utilizes natural selection and recombination under defined fitness criteria. The GA was chosen based on the findings of the optimization research area, which ensures that it has excellent performance, is light on computation and is easy to use [53,54]. Several kinds of research in the field of optimization using GA include electricity consumption and anomaly detection in the study by Qu et al. [55] their work combines GA with the AdaBoost ensemble model. In [1], Dowes, Nair and Sharma et al. developed a blood sample classification COVID-19 ensemble-based model that combines GA and machine learning, and in a study by Gao and Li [56], defects in small data samples were recognized by utilizing GA for the optimization of a CNN-based ensemble model.

A series of experiments with different classification algorithms was conducted to identify the best learners to be used in the framework. A total of five classifiers were selected due to their ability to generate better classification accuracy, including DT, RF, LASSO, RIGID, and XGBoost. Additionally, GA is utilized to define the heterogeneous integration of those five base learners to enhance the generalization ability of the framework; furthermore, the fitting ability of the model is improved by integrating the prediction results with meta-learners. Additionally, to reduce biases and improve model accuracy, the data predicted by the first-level learner are used to feed the second level in the model. Hence, predictions derived from the base learners and the original dataset are employed effectively to reduce biases and improve accuracy. In the next subsections, the different classification algorithms used in the ensemble model of the proposed GA-stacking model are introduced, including boosting DTs, XGBoost, LASSO, RIGID, and RF.

4.2.1 Decision Tree (DT)

DTs have been one of the most successful classifiers in recent studies, especially in CADx and eHealth. Moreover, the nature of the COVID-19 dataset used in the current study is a major factor for using DTs as the metric for calculating branch purity and results classification. While building a DT, all the input feature space is divided into smaller regions, and then it recursively categorizes each one independently [57]. Additionally, to maximize the performance, a criterion function is used to define the data splitting mechanism. In the current study, the information gain ratio was calculated as shown in Eq. (2).

IG(Ex,a)=H(Ex)=∑v∈values(a)(|x∈Ex||value(x,a)=v||Ex|).H(|x∈Ex||value(x,a)=v|)(2)

where IG = information gain, and IV = intrinsic information. The intrinsic information value is calculated using Eq. (3) as follows:

IG(Ex,a)=H(Ex)=∑v∈values(a)(|x∈Ex||value(x,a)=v||Ex|).log2×(|x∈Ex||value(x,a)=v||Ex|)(3)

where Ex = the training examples, and x∈Ex defines the value of a specific example x feature a. H= entropy is used to calculate information gain, and a = features.

4.2.2 Random Forest (RF)

An RF [58] is another machine-learning algorithm used for building the proposed model. A major advantage of using the RF model is its ability to identify which features are important for classification and use the scores of these features to reduce the dimensions of the problem at hand. To classify a vector space X = x1, x2, …, xm of m features, Sn, the training set with n observations, is divided into Y subsamples of similar proprieties. This process can be described in Eq. (4) as follows [59]:

Sn=(X1,Y1),(X2,Y2),…,(Xn,Yn),X∈Rm,Y∈R(4)

The subsample regression trees q = SΘ1n…, SΘqn modeling are constructed by selecting n from Sn, where Θq is an independent, identically distributed random vector feature. The final RF combines the outputs of all regression trees by computing the average value as follows: y^=1q∑j=1qh^(x,Sn1). If some feature q decreases the impurity (i.e., the variance) substantially, then this is indicative of an important feature. The impurity decrease is calculated by dividing the number of samples belonging to that tree by the total number of samples Tn [60]. Despite the excellent ability of RF models to rank the selected dataset features according to their importance, they do not identify the optimal number of features for modeling the problem at hand. To highlight the mentioned shortcoming of RF, the Recursive Feature Elimination (RFE) feature selection algorithm was utilized. RFE starts with all the significant feature spaces and then discards the feature (s) with the lowest important values. Subsequently, the remaining features are used to build the predictive model. Such a process will recursively continue until the threshold number of features remains.

4.2.3 Least Absolute Shrinkage and Selection Operator (LASSO)

Recently, the applications of LASSO as a feature classification technique have become more common among researchers with promising results [61]. It can minimize the model prediction error by identifying the subset of relevant (nonzero) variables. Accordingly, the LASSO estimator can be defined in Eqs. (5) and (6).

β^=(argmi n)β∑J=1n⁡[yi−βi−∑j=1q⁡xijβi]2s.t.∑j=1p⁡|βi|≤t(5)

β^=(argmi n)β∑J=1n⁡[yi−βi−∑j=1q⁡xijβi]2+λ∑j=1p⁡|βi|(6)

where λ ≥ 0 is a normalization parameter controlled by the amount of shrinkage and becomes a standard estimator if it reaches a zero value. Normally, when the value of λ increases, the number of zero coefficient variables increases accordingly. Hence, to improve the model classification performance, it is very important to optimize the value. In this study, the cross-validation technique to find the value of λ was utilized.

4.2.4 EXtreme Gradient Boosting (XGBOOST)

Gradient-Based Decision Tree (GBDT) [62] is a more robust machine learning approach for data classification. GBDT classifies the data (Xi Ni = 1), where Xi represents the sample, and N is the number of samples, by generating a correlated set of DTs h(x) using a loss function f (x) and integrating their prediction results. All the nodes are then combined in a linear format to build a new tree using the negative gradient of the loss function Ft−1(Xi) of previous (t-1) trees as the target value. Finally, the weighted sum of the prediction results of all trees is used as the final prediction result. XGBoost is based on the improvement of the GBDT. With XGBoost, the objective function is controlled by a regularization term in the objective function by a set of parameters. The objective function is similar to that of other boosting algorithms, except for the introduction of a regularization term. Consequently, this algorithm improves the computation efficiency and reduces the overfitting risk., i.e., for the n samples in the training set, the DT ft is constructed by the th-iteration using Eq. (7).

L^t=∑j=1n⁡l[yi,Ft−1(xi)+∑j=1t⁡Ω(ft)]2(7)

Suppose DT h(x) has J leaf nodes. The training sample set corresponding to the jth (j = 1, 2…, J) leaf node of the mth DT is recorded as Rmj. Let I(xi∈Rmj) be a binary function, and take 1 when (xi∈Rmj); otherwise, take 0. The logarithmic loss function is used in the classification problem, and Ω(ft) represents the regularization term, which is used to control the complexity of the model, as shown in Eq. (8).

Ω(ft)=γT+12λ∑j=1t⁡ωj2(8)

4.2.5 RIGID Regression

The RIGID learning algorithm was included in the study because it has been proven to be versatile and capable of high classification power. The RIGID regression algorithm proposed by [63] is as follows in Eq. (9).

β^∗T=(xTx+KI)−1xTy(9)

where k is the RIGID parameter, k ≥ 0, and I is the identity matrix. The RIGID regression proposed by Gisela and Kibria [63] can improve the estimated model coefficients when the RIGID parameter k is appropriate, even when there is a small deviation between the expected and real coefficient values. XTX is added to the RIGID matrix KI to utilize an estimated classification calculated by the function E(β^).

4.3 Classifier Stacking

In ensemble learning, stacking methods have been successfully applied to various fields in different ways [64]. In essence, stacked ensemble learning learns the interaction between individual models to combine their outputs to make the generalization of performance more effective by combining the outputs generated by each learner. Therefore, to improve the prediction accuracy of single models, first, it conducts an initial training for the base learner L1, L2…, Lm for N samples, and their distribution is adjusted according to the base learner performance. St = (X(n) t(n))N, where X(n) represents the nth feature vector of dataset features corresponding to target t(n).

Afterward, any out-of-fold prediction generated from the initial training process can be adjusted by the second base-learner training process. Finally, the results X^ i, X^ i…..X^ i from m using m base predictors, i.e., X^ j = Ci(Xi), are stacked and optimized to find the final prediction results. Therefore, for a query instance xq from the test data D Test, the predictions from the combination of base classifiers using the meta-classifiers was considered to obtain the final 348 results. Contrary to other ensemble learning models, the predictions made by the proposed model conducted by the first-level model are used as the inputs for the second-level in the model. This effectively uses the predictions of the base learners and original dataset to increase accuracy and decrease biases. There are many types of learners, each of which has different capabilities that are reflected in the output they produce. Subsequently, it is impossible to predict which learner combination and number from unseen data will outperform the others. Therefore, the genetic algorithm GA was initialized to select the optimal number and the best combination of the base learner. GA [65] is one of the most popular intelligent algorithms that maintains good performance in various fields.

GAs have unique properties that make them suitable for solving complex problems. These properties include nonlinearity, global optimization, and combinatorial optimization. Moreover, in comparison with traditional soft computing methods [19], GA has a significant advantage over other optimization algorithms in terms of being able to segment and address multipeak problems automatically; moreover, it can select and effectively define any pattern in a defined problem space.

In this study, a new algorithm that develops ideas from the genetic algorithm to apply to stacking ensemble configurations is proposed. This algorithm generates a better classification performance in terms of the Mean Squared Error (MSE) measure than the average performance of the state-of-the-art classification networks. The genetic ensemble first encodes the connection between initial base learners. Then, a combination of 363 candidate classifiers with the best fitness score performance is selected by the algorithm. The offspring of the selected classifiers are then created through a crossover process. Finally, a random selection of candidate learners is applied to the mutation process. For any genetics-based condition, the solution must be mapped into the search space of the algorithm. Additionally, for solutions to successfully be described as chromosome sequences of genes, one must find a suitable representation scheme. The genes might be expressed as binary numbers, floating numbers, or alphabets. For the proposed algorithm, learner combination is encoded using binary representation. Hence, for GA training, a new metadata of N sample points is constructed. St = X^ (n) t(n) at the meta-level training, an m-dimensional feature vector is formed, and the final predictions X^ m = X^ i, X^ i……X^ i} are obtained. In this way, the GA maps prediction vectors X^ (n) of base-level predictors to target labels t(n), represented as FΘ(X^), and is developed and used to build the final model classifiers. The conceptual model of GA-Stacking is illustrated in Fig. 3 The algorithm decodes each of the provided learner combinations based on the provided population to estimate the classification accuracy. Fitting scores are calculated based on the classification of these accuracies. In addition, the fitness is also viewed as an objective function of the GA algorithm, as it decides whether each chromosome will survive. In the proposed algorithm, an optimal fitness level (classification accuracy) for each chromosome was chosen, and the entire process is repeated until the Stacking-GAs model achieves this score. If the population is not able to achieve the optimal fitness score of the number of chromosomes, the proposed algorithm will select the fitness score using rank-based criteria, which ensures that chromosomes with the highest fitness scores survive. This process will result in faster convergence of the algorithm as it retains higher classification accuracy. Afterward, a uniform crossover process, c, makes the next generation of individuals from the whole pool of surviving chromosomes. Using a random variable, a random pair of parents is selected, and offspring are generated. Whenever this variable exceeds a predefined threshold, parent 1’s genes are taken. Otherwise, parent 2’s genes are selected. The last step involves applying a mutation to the survivor chromosomes. Algorithm 1 explains the methodology of GA-Stacking. Different classifiers L1, L2…, Ln were applied to the original training data D Train to generate the base classifiers. These base classifiers are tested on validation dataset D, and the best classifier is selected. The individual accuracies of base classifiers are calculated using GA, and the best performing individual base classifier from each cluster is chosen and sent to the meta-classifier M. The second step involves combining the forecasts made by the qualified base classifiers using LR as a meta-classifier.

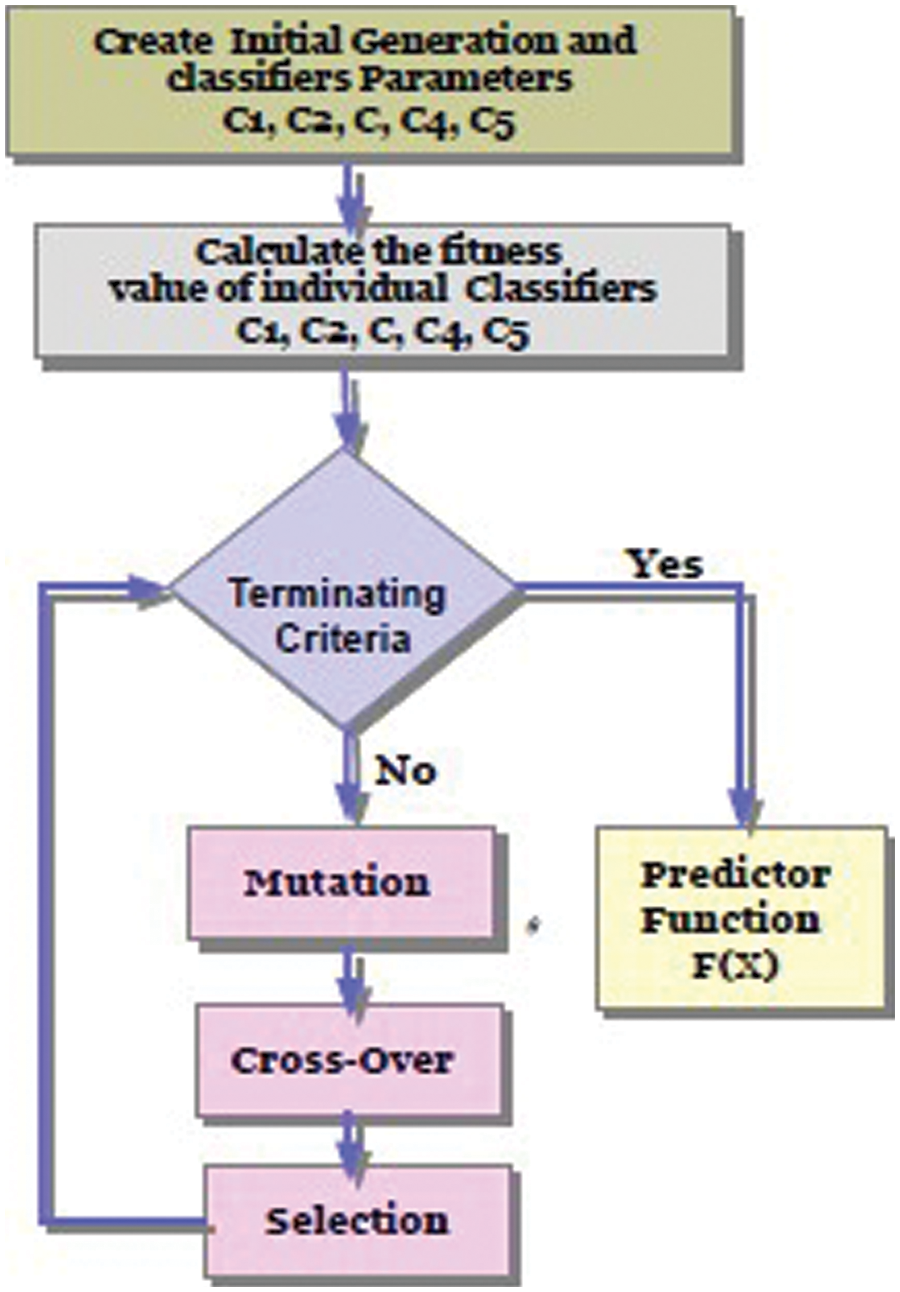
Figure 3: GA-Stacking conceptual model

Adjusting the number and combination of base learners involves reducing the number of operations considered between any nodes from a given generation Ω with time complexity O(n). This is done by selecting the most accurate prediction result based on the fitness function (RMSE) for all learners’ C search space in each generation α, where C represents the number of learners. For example, in Fig. 3, learners (C2, C3, C5) may be selected in α (2, 5) from the old search space α(2, 3, 5) to create a new search space α2. Here, the smaller search space Ω inherits/copies the weights from the previous search space. Therefore, given the GA input parameters (mutation, crossover, population selection), the complexity is O (Ω (nm + nm + n)), where Ω is the number of generations, n is the population size and c are the number of individuals. Therefore, the complexity is on the order of O(Ωnm)).

5  Experimental Results

To evaluate the performance of the proposed approach for forecasting the number of daily COVID-19 confirmed cases, three case studies were chosen: Russia (RUS), Europe (OWID_EUR) and Brazil (BRA). The goal is to accurately predict new cases of COVID-19 for each country. In fact, the countries are grouped according to the danger level, i.e., the accumulative number of new_deaths for each country. The country with a higher number of new_deaths is considered to be at a higher danger level. These three countries have been selected due to their high danger level. Fig. 4 shows the top 15 countries with high danger levels. To evaluate the prediction rates of the proposed approach, the MSE, the RMSE and the R2 measures were used. These measures are commonly deployed to predict the spread of infectious disease [5,6] by depicting the difference between predicted and real values. Fivefold cross-validation was used to avoid overfitting the model, where in each fold, the data are divided into 80% for the training set and 20% for the testing set.

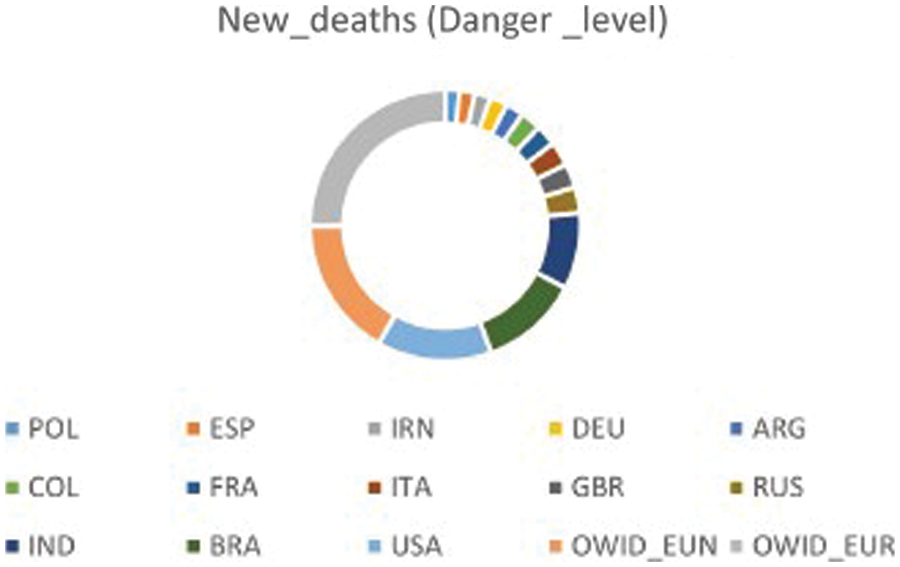
Figure 4: Level of danger for top 15 countries

5.1 Parameter Settings

For the implementation of the study, Anaconda notebook and Python as a programming language were used. The model with the highest predictive accuracy is selected out of all models. To tune the hyperparameters of the five base learners, a grid search process combined with five cross-validations is used to identify the best parameter values for each country individually. Tab. 4 illustrates the hyperparameters for each base learner. For any other hyperparameters that are not mentioned therein, their default value is used in the experiments. In addition, the parameters of the GA-Stacking are adjusted based on the optimization of a single learner in the first level. In contrast to the second level with LR (meta-learners), its default values of parameters produce high performance in comparison to any other values.

In GA, the following parameters are used: retain = 0.7, random_select = 0.1, and mutate_chance = 0.1; where retain represents the percentage of the population to be retained after each generation, random_select indicates a probability of a rejected network remaining in the population, and mutate_chance indicates thes probability of a randomly mutated network.

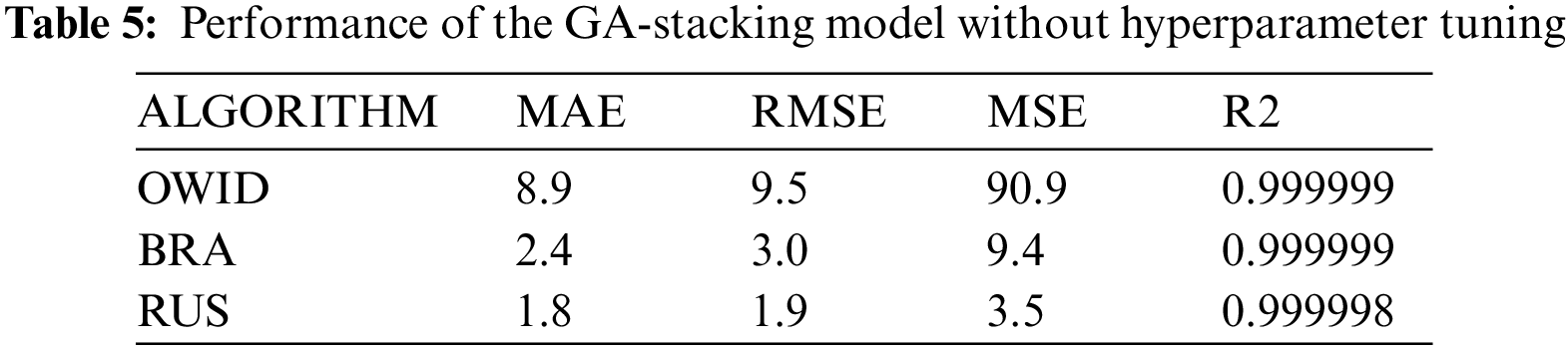
5.2 GA-stacking Results Without Hyperparameter Tuning

In this subsection, experiments are conducted using default settings of parameters for each base learner. The aim is to show that optimizing the hyperparameters of base learners affects the performance of the stacked ensemble model. Tab. 5 shows the results of the GA-Stacking approach without hyperparameters tuning (default parameters for each base learner), while Tabs. 6a, 6b, and 6c show the results with hyperparameters tuning. From these results, it is found that the GA-Stacking approach outperforms the individual classifiers, even in cases with no hyperparameter optimization of base learners.

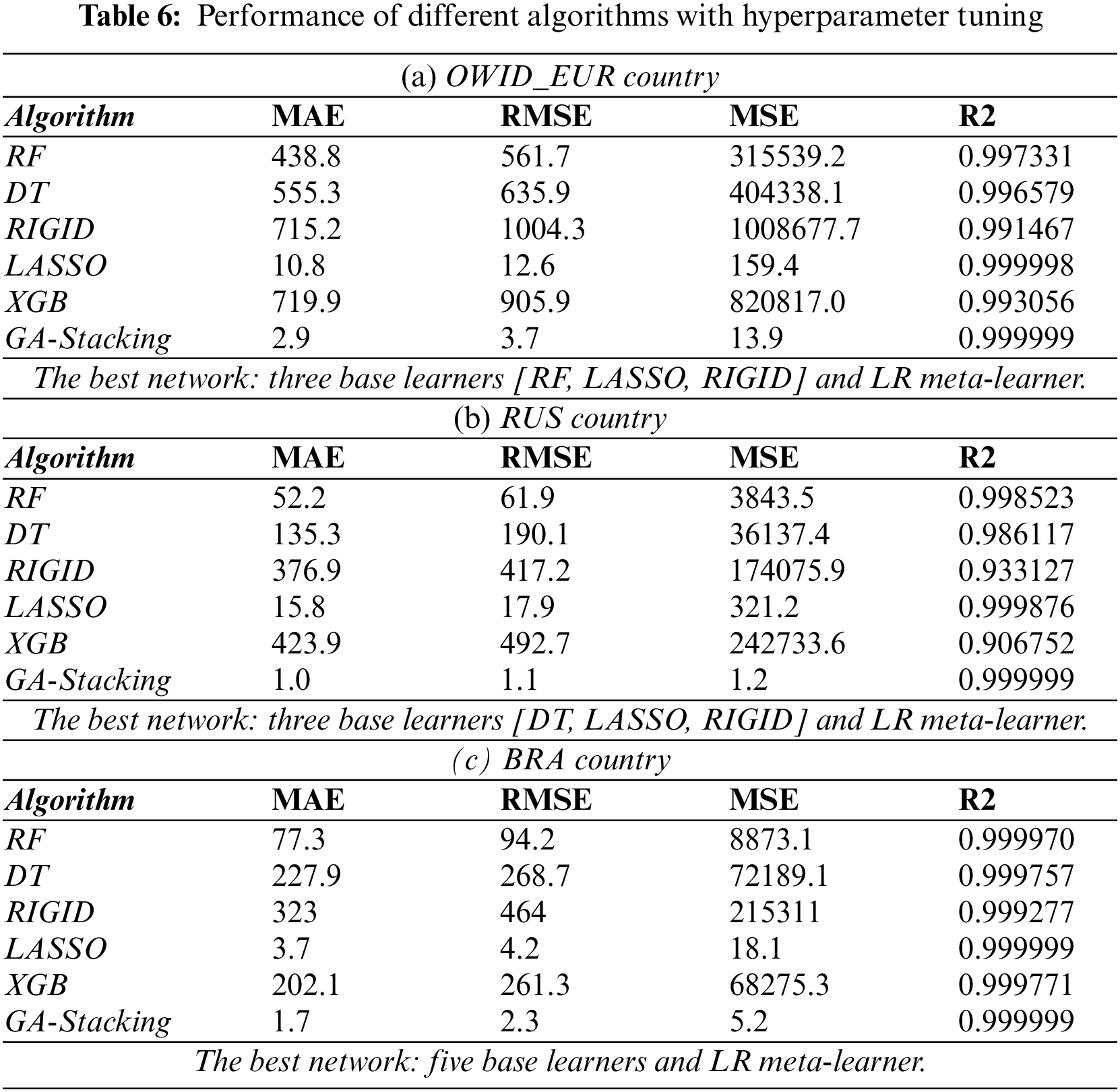
5.3 GA-Stacking Results with Hyperparameter Tuning

This subsection shows the effect of tuning the hyperparameters of the base classifiers on the results of single classifiers and the GA-Stacking approach. Fig. 5 shows the performance in terms of MAE of untuned GA-Stacking compared with the best tuned single classifier. It is clear that untuned GA-Stacking for all three countries still outperforms the single classifier even after tuning their hyperparameters. For each country, the detailed results for both single classifiers and GA-Stacking are presented in Tab. 6a, 6b, and 6c. For single classifiers, LASSO is best for OWID-EUR, but RIGID is the worst classifier in terms of MSE, RMSE and R2. The GA-Stacking approach achieves significant improvement over all single classifiers: 7.9% for MAE and 8.9% for RMSE compared with the best single classifier (LASSO). The GA-Stacking automatically identifies the best network for each country, e.g., in the case of OWID-EUR, the best network includes three base learners (RF, LASSO, RIGID) and LR as a meta-learner.

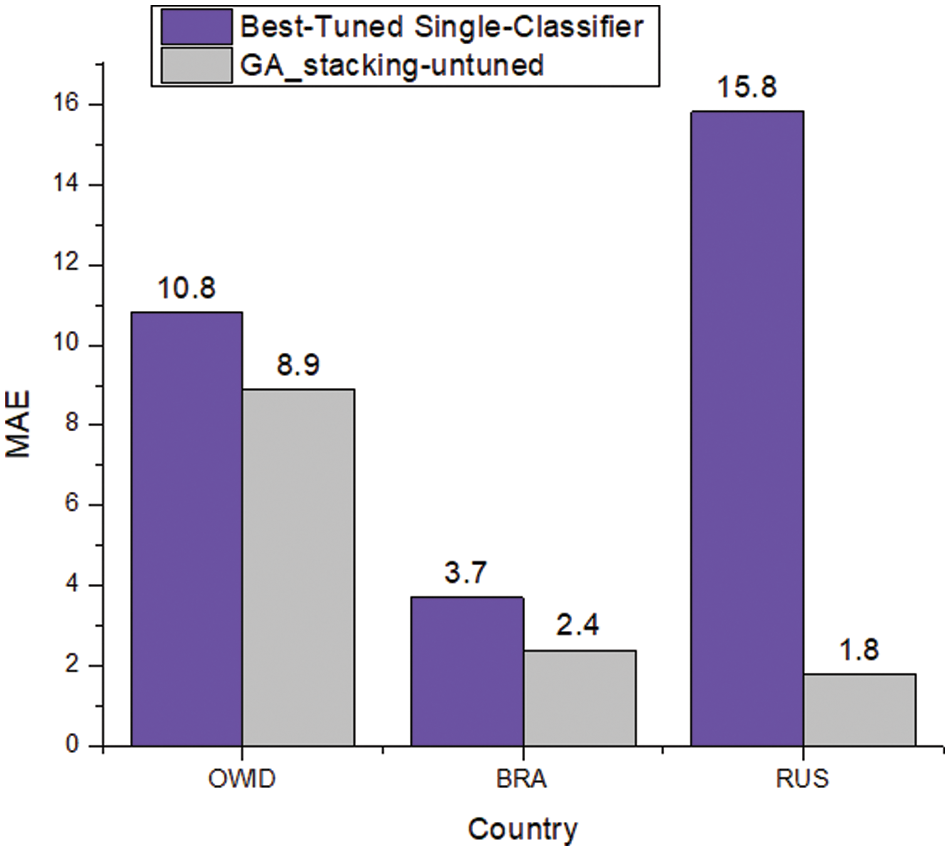
Figure 5: MAE of the best tuned single classifier compared with untuned GA-stacking

Using GA for optimizing the best combination of base learners in a stacked ensemble overcomes the performance of the individual classifiers. Specifically, for RUS countries, GA-Stacking achieves 1.1 RMSE, while the best RMSE obtained by a single classifier reaches 17.9%. The best network for RUS includes three base learners (DT, LASSO, RIGID) and LR as a meta-leaner. The best one for BRA consists of five base learners (RF, DT, XGB, LASSO, RIGID) and the LR meta-leaner. From the conducted experiments, the best combination of base learners for each country is different. Therefore, using the proposed approach to automatically select the best network is more effective than state-of-the-art approaches.

Tab. 7 clearly shows that the proposed GA-Stacking approach forecasts accurate values for 10 days from 25/07/2021 to 4/7/2021. As the actual and predicted values are very close, only the last two digits are used to represent values in the figures. For example, if the new_cases value is 20063, then it will be represented as 63. Fig. 6a, 6b and 6c illustrate curves for the three countries’ actual and predicted values of new_cases for the last 10 days. For the GA-Stacking approach, several runs are conducted using different generation numbers. The suitable generation number is 25 for two countries. Fig. 7 illustrates the average MSE over 25 generations for the three countries; starting from generation 10, the MSE value becomes more stable.

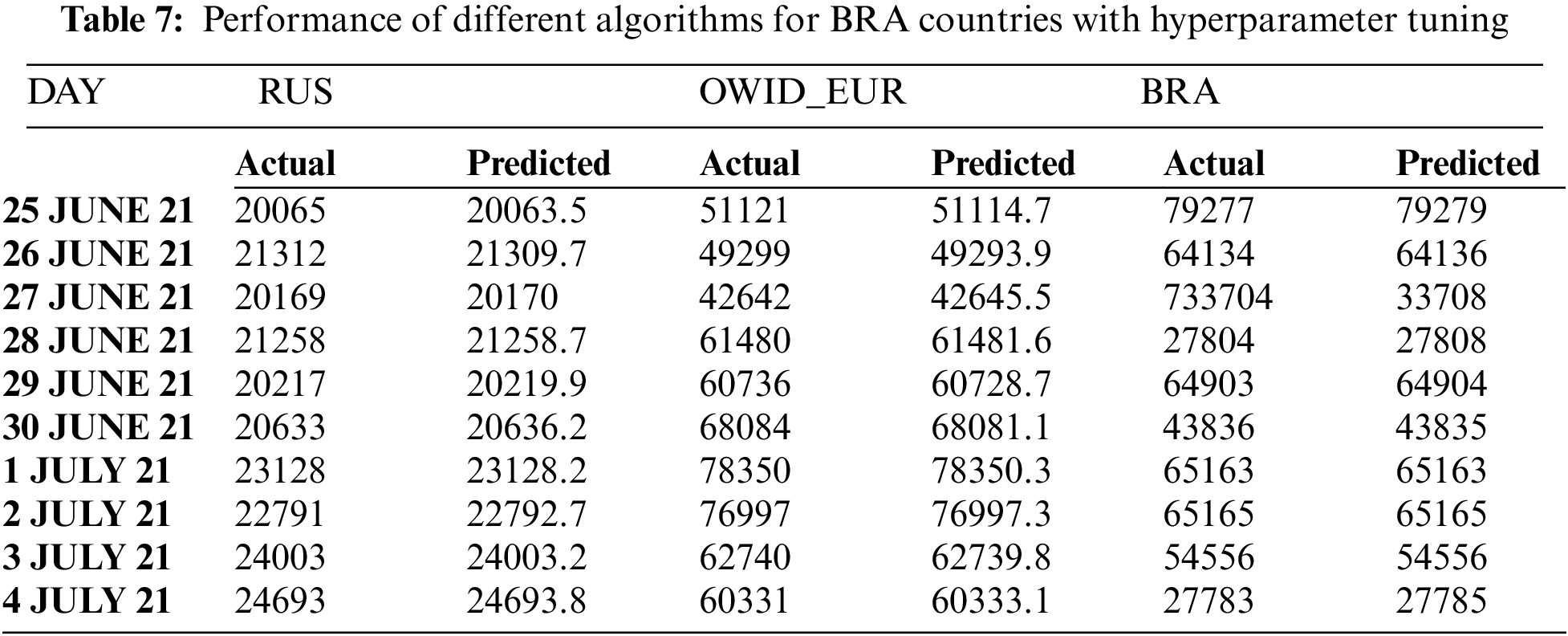
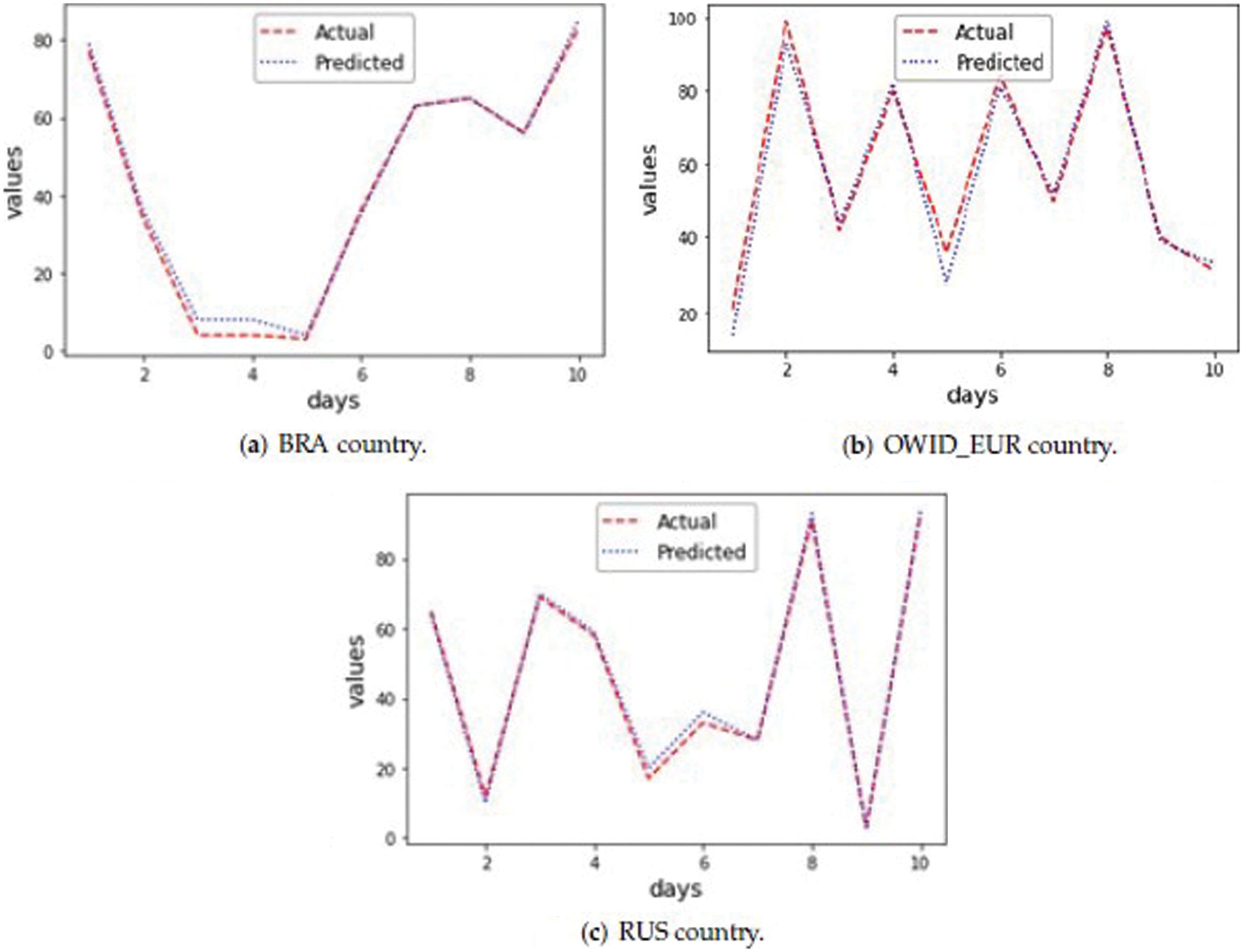
Figure 6: Actual New_cases compared with predicted New_cases by Stacked-GA

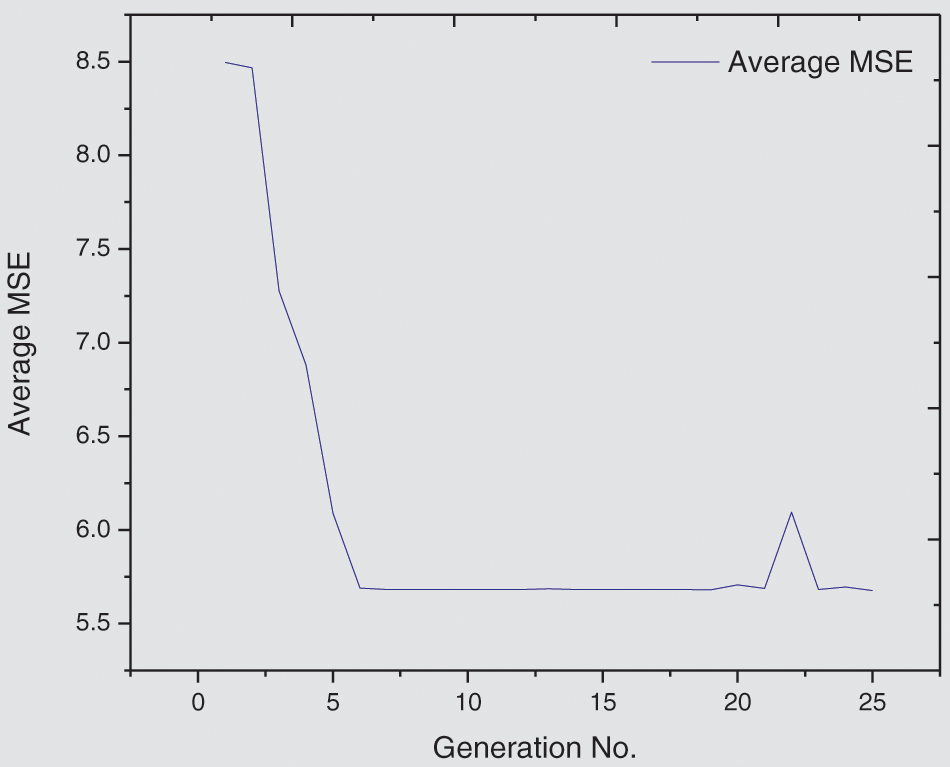
Figure 7: Stacked-GA average Mean Squared Error (MSE) for 25 generations for test data (Brazil (BRA) country)

5.4 Generalized Model

The aim of this experiment is to examine an augmented expectation by constructing stacked models determined from the RUS case study models to foresee the spread of COVID-19 in 50 other countries. All data time series for RUS are used for the training set GA-Stacking model, and the data from each country are used as a testing set. The results of 35 countries are presented in Tab. 8. From these results, it is concluded that this model can be used as a general model for testing any country’s data. There is diversity in the danger level for 35 countries, e.g., POL has a high danger level, while TCD has a low danger level. The GA-Stacking general model achieves effective performance over all 35 countries. As shown in Fig. 8, the countries are arranged by their cumulative new_cases as an indicator to visualize the performance of the general model and its relation to the spread of the epidemic in the country. The curve was divided into three areas: countries with limited, medium and widespread COVID-19. It was found that the general model works better for countries with limited and widespread COVID-19 than countries with a medium number of confirmed cases in terms of RMSE and MSE.

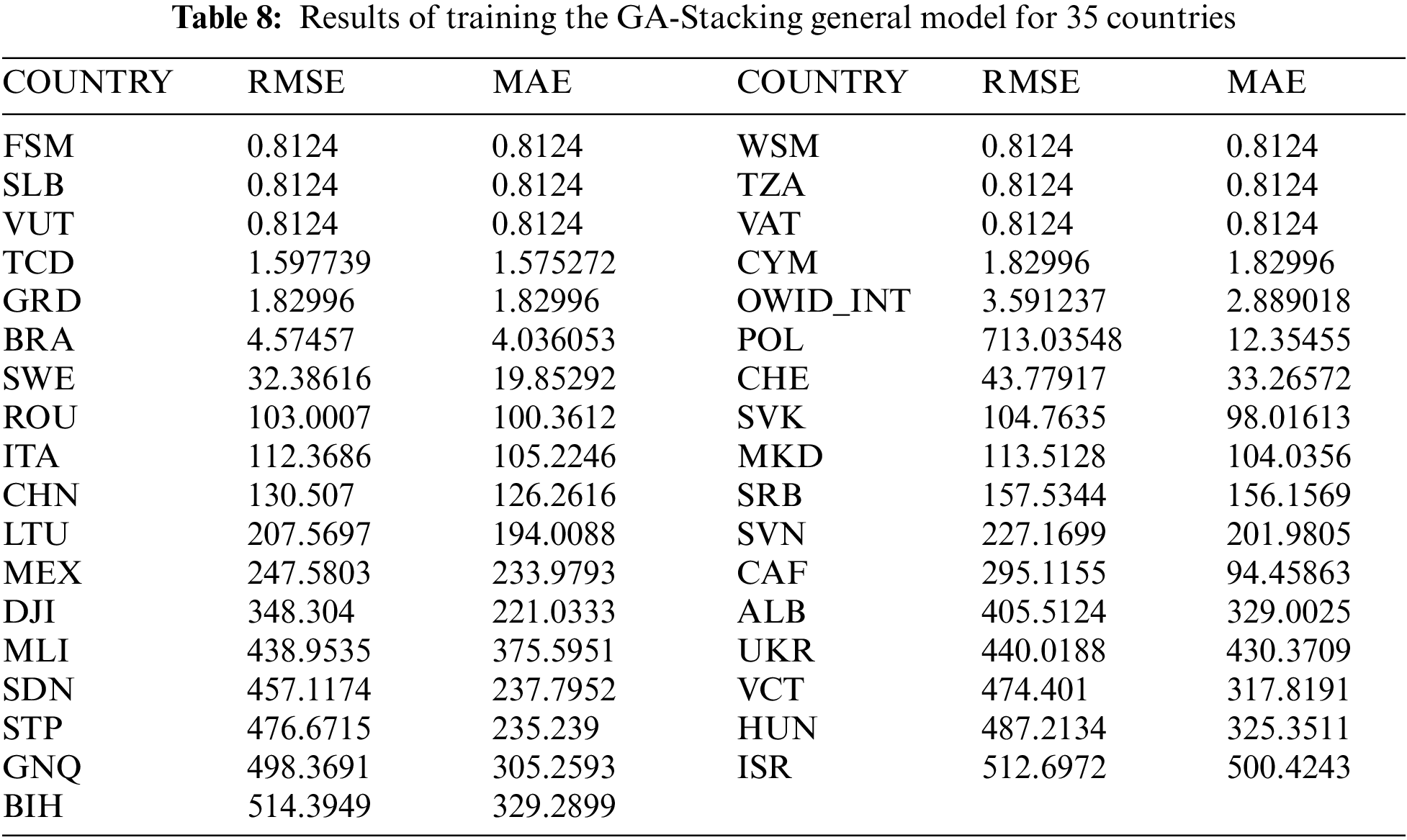
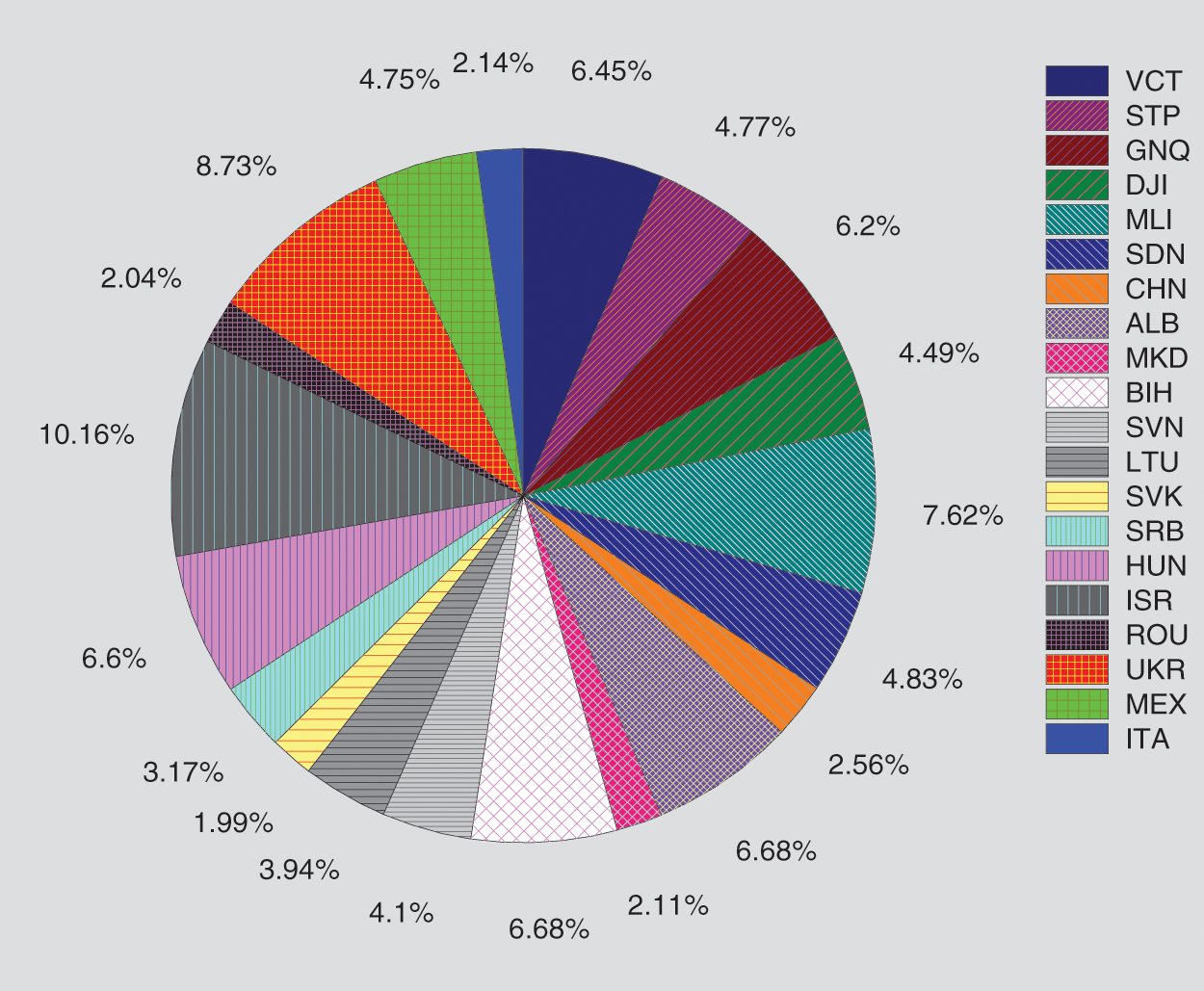
Figure 8: Performance of the GA-Stacking general model for 20 selected countries Mean Absolute Error (MAE) measure

5.5 GA-Stacking Ensemble vs. Hybrid Ensemble-Based Approaches

The hybrid ensemble-based model presented in [37] has combined several predictive models to improve the accuracy of predictions following a bagging ensemble in which the output of each classifier is fused based on a voting mechanism. By running the experiment of the OWID_EUR case study, using the methodology in [1] and while employing the GA abbreviated as Voting-GA to automatically combine the predictions of individual learners instead of the voting mechanism, it was found that through 25 generations, the GA-Stacking performs better than Voting-GA, as illustrated in Fig. 9. This is due to the effective performance of the proposed model compared with the voting method for combining the predictions of individual learners.

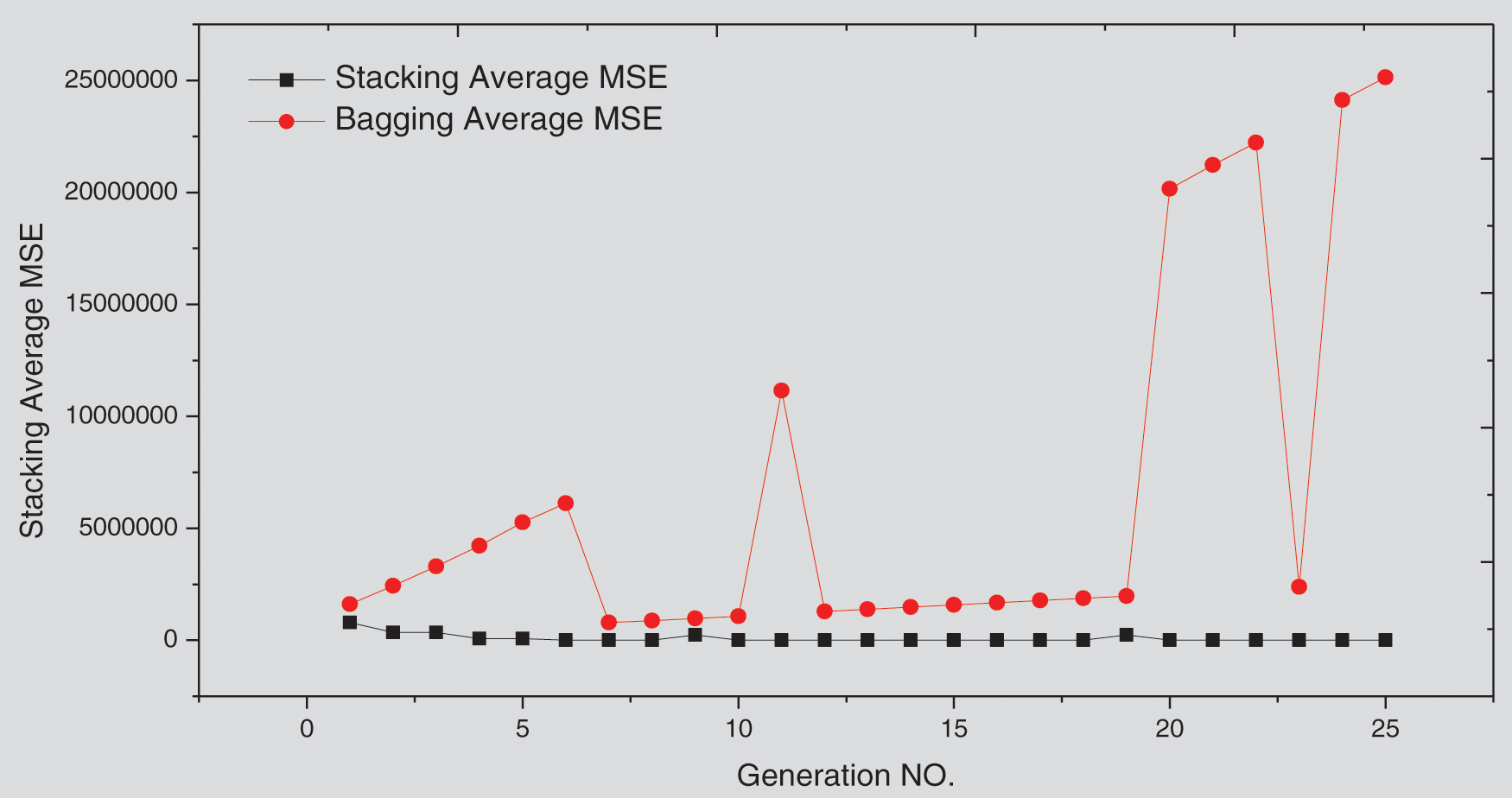
Figure 9: GA-Stacking vs. Voting-GA approach for the Europe (OWID_EUR) case study

5.6 Comparing GA-Stacking to Handcrafted Models

This section presents a comparison of the performance of the proposed GA-Stacking approach that selects base learners automatically based on a genetics algorithm to recent related work that manually selects base learners of the ensemble model presented in [66]. The recent work (2020) [65] used a group of handcrafted ensemble learners, including the voting classifier (RF, LR, KNN), voting classifier (LR, Lagrangian Support Vector Machine (LSVM), Classification And Regression Tree (CART)), boosting classifier (AdaBoost) and boosting classifier (XGBoost). Tab. 9 illustrates the results of the proposed GA-Stacking model and all handcrafted models. The models are applied to OWID-EUR country, where its samples are split into 80% train and 20% test sets.

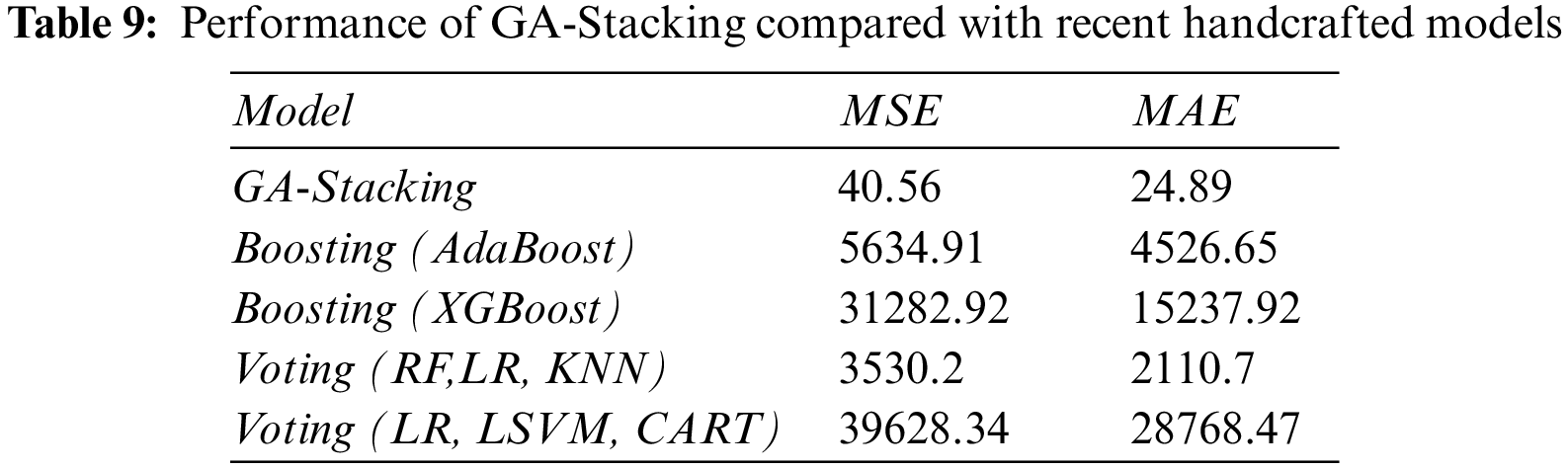
From Tab. 9, it is clear that the GA-Stacking model outperforms all the handcrafted models in terms of MSE and MAE metrics, thus ensuring the effectiveness of automatically selecting the base learners of the ensemble model.

5.7 The Impact of Vaccine Indicators on Predicting New Cases

This section aims to investigate the impact of adding vaccine indicators to the learning features of the general GA-Stacking model. The experiments are conducted using the same setting for forecasting the new_cases, with additional vaccine features, which are presented in Tab. 10. The OWID_EUR data are used as the training set to build a general model, and then the model uses the data from each country as a test set. Fig. 10 depicts the resulting prediction results.

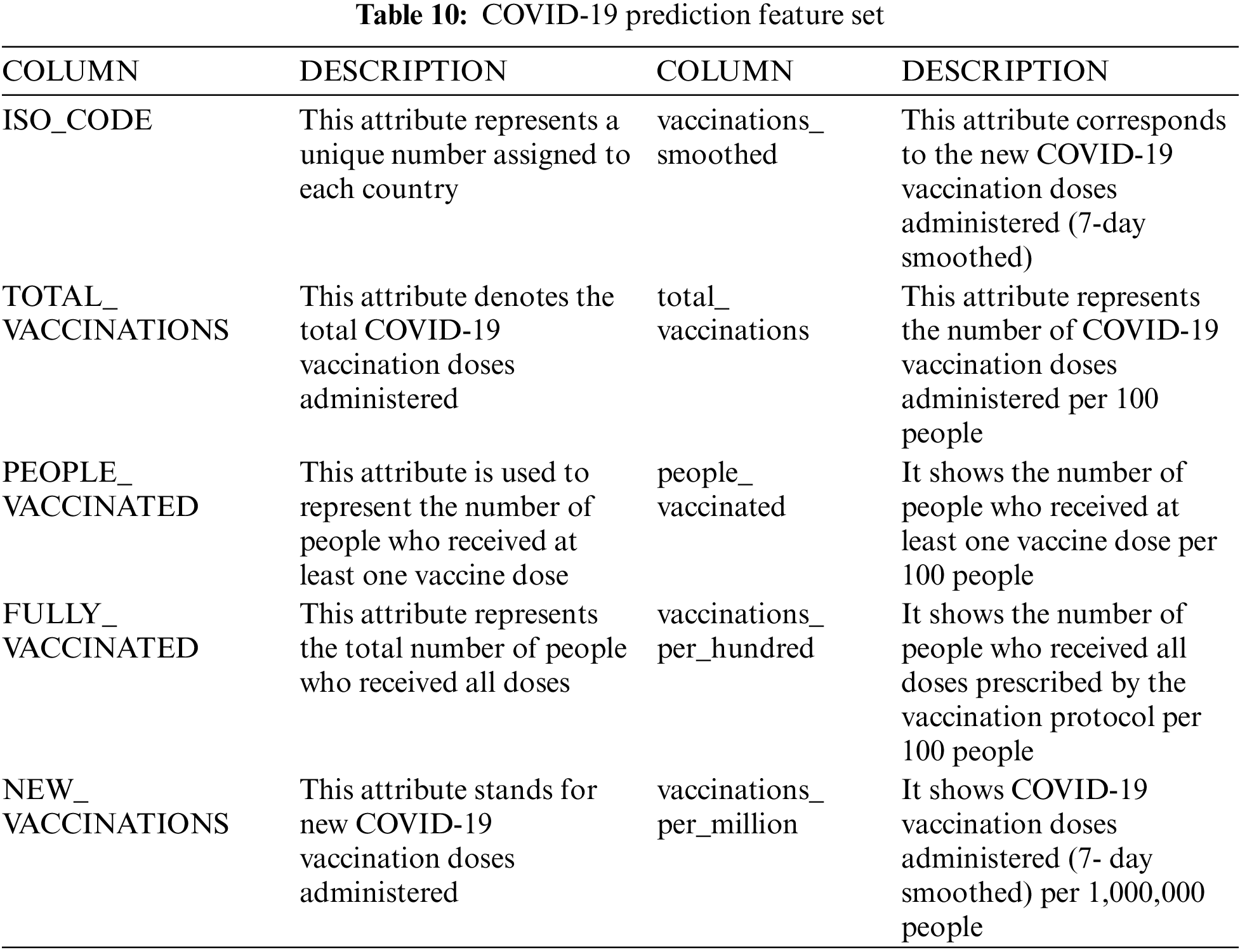
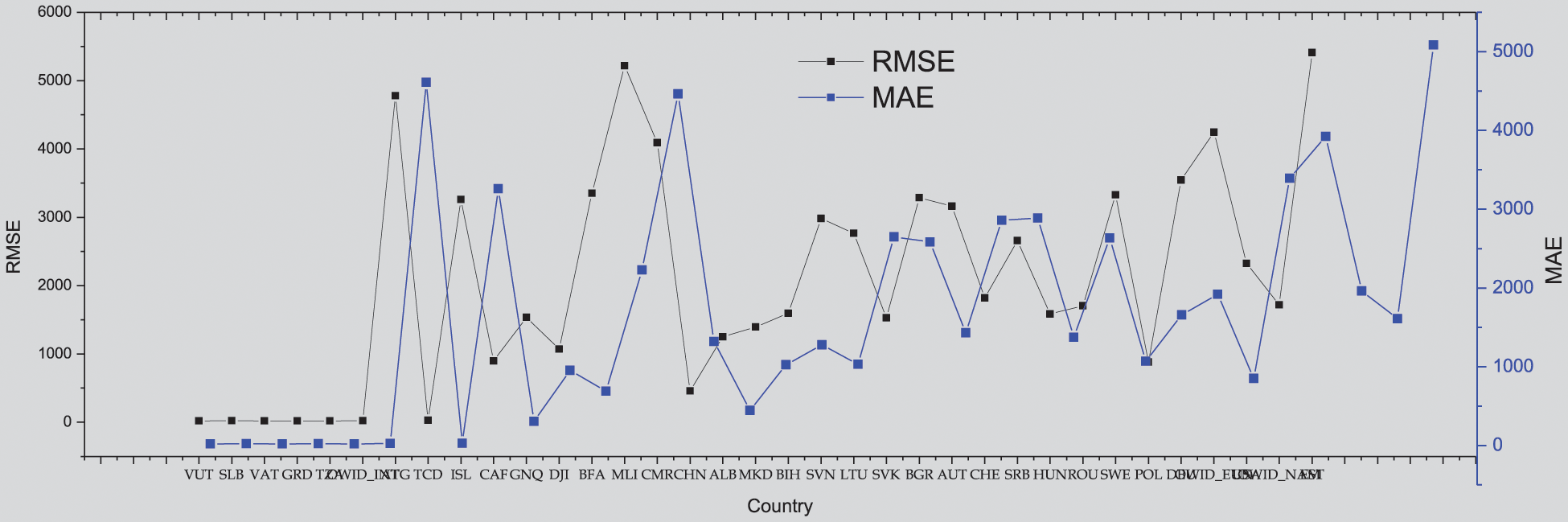
Figure 10: General GA-Stacking using vaccine features for 35 countries

In this part, the countries arranged by their cumulative new cases were selected as an indicator to visualize the performance of the GA-Stacking general model and its relation to the spread of the epidemic in the selected countries. As can be seen in Fig. 11, the general model works better for countries with limited and widespread COVID-19 than countries with a medium number of confirmed cases in terms of RMSE and MAE.

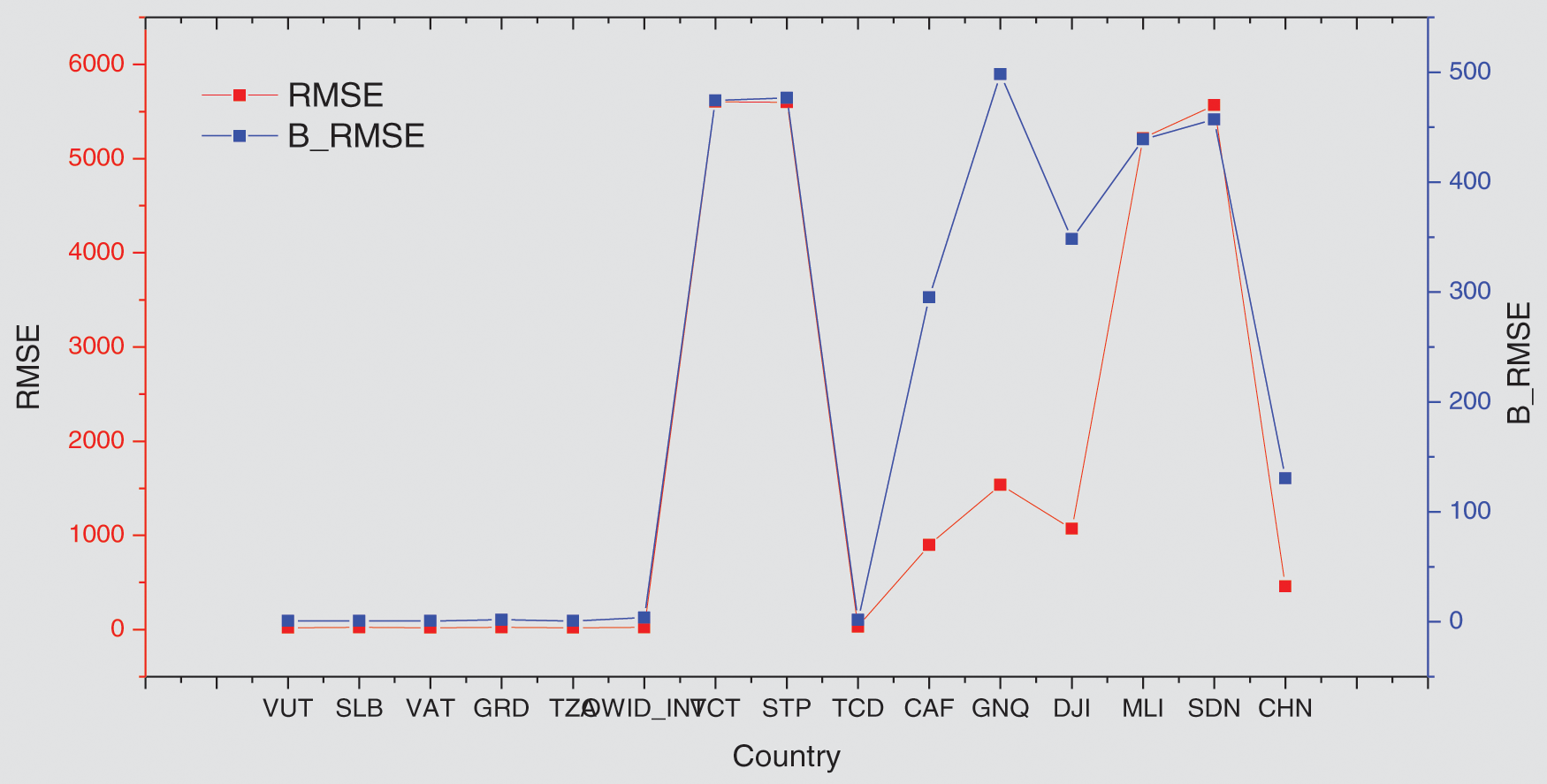
Figure 11: Comparing general GA-Stacking performance with and without adding vaccine features for 15 countries Root Mean Squared Error (RMSE)

To show the effect of adding vaccine indicators to the general model performance, the general model without (presented in Fig. 9) a baseline model was used. From Figs. 11 and 12, it is found that adding vaccine indicators impacts the general model and varies across countries. For some countries, the performance shows no change, such as SLB, VAT, OWID_INT and TCD countries. For other countries, such as VCT and CHN, the performance is decreased. For instance, for China, both RMSE and MAE are 130 for the baseline model but RMSE and MAE for GA-Stacking with adding Vaccine indicators. This may be because while these countries make efforts to increase the number of people vaccinated, there are not sufficient isolation wards and social distancing measures to contain the spread of the infection.

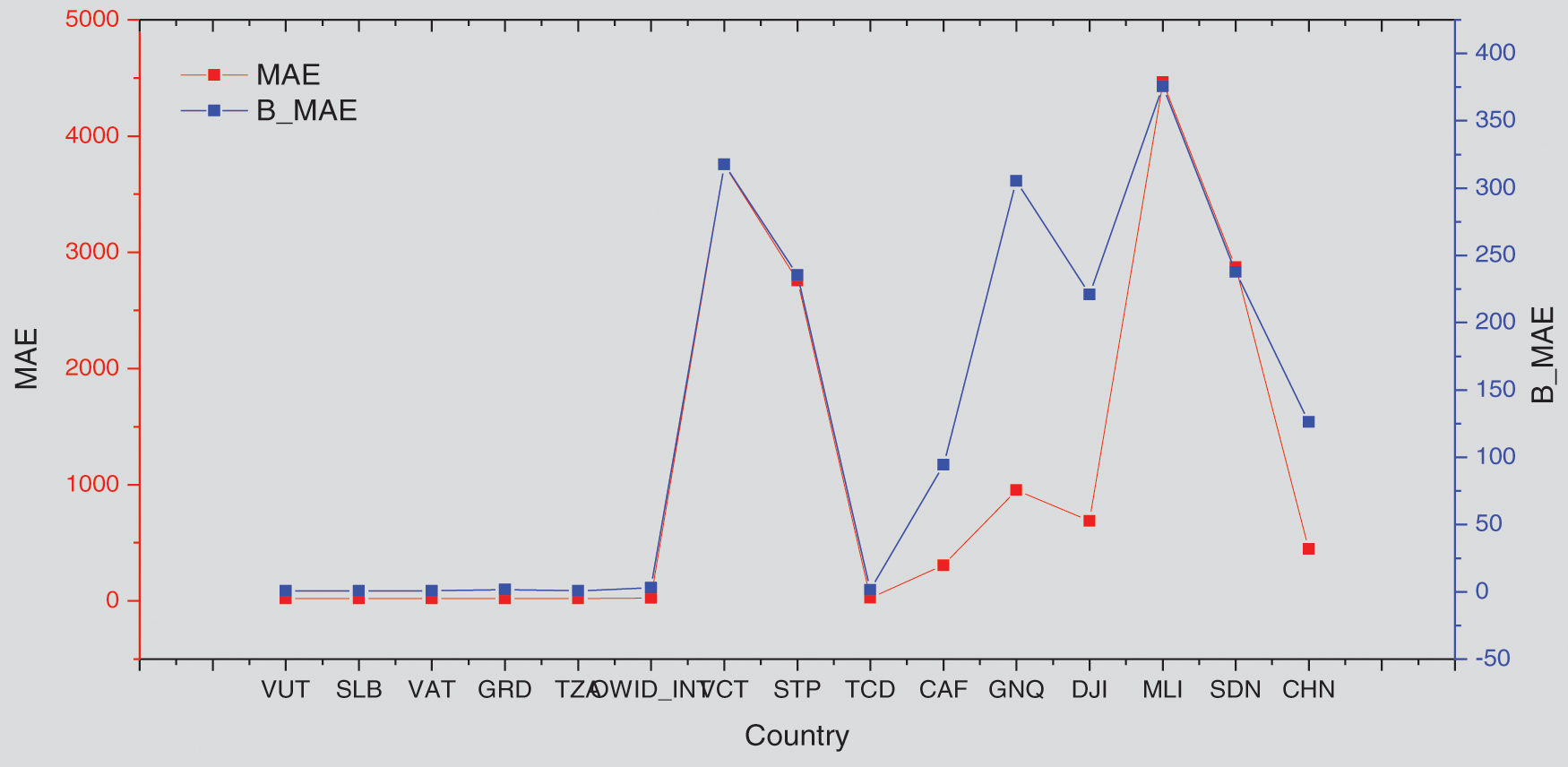
Figure 12: Comparing general GA-Stacking performance with and without adding vaccine features for 15 countries Mean Absolute Error (MAE)

6  Conclusions and Future Work

In this research, a GA-Stacking model is presented, which can be used as an accurate decision support tool to improve COVID-19 surveillance, infection control, and epidemic forecast management. Recently, most hybrid ensemble-based models have been deterministic and static, which means that all the model learners and combinations were known beforehand. Unfortunately, in real-world problems, determining all model details about the problem to be analyzed is not known at the outset. As a result, the ensemble of learners obtained by static ML can become invalid if unexpected situations occur, such as changing research area dataset types. Therefore, design methods must be used in order to build a general ensemble-based model automatically which can quickly react to changes in the search space or area under study, or prediction methods can be used so that there is the possibility of correcting it.

The proposed model employs GA-Stacking to select the best number and combination of stacking learners. The evaluation of the proposed method was conducted in three countries to measure the classification accuracy of the proposed model with and without hyperparameter optimization. The results show that optimization of base learners’ hyperparameters using the grid-search method improves the performance of both individual classifiers and the proposed GA-Stacking approach. Additionally, initializing GA for selecting the best base learners’ combination achieves high performance compared with individual classifiers. The proposed Stacked-GA model can be generalized for use in forecasting daily COVID-19 new cases in different countries. It was found that the general model works better for countries with limited and widespread COVID-19 than countries with a medium number of confirmed cases in terms of RMSE and MAE. The general GA-Stacking model was examined after adding vaccine indicators, and it has different impacts on the results from different countries. From the experiments conducted, it is recommended that vaccine features should be considered when building a forecasting model if precautionary measures are considered, such as sufficient social distancing and isolation measures. Otherwise, vaccine features will decrease the model performance, so they are not useful for accurate forecasting of daily COVID-19 spread. For future work, the model could be tested considering the GA as a meta-learner using a different number of machine learning models and artificial intelligence techniques. Moreover, different soft computing models for the long-term forecasting of COVID-19 could be proposed.

Funding Statement: This work received funding from the Deanship of Scientific Research at King Saud University.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  R. I. Doewes, R. Nair and T. Sharma, “Diagnosis of COVID-19 through blood sample using ensemble genetic algorithms and machine learning classifier,” World Journal of Engineering, vol. 19, no. 2, pp. 175–182, 2021. [Google Scholar]

 2.  M. Liang, Z. Chang, Z. Wan, Y. Gan, E. Schlangen et al., “Interpretable ensemble-machine-learning models for predicting creep behavior of concrete,” Cement and Concrete Composites, vol. 125, pp. 104295, 2021. [Google Scholar]

 3.  J. Devaraj, R. M. Elavarasan, R. Pugazhendhi, G. M. Shafiullah, S. Ganesan et al., “Forecasting of COVID-19 cases using deep learning models: Is it reliable and practically significant,” Results in Physics, vol. 21, pp. 103817, 2021. [Google Scholar]

 4.  J. Wu, J. Shen, M. Xu and M. Shao, “A novel combined dynamic ensemble selection model for imbalanced data to detect COVID-19 from complete blood count,” Computer Methods and Programs in Biomedicine, vol. 211, pp. 106444, 2021. [Google Scholar]

 5.  W. N. Ismail, M. M. Hassan, H. Alsalamah and G. Fortino, “CNN-Based health model for regular health factors analysis in internet-of-medical things environment,” IEEE Access, vol. 8, pp. 52541–52549, 2020. [Google Scholar]

 6.  S. Wollenstein-Betech, A. A. B. Silva, J. L. Fleck, C. G. Cassandras and I. C. H. Paschalidis, “Physiological and socioeconomic characteristics predict COVID-19 mortality and resource utilization in Brazil,” PloS One, vol. 15, no. 10, pp. e0240346, 2020. [Google Scholar]

 7.  J. Hao, X. Sun and Q. Feng, “A novel ensemble approach for the forecasting of energy demand based on the artificial bee colony algorithm,” Energies, vol. 13, no. 3, pp. 550, 2020. [Google Scholar]

 8.  L. Li and D. Wu, “Forecasting the risk at infractions: An ensemble comparison of machine learning approach,” Industrial Management & Data Systems, vol. 122, no. 1, pp. 1–19, 2021. [Google Scholar]

 9.  A. Telikani, A. Tahmassebi, W. Banzhaf and A. H. Gandomi, “Evolutionary machine learning: A survey,” ACM Computing Surveys (CSUR), vol. 54, no. 8, pp. 1–35, 2021. [Google Scholar]

10. T. N. Rincy and R. Gupta, “Ensemble learning techniques and its efficiency in machine learning: A survey,” in Proc.2nd IEEE Int. Conf. on Data, Engineering and Applications (IDEA), Bhopal, India, pp. 1–6, 2020. [Google Scholar]

11. X. Yin, Q. Liu, Y. Pan, X. Huang, J. Wu et al., “Strength of stacking technique of ensemble learning in rockburst prediction with imbalanced data: Comparison of eight single and ensemble models,” Natural Resources Research, vol. 30, no. 2, pp. 1795–1815, 2021. [Google Scholar]

12. N. Kardani, A. Zhou, M. Nazem and S. Shen, “Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data,” Journal of Rock Mechanics and Geotechnical Engineering, vol. 13, no. 1, pp. 188–201, 2021. [Google Scholar]

13. L. Zahedi, F. G. Mohammadi, S. Rezapour, M. W. Ohland and M. H. Amini, “Search algorithms for automated hyper-parameter tuning,” ArXiv, vol. arXiv:2104.14677, pp. 14677, 2021. [Google Scholar]

14. J. Hernandez-Gonzalez, D. Rodriguez, I. Inza, R. Harrison and J. A. Lozano, “Learning to classify software defects from crowds: A novel approach,” Applied Soft Computing, vol. 62, pp. 579–591, 2018. [Google Scholar]

15. H. Alibrahim and S. A. “Ludwig,” “Hyperparameter optimization: Comparing genetic algorithm against grid search and Bayesian optimization”, 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, pp. 1551–1559, 2021. [Google Scholar]

16. L. Ehwerhemuepha, S. Danioko, S. Verma, R. Marano, W. Feaster et al., “A super learner ensemble of 14 statistical learning models for predicting COVID-19 severity among patients with cardiovascular conditions,” Intelligence-based Medicine, vol. 5, pp. 100030, 2021. [Google Scholar]

17. N. Wang, S. Zhao, S. Cui and W. Fan, “A hybrid ensemble learning method for the identification of gang-related arson cases,” Knowledge-Based Systems, vol. 218, pp. 106875, 2021. [Google Scholar]

18. S. Cui, Y. Yin, D. Wang, Z. Li and Y. Wang, “A Stacking-based ensemble learning method for earthquake casualty prediction,” Applied Soft Computing, vol. 101, pp. 107038, 2021. [Google Scholar]

19. K. M. Hamdia, X. Zhuang and T. Rabczuk, “An efficient optimization approach for designing machine learning models based on genetic algorithm,” Neural Computing and Applications, vol. 33, no. 6, pp. 1923–1933, 2021. [Google Scholar]

20. Y. Rodkaew, “A genetic algorithm as a classifier,” in 2021 18th IEEE Int. Conf. on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, pp. 254–257, 2021. [Google Scholar]

21. Z. Soumaya, B. D. Taoufiq, N. Benayad, K. Yunus and A. Abdelkrim, “The detection of Parkinson disease using the genetic algorithm and SVM classifier,” Applied Acoustics, vol. 171, pp. 107528, 2021. [Google Scholar]

22. L. Wedlund and J. Kvedar, “New machine learning model predicts who may benefit most from COVID-19 vaccination,” NPJ Digital Medicine, vol. 4, no. 59, pp. 00425–4, 2021. [Google Scholar]

23. V. Carrieri, R. Lagravinese and G. Resce, “Predicting vaccine hesitancy from area-level indicators: A machine learning approach,” Health Economics, vol. 30, no. 12, pp. 3248–3256, 2021. [Google Scholar]

24. W. Wang, X. Huang, J. Li, P. Zhang and X. Wang, “Detecting COVID-19 patients in X-ray images based on MAI-nets,” International Journal of Computational Intelligence Systems, vol. 14, no. 1, pp. 1607–1616, 2021. [Google Scholar]

25. O. Shahid, M. Nasajpour, S. Pouriyeh, R. M. Parizi, M. Han et al., “Machine learning research towards combating COVID-19: Virus detection, spread prevention, and medical assistance,” Journal of Biomedical Informatics, vol. 117, pp. 103751, 2021. [Google Scholar]

26. N. P. Dharani, P. Bojja and P. R. Kumari, “Evaluation of performance of an LR and SVR models to predict COVID-19 pandemic,” Materials Today: Proceedings, 2021 (in press). [Google Scholar]

27. M. Ahmadi, A. Sharifi and S. Khalili, “Presentation of a developed sub-epidemic model for estimation of the COVID-19 pandemic and assessment of travel-related risks in Iran,” Environmental Science and Pollution Research, vol. 28, no. 12, pp. 14521–14529, 2021. [Google Scholar]

28. H. Lv, X. Yang, B. Wang, S. Wang, X. Du et al., “Machine learning driven models to predict prognostic outcomes in patients hospitalized with heart failure using electronic health records: Retrospective study,” Journal of Medical Internet Research, vol. 23, no. 4, pp. e24996, 2021. [Google Scholar]

29. H. Nasiri and S. Hasani, “Automated detection of COVID-19 cases from chest X-ray images using deep neural network and XGBoost,” ArXiv, vol. arXiv:2109.02428, 2021. [Google Scholar]

30. L. K. Shrivastav and S. K. Jha, “A gradient boosting machine learning approach in modeling the impact of temperature and humidity on the transmission rate of COVID-19 in India,” Applied Intelligence, vol. 51, no. 5, pp. 2727–2739, 2021. [Google Scholar]

31. M. Pourhomayoun and M. Shakibi, “Predicting mortality risk in patients with COVID-19 using artificial intelligence to help medical decision-making,” Smart Health (Amst), vol. 20, 2021. [Google Scholar]

32. K. Kumar, “Machine learning-based ensemble approach for predicting the mortality risk of COVID-19 patients: A case study,” In: M. Niranjanamurthy, S. Bhattacharyya, N. Kumar (Edsin Intelligent Data Analysis for COVID-19 Pandemic. Algorithms for Intelligent Systems, Singapore: Springer, pp. 1–25, 2021. [Google Scholar]

33. D. Tripathi, R. Cheruku and A. Bablani, “Relative performance evaluation of ensemble classification with feature reduction in credit scoring datasets,” Advances in Machine Learning and Data Science, vol. 705, pp. 293–304, 2018. [Google Scholar]

34. R. Florez-Lopez and J. M. Ramon-Jeronimo, “Enhancing accuracy and interpretability of ensemble strategies in credit risk assessment: A correlated-adjusted decision forest proposal,” Expert Systems with Applications, vol. 42, no. 13, pp. 5737–5753, 2015. [Google Scholar]

35. P. D. Singh, R. Kaur, K. D. Singh and G. Dhiman, “A novel ensemble-based classifier for detecting the COVID-19 disease for infected patients,” Information Systems Frontiers, vol. 23, pp. 1385–1401, 2021. [Google Scholar]

36. R. Malhotra, A. Kaur and Y. Singh, “Empirical validation of object-oriented metrics for predicting fault proneness at different severity levels using support vector machines,” International Journal of System Assurance Engineering and Management, vol. 1, no. 3, pp. 269–281, 2011. [Google Scholar]

37. V. Kadam, S. Jadhav and S. Yadav, “Bagging based ensemble of support vector machines with improved elitist ga-svm features selection for cardiac arrhythmia classification,” International Journal of Hybrid Intelligent Systems, vol. 16, no. 1, pp. 25–33, 2020. [Google Scholar]

38. T. Saba, I. Abunadi, M. N. Shahzad and A. R. Khan, “Machine learning techniques to detect and forecast the daily total COVID-19 infected and deaths cases under different lockdown types,” Microscopy Research and Technique, vol. 84, no. 7, pp. 1462–1474, 2021. [Google Scholar]

39. N. B. Yahia, M. D. Kandara and N. B. B. Saoud, “Deep ensemble learning method to forecast COVID-19 outbreak,” Research Square, 2020 (preprint). [Google Scholar]

40. M. Aljame, I. Ahmad, A. Imtiaz and A. Mohammed, “Ensemble learning model for diagnosing COVID-19 from routine blood tests,” Informatics in Medicine Unlocked, vol. 21, pp. 100449, 2020. [Google Scholar]

41. S. Ali and A. Majid, “Can-evo-ens: Classifier stacking based evolutionary ensemble system for prediction of human breast cancer using amino acid sequences,” Journal of Biomedical Informatics, vol. 54, pp. 256–269, 2015. [Google Scholar]

42. J. C. Monica, P. Melin and D. Sanchez, “Genetic optimization of ensemble neural network architectures for prediction of COVID-19 confirmed and death cases,” Fuzzy Logic Hybrid Extensions of Neural and Optimization Algorithms: Theory and Applications, vol. 940, pp. 85, 2021. [Google Scholar]

43. S. F. Ardabili, A. Mosavi, P. Ghamisi, F. Ferdinand, A. R. Varkonyi-Koczy et al., “Covid-19 outbreak prediction with machine learning,” Algorithms, vol. 13, no. 10, pp. 249, 2020. [Google Scholar]

44. J. Abdollahiand, B. Nouri-Moghaddam, “Hybrid stacked ensemble combined with genetic algorithms for diabetes prediction,” Iran Journal of Computer Science, pp. 1–16, 2022. [Google Scholar]

45. H. Widiputra, “GA-Optimized multivariate CNN-LSTM model for predicting multi-channel mobility in the COVID-19 pandemic,” Emerging Science Journal, vol. 5, no. 5, pp. 619–635, 2021. [Google Scholar]

46. A. Rodriguez, A. Tabassum, J. Cui, J. Xie, J. Ho et al., “Deepcovid: An operational deep learning–driven framework for explainable real-time covid-19 forecasting,” in Proc. AAAI Conf. on Artificial Intelligence, New York, United States of America, vol. 35, no. 17, pp. 15393–15400, 2020. [Google Scholar]

47. Y. Li, W. Jia, J. Wang, J. Guo, Q. Liu et al., “ALeRT-COVID: Attentive lockdown-aware transfer learning for predicting COVID-19 pandemics in different countries,” Journal of Healthcare Informatics Research, vol. 5, no. 1, pp. 98–113, 2021. [Google Scholar]

48. W. Liang, H. Liang, L. Ou, B. Chen, A. Chen et al., “Development and validation of a clinical risk score to predict the occurrence of critical illness in hospitalized patients with COVID-19,” JAMA Internal Medicine, vol. 180, no. 8, pp. 1081–9, 2020. [Google Scholar]

49. M. D. Hssayeni, A. Chala, R. Dev, L. Xu, J. Shaw et al., “The forecast of COVID-19 spread risk at the county level,” Journal of big Data, vol. 8, no. 1, pp. 1–6, 2021. [Google Scholar]

50. S. Wang, Y. Zha, W. Li, Q. Wu, X. Li et al., “A fully automatic deep learning system for COVID-19 diagnostic and prognostic analysis,” European Respiratory Journal, vol. 56, no. 2, pp. 1–11, 2020. [Google Scholar]

51. I. Priyadarshini and V. Puri, “A convolutional neural network (CNN) based ensemble model for exoplanet detection,” Earth Science Informatics, vol. 14, no. 2, pp. 735–47, 2021. [Google Scholar]

52. S. Shastri, K. Singh, M. Deswal, S. Kumar and V. Mansotra, “Cobid-net: A tailored deep learning ensemble model for time series forecasting of covid−19,” Spatial Information Research, vol. 30, no. 1, pp. 9–22, 2022. [Google Scholar]

53. Z. Zhang and X. Liu, “Study on optimal operation of natural gas pipeline network based on improved genetic algorithm,” Advances in Mechanical Engineering, vol. 9, no. 8, pp. 1–8, 2017. [Google Scholar]

54. S. Katoch, S. C. Sumit and K. Vijay, “A review on genetic algorithm: Past, present, and future,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 8091–8126, 2020. [Google Scholar]

55. Z. Qu, L. Hanxin, W. Zixiao, X. Juan, Z. Pei et al., “A combined genetic optimization with AdaBoost ensemble model for anomaly detection in buildings electricity consumption,” Energy and Buildings, vol. 248, 2021. [Google Scholar]

56. Y. Gao, G. Liang, L. Xinyu and W. Cuiyu, “A genetic algorithm-based ensemble convolutional neural networks for defect recognition with small-scale samples,” Advances in Swarm Intelligence (ICSI), vol. 12689, pp. 390–398, 2021. [Google Scholar]

57. S. R. Safavian and D. Landgrebe, “A survey of decision tree classifier methodology,” IEEE Transactions on Systems, man, and Cybernetics, vol. 21, no. 3, pp. 660–674, 1991. [Google Scholar]

58. M. Pal, “Random forest classifier for remote sensing classification,” International Journal of Remote Sensing, vol. 26, no. 1, pp. 217–222, 2005. [Google Scholar]

59. J. Li, S. Ma, T. Le, L. Liu and J. Liu, “Causal decision trees,” IEEE Transactions on Knowledge and Data Engineering, vol. 29, no. 2, pp. 257–271, 2016. [Google Scholar]

60. B. Charbuty and A. Abdulazeez, “Classification based on decision tree algorithm for machine learning,” Journal of Applied Science and Technology Trends, vol. 2, no. 1, pp. 20–28, 2021. [Google Scholar]

61. J. Ranstam and J. A. Cook, “LASSO regression,” Journal of British Surgery, vol. 105, no. 10, pp. 1348, 2018. [Google Scholar]

62. V. A. Dev and M. R. Eden, “Formation lithology classification using scalable gradient boosted decision trees,” Computers & Chemical Engineering, vol. 128, pp. 392–404, 2019. [Google Scholar]

63. M. Sewell, “Ensemble learning,” Research Note: UCL, vol. 11, no. 2, pp. 1–34, 2008. [Google Scholar]

64. G. Muniz and B. M. G. Kibria, “On some ridge regression estimators: An empirical comparison,” Communications in Statistics—Simulation and Computation, vol. 38, no. 3, pp. 621–630, 2009. [Google Scholar]

65. D. Whitley and A. M. Sutton, “Genetic algorithms-A survey of models and methods,” In: G. Rozenberg, T. Bäck, J. N. Kok, (Eds.in Handbook of Natural Computing, Berlin, Heidelberg: Springer, pp. 637–671, 2012. [Google Scholar]

66. I. Ahmad, M. Yousaf, S. Yousaf and M. O. Ahmad, “Fake news detection using machine learning ensemble methods,” Complexity, vol. 2020, pp. 1–11, 2020. [Google Scholar]