An Artificial Approach for the Fractional Order Rape and Its Control Model

1  Introduction

This study represents the naive susceptible population, which have not proper connection with the sex activities. The knowledgeable susceptible populations represent the previous information of sex. Nv shows the total susceptible girl’s population, which is separated into subclasses of susceptible naive Sn, infected knowledgeable Ik, susceptible knowledgeable Sk and infected naive In. Therefore, the total naive girl’s population is Nv = In + Sn + Ik + Sk. The factor NR represents the whole rapist population and is categorized into infective rapist IR and susceptible rapist SR, written as NR = IR + SR. All vulnerable recruitment classes are supposed to the naive susceptible population with immigration or/and birth at λv. The naive susceptible vulnerable girl’s population is enhanced by the infected naive, which can be improved without knowledgeable at γn. It is reduced by infection force Λv and the natural death rate ϕv with the actual rapist contacts. The infection force through the rapists to susceptible females is demonstrated as Λv=abIRNh, here a is rapist’s contact rate and b is infection force of vulnerable susceptible women, i.e., dSn(x)dx=λv−ϕnSn(x)+γnIn(x)−ΔvSn(x)−anSn(x)−μ1Sn(x).

The knowledgeable susceptible population of the vulnerable is produced by the naive healthier, which educated through the rate βn and growing susceptible naïve, which become knowledgeable without raped at αn rate. The infected knowledgeable individuals increased by improving the rate γk. It is decreased due to the force of infection Λv=abIRNv along with the natural death rate ϕv, i.e., dSkdx=αnSn−ϕvSk+γkIk−ΔvSk+βnIn−μ3Sk. The vulnerable population through the infected naive women is produced by using the vulnerable susceptible population based on the naive raped women. The infected recovered naive can be decreased by using the population based on the maintains or knowledgeable. The rate of natural death can be decreased at a rate ϕv along with the rape connected to death δn, i.e., dIndx=ΔnSn−(γn+βn+δn+ϕn)In−μ2In.

The infected knowledgeable vulnerable population girls are produced from the vulnerable susceptible population through the rapist based knowledgeable girls. That shows the infected/recovered knowledgeable girls, rape related death δk and natural death at a rate ϕv, i.e., dIkdx=ΔvSk−(γk+δk+ϕv)Ik−μ4Ik. The population of susceptible rapist is increased through the social difficulties, which produce the sexual strength at λR. The contact ration of the knowledgeable, vulnerable, and infected women decreased with the natural death ϕR along with the infection force i.e., ΛR=τkIkNR. The dynamical form of this representation is given as dSRdx=λR−ϕRSR−ΔRSR−μ5SR. The infective rapist’s population is enhanced by the susceptible rapist ΛR and decreased by ϕR (natural rate of death) is being caught δR, i.e., dIRdx=ΔRSR−(ϕR+δR)IR−μ6IR.

There are various studies that have been proposed to solve the dynamical models. To mention few of the studies are epidemic SIR models with equal death and birth rates have been proposed by the analytic schemes [1], stochastic procedures have been proposed to solve the HIV differential model [2], dynamical behavior and analytical solutions of nonlinear fractional differential systems arising in chemical reaction [3], nonlinear model based on dengue fever [4], nonlinear Parabolic dynamical wave equations [5], buckling of improved couples based functionally porous classified micro-plates [6], a system based on the phase-field using the fracture spread in the poroelastic media [7], dynamical studies of a fractional SITRS discrete system [8], dynamic study through the porous graded beam along with the sinusoidal rate of deformation shear model [9], the behavior of tumor as well as immune cells using the immunogenetic system based on the fractional kinds of the non-singular derivatives [10] and many more [11–29].

In this work, a fractional order mathematical rape and its control model is numerically discussed by using the strength of artificial neural networks (ANNs) together with the Levenberg-Marquardt backpropagation approach (LMBA), i.e., ANNs-LMBA.

The remaining parts of the paper are organized as: The design of fractional order model is described in Section 2. The stochastic applications are reported in Section 3. The structure of ANNs-LMBA is explained in Section 4. The simulations of the fractional order model are derived in Section 5. Conclusions are discussed along with future research in the last Section.

2  Mathematical Construction of the Fractional Order Mathematical Rape and Its Control Model

In this section, the design of fractional order mathematical rape and its control model is provided. The differential mathematical form of the nonlinear mathematical rape and its control model has six classes: susceptible native girls, infected immature girls, susceptible knowledgeable girls, infected knowledgeable girls, susceptible rapist population and infective rapist population. The mathematical form of the nonlinear mathematical rape and its control model is given as [30]:

{dSn(x)dx=λv−ϕnSn(x)+γnIn(x)−ΔvSn(x)−anSn(x)−μ1Sn(x),Sn(0)=l1,dIn(x)dx=ΔnSn(x)−(γn+βn+δn+ϕn)In(x)−μ2In(x),In(0)=l2,dSk(x)dx=αnSn(x)−ϕvSk(x)+γkIk(x)−ΔvSk(x)+βnIn(x)−μ3Sk(x),Sk(0)=l3,dIk(x)dx=ΔvSk(x)−(γk+δk+ϕv)Ik(x)−μ4Ik(x),Ik(0)=l4,dSR(x)dx=λR−ϕRSR(x)−ΔRSR(x)−μ5SR(x),SR(0)=l5,dIR(x)dx=ΔRSR(x)−(ϕR+δR)IR(x)−μ6IR(x),IR(0)=l6.(1)

The detail of each parameter of nonlinear mathematical rape and its control model is provided in Tab. 1.

The present work shows a nonlinear fractional order mathematical rape and its control model (1) based on the artificial intelligence (AI) together with the ANNs-LMBA. The construction of the fractional order mathematical rape and its control model is shown as:

{d(ν)Sn(x)dx(ν)=λv−ϕnSn(x)+γnIn(x)−ΔvSn(x)−anSn(x)−μ1Sn(x),Sn(0)=l1,d(ν)In(x)dx(ν)=ΔnSn(x)−(γn+βn+δn+ϕv)In(x)−μ2In(x),In(0)=l2,d(ν)Sk(x)dx(ν)=αnSn(x)−ϕvSk(x)+γkIk(x)−ΔvSk(x)+βnIn(x)−μ3Sk(x),Sk(0)=l3,d(ν)Ik(x)dx(ν)=ΔvSk(x)−(γk+δk+ϕv)Ik(x)−μ4Ik(x),Ik(0)=l4,d(ν)SR(x)dx(ν)=λR−ϕRSR(x)−ΔRSR(x)−μ5SR(x),SR(0)=l5,d(ν)IR(x)dx(ν)=ΔRSR(x)−(ϕR+δR)IR(x)−μ6IR(x),IR(0)=l6.(2)

where ν shows the fraction order derivative of the mathematical rape and its control model.

3  Novel Features and Frameworks of the Stochastic Solvers

In this section, the solutions of the fractional kind of mathematical rape and its control model are presented using the ANNs-LMBA. The stochastic computing performances through the ANNs based on the local and global operators have been implemented to solve several nonlinear, stiff, complex, and singular models [31–43]. Recently, these applications have been used to solve the Lane-Emden nonlinear system [44], functional order system [45], singular form of the fractional order equations [46–48], periodic differential system [49], delayed differential systems [50] and HIV infection based mathematical models [51,52].

The motive of this study is to provide the fractional order investigations based on the mathematical rape and its control model using the ANNs-LMBA. There are various applications related to the fractional order derivatives have been proposed based on the system conditions. Few of the fractional derivative applications based on the real-world system applications are provided in these references [53–55]. Furthermore, the stochastic procedures recently have been used to solve the fractional order models, like infection-based fractional-order nonlinear prey-predator system [56], seventh order singular system [57], fractional-order SIDARTHE COVID-19 pandemic differential model [58], fractional order dynamical nonlinear susceptible infected and quarantine differential model [59], immune-chemotherapeutic treatment for breast cancer [60], Bagley–Torvik mathematical model [61] and fractional infectious disease model [62]. The novel features of the designed stochastic ANNs-LMBA for the fractional order mathematical rape and its control model are designated as:

•   A design of the mathematical nonlinear model is constructed based on the fractional order mathematical rape and its control model.

•   The stochastic procedures have not been implemented before for the fractional order mathematical rape and its control model.

•   The investigations using the stochastic numerical paradigms are effectively accessible using the fractional order mathematical rape and its control model.

•   The design of LMBA using the procedures of AI is accessible for the fractional order mathematical rape and its control model.

•   The different variants of the fractional order mathematical rape and its control model have been proposed numerically to validate the consistency of the proposed ANNs-LMBA.

•   The comparison of the obtained and reference (Adams-Bashforth-Moulton) solutions indicate the brilliance of the proposed ANNs-LMBA.

•   The accuracy and convergence of the proposed numerical ANNs-LMBA scheme is performed through the performance of the absolute error (AE), which is accomplished in good order for the fractional order mathematical rape and its control model.

•   The STs, regression, MSE, correlation and regression performances support the constancy and dependability of the proposed ANNs-LMBA scheme for the fractional order mathematical rape and its control model.

4  Proposed Method: ANNs-LMBA

In this section, the proposed ANNs-LMBA structure for the fractional order mathematical rape and its control model is presented. The methodology ANNs-LMBA is divided in two sections. First, the critical performances of ANNs-LMBS operative are drawn. Whereas the implementation of ANNs-LMBA is executed for the fractional order mathematical rape and its control model.

Fig. 1 shows the multi-layer procedures of optimization through the numerical stochastic ANNs-LMBA. The statistical ANNs-LMBA solvers are indicated using the command ‘nftool’ in Matlab with the assortment of data as 70% for training, 14% for authorization and 16% for testing.

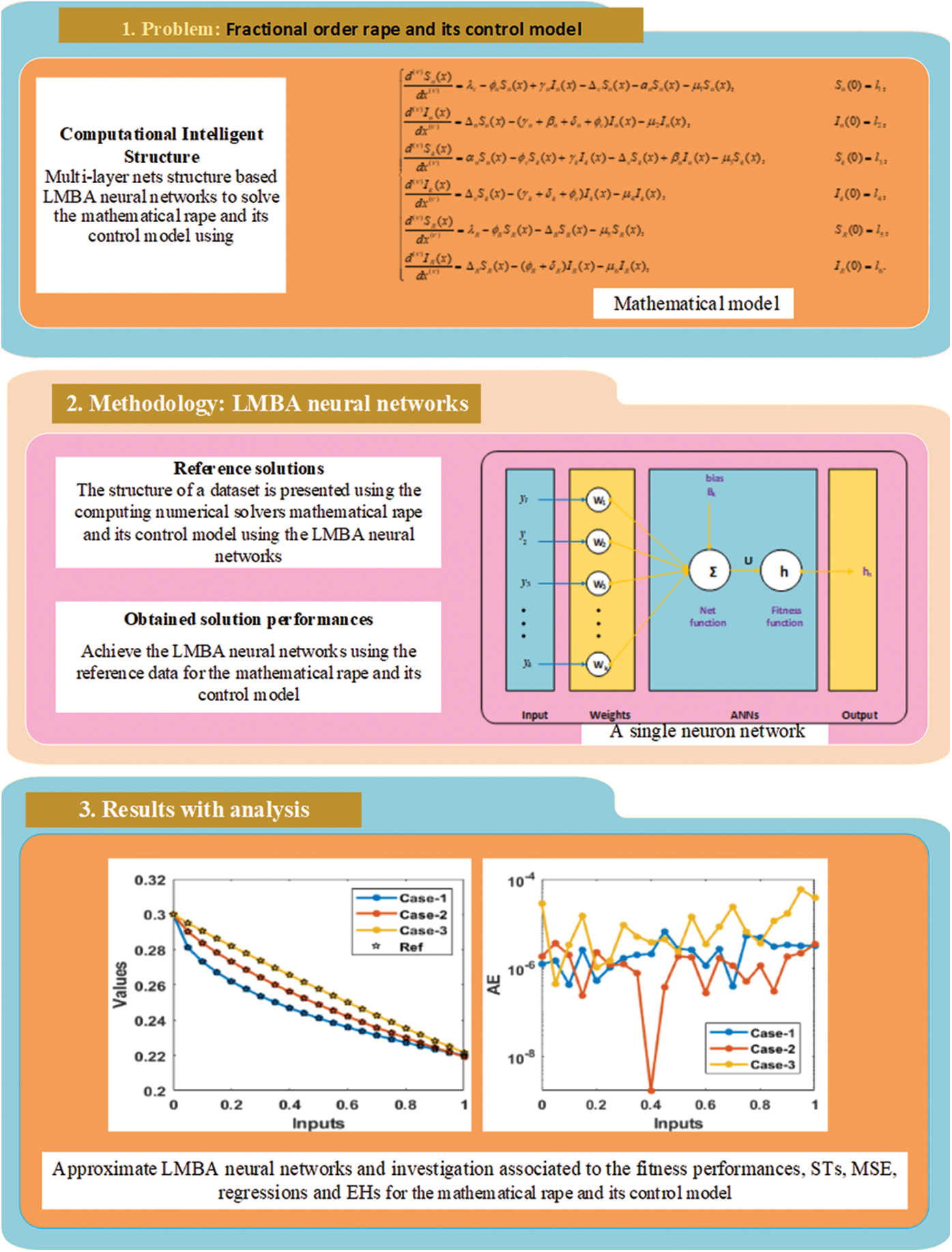
Figure 1: Workflow of ANNs-LMBA for the fractional order mathematical rape and its control model

5  Numerical Result Performances Using the Proposed Scheme

In this section, the mathematical rape and its control model along with three different variants is presented. The proposed scheme ANNs-LMBA is applied to find the numerical solutions of the mathematical rape and its control model, mathematically signified as:

Case 1: Consider a fractional order rape and its control model using the ν=0.5, λv=0.1, βn=0.1, δn=0.2, ϕv=0.2, ϕn=0.2, Δv=0.3, μ1=0.1, an=0.1, Δn=0.2, μ2=0.2, αn=0.1, δR=0.1, γk=0.2, δk=0.3, μ3=0.3, μ4=0.4, λR=0.3, ϕR=0.2, ΔR=0.1, μ5=0.5, l4=0.4, ΔR=0.2, l2=0.2, l1=0.1, l3=0.3, l6=0.6 and l5=0.5 is shown as:

{d(0.5)Sn(x)dx(0.5)=0.1−0.7Sn(x)+0.05In(x),Sn(0)=0.1,d(0.5)In(x)dx(0.5)=0.2Sn(x)−0.75In(x),In(0)=0.2,d(0.5)Sk(x)dx(0.5)=0.1Sn(x)−0.6Sk(x)+0.2Ik(x)+0.1In(x),Sk(0)=0.3,d(0.5)Ik(x)dx(0.5)=0.3Sk(x)−1.1Ik(x),Ik(0)=0.4,d(0.5)SR(x)dx(0.5)=0.3−0.8SR(x),SR(0)=0.5,d(0.5)IR(x)dx(0.5)=0.2SR(x)−0.9IR(x),IR(0)=0.6.(3)

Case 2: Consider a fractional order mathematical rape and its control model using the ν=0.7, λv=0.1, βn=0.1, δn=0.2, ϕv=0.2, ϕn=0.2, Δv=0.3, μ1=0.1, an=0.1, Δn=0.2, μ2=0.2, αn=0.1, δR=0.1, γk=0.2, δk=0.3, μ3=0.3, μ4=0.4, λR=0.3, ϕR=0.2, ΔR=0.1, μ5=0.5, l4=0.4, ΔR=0.2, l2=0.2, l1=0.1, l3=0.3, l6=0.6 and l5=0.5 is shown as:

{d(0.7)Sn(x)dx(0.7)=0.1−0.7Sn(x)+0.05In(x),Sn(0)=0.1,d(0.7)In(x)dx(0.7)=0.2Sn(x)−0.75In(x),In(0)=0.2,d(0.7)Sk(x)dx(0.7)=0.1Sn(x)−0.6Sk(x)+0.2Ik(x)+0.1In(x),Sk(0)=0.3,d(0.7)Ik(x)dx(0.7)=0.3Sk(x)−1.1Ik(x),Ik(0)=0.4,d(0.7)SR(x)dx(0.7)=0.3−0.8SR(x),SR(0)=0.5,d(0.7)IR(x)dx(0.7)=0.2SR(x)−0.9IR(x),IR(0)=0.6.(4)

Case 3: Consider a fractional order mathematical rape and its control model using the ν=0.9, λv=0.1, βn=0.1, δn=0.2, ϕv=0.2, ϕn=0.2, Δv=0.3, μ1=0.1, an=0.1, Δn=0.2, μ2=0.2, αn=0.1, δR=0.1, γk=0.2, δk=0.3, μ3=0.3, μ4=0.4, λR=0.3, ϕR=0.2, ΔR=0.1, μ5=0.5, l4=0.4, ΔR=0.2, l2=0.2, l1=0.1, l3=0.3, l6=0.6 and l5=0.5 is shown as:

{d(0.9)Sn(x)dx(0.9)=0.1−0.7Sn(x)+0.05In(x),Sn(0)=0.1,d(0.9)In(x)dx(0.9)=0.2Sn(x)−0.75In(x),In(0)=0.2,d(0.9)Sk(x)dx(0.9)=0.1Sn(x)−0.6Sk(x)+0.2Ik(x)+0.1In(x),Sk(0)=0.3,d(0.9)Ik(x)dx(0.9)=0.3Sk(x)−1.1Ik(x),Ik(0)=0.4,d(0.9)SR(x)dx(0.9)=0.3−0.8SR(x),SR(0)=0.5,d(0.9)IR(x)dx(0.9)=0.2SR(x)−0.9IR(x),IR(0)=0.6.(5)

The numerical simulations of the fractional order mathematical rape and its control model is obtained through the stochastic ANNs-LMBA with 15 numbers of neurons with the data selection are designated as 70% for training, 14% for authorization and 16% for testing. The output, input and hidden neuron’s construction is presented in Fig. 2.

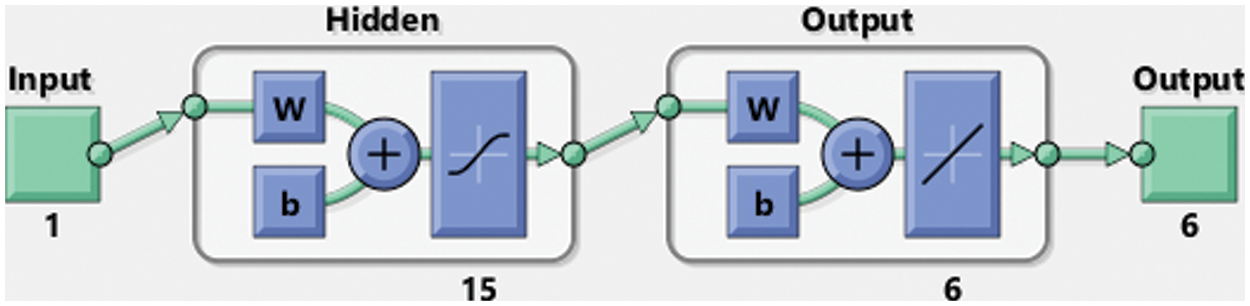
Figure 2: Proposed ANNs-LMBA for the fractional order mathematical rape and its control model

The graphical plots are demonstrated in Figs. 3–5 for the fractional order mathematical rape and its control model by applying the ANNs-LMBS procedures. To authenticate the best presentations and STs, Figs. 3 and 4 have been drawn. The values of the MSE and EHs using the training, authentication and best curves have been illustrated in Fig. 4 by applying the ANNs-LMBS procedures. The achieved best performances of the fractional order mathematical rape and its control model have been provided at epochs 49, 53 and 19 calculated as 1.4859 × 10−09, 4.9799 × 10−09 and 9.2361 ×10−09. The performances of the gradient values are depicted in Fig. 3 for the fractional order mathematical rape and its control model by applying the ANNs-LMBS procedures. The gradient measures have been performed around 9.6853× 10−08, 9.4888 × 10−08 and 2.866 × 10−06 for 1st, 2nd and 3rd case. These graphical plots show the convergence of the designed ANNs-LMBA for the fractional order mathematical rape and its control model. The first portion of Figs. 4 indicates the fitting curves performances for the fractional order mathematical rape and its control model. These illustrations indicate the comparative presentations of the obtained and reference solutions. The second part of the Fig. 4 represents the values the EHs. The values perform the values around 9.57 ×10−07, 7.83 × 10−06 and 5.55 × 10−06 for 1st, 2nd and 3rd case of the fractional order mathematical rape and its control model. The correlations are plotted to authenticate the regression presented in Fig. 5 of the fractional order mathematical rape and its control model. It is easy to understand that the correlation illustrations are calculated as 1 using the fractional order mathematical rape and its control system. The testing, authentication and training depictions signify the accuracy of the stochastic ANNs-LMBA for the fractional order mathematical rape and its control model. The MSE convergence using the training, complexity, verification, iterations, and testing is drawn in Tab. 2 for the fractional order mathematical rape and its control model using the ANNs-LMBA.

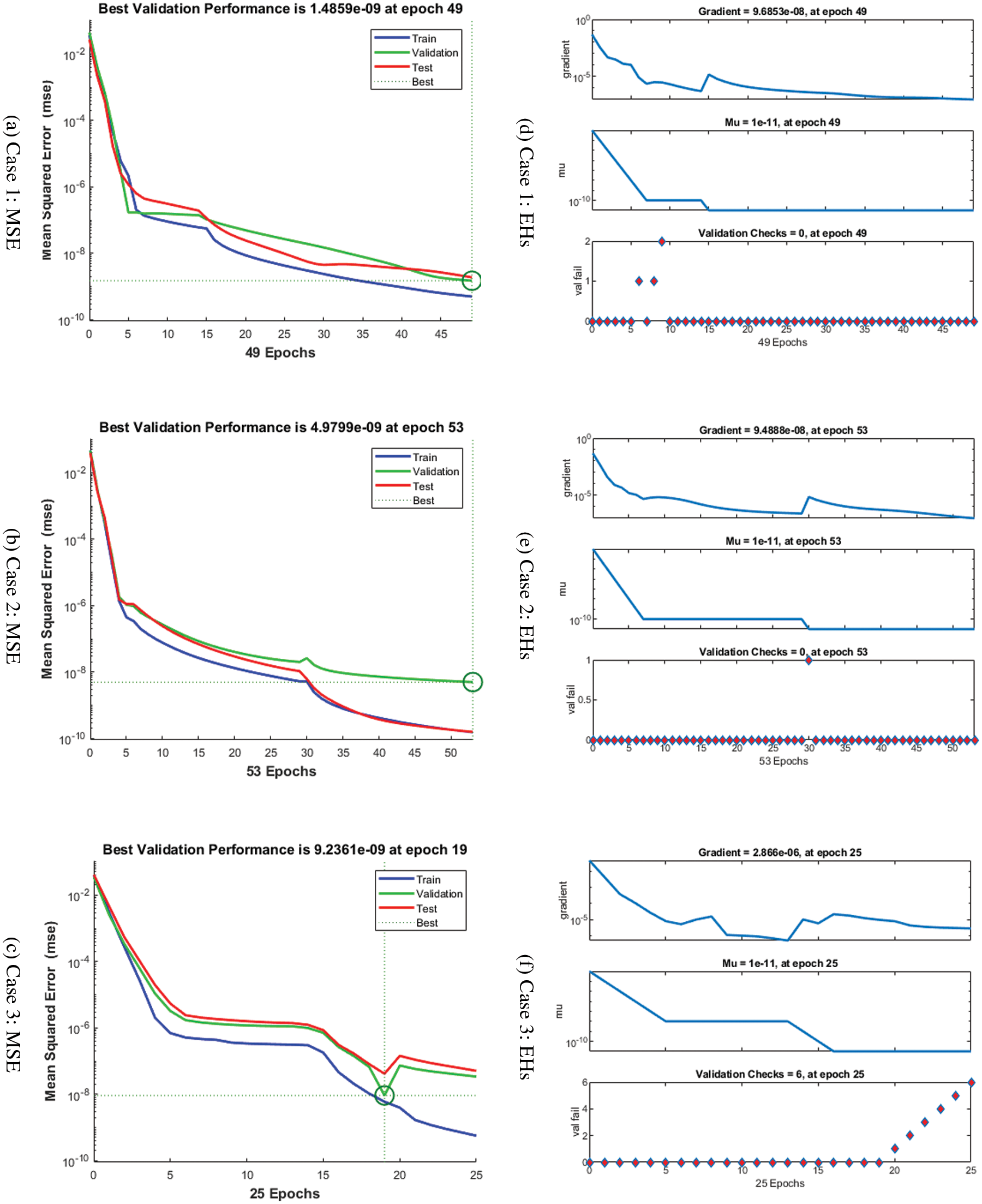
Figure 3: EHs and MSE for the fractional order mathematical rape and its control

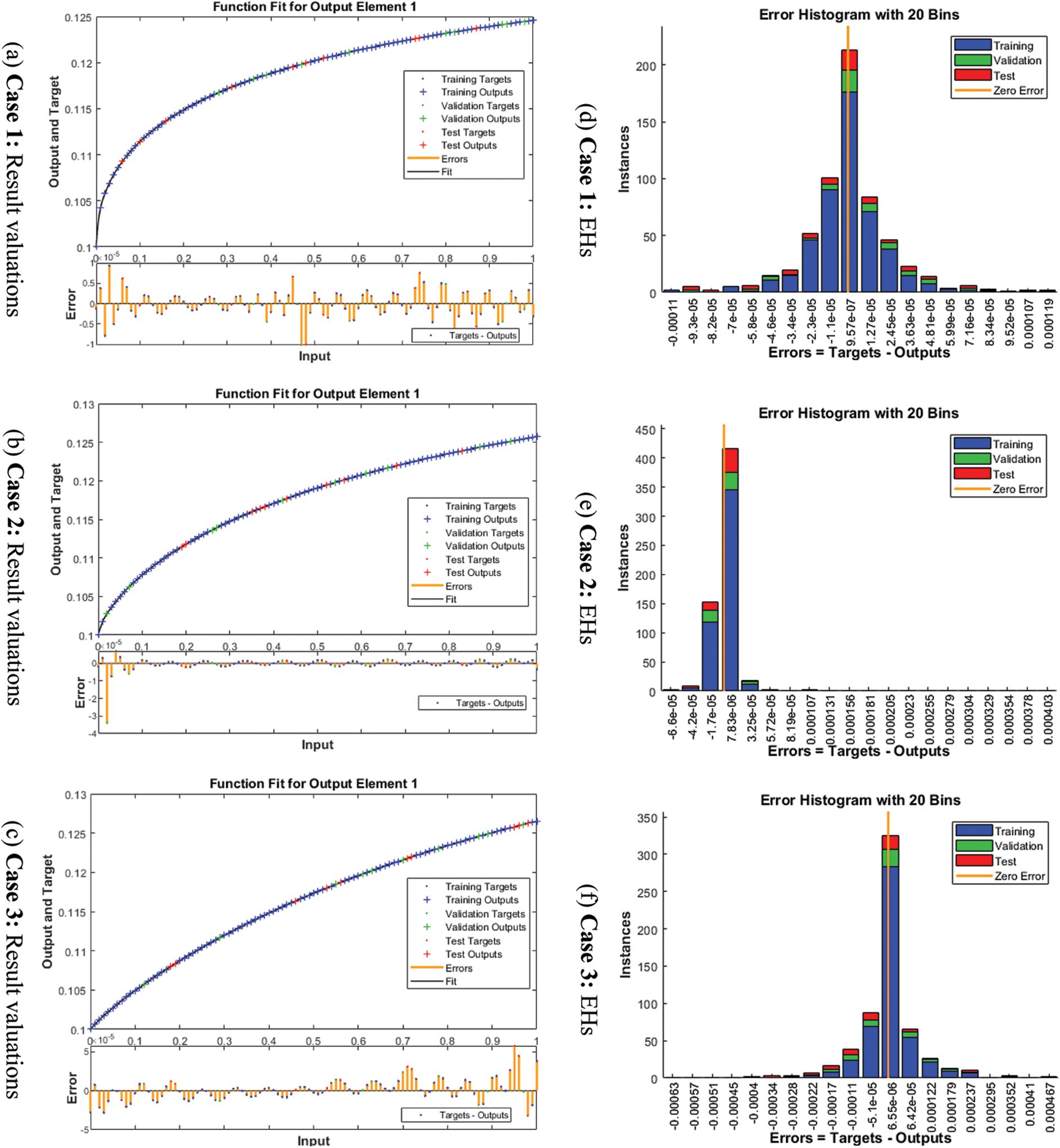
Figure 4: Valuations and EHs for the fractional order mathematical rape and its control system

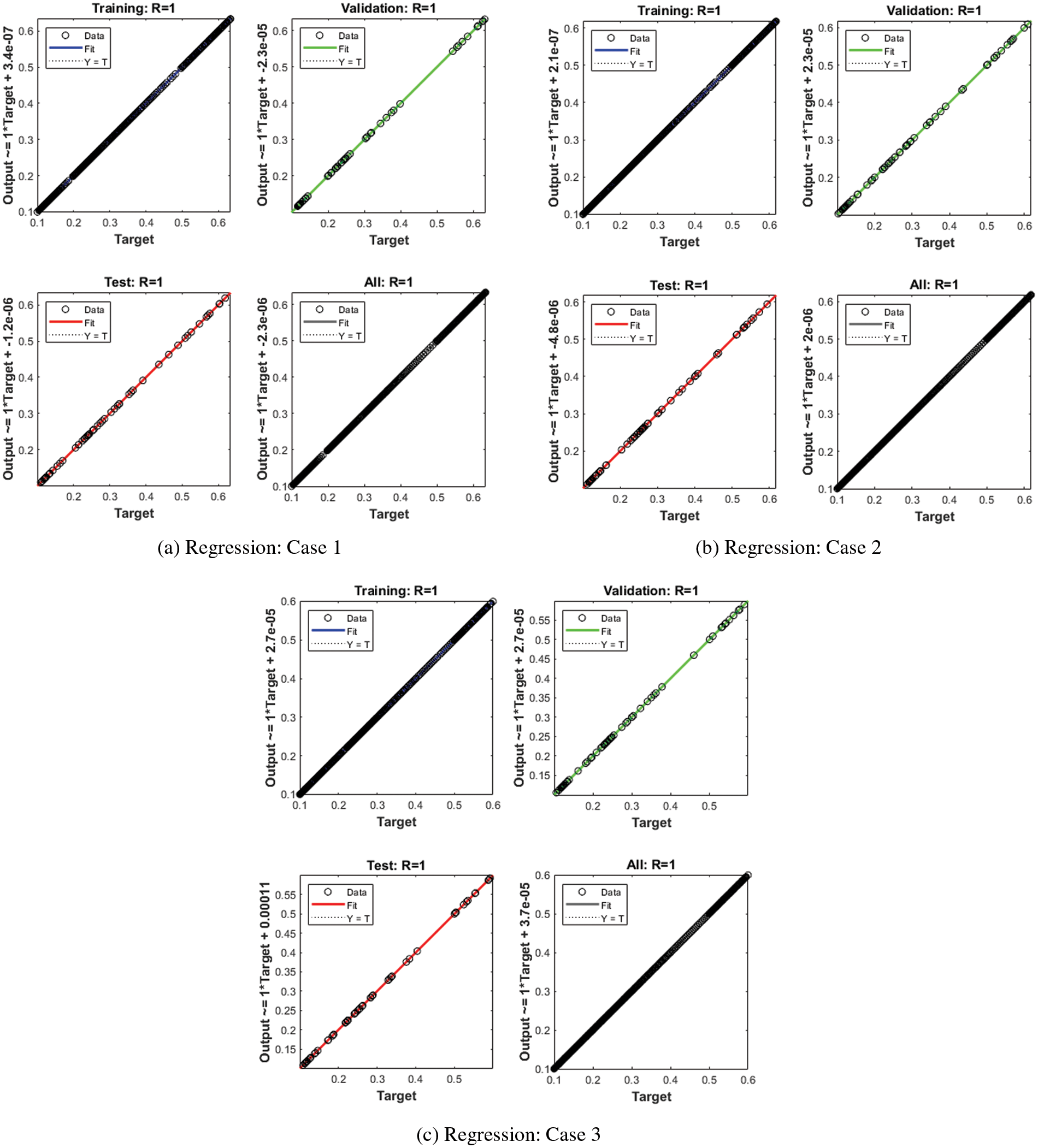
Figure 5: Regression for the fractional order mathematical rape and its control model

The result comparisons illustration along with AE have been drawn in Figs. 6–7. The numerical performances are derived to authenticate the fractional order mathematical rape and its control model using the stochastic ANNs-LMBA procedures. The obtained and reference numerical results have been plotted in Fig. 6 that shows the overlapping of the solutions. These exactly overlapping of the solution authenticates the correctness of the ANNs-LMBS for the fractional order mathematical rape and its control model. The AE for the susceptible native girls Sn(x), infected immature girls In(x), susceptible knowledgeable girls Sk(x), infected knowledgeable girls Ik(x), susceptible rapist population SR(x) and infective rapist population IR(x) for the fractional order mathematical rape and its control model are provided in Fig. 7. The susceptible native girls Sn(x) calculated as 10−06 to 10−08, 10−06 to 10−10 and 10−04 to 10−07 for 1st, 2nd and 3rd case of the fractional order mathematical rape and its control model. The infected immature girls In(x) class values are calculated as 10−04 to 10−07, 10−04 to 10−08 and 10−04 to 10−06 for 1st, 2nd and 3rd case of the fractional order mathematical rape and its control model. The susceptible knowledgeable girls Sk(x) category values are calculated as 10−05 to 10−06, 10−05 to 10−07 and 10−04 to 10−06 for 1st, 2nd and 3rd case of the fractional order mathematical rape and its control model. The infected knowledgeable girls Ik(x) category values are calculated as 10−05 to 10−06, 10−05 to 10−07 and 10−04 to 10−05 for 1st, 2nd and 3rd case of the fractional order mathematical rape and its control model. The susceptible rapist population SR(x) values are calculated as 10−04 to 10−06, 10−05 to 10−07 and 10−04 to 10−06 for 1st, 2nd and 3rd case of the fractional order mathematical rape and its control model. Likewise, the infective rapist population IR(x) values are calculated as 10−05 to 10−06, 10−05 to 10−07 and 10−04 to 10−05 for 1st, 2nd and 3rd case of the fractional order mathematical rape and its control model. These best AE indicate the precision of the ANNs-LMBA for the fractional order mathematical rape and its control model.

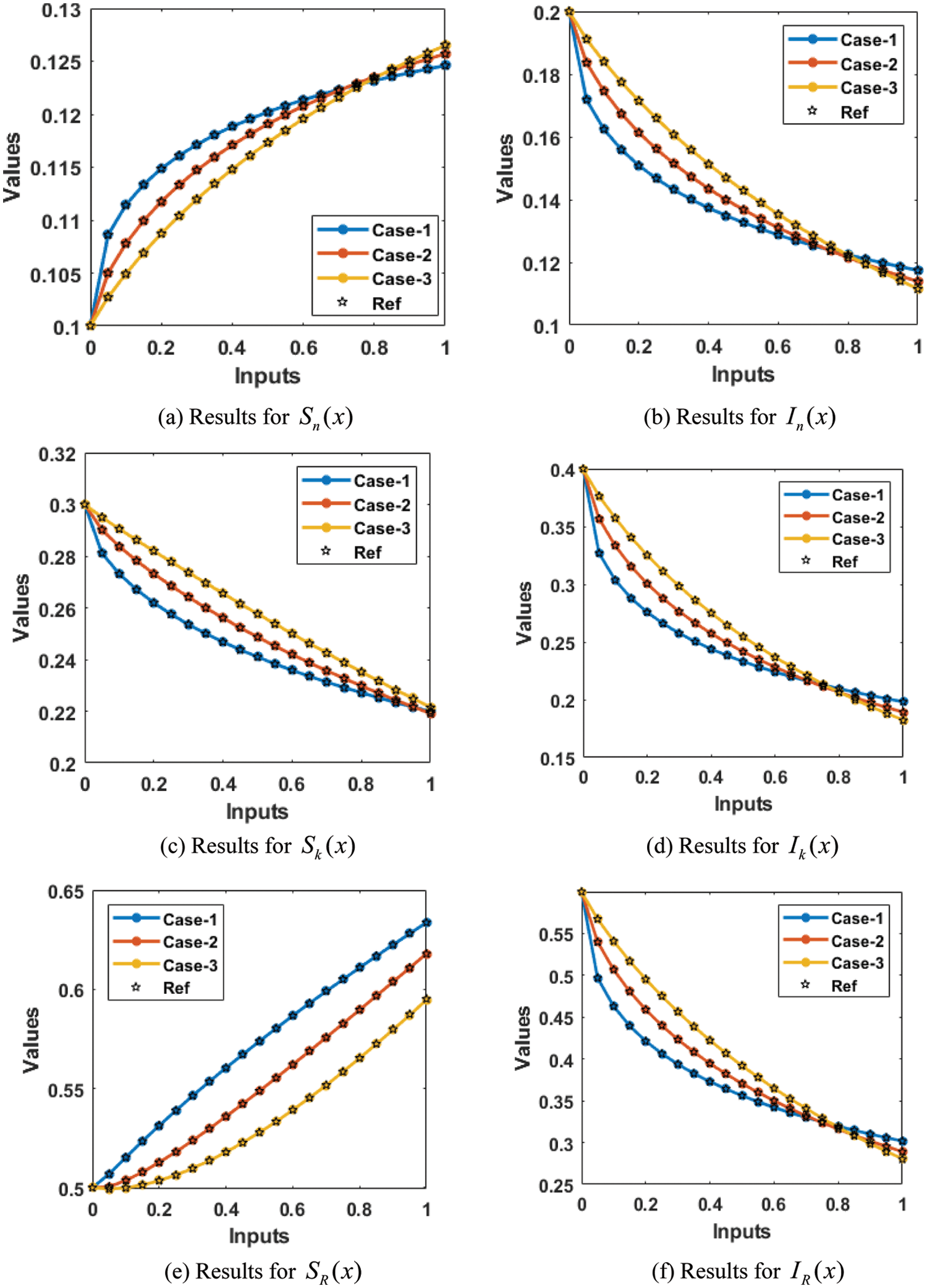
Figure 6: Result for the fractional order mathematical rape and its control model

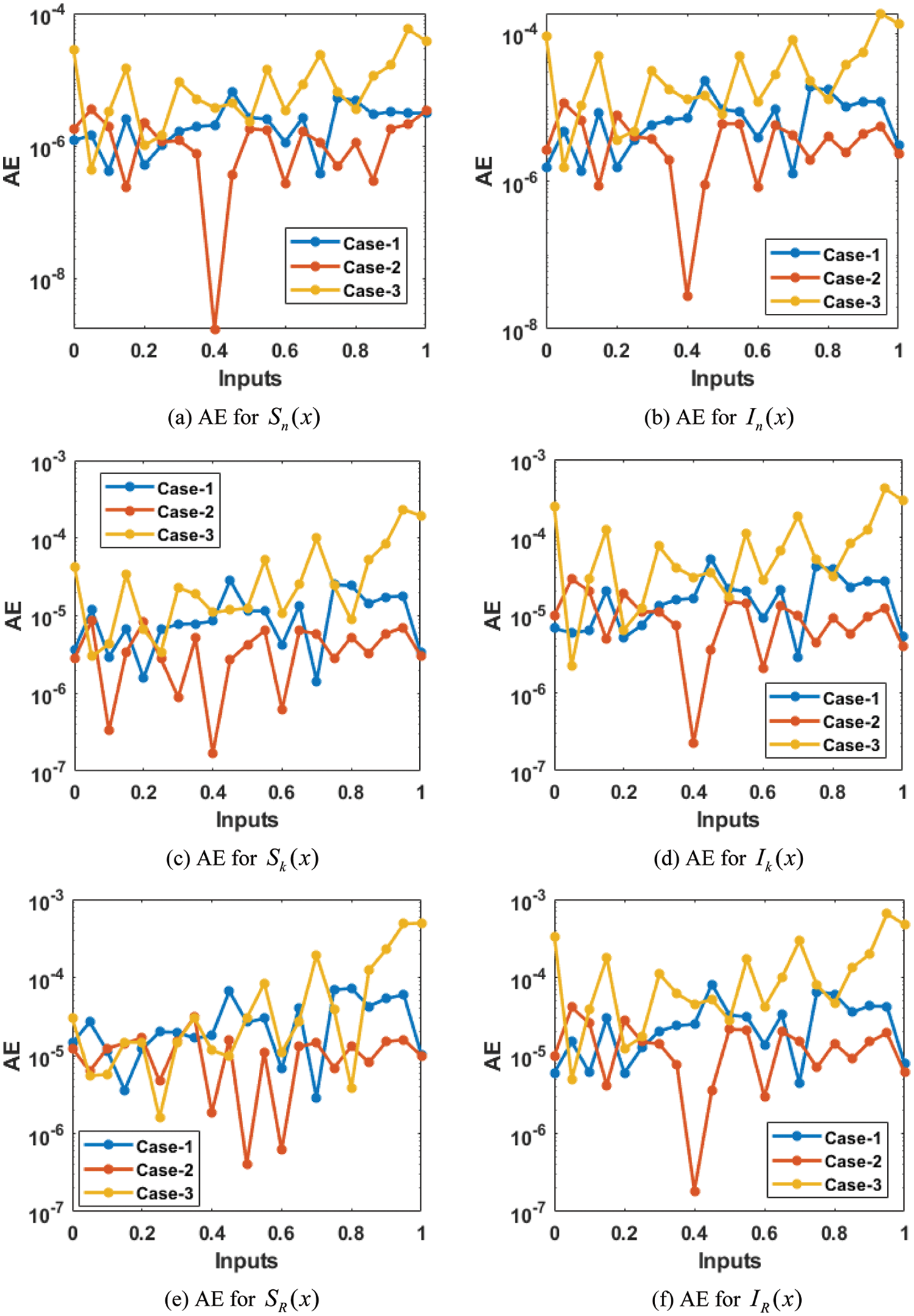
Figure 7: AE for the fractional order mathematical rape and its control model

6  Conclusion

In this study, a nonlinear fractional order mathematical rape and its control model are numerical simulated using the strength of ANNs along with the LMBA. The fractional order investigations have been provided to obtain more realistic results of the mathematical form of the rape and its control model. The fractional order mathematical rape and its control model are classified into six dynamics, susceptible native girls Sn(x), infected immature girls In(x), susceptible knowledgeable girls Sk(x), infected knowledgeable girls Ik(x), susceptible rapist population SR(x) and infective rapist population IR(x). The numerical routines for the fractional order mathematical rape and its control model have never been applied nor evaluated before through the stochastic ANNs-LMBS. Three different variants of the fractional order mathematical rape and its control model have been numerically solved to check the correctness of the proposed ANNs-LMBA. The data is used to present the rape and its control differential system is designated as 70% for training, 14% for authorization and 16% for testing. Fifteen neurons throughout the study have been used to solve the dynamical system. The dataset is proposed by the Adams-Bashforth-Moulton to check the comparison of results. The correctness is observed through the AE, which have been performed in best measures as 10−05 to 10−07 for each class of the fractional order mathematical rape and its control model. The dependability and capability of the proposed ANNs-LMBA is observed using the numerical performances through STs, MSE correlation, regression, and EHs. The precision of the ANNs-LMBA is observed via matching of results and AE values. The scheme performance is testified based on the constancy and reliability of proposed ANNs-LMBA.

Future Research Directions

In future, the designed ANNs-LMBA can be implemented to solve the fractional kind of derivatives [63–67] and sonic processes [68].

Funding Statement: This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  T. Harko, F. S. Lobo and M. Mak, “Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates,” Applied Mathematics and Computation, vol. 236, pp. 184–194, 2014. [Google Scholar]

 2.  Y. G. Sánchez, M. Umar, Z. Sabir, J. L. Guirao and M. A. Z. Raja, “Solving a class of biological HIV infection model of latently infected cells using heuristic approach,” Discrete & Continuous Dynamical Systems-S, vol. 14, no. 10, pp. 3611, 2021. [Google Scholar]

 3.  S. Sarwar and S. Iqbal, “Stability analysis, dynamical behavior and analytical solutions of nonlinear fractional differential system arising in chemical reaction,” Chinese Journal of Physics, vol. 56, no. 1, pp. 374–384, 2018. [Google Scholar]

 4.  M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, no. 2, pp. 1–9, 2020. [Google Scholar]

 5.  H. Ahmad, A. R. Seadawy, T. A. Khan and P. Thounthong, “Analytic approximate solutions for some nonlinear parabolic dynamical wave equations,” Journal of Taibah University for Science, vol. 14, no. 1, pp. 346–358, 2020. [Google Scholar]

 6.  J. Kim, K. K. Żur and J. N. Reddy, “Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates,” Composite Structures, vol. 209, no. 12, pp. 879–888, 2019. [Google Scholar]

 7.  S. Zhou, X. Zhuang and T. Rabczuk, “A phase-field modeling approach of fracture propagation in poroelastic media,” Engineering Geology, vol. 240, no. 1, pp. 189–203, 2018. [Google Scholar]

 8.  A. M. R. Elsonbaty, Z. Sabir, R. Ramaswamy and W. Adel, “Dynamical analysis of a novel discrete fractional SITRs model for COVID-19,” Fractals, vol. 29, no. 8, pp. 1–15, 2021. [Google Scholar]

 9.  F. Bourada, A. A. Bousahla, M. Bourada, A. Azzaz, A. Zinata et al., “Dynamic investigation of porous functionally graded beam using a sinusoidal shear deformation theory,” Wind and Structures, vol. 28, no. 1, pp. 19–30, 2019. [Google Scholar]

10. T. Rhodes and K. Lancaster, “Mathematical models as public troubles in COVID-19 infection control: Following the numbers,” Health Sociology Review, vol. 29, no. 2, pp. 177–194, 2020. [Google Scholar]

11. B. Ghanbari, S. Kumar and R. Kumar, “A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative,” Chaos Solitons & Fractals, vol. 133, no. 3, pp. 109619, 2020. [Google Scholar]

12. S. K. Mustafa, M. A. Ahmad, S. Sotnik, O. Zeleniy, V. Lyashenko et al., “Brief review of the mathematical models for analyzing and forecasting transmission of COVID-19,” Journal of Critical Reviews, vol. 7, no. 19, pp. 4206–4210, 2020. [Google Scholar]

13. Z. Sabir, T. Botmart, M. A. Z. Raja, R. Sadat, M. R. Ali et al., “Artificial neural network scheme to solve the nonlinear influenza disease model,” Biomedical Signal Processing and Control, vol. 75, no. 103594, pp. 1–13, 2022. [Google Scholar]

14. Z. Sabir, M. A. Z. Raja, T. Botmart and W. Weera, “A neuro-evolution heuristic using active-set techniques to solve a novel nonlinear singular prediction differential model,” Fractal and Fractional, vol. 6, no. 29, pp. 1–14, 2022. [Google Scholar]

15. R. N. Thompson, “Epidemiological models are important tools for guiding COVID-19 interventions,” BMC Medicine, vol. 18, no. 1, pp. 1–4, 2020. [Google Scholar]

16. G. B. Libotte, F. S. Lobato, G. M. Platt and A. J. S. Neto, “Determination of an optimal control strategy for vaccine administration in COVID-19 pandemic treatment,” Computer Methods and Programs in Biomedicine, vol. 196, no. 1, pp. 1–13, 2020. [Google Scholar]

17. I. Z. Sadiq, F. S. Abubakar and B. I. Dan-Iya, “Role of nanoparticles in tackling COVID-19 pandemic: A bio-nanomedical approach,” Journal of Taibah University for Science, vol. 15, no. 1, pp. 198–207, 2021. [Google Scholar]

18. A. B. Gumel, E. A. Iboi, C. N. Ngonghala and E. H. Elbasha, “A primer on using mathematics to understand COVID-19 dynamics: Modeling, analysis and simulations,” Infectious Disease Modelling, vol. 6, no. 5, pp. 148–168, 2021. [Google Scholar]

19. F. Ortenzi, E. Albanese and M. Fadda, “A transdisciplinary analysis of COVID-19 in Italy: The most affected country in Europe,” International Journal of Environmental Research and Public Health, vol. 17, no. 24, pp. 1–12, 2020. [Google Scholar]

20. P. Junswang, Z. Sabir, M. A. Z. Raja, S. Salahshour, T. Botmart et al., “An advanced stochastic numerical approach for host-vector-predator nonlinear model,” Computers, Materials and Continua, vol. 72, no. 3, pp. 5823–5843, 2022. [Google Scholar]

21. Z. Sabir, M. Umar, M. A. Z. Raja and D. U. M. I. T. R. U. Baleanu, “Applications of Gudermannian neural network for solving the SITR fractal system,” Fractals-an Interdisciplinary Journal on the Complex Geometry of Nature, vol. 28, no. 8, pp. 2150250, 2021. [Google Scholar]

22. S. Moore, E. M. Hill, M. J. Tildesley, L. Dyson and M. J. Keeling, “Vaccination and non-pharmaceutical interventions for COVID-19: A mathematical modelling study,” The Lancet Infectious Diseases, vol. 21, no. 6, pp. 793–802, 2021. [Google Scholar]

23. Y. Umar, “Theoretical studies of the rotational and tautomeric states, electronic and spectroscopic properties of favipiravir and its structural analogues: A potential drug for the treatment of COVID-19,” Journal of Taibah University for Science, vol. 14, no. 1, pp. 1613–1625, 2020. [Google Scholar]

24. A. J. I. D. M. Anirudh, “Mathematical modeling and the transmission dynamics in predicting the COVID-19-What next in combating the pandemic,” Infectious Disease Modelling, vol. 5, no. 3, pp. 366–374, 2020. [Google Scholar]

25. X. Chen, A. Zhang, H. Wang, A. Gallaher and X. Zhu, “Compliance and containment in social distancing: mathematical modeling of COVID-19 across townships,” International Journal of Geographical Information Science, vol. 35, no. 3, pp. 446–465, 2021. [Google Scholar]

26. Z. Zhang, A. Zeb, S. Hussain and E. Alzahrani, “Dynamics of COVID-19 mathematical model with stochastic perturbation,” Advances in Difference Equations, vol. 2020, no. 1, pp. 1–12, 2020. [Google Scholar]

27. M. Soumia, Z. Hanane, M. Benaissa, F. Z. Younes, A. Chakib et al., “Towards potential inhibitors of COVID-19 main protease Mpro by virtual screening and molecular docking study,” Journal of Taibah University for Science, vol. 14, no. 1, pp. 1626–1636, 2020. [Google Scholar]

28. A. A. Berryman, “The orgins and evolution of predator-prey theory,” Ecology, vol. 73, no. 5, pp. 1530–1535, 1992. [Google Scholar]

29. A. S. Bhadauria, R. Pathak and M. Chaudhary, “A SIQ mathematical model on COVID-19 investigating the lockdown effect,” Infectious Disease Modelling, vol. 6, no. 6, pp. 244–257, 2021. [Google Scholar]

30. I. A. Baba, A. Yusuf and M. Al-Shomrani, “A mathematical model for studying rape and its possible mode of control,” Results in Physics, vol. 22, no. 2, pp. 1–13, 2021. [Google Scholar]

31. D. Zhang, J. Hu, F. Li, X. Ding, A. K. Sangaiah et al., “Small object detection via precise region-based fully convolutional networks,” Computers, Materials and Continua, vol. 69, no. 2, pp. 1503–1517, 2021. [Google Scholar]

32. J. Wang, Y. Wu, S. He, P. K. Sharma, X. Yu et al., “Lightweight single image super-resolution convolution neural network in portable device,” KSII Transactions on Internet and Information Systems (TIIS), vol. 15, no. 11, pp. 4065–4083, 2021. [Google Scholar]

33. J. Wang, Y. Zou, P. Lei, R. S. Sherratt and L. Wang, “Research on recurrent neural network based crack opening prediction of concrete dam,” Journal of Internet Technology, vol. 21, no. 4, pp. 1161–1169, 2020. [Google Scholar]

34. J. Zhang, J. Sun, J. Wang and X. G. Yue, “Visual object tracking based on residual network and cascaded correlation filters,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 8, pp. 8427–8440, 2021. [Google Scholar]

35. Z. Sabir, M. A. Z. Raja, A. S. Alnahdi, M. B. Jeelani and M. A. Abdelkawy, “Numerical investigations of the nonlinear smoke model using the Gudermannian neural networks,” Mathematical Biosciences and Engineering, vol. 19, no. 1, pp. 351–370, 2022. [Google Scholar]

36. S. He, Z. Li, Y. Tang, Z. Liao, F. Li et al., “Parameters compressing in deep learning,” Computers, Materials & Continua, vol. 62, no. 1, pp. 321–336, 2020. [Google Scholar]

37. S. R. Zhou and B. Tan, “Electrocardiogram soft computing using hybrid deep learning CNN-ELM,” Applied Soft Computing, vol. 86, no. 4, pp. 1–11, 2020. [Google Scholar]

38. Z. Sabir, H. A. Wahab, S. Javeed and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 1–14, 2021. [Google Scholar]

39. S. R. Zhou, M. L. Ke and P. Luo, “Multi-camera transfer GAN for person re-identification,” Journal of Visual Communication and Image Representation, vol. 59, no. 1, pp. 393–400, 2019. [Google Scholar]

40. W. Wang, H. Liu, J. Li, H. Nie and X. Wang, “Using CFW-net deep learning models for X-ray images to detect COVID-19 patients,” International Journal of Computational Intelligence Systems, vol. 14, no. 1, pp. 199–207, 2021. [Google Scholar]

41. Z. Sabir, K. Nisar, M. A. Z. Raja, A. A. B. A. Ibrahim, J. J. P. C. Rodrigues et al., “Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations,” Alexandria Engineering Journal, vol. 60, no. 6, pp. 5935–5947, 2021. [Google Scholar]

42. W. Wang, Y. Jiang, Y. Luo, J. Li, X. Wang et al., “An advanced deep residual dense network (DRDN) approach for image super-resolution,” International Journal of Computational Intelligence Systems, vol. 12, no. 2, pp. 1592–1601, 2019. [Google Scholar]

43. W. Wang, Y. Yang, J. Li, Y. Hu, Y. Luo et al., “Woodland labeling in Chenzhou, China, via deep learning approach,” International Journal of Computational Intelligence Systems, vol. 13, no. 1, pp. 1393–1403, 2020. [Google Scholar]

44. Z. Sabir, J. L. Guirao and T. Saeed, “Solving a novel designed second order nonlinear Lane-Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, no. 3, pp. 1–12, 2021. [Google Scholar]

45. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Meyer wavelet neural networks to solve a novel design of fractional order pantograph Lane-Emden differential model,” Chaos, Solitons & Fractals, vol. 152, no. 2, pp. 1–14, 2021. [Google Scholar]

46. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. F. Aguilar, “FMNEICS: Fractional Meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane-Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]

47. Z. Sabir, M. A. Z. Raja, M. Umar, M. Shoaib and D. Baleanu, “FMNSICS: Fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane-Emden systems,” Neural Computing and Applications, vol. 34, no. 6, pp. 4193–4206, 2022. [Google Scholar]

48. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A novel design of fractional Meyer wavelet neural networks with application to the nonlinear singular fractional Lane-Emden systems,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2641–2659, 2021. [Google Scholar]

49. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems,” Frontiers in Physics, vol. 8, pp. 1–12, 2020. [Google Scholar]

50. S. Luemsai and T. Botmart, “Improved extended dissipativity results for T-S fuzzy generalized neural networks with mixed interval time-varying delays,” IEEE Access, vol. 10, pp. 2480–2496, 2022. [Google Scholar]

51. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, no. 6803, pp. 1–13, 2021. [Google Scholar]

52. Z. Sabir, M. Umar, M. A. Z. Raja, H. M. Baskonus and W. Gao, “Designing of Morlet wavelet as a neural network for a novel prevention category in the HIV system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250012, 2022. [Google Scholar]

53. B. Ghanbari and S. Djilali, “Mathematical analysis of a fractional-order predator-prey model with prey social behavior and infection developed in predator population,” Chaos, Solitons & Fractals, vol. 138, no. 4, pp. 1–13, 2020. [Google Scholar]

54. B. Ghanbari and S. Djilali, “Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative,” Mathematical Methods in the Applied sciences, vol. 43, no. 4, pp. 1736–1752, 2020. [Google Scholar]

55. Z. U. A. Zafar, H. Rezazadeh, M. Inc, K. S. Nisar, T. A. Sulaiman et al., “Fractional order heroin epidemic dynamics,” Alexandria Engineering Journal, vol. 60, no. 6, pp. 5157–5165, 2021. [Google Scholar]

56. Z. Sabir, T. Botmart, M. A. Z. Raja and W. Weera, “An advanced computing scheme for the numerical investigations of an infection-based fractional-order nonlinear prey-predator system,” PlOS ONE, vol. 17, no. 3, pp. 1–13, 2022. [Google Scholar]

57. Z. Sabir, M. A. Z. Raja, T. G. Nguyen, I. Fathurrochman, R. Sadat et al., “Applications of neural networks for the novel designed of nonlinear fractional seventh order singular system,” The European Physical Journal Special Topics, vol. 9, no. 6, pp. 1–15, 2022. [Google Scholar]

58. A. N. Akkilic, Z. Sabir, M. A. Z. Raja and H. Bulut, “Numerical treatment on the new fractional-order SIDARTHE COVID-19 pandemic differential model via neural networks,” The European Physical Journal Plus, vol. 137, no. 3, pp. 1–14, 2022. [Google Scholar]

59. T. Botmart, Z. Sabir, M. A. Z. Raja, W. Weera, R. Sadat et al., “A numerical study of the fractional order dynamical nonlinear susceptible infected and quarantine differential model using the stochastic numerical approach,” Fractal and Fractional, vol. 6, no. 3, pp. 1–13, 2022. [Google Scholar]

60. Z. Sabir, M. Munawar, M. A. Abdelkawy, M. A. Z. Raja, C. Ünlü et al., “Numerical investigations of the fractional-order mathematical model underlying immune-chemotherapeutic treatment for breast cancer using the neural networks,” Fractal and Fractional, vol. 6, no. 4, pp. 1–16, 2022. [Google Scholar]

61. G. L. Guirao, Z. Sabir, M. A. Z. Raja and D. Baleanu, “Design of neuro-swarming computational solver for the fractional Bagley-Torvik mathematical model,” The European Physical Journal Plus, vol. 137, no. 2, pp. 1–15, 2022. [Google Scholar]

62. Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “Solving an infectious disease model considering its anatomical variables with stochastic numerical procedures,” Journal of Healthcare Engineering, vol. 2022, no. 8, pp. 1–12, 2022. [Google Scholar]

63. A. O. Akdemir, E. Deniz and E. Yüksel, “On some integral inequalities via conformable fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 489–498, 2021. [Google Scholar]

64. M. Gürbüz and Ç. Yıldız, “Some new inequalities for convex functions via Riemann-Liouville fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 537–544, 2021. [Google Scholar]

65. W. Gao, P. Veeresha, D. G. Prakasha and H. M. Baskonus, “New numerical simulation for fractional Benney-Lin equation arising in falling film problems using two novel techniques,” Numerical Methods for Partial Differential Equations, vol. 37, no. 1, pp. 210–243, 2021. [Google Scholar]

66. E. İlhan and İ.O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]

67. A. Yokuş and S. Gülbahar, “Numerical solutions with linearization techniques of the fractional Harry Dym equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 35–42, 2019. [Google Scholar]

68. M. T. Gençoğlu and P. Agarwal, “Use of quantum differential equations in sonic processes,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 21–28, 2021. [Google Scholar]