Multi Criteria Decision Making for Evaluation and Ranking of Cancer Information

1  Introduction

Cancer is a class of diseases portrayed by erratic cell growth and the ability to infect and disperse several other tissues and organs. Electronic medical records (EMRs) have been adopted into healthcare communities to help with decision-making and to make finding medical solutions easier. Cancer treatment is also not well-served by Indian health services, which lack the required facilities and skills. Tobacco use is associated with a high rate of mortality and morbidity. Considering national priorities, cancer research has focused on etiology, including the detection of preventable risk factors, understanding the function of cancer progression, and operational research to reduce tobacco usage and common cancers using current infrastructures. Clinical, epidemiological, and basic science research, including advanced molecular techniques, were all part of the multidisciplinary study. Cancer registries aided in determining the extent and patterns of cancer incidence, as well as planning prevention and control activities. The programs of the task force listed above aided in addressing national goals. Supporting projects submitted by individual scientists, which covered virtually all specialties related to cancer and various locations in the body, were also given high priority.

1.1 Literature Review

Numerous studies have been conducted on the accuracy of online health-related information [1–3]. Most of this research suggested assessment criteria and frameworks for assessing the quality of knowledge [4–7]. The rate of increase in cancer patients can be determined by using some Multi-criteria decision-making (MCDM) technique [8–10]. Many applications of TOPSIS in medical and engineering are implemented by researchers [11–13]. In recent years, MCDM has become one of the extensively utilized methods for decision-making [14–17]. In [18] author presents the MCDM methodology for the supplier selection problem. Evaluation of cost-based supplier performance has been proposed by Monezka et al. [19]. Choi et al. [20] offered to manufacture delivery performance for supply chain management by MCDM. The Fuzzy theory is also widely utilized in decision-making approaches [21–24]. The idea of the Fuzzy set was initialized by Zadeh [25] in 1986. Afterward, the concept of Fuzzy MCDM was first suggested by Bellman et al. [26] in 1987. In Ref. [27] authors presented Fuzzy MCDM techniques. Wang [28] utilized Fuzzy MCDM in the supplier selection. Chu [29] offered the application of Fuzzy TOPSIS in selecting plant location. The authors in Ref. [30] suggested a different decision-making system depending on the interval-valued Fuzzy soft Matrix. Chen [31] described inclusion-based Fuzzy TOPSIS for MCDM. In Ref. [32] authors suggested a Fuzzy TOPSIS extension for decision-making problems. The authors in Ref. [33] offered a Fuzzy-MOORA technique for the selection of ERP systems. K. In Ref. [34] authors perform architect selection by using the integrated Fuzzy MCDM model. Lee [35] suggested a two-phase Fuzzy technique for evaluating service policies in a logistic approach.

1.2 Research Contribution

There exist numerous purposes of Fuzzy TOPSIS in literature for decision-making problems [33–36]. The main contributions of this research are:

1.    To assess the quality of online various cancer information in India using an MCDM technique in a fuzzy context, namely triangular fuzzy TOPSIS.

2.    The cancer data is accumulated from the Indian Council of Medical Research (ICMR) [9].

3.    The fuzzy triangular TOPSIS is applied to lungs, stomach, breast, oral, and melanoma cancer data for the year 2010 to 2015.

4.    To select the best possible selection of optimum causes of cancer based on a given data set by using expert scores.

5.    Since the experts’ options are not based on the binary operation which is based on possibly two options. The utilization of fuzzy set ideas widens opinion criteria for experts other than binary selection.

The remaining data is designed as follows: Section 2 offers some elementary preliminaries; Collected cancer data from ICMR is listed in Section 3; Fuzzy TOPSIS scheme is described in Section 4; In Section 5 we have implemented Fuzzy TOPSIS in the ranking of cancer data; Finally, the conclusion is drawn.

2  Some Basic Preliminaries

This section presents some basic theories associated with the Fuzzy set theory, which are the key components for understanding the Fuzzy TOPSIS.

2.1 Fuzzy Set

A Fuzzy set F∼ over a universal set U in which each element of universal is mapped to the set of real numbers in [0,1] by a membership function ηF∼(u). Mathematically, it can be denoted by:

ηF∼(u):u→[0,1].(1)

2.2 Fuzzy Triangular Number

The Fuzzy triangular number can be symbolized by the triplet F∼=(f1,f2,f3). The representation of triangular Fuzzy numbers is inferred as membership functions that satisfy the subsequent requirements in Fig. 1:

1.    f1 to f2 is increasing function.

2.    f2 to f3 is decreasing function.

3.    f1≤f2≤f3.

Figure 1: Triangular fuzzy number F∼=(f1,f2,f3)

The Fuzzy membership function is defined by:

ηF∼(u)={0foru<f1,u−f1f2−f1forf1≤u≤f2,f3−uf3−f2forf2≤u≤f3,0foru>f3.(2)

2.3 Equivalent Fuzzy Numbers

Consider F∼=(f1,f2,f3) and G∼=(g1,g2,g3) be two Fuzzy triangular numbers, these numbers are said to be equivalent if and only if f1=g1, f2=g2 and f3=g3.

2.4 Positive and Negative Fuzzy Numbers

A Fuzzy triangular number F∼=(f1,f2,f3) is said to be positive if all fi>0 for 1≤i≤3, and negative is all fi<0 for 1≤i≤3.

2.5 Operation of Fuzzy Numbers [11]

Consider F∼=(f1,f2,f3) and G∼=(g1,g2,g3) be two Fuzzy triangular numbers, the following four operations can be performed by:

a)   Addition: F∼+G∼=(f1+g1,f2+g2,f3+g3).

b)   Subtraction: F∼−G∼=(f1−g1,f2−g2,f3−g3).

c)   Multiplication: F∼×G∼=(min(f1g1,f1g3,f3g1,f3g3),f2g2,max(f1g1,f1g3,f3g1,f3g3)).

d)   Division: F∼/G∼=(min(f1/g1,f1/g3,f3/g1,f3/g3),f2/g2,max(f1/g1,f1/g3,f3/g1,f3/g3)).

3  Collected Cancer Data From ICMR

Cancer is a disease of inheritable factors. The smallest part of DNA is named genes which are the genius molecules of the cell gene that produce a protein that works as an alternative to the workhorse of cells. Through the existing health infrastructure in different countries, an operation is proposed to control the cancer disease in multidisciplinary approaches [9]. In this segment, we have shown cancer data from India from the year 2010 to 2015 collected from the Indian Council of Medical Research (ICMR) [9]. The number of patients with lung, stomach, breast, oral, and melanoma cancer from the years 2010 to 2015 is demonstrated in Tab. 1.

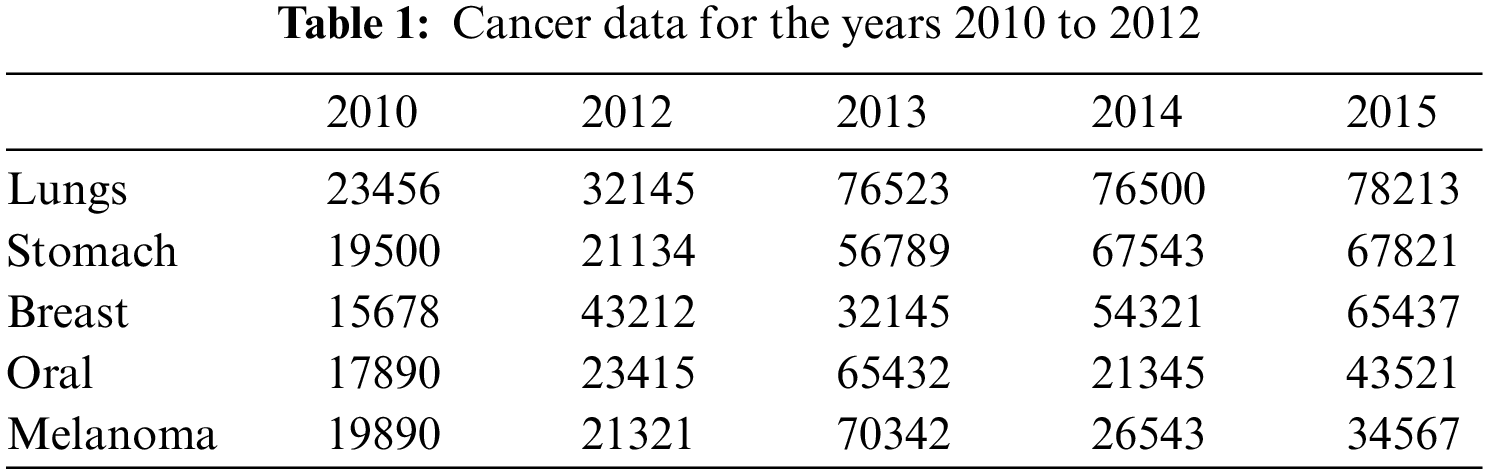
The bar chart illustration of cancer data for the years 2010 to 2012 is depicted in Fig. 2.

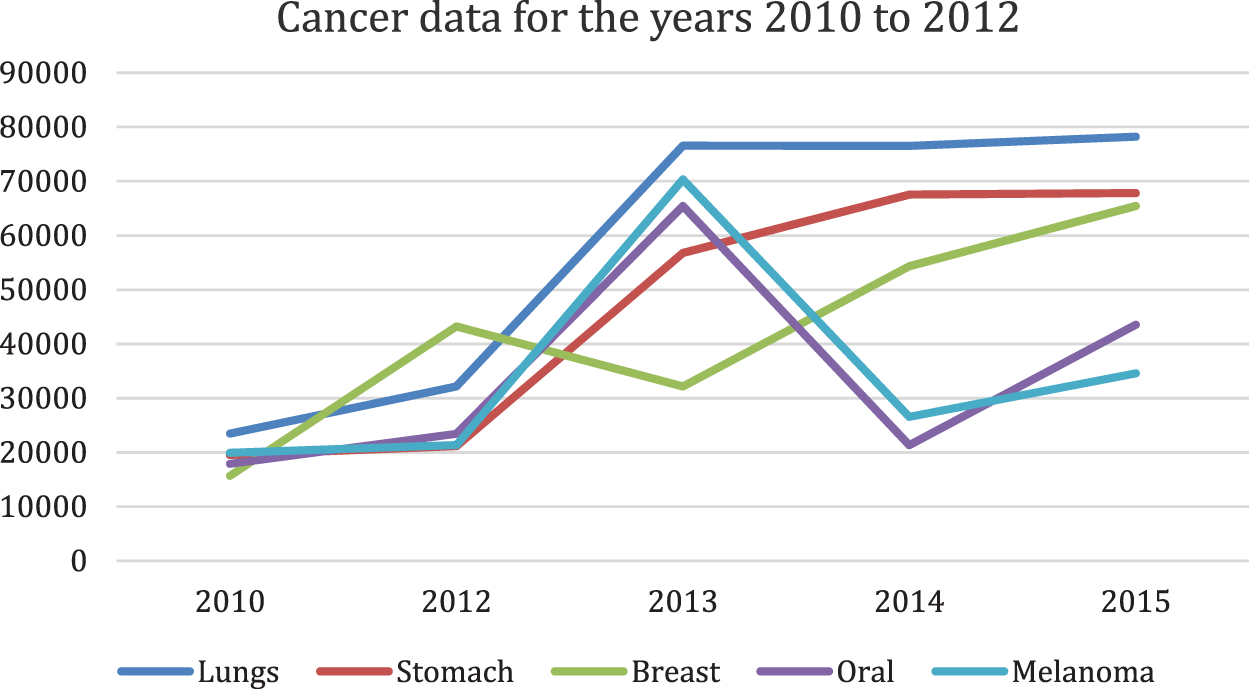
Figure 2: Bar chart representation of cancer data

4  Fuzzy TOPSIS Approach

TOPSIS was initially familiarized by Hwang et al. in 1981 [10]. This technique ranks all the possible choices created on the measurement of similarities to the ideal results. The objective of this technique is to determine the top possible option which has the nearest distance from the ideal result. In this segment, we have presented the mathematical structure of the TOPSIS method by using Fuzzy triangular sets.

TOPSIS Method by Fuzzy Triangular Sets

The TOPSIS method by using the Fuzzy triangular sets is defined by the subsequent steps:

Step 1: The first step is to describe the set of alternatives A, parameters P, and decision-makers DM by

A={A1,A2,…,Aa},(3)

P={P1,P2,…,Pb},(4)

DM={DM1,DM2,…,DMk}.(5)

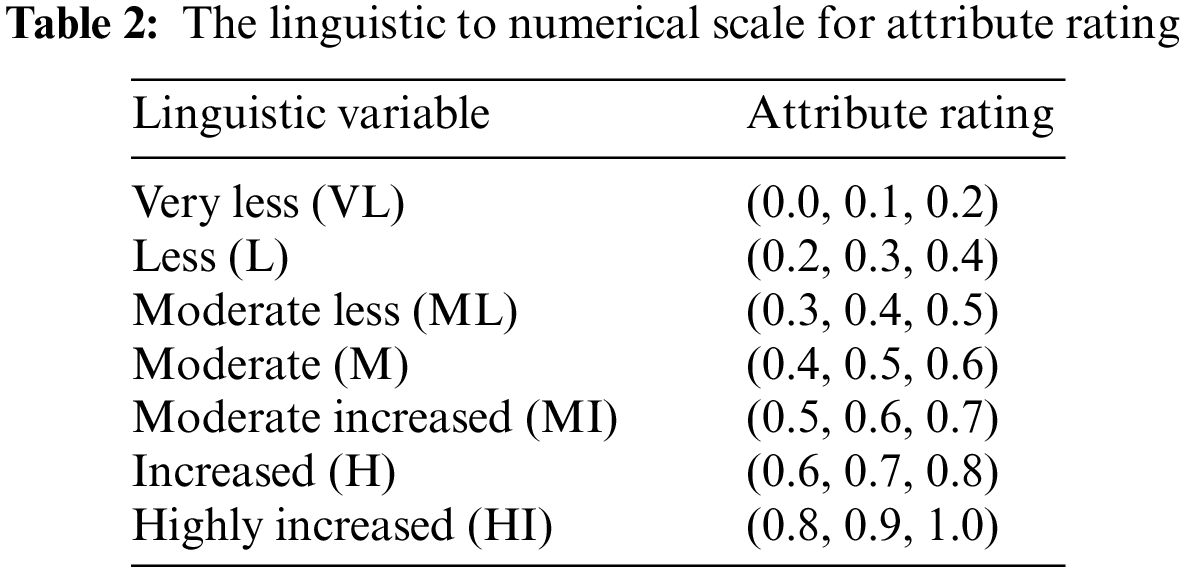
Step 2: The second step is the construction of triangular Fuzzy linguistics to a numeric scale. We have constructed a linguistic to numeric scale for the ratings of the attributes which is depicted in Tab. 2. The rating is assigned corresponding to the decision-makers. Suppose the number of decision-makers is K, then the rating attribute can be determined by

AabK=1K[Aab1+Aab2+…+AabK],(6)

AabK denotes the rating of a attributes according to the b parameters and K decision-makers.

Step 3: Now the triangular Fuzzy decision matrix (TFDM) is constructed centered on the attribute rating obtained in the previous step as follows:

TFDM=[A11A12⋯A1bA21A22⋯A2b⋮⋮⋱⋮Aa1Aa2⋯Aab],(7)

where Aab denotes the attribute, rating determined in the previous step.

Step 4: Next step is assigning weight to each alternative. The sample weight assigning is defined in Tab. 3.

Step 5: The subsequent step is the multiplication of weight vectors with the TFDM and the attained matrix can be written as:

Weighted_TFDM=Bab=[B11B12⋯B1bB21B22⋯B2b⋮⋮⋱⋮Ba1Ba2⋯Bab],(8)

where Bab=Aab×ψa.

Step 6: Positive ideal result B+ and the negative ideal result B− are selected from the weighted TFDM by getting the maximum and minimum fuzzy triangular numbers from each column, respectively.

Bb+=[max(B11,B21,…,Ba1),…,max(B1b,B2b,…,Bab)],(9)

Bb−=[min(B11,B21,…,Ba1),…,min(B1b,B2b,…,Bab)].(10)

Step 7: The distance between the ideal positive result and the ideal negative result with all other elements of the WTFDM is computed by utilizing the vertex technique. The distance between two Fuzzy triangular numbers f=(f1,f2,f3) and g=(g1,g2,g3) can be determined by:

d(f,g)=(f1−g1)2+(f2−g2)2+(f3−g3)23(11)

The positive and negative distance is summed up to get d+ and d− by:

db+=∑bd(Bab,Bb+),(12)

db−=∑bd(Bab,Bb−).(13)

Step 8: The closeness coefficients CCb can be obtained by using db+ and db− in the mathematical expression:

CCb=db−db++db−,(14)

Step 9: The last step is ranking the alternatives by the assessments of closeness coefficients. The largest assessment of the closeness coefficient ranks as the best alternative of the preference order and the smallest value is ranked as the worst alternative.

5  Application of Fuzzy TOPSIS in the Cancer Data Ranking

In this segment, we have implemented triangular Fuzzy TOPSIS in the ranking of cancer data. All possible alternatives to the problem are various cancer diseases and the year of each disease act as the parameter of the problem. The measures of Fuzzy TOPSIS in cancer ranking are defined by:

Step 1: The first step is defining the problem. Cancer of lungs, stomach, breast, oral, and melanoma are named as C1, C2, C3, C4, and C5 for Fuzzy TOPSIS method. The years 2010, 2012, 2013, 2014, and 2015 are named as Y1, Y2, Y3, Y4, and Y5. The input data of the Fuzzy TOPSIS structure is displayed in Tab. 4.

Step 2: The next step is the formation of a team of four decision-makers which are considered here as teams of four medical experts to analyze the situation of increase in cancer data. The linguistic terms are assigned to each cancer data and converted into numeric data by using the Fuzzy scale defined in Tab. 2. The average Fuzzy attribute ratings are calculated by using Eq. (6) with the number of decision-makers K is taken as four and the outcomes are depicted in Tab. 5.

Step 3: The average rating of alternatives concerning the decision of each medical expert team results in the form of a triangular Fuzzy decision matrix (TFDM) and is stated in Tab. 6.

Step 4: The next step is the construction of weight vectors according to the Fuzzy scale illustrated in Tab. 3. The weights are assigned according to the rate of patient increase in each cancer disease. The weight assigned to each disease is defined in Tab. 7.

Step 5: The next step is the multiplication of a triangular Fuzzy decision matrix with Fuzzy weight vectors assigned against each alternative as shown in Eq. (8). The attained weighted triangular Fuzzy decision matrix (WTFDM) is listed in Tab. 8.

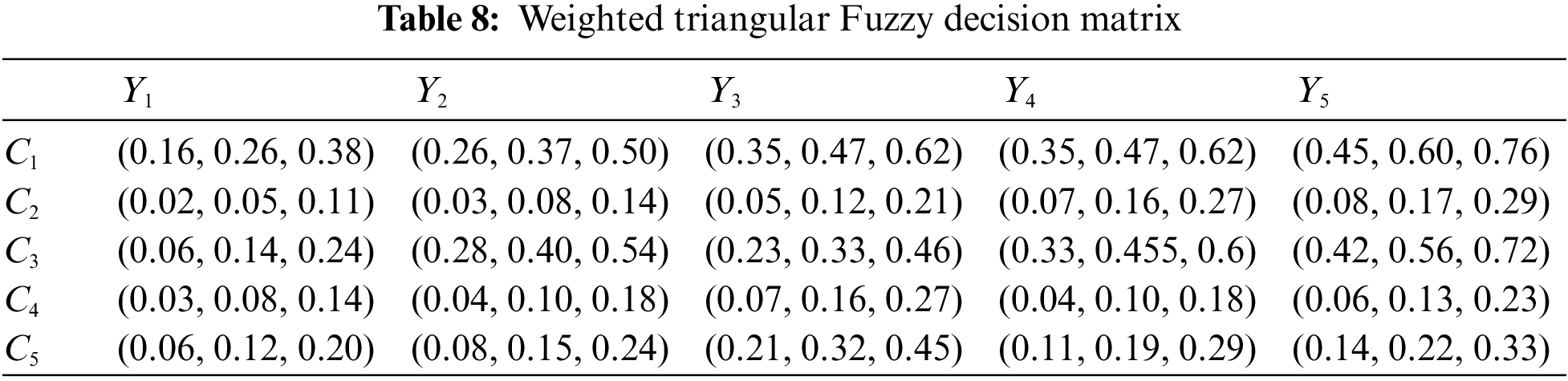
Step 6: The ideal positive results and ideal negative results are obtained from the weighted triangular Fuzzy decision matrix (WTFDM) and outcomes are exhibited in Eqs. (15) and (16).

Bb+=[(0.16,0.26,0.38),(0.28,0.40,0.54),(0.35,0.47,0.62),(0.35,0.47,0.62),(0.45,0.60,0.76)](15)

Bb−=[(0.02,0.05,0.11),(0.03,0.08,0.14),(0.05,0.12,0.21),(0.04,0.10,0.18),(0.06,0.13,0.23)](16)

Step 7: The distance of positive ideal results from all possible alternatives is determined by using Eqs. (11) and (12). The obtained positive distance is demonstrated in Tab. 9.

The distance between the negative ideal solution and all the. possible alternatives are computed by using Eqs. (11) and (13). The attained negative distance is listed in Tab. 10.

Step 8: The next step is the estimation of the closeness coefficient (CC) by using the positive and negative solutions as depicted in Eq. (14). The calculated results are presented in Tab. 11.

Step 9: The last step is the ranking of alternatives by the values of the closeness coefficient. The largest assessment of the closeness coefficient increases the ranking values as the best option and vice versa. In this data on Cancer, the disease C1 is ranked as the highly increasing disease, which is the lungs, Cancer. Tab. 11 shows the results of raking by using triangular Fuzzy TOPSIS.

The bar chart illustration of the relative closeness of each solution with ideal results for all possible diseases is depicted in Fig. 3. The depicted results indicate that lung cancer is the highest growing disease among all others.

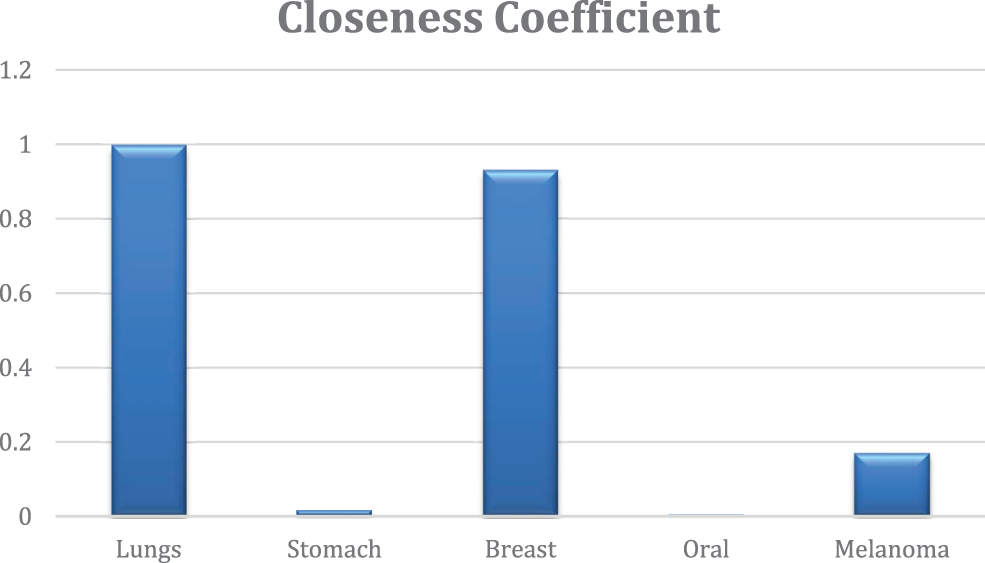
Figure 3: Bar chart representation of closeness coefficient of each disease

6  Conclusion and Future Recommendations

This study used triangular Fuzzy TOPSIS by using linguistic variables to evaluate the data on cancer in India from the years 2010 to 2015. The Fuzzy TOPSIS aids expert decision-makers as a team of medical experts in terms of subjectivity and ambiguity. The ranking by triangular Fuzzy TOSPSIS indicates that lung cancer is the most growing disease among all other types of cancers. Therefore, we can conclude that triangular Fuzzy TOPSIS can be effectively employed for the ranking of cancer data. The fuzzy-based MCDM provides accurate results with a complex implementation structure. In our future work, the fuzzy theory-based MCDM approaches can be utilized in other medical field data. The growth rate of other diseases can also be determined by using fuzzy MCDM. The fuzzy MCDM can also be utilized for the ranking of medical image encryption algorithms in the Internet of Things (IoT) and cryptography.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. I. Petrovic and M. Kankaras, “A hybridized IT2FS-DEMATEL-AHP-TOPSIS multicriteria decision making approach: Case study of selection and evaluation of criteria for determination of air traffic control radar position,” Decision Making: Applications in Management and Engineering, vol. 3, no. 1, pp. 146–164, 2020. [Google Scholar]

2. Ö. Yorulmaz, S. K. Yıldırım and B. F. Yıldırım, “Robust mahalanobis distance based TOPSIS to evaluate the economic development of provinces,” Operational Research in Engineering Sciences: Theory and Applications, vol. 4, no. 2, pp. 102–123, 2021. [Google Scholar]

3. D. Bozanic, D. Tešić, D. Marinković and A. Milić, “Modeling of neuro-fuzzy system as a support in decision-making processes,” Reports in Mechanical Engineering, vol. 2, no. 1, pp. 222–234, 2021. [Google Scholar]

4. M. Aslam, A. Fahmi, F. A. A. Almahdi and N. Yaqoob, “Extension of TOPSIS method for group decision-making under triangular linguistic neutrosophic cubic sets,” Soft Computing, vol. 25, no. 5, pp. 3359–3376, 2021. [Google Scholar]

5. M. Gulistan, N. Yaqoob, A. Elmoasry and J. Alebraheem, “Complex bipolar fuzzy sets: An application in a transport’s company,” Journal of Intelligent & Fuzzy Systems, vol. 40, no. 3, pp. 3981–3997, 2021. [Google Scholar]

6. A. Fahmi, N. Yaqoob and W. Chammam, “Maclaurin symmetric mean aggregation operators based on cubic Pythagorean linguistic fuzzy number,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 2, pp. 1925–1942, 2021. [Google Scholar]

7. A. Fahmi, F. Amin, M. Aslam, N. Yaqoob and S. Shaukat, “T-norms and T-conorms hesitant fuzzy Einstein aggregation operator and its application to decision making,” Soft Computing, vol. 25, pp. 47–71, 2021. [Google Scholar]

8. M. Akram, N. Yaqoob, G. Ali and W. Chammam, “Extensions of dombi aggregation operators for decision making under m-polar fuzzy information,” Journal of Mathematics, vol. 2020, no. 6, pp. 1–20, 2020. [Google Scholar]

9. Cancer research in ICMR achievements in nineties, 2000. [Online]. Available: https://www.icmr.nic.in/sites/default/files/guidelines/cancer_0.pdf. [Google Scholar]

10. C. L. Hwang and K. Yoon, Multiple Attributes Decision Making Methods and Applications, Berlin: Springer, 1981. [Google Scholar]

11. D. Dubois and H. H. Prade, “Operations of Fuzzy Number’s,” International Journal of Systems Science, vol. 9, no. 6, pp. 613–626, 1978. [Google Scholar]

12. C. T. Chen, “Extensions of the TOPSIS for group decision-making under fuzzy environment,” Fuzzy Sets and Systems, vol. 114, no. 1, pp. 1–9, 2000. [Google Scholar]

13. A. Awasthi, S. S. Chauhan and S. K. Goyal, “A multi-criteria decision-making approach for location planning for urban distribution centers under uncertainty,” Mathematical and Computer Modelling, vol. 53, no. 1–2, pp. 98–109, 2011. [Google Scholar]

14. D. Yong, “Plant location selection based on fuzzy TOPSIS,” The International Journal of Advanced Manufacturing Technology, vol. 28, no. 7–8, pp. 839–844, 2005. [Google Scholar]

15. M. Zulqarnain and M. Saeed, “An application of interval-valued fuzzy soft matrix (IVFSM) in decision making,” Science International, vol. 28, no. 3, pp. 2261– 2264, 2016. [Google Scholar]

16. M. Zulqarnain and M. Saeed, “Comparison between fuzzy soft matrix (FSM) and interval-valued fuzzy soft matrix (IVFSM) in decision making,” Science International, vol. 28, no. 5, pp. 4277–4283, 2016. [Google Scholar]

17. H. Zhang and L. Yu, “MADM method based on cross-entropy and extended TOPSIS with interval-valued intuitionistic fuzzy sets,” Knowledge-Based Systems, vol. 30, pp. 115–120, 2012. [Google Scholar]

18. R. Narasimhan, “An analytic approach to supplier selection,” Journal of Purchasing and Supply Management, vol. 1, pp. 27–32, 1983. [Google Scholar]

19. R. M. Monezka and S. J. Trecha, “Cost-based supplier performance evaluation,” Journal of Purchasing and Materials Management, vol. 24, no. 2, pp. 2–7, 1998. [Google Scholar]

20. J. Choi, S. X. Bai, J. Geunes and H. E. Romeijn, “Manufacturing delivery performance for supply chain management,” Mathematical and Computer Modelling, vol. 45, no. 1–2, pp. 11–20, 2007. [Google Scholar]

21. T. Chen, Y. Jin, X. Qiu and X. Chen, “A hybrid fuzzy evaluation method for safety assessment of food-waste feed based on entropy and the analytic hierarchy process methods,” Expert Systems with Applications, vol. 41, no. 16, pp. 7328–7337, 2014. [Google Scholar]

22. H. H. Nasab and A. S. Milani, “An improvement of quantitative strategic planning matrix using multiple criteria decision making and fuzzy numbers,” Applied Soft Computing, vol. 12, no. 8, pp. 2246–2253, 2012. [Google Scholar]

23. M. Li, L. Jin and J. Wang, “A new MCDM method combining QFD with TOPSIS for knowledge management system selection from the user’s perspective in intuitionistic fuzzy environment,” Applied Soft Computing, vol. 21, pp. 28–37, 2014. [Google Scholar]

24. H. C. Liu, X. J. Fan, P. Li and Y. Z. Chen, “Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment,” Engineering Applications of Artificial Intelligence, vol. 34, pp. 168–177, 2014. [Google Scholar]

25. L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]

26. R. E. Bellman and L. A. Zadeh, “Decision-making in a fuzzy environment,” Management Science, vol. 17, no. 4, pp. 141–164, 1970. [Google Scholar]

27. C. Kahraman, Fuzzy Multi-Criteria Decision Making: Theory and Applications with Recent Developments, 1st ed., vol. 16. New York, USA: Springer Science and Business Media, 2008. [Google Scholar]

28. Y. X. Wang, “Application of fuzzy decision optimum model in selecting supplier,” The Journal of Science Technology and Engineering, vol. 5, no. 15, pp. 1100–1103, 2005. [Google Scholar]

29. T. C. Chu, “Selecting plant location via a fuzzy TOPSIS approach,” The International Journal of Advanced Manufacturing Technology, vol. 20, no. 11, pp. 859–864, 2002. [Google Scholar]

30. M. Zulqarnain and M. Saeed, “A new decision-making method on interval valued fuzzy soft matrix (IVFSM),” British Journal of Mathematics & Computer Science, vol. 20, no. 5, pp. 1–17, 2017. [Google Scholar]

31. T. Y. Chen, “The inclusion-based TOPSIS method with interval-valued intuitionistic fuzzy sets for multiple criteria group decision making,” Applied Software Computing, vol. 26, pp. 57–73, 2015. [Google Scholar]

32. G. R. Jahanshahloo, F. H. Lotfi and M. Izadikhah, “Extension of the TOPSIS method for decision-making problems with fuzzy data,” Applied Mathematics and Computation, vol. 181, no. 2, pp. 1544–1551, 2006. [Google Scholar]

33. P. Karande and S. Chakraborty, “A Fuzzy-MOORA approach for ERP system selection,” Decision Science Letters, vol. 1, pp. 11–21, 2012. [Google Scholar]

34. V. Keršulienė and Z. Turskis, “Integrated fuzzy multiple criteria decision making model for architect selection,” Technological and Economic Development of Economy, vol. 17, no. 4, pp. 645–666, 2011. [Google Scholar]

35. K. L. Lee, “Two-phase fuzzy approach for evaluating service strategies in an airports international logistic system,” Journal of the Chinese Institute of Industrial Engineers, vol. 27, no. 3, pp. 209–225, 2010. [Google Scholar]

36. J. Lu, G. Zhang, D. Ruan and F. Wu, Multi-Objective Group Decision Making: Methods, Software, and Applications With Fuzzy Set Techniques, 1st ed., vol. 6. Singapore: World Scientific, 2007. [Google Scholar]