Rooted Tree Optimization for Wind Turbine Optimum Control Based on Energy Storage System

1  Introduction

Renewable energies (hydraulic, solar, wind, geothermal, and biomass) are developing intensively throughout the world, driven by the fixture to combat global heating by degrading greenhouse gas emissions. Wind energy has a specific place, particularly in remote areas where grid-supplied electricity is either unavailable or prohibitively expensive [1,2].

In variable speed wind turbine (VSWT), despite the wide range of generators that could be utilized, the PMSG “without gearbox” is still a good option for both offshore and onshore implementations. Indeed, compared to competing machines (squirrel cage induction machine (SCIG) and doubly-fed induction generator (DFIG)), the PMSG offers several benefits, including high energy output, improved reliability, a good power/weight ratio, together with a high potential for the optimization of energy output. [3,4].

The efficiency and service life of the proposed system configuration depend primarily on the dimensioning of the system’s various components like vertical or horizontal WT selection and the presence of absence of an energy storage system (ESS). Other factors that can also affect those properties include the management approach that is selected (type of power converter controller together with the wind turbine operating region), which is designed according to performance requirements [5]. This is why a reliable and efficient control system is required to ensure safety and optimal performance. In this respect, an important body of research has been consecrated to the development of strong control algorithms for WT generators [6–13]. This can be achieved by considering whether it is possible to extend the turbine operation at two regions whilst guaranteeing higher power fed into the grid [4].

Over the recent years, novel control approaches have appeared to address the shortcomings of classical control techniques with better efficiency and performance. These include fractional-order PI (FOPI) [7], predictive control (NPC) [8,9], fuzzy logic control (FLC) [10], artificial neural network (ANN) [11], back-stepping control (BSC) [12] and sliding mode control (SMC) [13]. Despite the numerous advantages offered by predictive control strategy, the latter is quite burdensome, since it needs suitable model identification from the system, which in turn negatively affects the system’s performance [9]. Fuzzy control logic (FLC) is the most widely employed approach; however, it suffers from some drawbacks such as the requirement for a large memory, which results in longer time to access the better solution. Moreover, this approach lacks specifics on the determination of fuzzification, inferences and defuzzification [14]. The ANN-based control technique holds great promises but the absence of a well-defined process for the identification of the appropriate topology of the network and the numbers of neurons to be integrated into the hidden layer pose a serious challenge. Indeed, control performance could be significantly reduced by randomly setting the network weights starting values and the definition of the learning stage [15]. The biggest hindrance of the BSC resides in the explosion of complexity generated by the consecutive derivations of the virtual controls at every stage of the back-stepping design [12]. The SMC can handle uncertainties with minimal error of tracking and quick response time with a remarkable ease for practical implementation. However, since the sign function is discontinuous in nature, it produces oscillations at the control input at a steady-state. The latter phenomenon is known as chattering [16,17].

The classical control method based on (PI) [1,4] has significant advantages: fast response and simple physical realization [18,19]. This method requires optimal tuning for the model to work properly. Therefore, WTs performance is closely related to the suitable selection of PI gains. Regulating PI parameters by conventional trial and error technique is time-consuming and onerous in nonlinear systems [20], such as (VSWT-PMSG-ESS) configuration. Therefore, modern intelligent amelioration algorithms from which: FLC [6,10,14], ANN [21], mimetic algorithm [22], Genetic Algorithm (GA) [23], Particle Swarm Optimization (PSO) [14], Artificial Bee Colony (ABC) [24], Grey Wolf Optimizer (GWO) [25], Ant Colony Optimization (ACO) [26], and Democratic Joint Operations algorithm (DJO) [3] have been successfully employed to make adjustments to the right parameters of PI controller. Meanwhile, there is room for performance improvement by developing the right optimizer, with appropriate parameters settings. In this work, a DPC-SVM-PI based (RTO) algorithm is proposed to obtain optimal gains (Kp and Ki) in order to decrease the harmonic distortion in grid current, to guarantee a loud quality of the inserted power to the network, and to increase the system rapidity and stability.

The reminder of the present paper is comprised of five section ordered as follows: Section 2 briefly defines work related to our study; Section 3 provides mathematical model for the main constituents of the PMSG-basis VSWT backed through an ESS. The design from the DPC-SVM-PI control system-basis RTO improver is covered in division four. Simulations beneath MATLAB/Simulink and the results are presented in division 5 to confirm the efficiency of the suggested control approach. Finally, the findings are summarized in Section 6.

2  Literature Review

Nowadays, several works have been proposed using Meta-heuristics and Artificial Intelligence in order to adjust the optimal parameters allowing achieving better control performances and adequate active and reactive power management whoever the system generation to the grid. This can be obtained by taking into account difficulties associated with nonlinearities of the selected control topology. Reference [27] the authors have used artificial bee colony optimization (ABCO), mine blast algorithms (MBA) to achieve best gains from the nonlinear SMC for the purpose of controlling voltage source converter (VSC) in order to high-voltage direct current systems. Reference [28] have proposed GWO to minimize ESS size and thereby improve the actuating cost of the micro-grid. The numerical simulation, along with results comparison, has shown the effectiveness of the proposed algorithm. Meta-heuristic Optimization Techniques (MOTs) are targeting improvement in wind power plant’s dynamic behavior where ABCO and GWO have been utilized for the optimization of the gains of the blade pitch control system [29]. Whereas in Tan et al. [30], the PSO algorithm has been utilized for a multimodal design of DFIG to reach higher efficiency and optimal machine design. Furthermore, PSO has been applied to optimum capacitor allocation of a wind energy generation system connected to a distribution system [31]. In order to enhance the control performances of a hybrid power system under a wide range of environmental conditions, the chaotic GWO has been utilized by [32] introduced the adaptive control and fuzzy neural network control techniques for single-phase inverters to improve voltage tracking performance and keep its robustness higher when sources of uncertainty are present in the Photovoltaic (PV) systems. Furthermore, an adaptive PI controller is used in [33] to reinforce the DC-link voltage in a single-stage PV system linked to the grid [34] have conducted several comparative studies between conventional PID and fuzzy controllers to demonstrate the superiority of fuzzy controllers. A real-time implementation of an intelligent Fuzzy PI Regulator based on 33 level-switched multilevel capacitor inverters for permanent magnet synchronous motor (PMSM) drives has been suggested by [35]. The performance evaluation based on a neuro-fuzzy hybrid intelligent PI control method for four regions jointed thermal, hydropower plant is proposed by [36,37] presented in their work fuzzy logic as an intelligent controller to optimize PID parameters applied to control two active and reactive power channels based on the DFIG direct-current vector control design. The authors in [38] have introduced PI-H∞ to regulator the rotor currents of a DFIG, to enhance robustness, and to guarantee harmonic currents mitigation, and performance stability in case of main voltage distortion and generator parameter variation.

3  Theoretical Developments and Method

This section reviews a simulation analysis of the entire system before the actual implementation stage. Fig. 1 appears the form of the wind energy system (WEs). The rotor of the three-bladed horizontal axis wind turbine is coupled a shaft of the PMSG without a gearbox. The electronic power device is comprised of two back-to-back AC/DC/AC IGBT bridges linked via a shared DC bus that transfers the power generated by the PMSG to the network. This WT is fed by an ESS connected to a DC bus system comprised of a lead-acid battery and a bi-directional DC/DC converter.

Figure 1: Studied wind generation system

3.1 Model of the Wind Turbine

The Wind sail performs the conversion of air mass-energy into motion when wind circulates on active surface S. The air mass (Pt) power is given by Eq. (1) [39]:

Pt=12ρ.S.v3(1)

where ρ denotes air density and v wind speed. This power is then transferred to the generator shaft in the form of the turbine power or aerodynamic power, manifested by Eq. (2) [39]:

Pω=12ρ.SCp(λ,β).v3(2)

Denotes R the wind blade radius, the blade pitch angle is β, λ the tip speed ratio (TSR), power coefficient is Cp the provided by Eq. (3) [17]:

Cp=0.073(151λ′−0.058β−0.002β2.14−13.2)e−18.4λ′(3)

As the aerodynamic efficiency varies with λ, as expressed by Eq. (3), Cp reaches its maximum values when λ is optimal λopti. Fig. 2 shows the resultant Cp as a function of λ when β is zero or fixed [13].

Figure 2: Power coefficient (Cp) vs. specific speed curve (λ)

3.2 Model of the PMSG

The model of the PMSG is expressed by equations that are based entirely on the stator voltage Vd and Vq inside the park model as shown by Eq. (4) [11].

{Vd=RsId+LddIddt−ωLqIqVq=RsIq+LqdIqdt+ω(LdId+ψf)(4)

The electromagnetic torque (Te) is determined by Eq. (5) [12]:

Te=32p[(Ld−Lq)IdIq+Idψf](5)

where, the number of poles is p, Rs the resistance of the stator, Id its direct current and Iq its quadrature current, Ld its direct inductance Lq its inductance quadrature, ω is the electrical pulsation, and ψf is the field flux.

3.3 Grid Model

The network model in the d-q field is given by Eqs. (6) and (7) [13]:

Vdg=Vdi−RgIdg−LdgdIdgdt+LqgωgIqg(6)

Vqg=Vqi−RgIqg−LqgdIqgdt−LdgωgIdg(7)

While g returns to the generator. Hence, the active and reactive powers are provided by Eqs. (8) and (9), respectively [13]:

Pg=32(VdgIdg+VqgIqg)(8)

Qg=32(VdgIqg−VqgIdg)(9)

4  Control Scheme

Usually, the suggested control schemes can be allocated in machine side converter (MSC), battery side converter (BSC), and grid side converter (GSC), as presented in Fig. 3. The MSC is clearly in charge of obtaining available mechanical power from wind and transforming it into electrical power in both regions (2 and 3) [40]. The BSC is monitored so as to keep the DC bus voltage close to the nominal worth (800 V) together operating conditions [39]. The output electrical power is corrected then transferred to the GSC through the DC-Link capacitor supported by ESS. To cope with the electrical network necessities, the GSC controls the reactive and active powers which are injected into the utility grid.

Figure 3: The complete control description of the studied wind system/ESS

4.1 Grid Side Converter Controller

Utilizing the GSC is essential in ensuring that customers receive the energy they desire, regardless of the operating conditions. Considering that, a novel DPC-SVM-based PIRTO algorithm is proposed for the management the amount of active and reactive power that is supplied to the grid. The schematics of the GSC control strategy are explained in Fig. 3c. By difference to the conventional vector approach, the DPC-SVM-based PIRTO the GSC receives the voltage directly from the grid.

4.2 Design of Proposed PI-RTO Controller

The proposed rooted tree optimization algorithm (RTO) has a complicated system to bring underground water. That’s social behavior became a trendy technology. The base concept of roots system is that the various roots, which begin to find underground water in the first layer, get from the tree’s first kink [41]. It is the first solution randomly [42]. Fig. 4 shows that it can be obtained a new generation and the grade of fitness by the nearest roots to the goal. Furthermore, the roots distant from the objective are removed.

Figure 4: The roots of desert plants (Palm) searching for water

The tree roots of the desert plants are characterized by their behavior, which is looking for underground water based on the wetness degree under the ground. This behavior has inspired the strategy of this algorithm.

Applying the RTO algorithm requires explaining some variables. Those concerns:

•   Root: Presents a suggested or candidate solution.

•   Wetness degree (Dw): Decides the fitness degree among the population.

Where the variables (Rr,Rc,Rn) are the rates that impressionable in the convergence in order to achieve the best result.

Step 1: In order to arrive at a new population, by the roots closest to the water randomly, a new generation is started. The initial solution is proposed by the members of the new generation [43]. The novel population is computed using the following formula:

Ynew(k,it+1)=Yr(it)+b3×Dw(k)×randn×mit(10)

Yr(it): The preceding candidate to the iteration,

b3: The adjustable parameter.

Step 2: The tree root system’s technology is characterized by selection the better roots that gather about the wet spot, from which a novel generation is formed, and the faraway roots are removed.

Taking the number of applicants into account, the new generation is given by:

Ynew(k,it+1)=Ybest(it)+b1×Dw(k)×randn×(mN×it)(11)

Step 3: A nouveau generation is born from the roots that have arrived at the nearest location, whose roots continue to bring water. To calculate a new population, the following expression is used:

Ynew(k,it+1)=Y(k,it)+b2×Dw(k)×rand×(Ybest(it)−Y(k,it))(12)

where b2 is the adjustable parameter and Y(k,it) the preceding candidate to the next iteration.

Step 4: In accordance with Dw(k) reorder, the whole population then take the best solution and reorganize the entire population according to Dw(k), then choose the better option. Whereas the wetness degree changes from [0–1].

According to Dw(k),

Dw(k)={fkmaxfkforthemaximumobjective1−fkmaxfkfortheminimumobjective(13)

where k = 1, 2, 3…., N and fk degree of fitness.

Best solution for the entire population, given by the individual, is to select the optimum values of PI to regulator the PMSG [44–48]. To select the values of the objective function, the adequate search algorithm presented in Fig. 5.

Figure 5: Search algorithm of the RTO–PI control

Fig. 6 shows how the fitness function evolves with the use of the RTO algorithm, where the relative optimum values are Kp=10.410 and Ki=26.050. Furthermore, Tab. 1 illustrates the optimal gains for the five iterations and their fitness functions.

Figure 6: The variation of the fitness function

5  Simulations and Results Analysis

So as to evaluate the efficacy of the control and management approach proposed, a series of emulate were directed using MATLAB/Simulink, under changed wind speed profile.

To confirm the reliability of the system’s topology together with the proposed control strategy, the system was implemented in different areas under changing operating conditions. Mutable wind speeds were applied at a period of 19 s with an average value of 11.75 m/s as shown in Fig. 7a. During the tests, the WT operated at maximum power point tracking (MPPT) at the mode of region two under wind speed less than the design value. The suggested MPPT method relies on optimal control of torque and sliding mode control (OTC-SOSMC). This approach allows tracking wind speed changes and attains the global maximum power point (MPP). To protect the VSWT, the OTC-SOSMC seamlessly switches the operation mode to region 3 when wind speed exceeds the nominal value. From Figs. 7b and 7c, the suggested OTC-SOSMC based MPPT technique is shown to be robust and reliable, as can be seen from the characterized values Cpmax=0.48 and λoptim=8.1 in regions 2 and 3. The curve is shown in Fig. 7d confirms the effectiveness and adaptability of the control (switching) in regions (2 and 3).

Figure 7: MPPT/limitaion based in OTC-SOSMC

To assess the performance of the suggested DPC-SVM-PI controller-based RTO algorithm in the GSC, the required power was incremented, as can be seen form Fig. 8b. Initially, the desired power reference was set to 3000 W for 5 s. For t in the range 5–10 s, the demand was augmented up to 4000 W, and then it continued to rise till it reached 5000 W in the range 10–15 s. Finally, in the time range 15–19 s, the power was increased to 7000 W.

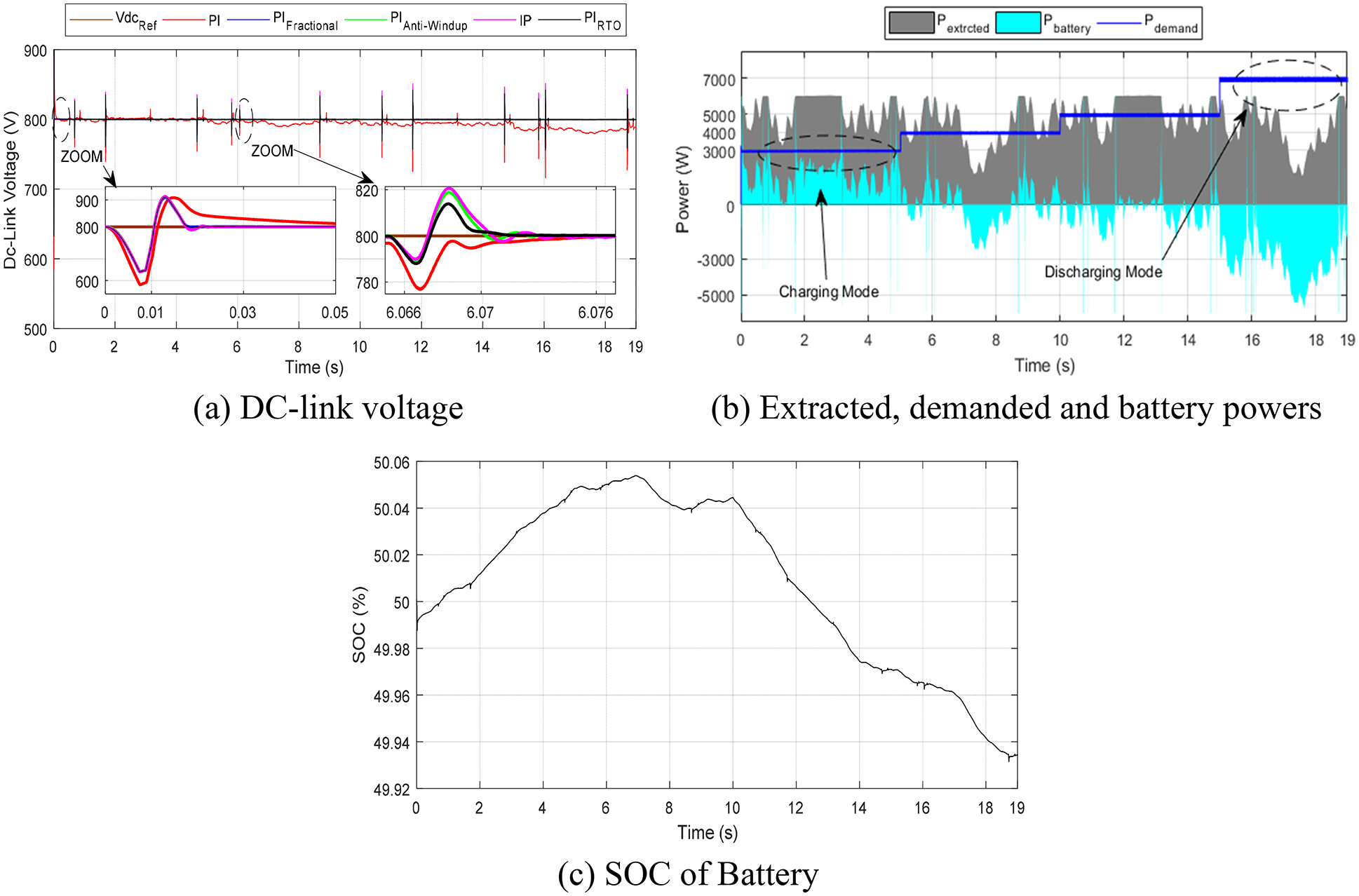
Figure 8: ESS control

One such scenario enables us to evaluate the ephemeral and steady-state performance of the suggested DPC-PI-based RTO algorithm. For the sake of comparing the robustness of the proposed PIRTO algorithm, a number of controllers were utilized, among which PI, PIFractional, PIanti-windup, and IP. The dynamic behavior of the DPC-SVM-PIRTO implemented in the GSC was investigated, and the results are provided in Tabs. 2 and 3. The results illustrate performance with regard to ripple reduction, tracking rapidity, efficiency and settling time regardless of the instantaneous variations of the required or available wind power, the electric power exchanged with the grid is confirmed only in the case when DC-bus is set as a constant nominal value.

The battery side converter (DC-ESS) is set to reservation the DC-link voltage nigh to the nominal value of 800 V, as indicated by Fig. 8a. The system performances are ameliorated in the situation of DPC-SVM-PIRTO controllers in both control loops (Pg and Qg) with regard to overshoot, undershoot, rise time, residing time, and steady-state mistake. Different residing times (s) provided by PIRTO is 16.11e-3, meanwhile it is 23.65e-3, 16.13e-3, 16.14e-3, 16.16e-3 for PI, PIFractional, PIanti-windup and IP respectively. Furthermore, the average Vdc (V) is 799.989 of by means of PIRTO controller; however, it is 793.395,799.951,799.791 and 799.527 for PI, PIFractional, PIanti-windup, and IP consecutively. The minimum overshoot (%) percentage is reduced by 13.60e-2 by using PIRTO, but it is 13.73e 3, 13.75e-2, 14.10e-2, and 14.10e-2 for PI, PIFractional, PIanti-windup, and IP, respectively. In addition, the average error of Vdc (V) is 0.010 when using PIRTO. From Tab. 2, the transient reply indicates the superiorities of the PIRTO and its ability to provide improved performances to other regulators (PI, PIFractional, PIanti-windup, and IP).

The turbine’s power extract, its nominal power together with the battery required and stored power are shown in Fig. 8. The latter shows clearly that the objectives set for the proposed system management and control was attained. The energy storage system (battery) can operate under changing weather conditions and handle various constraints. As can be seen, the load power demand is consistently satisfied. The operational stability in both regions (2 and 3) is uniform and covers simultaneously the scenarios of charge/discharge/MMPT/power limitations. As can be seen from Fig. 8, the state of charge (SOC) adjusts quickly to obtain charge/discharge of the battery, cycle at all instant. This difference is primarily dependent on battery current, load demand and power production.

Electrical energy injected into the grid under the controlled of DPC-SVM-PI-based RTO and four other controllers is shown in Fig. 9. The controllers were shown to be capable of tracking accurately the set point (Figs. 9a and 9b). However, the active and reactive power levels indicate that the PIRTO exhibits a better behavior than the other techniques. Simulation results are compiled in Tab. 3. The latter illustrate the superior performance of the suggested PIRTO algorithm compared to another controller. Indeed, as exposed in Figs. 9a and 9b the simulation dynamic response of the GSC is enhanced with the use of PIRTO. Moreover, the minimum overshoot (%) percentage is 12.3e-3 in the case of the PIRTO application. Meanwhile, it is 15.5e-3, 23.7e-3, 21.3e-3 and 15.5e-3 by means of PI, PIFractional, PIanti-windup and IP respectively. The rise times (s) of the competing controllers are 49.6e-5, 20.2e-5, 18e-5, 20.6e-5 by means of PI, PIFractional, PIanti-windup and IP respectively. But it is 37.062e-5 by means of PIRTO. Their relative settling times (s) of the for techniques (PI, PIFractional, PIanti-windup and IP) are 512e-4, 13.99e-4, 8.96e-4 and 112.50e-4, consecutively. However, it is 5.42e-4 in the case of using PIRTO. Also, the Pg average power (W) injected in the grid is 4.729e+3, 4.723e+3, 4.707e+3, and 4.728e+3 by using PI, PIFractional, PIanti-windup, and IP, respectively; meanwhile, it is 4.730e+3W when PIRTO is used.

Figure 9: Grid power used DPC-SVM based an (PI, PIfractional, PI anti-windup, IP and PI RTO) controllers

PIRTO gives the best energy efficiency estimated at 99.59% compared to PI (99.57%), PIFractional (99.44%), PIanti-windup (99.11%) and IP (99.54%). The relative settling times (s) are 512e-4, 13.99e-4, 8.96e-4, and 112.50e-4, which are higher than that given by PIRTO (5.42e-4). Furthermore, the grid power injection’s mean error (W) is 20.555, 26.500, 42.299, 21.971, and 19.669 in case of using PI, PIFractional, PIanti-windup, IP, and PIRTO, consecutively. It is obvious from Tab. 3. That the dynamic system responses are clearly enhanced when PIRTO is used compared to the dynamic responses by means of the competing techniques. The reactive power is set to zero for a unity power factor, Fig. 9c illustrates that. It could be observed that the reactive power follows the set point value seamlessly with less oscillations and static errors for all significant algorithms.

To asseverate the efficacy of the suggested control method (DPC-SVM-PIRTO) based optimizer parameter identification, an examination of harmonic distortion of grid current was performed for each regulator, as shown in Figs. 10 and 11.

Figure 10: Grid current for DPC-SVM technique for different controllers under power variation

Figure 11: THD of different controllers under power variation

Fig. 10 shows the injected current into phase ‘A’ using the five controllers, of the grid. Figure shows the superior performance in terms of the suggested PIRTO algorithm, displaying a distortion-free and smooth waveform in comparison to other algorithms (Fig. 10f).

As one can note from Figs. 11a–11c, the gross harmonic distortion (THD) of Iag is 1.79%, 0.95%, and 1.05% for a fundamental frequency of the power grid (fr) of 15.01 Hz. This implies the appearance of a distorted form and very undesirable current (phase A) during the simulation, which can be seen in the zoomed-in section (Figs. 10b–10d). This is an indication that the implementation of PI, PIFractional, and PIanti-windup generates a poor-quality injected power, which may cause, in turn, a degradation of the power grid. On the other hand, Figs. 11d and 11e shows a reduce the better current distortion by 0.54% and 0.36% for IP and PIRTO, respectively. PIRTO exhibits a superior performance as shown by the current’s smooth shape, attributable to the elimination of odd harmonics. THD reduction is recommended for power reference applications (3000 W) through filtering out the odd harmonics, and obtaining thereby a waveform that is smooth and distortion-free.

The THD provided by the PIRTO algorithm is significantly reduced based on Fig. 12 and the results discussed above. It outperforms the other techniques in terms of power quality.

Figure 12: Comparison of five controller types

6  Conclusion

In the present work, a PMSG Wind turbine enhanced by an energy storage system is proposed to assure the availability of power under an ambit of wind conditions. This design is based on a DPC-SVM-PI controller supported by an advanced control and management system. The optimal control gains of DPC-PI are achieved by RTO optimizer to enhance the system performances, in terms of reference tracking precision, stability, harmonic mitigation, the rapidity and quality of the energy fed at the grid. For different working conditions, simulations in MATLAB/Simulink, The control topology’s efficiency is confirmed and compared to PI. PIfractional, PIanti-windup, and PI controller’s results. The simulation results showed that PIRTO exhibits better efficiency than the competing controllers. It is noted that the PIRTO based supervisor simply trajectories the power grid references in different operational conditions. Consequently, the storage system has solved VSWT the disadvantages of wind’s inherent sporadic nature. It is also observed that the use of a backup source in VSWT raises the reliability and power grid operational safety in order to balance supply and demand. The control and management system showed that the operational freedom in zones 2 and 3 together, could be extended with high conservation of wind speed nominal. Moreover, higher consistency and similarity between the four operating modes (MPPT, limiting, loading, unloading) is obtained in the presence of a powerful management algorithm. The proposed RTO optimizer-based control conducted by DPC-PI optimal control parameters has successfully improved the performance of the energy fed into the grid. The amount of power provided by the grid utilizing the DPC-SVM-PI strategy has also shown smooth waveforms through high following indices and high accuracy. Finally, it is possible to conclude that RTO based regulator has best dynamic and stable performance, very fast time response, low undershoot, reduced THD, and better current waveform compared to other controllers.

Acknowledgement: The authors would like express their gratitude to Prince Sultan University for taking care of the present Article Processing Charges (APC). Special acknowledgement to Automated Systems & Soft Computing Lab (ASSCL), Prince Sultan University, Riyadh, Saudi Arabia.

Funding Statement: The work is funded by Prince Sultan, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Dahbi, A. Reama, H. Messaoud, N. Nait-Said, M. -S. Nait-Said et al., “Control and study of a real wind turbine,” Computers & Electrical Engineering, vol. 80, no. 21, pp. 106492, 2019. [Google Scholar]

 2.  B. Madaci, R. Chenni, E. Kurt and K. E. Hemsas, “Design and control of a stand-alone hybrid power system,” International Journal of Hydrogen Energy, vol. 41, no. 29, pp. 12485–12496, 2016. [Google Scholar]

 3.  B. Yang, T. Yu, H. Shu, X. Zhang, K. Qu et al., “Democratic joint operations algorithm for optimal power extraction of PMSG based wind energy conversion system,” Energy Conversion and Management, vol. 159, no. 5, pp. 312–326, 2018. [Google Scholar]

 4.  A. Azar, S. Vaidyanathan and A. Ouannas, “Fractional order control and synchronization of chaotic systems,” Springer, vol. 688, pp. 1–12, 2017. [Google Scholar]

 5.  L. Barelli, D. Ciupageanu, A. Ottaviano, D. Pelosi and G. Lazaroiu, “Stochastic power management strategy for hybrid energy storage systems to enhance large scale wind energy integration,” Journal of Energy Storage, vol. 31, no. 6, pp. 101650, 2020. [Google Scholar]

 6.  H. Li, B. Song, T. Chen, Y. Xie and X. Zhou, “Adaptive fuzzy PI controller for permanent magnet synchronous motor drive based on predictive functional control,” Adaptive Fuzzy PI Controller for Permanent Magnet Synchronous Motor Drive Based on Predictive Functional Control, vol. 358, no. 15, pp. 7333–7364, 2021. [Google Scholar]

 7.  A. Jain and R. Saravanakumar, “Comparative analysis of fractional order PI and integer order PI based controller for hybrid standalone wind energy conversion system,” Environment Progress & Sustainable Energy, vol. 39, no. 2, pp. 1–9, 2020. [Google Scholar]

 8.  M. Alizadeh and S. Kojori, “Small-signal stability analysis, and predictive control of Z-Source Matrix Converter feeding a PMSG-WECS,” International Journal of Electrical Power & Energy Systems, vol. 95, no. December, pp. 601–616, 2018. [Google Scholar]

 9.  B. Babaghorbani, M. Beheshti and H. Talebi, “A Lyapunov-based model predictive control strategy in a permanent magnet synchronous generator wind turbine,” International Journal of Electrical Power & Energy Systems, vol. 130, no. 10, pp. 106972, 2021. [Google Scholar]

10. K. Naik, C. Gupta and E. Fernandez, “Design and implementation of interval type-2 fuzzy logic-PI based adaptive controller for DFIG based wind energy system,” International Journal of Electrical Power & Energy Systems, vol. 115, no. 8, pp. 105468, 2020. [Google Scholar]

11. C. Wei, Z. Zhang, W. Qiao and L. Qu, “An adaptive network-based reinforcement learning method for MPPT control of PMSG wind energy conversion systems,” IEEE Transactions on Power Electronics, vol. 31, no. 11, pp. 7837–7848, 2016. [Google Scholar]

12. Y. El Mourabit, A. Derouich, A. El Ghzizal, N. El Ouanjli and O. Zamzoum, “Nonlinear backstepping control for PMSG wind turbine used on the real wind profile of the Dakhla-Morocco city,” International Transaction on Electrical Energy Systems, vol. 30, no. 4, pp. 1–28, 2020. [Google Scholar]

13. B. Meghni, D. Dib and A. Azar, “A second-order sliding mode and fuzzy logic control to optimal energy management in wind turbine with battery storage,” Neural Computing and Applications, vol. 28, no. 6, pp. 1417–1434, 2017. [Google Scholar]

14. N. Bounar, S. Labdai and A. Boulkroune, “PSO-GSA based fuzzy sliding mode controller for DFIG-based wind turbine,” ISA Transactions, vol. 85, no. 1, pp. 177–188, 2019. [Google Scholar]

15. H. Chojaa, A. Derouich, S. Chehaidia, O. Zamzoum, M. Taoussi et al., “Integral sliding mode control for DFIG based WECS with MPPT based on artificial neural network under a real wind profile,” Energy Reports, vol. 7, no. 5, pp. 4809–4824, 2021. [Google Scholar]

16. A. Benamor, M. Benchouia, K. Srairi and M. Benbouzid, “A novel rooted tree optimization apply in the high order sliding mode control using super-twisting algorithm based on DTC scheme for DFIG,” International Journal of Electrical Power & Energy Systems, vol. 108, no. 1, pp. 293–302, 2019. [Google Scholar]

17. B. Kelkoul and A. Boumediene, “Stability analysis and study between classical sliding mode control (SMC) and super twisting algorithm (STA) for doubly fed induction generator (DFIG) under wind turbine,” Energy, vol. 214, no. Issue 11, pp. 118871, 2021. [Google Scholar]

18. M. Qais, H. Hasanien and S. Alghuwainem, “A novel LMSRE-based adaptive PI control scheme for grid-integrated PMSG-based variable-speed wind turbine,” International Journal of Electrical Power & Energy Systems, vol. 125, no. 9, pp. 106505, 2021. [Google Scholar]

19. S. Soued, M. Chabani, M. Becherif, M. Benchouia, H. Ramadan et al., “Experimental behaviour analysis for optimally controlled standalone DFIG system,” IET Electric Power Applications, vol. 13, no. 10, pp. 1462–1473, 2019. [Google Scholar]

20. T. Carneiro, S. Melo, P. Carvalho and A. Braga, “Particle swarm optimization method for estimation of weibull parameters: A case study for the brazilian northeast region,” Renewable Energy, vol. 86, no. 1, pp. 751–759, 2016. [Google Scholar]

21. J. Fei and C. Lu, “Adaptive fractional order sliding mode controller with neural estimator,” Journal of the Franklin Institute, vol. 355, no. 5, pp. 2369–2391, 2018. [Google Scholar]

22. Y. Mousavi and A. Alfi, “A memetic algorithm applied to trajectory control by tuning of fractional order proportional-integral-derivative controllers,” Applied Soft Computing, vol. 36, no. 3, pp. 599–617, 2015. [Google Scholar]

23. C. Ko, T. Lee, H. Fan and C. Wu, “Genetic auto-tuning and rule reduction of fuzzy PID controllers,” in IEEE Int. Conf. on Systems, Man and Cybernetics, Taipei, Taiwan, vol. 2, pp. 1096–1101, 2006. [Google Scholar]

24. A. Bagheri, A. Jabbari and S. Mobayen, “An intelligent ABC-based terminal sliding mode controller for load-frequency control of islanded micro-grids,” Sustainable Cities and Society, vol. 64, pp. 102544, 2021. [Google Scholar]

25. Y. Zhang, J. Zhou, Y. Zheng and Y. Xu, “Control optimisation for pumped storage unit in micro-grid with wind power penetration using improved grey wolf optimiser,” IET Generation, Transmission & Distribution, vol. 11, no. 13, pp. 3246–3256, 2017. [Google Scholar]

26. H. Boubertakh, M. Tadjine, P. Glorennec and S. Labiod, “Tuning fuzzy pid controllers using ant colony optimization,” in Mediterranean Conf. on Control and Automation, Thessaloniki, Greece, pp. 13–18, 2009. [Google Scholar]

27. H. Ramadan, A. Fathy and M. Becherif, “Optimal gain scheduling of VSC-HVDC system sliding mode control via artificial bee colony and mine blast algorithms,” IET Generation, Transmission & Distribution, vol. 12, no. 3, pp. 661–669, 2018. [Google Scholar]

28. S. Sharma, S. Bhattacharjee and A. Bhattacharya, “Grey wolf optimisation for optimal sizing of battery energy storage device to minimise operation cost of microgrid,” IET Generation, Transmission & Distribution, vol. 10, no. 3, pp. 625–637, 2016. [Google Scholar]

29. S. Soued, M. Ebrahim, H. Ramadan and M. Becherif, “Optimal blade pitch control for enhancing the dynamic performance of wind power plants via metaheuristic optimisers,” IET Electric Power Applications, vol. 11, no. 8, pp. 1432–1440, 2017. [Google Scholar]

30. Z. Tan, N. Baker and W. Cao, “Novel optimisation algorithm of electrical machines,” in 8th IET Int. Conf. on Power Electronics, Machines and Drives, Glasgow, United Kingdom, pp. 1–6, 2016. [Google Scholar]

31. H. Ramadan, A. Bendary and S. Nagy, “Particle swarm optimization algorithm for capacitor allocation problem in distribution systems with wind turbine generators,” International Journal of Electrical Power & Energy Systems, vol. 84, no. 2, pp. 143–152, 2017. [Google Scholar]

32. R. Wai, M. Chen and Y. Liu, “Design of adaptive control and fuzzy neural network control for single-stage boost inverter,” IEEE Transactions on Industrial Electronics, vol. 62, no. 9, pp. 5434–5445, 2015. [Google Scholar]

33. A. Shawqran, A. El Marhomy, M. Attia, A. Abdelaziz and H. Alhelou, “Enhancement of wind energy conversion system performance using adaptive fractional order PI blade angle controller,” Heliyon, vol. 7, no. 10, pp. e08239, 2021. [Google Scholar]

34. A. Boudia, S. Messalti, A. Harrag and M. Boukhnifer, “New hybrid photovoltaic system connected to superconducting magnetic energy storage controlled by PID-fuzzy controller,” Energy Conversion and Management, vol. 244, no. 7, pp. 114435, 2021. [Google Scholar]

35. N. Lakshmipriya, N. Ananthamoorthy, S. Ayyappan and P. Hema, “An intelligent fuzzy PI controller based 33 level switched capacitor multilevel inverter for PMSM drives,” Materials Today Proceedings, vol. 45, no. 6, pp. 2861–2866, 2021. [Google Scholar]

36. S. Prakash and S. Sinha, “Simulation based neuro-fuzzy hybrid intelligent PI control approach in four-area load frequency control of interconnected power system,” Applied Soft Computing, vol. 23, no. August (3), pp. 152–164, 2014. [Google Scholar]

37. T. Nguyen, D. Nguyen and Q. Ngo, “The power-sharing system of DFIG-based shaft generator connected to a grid of the ship,” IEEE Access, vol. 9, pp. 109785–109792, 2021. [Google Scholar]

38. Y. Wang, Q. Wu, W. Gong and M. Gryning, “H∞ robust current control for DFIG-based wind turbine subject to grid voltage distortions,” IEEE Transactions on Sustainable Energy, vol. 8, no. 2, pp. 816–825, 2017. [Google Scholar]

39. B. Meghni, D. Dib, A. T. Azar and A. Saadoun, “Effective supervisory controller to extend optimal energy management in hybrid wind turbine under energy and reliability constraints,” International Journal of Dynamics and Control, vol. 6, no. 1, pp. 369–383, 2018. [Google Scholar]

40. A. Benamor, M. Benchouia, K. Srairi and M. Benbouzid, “A new rooted tree optimization algorithm for indirect power control of wind turbine based on a doubly-fed induction generator,” ISA Transactions, vol. 88, no. 4, pp. 296–306, 2019. [Google Scholar]

41. Y. Labbi, D. Ben Attous, H. Gabbar, B. Mahdad and A. Zidan, “A new rooted tree optimization algorithm for economic dispatch with valve-point effect,” International Journal of Electrical Power & Energy Systems, vol. 79, no. 8, pp. 298–311, 2016. [Google Scholar]

42. L. Ow and E. Sim, “Detection of urban tree roots with the ground penetrating radar,” Plant Biosystems, vol. 146, no. 3, pp. 288–297, 2012. [Google Scholar]

43. A. Benamor, M. Benchouia, K. Srairi and M. Benbouzid, “A new rooted tree optimization algorithm for indirect power control of wind turbine based on a doubly-fed induction generator,” ISA Transactions, vol. 88, no. 4, pp. 296–306, 2019. [Google Scholar]

44. S. Zhang and J. Yang, “Analysis of user critical interests based on an improved shortest root tree algorithms,” in 2010 IEEE Int. Conf. on Progress in Informatics and Computing, Shanghai, China, vol. 2, no. 1, pp. 1189–1193, 2010. [Google Scholar]

45. T. Perry, “The ecology of tree roots and the practical significance thereof,” Journal of Arboriculture, vol. 8, no. August, pp. 197–211, 1982. [Google Scholar]

46. A. Ibrahim, S. Mirjalili, M. El-Said, S. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, no. 1, pp. 125787–125804, 2021. [Google Scholar]

47. E. -S. M. El-kenawy, Marwa and Eid, “Hybrid gray wolf and particle swarm optimization for feature selection,” International Journal of Innovative Computing, Information & Control, vol. 16, no. 1, pp. 831–844, 2020. [Google Scholar]

48. E. -S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, no. 1, pp. 107635–107649, 2020. [Google Scholar]