Identity-Based Edge Computing Anonymous Authentication Protocol

1  Introduction

With sensor technology and wireless communication technology development, the application range of edge computing has become more extensive [1]. In an edge computing system, the computing power of edge devices such as wireless terminals may become the bottleneck of system performance. It is often necessary to offload to improve computing efficiency. When many terminals are offloading computing, the MEC server must process the offloaded task according to priority [2–4]. However, the data of some terminals have the characteristics of information sensitivity and timeliness, which requires faster offloading of computing tasks and higher priority [5]. Such terminals are privileged users. Since wireless terminals are bound to user identities, privileged users will authorize signatures to other terminals in order to complete the signatures together more efficiently [6]. How to protect the privacy of the wireless terminal’s identity while completing the data transmission between the wireless terminal and the MEC, which has essential research significance [7,8]. At present, the common methods mainly include group signature, ring signature, proxy signature, etc.

An identity-based proxy threshold ring signature for edge computing is proposed in this paper. The original signature scheme is optimized, and the proxy signature is combined with the ring signature to improve the efficiency of signatures and ensure the identity privacy of the proxy signer and use the threshold method prevents the influence of a single node’s malicious actions on the signature; combined with edge computing, the computing power of the MEC server is used to reduce the burden on the wireless terminal further.

The arrangement of the remaining chapters of this article: Section 2 introduces the research work related to this article and briefly introduces and analyzes these results. Section 3 describes the authentication process between the original signer, the proxy signer, and the MEC server. Section 4 describes in detail the identity-based anonymous authentication protocol in the context of edge computing. Sections 5 and 6 analyze the scheme from three aspects: correctness, security and computational efficiency. The Section 7 summarizes the content of the full text, and puts forward the research direction of the follow-up work.

2  Related Work

Edge computing is a distributed service architecture that migrates computing and storage resources from the cloud platform to the network edge. It consists of multiple edge nodes located between cloud servers and local devices to complete data analysis tasks. Because it is closer to the local device, it can provide services with less latency, such as autonomous driving, virtual reality, smart cities, etc. But since edge nodes are usually located in untrusted environments, they also face various security and privacy threats. For example, the local device may add poisoned samples or send low-quality data to the edge node, and the edge node may speculate the data privacy of the local device, or tamper with the calculation result to destroy the execution of the protocol. Therefore, it is very important to build a more robust privacy protection and information security mechanism. The following mainly introduces the literature related to privacy protection and anonymous authentication in the edge computing environment.

Elliptic curve is a commonly used encryption method at present. It has high security, but it also consumes a lot of computation. Literature [9] proposed a lightweight anonymous authentication protocol for Internet of things terminals. The protocol uses certificateless signature, elliptic curve and signcryption technology. Through random oracle analysis, the model can realize anonymous authentication and privacy protection, and has low computing and communication costs. Literature [10] combined ring signature and elliptic curve cryptosystem and proposed a verifiable ring signature scheme using ECC anonymous sign-crypt. This scheme has the advantages of anonymity of ring signature, low computational cost, and high security of elliptic curve cryptosystem. Literature [11] combines the characteristics of group signature and threshold signature. This paper proposes a threshold group signature scheme based on the elliptic curve and realized the group members and administrators of two-way authentication. The program has anonymity and traceability also can resist collusion attacks to solve the Internet of things terminal, tampered with, such as counterfeiting threats are easy to be tapped. According to the characteristics of group signature and threshold signature, the scheme in reference [12] proposes a threshold group signature scheme based on elliptic curve, which realizes the two-way authentication between group members and group administrators. This method has anonymity and traceability, and solves the threat that the Internet of things terminal is easy to be eavesdropped, tampered and forged. However, the improvement of security has a certain impact on the efficiency of computing and communication.

Group signature scheme is a common method of anonymous authentication. Literature [13] proposes a group signature scheme that can be modified to provide privacy protection certification. For many revocable group signature schemes, this scheme introduces a contained backward security model of the definition of safety compared with previous schemes. This scheme is efficient and scalable, and more practical in actual application. Literature [14] proposed an efficient full-dynamic group signature scheme for the group signature that allows users to register and cancel within the group. The technology uses a merkle tree to record the information of registered users and uses a trusted third party to generate public and private keys. Thus, the computational efficiency of the scheme is improved. Literature [15] proposes an anonymous authentication scheme suitable for doctor-patient relationship. The scheme uses single hash function and user behavior tracking system to protect user privacy and improve system performance. At the same time, through experimental analysis, the scheme can resist most attacks and has high security.

Proxy signature is often used to reduce the consumption of self-signature. Literature [16] puts forward a kind of according to industrial IoT environment efficiently and to prove that the proxy signature scheme based on the certificate without pairing, this scheme can solve common password scheme based on certification of identity or secret key escrow and secret key distribution problems, at the same time, at different stages of the cost and the length of the signature than other signature schemes have reduced. Reference [17] proposed a lattice-based quantum proof anonymous proxy signature. Anonymity is achieved by using ring signatures. The experimental analysis proves that the scheme has adaptive security against the stability of the selected message attack on the small integer solution problem. Reference [18] proposes a decentralized electronic reporting scheme based on proxy signature and blockchain privacy protection. The scheme uses lattice ciphers to protect privacy while also resisting quantum attacks. Reference [19] proposed an efficient heterogeneous cross-domain authentication scheme based on proxy blind signature in cloud environment. This scheme gives the authority of the third-party legal agent by introducing a trusted certification center between the clouds. The authentication process is optimized by a trusted third party, but is prone to a single point of failure.

3  Identity Authentication Protocol

3.1 Protocol Description

The specific process of the scheme is shown in Fig. 1 below.

Figure 1: Anonymous authentication protocol structure diagram

The original signer hides his identity information by constructing a ring, sends the entrusting certificate to the proxy signer as a ring, and distributes the information that can represent his identity to the proxy signer in the way of the threshold. After receiving the entrusting certificate and key fragment, the proxy signer shares the information with the members in the ring to calculate and generate the proxy threshold ring signature.

Privileged member A, proxy signature terminal N, edge computing server MEC and key generation center (KGC) have shared keys, but they do not have identity authentication keys between them. Therefore, through the following protocol process, privileged members can be made A shared identity key kan is obtained between A and the proxy signature terminal N, and a shared identity key kmn is obtained between the proxy signature terminal N and the edge computing server MEC. The specific process is as follows:

(1)   Privileged member A sends his identity information IDA and request req1 to obtain the shared identity key to the proxy signature terminal N.

(2)   N packs the received information of A with its own identity information IDN and request req2 and sends it to the edge server MEC.

(3)   MEC packs the received information of N with its own identity information IDM and request req3 and sends it to the key generation center KGC.

(4)   After the KGC receives the information from the MEC, it generates three random numbers rK1,rK2,rK3 and returns it to the MEC. The MEC keeps one of its own and sends the remaining two to N, and N repeats the above steps. MEC, N, and A obtain the random number rK3,rK2,rK1 generated by KGC, respectively.

(5)   A generates a random number rA, encrypts the shared identity key information that it wants to obtain with the shared key between KGC and sends it to N together with the random number. N is the same as above, packs its random number rN, encrypted information, and received information to MEC. MEC sends {rK1||rA||IDA||IDN}Kak,rA,{rK3||rM||IDM||IDN}Kmk,rM,{rK2||rN||IDN||IDA||IDM}Knk,rN to KGC.

(6)   After receiving the information, the KGC obtains the needs of different users through decryption and returns the requested information {rA||kan||IDK}Kak,{rN||kan||kmn||IDK}Knk,{rM||kmn||IDK}Kmk to the MEC.

(7)   After MEC receives the information, it sends the information to N and A layer by layer.

(8)   After A, N, and MEC decrypt the received information, they obtain the identity keys kan and kmn.

3.2 Safety Analysis

The security analysis of this scheme can be proved by formal methods (including BAN logic, model checking (CSP), theorem-proof (string space) and other methods). BAN logic is mainly used to analyze whether the cryptographic protocol can normally work, what content has been completed by the protocol, the assumptions required by the protocol, and the rationality of the assumptions [20]. BAN logic is a logical analysis method based on knowledge and belief. The BAN logic definition and derivation formula used in the proof of this article are as follows.

3.2.1 Protocol Description

A−>N:IDA,req1N−>M:IDA,req1,IDN,req2M−>K:IDA,req1,IDN,req2,IDM,req3K−>M:rK1,rK2,rK3M−>N:rK1,rK2N−>A:rK1A−>N:{rK1||rA||IDA||IDN}Kak,rAN−>M:{rK1||rA||IDA||IDN}Kak,rA,{rK2||rN||IDN||IDA||IDM}Knk,rNM−>K:{rK1||rA||IDA||IDN}Kak,rA,{rK2||rN||IDN||IDA||IDM}Knk,rN{rK3||rM||IDM||IDN}Kmk,rMK−>M:{rA||kan||IDK}Kak,{rN||kan||kmn||IDK}Knk,{rM||kmn||IDK}KmkM−>N:{rA||kan||IDK}Kak,{rN||kan||kmn||IDK}KnkN−>A:{rA||kan||IDK}Kak

3.2.2 Inference Rules

(1)   Message meaning rules

P|≡Q⟷KP,P⊲{X}KP|≡Q∼X(1)

(2)   Temporary value validation rules

P|≡#(X),P|≡Q|∼XP|≡Q|≡X(2)

(3)   Arbitration rules

P|≡Q|⇒P,P|≡Q|≡XP|≡X(3)

(4)   Freshness rules

P|≡#(X)P|≡#(X,Y)(4)

According to the logic initialization hypothesis:

(1)   A|≡A⟷KakK

(2)   K|≡A⟷KakK

(3)   N|≡N⟷KnkK

(4)   K|≡N⟷KnkK

(5)   M|≡M⟷KmkK

(6)   K|≡M⟷KmkK

(7)   K|≡#(rK1)

(8)   K|≡#(rK2)

(9)   K|≡#(rK3)

(10)   A|≡#(rA)

(11)   N|≡#(rN)

(12)   M|≡#(rM)

(13)   A|≡K|⇒A

(14)   N|≡K|⇒N

(15)   M|≡K|⇒M

3.2.3 Logical Inference

(1)   Proof of K|≡A⟷kcnN:

        K⊲{rK1||rA||IDA||IDN}Kak,{rK2||rN||IDN||IDA||IDM}Knk

         From the initialization assumptions (2), (4) and rule (1), we can get:

          K|≡A∼{rK1||rA||IDA||IDN}K|≡N∼{rK2||rN||IDN||IDA||IDM}

         From the initialization assumptions (7), (8) and rule (4), we can get:

          K|≡#{rK1||rA||IDA||IDN}K|≡#{rK2||rN||IDN||IDA||IDM}

         From the above results and rule (2), we can get:

          K|≡A|≡{rK1||rA||IDA||IDN}K|≡N|≡{rK2||rN||IDN||IDA||IDM}

         So: K|≡A⟷kcnN

(2)   Proof of K|≡M⟷kmnN:

         K⊲{rK2||rN||IDN||IDA||IDM}Knk,{rK3||rM||IDM||IDN}Kmk

         From the initialization assumptions (4), (6) and rule (1), we can get:

          K|≡N∼{rK2||rN||IDN||IDA||IDM}K|≡M∼{rK3||rM||IDM||IDN}

         From the initialization assumptions (8), (9) and rule (4), we can get:

          K|≡#{rK2||rN||IDN||IDA||IDM}K|≡#{rK3||rM||IDM||IDN}

         From the above results and rule (2), we can get:

          K|≡N|≡{rK2||rN||IDN||IDA||IDM}K|≡M|≡{rK3||rM||IDM||IDN}

         So: K|≡M⟷kmnN

(3)   Proof of M|≡M⟷kmnN:

          M⊲{rM||kmn||IDK}Kmk

         From the initialization assumptions (5) and rule (1), we can get:

          M|≡K∼{rM||kmn||IDK}

         From the initialization assumptions (12) and rule (4), we can get:

          M|≡#{rM||kmn||IDK}

         From rule (2), we can get:

          M|≡K|≡M⟷kmnN

         From the initialization assumptions (15) and rule (3), we can get:

          M|≡M⟷kmnN

(4)   Proof of N|≡M⟷kmnN,N|≡A⟷kanN:

          N⊲{rN||kan||kmn||IDK}Knk

         From the initialization assumptions (3) and rule (1), we can get:

          N|≡K∼{rN||kan||kmn||IDK}

         From the initialization assumptions (11) and rule (4), we can get:

          N|≡#{rN||kan||kmn||IDK}

         From rule (2), we can get:

          N|≡K|≡M⟷kmnNN|≡K|≡A⟷kanN

         From the initialization assumptions (14) and rule (3), we can get:

          N|≡M⟷kmnNN|≡A⟷kanN

(5)   Proof of A|≡A⟷kanN:

         A⊲{rA||kan||IDK}Kak

         From the initialization assumptions (1) and rule (1), we can get:

          A|≡K∼{rA||kan||IDK}

         From the initialization assumptions (10) and rule (4), we can get:

          M|≡#{rA||kan||IDK}

         From rule (2), we can get:

          A|≡K|≡A⟷kanN

         From the initialization assumptions (13) and rule (3), we can get:

          A|≡A⟷kanN

4  Signature Scheme

4.1 Key Generation Algorithm

Let q be a large prime number, point P be the generator of the additive cyclic group G1 of order q, G2 be the multiplicative cyclic group of the same order, and bilinear mapping e:G1×G1→G2. Hash:H1{0,1}∗→G1, Hash:H2{0,1}∗→Zq∗ is a hash function, H1 maps any bit string to a point in the group G1, H2 maps any bit string to a number in G1. Select s as the primary key and Ppub=sP as the system public key randomly. Expose the system parameter <G1,G2,e,q,P,Ppub,H1,H2>.

The signer can send his identity information to the Key Generation Center (KGC) to obtain his private key. After KGC confirms his identity, it hashes the ID, QID=H1(ID), which can be used as his public key, and then calculates his private key SID=sQID. KGC sends the public and private key pair (QID,SID) to the corresponding member through the private channel.

4.2 Agent Generation Algorithm

4.2.1 Pretreatment Stage

The original signer A is a privileged user whose identity information is ID0. The proxy signer is a wireless terminal device. The ring L={ID1,…,IDn} has n members and consists of a wireless terminal device. The identity information of L is IDs=H1(ID1||…||IDn). At this time, the private keys of the original signer and the proxy signer are SID0=sQID0,SIDs=sQIDs. N members hold a private key fragment of the proxy signer’s private key in a threshold manner. The KGC selection threshold polynomial is generated as follows:

f(x)=SIDc+(∑i=2tai−1xi−1)QIDc=(s+∑i=2tai−1xi−1)QIDc(5)

Each proxy signer IDi(i=1,…,n) gets the corresponding key fragment f(IDi).

4.2.2 Agent Phase

(1)   The signature information is m, and the original signature is generated into a delegation certificate m. The delegation certificate includes the ring’s information where the original signer and the proxy signer are, the time stamp, the information of the file to be signed, etc. The timestamp is used to limit the validity of the signature. Calculate h=H2(m||W||L).

(2)   The original signer A randomly selects r∈Zq∗, calculates and publishes the rP, then calculates the rPpub and sends it to the member MEC server IDc.

Original signer selection threshold polynomial:

h(x)=rPpub+(∑i=2tai−1xi−1)QIDP(6)

Each proxy signer IDi(i=1,…,n) obtains the corresponding fragment h(IDi).

4.3 Signature Generation Algorithm

(1)   The proxy signer IDi(i=1,…,t,i≠c) participating in the signing selects Ui∈G1 and calculates hi=H2(m||W‖L‖Ui), ∀i∈{1,…,t}∖{c}

(2)   MEC server IDc selects a random rc∈Zq∗, calculates Uc=rcQIDc−∑i≠c{Ui+hiQIDi} and hc=H2(m‖W‖L‖Uc). The MEC calculates rc+hc and returns it to the proxy signer IDi.

(3)   Proxy signer IDi calculates Vi=(rc+hc)f(IDi)+h(IDi) and sends it to MEC server IDc.

(4)   The MEC server IDc calculates V=∑i=1tλiVi and λi as Lagrange multipliers and outputs the proxy signature σ of the message m:σ={Ui=1t{Ui},V}.

5  Signature Verification

The MEC performs the following verification after receiving the signature information:

Verify that e(Ppub,∑i=1t(Ui+hiQIDi)+rP)=e(P,V) is valid. If yes, the signature is accepted. The specific process is as follows:

e(Ppub,∑i=1n(Ui+hiQIDi)+rP)=e(Ppub,(Uc+hcQIDc)+∑i=1,i≠cn(Ui+hiQIDi)+rP)=e(Ppub,rcQIDc+hcQIDc+rP)=e(P,V)(7)

6  Performance Analysis

6.1 Security Analysis

The scheme in this paper is based on the typical Shamir threshold and bilinear technique to construct the signature. According to the characteristics of the threshold, the following conclusions can be drawn: any node whose weight sum is less than the threshold value cannot complete the signature, and any node whose weight sum is greater than or equal to the threshold value can complete the signature. Therefore, the scheme can resist the collusive attack of any member whose sum is less than the threshold. At the same time, a typical security analysis scheme is adopted, and the security of this scheme can be reduced to a discrete logarithm problem. The difficulty of the proposed scheme is equivalent to solving the discrete logarithm problem.

Discrete logarithm problem: given a random number Z∈G, the finding r(r>1) makes rP=Z difficult for the group. The variant form is as follows: Given R∈G,h∈Zq, it is difficult to find T∈G that satisfies h=e(R,T).

Theorem 1: Suppose there is an adaptive selection message and identity of the attacker F with a non-negligible probability ε to break the scheme within PPT time. Then, algorithm C solves the discrete logarithm problem with a non-negligible probability ε′=O(ε) in PPT time. Where O(ε) represents the quantity that ε is not less than a certain constant (which is related to the capability of the random predictor qH1, qH2, qL, but independent of the safety parameter K).

Proof: Assuming C is a challenger, C’s goal is to call F to solve the discrete logarithm problem eventually.

(1)   Setup: C runs the setup algorithm. C maintains T signature ID1,…,IDN public keys and constructs two predictors H1 and H2 (see the structure below for the structure of H1 and H2). C sends data {ID1,…,IDN,H1,H2} to attacker F as a public parameter.

(2)   H1 Query: C maintains a list H1L with the array {IDi,Qi}. C prepared qH1 responses Q1,…,QqH1 randomly. When F accesses the value H1 of IDi, C retrieves {IDi,Qi} from the list H1L and sends Qi to F.

(3)   H2 Query: C maintains a list H2L with {IDi,mj,Ui,hi}. C prepared qH2 responses to h1,…,hqH2 randomly. When F accesses H2 value of IDi,mj,Ui, C retrieves {IDi,mj,Ui,hi} from the list H2L and sends hi to F.

(4)   Signature Query: C maintains a list LL containing qL an array LL. F makes a signature query to mi, C first checks whether mi is in the list H2L, then restores {mi,σi} and sends σi to F.

Attacker F interacts with attacker C and C outputs based on the preceding policy.

When F stops asking, F outputs a signature σj about mj (whose signature was never asked) that satisfies Ver(mj,σj)=1. C restores {IDi,mj,Ui,hi} from the list H2L and {IDi,Qi} from the list H1L. Set h=e(Ppub,∑i=1n(Ui+hiQIDi)+rP), then e(P,V)=h. Since h has not been asked, the discrete logarithm problem is solved correctly.

If h is equal to some value that has already been queried, the probability is qL2n according to the drawer principle. So the probability that C successfully solves the discrete logarithm problem is still ε′=O(ε)+qL2n=O(ε).

6.2 Efficiency Analysis

Tab. 1 shows the time complexity of each operation.

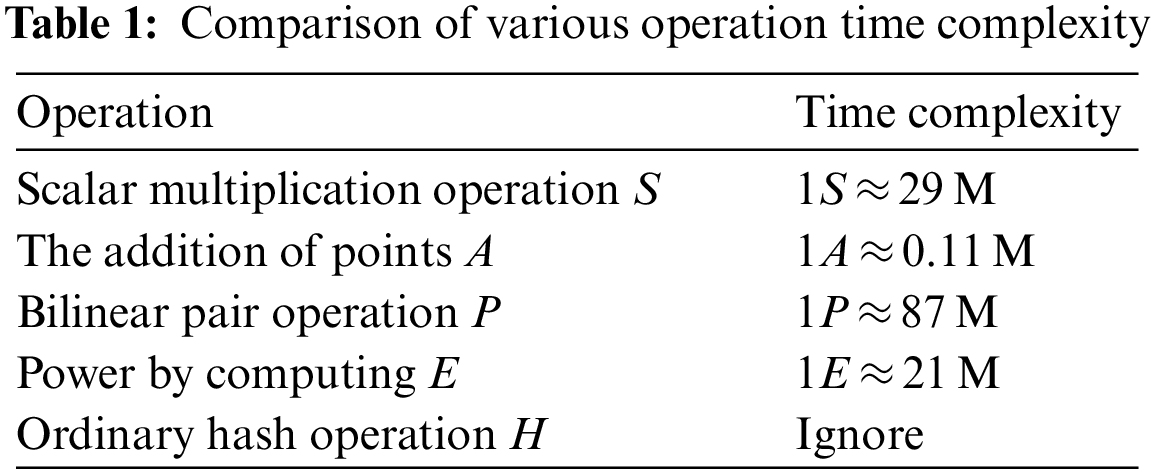
Comparison data refer to reference [21]. And P represents the bilinear pair operation, S represents the scalar multiplication operation on the elliptic curve, A represents the addition operation of two points on the elliptic curve, E represents the power multiplication operation, and M represents the dot multiplication operation. Reference [22] tested the calculation time of number multiplication on an elliptic curve on a 900 KHz sensor is about 2.6 s. Considering the intelligent terminal of the latest CortexA9 1.2 GHz microprocessor, the calculation time of number multiplication on the elliptic curve is about 0.00195 s (1S). The efficiency of each stage of the scheme is as Tab. 1.

It can be seen from Tab. 2 that the calculation time of the key generation stage is linear with the total number of members. When the number of members increases, the calculation time also increases. The calculation time of the signature generation and verification stage has a linear relationship with the threshold value. The larger the threshold value is, the longer the calculation time is. The calculation time of the agent stage is certain and has nothing to do with the total number of members and the threshold value.

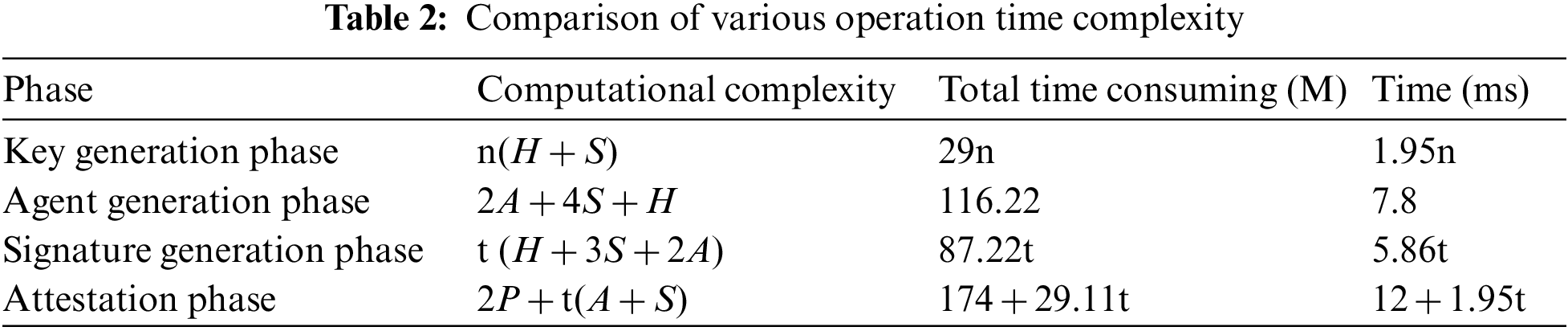
The performance comparison between the proposed scheme and the node without edge computing server is given below to evaluate better the influence of proxy threshold signature in the edge computing environment. As can be seen from Tab. 3, edge computing offloading optimizes the computing structure of the original signature scheme, offloads some high-consumption computations to edge computing servers, and greatly improves the computing efficiency of terminal nodes.

7  Conclusion

An identity-based anonymous authentication protocol for edge computing is proposed in this paper. This scheme combines proxy signature and ring signature, and at the same time, incorporates (t, n) threshold into it. And through correctness verification and security analysis, it is concluded that the signature has the characteristics of unforgeability and resistance to collusion attacks, which can provide timely response to information with timeliness and other characteristics, improve the efficiency of the signature, and ensure the identity of the proxy signer privacy. Through efficiency analysis, it can be seen that applying the solution in this paper to an edge computing system can make full use of the computing power of the MEC server, reduce the burden on wireless terminals, and improve system performance. Although the solution in this paper further releases the computing power of the terminal under the premise of ensuring anonymity, ensuring anonymity is redundant and complicated and not concise enough. We will further optimize the program to achieve better efficiency in the future.

Funding Statement: This paper was sponsored in part by Beijing Postdoctoral Research Foundation (No. 2021-ZZ-077, No. 2020-YJ-006) and Chongqing Industrial Control System Security Situational Awareness Platform, 2019 Industrial Internet Innovation and Development Project-Provincial Industrial Control System Security Situational Awareness Platform, Center for Research and Innovation in Software Engineering, School of Computer and Information Science (Southwest University, Chongqing 400175, China), and Chongqing Graduate Education Teaching Reform Research Project (yjg203032).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  T. Shanshan, M. Waqas, S. Rehman, T. Mir, Z. Halim et al., “Social phenomena and fog computing networks: A novel perspective for future networks,” IEEE Transactions on Computational Social Systems, vol. 9, no. 1, pp. 32–44, 2021. [Google Scholar]

 2.  Y. Liu, Y. Ren, Q. Wang and J. Xia, “The development of proxy re-encryption,” Journal of Cyber Security, vol. 2, no. 1, pp. 1–8, 2020. [Google Scholar]

 3.  N. Ahamed and N. Duraipandian, “Secured data storage using deduplication in cloud computing based on elliptic curve cryptography,” Computer Systems Science and Engineering, vol. 41, no. 1, pp. 83–94, 2022. [Google Scholar]

 4.  S. Tu, M. Waqas, S. Rehman, T. Mir, G. Abbas et al., “Reinforcement learning assisted impersonation attack detection in device-to-device communications,” IEEE Transactions on Vehicular Technology, vol. 70, no. 2, pp. 1474–1479, 2021. [Google Scholar]

 5.  K. Shankar and S. Venkatraman, “A secure encrypted classified electronic healthcare data for public cloud environment,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 765–779, 2022. [Google Scholar]

 6.  A. Berguiga and A. Harchay, “An IoT-based intrusion detection system approach for tcp syn attacks,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3839–3851, 2022. [Google Scholar]

 7.  S. Oliver and T. Purusothaman, “Lightweight and secure mutual authentication scheme for IoT devices using coap protocol,” Computer Systems Science and Engineering, vol. 41, no. 2, pp. 767–780, 2022. [Google Scholar]

 8.  P. Ranaweera, A. Jurcut and M. Liyanage, “MEC-Enabled 5G use cases: A survey on security vulnerabilities and countermeasures,” ACM Computing Surveys, vol. 54, no. 9, pp. 186:1–186:37, 2022. [Google Scholar]

 9.  X. Ding, X. Wang, Y. Xie and F. Li, “A lightweight anonymous authentication protocol for resource-constrained devices in internet of things,” IEEE Internet of Things Journal, vol. 9, no. 3, pp. 1818–1829, 2022. [Google Scholar]

10. P. Gupta and M. Kumar, “A verifiable ring signature scheme of anonymous signcryption using ECC,” International Journal of Mathematical Sciences and Computing, vol. 7, no. 2, pp. 24–30, 2021. [Google Scholar]

11. B. Gong, X. Zhang, Y. Cao, Z. Li, J. Yang et al., “A threshold group signature scheme suitable for the internet of things,” Concurrency and Computation: Practice and Experience, vol. 33, no. 13, 2021. [Google Scholar]

12. T. Preethi and B. Amberker, “Lattice-based group signature scheme without random oracle,” Information Security Journal: A Global Perspective, vol. 29, no. 6, pp. 366–381, 2020. [Google Scholar]

13. X. Yue and M. Xi, “A revocable group signatures scheme to provide privacy-preserving authentications,” Mobile Networks and Applications, vol. 10, pp. 1–5, 2020. [Google Scholar]

14. Y. Sun, Y. Liu and B. Wu, “An efficient full dynamic group signature scheme over ring,” Cyber Security, vol. 1, no. 1, pp. 15, 2019. [Google Scholar]

15. J. Subramani, A. Maria, A. Rajasekaran and F. Al-Turjman, “Lightweight privacy and confidentiality preserving anonymous authentication scheme for WBANs,” IEEE Transactions on Industrial Informatics, vol. 18, no. 5, pp. 3484–3491, 2022. [Google Scholar]

16. G. Verma and B. Singh, “An efficient and provable certificate-based proxy signature scheme for IIoT environment,” Information Sciences, vol. 518, pp. 142–156, 2020. [Google Scholar]

17. R. Swati and P. Sahadeo, “A quantum resistant anonymous poxy signature scheme,” Sādhanā, vol. 47, no. 1, 2022. [Google Scholar]

18. H. Zou, X. Liu, W. Ren, T. Zhu and M. Alazab, “A decentralized electronic reporting scheme with privacy protection based on proxy signature and blockchain,” Security and Communication Networks, vol. 2022, pp. 5424395:1–8, 2022. [Google Scholar]

19. J. ZeTao and X. JuanJuan, “Efficient heterogeneous cross domain authentication scheme based on proxy blind signature in cloud environment,” Computer Science, vol. 47, no. 11, pp. 60–67, 2020. [Google Scholar]

20. M. Burrows, M. Abadi and R. Needham, “A logic of authentication,” ACM Transactions on Computer Systems, vol. 8, no. 1, pp. 18–36, 1990. [Google Scholar]

21. S. Islam and G. Biswas, “A Pairing-free identity-based authenticated group key agreement protocol for imbalanced mobile networks,” Annals of Telecommunications, vol. 67, no. 11, pp. 547–558, 2012. [Google Scholar]

22. Y. Lin, “Design and implementation of identity authentication scheme based on elliptic curve cryptography on WSN,” Ph.D. Dissertation, Zhejiang University of Technology, China, 2008. [Google Scholar]