A Robust Asynchrophasor in PMU Using Second-Order Kalman Filter

1  Introduction

A smart grid is an advanced electrical grid that enables the management of grid operation. In addition, it remotely monitors the performance of the electrical grid by taking readings of its state and its components throughout devices, transformers, and feeder lines. To do this, it uses smart meters sent to the monitor and control room to ensure the reliability of the power flow as shown in Fig. 1. Therefore, it is an integrated and optimized electrical grid system that includes various power sources as well as control devices with wider accessibility and autonomous capabilities. Its working principle is based on automation techniques that require controls, computers, and sensors in a collaborative working environment using communication systems. The framework of the smart grid enables the grid to provide a unidirectional flow of electricity as well as network status data through a digital communication system which allows the amount of change in the grid to be monitored. The change results from user behavior and equipment malfunction and interactions with such necessary procedures to ensure the reliability of the grid and the conductivity of the power system to operate smoothly and securely. Thereby, it has several capabilities; most notably, is the possibility of self-restoration and enabling consumers to become producers simultaneously. Additionally, it has the potential to rapidly restore and enable consumers to become producers simultaneously. It reinforces the idea of a micro-grid with independent operating capabilities if required [1].

Figure 1: Elements of smart grid

The smart grid originated in the power system’s operating system through a mechanism that relies on remote control access for monitoring the grid. The principle of the system’s work depends on a communication system to transmit data about the state of the system to take an accurate perception of the state of the grid. The phase measurements took from the PMU is being dispatched to the control facility to make the most appropriate decision according to the system’s hosting capacity of each feeder to ensure the stability and power quality of grid. Smart grid development has allowed the ability to deal with bidirectional power flow, enhancing the opportunities for distributed generation at the consumer site. Therefore, the network system has been dealing with the increase of a large amount of data with such sensitivity throughout Phasor Measurement Units (PMUs), Supervisory Control Systems And Data Acquisition (SCADA), and the like, which requires further development and improvement to ensure its protection and reliability [2].

A power systems’ state estimation has become an essential and effective tool to monitor and control the power grid to ensure the grid’s reliability and safety for all stakeholders. Therefore, the PMU represents the most effective and substantial control device due to its capability. This is based on the synchronization of a GPS time-stamped signal through a GPS signal receiver to determine the time and location of a certain phase in real-time. Such a real-time system process is relied on by an advanced communication system to ensure a speedy sampling rate. However, it is expensive and requires further development to reduce costs with high performance. In [3], the author discussed the optimal allocation of PMUs to cover the grid with a minimum number of PMUs for microgrids.

The continuity of smart grid improvement and introduction of Distributed Energy Resources (DERs) with a limited production capability has led to the formation of several micro-grids. These micro-grids are self-sufficient in handling the required energy for consumption partially or completely. A microgrid is based on a decentralized set of small-scale Distributed Generation (DG) near the local loads, as illustrated in Fig. 2, which operates in grid-connected mode to the main grid with such formation creating the concept of a decentralized power system [4]. Its working principle is based on full operation separately from the main grid known as an off-grid mode in the case of power or system failure. However, the high Photovoltaics (PV) penetration into the Low Voltage (LV) networks causes technical difficulties in network stability and power quality which could lead to an electric outage and load increase in the local grid. Such a problem occurs due to overvoltage by DG. PV in the LV network has raised concerns to overcome the problem. Therefore, the necessity for a developed control system masterly estimates the changes and increases in voltage and the level of loads in the local low voltage network with the instant control feature that enables it to ensure the reliability of the network operation for the microgrid as well as the main grid as a whole [5].

Figure 2: Micro-gird diagram

1.1 Phasor Measurement Unit

Phasor Measurement Unit (PMU) can be recognized as monitoring device to assist estimating the amount of the signal magnitude and phase at certain point in the grid based on synchronized common time source. The PMU measures the voltage and current signal amount at numerous spots along the power grid for monitoring. The importance of phasor approximation extensively propagated to enhance in monitor, control, and system protection design. The cost function of a power station remains proportionally to a system’s phase error.

The data obtained to the PMU are GPS timely stamped to effortlessly promote better monitoring for wide grid to take sample measurement of the voltage and current in timely fashion. Some of the PMU estimation approach has been introduced in [6] include Discrete Fourier transform (DFT), and zero crossing which assist to monitor the system’s conditions considering phasor data. The DFT estimation approach of the PMU was considered using symmetric component distance relay process where those units offer widely supervision to the grid condition, to abstain from blackout and maintain network stability. Such optimal grid operation would promotes the flexibility to integrate with Smart grid steadily take into consideration the grid data analysis for network operation tuning and communication protection. The key units of the PMU device contain synchronization clock, measurement, and transmission unit. This paper [6] illustrates numerous approaches to estimate the system’s phase including Kalman Filters as well as the PMU framework which identifies the synchronization, measurement, and data units.

The acquired data to the PMU has been gathered from numerous locations around the grid to monitor the health of the grid operation, those date are real-time Global Positioning System (GPS) stamped [6,7]. The functionality of the PMU relies on taking the sample measurement of voltage and current beside the system phasor timely-stamped GPS forming so-called Synchrophasor. Synchrophasor can simply be defined by the amount of synchronized phasor which represents the power state at certain location of the gird. Typically, it is formed in a complex order where signal shaped in sinusoidal waveform contains magnitude and phase. Noteworthy, the extracted phasor of the PMU encloses crucial data about voltage and current by 1 μs. Power grid operator gathers the data all over the gird to avoid improper action may occur along the grid.

The PMU measurements rely on synchronized time-stamped data using GPS [7]. It is used for the phasor measurement of the power system to ensure the operation of the grid’s reliability. It plays a significant role to control, monitor, and protect the state of the power system. It is a state estimation application to estimate the phasor for every bus in the system. The input data to the PMU comes in an instantaneous form which presents either voltage or current magnitude and phase to a specific Point of Interconnection (POI) across the grid. Those PMUs locations are considered the most critical locations such as transformers to safeguard the grid. The phasor measurement signifies the designing of various protection elements and control mechanism to the gird. The cost of operation for an energy source is proportional to inaccurate phase. It is essential to work on the introduction of an enhanced phasor estimation technique in which to outperform the system’s reliability as it has been introduced in this paper which is Second-Order Kalman Filter (SOKF). The conceptual work of the PMU is based on gathering real-time data from certain positions around the power grid. These data represent voltage or current phase measurements which are enveloped in time-stamped GPS signals to form Synchrophasor where it is formed in a complex value of the sinusoidal waveform for amplitude and phase to identify the state of the power system. This unit has helped the network operator to keep up with the real-time state of the system, but it requires working on development and operation cost. The PMU produces the state phasor of the power system at the desired site to control the power system and take the appropriate action for such conditions of the dynamic system.

The presented PMU mechanism which is to evaluate the state of the system phase in [8] considers the synchronization technique with employment of Kalman Filter (KF) approach to reach the desired network accuracy for enhanced operation. PMU can deliver around 50 samples of voltage or current magnitude and phase per second. The PMU data can be analyzed to define the system frequency and its abnormality while those records are timely stamped Global Positioning System (GPS) data. PMU functionality led to estimates and identifies the system stability throughout the collection for either voltage or current magnitude and phase for each feeder line of the grid.

In case, multiple power stations operate out of phase at different degrees, the lower power station level would reversely operate against the other station creating resistance mode due to massive power loss across the power grid and substations. Weak grid supervision may result in severe damages to system’s equipment due to least monitor and inaccurate estimation.

The PMU primary role is to ensure grid stability considering the phasor of the system by taking the GPS time-stamped system’s phasor measurement where the phasor data of either voltage or current are instantaneously produced in analog input form to the PMU. Those data collected from various highly effective locations along the gird to ensure the power quality and the safety of the power grid. While the importance of PMU is raising, the necessitate to development the PMU has to lay out less complex and low-cost grid operation to overcome the Photovoltaics (PVs) penetration of the Distributed Generation (DG). The DG integration necessitates faster response with lower operation cost and complexity reduction. Consequently, this research work proposes optimized mathematical technique for the PMU using SOKF that is robust and optimal.

The suggested work focuses on the capabilities to handle the excessive PV penetration of the DG and its challenge to the local gird due to the expansion of DG sources at the Low Voltage (LV) network level.

In [8], the author addressed Kalman Filter to estimate the synchronized phasor of the system through the distributed PMUs along the power grid for monitoring and control. The author addressed a KF for simultaneous phase estimation of the system through phase measurement units spread across the power grid to monitor and control performance reliability. Such measurement required linearization step process and synchronization clock units for the Synchrophasor.

The paper [9] discussed the rising challenges of the integration of Distributed Generation (DG) in the micro-grid. The authors addressed a proposed model considering Weighted Least Squares (WLS) process to handle the penetration of DG sources mainly Photovoltaics (PVs) to the low voltage distribution networks with respect to the PMU position along with the network.

1.2 PMU Structure

The PMU Structure consists of three main units, these units are the synchronization, measurement, and data unit as shown in Fig. 3 below. The synchronization unit provides the synchronized phasor to the measurement unit. The role of the measurement unit is to ensure the bandwidth of the signal is to be sampled within the limited range of the required frequency. So that the data unit transmits the processed signal throughout the transmission system.

Figure 3: PMU structure

The PMU is the phasor of the system measurement device which is used for monitoring and control of the power grid to certify the power connection reliability. It takes the phasor of the system for the voltage and current with GPS time-stamped for validity and allocation. The PMU principals’ work as shown in Fig. 4 takes place with the synchronization unit which includes a GPS receiver and a Phase-Locked Oscillator to deliver the sample clock for the measurement unit. The GPS receiver is a sinusoidal signal which carries the amplitude and frequency. PLL/PLO is to aliens the reference phase with the transmitter phase. The measurement unit contains an anti-aliasing filter to certify that the sampled bandwidth of the signal is within the permissible frequency range, the analog-to-digital converter, and the phase processor., analog to digital converter, and phasor processor. The data transmission unit receives the data from measurement unit to be transmitted through the Modem [10,11].

Figure 4: PMU principals’ work

Considering the PMU principals’ work in Fig. 4, GPS receiver and phase-locked oscillator forms a sample clock to the measured data throughout the anti-aliasing filter assuring the required frequency range of the bandwidth of the signal, analog to digital converter to converts the input analog signal to digital signal and process the phasor to the data unit. The data unit collects the processed phasor coming from the measurement unit.

The existing PMU has demonstrated technical challenges due to the rapid development and changing patterns of smart grid operation with the integration of DGs. Therefore, Synchrophasor may present tremendous error due to the traditional synchronization process where the traditional technique is based on a synchronization process [12].

1.3 KALMAN FILTER

Kalman Filter is an estimation approach that was introduced by Dr. Rudolf E. Kalman in his 1960 publication. It is a set of mathematical estimation processes based on prediction and updating the state measurement using a mathematical model to provide the best solution out of the system. Kalman Filter’s application is vastly known in signal processing and control systems applications. It stands out as one of the most sensing and highly accurate Linear Quadratic Estimation (LQE) algorithms for predicting data today. This is due to its low cost and the redundancy characteristic, which is based on updating the state of measurement to correct the previous estimation state. Kalman Filter capabilities reach far and beyond many kinds of noises including Gaussian and Non-Gaussian noise. The Kalman Filter estimation process is widely considered to filter the signal from noise and distortion. It relies on updating the filtered system state by knowing the dynamic of system behavior in advance, and then updating the prediction of the next state and then correcting the prediction result [12].

Kalman Filter is a recursive estimation process as shown in Fig. 5. It begins with an initial estimate to predict the projection of the next state, and error covariance, and then computes the Kalman gain, and updates the measurement estimation and error covariance. So, it’s simply predicting the next state through the mathematical model and then updating the state estimation measurement. It works by predicting the next state using a mathematical model and then updating the state estimation measurement with feedback gain [12].

Figure 5: Kalman filter process

Extended Kalman Filter (EKF) is a linearization process for non-linear systems which enables the linearization of the state space of every step to the updated state estimation using either Taylor approximation or the Jacobian approach for a non-linear system. The existing applications mostly involve a non-linear differential equation whether it is the system or the state measurement [13,14].

State estimation enables control of the online network due to the sensitivity of the state of the network to ensure efficient operation particularly for microgrids that may rely on DG at certain conditions.

1.4 Signal Noise

Signal systems are exposed to many phenomena that affect their performance and cause signal weakness due to several factors which could be resulting from communication, device, and equipment condition, as well as external interference to the signal as a result of natural surrounding conditions.

1.4.1 Gaussian Noise

Gaussian noise is a normal distribution that helps to figure out the noise effectiveness applied to the signal of the system to validate the quality of the signal throughout the noise. The Additive White Gaussian Noise (AWGN) represents the most common type of Gaussian noise in a signal channel. In fact, AWGNs occur due to the high load on the electronic devices which cause noise, transmission environments, or communication interference. It allows us to identify the affected signal considering the disturbance and noise along with the transmitted signal as shown in Fig. 6 below [15].

Figure 6: Additive white gaussian noise channel

1.4.2 Non-Gaussian Noise

Since communication and signal systems are exposed to numerous various types of noises which may be different from Gaussian noise, it is essential to frame a highly disruptive environment. Therefore, non-Gaussian noise has been included to validate the system’s signal robustness to tackle the system’s signal in such severe environmental conditions. Non-Gaussian noise is basically a mixture of multiple Gaussian noises forming a severe noise environment as shown in Fig. 7 below. In this paper, the proposed method is considered under different environments to test the system’s robustness [15].

Figure 7: Non-gaussian noise

2  Related Work

The rapid increase of the data rate in the PMUs has required extreme development. Yet, the higher data collection rate has allowed better situational awareness along with the development of better tools. However, it has created a significant concern to handle these data efficiently with less cost consumption and lower error rates. Thus, there is an imperative need for highly efficient mathematical tools that ensure a lower error rate with fewer operation costs and complexity [16,17].

In [18] the research proposes an improved method for dealing with bad data in power systems via the PMU while the high PMU rate measurement. This proposed method introduces an algorithm that checks the measured data to identify the bad data. It detects the wrong measurement condition and its location to enhance the accuracy of the measurement. Moreover, the performance of the proposed model was verified by testing it under several environments to ensure the robustness of the model in different operational conditions.

This paper [19] presented the application of KF for phase tracking in Binary Phase Shift Keying (BPSK) in the ZigBee system to optimize the phase changes with consideration of the presence of the Additive White Gaussian Noise (AWGN). The outcome of the proposed method was promising due to its high accuracy to track the phase changes in the presence of AWGN which encouraged it to expand the research work on the phase optimization process.

In this paper [20], the authors investigated the effectiveness of Extended Kalman Filter (EKF) to track the phase changes mainly Binary Phase Shift Keying (BPSK) using ZigBee receivers. The proposed method was applied for the optimization of the phase changes to minimize the phase error under different types of environments.

In this paper [21], the authors deal with the method of using the Kalman filter residuals to expose the transient state in the PMU by recognizing the differences between the measurement and estimated values. Note that the difference is close to zero at the steady-state, which is exactly the opposite when the unforeseen shifts present a greater raise to show the extent of the unalike between the measurement and estimated values. Therefore, the authors resorted to studying the performance to discover the magnitude and phasor of the system along with the power quality of the system including the frequency shifts and the grid state of power transient.

The proposed method in this paper [22] used multiple Linear Kalman Filters (LKF) connected to each other to form a new form of phase tracking with enhanced prior knowledge about the phase. The method considered the Kalman Filters to be tested under different types of noises to validate the robustness of the proposed solution to the system’s phase tracking. The system’s novelty was verified by considering Mean Square Error (MSE) in consideration of Signal to Noise Ratio (SNR).

The PMU measures the amplitude and phase of the voltage and current along with various locations along the electrical grid. Its primary work is based on the value of the phase for the collected data using an optimal estimation process. With the enormous role of the PMU in controlling and protecting the grid systems in various circumstances and locations, it is highly important to work on advancing phasor estimation technique to contribute to raising the level of accuracy at a lower cost and with higher efficiency.

The authors [23] discussed two types of nonlinear Kalman Filters for estimating battery system state behavior. One of which is the Extended Kalman Filter (EKF) that requires a linearization step process to its state space equation. In contrast, the Unscented Kalman Filter (UKF) relies on unscented transformation [24,25].

The purpose of this paper [26] was to examine the replacement of the Phase Locked-Loop (PLL) with the LKF for phase changes optimization process within the ZigBee receiver through different operation conditions. The implication of LKF revealed accurate estimation for the phase changes with respect to different types of noises. Such application outcome encourages to develop an optimization to a similar system’s condition.

PMU stands out as one of the most useful tools for monitoring and controlling the smart grid. It forms a significant functionality in control and supervision of the smart grid systems by taking the system’s phasor in different parts of the network to ensure the reliability of operation. The ultimate use of PMU is to detect the measurement of the magnitude and phase for the voltage or current at a certain time and location synchronized with a time stamped GPS clock. Therefore, the existing PMU highlights the importance of optimization to save the cost with less complexity to handle the existing network deals with the penetration of distributed Photovoltaics (PV).

In this paper [27], the H∞ filter has been introduced referring to the Extended Kalman Filter. The proposed model formed what so-called H∞ Extended Kalman Filter (HEKF) to enable the dynamic control system to face the operation challenges for various power system conditions. Therefore, it requires a solid control system that is capable of bypassing these variables steadily and ensuring the network conductivity safely. The proposed model was tested using IEEE 39-bus system for the effectiveness verification. The paper considered EKF and UKF for comparison with HEKF which outperformed them in two different cases. Note that the proposed model requires a linearization step using the Jacobian matrix.

The authors [28] discussed the parametric variables on the dynamic state estimates for Phasor Measurement Units of the synchronous power generation systems employing Monte Carlo method. Both Extended Kalman Filter (EKF) with unknown inputs and Unscented Kalman Filter (UKF) were investigated to recognize the out of which these filters fit effectively on the estimation process due to parametric variabilities using the IEEE 39 bus system. The authors concluded this paper by assuring that the selection of the type of Kalman filter would not impact the estimation process looking at the deviation of the parametric variation where UKF has lower MSE while EKF has shown the opposite.

This paper [29] discussed several models for state estimation process for the Phasor Measurement Units (PMU) associated with the generation side, where the focus was on the Least Square Errors (LSE), Extended Kalman Filter (EKF), Unscented Kalman Filter (UKF) for each of the parameters and states.

In [30], a study has been conducted to illustrate the differences among several methodological tools within the Bayesian framework for dynamic system estimation for the PMUs outcome data. This study includes Extended Kalman Filter (EKF), Unscented Kalman Filter (UKF), Ensemble Kalman filter (EnKF), and the Particle Filter (PF) where each method has been gone through robustness validation work including different type of noise. The studies show how the EnKF outperformed the other methods in terms of accuracy to estimate the PMUs data while PF requires a high number of samples among the other methods for better accuracy. The performance of both EKF and UKF methods have demonstrated a greater robustness with lower sensitivity while EnKF required more time to present better accuracy tracking data.

In [31] there were two types of KF estimation process applied to this paper to track the system’s phase using high-speed data across PMUs of the power system grid which are EKF and the UKF. It was found throughout this research using MATLAB simulation tools that UKF could evaluate the mean and covariance to third degree and EKF able to the first degree. However, EKF performed better with real-time implementations.

An investigation has been conducted to determine the optimal estimation approach among Least Square estimator and Kalman Filter (KF) for the voltage sag within the power grid by estimating the systems’ power phasors. A comparison-based assessment of the capabilities of Least Square and KF designed to better estimate the phasor where the results showed the Least Square to excel for less than one cycle compared to the KF process [32].

The research in [33] introduced a Second-Order Kalman Filter (SOKF) to minimize the phase error as a new optimization method to reduce the phase signal error received from an access point based on a less complicated mathematical model of phase estimation process for the PMU. However, instead of applying the Extended Kalman Filter to enhance the estimation of the result, the Second-Order Kalman Filter indicates that the optimization of the result resulted in less system complexity and a result closer to the reference.

In this paper, the robustness of the new optimal method proposed in [33] has been analyzed where the system performance has been extensively tested using Mean Square Error (MSE) with respect to Signal to Noise Ratio (SNR) values. It shows more robustness with no linearization technique implemented. The simplified mathematical approach excludes the circuit to detect the system phase which is known as Asynchrophasor technique. It is well known that Asynchrophasor is less expensive than Synchrophasor. The proposed method has been verified in the presence of different nominal propagation where the solution results in a phase error minimization.

3  Methodology

3.1 Second Order Kalman Filter for PMU Phase Signal Detector

The Asynchrophasor technology has been formulated to overcome many challenges centered on eliminating the need for synchronous processes. The introduction of the Asynchrophasor has helped to ensure low cost and reduce complexity resulting in less error of the outputs of the PMU. Asynchrophasor estimation technique relies on a Second-Order Kalman Filter (SOKF) to reduce errors and complexity associated with the synchronization process. The working principle of this introduced technique does not require a synchronization process as shown in Fig. 8 which helps to reduce the cost. The synchronization process is an old technique to detect the Synchrophasor which was replaced in this proposed method by an efficient algorithm that is based on SOKF to detect phase changes as shown in Fig. 8 below. Such a new method will help to optimize the device and reduce and narrow down the cost with less error.

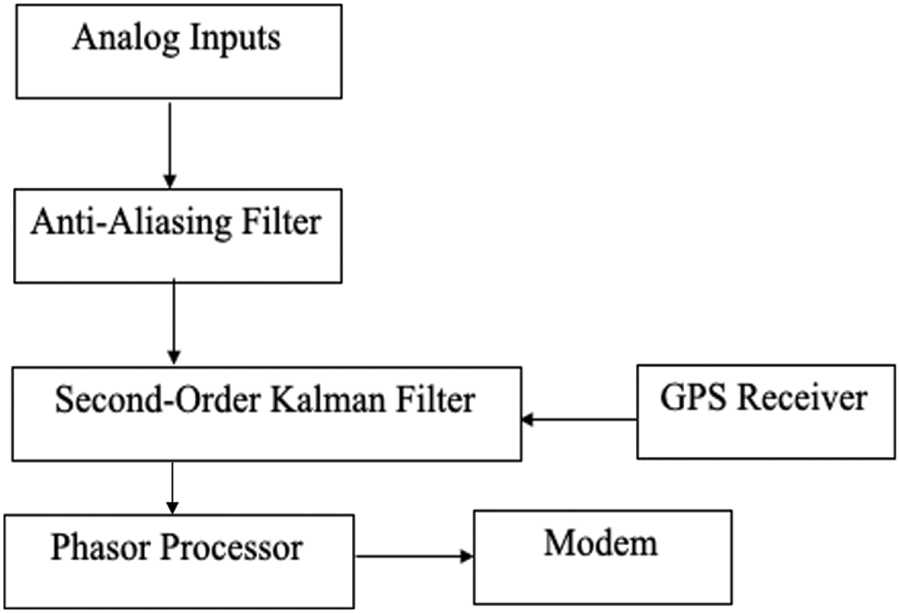
Figure 8: Asynchrophasor PMU structure

The optimized Asynchrophasor approach presented in this paper has been modeled using a Second-Order Kalman Filter (SOKF) to minimize the phasor error of the PMU. The intention of the proposed solution is to optimize the PMU to lower the cost and complexity which replaces the synchronization circuit by Asynchrophasor approach in the PMU layout. This proposed method includes a minimization process of phasor error based on Mean Square Error (MSE) with no linearization techniques needed. Such an intended method has shown how costless and robust the system is by considering the system outcome to be tested in the presence of Gaussian and non-Gaussian. Instead of Synchrophasor for the synchronous phase technique, the developed technique of the proposed solution within the PMU relies on an asynchronous phase technique which is known as Asynchrophasor.

The PMU signal is a sinusoidal function. The mathematical model of the PMU signal can be expressed as follows:

x(t)=Mcos(ωt+θ)(1)

Note that M is the amplitude of the sinusoidal function, where ω represents the angular frequency, and θ forms the variant of phase angle of the wave signal [34,35].

3.2 The Model Function of the PMU

The model function of the PMU is as addressed below (2) to employ the Second-Order Kalman Filter for phase detectors [36].

x(k+1)=Fx(k)+w(k)(2)

F=[01−w20][−w sin sinwt−w2cos coswt](3)

The time update equation x(k+1) includes the transition matrix F multiplied by the PMU’s general plant solution x(k) summed by the Gaussian noise which is noted by w(k).

z(k)=Hx(k)+v(k)(4)

H=[10](5)

The measurement equation is expressed by z(k), which involves the observation matrix H, and the measurement noisev(k). The application of the second-order Kalman filter indicates a mathematical model for the system’s phase in the state space variables where the time update equation includes the transition matrix with the addition to the noise in (3). The PMU’s general plant dynamical solution takes its place in both the time update equation and the measurement equation to update the estimation process to the phase error minimization. Such an asynchronous phasor process supersedes the existing synchronization process.

3.3 Kalman Filter Algorithm

In this section, the Kalman Filter algorithm has been utilized to predict and update the state space of the filter for the state of the phase accordingly. The estimation process of Kalman Filter begins with the prediction of the system’s phase with the initial estimate X0 along with the update error matrix P0. Then, the Kalman Filter Gain G is calculated for prediction correction. The error constraints are considered to update the estimation according to with and without the consideration of the deviation. Since Kalman Filter is a recursive process, the prediction and correction processes are implemented according to each time step n.

The following Tab. 1 describes the computing process:

4  Results

In this section, the optimal mathematical model was implemented using MATLAB simulation software to demonstrate the optimal Asynchrophasor technique in PMU as shown in Fig. 9 which is based on Second-Order Kalman Filter (SOKF) to track the system’s signal phasor across the PMUs allocated all over the grid. The simulation works for the proposed method include testing under different environments to present the robustness of the proposed model. This solution results in a phase error minimization. Note, that the figures below are considering the phase in radians vs. the number of samples.

Figure 9: PMU signal’s phase

In Fig. 10 the proposed method in the PMU has been considered in the presence of Gaussian noise as shown above where the Second-Order Kalman Filter has picked up the value of the Asynchrophasor as it takes a larger number of samples with very close results to the reference phase which Asynchrophasor results have performed better and closer than the Synchrophasor as it is represented in the blue line under Gaussian noise. The proposed model excels in the presence of Gaussian noise by using MSE to measure the effectiveness of the proposed technique based on SOKF, as it was shown that is able to better track the phase of the system in the presence of Gaussian noise. Notice that at the rate of 5 dB show the improvement whereby 21.45% under Gaussian noise.

Figure 10: MSE in presence of gaussian noise

Where in Fig. 11 the simulation results were considered in the presence of non-Gaussian noise. The Asynchrophasor approach in the PMU has performed better than Syncrhophasor under severe environmental conditions that show the robustness and effectiveness of the optimal method SOKF. Apparently, the SOKF approach has worked much better than the existing model in the presence of non-Gaussian noise that’s evaluated by MSE. Therefore, it’s crucial to have SOKF in place of the presence of non-Gaussian noise. It can be noticed how much improvement at the rate at 5 dB by 16.2% for the presence of non-Gaussian.

Figure 11: MSE in presence of non-gaussian noise

5  Conclusion

In this paper, a mathematical model is proposed using Second-Order Kalman filter (SOKF) in the PMU to reduce phase error and reduce operational cost. So, this simplified model is based on replacing the Asynchrophasor technique with Synchrophasor which outperforms the synchronization process. The simulation results of the proposed model explicate the robustness of the proposed method to minimize the phase error and reduce the cost in the presence of different environments which includes the presence of Gaussian noise and non-Gaussian noise. The outcomes of this optimization technique were verified by taking mean square error (MSE) with respect to SNR values to measure the phase error deviation of the signal. The proposed method includes the minimization of the phasor error that is based on Mean Square Error (MSE) and no linearization technique was needed. The optimal solution of the proposed method has obtained an effective and significant role in place of the present model. This research introduces the significance development for the proposed estimation approach in terms of operation cost and its affect. The estimated SOKF outcome offered better results compares to the Synchrophasor PMU with lower cost and robust values. Such development is highly effective due to the increase in the system stability in the presence of different environments, including in the presence of Gaussian noise and non-Gaussian noise.

Acknowledgement: This research is part of my PhD research work that is sponsored by King Faisal University, Al-Ahsa, Saudi Arabia through my studies at Oakland University, Rochester, MI, USA.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  I. Colak, R. Bayindir and S. Sagiroglu, “The effects of the smart grid system on the national grids,” in 8th Int. Conf. on Smart Grid (IcSmartGrid), Paris, France, pp. 122–126, 2020. [Google Scholar]

 2.  A. Shobol, M. Ali, M. Wadi and M. TüR, “Overview of big data in smart grid,” in 8th Int. Conf. on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, pp. 1022–1025, 2019. [Google Scholar]

 3.  K. Amiri, R. Kazemzadeh and O. Eghbali, “A novel optimal pmu location method in smart grids,” in Smart Grid Conf. (SGC), Sanandaj, Iran, pp. 1–5, 2018. [Google Scholar]

 4.  X. Xing, L. Xie and H. Meng, “Cooperative energy management optimization based on distributed MPC in grid-connected microgrids community,” International Journal of Electrical Power & Energy Systems, vol. 107, no. 19, pp. 186–199, 2019. [Google Scholar]

 5.  N. Alqahtani, S. Ganesan, M. Zohdy and R. Olawoyin, “Overvoltage mitigation in distributed networks connected to DG systems,” in Int. Conf. on Computing and Information Technology (ICCIT-1441), Tabuk, Saudi Arabia, pp. 1–6, 2020. [Google Scholar]

 6.  P. Nanda, C. K. Panigrahi and A. Dasgupta, “Phasor estimation and modelling techniques of pmu-a review,” Energy Procedia, vol. 109, no. 10, pp. 64–77, 2017. [Google Scholar]

 7.  A. Reis, F. Guarda and C. Gastaldini, “Simulation of a phasor measurement unit in real time using typhoon virtual hil,” in IEEE PES Innovative Smart Grid Technologies Conf.-Latin America, Gramado, Brazil, pp. 1–5, 2019. [Google Scholar]

 8.  S. Almasabi and J. Mitra, “An overview of synchrophasors and their applications in smart grids,” in ICICPI, Kolkata, India, pp. 179–183, 2016. [Google Scholar]

 9.  D. Macii, G. Barchi and L. Schenato, “On the role of phasor measurement units for distribution system state estimation,” in IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems Proc., Naples, Italy, pp. 1–6, 2014. [Google Scholar]

10. V. Centeno, A. Phadke and A. Edris, “Adaptive out-of-step relay with phasor measurement,” in Sixth Int. Conf. on Developments in Power System Protection, Nottingham, UK, pp. 210–213, 1997. [Google Scholar]

11. B. Pinte, M. Quinlan, A. Yoon, K. Reinhard and P. W. Sauer, “A One-phase, distribution-level phasor measurement unit for post-event analysis,” in IEEE PECI, Champaign, IL, USA, pp. 1–7, 2014. [Google Scholar]

12. R. Brown and P. Hwang, in Introduction to Random Signals and Applied Kalman Filtering, Hoboken, NJ, USA: John Wiley and Sons, 2012. [online]. Available: https://onlinelibrary.wiley.com/doi/abs/10.1002/acs.4480060509. [Google Scholar]

13. P. Zarchan and H. Musoff, “Fundamentals of kalman filtering: A practical approach,” in Astronautics and Aeronautics Progress, 3rd ed., Reston, VA, USA: American Institute of Aeronautics and Astronautics, vol. 232, pp. 257, 2009. [Google Scholar]

14. M. Rhudy, R. Salguero and K. Holappa, “A kalman filtering tutorial for undergraduate students,” International Journal of Computer Science & Engineering Survey, vol. 8, no. 1, pp. 1–18, 2017. [Google Scholar]

15. J. Proakis and M. Salehi, in Digital Communications, 5th ed., New York, NY, USA: McGraw-Hill, 2008. [Google Scholar]

16. J. Chen and A. Abur, “Placement of pmus to enable bad data detection in state estimation,” IEEE Transactions on Power Systems, vol. 21, no. 4, pp. 1608–1615, 2006. [Google Scholar]

17. P. Ashton, G. Taylor, M. Irving, I. Pisica, A. Carter et al., “Novel application of detrended fluctuation analysis for state estimation using synchrophasor measurements,” IEEE Transactions on Power Systems, vol. 28, no. 2, pp. 1930–1938, 2013. [Google Scholar]

18. M. Pignati, L. Zanni, S. Sarri, R. Cherkaoui, J. -Y. Le Boudec et al., “A Pre-estimation filtering process of bad data for linear power systems state estimators using PMUs,” in IEEE Power Systems Computation Conf., Wroclaw, Poland, pp. 1–8, 2014. [Google Scholar]

19. A. Alqahtani and M. Zohdy, “Zigbee signal phase tracking using a discrete kalman filter estimator under awgn channel,” Journal of Computer and Communications, vol. 07, no. 01, pp. 10–17, 2019. [Google Scholar]

20. A. Alqahtani, M. Zohdy, S. Ganesan and R. Olawoyin, “A novel phase tracking in zigbee receiver using extended kalman filtering over awgn channel,” in IEEE 10th Annual UEMCON, New York, NY, USA, pp. 0158–0162, 2019. [Google Scholar]

21. M. de Ápraiz, R. I. Diego and J. Barros, “Transient detection in phasor measurement units with kalman filtering,” in ICHQP, Ljubljana, Slovenia, pp. 1–6, 2018. [Google Scholar]

22. A. Alqahtani, S. Ganesan, M. Zohdy and R. Olawoyin, “A novel non-coherent oqpsk detection based on interactive kalman filtering with applications in zigbee receiver,” in IEEE Int. Conf. on Electro Information Technology, Chicago, IL, USA, pp. 601–608, 2020. [Google Scholar]

23. I. Jokić, Ž Zečević and B. Krstajić, “State-of-charge estimation of lithium-ion batteries using extended kalman filter and unscented kalman filter,” in 23rd Int. Scientific-Professional Conf. on Information Technology, Zabljak, Montenegro, pp. 1–4, 2018. [Google Scholar]

24. G. Welch and G. Bishop, “An introduction to the kalman filter,” 1995. [Online]. Available: https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf. [Google Scholar]

25. Q. Yu, R. Xiong, C. Lin, W. Shen and J. Deng, “Lithium-ion battery parameters and state-of-charge joint estimation based on h-infinity and unscented kalman filters,” IEEE Transactions on Vehicular Technology, vol. 66, no. 10, pp. 8693–8701, 2017. [Google Scholar]

26. A. Alqahtani and M. Zohdy, “An investigation into using kalman filtering for phase estimation in ieee 802.15.4/zigbee receivers running on adjacent channel interference,” in IEEE Int. Conf. on Electro Information Technology, Brookings, SD, USA, pp. 058–062, 2019. [Google Scholar]

27. J. Zhao, “Dynamic state estimation with model uncertainties using h∞ extended kalman filter,” IEEE Transactions on Power Systems, vol. 33, no. 1, pp. 1099–1100, 2018. [Google Scholar]

28. A. Paul, G. Joos and I. Kamwa, “Parameter validation for kalman filter based dynamic state estimation of power plant dynamics,” in IEEE EPEC, Saskatoon, SK, Canada, pp. 1–6, 2017. [Google Scholar]

29. L. Fan, “Least squares estimation and kalman filter based dynamic state and parameter estimation,” in IEEE Power & Energy Society General Meeting, Denver, CO, USA, pp. 1–5, 2015. [Google Scholar]

30. N. Zhou, D. Meng, Z. Huang and G. Welch, “Dynamic state estimation of a synchronous machine using PMU data: A comparative study,” in IEEE Power & Energy Society General Meeting, Denver, CO, USA, pp. 1–1, 2015. [Google Scholar]

31. H. Tebianian and B. Jeyasurya, “Dynamic state estimation in power systems using kalman filters,” in IEEE Electrical Power & Energy Conf., Halifax, NS, Canada, pp. 1–5, 2013. [Google Scholar]

32. Y. Amirat, Z. Oubrahim, G. Feld and M. Benbouzid, “Phasor estimation for power quality monitoring: Least square versus kalman filter,” in IECON 2017–43rd Annual Conf. of the IEEE Industrial Electronics Society, Beijing, China, pp. 4339–4343, 2017. [Google Scholar]

33. N. Alqahtani, S. Ganesan, M. Zohdy and R. Olawoyin, “Optimal asynchrophasor in PMU using second order kalman filter,” in IEEE Int. Conf. on Electro Information Technology, Chicago, IL, USA, pp. 635–637, 2020. [Google Scholar]

34. L. Du, J. -k. Huang and Q. -y. Liu, “A realization of measurement unit for phasor measurement unit based on DSP,” in 2012 Asia-Pacific Power and Energy Engineering Conf., Shanghai, China, pp. 1–3, 2012. [Google Scholar]

35. A. V. Linimol, J. Thomas and F. Fernandez, “Experimental analysis on FireFly and grey wolf optimization for phasor estimation in PMU,” in 2018 Int. Conf. on Circuits and Systems in Digital Enterprise Technology (ICCSDET), Kottayam, India, pp. 1–7, 2018. [Google Scholar]

36. P. Madhukar and L. Prasad, “State estimation using extended kalman filter and unscented kalman filter,” in 2020 Int. Conf. on Emerging Trends in Communication, Control and Computing (ICONC3), Lakshmangarh, India, pp. 1–4, 2020. [Google Scholar]