Robust and Reusable Fuzzy Extractors from Non-Uniform Learning with Errors Problem

1  Introduction

Authentication necessitates the use of a secret derived from some source with sufficient entropy. Because of their uniqueness and usability, biometric information such as fingerprints, iris patterns, and facial features can be a promising candidate, as can physical unclonable functions and quantum sources. Biometric authentication, in particular, makes a user’s life much easier because biometric information does not require a user to memorize or securely store anything in order to authenticate. However, two challenges are found to using biometric data. First, because biometric information is immutable, it is difficult to change once it has been leaked to an adversary. As a result, provable cryptographic security is critical for biometric storage systems. Second, whenever biometric data are generated, small errors occur as a result of the various conditions and environments. In other words, the biometric data provide similar but not identical readings at each measurement.

Since Dodis et al. [1] proposed the concept of a fuzzy extractor to address these issues, it has been regarded as one of the candidate solutions for key management using biometric data. A fuzzy extractor can extract the same random string from a noisy source without storing the source itself. A fuzzy extractor is made up of two algorithms (Gen, Rep). The generation algorithm Gen takes as input w (= an initial reading of the noisy source) and outputs an extracted string R and a helper data P. The reproduction algorithm Rep will reproduce R from w′ (= a second reading of the same source) with the help of P if w and w′ are close enough, i.e., the distance between w and w′ is small enough. The correctness of fuzzy extractor guarantees that the same string R is reproduced if the fuzzy data are generated from the same source. Furthermore, the security of the fuzzy extractor guarantees that the helper data does not reveal any information about the biometric data.

The majority of the fuzzy extractors are built on the sketch-then-extract paradigm, with a secure sketch and a randomness extractor as building blocks [2–5]. A secure sketch is an information-reconciliation protocol, which can recover the original value w from w′ if w and w′ are close enough, and then, the random string will be extracted from the recovered w using a randomness extractor. However, secure sketch has been shown to cause a small leakage of biometric data from helper data, resulting in security loss [6]. As a result, a fuzzy extractor based on secure sketch requires high entropy source data. Fuller stated in [6] that constructing secure sketches with computational unpredictability of w given helper data is still an open problem.

Fuller et al. [6] proposed a computational fuzzy extractor based on the learning with errors (LWE) problem that does not use a secure sketch nor a randomness extractor to avoid the negative result for secure sketches. The random string is not extracted from w in Fuller’s computational fuzzy extractor scheme; rather, w “encrypts” the random string in a way that can be decrypted with the knowledge of some close w′. Their approach prevents biometric data leakage from the helper data because the helper data hides secret randomness (the random string) using w, rather than extracting it from w. However, their construction is significantly inefficient and can only tolerate sub-linear errors due to the construction of the decoding algorithm during the reproduction phase, which is limited to guessing a subset of error locations and checking if the chosen part contains any errors. However, in order to be widely used in practice, a fuzzy extractor must be efficient in terms of costing time including generation algorithm and reproduction algorithm and be able to tolerate more than a certain level of error. Some biometric data, such as iris codes, exhibit linear errors. Repeated readings of the same iris demonstrate an average error rate of 10%–30% [7] for the iris code, which is proposed to represent human iris features [8].

Moreover, Fuller’s construction does not guarantee reusability or robustness. Boyen [2] formalized the concept of reusability, which is the security notion in the case that several pairs of extracted string and related helper data issued from correlated biometric data are revealed to an adversary. For multiple correlated samples (w,w1,…,wt) of the same source, reusability guarantees the (pseudo) randomness of R conditioned on (P,{Pi,Ri}i=1,…t) where (Pi,Ri)←Rep(wi). Robustness is the security notion in the case that an adversary modifies the helper data P before P is given to the user. A robust fuzzy extractor has been studied in order to protect against malicious alteration of helper data and to support mutual authentication between a user and a server. Robustness requires that any modification of P by an adversary will be detected. Boyen et al. [9] introduced the concept of robust fuzzy extractor, and Dodis et al. [10] strengthened robustness, which guarantees that the fuzzy extractor will detect any modification of P by an adversary who also has access to R. Both security concepts must be satisfied in order to use a fuzzy extractor as a secure authentication method in real life.

Canetti et al. [11] proposed a fuzzy extractor construction with inputs from low-entropy distributions that relies on a strong cryptographic primitive called digital locker to avoid the negative result for secure sketches as well. Their strategy is to sample many partial strings from a noisy input string and then independently lock one secret key with each partial string. This sample-then-lock method, however, necessitates an excessive amount of storage space for the helper value in order to store the hashed values of multiple subsets of the noisy data. To be widely used in practice, a fuzzy extractor must have a small size of helper data, which is stored in a server for authentication. Cheon et al. [12] later tweaked this scheme to reduce the size of the helper data. However, the computational cost of the reproduction algorithm significantly increased.

1.1 Contribution

We propose a new computational fuzzy extractor in this paper that does not rely on a secure sketch or digital locker. As a result, our scheme is efficient, and thanks to the new decoding algorithm, it can tolerate linear errors. To address the error caused by the difference between the biometric data used for registration and the biometric data used for authentication, we encode the extracted key using two cryptographic primitives: error correction code (ECC) and the EMBLEM encoding method [13]. We eliminated the recursive decoding algorithm from the previous fuzzy extractor [6], which improved the efficiency of our scheme. Unlike Fuller’s scheme, the decoding time for our scheme does not increase when the error rates increase. These points result to increased efficiency for the reproduction algorithm and error tolerance for the biometric data. For example, the reproduce algorithm for our scheme including decoding algorithm takes only 0.28 ms for 80-bit security with 30% error tolerance rates, whereas Fuller’s reproduce algorithm takes more than 30 s with 1.3% error tolerance rates [14]. Meanwhile, Canetti’s scheme [11], which is based on digital locker, requires a large size of helper data in order to store the hashed values of multiple subsets of the biometric data. For example, the helper data of their construction require approximately 33 GB of storage for 128-bit security with 19.5% error tolerance rates [13]. Meanwhile, the helper data for our construction require only 543 bytes for 128-bit security with 20% error tolerance rates. As a result, we demonstrate that our scheme is much more efficient because it has an efficient decoding algorithm compared to Fuller’s fuzzy extractor and has much smaller size of helper data compared to Canetti’s fuzzy extractor.

In addition, we extend our fuzzy extractor to robust and reusable. Both security concepts must be satisfied in order to use a fuzzy extractor as a secure authentication method in real life. Moreover, we present formal security proof for the proposed fuzzy extractor based on the non-uniform LWE (NLWE) problem [15] as well as concrete bit hardness for our scheme using a LWE-estimator. Furthermore, we provide parameter sets that meet the security requirements and present the performance of our fuzzy extractor’s implementation. As a result, in comparison to previous fuzzy extractor schemes, we build the computational fuzzy extractor that supports a much more efficient implementation with a smaller size of helper data, compared to previous fuzzy extractor schemes.

To ensure the security of our fuzzy extractor, we must assume that the biometric data are drawn from a uniform distribution. Also, we are well aware that in reality, many fuzzy sources, including biometric data, do not provide uniform distributions. The purpose of this paper is to inspire researchers to create an efficient computational fuzzy extractor based on our construction.

1.2 Related Works

Dodis et al. introduced the fuzzy extractor in 2004, which generates a cryptographically secure key using the user’s biometric data and is based on secure sketch [1].

Reusable fuzzy extractor: In 2004, Boneh et al. defined a reusable fuzzy extractor based on secure sketch and demonstrated that informational theoretic reusability necessitates a significant decrease in security, implying that the security loss is necessary [2]. In 2016, Canetti et al. [11] constructed a reusable fuzzy extractor based on the powerful tool “digital locker,” which is a symmetric key cryptographic primitive. The concept of the scheme is sample-then-lock, which hashes the biometric in an error-tolerant manner. In particular, multiple random subsets of the biometric data are hashed, and then, the values are used as a pad for a (extracted) cryptographic key. Following the second measurement, the cryptographic key is determined by hashing multiple random subsets of the biometric data. Correctness follows if it is likely that the first measurement and the second measurement is identical in at least one subset of biometric data. This scheme based on a digital locker requires a large size of helper data to store the hashed values of multiple subsets of the biometric data. The size of helper data of Canetti’s construction is too large to use the fuzzy extractor practically and the performance of reproduction algorithm is inefficient. To reduce the size of the helper data, Cheon et al. [12] modified Canetti's scheme in 2018. However, the computational cost of the reproduction algorithm even increased.

In 2017, Apon et al. [16] improved Fuller’s construction [6] to satisfy the reusability requirement using either a random oracle or a lattice-based symmetric encryption technique. However, it falls short of overcoming Fuller’s construction limitations: logarithmic fraction of error tolerance due to the time-consuming process of reproduction algorithm even with a small number of errors. Wen et al. [3] proposed a reusable fuzzy extractor based on the LWE problem in 2018, and their scheme is resilient to linear fractions of errors. However, their scheme is based on a secure sketch, and this point results in a leakage of biometric information.

Robust fuzzy extractor: In 2004, Boyen et al. [9] introduced the concept of robustness, and they proposed a general method for converting a fuzzy extract to a robust one using a secure sketch in a random oracle model. Dodis et al. [10] extended post-application robustness by requiring that any modification of P by an adversary who also sees R be detected. Since then, many works introduced information-theoretic fuzzy extractors with robustness [17,18].

Robust and reusable fuzzy extractor: In 2018, Wen et al. [5] defined the concept of robust and reusable fuzzy extractor in the common reference string model based on the decisional diffie-hellman (DDH) and the decision linear (DLIN) assumptions in the standard model, which is not post-quantum resistant. Traditional cryptography relies on the hardness of number-theoretic problems like integer factorization and discrete logarithm to ensure its security. With the advent of quantum computers, researchers demonstrated that quantum algorithms can solve problems such as DDH and DLIN in polynomial time. Also, Wen’s scheme is based on a secure sketch. Later, Wen et al. [19] proposed two frameworks for developing robust and reusable fuzzy extractors and presented two instantiations in 2019, one of which is an LWE-based one that supports a sub-linear fraction of errors. The second is a DDH-based one that does not support linear fraction of errors and is not quantum resistant. Moreover, their scheme employs a secure sketch, resulting in a leakage of biometric information, a biometric source with high entropy is required.

1.3 Outline

The remainder of this paper is organized as follows: In Section 2, we introduce notation, mathematical problems, and the error correcting mechanism on which our scheme is based on. We briefly introduce Fuller’s fuzzy extractor [6] in Section 2 as well. Then, in Section 3, we define fuzzy extractor and their security models including reusability and robustness. In Section 4, we present our reusable fuzzy extractor and demonstrate how to prove its security, such as reusability. In Section 5, we present our reusable fuzzy extractor with robustness and demonstrate how to prove its robustness. We discuss security requirements and concrete parameters for our construction in Section 6. In Section 7, we present the result as well as performance of implementation and we conclude this paper in Section 8.

2  Preliminaries

2.1 Notation

Let Zq denote the quotient ring of integers modulo q. Vectors with entries in Zq are referred to as column vectors and are denoted by lowercase letters, such as., x,y. Matrices with entries in Zq are denoted by bold capital letters, such as A,B.

For finite set S, we denote sampling the element s uniformly from S with s←r or simply s←r. Let X be a distribution over Z, then we write x←X if x is sampled in accordance with X. Furthermore, we denote sampling each coordinate of a matrix A∈Zm×n with distribution X by A←Xm×n with m,n∈Z>0. For an algorithm A, the value y←A(x) denotes the output of A on input x; if A employs randomness, then A(x) is a random variable. The min-entropy of X is H∞(X)=−log⁡(maxxPr[X=x]) where X is a random variable, and x is a particular outcome.

2.2 LWE Problem [20]

The LWE and NLWE problems are defined here. The LWE problem was defined in [20], and the error distribution is typically a discrete Gaussian distribution. The hardness of the decisional LWE problem is guaranteed by the worst-cased hardness of the decisional version of the shortest vector problem (GapSVP).

For integers n,m,q and distributions Ds,De over Zq, given an instance (A,b)∈Zqm×n×Zqm, the decisional LWE problem (Zq,n,m,Ds,De)-LWE is to determine if s←Dsn exists such that the instance is of the form (A,b=As+e) with A←R or the instance is of the form (A,u) sampled from Zqm×n×Zqm uniformly.

The advantage of an adversary A in solving decisional LWE problem is defined as follows:

AdvLWEq,n,m,Ds,De(A)=|Pr[A(A,b)=1]−Pr[A(A,u)=1]|.(1)

2.3 NLWE Problem [15]

For integers n,m,q, an error distribution X over Zq, and a distribution η over Zq given an instance (A,b)∈ηm×n×Zqm, the non-uniform LWE problem (Zq,n,m,X,η)-NLWE is to determine if s←Zqn exists such that the instance is of the form (A,b=As+e) with A←R or the instance is of the form (A,u) sampled from ηm×n×Zqm uniformly.

The advantage of an adversary A in solving a decisional NLWE problem is defined as follows:

AdvNLWEq,n,m,X,η(A)=|Pr[A(A,b)=1]−Pr[A(A,u)=1]|.(2)

According to reference [15], for some k≥1, a reduction occurs from (Zq,n,m,Ds,De)-LWE to (Zq,n,m,X,η)-NLWE for certain choices of the distribution η. As a result, the NLWE problem is at least as difficult as the standard LWE problem. In the paper [15], researchers demonstrated that NLWE is as difficult as LWE for a distribution η which is coset sampleable, i.e., there are two probabilistic polynomial-time (PPT) algorithms (MatrixGen, SamplePre) such that:

–   MatrixGen(1k,n,q) outputs a matrix A∈Zqn×k and auxiliary data t.

–   SamplePre(u∈Zqn,t) outputs a vector e∈Zqk satisfying Ae=u.

Furthermore, if u is distributed uniformly in Zqn, then the output of SamplePre(u,t) is distributed statistically close to η. We present the following theorem.

Theorem 2.1. ([15]) Let η be a coset-sampleable distribution. Assume there exists a PPT algorithm A that solves the (Zq,k⋅n,m,X,η)-NLWE problem with advantage ϵ. Then, η is an n-coset sampleable distribution, and there exists a PPT algorithm B that solves the (Zq,n,m,X)-LWE problem with the same advantage ϵ.

For some distributions η, such as the uniform distribution on {0,1}, a discrete Gaussian distribution, a uniform distribution over a sufficiently large linear subspace of Zq, reference [15] shows that for proper parameters, NLWE is as hard as LWE. The following corollary shows the relationship between LWE and NLWE problems when η is the uniform distribution on {0,1}.

Corollary 2.1. ([15]) Let η be the uniform distribution on {0,1}. Assume there exists a PPT algorithm A that solves the (Zq,⌈log2⁡q⌉⋅n,m,X,η)-NLWE problem with advantage ϵ. Then, η is an n-coset sampleable distribution, and there exists a PPT algorithm B that solves the (Zq,n,m,X)-LWE problem with the same advantage ϵ.

The relationship between LWE and NLWE problems is easily generalizable, and the proof of [15] can be directly applied to the following corollary, so the proof is omitted in this paper.

Corollary 2.2. Let η=[−L/2,L/2]. Assume there exists a PPT algorithm A that solves the (Zq,⌈logL⁡q⌉⋅n,m,X,η)-NLWE problem with advantage ϵ. Then, η is an n-coset sampleable distribution, and there exists a PPT algorithm B that solves the (Zq,n,m,X)-LWE problem with the same advantage ϵ.

2.4 ECC

We encode the extracted key with two cryptographic primitives to account for the error caused by the difference between the biometric data used for registration and the biometric data used for authentication: EMBLEM encoding method and ECC.

The basic idea behind ECC is that the sender encodes the message with redundancy bits to allow the receiver to detect and correct a limited number of errors that may occur anywhere in the message without re-transmission. In this paper, we use the (nECC,kECC,tECC) Bose-Chaudhuri-Hocquenghem (BCH) code, which used in a variety of applications in digital communications and storage. nECC is the block length, kECC is the message length, and tECC is the hamming weight of error such that kECC>tECC.

•   ECC.Encode: It takes as input a message m∈{0,1}kECC and outputs a codeword c∈{0,1}nECC

•   ECC.Decode: It takes as input a codeword c∈{0,1}nECC and outputs a message m∈{0,1}kECC

•   Correctness: For all messages m∈{0,1}kECC and for all errors e∈{0,1}nECC such that hamming weight of e is less than tECC, it holds that ECC.Decode(Ecc.Encode(m)⊕e)=m.

2.5 EMBLEM Encoding Method [13]

We use an additional encoding method, EMBLEM encoding, with ECC encoding to tolerate errors caused by differences between the biometric data used for registration and the biometric data used for authentication. EMBLEM is a new multi-bit encoding method used in LWE-based encryption schemes [13]. Because both the public key and the ciphertext in an LWE-based encryption scheme contain errors, an additional error-handling mechanism is required to obtain the correct plaintext during the decryption algorithm. During the EMBLEM encoding, the tEMB-bit message is encoded by concatenating the bit strings 1||0d where d is a pre-defined error tolerance parameter. As long as the size of the error term is less than 2d, the error cannot affect the message part. As a result, the message part can be extracted in its entirety. That is, EMBLEM decoding is accomplished by simply extracting the most significant tEMB-bit from each coefficient. For a message m∈{0,1}tEMB, EMBLEM.Encode and EMBLEM.Decode work as follows:

•    EMBLEM.Encode. it proceeds as follows:

•    EMBLEM.Decode. it proceeds as follows:

•    Correctness: For all messages m∈{0,1}tEMB and for all errors e∈ZqtEMB where the infinite norm of e is less than 2d−1, it holds that EMBLEM.Decode(EMBLEM.Encode(m)+e)=m.

2.6 Fuller’s Computational Fuzzy Extractor [6]

In 2017, Fuller et al. [6] introduced a computational fuzzy extractor based on the LWE problem. In order to reduce entropy loss, their construction did not use secure sketch. As a result, the scheme can extract a string whose length equals the entropy of the source. Furthermore, the Gen procedure takes w←W, where W is a uniform distribution over Zρqm for ρ∈(0,1). In other words, they assume that w←W where W=Zρqm. Also, due to the decoding algorithm, their construction is inefficient and can only tolerate a sub-linear fraction of errors. In more detail, their construction is comprised of two algorithms, Gen and Rep, as follows:

•    Gen(w): It proceeds as follows:

•    Rep(w′,P): It proceeds as follows:

•    Decodet(A,b=As+w−w′): It proceeds as follows:

The Decodet algorithm proceeds recursively until Step (1) of the algorithm drops all rows containing errors. As a result, the more errors the value b demonstrates, the longer the decoding algorithm takes. To ensure efficient decoding, their design can only tolerate a limited number of errors. Huth et al. [14] present a device-server authentication system with pre-application robustness based on Fuller’s construction, as well as the first implementation of a lossless computational fuzzy extractor in which the entropy of the source equals the entropy of the extracted key, in 2017. Furthermore, they provide parameter sets for 80-bit, 128-bit, and 256-bit security. Their fuzzy extractor can correct t=O(log⁡n) errors as well. With their implementation, their scheme can correct up to tm=10768=1.3% errors in the lossless setting [14].

3  Definitions

3.1 Computational Fuzzy Extractor

Fuzzy extractor extracts an almost uniformly random string R from a noisy source w. R can be recovered from any w′ that is sufficiently close to w using a public helper string P, and R remains computationally close to uniform even when P is given. Two PPT algorithms make up a fuzzy extractor (Gen, Rep). Gen is the generation algorithm which takes as input w∈W and outputs (P,R) with a public helper string P and an extracted string R∈{0,1}ℓ, and Rep is the reproduction algorithm which takes the public helper string P and w′∈W and outputs an extracted string R′∈{0,1}ℓ.

It holds the following properties.

•   Correctness. It holds that R′=R with overwhelming probability for any w,w′∈W such that δ=w−w′∈M, where M is an admissible error distribution for all (P,R)← Gen (w) and R′← Rep (P,w′).

•   Security (pseudo-randomness). The extracted string R is pseudo-random conditioned on P if (R,P)← Gen (w), that is A((R,P),(Uℓ,P))≤ε for any computationally bounded adversary A and any distribution W on M.

The reusability is the security notion in the case that several pairs of extracted string and related helper data issued from correlated biometric data are revealed to an adversary, which is clearly a much stronger security guarantee. More formally, it is the security of a reissued pair (R,P)← Gen (w), given some pairs (Ri,Pi)← Gen (wi) for correlated w and wi. We follow the security model in [10].

•   Reusability. For any distribution W over metric space M and any PPT adversary A, its advantage defined below satisfies

AdvFE,Areu:=|Pr[ExpFE,Areu(1)⇒1]−|Pr[ExpFE,Areu(0)⇒1]≤ε(3)

where ExpFE,Areu(β) describes the reusability experiment conducted by a challenger C and an adversary A as follows:

ExpFE,Areu(β):

1.    Challenger samples w←W and gets (P,R)← Gen(w). If β=0, the challenger it returns (P,R) to A; If β=1, chooses UR randomly and returns (P,UR).

2.    A may adaptively make at most qw queries of the following form:

When A outputs a guessing bit b′, the experiment outputs b′.

The robustness is a security notion that applies when an adversary modifies the helper data P before P is given to the user. The robustness of fuzzy extractor requires that any change of P by an adversary will be detected. Boyen et al. [9] introduced robust fuzzy extractor, and Dodis et al. [10] strengthened robustness to post-application robustness, which guarantees that the fuzzy extractor will detect any modification of P by an adversary who also has an access to R. In 2018, Wen et al. [5] proposed a robust and reusable fuzzy extractor in 2018 and generalized the concept of post-application robustness of reusable fuzzy extractor, allowing the adversary to ask the generation oracle with shift δi∈M to get (Pi,Ri)←Gen (w+δi). More formally, it is the security of a modified helper data P^, given some pairs (R,P)← Gen(w) and (Ri,Pi)← Gen(wi) for correlated w and wi. We follow the security model in [5].

•   Robustness. For any distribution W over metric space M and any PPT adversary A, its advantage defined below satisfies

AdvFE,Arob :=|Pr[ExpFE,Arob(1λ)⇒1]≤ε(4)

where ExpFE,Arob(1λ) describes the robustness experiment conducted by a challenger C and an adversary A as follows:

ExpFE,Arob(1λ):

1.     Challenger samples w←W, gets (P,R)← Gen (w) and returns (P,R) to A.

2.    A may adaptively make at most qw queries of the following form:

3. A submits its forgery (P^,δ^) to C.

4  Computational Fuzzy Extractor with Reusability

The main idea our scheme is that the biometric data w←W encrypts the random string R in a way that can be decrypted with the knowledge of some close w′. In this paper, we consider a uniform source W=Zqn. The construction first chooses A and e from small range and chooses a random R to be used as the output of the fuzzy extractor. Then we compute the helper data b by using w as the secret key of a symmetric LWE-based encryption scheme, i.e., b=Aw+e+R. Based on the LWE problem, the value Aw+e looks like a random value. Therefore, b hides the value Encode (R) securely. During the reproduction phase, one computes c=b−Aw′=A(w−w′)+e+R. Since A and e are sampled from small ranges and w−w′ is small, c=R+e′ where e′ is a small. To extract the string R from the helper data c, the random string R is encoded with EMBLEM encoding method and ECC before adding to Aw+e to compute b. Then one can extract R from c= Encode(R)+e′ if e′ is small enough.

4.1 Construction

We present a computational reusable fuzzy extractor based on the NLWE problem in this paper as shown in Fig. 1. The following are the specifics of our construction. We assume that w←W where W=Zqn.

•    Gen(w): To generate a helper data P and an extracted string R, it proceeds as follows:

•    Rep(w′,P): To reproduce the string R from the helper data P=(A,b) and w′, it proceeds as follows:

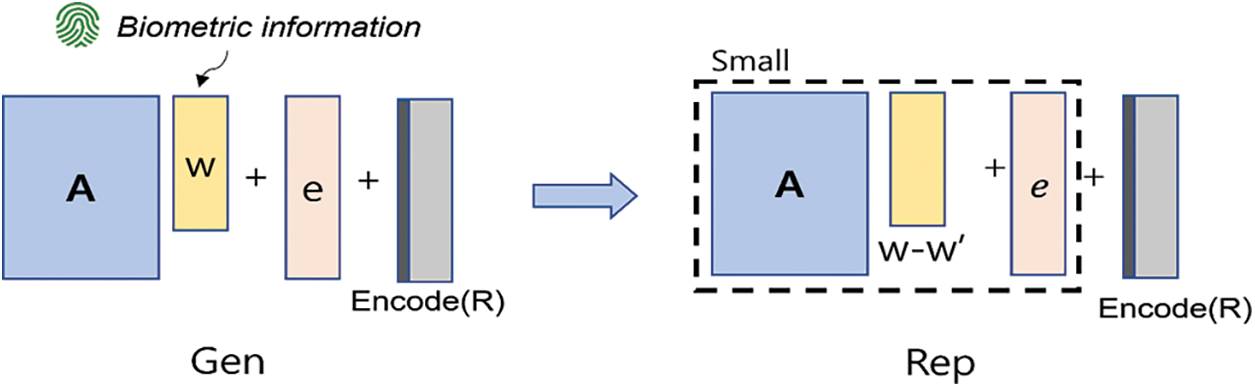
Figure 1: Construction of proposed fuzzy extractor scheme

4.2 Correctness

In this paper, we assume that the admissible error distribution δ:=w−w′exhibits three types:

(1)    δ∈Zqn has all zeros components except less than t out of n components are in {1,−1},

(2)   δ∈Zqn has all zeros components except less than t out of n components are in {2,1,−1,−2},

(3)   δ∈Dρ is sampled from a Gaussian distribution with its standard deviation ρ.

If w,w′ are close enough, then we can set ||A(w−w′)+e||∞≤2d−1 where d=⌊log⁡q⌋−1 with overwhelming probability through proper parameter setting. If it is the case, then by the correctness of EMBLEM encoding method, EMBLEM.Decode(c)=ECC.Encode(R). Now, it is easy to get R with ECC.Decode. If ||A(w−w′)+e||∞≥2d−1, then EMBLEM.Decode(c)=ECC.Encode(R)⊕e′. If the hamming weight of e′ is less than tECC with proper parameter setting, then, by the correctness of ECC, we can get ECC.Decode(EMBLEM.Decode(c))=R.

4.3 Security

Theorem 4.1. If the NLWE problem is difficult, our construction presented in Chapter 4.1 is a reusable computational fuzzy extractor.

Proof. We demonstrate the reusability of our construction by defining a sequence of games and proving that the adjacent games are indistinguishable. For each Gi for i=0,…,4,γi is defined as the event that an adversary A correctly guesses.

Game G0: It is the original game ExpFE,Areu(0) in which P=(A,b)← Gen (w) where challenger C samples A←rηm×n,e←rXn,R←r{0,1}ℓ, sets b=Aw+e+Encode(R). Finally, it returns (P,R) to A. On receipt of a δi∈M from A, challenger C samples Ai←rηm×n, ei←rXn,Ri←r{0,1}ℓ, sets bi=Ai(w+δi)+ei+Encode(Ri). In other words, challenger get Pi=(Ai,bi)← Gen(w+δi). Finally, it returns (Pi,Ri) to A. When A outputs a guessing bit β′, the experiment outputs β′. Clearly, we have Pr[γ0]=Pr[ExpFE,Areu(0)⇒1].

Game G1: It is the same as G0, except that Pi← Gen(w+δi), now is changed to bi=Aiw+Aiδi+ei+Encode(Ri) where Ai∈ηm×n, Ri∈{0,1}ℓ. Clearly, we can get Pr[γ0]=Pr[γ1].

Game G2: It is the same as G1, except that Pi← Gen(w+δi) and P← Gen(w), now is changed tobi=Ui+Aiδi+ENC(Ri),Pi=(Ai,bi), b=U+Encode(R),and P=(A,b) where A,Ai∈ηm×n, U,Ui∈Zqn, R,Ri∈{0,1}ℓ. As a result, |Pr[γ1]−Pr[γ2]|≤AdvNLWEn,(qw+1)m,q,k,X,η(A).

Game G3: It is the same as G2, except that the coin β=0 is replaced to β=1,that is, the challenger gives (P,UR) and (Pi,URi) to the adversary. In this game, the helper data P and all Pi for i=1,…,qw have no information about w, and U,Ui are uniformly random. As a result, Pr[γ2]=Pr[γ3].

Game G4: It is the same as G3, except that bi=Ui+Encode(Ri) and b=U+Encode(R) now is changed back to bi=Aiw+ei+Encode(Ri)+Aiδi and b=Aw+e+Enc(R). We get |Pr[γ3]−Pr[γ4]|≤AdvNLWEn,(qw+1)m,q,k,X,η(A).

Game G5: It is the same as G4, except that bi=Aiw+ei+Encode(Ri)+Aiδi now is changed back to bi=Ai(w+δi)+ei+Encode(Ri). Clearly, we can get Pr[δ4]=Pr[δ5]. Furthermore, this game is the original game ExpFE,Areu(1). As a result, we have Pr[δ5]=Pr[ExpFE,Areu(1)⇒1]. As a result, we get |Pr[ExpFE,Areu(1)⇒1]−|Pr[ExpFE,Areu(0)⇒1]≤2⋅AdvNLWEn,(qw+1)m,q,k,X,η(A).

5  Extension to Robust and Reusable Computational Fuzzy Extractor

Boyen et al. [9] utilizes a hash function to the fuzzy extractor scheme for robustness by feeding the biometric data into the hash function, i.e., σ=H(w,pub) where pub is a public data. In reproducing phase, the user who has w′(=w+δ) can restore w using secure sketch. As a result, the robustness can be validated by a user. Because our scheme is not based on a secure sketch, we cannot use the general method in [9] for robustness. To achieve robustness in our scheme, two keys R and K are generated by a random string r, which is the helper data b is encrypting. Then, R is regarded as an extracted key, and K is regarded as an authentication key for hash function to provide robustness. Despite the fact that the extracted key R is revealed to the adversary through helper data, the adversary cannot forge σ without the authentication key K. In other words, our fuzzy extractor provides post-application robustness, because the only valid user can decrypt the helper data b using w′ and obtain the random string r to compute the authentication K.

5.1 Construction

We present a computational reusable fuzzy extractor with robustness based on the construction of computational fuzzy extractor with reusability presented in Chapter 4. The details of our construction are as follows. We assume that w←W where W=Zqn.

•    Gen(w): To generate a helper data P and an extracted string R, it proceeds as follows:

•    Rep(w′,P): To reproduce the string R from the helper data P=(A,b,σ) and w′, it proceeds as follows:

5.2 Correctness

The correctness of the robust and reusable fuzzy extractor scheme in construction 5.1 follows from the correctness of the underlying reusable fuzzy extractor scheme in construction 4.1.

If w,w′ are close enough, then we can set ||A(w−w′)+e||∞≤2d−1 where d=⌊log⁡q⌋−1 with overwhelming probability with proper parameter settings. If this is the case, then by the correctness of EMBLEM encoding method, EMBLEM.Decode(c)=ECC.Encode(r). Now, obtaining r using ECC.Decode is simple. If ||A(w−w′)+e||∞≥2d−1, then EMBLEM.Decode(c)=ECC.Encode(r)⊕e′. If the hamming weight of e′ is less than tECC with proper parameter setting, then, by the correctness of ECC, we can get ECC.Decode(EMBLEM.Decode(c))=r.

5.3 Security

Theorem 5.1. If the NLWE problem is difficult, our construction presented in Chapter 5.1 is a computational fuzzy extractor with reusability.

The reusability of the fuzzy extractor scheme presented in construction 5.1 is guaranteed in the same way that Theorem 4.1 is guaranteed. We sketch a proof of reusability here. To achieve robustness, our scheme has some changes compared to the scheme in Chapter 4.1. First, b is encrypting a random string r, not an extracted string R directly. Second, two keys R and K are generated by a random string r with a random oracle. Lastly, the helper data are made up of A,b and σ=H2(K,A,b). Despite giving additional information about σ to the adversary, the adversary’s advantage does not increase at all because there is no relationship between R and K. Therefore, the rest of the proof of reusability is same to the proof of theorem 4.1. Now, the proof of robustness for fuzzy extractor is presented.

Theorem 5.2. If the NLWE problem is difficult, then our construction in Chapter 5.1 is a computational fuzzy extractor with robustness.

Proof. We prove the robustness of our construction, similar to the proof of reusability in Theorem 4.1, by defining a sequence of games and proving the adjacent games indistinguishable. For each Gi for i=0,…,4,γi is defined as the event that an adversary A wins.

Game G0: It is the original game ExpFE,Arob(1λ) in which P=(A,b,σ)← Gen (w) where challenger C samples A←rηm×n,e←rXn,r←r{0,1}ℓ, sets b=Aw+e+Encode(r), and gets (R,K)=H1(r,A,b) and σ=H2(K,A,b). Finally, it returns (P,R) to A where P=(A,b,σ). On receipt of a δi∈M from A, challenger C samples Ai←rηm×n,ei←rXn,ri←r{0,1}ℓ sets bi=Ai(w+δi)+ei+Encode(Ri) and gets (Ri,Ki)=H1(ri,Ai,bi) and σi=H2(Ki,Ai,bi). In other words, challenger get Pi=(Ai,bi,σi)← Gen (w+δi). Finally, it returns (Pi,Ri) to A. Then, A submits to C its forgery (P^,δ^) with P^=(A^,b^,σ^). A wins if dis (δ^)≤t, P^≠P or any other Pi s and Rep (w+δ^,P^)≠⊥. Recall that Rep (w+δ^,P^)≠⊥ if and only if dis (w,w+δ^)≤t and σ^′=σ^ holds, where σ^′=H2(K^′,A^,b^), (R^′,K^′)=H1(r^′,A^,b^) and r^′= Decode (b^−A^(w+δ^)). The game outputs 1 if A wins and 0 otherwise. Clearly, we have Pr[γ0]=Pr[ExpFE,Arob(1λ)⇒1].

Game G1: It is the same as G0, except that Pi← Gen (w+δi) now is changed to bi=Aiw+Aiδi+ei+Encode(ri) where Ai∈ηm×n, ri∈{0,1}ℓ. Clearly, we can get Pr[γ0]=Pr[γ1].

Game G2: It is the same as G1, except that Pi← Gen (w+δi) and P← Gen (w) now is changed to b=U+Encode(r),bi=Ui+Aiδi+Encode(ri) where A,Ai∈ηm×n,U,Ui∈Zqn, and r,ri∈{0,1}ℓ. As a result, |Pr[γ1]−Pr[γ2]|≤AdvNLWEn,(qw+1)m,q,k,X,η(A).

Game G3: It is the same as G2, except that σ=H2(K,A,b) and σi=H2(Ki,Ai,bi) now is changed to σ,σi←r{0,1}ℓ2. Because H2 is a random oracle, the adversary cannot tell the difference between Game G3 and G4. As a result, we can get Pr[γ2]=Pr[γ3].

Game G4: It is the same as G3, except that (R,K)=H1(r,A,b) and (Ri,Ki)=H1(ri,Ai,bi) now is changed to R,Ri,K,Ki←r{0,1}ℓ1. Because H1 is a random oracle and b, bi have no information about r, ri, the adversary cannot tell the difference between Game G3 and G4. As a result, we can get Pr[γ3]=Pr[γ4].

In this game, the helper data P and all Pi for i=1,…,qw exhibit no information about w. Also, because A cannot learn any information about w from queries, A must determine an appropriate value for σ^ of the forgery (P^,δ^) to win this game; i.e., if A “guesses” that K^=H1(r^,A^,b^) and r^=Decode(b^−A^w^) for a particular choice of (A^,b^), then a “winning” strategy is for A to obtain σ^=H2(K^,A^,b^) and output P^=(A^,b^,σ^).

Decode is a deterministic function determined by the inputs. Therefore, when (A^,b^) are fixed, then r^=Decode(b^−A^w^) is fixed where w−w^∈M, and the value σ^=H2(K^, A^,b^)is fixed as well because the value K^ is determined by the values r^,A^,b^. As a result, if A ever outputs P^=(A^,b^,σ^) with (A^,b^)=(Ai,bi) for some i≤qw, then σ^ should be equal to σ, and so, the response is always ⊥. Thus, we simply assume that (A^,b^)≠(Ai,bi) for all i≤qw.

Assume for a moment that there are no collisions in the outputs of any of the adversary’s random oracle queries. The probability that the forgery is “successful” is at most the probability that A asked a query of the form H2(K^,A^,b^) for the correct K^ to get the value σ^ (where (A^,b^)≠(Ai,bi) for all i≤qw and K^=H1(r^,A^,b^)) plus the probability that such a query was not asked, yet A nevertheless managed to predict the value H2(K^,A^,b^). We can easily see that the second case occurs with a probability of no more than 2−ℓ2.

In the first case, the probability that the adversary A asked a query of the form H2(K^,A^,b^) for the correct K^ is at most the probability that A asked a query of the form H1(r^,A^,b^) for the correct r^ to get the value K^ plus the probability that such a query was not asked, yet A nevertheless managed to predict the value H1(r^,A^,b^). Obviously, the latter case occurs with a probability of not more than 2−ℓ1. There is at most one K^ such that H2(K^,A^,b^)=σ^ for any σ^ and at most one r^ such that H1(r^,A^,b^)=K^, since no collisions are found in these random oracle H1, H2 queries by assumption. Thus, the adversary is successful if this r^ equals the correct value Decode(b^−A^w^). To get the correct value, the adversary either “predicts” the value r^ itself or compute Decode(b^−A^w^) by “guessing” w^ for which dis (w,w^)≤t. By what we just argued, the probability that this occurs is at most 2−ℓ1+2H∞(W^|pub). Furthermore, by the birthday bound the probability of a collision is at most qH1222ℓ1 and qH222ℓ2 for hash oracle H1 and H2, respectively [9]. Therefore, we find that Pr[γ4]≤2−ℓ1+qH12⋅2−2ℓ1+(qH22+1)⋅2−ℓ2+2H∞(W^|pub). By assumptions of the NLWE problem and the biometric data distribution, 2H∞(W^|pub)≤2n⋅log2⁡q. In conclusion, Pr[ExpFE,Arob(1λ)⇒1]≤AdvNLWEn,(qw+1)m,q,k,X,η(A)+2−ℓ1+qH12⋅2−2ℓ1+(qH22+1)⋅2−ℓ2+2n⋅log2⁡q.

6  Concrete Parameter Settings

6.1 System Parameters

Let λ be the security parameter, which is the targeted bit security of the fuzzy extractor. We set the modulus q=256 for all parameter settings in our scheme. The matrix A is sampled from the distribution η in Zq, where η=[−L/2,L/2] and L be the value indicating the range used to sample the matric A, and we set L=q1/2 in this paper. To mitigate the heavy cost of Gaussian sampling, we use a centered binomial distribution to simulate a Gaussian distribution for an error distribution, as described in [21]. A centered binomial distribution with the standard deviation of k/2 can be generated as Σi=1k(bi−bi′), where bi,bi′ are uniformly random bits, as described in [22].

As previously stated, we use (nECC,kECC,tECC) BCH code, where nECC (the number of NLWE instances) is the block length, kECC (the length of an extracted key) is the message length, and tECC is the hamming weight of error such that nECC>kECC. As in Section 5, we use SHAKE as the hash function.

6.2 Concrete Hardness of the NLWE Problem

We use the method presented by [23], which is a software for estimating the hardness of LWE and a class of LWE-like problems, to estimate the hardness of the NLWE problem on which the security of our fuzzy extractor scheme is based. As previously stated, because the LWE problem can be reduced to the NLWE problem using Theorem 4.1 in Section 4, we can estimate the hardness of the NLWE problem. The LWE-estimator outputs an upper bound on the cost of solving NLWE using currently known attacks, such as the primal lattice attack described in [22,24,25] and the dual lattice attack described in [26,27].

The most important building block in most efficient NLWE attacks is the blockwise Korkine-Zolotarev (BKZ) lattice reduction algorithm [28]. As a result, our estimator calculates the overall hardness against NLWE solvers by estimating the cost of the BKZ algorithm. Several methods exist for calculating the running time of BKZ [22,28,29]. We determined to adopt the BKZ cost model of (0.292)⋅β where β is the BKZ block size. Shortest vector problem (SVP) solver is the foundation of the BKZ algorithm. In terms of the number of SVP oracle calls made by the BKZ algorithm, the core-SVP model [22] assumes that an SVP oracle is required to be called only once in a conservative model. The best-known classical SVP solver runs in time ≈20.292⋅β. Tab. 1 shows that our fuzzy extractor under the chosen parameters provides at least λ bit security against NLWE problem.

6.3 Concrete Parameters

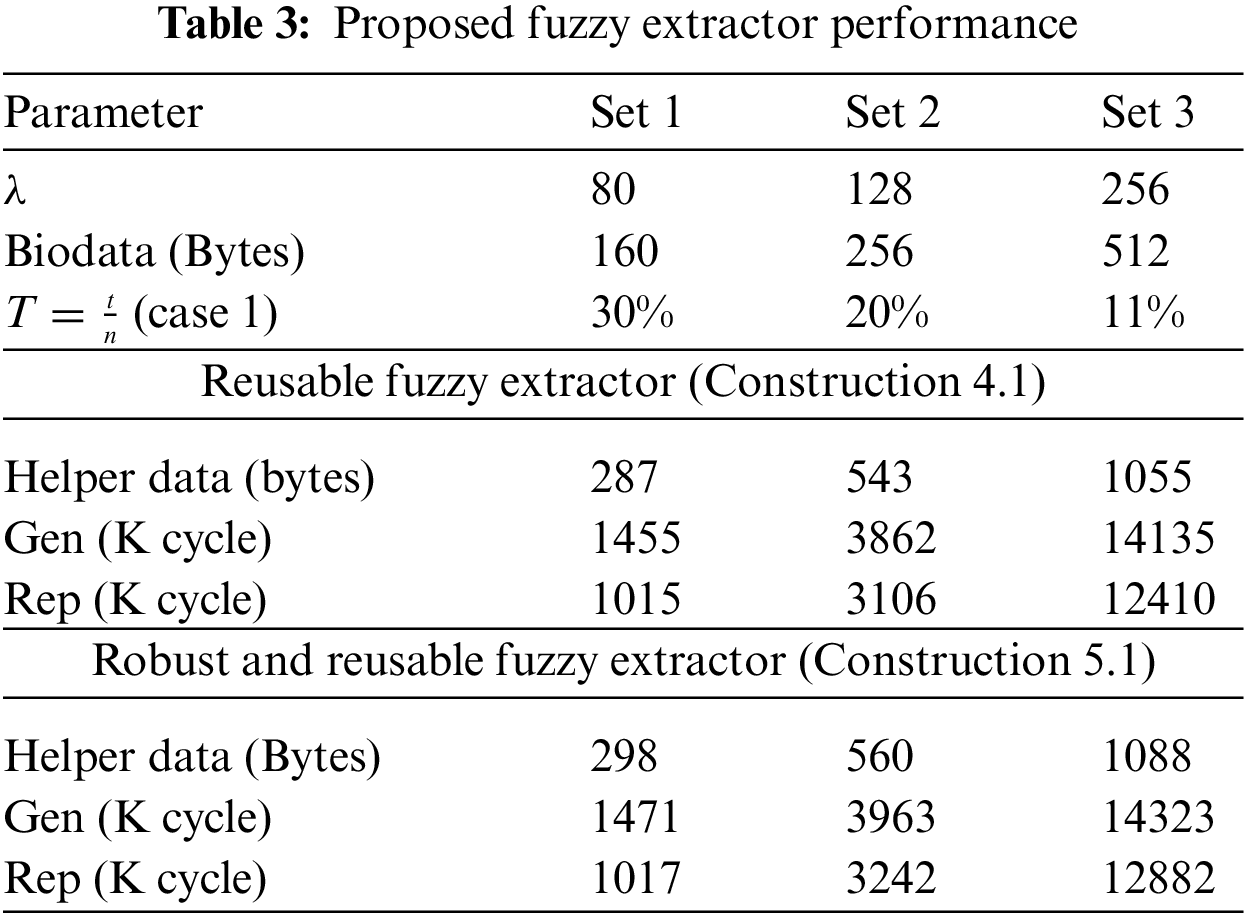
The helper data are made of A and b where A can be constructed with a 256-bit seed easily. As a result, the helper data are (256+m⋅log2⁡q)/8 bytes for our reusable fuzzy extractor. Furthermore, for our robust and reusable fuzzy extractor, the helper data consist of seedA, b and σ. Therefore, the helper data are (256+m⋅log2⁡q+ℓ)/8 bytes since the helper data are increased by only ℓ/8 bytes. As previously stated, in this paper, we assume three cases of the vector δ=w−w′: case (1): δ∈Zqn has all zeros components except less than t out of n components are in {1, −1}, case (2): δ∈Zqn has all zeros components except less than t out of n components are in {2, 1, −1, −2}, case (3): δ∈Dρ is sampled in a Gaussian distribution with its standard deviation ρ. As a result, we provide error tolerance rates based on these scenarios.

Tab. 1 shows three parameter sets that target 80, 128, and 256 bits of security against adversaries, respectively. Fig. 2 presents the false rejection rates (FRRs) of reproduction algorithm when the error rates (=t/n) increase. To get the average FRRs, we repeat our experiment 10,000 times each. For the 80-bit security with 30% error tolerance rates in case (1), we set n=160,m=255,ℓ=87,k=108, and we choose BCH (255,87,26) as an ECC encoding algorithm. For the 128-bit security with 20% error tolerance rates in case (1), we set n=256,m=511,ℓ=130,k=84, and we choose BCH (511,130,55) as an ECC encoding algorithm. Finally, for the 256-bit security level with 11% error tolerance rates in case (1), we set n=512,m=1023,ℓ=258,k=60, and we choose BCH (1023,258,106) as an ECC encoding algorithm. Then, the FRRs for these three parameter sets are all zero. In case (2), the error tolerance rates for 80, 128, and 256-bit security are 12%, 8%, and 5%, respectively. In case (3), the FRRs are all zero until the error is sampled from a Gaussian distribution with a standard deviation of 0.5, 0.35, and 0.25 for the 80, 128, and 256-bit security levels, respectively.

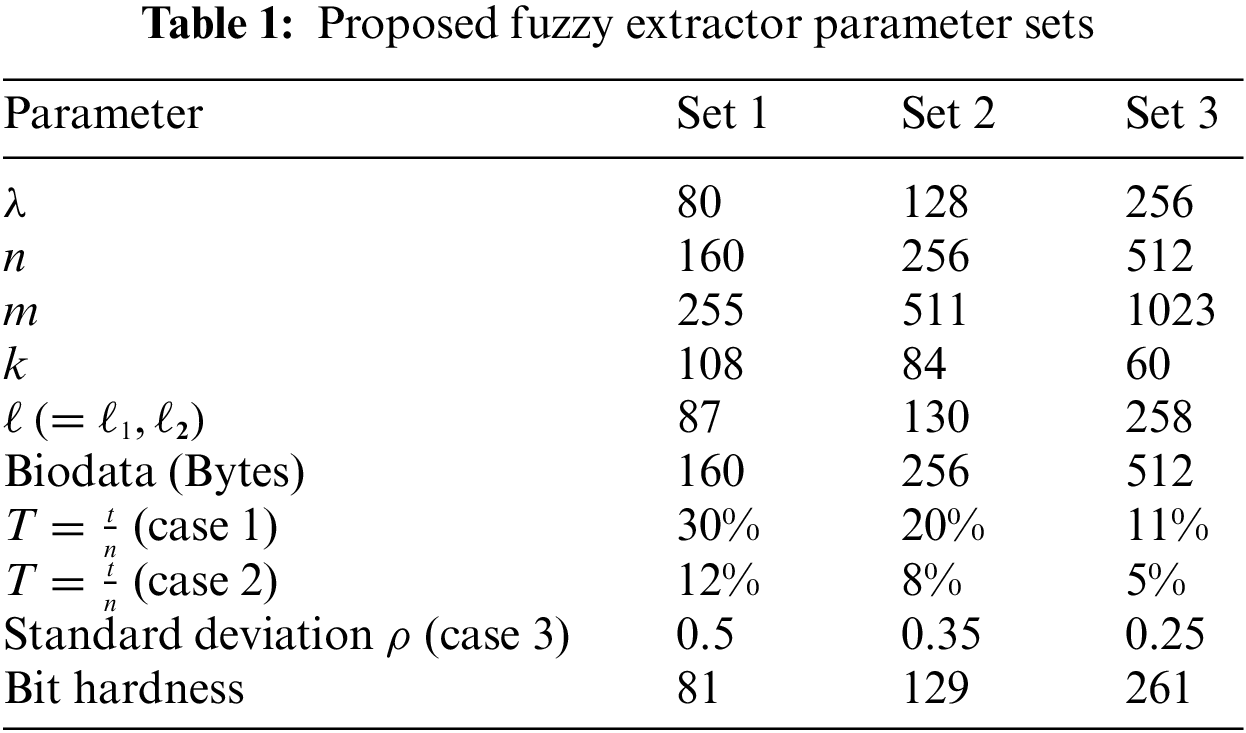
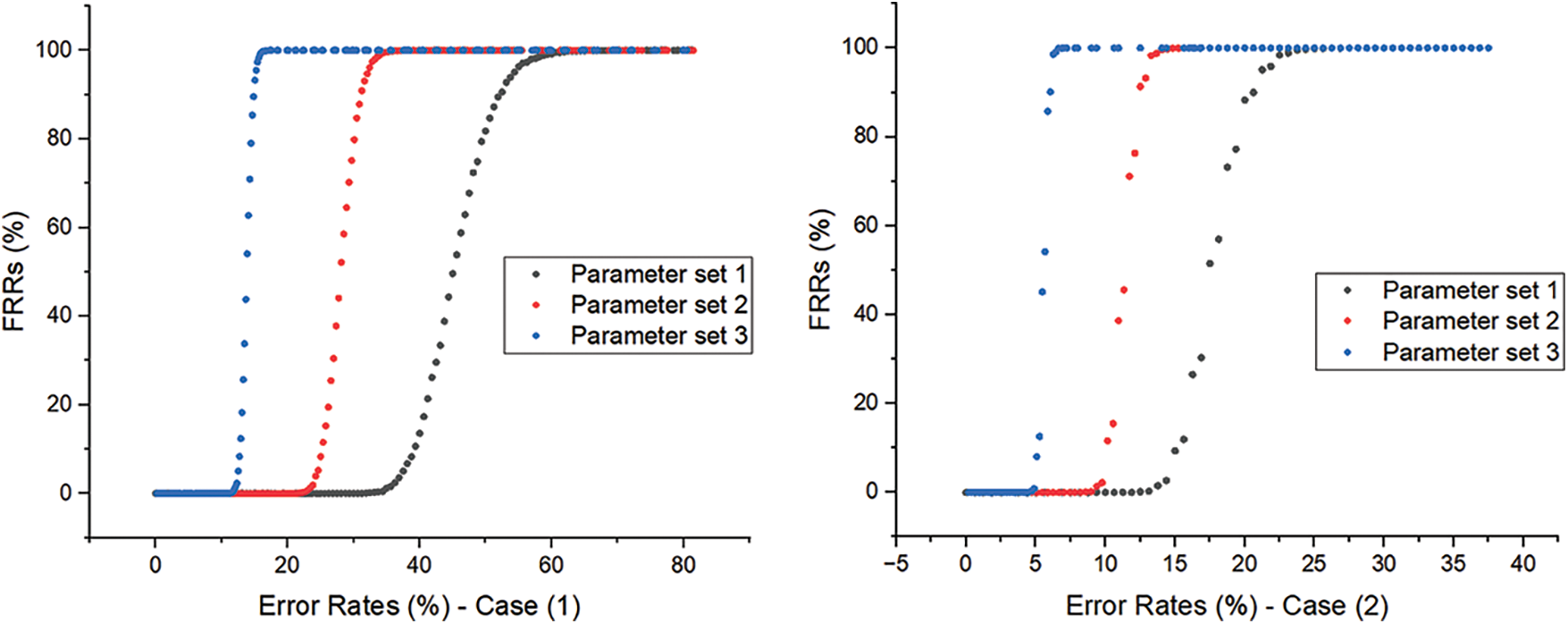
Figure 2: Simulation of reproduction algorithm

7  Results

7.1 Performance Analysis and Comparison

In this section, we describe the performance of our fuzzy extractor scheme. We evaluate the performance of our implementation on a 3.7GHz Intel Core i7-8700 k running Ubuntu 20.04 LTS. Our implementation codes are available to https://github.com/KU-Cryptographic-Protocol-Lab/Fuzzy_Extractor.

Huth et al. [14] improved on Fuller’s construction [6] in terms of decoding efficiency. However, their fuzzy extractor is bounded by the same limitations as Fuller’s, one of which is an error tolerance. The other one is that the decoding time increases with an increasing error t. As a result, they set a time limit for the decoding attempt to be less than 100 s. As a result, they can correct up to 1.3% error tolerance without false rejection, and the decoding time is more than 30 s on a machine with a 3.2 GHz single core and 8 GB RAM [14].

Canetti et al. [11] proposed a reusable fuzzy extractor based on a cryptographic digital locker in 2016, and their scheme requires a large size of helper data in order to store the hashed values of multiple subsets of the biometric data. For example, the helper data of their construction require approximately 33 GB of storage for 128-bit security with 19.5% error tolerance rates. Chen et al. [12] improved Canetti’s construction [11] by reducing the storage space for helper data. However, their storage space for helper data still requires significantly more space than ours. More than 3 MB of storage space is required for 80-bit security with 20% error tolerance. Furthermore, the time complexity of these schemes’ reproduction algorithms, which rely on the use of a digital locker to generate helper data, is involved with the computation of a significantly large number of hash values. For example, for 80-bit security with 20% error tolerance, Chen’s scheme [12] requires 53.6×103 subsets to be hashed, according to [30]. Assuming that the digital locker of these schemes is instantiated with the SHA-256 hash function and that the computation of SHA-256 takes 1 ms, then decoding takes about 1 min. Tab. 2 indicates comparison between our scheme and previous fuzzy extractor schemes.

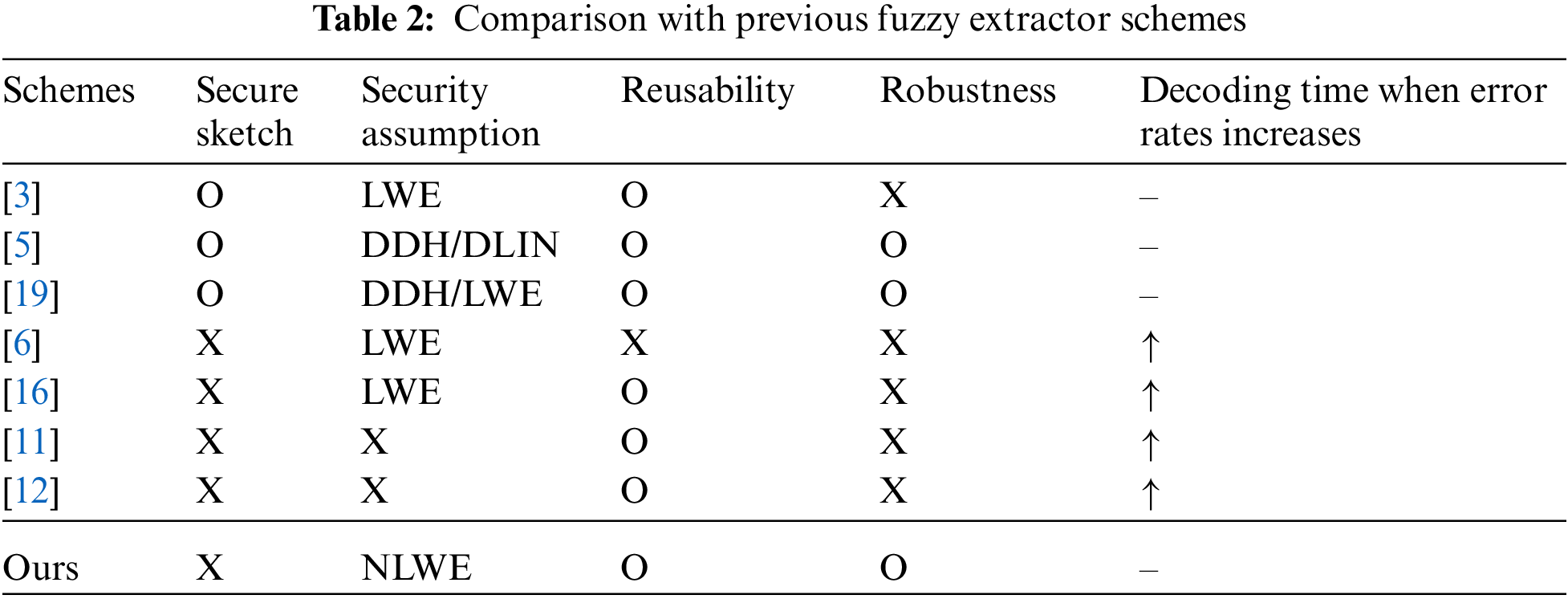
Conversely, our scheme does not increase the decoding time or storage space for helper data with an increasing error t. Regardless of an increasing error, the reproducing algorithm for our scheme, which includes the decoding algorithm takes 0.28, 0.89, and 3.42 ms, and the storage space requires only 298, 543, and 1,055 bytes for 80, 128, and 256-bit security, respectively, as shown in Tab. 3.

8  Conclusions and Future Work

In this paper, we propose a new computational fuzzy extractor that is more efficient and has small size of helper data. As a result, our scheme is reusable and robust, and it can tolerate linear errors thanks to a new decoding algorithm that employs ECC and the EMBLEM encoding method. These points contribute to increasing the efficiency of the reproduction algorithm and supporting the linear fraction of errors for biometric data. Furthermore, as the error increases, our scheme does not increase the decoding time or storage space for helper data. We present the formal security proof for the proposed fuzzy extractor using the non-uniform LWE problem, as well as the concrete bit hardness for our scheme using the LWE-estimator. To ensure the security of our fuzzy extractor, we must assume that the biometric data are drawn from a uniform distribution, i.e., w←Zqn, which is an ideal distribution for our scheme. We are well aware that in reality, many fuzzy sources including biometric data, do not provide uniform distributions. The purpose of this paper is to inspire researchers to design an efficient computational fuzzy extractor based on our construction. As future work we want to investigate the hardness of the NLWE problem with non-uniform secret distribution, not just uniform distribution. Also, we want to investigate the feature extraction technique using a deep neural network, which can be of independent interest.

Funding Statement: This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No. 2022-0-00518, Blockchain privacy preserving techniques based on data encryption).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Y. Dodis, L. Reyzin and A. D. Smith, “Fuzzy extractors: How to generate strong keys from biometrics and other noisy data,” in Int. Conf. on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, pp. 523–540, 2004. [Google Scholar]

 2.  X. Boyen, “Reusable cryptographic fuzzy extractors,” in Proc. of the 11th ACM Conf. on Computer and Communications Security, Washington, DC, USA, pp. 82–91, 2004. [Google Scholar]

 3.  Y. Wen and S. Liu, “Reusable fuzzy extractor from LWE,” in Australasian Conf. on Information Security and Privacy, Wollongong, NSW, Australia, pp. 13–27, 2018. [Google Scholar]

 4.  Y. Wen, S. Liu and S. Han, “Reusable fuzzy extractor from the decisional Diffie-Hellman assumption,” Designs, Codes and Cryptography, vol. 86, no. 11, pp. 2495–2512, 2018. [Google Scholar]

 5.  Y. Wen and S. Liu, “Robustly reusable fuzzy extractor from standard assumptions,” in Int. Conf. on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia, pp. 459–489, 2018. [Google Scholar]

 6.  B. Fuller, X. Meng and L. Reyzin, “Computational Fuzzy Extractors,” in Int. Conf. on the Theory and Application of Cryptology and Information Security,, Bengaluru, India, pp. 174–193, 2013. [Google Scholar]

 7.  S. Simhadri, J. Steel and B. Fuller, “Cryptographic authentication from the iris,” in Int. Conf. on Information Security, New York City, NY, USA, pp. 465–485, 2019. [Google Scholar]

 8.  J. Daugman, “How iris recognition works,” in International Conference on Image Processing, Rochester, New York, USA, pp. 33–36, 2002. [Google Scholar]

 9.  X. Boyen, Y. Dodis, J. Katz, R. Ostrovsky and A. Smith, “Secure remote authentication using biometric data,” in Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, pp. 147–163, 2005. [Google Scholar]

10. Y. Dodis, J. Katz, L. Reyzin and A. Smith, “Robust fuzzy extractors and authenticated key agreement from close secrets,” in Annual Int. Cryptology Conf., Santa Barbara, California, USA, pp. 232–250, 2006. [Google Scholar]

11. R. Canetti, B. Fuller, O. Paneth, L. Reyzin and A. Smith, “Reusable fuzzy extractors for low-entropy distributions,” Journal of Cryptology, vol. 34, no. 1, pp. 1–33, 2021. [Google Scholar]

12. J. H. Cheon, J. Jeong, D. Kim and J. Lee, “A reusable fuzzy extractor with practical storage size,” in Australasian Conf. on Information Security and Privacy, Wollongong, NSW, Australia, pp. 28–44, 2018. [Google Scholar]

13. M. Seo, S. Kim, D. H. Lee and J. H. Park, “EMBLEM: (R) LWE-based key encapsulation with a new multi-bit encoding method,” International Journal of Information Security, vol. 19, no. 4, pp. 383–399, 2020. [Google Scholar]

14. C. Huth, D. Becker, J. G. Merchan, P. Duplys and T. Güneysu, “Securing systems with indispensable entropy: LWE-based lossless computational fuzzy extractor for the Internet of Things,” IEEE Access, vol. 5, pp. 11909–11926, 2017. [Google Scholar]

15. D. Boneh, K. Lewi, H. Montgomery and A. Raghunathan, “Key homomorphic PRFs and their applications,” in Annual Cryptology Conf., Santa Barbara, CA, USA, pp. 410–428, 2013. [Google Scholar]

16. D. Apon, C. Cho, K. Eldefrawy and J. Katz, “Efficient, reusable fuzzy extractors from LWE,” in Int. Conf. on Cyber Security Cryptography and Machine Learning, Beer-Sheva, Israel, pp. 1–18, 2017. [Google Scholar]

17. R. Cramer, Y. Dodis, S. Fehr, C. Padró and D. Wichs, “Detection of algebraic manipulation with applications to robust secret sharing and fuzzy extractors,” in Annual Int.Conf. on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, pp. 471–488, 2008. [Google Scholar]

18. B. Kanukurthi and L. Reyzin, “An improved robust fuzzy extractor,” in Int. Conf. on Security and Cryptography for Networks, Amalfi, Italy, pp. 156–171, 2008. [Google Scholar]

19. Y. Wen, S. Liu and G. Dawu, “Generic constructions of robustly reusable fuzzy extractor,” in IACR Int. Workshop on Public Key Cryptography, Beijing, China, pp. 349–378, 2019. [Google Scholar]

20. O. Regev, “On lattices, learning with errors, random linear codes, and cryptography,” Journal of the ACM (JACM), vol. 56, no. 6, pp. 1–40, 2009. [Google Scholar]

21. X. Lu, Y. Liu, Z. Zhang, D. Jia, H. Xue et al., “LAC: Practical ring-LWE based public-key encryption with byte-level modulus,” Cryptology ePrint Archive, vol. 1009, pp. 1–36, 2018. [Google Scholar]

22. E. Alkim, L. Ducas, T. Pöppelmann and P. Schwabe, “Post-quantum key exchange-A new hope,” in 25th USENIX Security Symp. (USENIX Security 16), Austin, TX, USA, pp. 327–343, 2016. [Google Scholar]

23. M. R. Albrecht, B. R. Curtis, A. Deo, A. Davidson, R. Player et al., “Estimate all the {LWE, NTRU} schemes!,” in Int. Conf. on Security and Cryptography for Networks, Amalfi, Italy, pp. 351–367, 2018. [Google Scholar]

24. M. R. Albrecht, F. Göpfert, F. Virdia and T. Wunderer, “Revisiting the expected cost of solving uSVP and applications to LWE,” in Int. Conf. on the Theory and Application of Cryptology and Information Security, Hong Kong, China, pp. 297–322, 2017. [Google Scholar]

25. S. Bai and S. D. Galbraith, “Lattice decoding attacks on binary LWE,” in Australasian Conf. on Information Security and Privacy, Wollongong, NSW, Australia, pp. 322–337, 2014. [Google Scholar]

26. M. R. Albrecht, “On dual lattice attacks against small-secret LWE and parameter choices in HElib and SEAL,” in Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, Paris, France, pp. 103–129, 2017. [Google Scholar]

27. D. Micciancio and O. Regev, “Lattice-based cryptography,” in: Post-Quantum Cryptography, Berlin, Heidelberg: Springer, pp. 147–191, 2009. [Google Scholar]

28. Y. Chen and P. Q. Nguyen, “BKZ 2.0: Better lattice security estimates,” in Int. Conf. on the Theory and Application of Cryptology and Information Security, Seoul, South Korea, pp. 1–20, 2011. [Google Scholar]

29. M. R. Albrecht, R. Player and S. Scott, “On the concrete hardness of learning with errors,” Journal of Mathematical Cryptology, vol. 9, no. 3, pp. 169–203, 2015. [Google Scholar]

30. I. Lim, M. Seo, D. H. Lee and J. H. Park, “An improved fuzzy vector signature with reusability,” Applied Sciences, vol. 10, no. 20, pp. 7141, 2020. [Google Scholar]