Fractional Order Environmental and Economic Model Investigations Using Artificial Neural Network

Wajaree Weera; Chantapish Zamart; Zulqurnain Sabir; Muhammad Asif; Afaf Alwabli; S. Mahmoud; Supreecha Wongaree; Thongchai Botmart

doi:10.32604/cmc.2023.032950

Table of Content

Abstract
Introduction
Designed Scheme: ANNs-LMBM
Results and Simulations
Concluding Remarks
References

Open Access

ARTICLE

Fractional Order Environmental and Economic Model Investigations Using Artificial Neural Network

Wajaree Weera¹, Chantapish Zamart¹, Zulqurnain Sabir^2,3, Muhammad Asif Zahoor Raja⁴, Afaf S. Alwabli⁵, S. R. Mahmoud⁶, Supreecha Wongaree⁷, Thongchai Botmart^1,*
1 Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
2 Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
3 Department of Mathematical Sciences, UAE University, P. O. Box 15551, Al Ain, UAE
4 Future Technology Research Center, National Yunlin University of Science and Technology, 123 University Road, Section 3, Douliou, Yunlin, 64002, Taiwan
5 Department of Biological Sciences, Rabigh College of Science and Arts, King Abdulaziz University, Rabigh, Saudi Arabia
6 GRC Department, Faculty of Applied Studies, Jeddah, King Abdulaziz University, Rabigh, Saudi Arabia
7 Institute of General Education, Udon Thani Rajabhat University, Udon Thani, 41000, Thailand
* Corresponding Author: Thongchai Botmart. Email:

Computers, Materials & Continua 2023, 74(1), 1735-1748. https://doi.org/10.32604/cmc.2023.032950

Received 02 June 2022; Accepted 12 July 2022; Issue published 22 September 2022

Abstract

The motive of these investigations is to provide the importance and significance of the fractional order (FO) derivatives in the nonlinear environmental and economic (NEE) model, i.e., FO-NEE model. The dynamics of the NEE model achieves more precise by using the form of the FO derivative. The investigations through the non-integer and nonlinear mathematical form to define the FO-NEE model are also provided in this study. The composition of the FO-NEE model is classified into three classes, execution cost of control, system competence of industrial elements and a new diagnostics technical exclusion cost. The mathematical FO-NEE system is numerically studied by using the artificial neural networks (ANNs) along with the Levenberg-Marquardt backpropagation method (ANNs-LMBM). Three different cases using the FO derivative have been examined to present the numerical performances of the FO-NEE model. The data is selected to solve the mathematical FO-NEE system is executed as 70% for training and 15% for both testing and certification. The exactness of the proposed ANNs-LMBM is observed through the comparison of the obtained and the Adams-Bashforth-Moulton database results. To ratify the aptitude, validity, constancy, exactness, and competence of the ANNs-LMBM, the numerical replications using the state transitions, regression, correlation, error histograms and mean square error are also described.

Keywords

Environmental and economic model; artificial neural networks; fractional order; nonlinear; Levenberg-Marquardt backpropagation

1 Introduction

The researcher’s community is taking keen interest for solving the nonlinear environmental and economic (NEE) model as it has several applications in industrial organizations. Conceptual investigations based on the association of the supply chain are implemented to the strategic relationships to increase the operational and financial interest in the industrial presentations and to decrease the cost catalogues in the supply chain management (SCM) [1–3]. Different studies have been presented related to the SCM, e.g., the affiliating nature of inter-firm in the SCM has been accessed by Mentzer et al. [4]. The quantity of the industrial growing categories using the strategic consequence of controlling, planning is also presented along with the SCM design moderately. The association between the industrial groups is related to increase the shared prospect for these cultures with fine advantages [5,6]. Min et al. [7] applied the modeling of the SCM procedure with the key challenges and opportunities to model the systems of the supply chain.

The mathematical system represents the numerous differential models, e.g., SITR covid model [8], dengue virus model [9], nervous stomach model [10], vector disease model [11] and mosquito dispersal model [12]. To predict the unified growth of the economy, the growth rate of the low-level economies does not unstable, when the prominent economies of the world faced troubles in case of economic disaster. The design of the “predator-victim” model presents the authorizations of the mathematical systems to describe their reports. The mathematical presentations of the NEE model have three classes, new procedural diagnostics and cost of control principles (X), exclusion costs of disasters values (Y) and the competence of the system based on the industry fundamentals (Z). The mathematical structure to express these quantities is provided as [13–15]:

{X′(ω)=K3Z(ω)+K1X(ω)(a−X(ω))−K2Y(ω),X0=l1,Y′(ω)=K4X(ω)(a−X(ω))+K6Z(ω)−K5Y(ω)(b−Y(ω)),Y0=l2,Z′(ω)=K7X(ω)−K8Y(ω),Z0=l3.(1)

The system (1) is known as fractional order (FO) derivatives in the NEE model, i.e., FO-NEE model, where, K1, K2,…., K8 are the constant coefficients. The initial conditions are represented as l1, l2 and l3. The aim of this work is to provide the importance and significance of the FO-NEE model by applying the artificial neural networks (ANNs) and the Levenberg-Marquardt backpropagation method (ANNs-LMBM). The extended form of the FO-NEE model is given as:

{Xα(ω)=K3Z(ω)+K1X(ω)(a−X(ω))−K2Y(ω),X0=l1,Yα(ω)=K4X(ω)(a−X(ω))+K6Z(ω)−K5Y(ω)(b−Y(ω)),Y0=l2,Zα(ω)=K7X(ω)−K8Y(ω),Z0=l3,(2)

where, α represents the fractional order Caputo derivative that is taken between 0 and 1.

The computing stochastic solvers based on the ANNs-LMBM are derived to solve the FO form of the derivative using the NEE model. The stochastic solvers have been tested through the local and global operator performances to solve a few nonlinear, singular, and complicated differential models. Few applications of the stochastic applications are COVID-19 systems [16,17], fractional order models [18,19], functional order system [20], periodic differential system [21], third kind of nonlinear singular system [22] delay singular model [23], dynamics of the food chain models [24], and singular explosion theory models [25].

The aim of the current study is to present the numerical investigations of the FO mathematical system, which is based on the NEE model by using the stochastic performances of the ANNs-LMB. The time-fractional form of the derivative has a number of submissions in various networks. The integer order shows remembrance, whereas, the memory function represents the form of FO. The FO form is applied to the application of the real-world systems [26–34]. Few novel features of the ANNs-LMBM for the FO-NEE model are provided as:

• A design of a fractional order economic and environmental nonlinear mathematical model is presented.

• The stochastic performances have never been applied before to solve the mathematical nonlinear FO-NEE model.

• The solutions of the mathematical nonlinear FO-NEE model have been successfully presented by using the stochastic ANNs-LMBM.

• Three different cases using the FO derivative have been examined to present the numerical performances of the mathematical FO-NEE model.

• The brilliance of the stochastic ANNs-LMBM procedures is authenticated by using the comparison of the reference (Adams-Bashforth-Moulton) and calculated results.

• The performance through the absolute error (AE) is validated with the matching of order 4 to 6 to solve the mathematical FO-NEE model.

• The reliability and constancy of the proposed ANNs-LMBM is tested using the EHs, correlation, STs, MSE and regression to solve the mathematical FO-NEE model.

The other parts are provided as: The proposed ANNs-LMBM is described in Section 2. The simulations of the FO-NEE model are narrated in Section 3. Conclusions are provided in the last Section.

2 Designed Scheme: ANNs-LMBM

In this section, the proposed artificial neural networks, and the Levenberg-Marquardt backpropagation method (ANNs-LMBM) structure is presented to solve the mathematical fractional order nonlinear environmental and economic (FO-NEE) model. The designed ANNs-LMBM methodology is divided in two phases as: the essential steps using the ANNs-LMBM are provided, while the execution method via designed procedures is described to solve the mathematical FO-NEE model.

Fig. 1 represents the multi-layer optimization performance using the stochastic ANNs-LMBM. Whereas, the single layer neuron structure is provided in Fig. 2. The data is selected to solve the FO-NEE system is executed as 70% for training and 15% for both testing and certification.

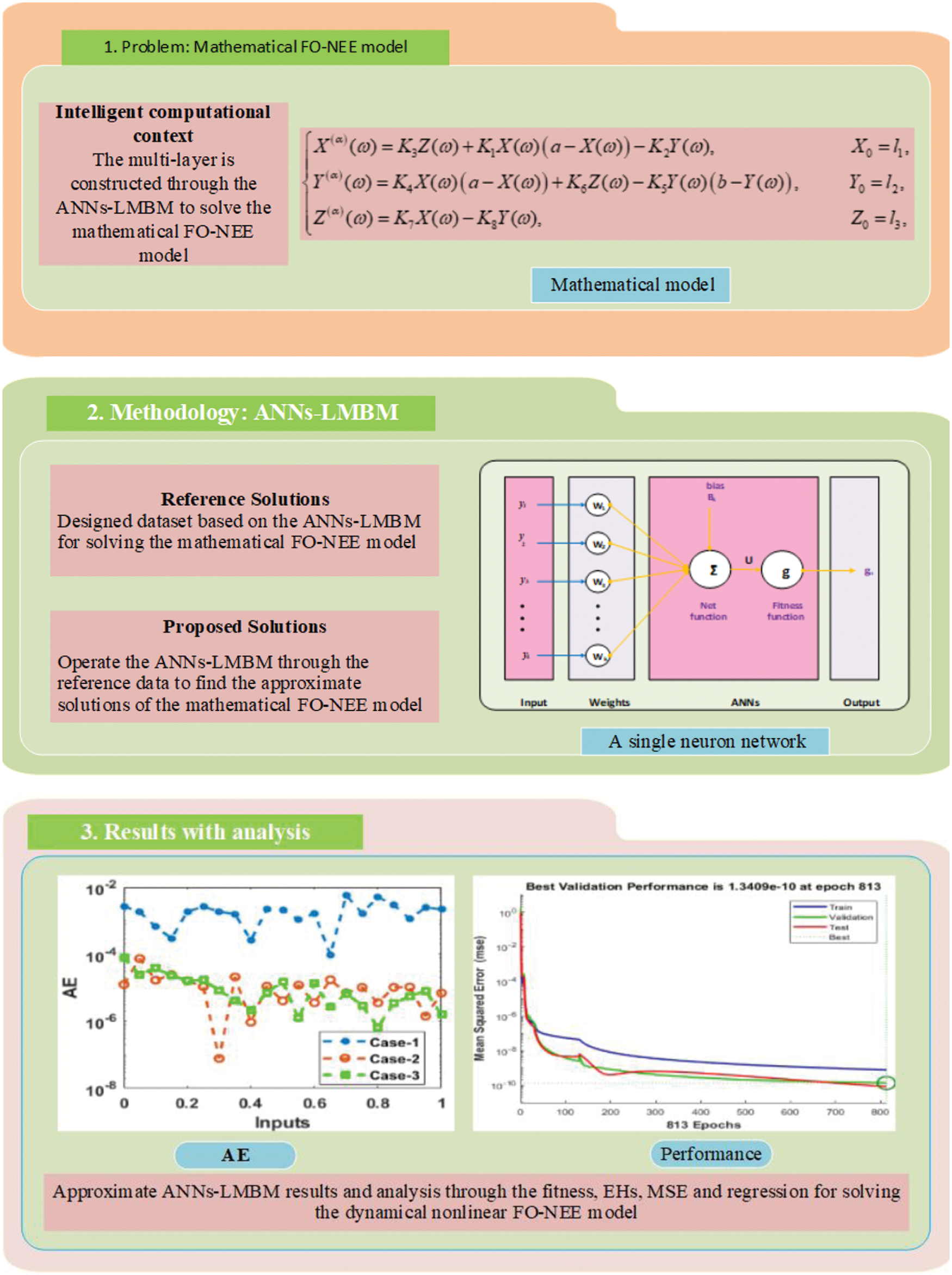
images

Figure 1: Illustrations of the ANNs-LMB procedure for the mathematical FO-NEE model

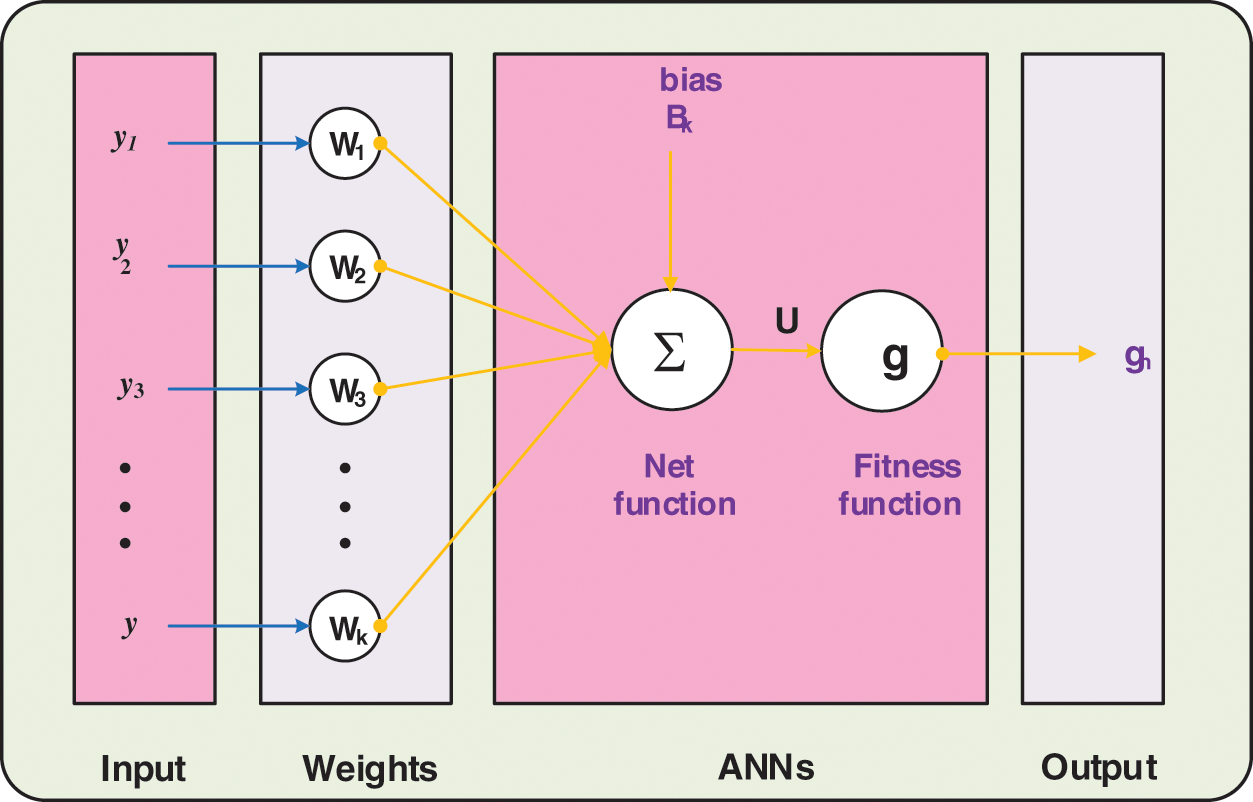
images

Figure 2: A single layer structure

3 Results and Simulations

This section shows three different variations based on the fractional order (FO) derivative to solve the mathematical fractional order nonlinear environmental and economic (FO-NEE) model using the artificial neural networks and the Levenberg-Marquardt backpropagation method (ANNs-LMBM) structure. The mathematical form of each case is presented as:

Case 1: Consider the mathematical FO-NEE model with the appropriate parameter values along with the FO derivative α=0.5 is given as:

{X0.5(ω)=0.4Z(ω)+0.2X(ω)(10−X(ω))−0.3Y(ω),X0=2,Y0.5(ω)=0.2X(ω)(10−X(ω))+0.3Z(ω)+0.3Y(ω)(5−Y(ω)),Y0=4,Z0.5(ω)=−0.3Y(ω)+0.4X(ω),Z0=3.(3)

Case 2: Consider the mathematical FO-NEE model with the appropriate parameter values along with the FO derivative α=0.7 is given as:

{X0.7(ω)=0.4Z(ω)+0.2X(ω)(10−X(ω))−0.3Y(ω),X0=2,Y0.7(ω)=0.2X(ω)(10−X(ω))+0.3Z(ω)+0.3Y(ω)(5−Y(ω)),Y0=4,Z0.7(ω)=−0.3Y(ω)+0.4X(ω),Z0=3.(4)

Case 3: Consider the mathematical FO-NEE model with the appropriate parameter values along with the FO derivative α=0.9 is given as:

{X0.9(ω)=0.4Z(ω)+0.2X(ω)(10−X(ω))−0.3Y(ω),X0=2,Y0.9(ω)=0.2X(ω)(10−X(ω))+0.3Z(ω)+0.3Y(ω)(5−Y(ω)),Y0=4,Z0.9(ω)=−0.3Y(ω)+0.4X(ω),Z0=3.(5)

The numerical simulations of the FO-NEE model are presented using the ANNs-LMBM with 15 numbers of neurons together with the selection of data to solve the FO-NEE system is executed as 70% for training and 15% for both testing and certification. The structure of the input, hidden and output layers with 15 neurons are plotted in Fig. 3.

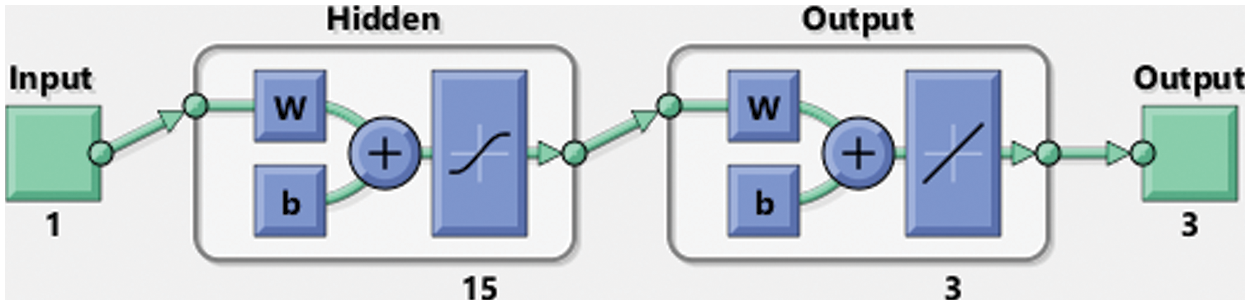
images

Figure 3: Proposed ANNs-LMBM structure for the mathematical FO-NEE model

Fig. 4 shows the graphical illustrations to solve the mathematical NEE model using the stochastic structure of the ANNs-LMBM. The graphical representations are provided in the plots 4 and 5 present the STs and the best performances. The MSE and STs values based on the best curves, training and authentication are shown in Fig. 4 for the mathematical FO-NEE model. The best performances obtained via ANNs-LMBM for the mathematical FO-NEE model at epochs 81, 813 and 850. These values are calculated as 1.1158 × 10−04, 1.3409 × 10−10 and 2.2393 × 10−10, respectively. The gradient values have been calculated through the ANNs-LMBM for the mathematical FO-NEE system. These values calculated around 4.1547 × 10−03, 9.9851 × 10−08 and 9.8482 × 10−08. These illustrations show the convergence of the proposed ANNs-LMBM for the mathematical FO-NEE model. The values of the fitting curves are provided through the comparison of the achieved and reference outcomes in Fig. 5. The error illustrations have been drawn through the training, testing and authentication procedures for each case of the FO-NEE system using the ANNs-LMBM procedures. The EHs plots are provided in Figs. 5a–5c, while the regression illustrations are authenticated in Figs. 5d–5f to solve the mathematical FO-NEE model. The EHs are calculated as 3.24 × 10−04, 9.21 × 10−06 and 8.04 × 10−06 for case 1–3. The correlation is given in Fig. 6 to demonstrate the regression performance. One can observe that the correlation values for each case of the model are computed as 1, which represents the perfect modelling. The testing, certification and training measures label the correctness of ANNs-LMBM procedure for the mathematical FO-NEE model. The convergence through the MSE is observed to check the complexity measures, training, iterations, backpropagation, testing and validation, which is provided in Tab. 1 for the mathematical FO-NEE system.

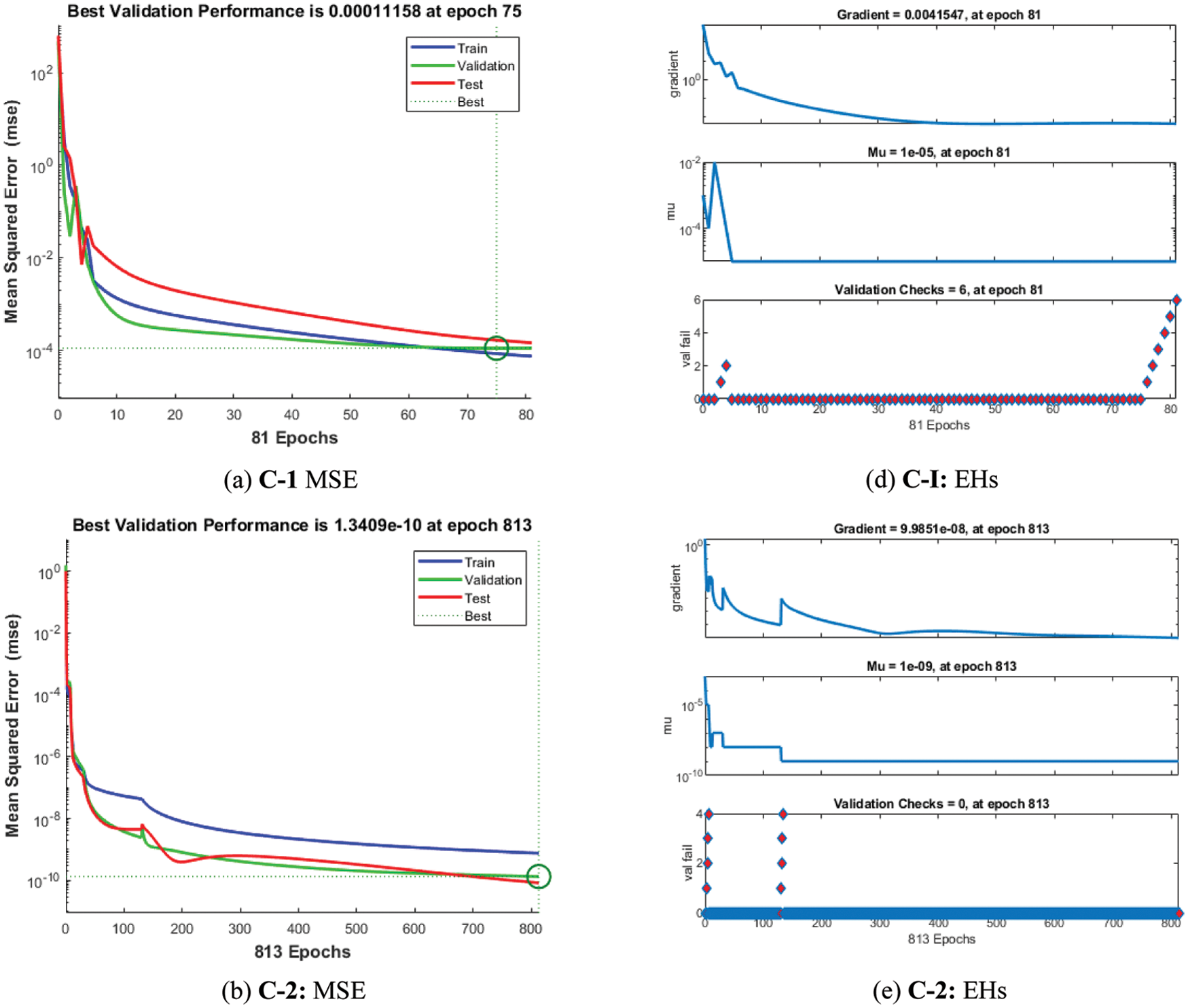
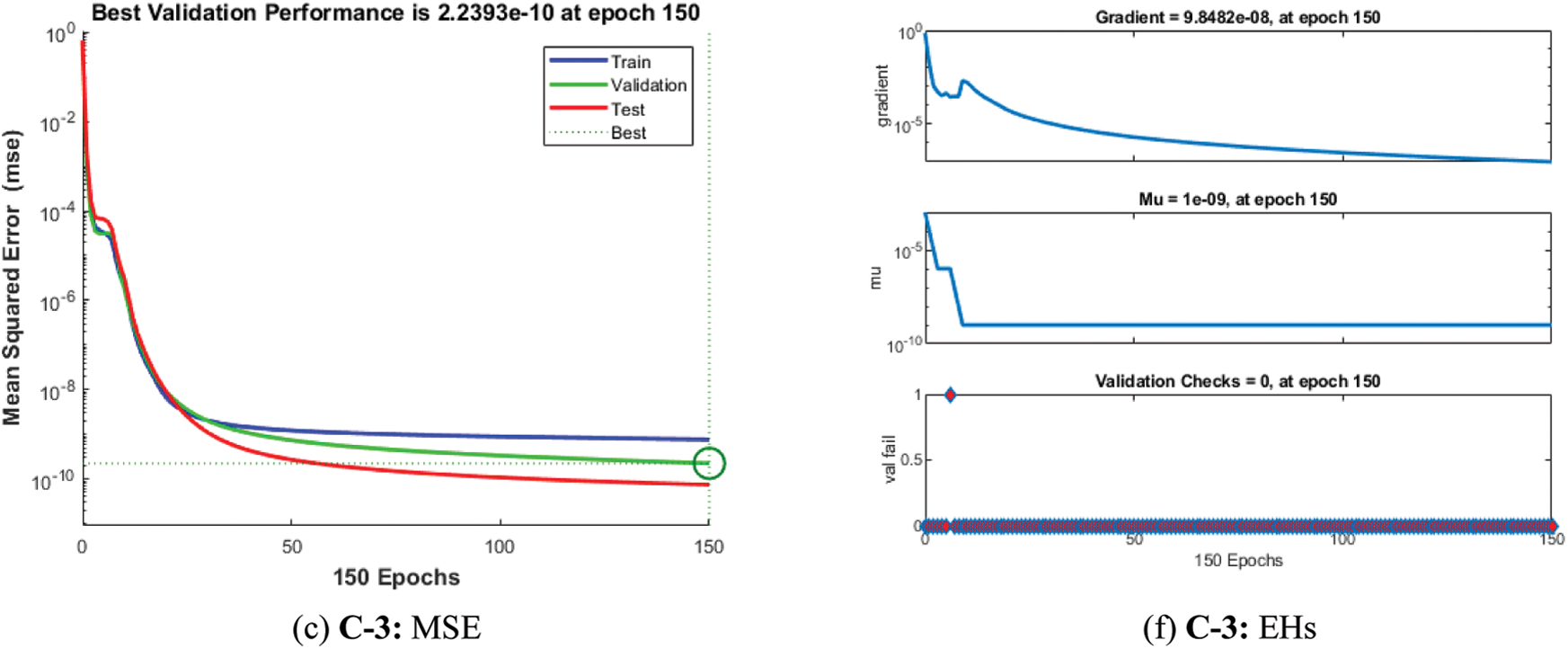
images images

Figure 4: STs and MSE for the mathematical FO-NEE system

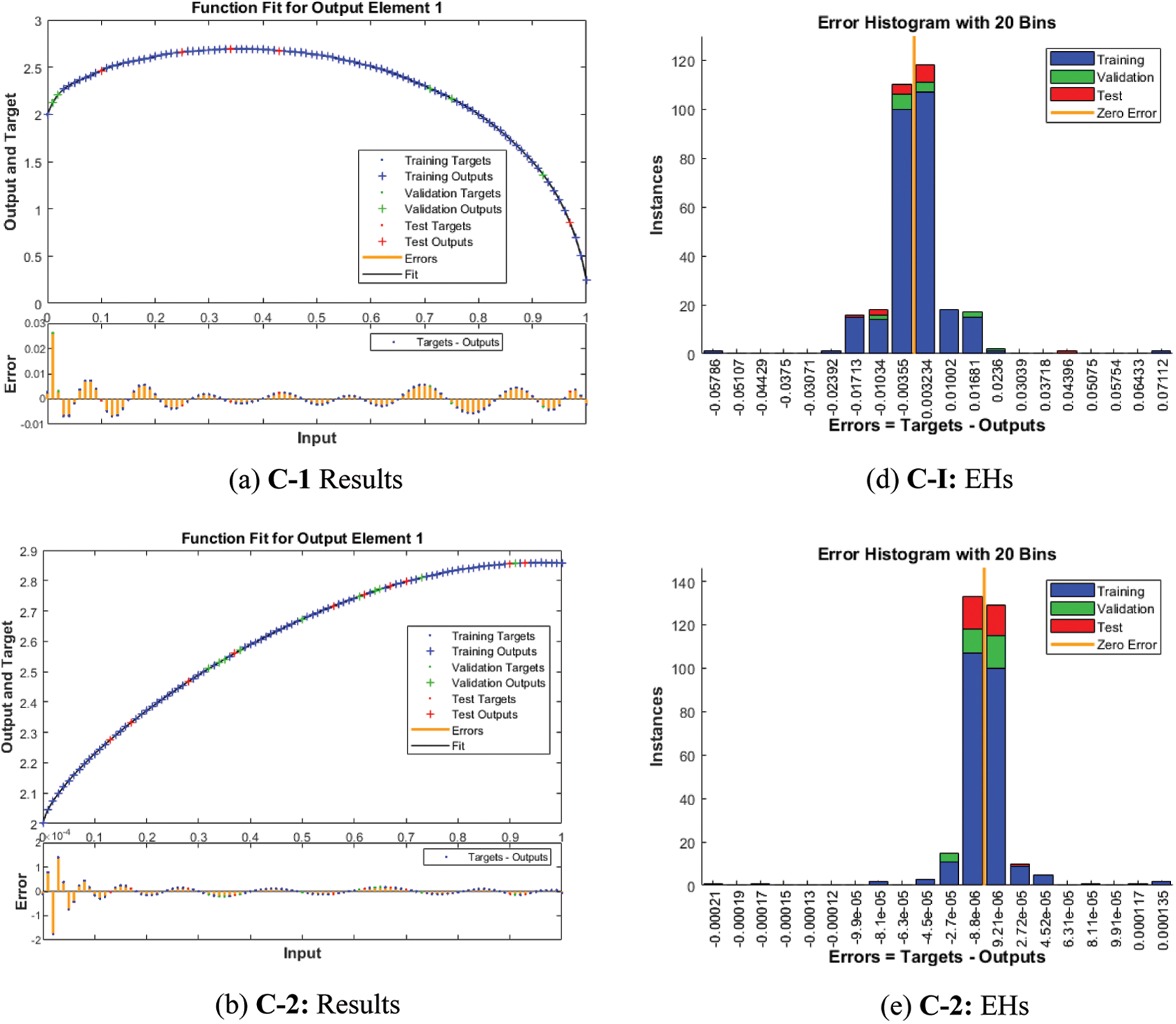
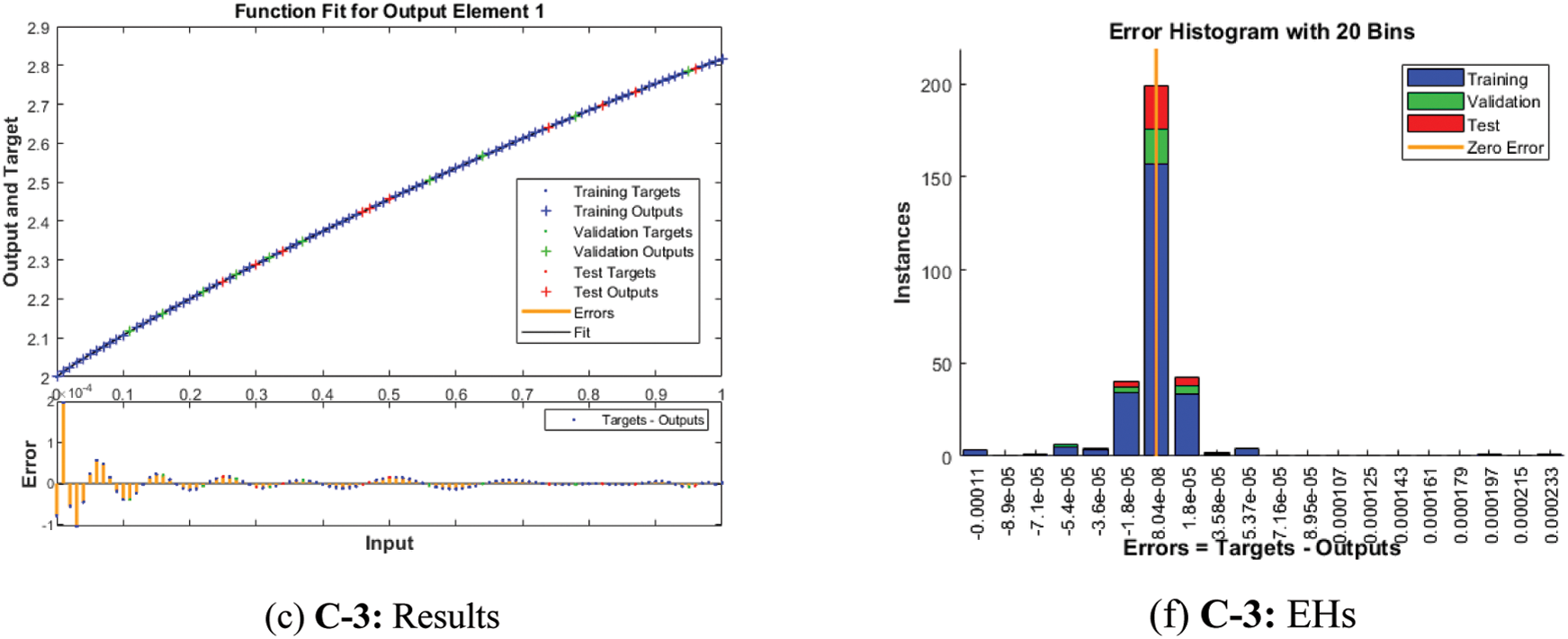
images images

Figure 5: Results valuations and EHs based on the mathematical FO-NEE system

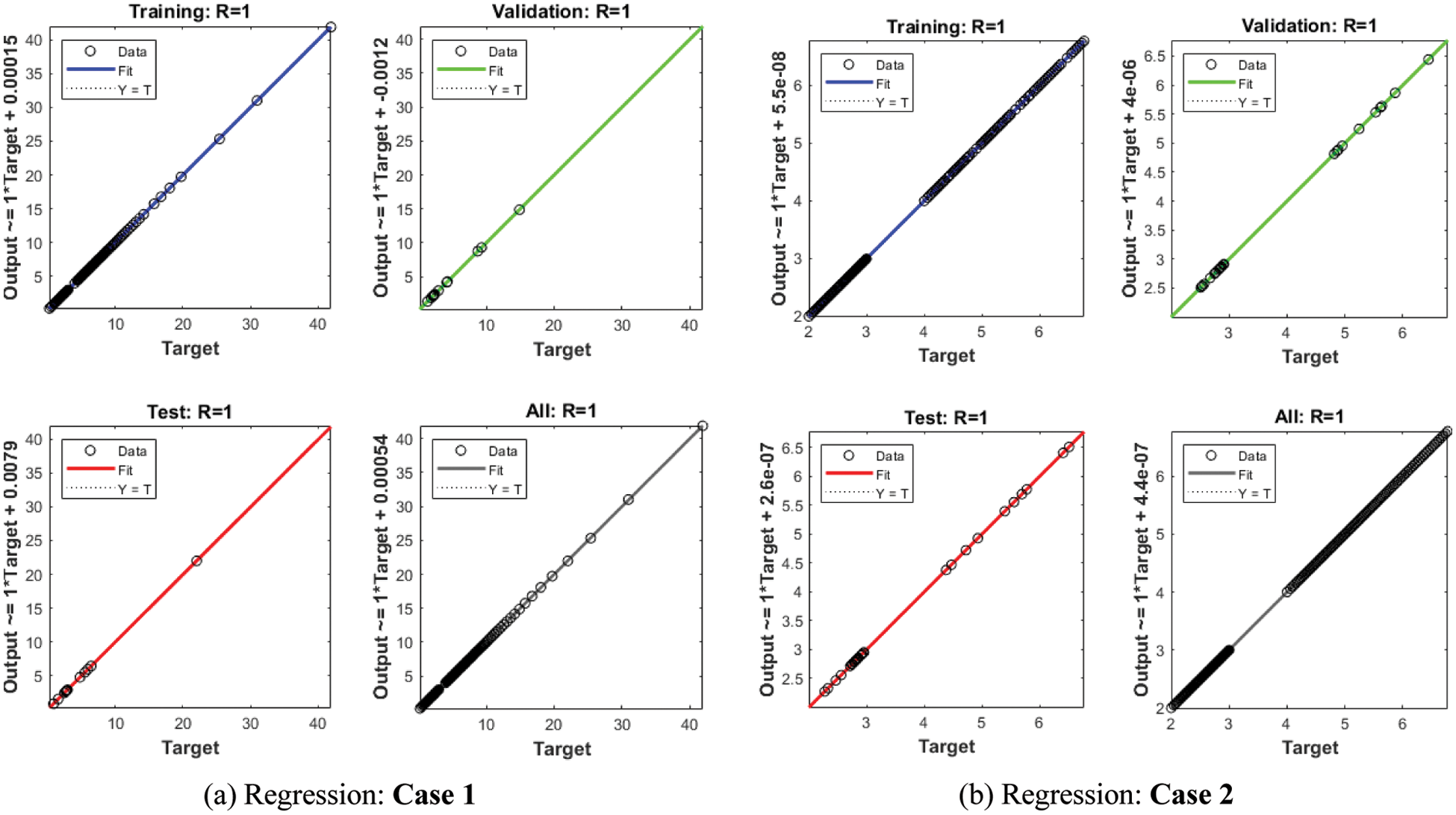
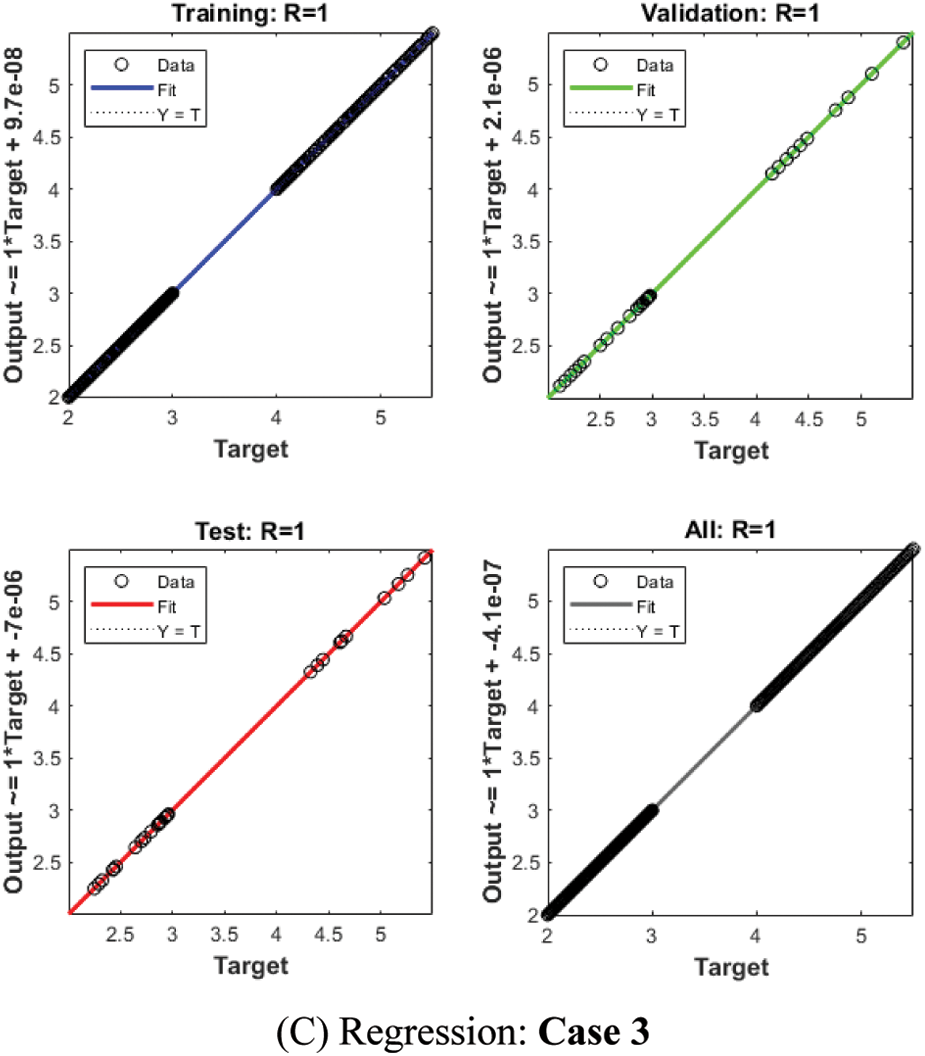
images images

Figure 6: Regression plots for the mathematical FO-NEE system

images

The comparison performances through the overlapping of the results along with the AE values have been provided in Figs. 7 and 8 for the mathematical FO-NEE system. The numerical representations for each class of the mathematical FO-NEE system have been discussed using the stochastic procedures based on the ANNs-LMBM. The depiction of proposed and reference solutions is provided in Fig. 7 that shows the overlapping of the results. These overlapped performances authenticate the exactness of the stochastic ANNs-LMBM for the mathematical FO-NEE model. The performances of the AE are provided in Fig. 8 for solving the mathematical FO-NEE model. The AE for X(ω) found around 10−02 to 10−04, 10−04 to 10−06 and 10−04 to 10−08 for case 1 to 3 based on the mathematical FO-NEE model. The AE values for Y(ω) are calculate as 10−02 to 10−04 for case 1, 10−04 to 10−06 for case 2 and 3 for the mathematical FO-NEE model. The AE for Z(ω) found 10−03 to 10−05 for case 1, 10−05 to 10−07 for case 2 and 3 based on the mathematical FO-NEE model. These good AE performances show the accuracy of the ANNs-LMB-NNs for the mathematical FO-NEE model.

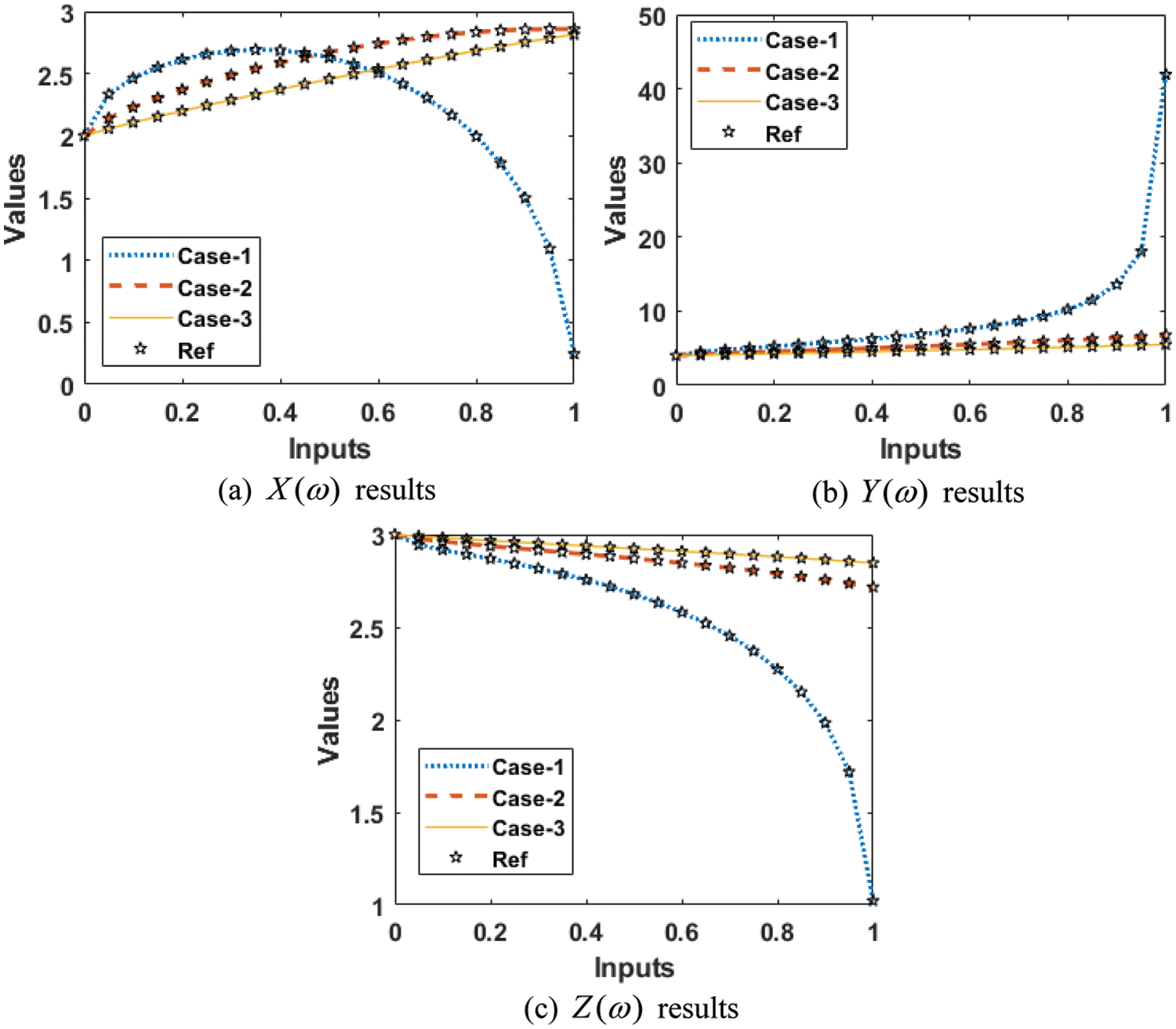
images

Figure 7: Result for the mathematical FO-NEE system

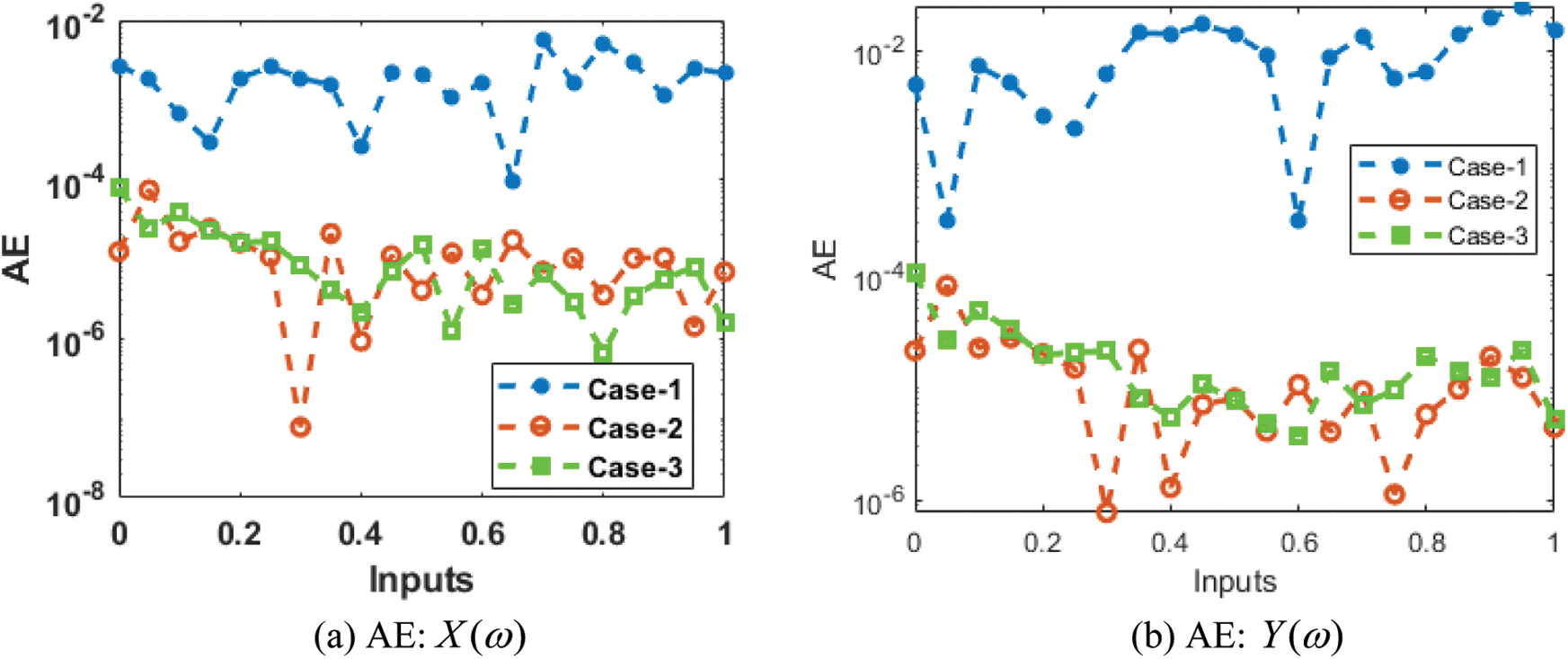
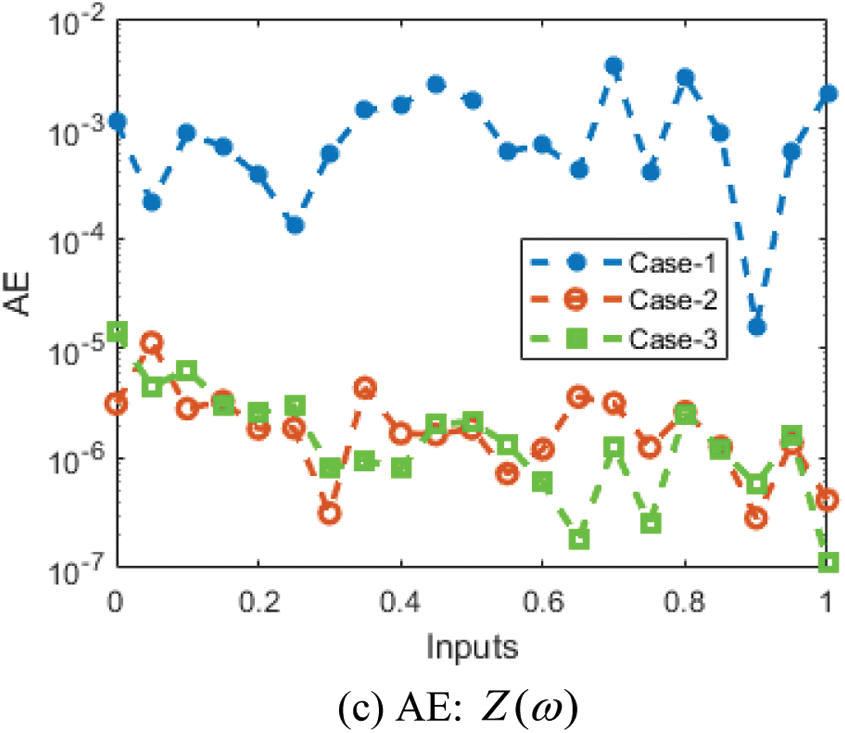
images images

Figure 8: AE for the mathematical FO-NEE system

4 Concluding Remarks

The purpose of this work is to introduce a stochastic numerical procedure for the fractional order derivatives using the mathematical form of the environmental and economic system. The dynamics of the nonlinear environmental and economic model become more accurate and precise with the involvement of the fractional order derivative. The composition of the FO-NEE model is classified into three classes, execution cost of control, system competence of industrial elements and a new diagnostics technical exclusion cost. The dynamics of the fractional order NEE model has never been tested before through the stochastic solvers. The ANNs-LMBM method have been presented for the numerical solutions of the mathematical FO-NEE system. Three different cases using the FO derivative have been examined to indicate the performances of the FO-NEE model. The selection of the data to solve the mathematical FO-NEE system is executed as 70% for training and 15% for both testing and certification. Fifteen neurons have been applied for the mathematical NEE system throughout this study and the obtained measures have been compared with the reference Adams-Bashforth-Moulton. The absolute error is calculated in good measures to solve the fractional order derivatives using the mathematical form of the environmental and economic system. To reduce the MSE performances that the numerical results have been performed through ANNs-LMBM. To authorize the aptitude, reliability of the ANNs-LMBM, the simulations have been performed through EHs, STs, MSE, correlation and regression. The accuracy of ANNs-LMBM is observed for the mathematical FO-NEE system through the overlapping of the proposed and reference outcomes. Moreover, the performance is indicated to authenticate the consistency of the ANNs-LMBM scheme.

In future studies, the ANNs-LMBM approaches have been used to solve the numerical performance of the nonlinear models [35–42].

Funding Statement: This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Whang, “Coordination in operations: A taxonomy,” Journal of Operations Management, vol. 12, no. 3–4, pp. 413–422, 1995.
2. D. J. Reyniers, “Supplier-customer interaction in quality control,” Annals of Operations Research, vol. 34, no. 1, pp. 307–330, 1992.
3. C. R. Sox, L. J. Thomas and J. O. McClain, “Coordinating production and inventory to improve service,” Management Science, vol. 43, no. 9, pp. 1189–1197, 1997.
4. J. T. Mentzer, S. Min and Z. G. Zacharia, “The nature of interfirm partnering in supply chain management,” Journal of Retailing, vol. 76, no. 4, pp. 549–568, 2000.
5. J. Mohr and R. Spekman, “Characteristics of partnership success: Partnership attributes, communication behavior, and conflict resolution techniques,” Strategic Management Journal, vol. 15, no. 2, pp. 135–152, 1994.
6. M. S. Mentzer, “Two heads are better than one if your company spans the globe,” Academy of Management Perspectives, vol. 13, no. 2, pp. 89–90, 1999.
7. H. Min and G. Zhou, “Supply chain modeling: Past, present and future,” Computers & Industrial Engineering, vol. 43, no. 1–2, pp. 231–249, 2002.
8. M. Umar, Z. Sabir, M. A. Z. Raja, F. Amin, T. Saeed et al., “Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19,” Alexandria Engineering Journal, vol. 60, no. 3, pp. 2811–2824, 2021.
9. M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, no. 2, pp. 1–9, 2020.
10. Y. G. Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020.
11. Z. Sabir, M. Umar, G. M. Shah, H. A. Wahab and Y. G. Sánchez, “Competency of neural networks for the numerical treatment of nonlinear host-vector-predator model,” Computational and Mathematical Methods in Medicine, vol. 2021, pp. 1–13, 2021.
12. M. Umar, M. A. Z. Raja, Z. Sabir, A. S. Alwabli and M. Shoaib, “A stochastic computational intelligent solver for numerical treatment of mosquito dispersal model in a heterogeneous environment,” The European Physical Journal Plus, vol. 135, no. 7, pp. 1–23, 2020.
13. A. Oliinyk and L. Feshanych, “The use of the apparatus of ordinary differential equations in simulation of economic and environmental systems,” in Int. Scientific and Technical Conf.-ITMM, Dnipro, Ukraine, pp. 216–220, 2020.
14. A. K. Kiani, W. U. Khan, M. A. Z. Raja, Y. He, Z. Sabir et al., “Intelligent backpropagation networks with bayesian regularization for mathematical models of environmental economic systems,” Sustainability, vol. 13, no. 17, pp. 1–19, 2021.
15. K. Nisar, Z. Sabir, M. A. Z. Raja, A. A. A. Ibrahim, S. R. Mahmoud et al., “Numerical study of the environmental and economic system through the computational heuristic based on artificial neural networks,” Sensors, vol. 21, no. 19, pp. 1–18, 2021.
16. M. Umar, Z. Sabir, M. A. Z. Raja, M. Shoaib, M. Gupta et al., “A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics,” Symmetry, vol. 12, no. 10, pp. 1–17, 2020.
17. T. Botmart, Z. Sabir, M. A. Z. Raja, W. Weera, R. Sadat et al., “A numerical study of the fractional order dynamical nonlinear susceptible infected and quarantine differential model using the stochastic numerical approach,” Fractal and Fractional, vol. 6, no. 3, pp. 1–13, 2022.
18. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Meyer wavelet neural networks to solve a novel design of fractional order pantograph Lane-Emden differential model,” Chaos, Solitons & Fractals, vol. 152, no. 2, pp. 1–14, 2021.
19. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Solution of novel multi-fractional multi-singular Lane-Emden model using the designed FMNEICS,” Neural Computing and Applications, vol. 33, no. 24, pp. 17287–17302, 2021.
20. J. L. Guirao, Z. Sabir and T. Saeed, “Design and numerical solutions of a novel third-order nonlinear Emden-Fowler delay differential model,” Mathematical Problems in Engineering, vol. 2020, no. 3, pp. 1–9, 2020.
21. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems,” Frontiers in Physics, vol. 8, pp. 1–12, 2020.
22. Z. Sabir, M. A. Z. Raja, C. M. Khalique and C. Unlu, “Neuro-evolution computing for nonlinear multi-singular system of third order Emden-Fowler equation,” Mathematics and Computers in Simulation, vol. 185, no. 1, pp. 799–812, 2021.
23. Z. Sabir, J. L. Guirao and T. Saeed, “Solving a novel designed second order nonlinear Lane-Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, no. 3, pp. 1–12, 2021.
24. Z. Sabir, “Stochastic numerical investigations for nonlinear three-species food chain system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250005, 2022.
25. Z. Sabir, “Neuron analysis through the swarming procedures for the singular two-point boundary value problems arising in the theory of thermal explosion,” The European Physical Journal Plus, vol. 137, no. 5, pp. 638, 2022.
26. A. Yokuş and S. Gülbahar, “Numerical solutions with linearization techniques of the fractional Harry Dym equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 35–42, 2019.
27. U. Ali, A. Iqbal, M. Sohail, F. A. Abdullah and Z. Khan, “Compact implicit difference approximation for time-fractional diffusion-wave equation,” Alexandria Engineering Journal, vol. 61, no. 5, pp. 4119–4126, 2022.
28. F. M. Salama, N. N. Abd Hamid, N. H. M. Ali and U. Ali, “An efficient modified hybrid explicit group iterative method for the time-fractional diffusion equation in two space dimensions,” AIMS Mathematics, vol. 7, no. 2, pp. 2370–2392, 2022.
29. Z. Sabir, M. Munawar, M. A. Abdelkawy, M. A. Z. Raja and C. Ünlü, “Numerical investigations of the fractional-order mathematical model underlying immune-chemotherapeutic treatment for breast cancer using the neural networks,” Fractal and Fractional, vol. 6, no. 4, pp. 1–16, 2022.
30. A. H. Ganie, A. M. Saeed, S. Saeed and U. Ali, “The Rayleigh-Stokes problem for a heated generalized second-grade fluid with fractional derivative: An implicit scheme via Riemann-Liouville integral,” Mathematical Problems in Engineering, vol. 2022, no. 1, pp. 1–13, 2022.
31. T. A. Sulaiman, H. Bulut and S. S. Atas, “Optical solitons to the fractional Schrdinger-Hirota equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 535–542, 2019.
32. E. İlhan and İ. O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020.
33. A. O. Akdemir, E. Deniz and E. Yüksel, “On some integral inequalities via conformable fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 489–498, 2021.
34. H. Durur, O. Tasbozan and A. Kurt, “New analytical solutions of conformable time fractional bad and good modified boussinesq equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 447–454, 2020.
35. H. M. Baskonus, M. S. Osman, M. Ramzan, M. Tahir and S. Ashraf, “On pulse propagation of soliton wave solutions related to the perturbed Chen-Lee–Liu equation in an optical fiber,” Optical and Quantum Electronics, vol. 53, no. 10, pp. 1–17, 2021.
36. E. Ilhan, P. Veeresha and H. M. Baskonus, “Fractional approach for a mathematical model of atmospheric dynamics of CO2 gas with an efficient method,” Chaos Solitons & Fractals, vol. 152, no. 4, pp. 1–10, 2021.
37. M. Alesemi, N. Iqbal and T. Botmart, “Novel analysis of the fractional-order system of non-linear partial differential equations with the exponential-decay kernel,” Mathematics, vol. 10, no. 4, pp. 1–17, 2022.
38. G. Yel, C. Cattani, H. M. Baskonus and W. Gao, “On the complex simulations with dark-bright to the hirota-maccari system,” Journal of Computational and Nonlinear Dynamics, vol. 16, no. 6, pp. 1–9, 2021.
39. A. Ciancio, G. Yel, A. Kumar, H. M. Baskonus and E. Ilhan, “On the complex mixed dark-bright wave distributions to some conformable nonlinear integrable models,” Fractals, vol. 30, no. 1, pp. 1–14, 2022.
40. T. A. Sulaiman, H. Bulut and H. M. Baskonus, “On the exact solutions to some system of complex nonlinear models,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 29–42, 2021.
41. Z. Sabir, M. G. Sakar, M. Yeskindirova and O. Saldir, “Numerical investigations to design a novel model based on the fifth order system of Emden-Fowler equations,” Theoretical and Applied Mechanics Letters, vol. 10, no. 5, pp. 333–342, 2020.
42. Z. Sabir, J. L. Guirao, T. Saeed and F. Erdoğan, “Design of a novel second-order prediction differential model solved by using adams and explicit Runge-Kutta numerical methods,” Mathematical Problems in Engineering, vol. 2020, no. 3, pp. 1–7, 2020.

Cite This Article

W. Weera, C. Zamart, Z. Sabir, M. A. Z. Raja, A. S. Alwabli et al., "Fractional order environmental and economic model investigations using artificial neural network," Computers, Materials & Continua, vol. 74, no.1, pp. 1735–1748, 2023.

This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.