Analysis of LDPC Code in Hybrid Communication Systems

1  Introduction

With the global demand for higher bandwidth and speed, FSO has become a promising field to fulfill this necessity. Optical communication is becoming more popular as a potential opportunity to satisfy the bottleneck’s reliability issue and complement extra traditional RF/microwave links. However, the simple FSO system has the downside of information loss while transmitted via a turbulent atmosphere. The loss may be extreme, resulting in a complete communication channel blackout [1]. To overwhelm this issue, the hybrid FSO/RF is developing gradually as a communication field, which will act as a potential backhaul if the FSO goes down. When the core link degrades by cause of fog, haze, rain, snow, catastrophe, or anthropomorphic, a mmWave RF link that is a hybrid FSO/RF is employed to produce the data to the receiver. This method offers high bandwidth, license-free frequencies, and high-speed data communication [1]. Coding techniques can be considered to improve the data rate of such links.

Error control coding has maximized the error correction capability of the optical link by using various forward error correction (FEC) methods consisting of convolutional codes, Reed-Solomon (RS) codes, Turbo codes, Trellis coded modulation (TCM), and LDPC. The study of error behavior using error correction codes within the fading channel has been a research topic for several years [2]. LDPC codes are preferable to turbo codes for terribly high-rate transmission due to their lower decoding complexity and computation time. The variable rate of LDPC codes can maximize the link capability and offer accurate coding gain [3]. Different assessments have been made for using LDPC codes in systems [4,5]. A complete list of acronyms is provided in Tab. 1.

Gallager developed LDPC codes in 1960 [4]. These codes belong to a specific class of Shannon-capacity approaching codes. Gallager’s work was overlooked for twenty years. In 1981, Tanner worked on LDPC codes and used graphs to represent LDPC codes. Later in the 1990s, David Mackay relieved Tanner’s work [5]. Long LDPC codes decoded by belief propagation are closer to Shannon’s theoretical limit. Due to this advantage, LDPC codes are strong competitors over other codes used in a communication system, such as turbo codes. LDPC is the basic example of ECC, which has become very famous as it achieves near Shannon capacity in the additive white Gaussian noise (AWGN) [6]. LDPC codes have parallelism features supporting various speeds, performances, and memory consumption [7]. LDPC codes are easy to design with code rate and block length, and also, the rate adaptability can be easily achieved in LDPC codes. Extrinsic information transfer (EXIT) is a simple technique to show LDPC code convergence behavior. EXIT analysis is an efficient tool for designing the iterative decoding system [8]. EXIT chart comprises two components decoder, which is variable node decoder (VND) and Check node decoder (CND) [9].

In this paper, we first consider a regular binary code, and then an irregular LDPC code is evaluated. Evaluation of the LDPC code threshold with a certain degree distribution is vital for designing a coding system approaching the Shannon limit. But it is complicated to optimize degree distribution direct using density evolution due to its exhaustive calculations. Alternatively, using Gaussian approximation (GA) of the message densities for both regular and irregular LDPC codes is very simple. For LDPC, EXIT charts are used to evaluate the sum-product Algorithm. This paper optimized the codes by applying curve-fitting on EXIT charts. Thus, the analysis of EXIT charts predicts an optimistic value for the convergence threshold. LDPC code gives exceptional BER performance nearly close to the Shannon limit. We also computed the BER by soft decision and compared it to the proposed FSCS.

The paper outline is as follows. In Section 2, we develop a system model under consideration. We formalize the LDPC code with factor graph and decoding algorithms in Section 3. In Section 4, we also introduce the LDPC code notations. Section 5 also introduces the code convergence measuring tools useful for following analysis and EXIT chart behavior in the proposed system. In Section 6, we present some numerical results. Section 7 concludes the proposed research work.

2  System Model

The proposed free-space communication system (FSCS) in which optical and radio channels are considered parallel is given in Fig. 1. It comprises two parallel RF and FSO channels with a transmitter (encoder) pair and a receiver (decoder). The modulating data is encoded into the codeword of n-bits. It is divided into two ways, namely optical channel bits no=nF and RF channel bits nr=n(1−F), where F is used to divide the bits over the optical and radio channel.

Figure 1: Block diagram of a proposed Free-Space Communication System (FSCS)

Binary mapping schemes are used on each link to map the channel bits. The mapped symbols of each channel are transmitted over the respective link. Thus, each stream from the encoder is mapped to create consistent RF and FSO symbols sent respectively on the particular link. The signal is modulated by RF link to a mmWave carrier frequency of RF, even though FSO link. The single encoder aims to minimize the computational complexity and the communication cost using a single pair of encoder and decoder having slow varying channels.

2.1 FSO Channel Model

At the transmit side, codewords are mapped to channel symbols employing binary modulation schemes. The on-off keying (OOK) modulated optical signal comes from the transmitter. A simple signal model from the FSCS communication system over an optical link is given by, See Eq. (1)

y= TX+z(1)

where y called the received FSO symbols, T=ηPh, where X is the optical symbols, η represents the conversion detectors efficiency, P represents the transmitted optical power, and h denotes the FSO channel fading. In the presented work, we exploit the additive white Gaussian noise (AWGN) model, where z denotes an independent and identically distributed (i.i.d) random variable (zero mean and unit variance).

2.2 RF Channel Model

Considering the RF power P, the received RF signal is expressed by

y^=T^X^+z^(2)

where y^ is the received RF signal T^=P^h^, X^ represents the radio channel symbols transmitted by employing the binary phase-shift keying (BPSK), P^ represent the RF receive power. z^ denotes a Gaussian random variable (zero mean and unit variance).

3  LDPC Code

The Initial letter of each notional word in all headings is capitalized. LDPC code is most efficiently employed linear code along with a sparse parity check matrix (H). LDPC code may be signified through a Tanner graph. LDPC code can be regular type as well as irregular type LDPC code. For regular LDPC code, hamming weight (i.e., wc) of every column are the same as well as the same hamming weight (i.e., wr) of every row of H. While for the irregular LDPC code wr≠wc [10]. In the presented work, the focus is on the regular codes. LDPC codes can be decoded using bit flipping, minimal decoding, and belief propagation (BP) [11]. LDPC code represented by H is preferred for hardware implementation, giving an endless number of edges of the variable and check nodes. LDPC code (j,k) such as (N×M) where wr denotes the range of 1’s in rows as well as wc represents the range of 1’s in columns. These conditions are related to the LDPC matrix, which are wc"N and wr"M. The LDPC code H may be represented graphically using Tanner graph; see Fig. 2 below.

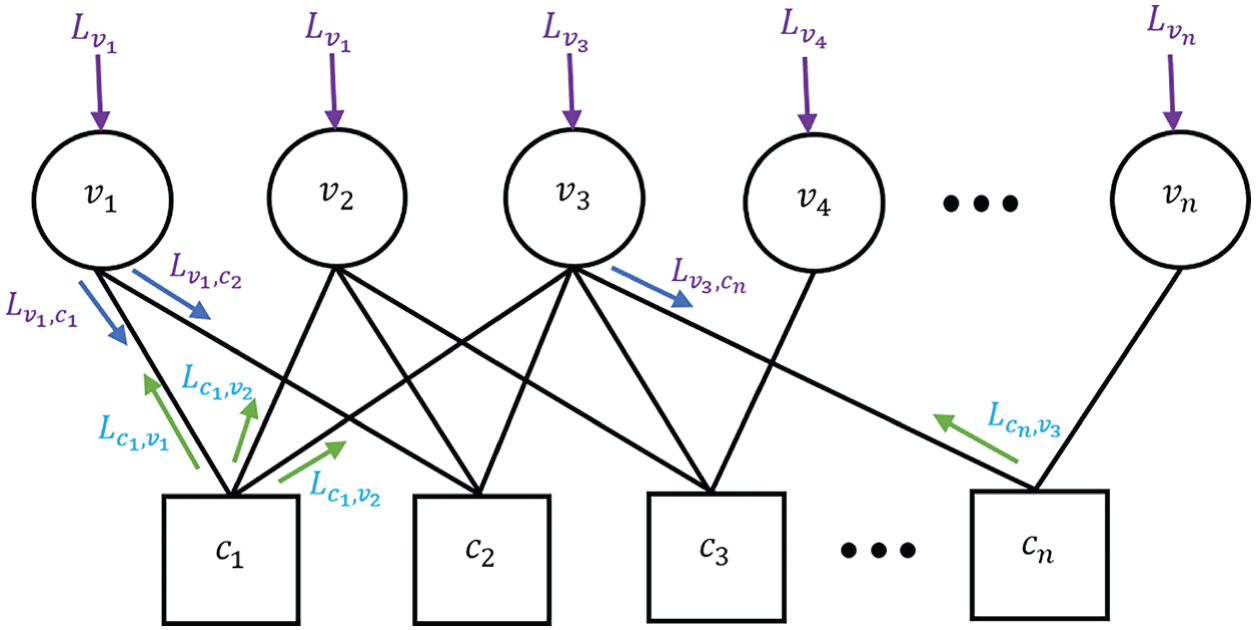
Figure 2: Parity check matrix factor graph

In LDPC code, Optical and RF channels are considered with various mapping schemes. In this case, the codeword is divided into two ways, which are optical and RF links.

n=no+nr(3)

where no=nF, nr=nF^, F^=(1−F) and F(F^) are the bit dividing factors for the FSO and RF channels. The more precise and general system is considered, and it might be impartial on real block length, i.e., n of encoded bits, to simplify the system simulation. For practical measurements, F(F^) that is mentioned above. After mapping implement, the bits of the optical channel are specified as,

no=nF=Ns1−p(4)

where N is the number of FSO channel symbols sent over the optical channel, p is the optical channel symbols fraction, and s optical bits per symbol, i.e., s=log2⁡(M). Now for RF channel bits are specified as

nr=nF^=N^s^1−p^(5)

where N^ is that the range of transmitted RF channel symbols, p^ denotes RF channel symbols fraction and s^ optical bits per symbol, i.e., s^=log2⁡(M^).

3.1 Bit Flipping (BF) Algorithm

Gallager developed the Bit Flipping (BF) along with all the LDPC codes [12]. The Algorithm belongs to the group of iterative decoding algorithms and is primarily based upon a calculation of the syndrome vector in the parity matrix H. The channel symbols are converted into 1s and 0s based on hard decoding a. At each iteration, it calculates full check-sums, in addition to a range of unsuccessful parity checks regarding every n bit of the codeword. Subsequently, the inverted bits are if they result in the most important content of unsuccessful parity checks. The technique must be repeated till check-sums are satisfied or until it reaches a defined range of iterations.

3.2 Sum-Product (SP) Decoding Algorithm

The sum-product (SP) decoding is identical to the bit flipping decoding. The SP decoding algorithm is based on a soft decision [12]. However, in this case, the messages are now represented as soft values. In such a way, we can call the bit flipping decoding hard decision decoding; moreover, the SP decoding is denoted as soft-decision decoding [13]. The received probabilities are referred to as received bit prior probabilities.

4  LDPC Code Definitions and Notations

Recently LDPC codes have gained much attention in coding theory owing to their near Shannon capacity performance for many data transmission and storage channels. LDPC codes provide many other benefits, such as less computational complexity, and its decoding can be counted, so that correct decoding is detectable [13]. Variable nodes (VN) are designated by dv while the check nodes (CN) are represented by dc. The check and variables nodes degree for an irregular LDPC code profiles are expressed as two polynomials,

λ(x)=∑i=2dvλixi−1(6)

ρ(x)=∑j=2dcρjxj−1(7)

where λi and ρj are the fraction of the edges that is related to the degree of VN and CN with i and j indexes respectively. We are considering the both the BPSK and OOK, the log-likelihood ratio (LLR) value of X conditioned on the matched filtered outputs and considered as,

L=log⁡P(X=0|y)P(X=1|y)(8)

=∑X∈X0(y|X)∑X∈X1(y|X)(9)

where P(y|X) is specified as

P(y|X)=∫0∞P(y|X,r)P(r)dr(10)

=∫0∞12πσ2exp(−(y−rX)22σ2)×2rexp(−r2)dr(11)

For BPSK

=logψ(y/2σ~)ψ(−y/2σ~)(12)

where σ~=σ2(1+2σ2) and ψ=1+πxexp(X2)erfc(−X). The calculation of Eqs. (8) and (9) is so complicated that several works have tried to reduce the computational by approximation. The channel transition probability P(y|X) is,

p(y|X0=1)(13)

p(y|X1=0)(14)

p(y)=12[p(y|1)+p(y|0)](15)

where p(y|X0=1)=p(y|X1=0)=0.5 is assumed. Now it is calculated in the LLR equation as

L=log⁡p(y|X0=1)p(y|X1=0)(16)

Subsequently, the channel is symmetric by supposing the entirely zero codewords are transmitted when analyzing the decoding algorithm. The channel information’s probability density function (PDF) is Gaussian sufficient for the following symmetry situation.

f(x)=exf(−x)(17)

The researchers evidenced that the situation is gratified for channel messages after symmetry. For all of the values, the identity is preserved in following iterations within the sum-product interpreting set of rules [14]. Let L as an intermittent data within the decoder, which can either be from a CN to a VN or a soft value from a VN to a CN. To represent the mutual information (MI) among L and X, the operator of the mutual fact T on f1 is given by,

T(f1)=I(L;X)(18)

The PDF is symmetrical, and it is supposed that all zero codewords are transmitted [14],

T(f1)=1−E[log2⁡(1+e−L)](19)

where E represents the expectation operator. We describe the feature J(σ) because of the mutual information, which is the PDF is symmetric Gaussian density that implies σ2/2 and the variance σ2 as in [15].

J(σ)=T(N(σ2/2),σ2)=1−12πσ∫−∞∞e(x−σ2/2)22σ2log2⁡(1+e−x)dx(20)

5  Behavior of EXIT Chart

EXIT chart was made-up to investigate the code convergence behavior [9]. The convergence behavior of the LDPC code is analyzed by employing the EXIT chart. A much-detailed analysis of the EXIT charts and the EXIT functions’ evaluation over each CV and VN is given in [16]. The EXIT function is designed by modeling the soft values over each node are also provided in [16]. This paper presents two techniques such as curve fitting and regular LDPC code.

5.1 Curve-Fitting Technique

In the curve-fitting technique, analysis is applied by the fitting optimization functions IEV and IEV−1 for a certain error (noise with a standard deviation σ0) despite the fact of observing the convergence criterion. It was developed for the BEC channel based on the surface property tested for a particular channel [17]. The space between the EXIT chart curves is dependent on the loss as per the area property. Therefore, the transfer curves must match to reduce the speed loss. The optimization approach has been prolonged to additional channels such as AWGN. Though area possession has not been retained. Now, we describe a curve-fitting design that leads to smart performance codes. The function IEV is a noise standard deviation dependent function, while IEC−1 independent. Supposing the code grade profiles are selected by fitting the graphs with a given σ0 satisfying the convergence criterion. For the value above the σ0, the IEV curve moves down and cuts off IEC−1. The curves match at that σ0. The code does now no longer converge for a value larger than the σ0. The best converging value for the specified design parameters can lead to the adaptation of the curves to the smart performance of the codes.

By optimizing, we can design better codes for the projected threshold. The look-up table (curve fitting) has created two codes with the same parameters. In Tab. 2, the code parameters are specified. The transfer curves are very intently similar. Therefore, the projected convergence threshold is 0.94, see Fig. 3. We simulate the performance of those two codes for iterations of different lengths. Codes are made employing a random edge interleaved. The simulation results (in terms of bit error rate (BER)) are presented in Fig. 4. Therefore, the code with a higher projected convergence threshold performs better.

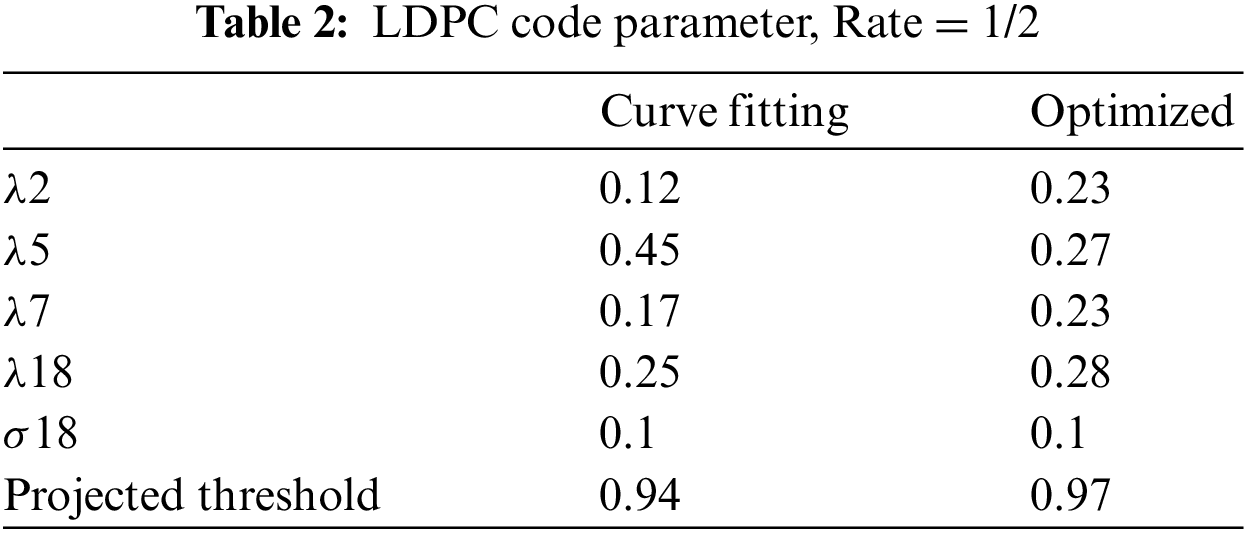
Figure 3: EXIT chart by using curve fitting technique

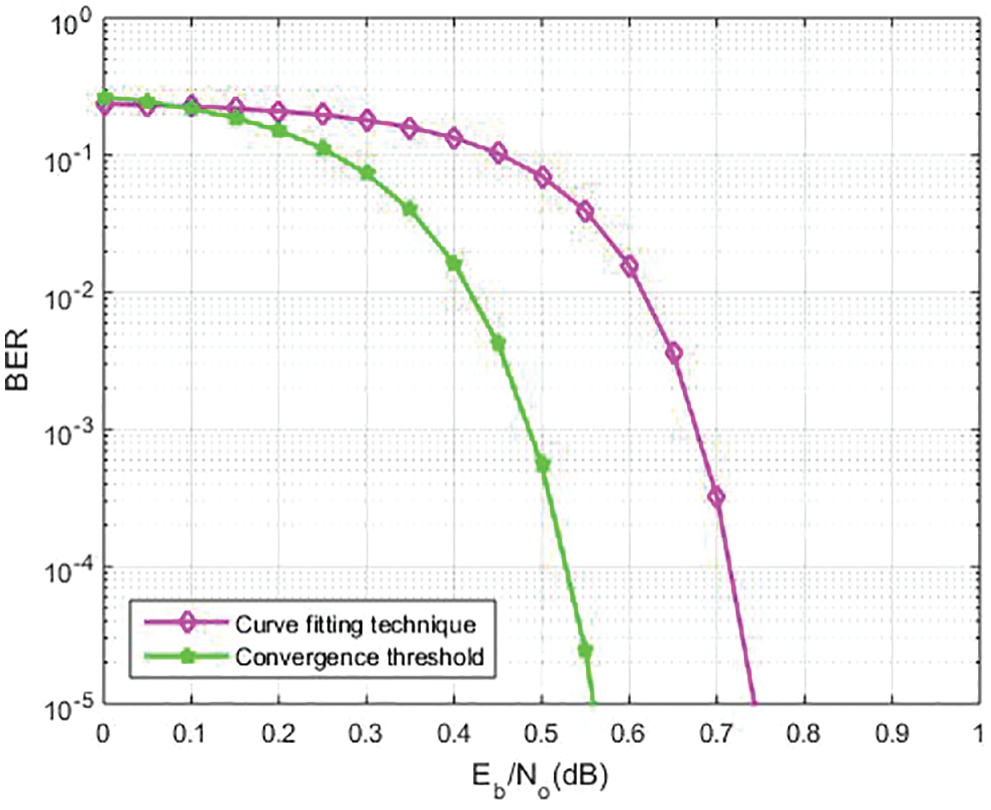
Figure 4: BER comparison between curve fitting technique and convergence threshold

5.2 Regular LDPC Codes

The division of the output messages of CNs is not always assumed to be a Gaussian symmetry [6]. The VN detector of the EXIT function is evaluated to analyze the CNs information using a normal histogram. The failure of the VN detector optimization function owing to the defined approximation can be ignored. Assuming IAV extrinsic MI of CN messages and the channel message variance is σch, then the optimized IEV is expressed as

IEV=((dv−1)[J−1(IAV)]2+σch2)(21)

The decoding operation of a CN is comparable to it of one single parity check code. The distribution of messages from VNs to test nodes but independent and identically distributed (i.i.d) inputs are transmitted to the VNs [6]. If IAC are the output messages of the VNs, then the VN detector of the EXIT function is evaluated by using the same method as in [14]. Tab. 3 suggests the values obtained during the convergence by exploiting the EXIT charts and Gaussian approximation (GA). According to the table, the expected convergence threshold error for the EXIT charts is far lower to 0.01dB. It is also far smaller than the convergence threshold error expected use of GA mainly based on the mean.

5.3 Irregular LDPC Codes

For regular LDPC codes, σi2 the output messages are evaluated by,

σi2=(i−1)[J−1(IAV)2]2+σch2(22)

In [6], due to the variable nodes of numerous degrees, the distribution of variable nodes is a symmetric Gaussian mixture for the output messages.

fv=∑i=2dvλi.N(σi22,σi2)(23)

The variable node detector of the EXIT function is given as

IEV=∑i=2dvλiJ(σi)(24)

The CN decoder EXIT function is [14],

IECi=1−J(i−1J−1(1−IAC))(25)

IEC(IAC)=∑i=2dcρiIECi(26)

We display that this calculation results in a better EXIT curve for the check node detector than the actual function. As an anticipated result, the thresholds for convergence are improved than the actual values.

6  Simulation Results

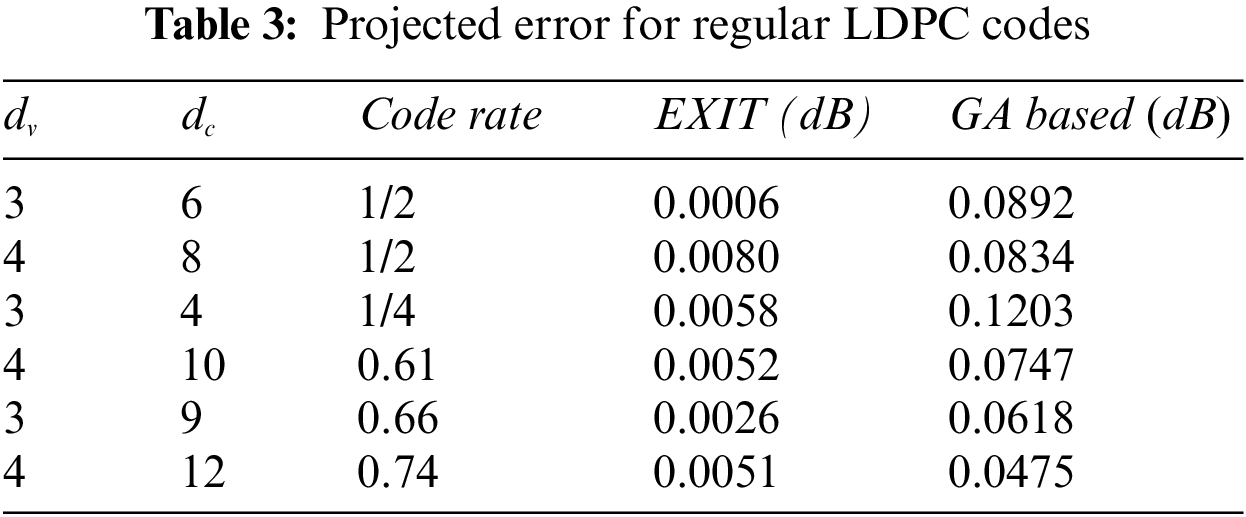
In Figs. 5 and 6, it shows the simulation results obtained using the EXIT technique considering the regular and irregular LDPC code with Rc=0.5. It is seen that the distance in simulation curves obtained for both the CN and VNs of the irregular code is very less compared to the ones obtained for VN and CN of the regular code. It is also noted that the computational complexity in the case of the irregular LDPC code is greater because it needs a greater number of iterations to reach the desired solution. Figs. 5 and 6 show that the converging values of the SNR in the case of the regular and irregular LDPC code are calculated as −1.70dB and −2.50dB, respectively. The smaller value of the SNR in the case of the irregular code proves that the irregular LDPC codes can get better performance gain under the waterfall region than the regular codes.

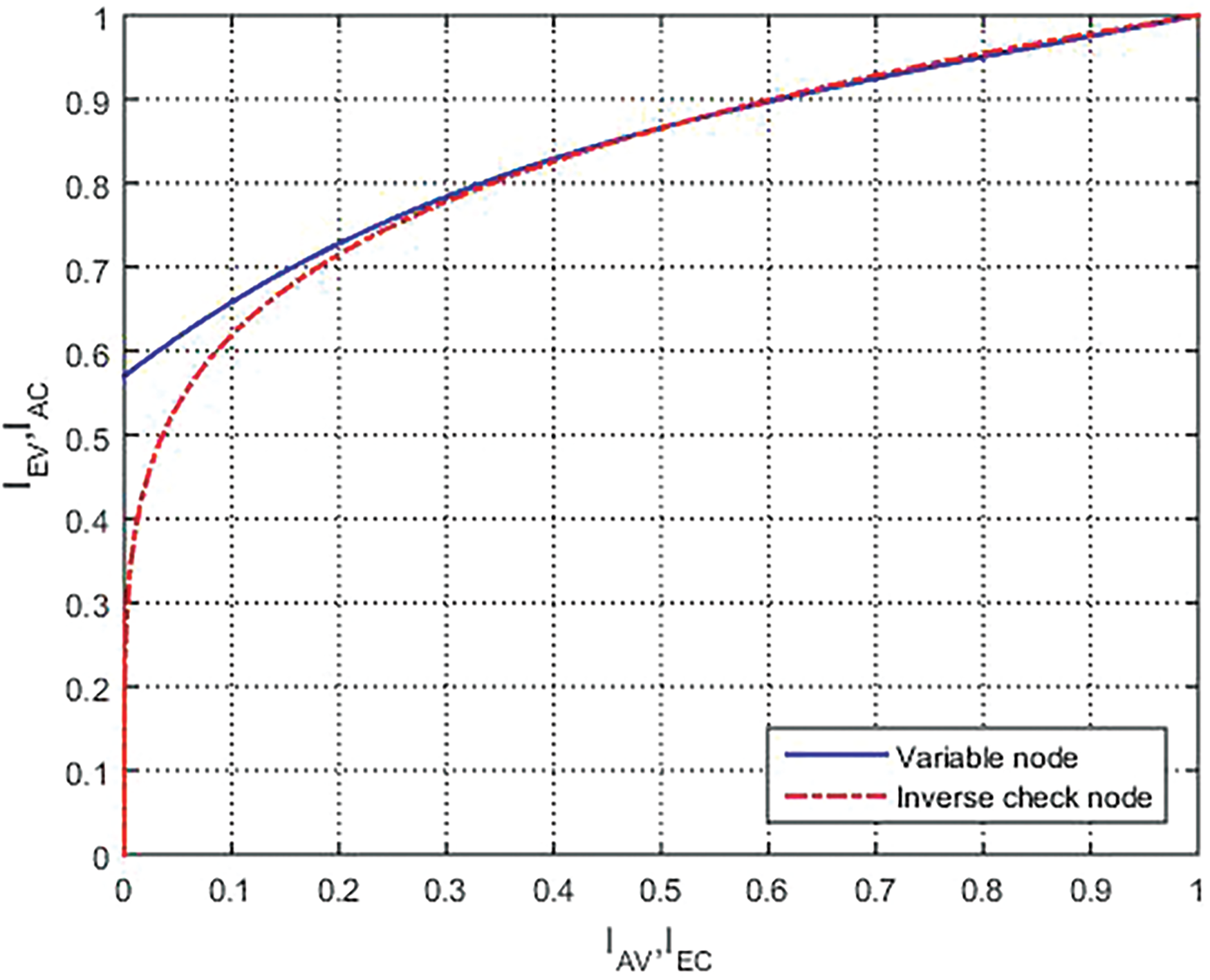
Figure 5: EXIT chart for regular LDPC codes

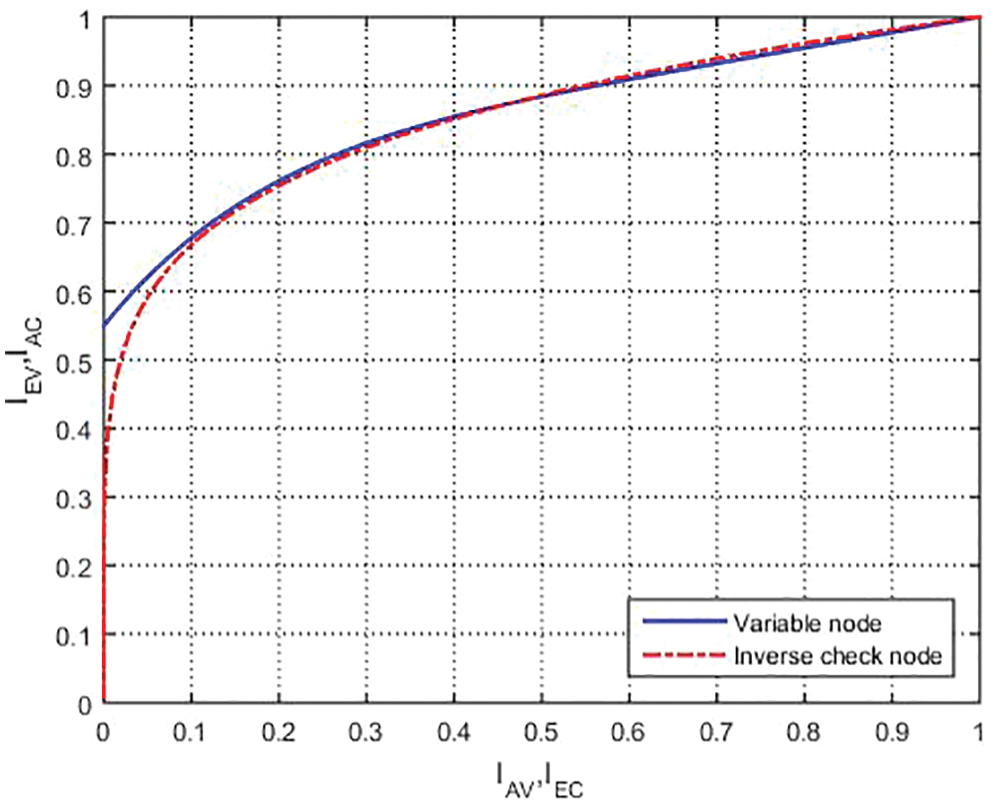
Figure 6: EXIT chart for irregular LDPC codes

In Fig. 7, it is shown that we conduct the number of iterations to analyze the bit error rate (BER) performance based on M and N that is check nodes and variable nodes, respectively. We are calculating the LLRs for OOK and BPSK, making the soft decision, and counting the number of bit errors. The results are performed on our proposed system and calculated the Eb/N0. The simulation results are conducted over 10−5 with different numbers of check nodes M=1K,2K,3K concerning variable nodes N=2K,4K,6K, and the codes are 0.9dB away. These codes are 2.9dB to 5.3dB away from the Shannon limit for the binary AWGN channel considering a BER equivalent to 10−5. We can also see that the LDPC code is 3dB better at 10−5. According to the simulation conclusion, increasing the M can dramatically reduce the Shannon limit to the same BER. In Fig. 8, it is also seen that it is near the Shannon limit with respect to FSO and RF. Hence, the comparison of simulation results is better in the FSCS case.

Figure 7: BER performance at different M

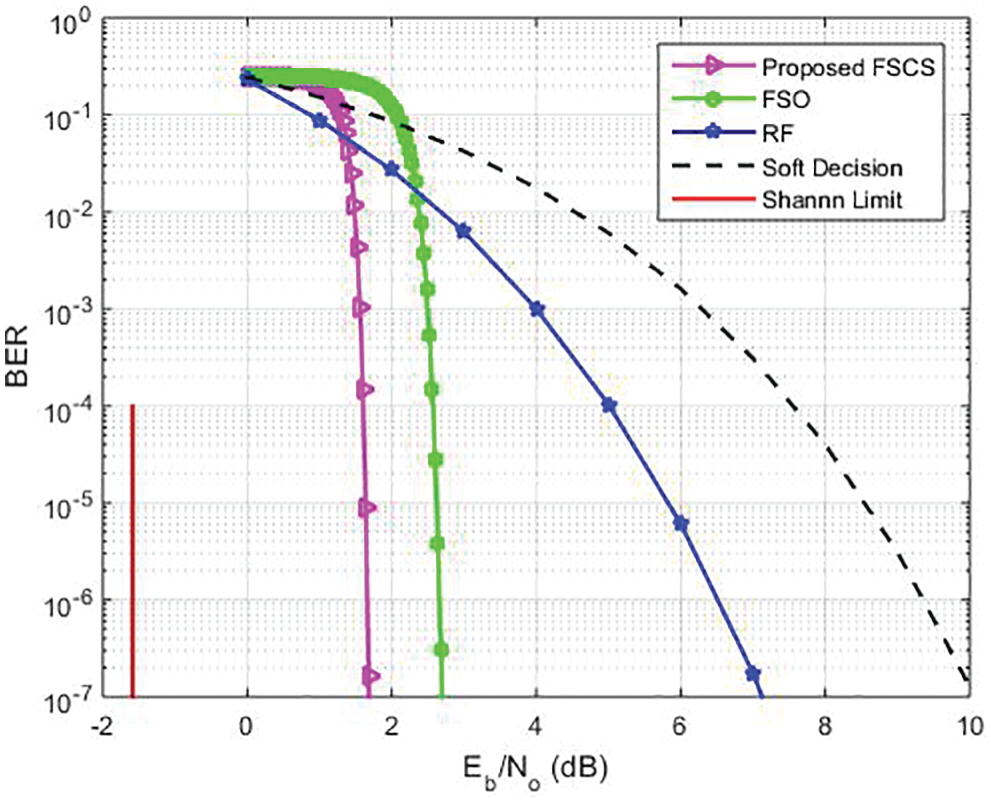
Figure 8: Comparison of our proposed FSCS at the same M

7  Conclusion

The proposed research work analyzes the curve-fitting approach to developing the LDPC codes. The optimization technique is also developed and is solely based on a convergence criterion that gives better results. The primitive principles of code design tools and the EXIT chart for FSCS are outlined. This work provides a vision of the performance of the proposed system for regular LDPC code and shows how the BER performance of FSCS links may be improved. It is observed that the presented work is well adapted to a range of decoding algorithms. The simulation results for the LDPC code indicate that the SP algorithm is optimal since its BER is stable and low for the bit flipping over given iterations. We also analyze the BER and investigate the performance of OOK and BPSK modulation schemes. We computed the LLR mapping, OOK and BPSK have been derived. From the simulation results, it is seen that our proposed FSCS is better than FSO and RF.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

 1.  Z. Ghassemlooy, W. Popoola and S. Rajbhandari, Optical Wireless Communications: System and Channel Modelling with Matlab. Boca Raton, Florida, USA: CRC press, 2017. [Google Scholar]

 2.  J. Hagenauer and E. Lutz, “Forward error correction coding for fading compensation in mobile satellite channels,” IEEE Journal on Selected Areas in Communications, vol. 5, no. 2, pp. 215–225, 1987. [Google Scholar]

 3.  C. Fewer, M. Flanagan and A. Fagan, “A versatile variable rate LDPC codec architecture,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 54, no. 10, pp. 2240–2251, 2007. [Google Scholar]

 4.  R. G. Gallager, “Low density parity check codes,” IEEE Transactions on Information Theory, vol. 10, no. 2, pp. 172, 1964. [Google Scholar]

 5.  D. J. C. MacKay and R. M. Neal, “Near shannon limit performance of low density parity check codes,” Electronics Letters, vol. 33, no. 6, pp. 457–458, 1997. [Google Scholar]

 6.  S. Garg, A. Dixit and V. Jain, “Analysis of LDPC codes in FSO communication system under fast fading channel conditions,” IEEE Open Journal of Communications Society, vol. 2, pp. 1663–1673, 2021. [Google Scholar]

 7.  Z. Zhang, L. Zhou and Z. H. Zhou, “Design of a parallel decoding method for LDPC code generated via primitive polynomial,” Electronics MDPI, vol. 10, no. 4, pp. 425, 2021. [Google Scholar]

 8.  H. Bao, C. Zhang and S. Gao, “Design and analysis of joint source-channel code system with fixed-length code,” Information MDPI, vol. 13, no. 6, pp. 281, 2022. [Google Scholar]

 9.  H. Kashif and M. N. Khan, “Future of free space communication systems (FSCSAn overview,” in Intermountain Engineering, Technology and Computing (IETC), Utah Valley University Orem, USA, pp. 1–5, 2020. [Google Scholar]

10. R. G. Gallager, “Low-density parity-check codes,” IEEE Transaction on Information Theory, vol. 8, no. 1, pp. 21–28, 1962. [Google Scholar]

11. T. Richardson and R. L. Urbanke, “The capacity of low-density parity check codes under message-passing decoding,” IEEE Transactions on Information Theory, vol. 47, no. 2, pp. 599–618, 2001. [Google Scholar]

12. F. R. Kschischang, B. J. Frey and H. A. Loeliger, “Factor graphs and the sum-product algorithm,” IEEE Transactions on Information Theory, vol. 47, no. 2, pp. 498–519, 2001. [Google Scholar]

13. M. N. Khan and M. Jamil, “EXIT chart behaviour for the hybrid FSO/RF communication system,” in Int. Conf. on Information, Communications and Signal Processing (ICICS), Singapore, 2015. [Google Scholar]

14. T. J. Richardson, M. A. Shokrollahi and R. L. Urbanke, “Design of capacity approaching irregular low-density parity-check codes,” IEEE Transactions on Information Theory, vol. 47, no. 2, pp. 619–637, 2001. [Google Scholar]

15. M. N. Khan, S. O. Gilani, M. Jamil, A. Rafay, Q. Awais et al., “Maximizing throughput of hybrid FSO-RF communication system: An algorithm,” IEEE Access, vol. 6, pp. 30039–30048, 2018. [Google Scholar]

16. M. N. Khan, M. Jamil and M. Hussain, “Adaptation of hybrid FSO/RF communication system using puncturing technique,” Radio Engineering, vol. 25, no. 4, pp. 12–19, 2016. [Google Scholar]

17. A. Ashikhmin, G. Kramer and S. T. Brink, “Extrinsic information transfer functions: model and erasure channel properties,” IEEE Transactions on Information Theory, vol. 50, no. 11, pp. 2657–2673, 2004. [Google Scholar]