Blockchain Driven Metaheuristic Route Planning in Secure Wireless Sensor Networks

1  Introduction

The rapid development of the WSN technologies received a demand for IoT applications which forms the other pervasive very efficient. IoT was used to provide the network constantly all over the world [1]. Moreover, the IoT goes with the principle which can be things or objects, and take part on the basis of wireless connections with one another to assuring ubiquitous communications. Along with that, the IoT was indulged with numerous applications that are smart homes, military, agriculture, cities, etc [2]. In several IoT applications, the sensor node (SN) transfers sensed data into the Base Station (BS) for enhancing the scalability, the energy efficiency, and data broadcast, in the WSNs which builds network further practicable [3]. Conversely, with the efficient and resourceful communication protocol for IoT or WSNs, there come numerous difficulties like undependability of low power wireless links and the less sources which were absent in relation to Quality of Service (QoS) requirements [4]. According to the demand in before line, the growth of multipath aware routing protocol becomes vital prerequisite which might assure minimum energy consumption, loss rate, delay, and the latency for numerous applications from IoT [5,6]. Fig. 1 depicts the framework of IoT supported WSN.

Figure 1: Structure of IoT assisted WSN

The WSNs consist of limited life because of the limited energy capability of deployed SNs. So, energy-efficient routing turns out to be a challenging research field in WSN [7,8]. Numerous current policies were offered for presenting energy efficient (EE) routing in WSNs. But, clustering-related protocols were mostly used for routing [9,10]. The energy can be effectively used when sending the data packets to the BS. Many routing related prevailing research works are basically aimed at effectual power utilization [11]. SNs produce a vast volume of data and transfer of the enormous volume of data may lead to collision. A multi-channel communication method was used for reducing disputes amongst SNs [12]. Numerous conventional routing plans leveraged composite event recognition for diminishing power consumption. But then, centroid oriented routing improves the network performance by using effective energy [13]. If transmission between BS and SNs was over, a black hole attack appears because of random selection

Shen et al. [14] suggest a novel EE centroid-oriented routing protocol (EECRP) for WSN-supported IoT for improving network performance. The presented EECRP has 3 main segments they are a newly distributed cluster formation approach which allows the self-organization of local sensors, and innovative sequences of systems to adapt cluster and rotate the CH in accordance with the centroid position to equally allocate the energy load between every SNs. The researchers in [15] suggest a new Secure DL (SecDL) methodology for dynamic cluster-related WSN-IoT network systems. In order to improvise the productivity of energy, the network was made that is Bi-Concentric Hexagons together with Mobile Sink technology. Dynamic clusters were generated inside Bi-Hex network and optimal CHs are selected by Quality Prediction Phenomenon (QP2) which assures energy efficiency and QoS. Data aggregation was permitted in all the clusters and managed with a Two-way Data Elimination after Reduction structure.

The authors in [16] present Scalable and EE routing protocol (SEEP). SEEP uses the multi-hop hierarchical routing strategy for reducing power consumption. In order to attain scalably as well as EE networks, SEEP uses a multi-tier related clustering structure. The network region in SEEP can be segregated into several regions by using suggested subarea division system. The zones in the network can be raised as size of the network rises to ignore long distance transmission. In [17], an original EE SN-deployment scheme for two stage routing protocol (EE-DSTRP) was suggested for minimizing the power utilization of SNs and expanding the network lifespan. SN deployment was a new method that depends upon the golden ratio. Every conventional protocol segregates network regions for transmission. Priyanga et al. [18] suggest an energy aware multiuser& multi-hop hierarchical-related routing protocol (EAMMH-RP) has multi-hop transmission that equally dispenses the energy load between every SNs in cluster formation, novel sequence of systems to adapt and rotate clusters, and brand-novel process for reducing the power utilization for remote transmission.

This paper presents a new blockchain with Enhanced Hunger Games Search based Route Planning (BCEHGS-RP) scheme for IoT assisted WSN. The presented BCEHGS-RP model majorly employs BC technology for secure communication in the IoT supported WSN environment. In addition, an effective multihop route planning technique was designed with the use of EHGS technique. The proposed EHGS technique is derived from the concept of Hill Climbing strategy (HCS) and HGS algorithm. Moreover, a fitness function with two parameters namely residual energy (RE) and inter-cluster distance to elect optimal routes. The performance validation of the BCEHGS-RP model has been experimented with under diverse number of nodes.

2  The Proposed Model

In this study, a novel BCEHGS-RP approach was established for secure communication in the IoT assisted WSN. Besides, the presented BCEHGS-RP model majorly employed BC technology for secure communication from the IoT supported WSN environment. Mover, an effective multihop route planning technique is designed by the use of EHGS technique.

2.1 BC Enabled Secure Transmission

Blockchain (BC) is a distributed dataset, where each node must agree and participate in the conclusion of appending novel blocks of dataset in BC and must have a counterfeit of that dataset [19]. BC is a distributed ledger with data traceability, tamper-proof, and decentralization features. BC is utilized for improving the robustness and trustworthiness of the routing dataset. Then, apply the BC for recording the routing table database. The procedure of agreeing and participating in a majority or common decision is named consensus. Here, we introduced an AI-based lightweight consensus approach relevant to WSN. At present, the most consensus algorithm utilized is not relevant for WSN since this algorithm consumes energy and processing power to reach consensus assumption appending a novel block in BC. The widely employed consensus algorithm is Proof of Stake (PoS) and Proof of Work (PoW). In PoW approach, every mining node takes part in the consensus procedure, and the node using additional assets, that is., hashing or computing power could assign novel block. In PoS, the nodes using additional stakes have higher possibility to assign the novel block. The drawback of algorithm is time delay and energy consumption to process novel blocks that make the algorithm inappropriate for WSN due to less computing power and lower battery power. BC encompasses three major elements chain, transactions or blocks, and consensus algorithm.

2.2 Design of EHGS Algorithm

Yang et al. [20] developed an HGS algorithm that is a population-based and gradient-free optimizer, which imitate the collaborative foraging activity of social animal whose behavior is related to the hunger degree. Especially, an adoptive weight is applied in HGS for stimulating the impact of hunger in the logical rule (game) on every searching phase, which provides a simple, however, active structure with higher efficiency. Because hunger is assumed to be the critical factor in preserving homeostatic balance and affect animal decision and action, craving for food increase as starving. Furthermore, game refers to logical rules adopted by nearly every animal for survival, namely searching for food and defending itself from the predator. Once there is a constrained number of food, a logical game starts among hungry animals that will struggle to discover food resources and win the present competition. In the following, HGS can be mathematically modelled as follows.

2.2.1 Approach Food

This section demonstrates collaborative and independent predatory behavior of social animals, which derive updating mechanism of the location in all the iterations. Even though social animal frequently collaborates in group for hunting the prey, there exists the possibility that a certain individual doesn’t contribute to teamwork. In that respect, three games are adapted for expressing the behavior approaches to food in the following [21]:

X(t+1)⟶={X(t)⟶⋅(1+randn(1)),r1<lW1⟶⋅Xb(t)⟶+R⟶⋅W2⟶⋅|Xb(t)⟶−X(t)⟶|,r1>l,r2>EW1⟶⋅Xb(t)⟶−R⟶⋅W2⟶⋅|Xb(t)⟶−X(t)⟶|,r1>l,r2<E(1)

From the expression, t represents the existing iteration; X(t)⟶ indicates every individual position; Xb(t)⟶ signifies the position of the finest individual in the existing iteration; W1⟶ and W2⟶ characterize weight of hunger, randn (1) denotes an arbitrary value fulfilling standard distribution; r1 and r2 denotes two arbitrary value ranges within [0, 1]; l represents a variable developed for enhancing the approach. Here, |Xb(t)⟶−X(t)⟶| model “range of activity” for every agent (individual), and R⟶ is constrained within [−a,a] extended. E served as a control variation determined as follows.

R⟶=a×(2×r3−1)(2)

a=2×(1−tT)(3)

E=sech(|F(i)−Fbest|)(4)

From the equation, T denotes the maximal iteration count; r3 indicates an arbitrary value ranges from [0, 1]; i∈1,2,…n and F(i) signifies the fitness value of all the agents; Fbest signifies the fitness value of optimal agent; sech characterizes the hyperbolic function as (x)=2eχ+e−χ.

In this section, three guidelines are classified into two factors for the population, that is, X⟶-based and Xb⟶-based. The initial game focused on autonomous hunting behaviors without team work for some individuals. The final two games simulate the collective foraging activity using R⟶,W1⟶ and W2⟶. Such laws offer each individual different potential positions for exploring the optimum solution in the searching space. Fig. 2 illustrates the flowchart of HGS approach.

Figure 2: Flowchart of HGS algorithm

2.2.2 Hunger Role

In this part, the hunger-driven features are modelled arithmetically. In another word, the impact of hunger on every searching stage in the game setting is formulated.

The description of “weight of hunger” (i.e.,W1⟶andW2⟶) are evaluated by:

W1(ι)⟶={hungry(i)⋅NSHungry×r4,r3<l1,r3>l(5)

W2(ι)⟶=(1−exp(−|hungry(i)−Hungry|))×r5×2(6)

In the equation, hungry(i) signifies the hunger stage of all the agents; SHungry denotes a sum of hungry quantity of every agent, viz., sum (hungry);N symbolizes the amount of agents; r3,r4 and r5 indicates arbitrary integer lies within [0l1].

The hungry(i) is provided in the following:

hungry(i)={0,F(i)=Fbesthungry(i)+HF(i)≠Fbest(7)

From the formula, the hunger stage of the optimal individual in all the iterations is often fixed as zero that produces hungry (Xb⟶)=0. For each other, a novel hunger sensation (H) is appended to the actual hunger stage for generating individual diversification.

The equation of H is shown below.

H={LH×(1+r6)lTH<LHTH,TH≥LH(8)

TH=F(i)−FbestFworst−Fbest×r7×2×(ub−lb)(9)

In the formula, LH indicates lower limits of the hunger sensation H;r6 and r7 denotes the two arbitrary number ranges within [0, 1]; Fworst denotes the fitness values of worst agent; ub and lb indicate the upper and lower limits of the searching region, correspondingly.

From the above expression, F(i)−FbestFworst−Fbest denotes the hunger ratio, where F(i)−Fbest indicates the quantity of food that agent demands to accomplish the comprehensive non-hungry state, and Fworst−Fbest denotes the highest foraging ability of the agent in the present iteration.

The proposed EHGS technique is derived from the concept of HCS and HGS algorithm. The HCS refers to local search form [22]. Firstly, arbitrary solution is initiated and frequently moves downhill from a present solution till the neighborhood solution with best quality is reached. It is applied in various challenges of optimization tasks. The HCS initiated by a random solution for the candidate’s problems Hi={Hi1,Hi2,…,Hin}, and later Neighborhood navigation (N-operator) and β operators are applied to repetitively produce novel solution Hi′={Hi′1,Hi′2,…,Hi′n}. In all the iterations of HCS, the N-operator phase is implemented by the random walk model for obtaining the (Hi′) neighboring solution of the Hi solution in the following:

Hi′k=Hik±U(0,1)×BW∃!k∈[1,n](10)

Now, BW=UBk−LBk.

At the same time, β operator is used to allocate new values for the Hi′ solution through the original value of Hi or the novel one as follows:

Hi′k={Hirifrand≤βHikotherwise(11)

The β-operator increases the exploration of HCS by roaming from a searching region to others. Moreover, exploitation is implemented by the N-operator phase that helps the neighborhood search for the existing solution. Using this operator, the HCS could prevent falling into the local minimal.

2.3 Process Involved in Route Planning

In this study, an effective multihop route planning technique is designed by the use of EHGS technique with a fitness function with two parameters namely residual energy (RE) and inter-cluster distance to elect optimal routes [23–25]. In the case of routing, the dimension of every single population in the EHGS algorithm is similar to CH and the further position is added in the BS. Given that, θi=(θ1i,θ2i|θp+1i) refers to a ith bacterium, θnii that denotes real values amongst [0, 1]. Next, the proposed mapping function is utilized to evaluate the next-hop to BS. A mapping function is represented as follows.

f(x)={i,forwhich|(ik−Xifj)|isminimum,∀i1≤i≤k(12)

In Eq. (12), the primary goal is to select the optimal path among BS and CHs. It is achieved by utilizing the fitness function by assuming objectives such as Euclidean distance, and RE. At first, the RE of succeeding hop is preferred as a relay to BS. For transmission purposes, the succeeding hop attains and gathers information and transmits them to BS. Therefore, the maximal RE for next-hop is greatly preferable. Hence, initial sub-objective interms of RE is f1 upgraded by using Eq. (13):

f1=∑i=1mECHi(13)

Following, Euclidean distance is applied to describe the distance amongst the CH to BS and next-hop. Energy reduction is in equal proportion to a transmission distance. Once a distance is low, then its minimal quantity of energy is exhausted. Therefore, the secondary objective is to minimalize the distance amongst BS and CH. At last, it improves the lifetime of the network. Therefore, the secondary sub-objective using distance is f2 is represented by using:

f2=1∑i=1mdis(CHi,NH)+dis(NH,BS)(14)

The abovementioned sub-objective transforms the normalization function at different ranges. Next, the weighted sum method was utilized for sub objective and changed to a single objective. Here, α1 and α2 implies the weight assigned for each sub-objective.

Fitness=α1(f1)+α2(f2),where∑i=12αi=1αiε(0,1);(15)

3  Experimental Validation

The experimental validation of the BCEHGS-RP model is tested on MATLAB tool. The results are inspected under two scenarios: node count of 100 and node count of 150. Tab. 1 and Fig. 3 provide a brief average residual energy (ARE) inspection of the BCEHGS-RP approach with existing methodologies under 100 nodes. The obtained values inferred that the BCEHGS-RP algorithm has shown better results with maximum values of ARE. For instance, with 10 rounds, the BCEHGS-RP model has demonstrated higher ARE of 9.28 J while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have attained lower ARE of 9.01, 8.91, 8.86, 8.98, and 9.13 J respectively. In addition, with 50 rounds, the BCEHGS-RP model has exhibited improvised ARE of 6.68 J but the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has depicted reduced ARE of 5.68, 4.71, 5.00, 5.15, and 6.07 J respectively. Moreover, with 100 rounds, the BCEHGS-RP model has exposed maximum ARE of 2.79 J where the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has portrayed decreased ARE of 1.36, 0.48, 0.09, 0.17, and 2.08 J respectively.

Figure 3: ARE analysis of BCEHGS-RP approach under 100 nodes

Tab. 2 and Fig. 4 offer a detailed link lifetime (LLT) examination of the BCEHGS-RP approach with recent methodologies under 100 nodes. The attained values exposed that the BCEHGS-RP approach has outperformed optimum outcomes with maximal values of LLT. For instance, with 10 rounds, the BCEHGS-RP algorithm has outperformed superior LLT of 1.326 s but the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have gained lower LLT of 0.027, 0.464, 0.157, 0.044, and 0.150 s correspondingly. Moreover, with 50 rounds, the BCEHGS-RP model has exhibited improvised LLT of 0.604 s while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have illustrated lower LLT of 0.007, 0.092, 0.126, 0.024, and 0.157 s correspondingly. Moreover, with 100 rounds, the BCEHGS-RP system has exposed maximal LLT of 0.278 s while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have depicted lower LLT of 0.017, 0.232, 0.010, 0.017, and 0.174 s correspondingly.

Figure 4: LLT analysis of BCEHGS-RP approach under 100 nodes

Tab. 3 and Fig. 5 provide a brief average packet deliver ratio (PDR) review of the BCEHGS-RP technique with recent methods under 100 nodes. The obtained values inferred that the BCEHGS-RP model has shown better results with maximum values of PDR. For instance, with 10 rounds, the BCEHGS-RP model has demonstrated higher PDR of 77.94% while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have attained lower PDR of 70.80%, 40.40%, 58.91%, 20.86%, and 74.71% correspondingly. In addition, with 50 rounds, the BCEHGS-RP model has exhibited improvised PDR of 83.37% while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has depicted reduced PDR of 76.24%, 78.11%, 78.79%, 80.66%, and 77.60% correspondingly. In addition, with 100 rounds, the BCEHGS-RP algorithm has exposed maximal PDR of 91.70% while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has outperformed decreased PDR of 88.13%, 81.68%, 82.86%, 85.24%, and 88.02% correspondingly.

Figure 5: PDR analysis of BCEHGS-RP approach under 100 nodes

Tab. 4 and Fig. 6 demonstrate a detailed ARE examination of the BCEHGS-RP system with recent approaches under 150 nodes. The obtained values inferred that the BCEHGS-RP model has shown better results with higher values of ARE. For instance, with 10 rounds, the BCEHGS-RP model has demonstrated higher ARE of 9.27 J but the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has attained minimal ARE of 9.00, 8.92, 9.00, 8.92, and 8.97 J respectively. Similarly, with 50 rounds, the BCEHGS-RP model has exhibited improvised ARE of 6.19 J where the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has depicted reduced ARE of 5.60, 5.16, 5.18, 5.14, and 5.95 J respectively. Eventually, with 100 rounds, the BCEHGS-RP model has shown maximum ARE of 2.38 J while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has exhibited decreased ARE of 1.10, 0.42, 0.59, 0.44, and 1.61 J correspondingly.

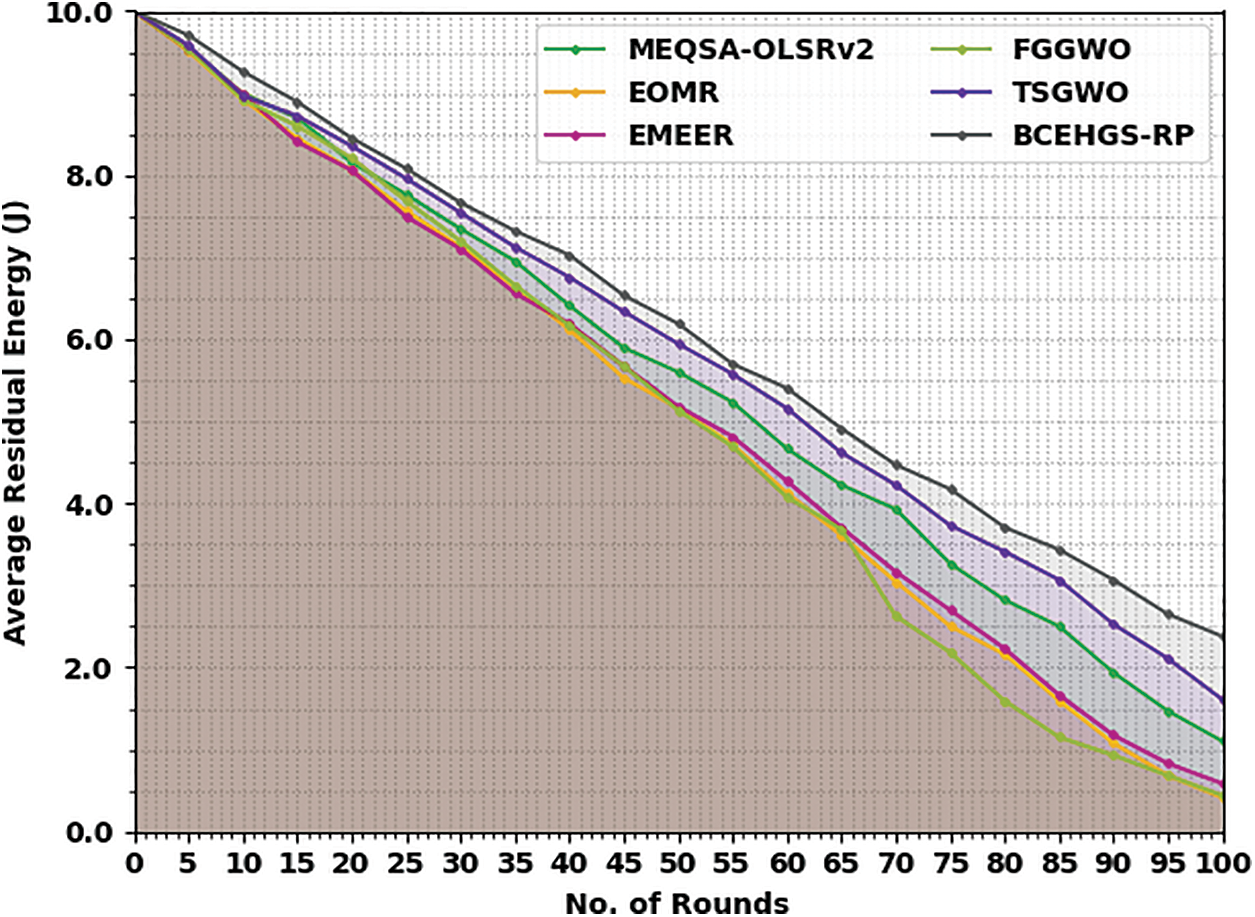
Figure 6: ARE analysis of BCEHGS-RP approach under 150 nodes

Tab. 5 and Fig. 7 depict a brief LLT inspection of the BCEHGS-RP approach with existing models under 150 nodes. The obtained values inferred that the BCEHGS-RP methodology has depicted better outcomes with higher values of LLT. For instance, with 10 rounds, the BCEHGS-RP model has demonstrated higher LLT of 0.725 s while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have reached lower LLT of 0.006, 0.010, 0.010, 0.033, and 0.566 s respectively. Followed by, 50 rounds, the BCEHGS-RP model has exhibited improvised LLT of 0.304 s but the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have depicted lesser LLT of 0.004, 0.018, 0.008, 0.010, and 0.021 s correspondingly. Lastly, with 100 rounds, the BCEHGS-RP model has demonstrated maximum LLT of 0.208 s where the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has outperformed decreased LLT of 0.012, 0.006, 0.017, 0.025, and 0.033 s correspondingly.

Figure 7: LLT analysis of BCEHGS-RP approach under 150 nodes

Tab. 6 provide a brief average PDR inspection of the BCEHGS-RP system with existing methods under 100 nodes. The attained values revealed that the BCEHGS-RP methodology has depicted optimum outcomes with maximal values of PDR.

For sample, with 10 rounds, the BCEHGS-RP approach has demonstrated higher PDR of 57.94% but the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology have attained lower PDR of 50.64%, 55.32%, 20.31%, 21.01%, and 20.49% correspondingly. Additionally, with 50 rounds, the BCEHGS-RP model has exhibited improvised PDR of 76.99% where the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has depicted decreased PDR of 63.29%, 65.72%, 68.84%, 72.13%, and 73% correspondingly. In addition, with 100 rounds, the BCEHGS-RP model has represented superior PDR of 85.09% while the MEQSA-OLSRv2 method, EOMR algorithm, EMEER approach, FGGWO system, and TSGWO methodology has outperformed decreased PDR of 73.87%, 78.20%, 75.77%, 79.24%, and 82.88% correspondingly.

4  Conclusion

In this study, a novel BCEHGS-RP approach was established for secure communication in the assisted WSN. Besides, the presented BCEHGS-RP model majorly employed BC technology for secure communication from the IoT supported WSN environment. Mover, an effective multihop route planning approach was designed with utilize of EHGS technique. The proposed EHGS technique is derived from the concept of HCS and HGS algorithm. Moreover, a fitness function with two parameters namely RE and inter-cluster distance to elect optimal routes. The performance validation of the BCEHGS-RP model has been experimented with under diverse number of nodes. Extensive experimental outcomes highlighted the better performance of the BCEHGS-RP approach on existing approaches. In futureIoT, data aggregation and compression systems are planned for improving the longevity of the network.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R237), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4310373DSR30).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Arjunan and P. Sujatha, “Lifetime maximization of wireless sensor network using fuzzy based unequal clustering and ACO based routing hybrid protocol,” Applied Intelligence, vol. 48, no. 8, pp. 2229–2246, 2018. [Google Scholar]

 2.  M. Shafiq, H. Ashraf, A. Ullah, M. Masud, M. Azeem et al., “Robust cluster-based routing protocol for IoT-assisted smart devices in WSN,” Computers, Materials & Continua, vol. 67, no. 3, pp. 3505–3521, 2021. [Google Scholar]

 3.  S. Arjunan and S. Pothula, “A survey on unequal clustering protocols in wireless sensor networks,” Journal of King Saud University-Computer and Information Sciences, vol. 31, no. 3, pp. 304–317, 2019. [Google Scholar]

 4.  N. Chouhan and S. C. Jain, “Tunicate swarm grey wolf optimization for multi-path routing protocol in IoT assisted WSN networks,” Journal of Ambient Intelligence and Humanized Computing, 2020, https://htts://doi.org/10.1007/s12652-020-02657-w. [Google Scholar]

 5.  S. Arjunan, S. Pothula and D. Ponnurangam, “F5 N-based unequal clustering protocol (F5NUCP) for wireless sensor networks,” International Journal of Communication Systems, vol. 31, no. 17, pp. e3811, 2018. [Google Scholar]

 6.  I. Abunadi, M. M. Althobaiti, F. N. Al-Wesabi, A. M. Hilal, M. Medani et al., “Federated learning with blockchain assisted image classification for clustered UAV networks,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1195–1212, 2022. [Google Scholar]

 7.  T. Durgam and R. Sadiwala, “Dynamic time assisted authentication protocol (DTAAP) for client-server in WSN-IoT environment,” in 2021 Int. Conf. on Emerging Smart Computing and Informatics (ESCI), Pune, India, pp. 583–586, 2021. [Google Scholar]

 8.  A. M. Hilal, J. S. Alzahrani, I. Abunadi, N. Nemri, F. N. Al-Wesabi et al., “Intelligent deep learning model for privacy preserving IIoT on 6G environment,” Computers, Materials & Continua, vol. 72, no. 1, pp. 333–348, 2022. [Google Scholar]

 9.  N. Chouhan, “Artificial intelligence–based energy-efficient clustering and routing in IoT-assisted wireless sensor network,” In Artificial Intelligence for Renewable Energy Systems, pp. 79–91, 2022, https://htts://doi.org/10.1002/9781119761686.ch3. [Google Scholar]

10. F. Alrowais, A. S. Almasoud, R. Marzouk, F. N. Al-Wesabi, A. M. Hilal et al., “Artificial intelligence based data offloading technique for secure mec systems,” Computers, Materials & Continua, vol. 72, no. 2, pp. 2783–2795, 2022. [Google Scholar]

11. M. Y. Arafat, M. A. Habib and S. Moh, “Routing protocols for UAV-aided wireless sensor networks,” Applied Sciences, vol. 10, no. 12, pp. 4077, 2020. [Google Scholar]

12. R. K. Lenka, A. K. Rath and S. Sharma, “Building reliable routing infrastructure for green IoT network,” IEEE Access, vol. 7, pp. 129892–129909, 2019. [Google Scholar]

13. S. Famila, A. Jawahar, A. Sariga and K. Shankar, “Improved artificial bee colony optimization based clustering algorithm for SMART sensor environments,” Peer-to-Peer Networking and Applications, vol. 13, no. 4, pp. 1071–1079, 2020. [Google Scholar]

14. J. Shen, A. Wang, C. Wang, P. C. K. Hung and C. -F. Lai, “An efficient centroid-based routing protocol for energy management in wsn-assisted IoT,” IEEE Access, vol. 5, pp. 18469–18479, 2017. [Google Scholar]

15. S. Sujanthi and S. N. Kalyani, “SecDL: QoS-aware secure deep learning approach for dynamic cluster-based routing in wsn assisted IoT,” Wireless Personal Communications, vol. 114, no. 3, pp. 2135–2169, 2020. [Google Scholar]

16. A. Shukla and S. Tripathi, “A multi-tier based clustering framework for scalable and energy efficient WSN-assisted IoT network,” Wireless Networks, vol. 26, no. 5, pp. 3471–3493, 2020. [Google Scholar]

17. A. K. Dwivedi, A. K. Sharma and P. S. Mehra, “Energy efficient sensor node deployment scheme for two stage routing protocol of wireless sensor networks assisted IoT,” ECTI Transactions on Electrical Engineering,” Electronics, and Communications, vol. 18, no. 2, pp. 158–169, 2020. [Google Scholar]

18. M. Priyanga, S. L. S. Vimalraj and J. Lydia, “Energy aware multiuser & multi-hop hierarchical–based routing protocol for energy management in WSN-assisted IoT,” in 2018 3rd Int. Conf. on Communication and Electronics Systems (ICCES), Coimbatore, India, pp. 701–705, 2018. [Google Scholar]

19. M. Kaur, M. Z. Khan, S. Gupta, A. Noorwali, C. Chakraborty et al., “MBCP: Performance analysis of large scale mainstream blockchain consensus protocols,” IEEE Access, vol. 9, pp. 80931–80944, 2021. [Google Scholar]

20. Y. Yang, Y. Wu, H. Yuan, M. Khishe and M. Mohammadi, “Nodes clustering and multi-hop routing protocol optimization using hybrid chimp optimization and hunger games search algorithms for sustainable energy efficient underwater wireless sensor networks,” Sustainable Computing: Informatics and Systems, vol. 35, pp. 100731, 2022. [Google Scholar]

21. S. Chakraborty, A. K. Saha, R. Chakraborty, M. Saha and S. Nama, “HSWOA: An ensemble of hunger games search and whale optimization algorithm for global optimization,” International Journal of Intelligent Systems, vol. 37, no. 1, pp. 52–104, 2022. [Google Scholar]

22. T. C. Ou, W. F. Su, X. Z. Liu, S. J. Huang and T. Y. Tai, “A modified bird-mating optimization with hill-climbing for connection decisions of transformers,” Energies, vol. 9, no. 9, pp. 671, 2016. [Google Scholar]

23. G. N. Nguyen, N. H. L. Viet, M. Elhoseny, K. Shankar, B. B. Gupta et al., “Secure blockchain enabled cyber-physical systems in healthcare using deep belief network with ResNet model,” Journal of Parallel and Distributed Computing, vol. 153, pp. 150–160, 2021. [Google Scholar]

24. B. L. Nguyen, E. L. Lydia, M. Elhoseny, I. V. Pustokhina, D. A. Pustokhin et al., “Privacy preserving blockchain technique to achieve secure and reliable sharing of IoT data,” Computers, Materials & Continua, vol. 65, no. 1, pp. 87–107, 2020. [Google Scholar]

25. M. N. A. Mhiqani, R. Ahmad, Z. Z. Abidin, K. H. Abdulkareem, M. A. Mohammed et al., “A new intelligent multilayer framework for insider threat detection,” Computers & Electrical Engineering, vol. 97, pp. 107597, 2022. [Google Scholar]