Wind Power Prediction Based on Machine Learning and Deep Learning Models

1  Introduction

Wind energy is crucial to reducing global carbon emissions. Wind turbine producers’ power curves are an efficacious way of showing wind turbine overall effectiveness. Nevertheless, wind power prediction is difficult because of the complexities of offshore wind turbine dynamics and the surrounding cruel environment but prediction is necessary to permit condition monitoring [1]. Wind energy production has a significant influence not just on power markets, but also on retail market and wholesale layouts. Jointly, technological challenges occur as an output of the requirement to assure the power grid’s proper operation. High-quality, long-term wind data values are necessary to create technique findings which resulting in good policy suggestions. Middle and long-term prediction requirements (e.g., reliability, thoroughness and rapidity) are more stringent, making it challenging to generate trustworthy findings [2].

Wind forecasting technologies have been the focus of global research, serving as the foundation for power system planning and operation, power dispatch reference and optimum energy flow distribution. With the advancement of information, artificial intelligence technologies and edge computing devices, forecasting approach is evolving toward surveillance refinement. The real-time forecasting of wind power can help wind turbines improve their overall productivity by enabling sophisticated wind turbine adjustment planning and pre-setting of pitch, yaw surveillance devices [3]. Wind power prediction is important for power traders’ unit obligation, maintenance scheduling and profit optimization. The present progress of effective and precise wind power prediction methodologies provides an improved cost-effective operating and maintenance strategies for futuristic wind turbines [4].

AI techniques have showed great accuracy, enhanced generalization performance, and better learning capability, making them excellent for dealing with unreliable, inflexible, and discontinuous wind power. Because of its high thoroughness, versatility, and enhanced efficiency, AI-based hybrid techniques for wind power prediction such as deep learning, classification and regression, neural network and rule-based techniques have recently gained popularity [5]. Accurate wind power and wind speed (WP/WS) prediction has steadily become more important in reducing wind power variability in network deployment management. Because of their greater capacity to cope with complicated nonlinear issues, data uncertainties, and missing features, deep learning techniques are widely being evaluated for WP/WS prediction as intelligent methodologies, particularly deep learning [6].

Wind power forecasting has evolved through the years into a method of addressing the high fluctuation issues produced by large-scale integration. Improved forecast accuracy is essential for improving power grid reliability and economics. Machine learning techniques have been used to improve wind power forecasting. Bagging Neural Networks, Adaptive Boosting, Gradient Boosting and Random Forest. Machines are some of the methods utilized for prediction. Ensembles increase predicting accuracy by diversifying the model and are appropriate for middle and long-term prediction. Optimization algorithms, signal decomposition techniques and several of mentioned algorithms are integrated into hybrid models, which encompass the integration of both unsupervised and supervised algorithms employing clustering models such as Spectral and Bayesian, and clustering analysis is performed using K-means [7]. Aside from traditional machine learning techniques, the effective employment of deep learning in object classification have attracted an increasing number of academics and experts in the field of prediction. Given deep learning’s distinct advantages in time-dependent depictions and feature extraction, it is appropriate to integrate it with auxiliary mode decomposition in forecasting of wind power [8]. Furthermore, when a substantial quantity of hidden layers are employed in the building of a prediction models, deep learning techniques improve computational and statistical approaches, although they are attacked for their comparatively poor learning rates [9].

Wind power prediction relies heavily on assessment. Evaluating suggested prediction models enables for ongoing comparison of alternative models and, as a result, their continuous evolution. Both probabilistic and deterministic forecasts require evaluation. Over the years, basic comparison measures like as Mean Squared Error (MSE), Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) have been employed in deterministic prediction to assess the effectiveness of prediction methods. Furthermore, assessing probabilistic projections is more difficult than assessing point predictions. While the variance between anticipated and measured power values is used to evaluate point predictions, this is not viable in probabilistic prediction since such a comparison is not achievable explicitly [10].

Our contributions can be stated as follows. (1) Data preprocessing and data cleaning were performed to the chosen dataset. (2) Deep neural network (DNN) model, k-nearest neighbor (KNN) regressor model, long short-term memory (LSTM) model, averaging model, random forest (RF) regressor model, bagging regressor model, and gradient boosting (GB) regressor model are used as regression models for predicting wind power. (3) Five evaluation criteria namely, mean absolute error (MAE), median absolute error (MedAE), mean square error (MSE), coefficient of determination (R2), root mean squared error (RMSE) were utilized to estimate the efficiency of the regression models. Fig. 1 illustrates the framework of the recommended methodology for wind power prediction.

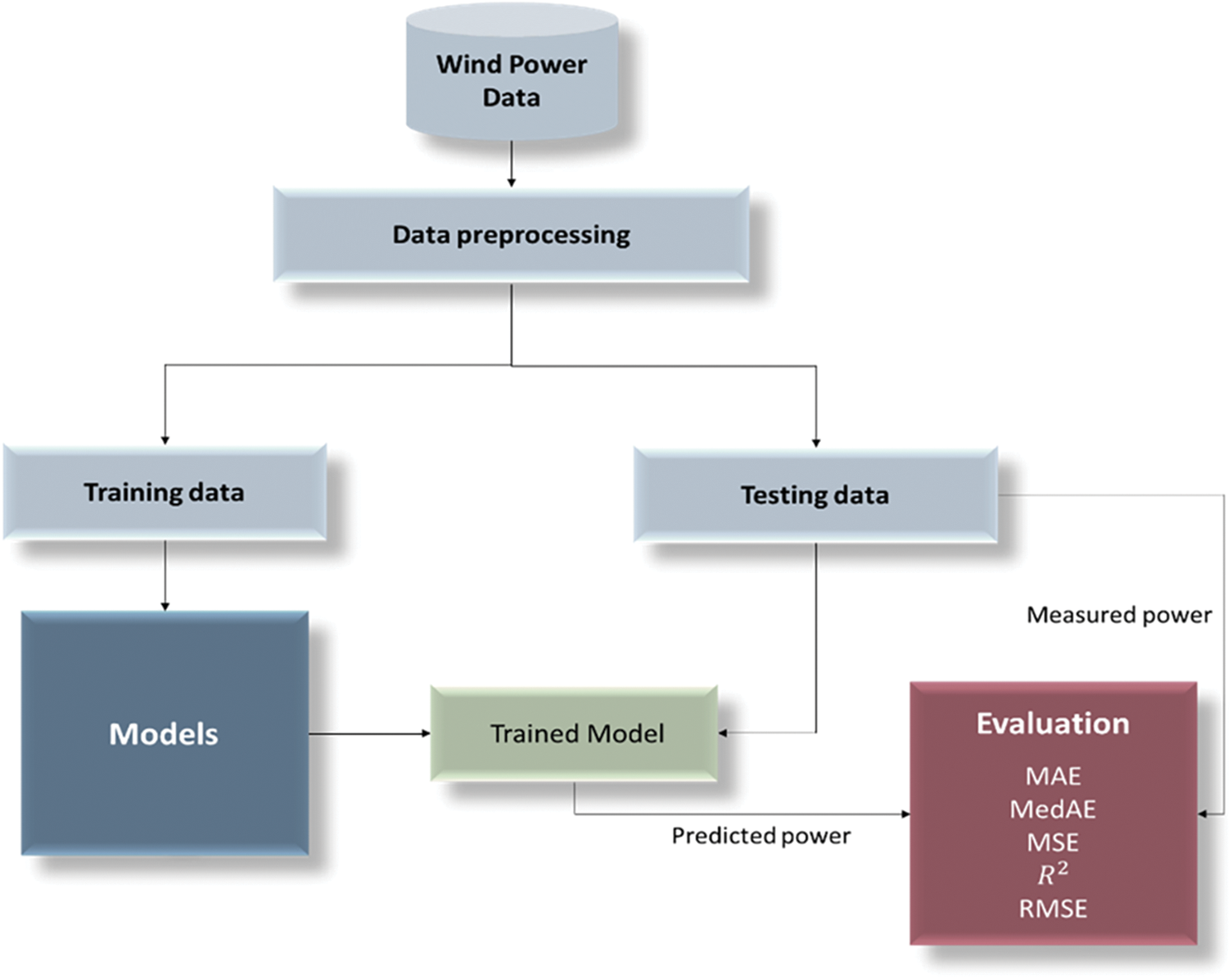
Figure 1: Framework for the proposed wind power prediction

The rest of the paper is organized as follows. The categorization of existing wind power forecasting systems was presented in Section 2. Section 3 discussed the different ML/ DL strategies that may be utilized to increase wind power forecasting performance. Section 4 presented the proposed model for wind power prediction. Performance evaluation and results discussion were provided in Section 5. At last, conclusion and future work are mentioned in Section 6.

2  Related Works

Machine learning approaches are currently utilized in many applications to classify and predict the enrolled features based on supervised learning [11]. Furthermore, its ability to cluster the data and reduce the dimensionality size of the features based on unsupervised learning. Deng et al. [12] used a bidirectional gated recurrent unit approach with deep learning system to anticipate wind power. The findings demonstrate the model’s capacity to spontaneously simulate the link between wind direction, speed and power. Yildiz et al. [13] presented a Convolutional Long Short-Term Memory network (Conv-LSTM) for short-term wind power prediction. To remove any irregularities in the raw data, Variational Mode Decomposition (VMD) was applied. Following that, Conv-LSTM is used to generate early forecasting findings, along with extract spatiotemporal data from the forecasted samples. In two separate studies, the suggested model outperformed the other models in terms of RMSE, MSE, MAE, and MRE error metrics. Authors in [14] suggested a two-step revolutionary deep learning technique for wind power forecasting: feature extraction based on VMD, followed by an enhanced CNN to predict wind power. Due to its competitive effectiveness, the suggested technique surpassed the other systems and provided impressive outcomes for extremely short-term prediction.

Authors in [15] suggested SVM-based approach with Improved Dragonfly Algorithm (IDA) for a hybrid wind power forecasting approach. When compared against existing models, such as the Gaussian Process Regression and Back Propagation Neural Network (BPNN), the suggested model outperformed them (GPR). The suggested IDA-SVM model outperformed the other techniques for winter and fall datasets using the R2, NMAE, MAPE and NRMSE error metrics. Authors in [16] suggested a new deep transfer learning strategy based on a one-of-a-kind serio-parallel CL feature extractor for multi-step forward wind power forecasting of targeted wind ranches in the absence of wealthy historical information. The findings validated the supremacy of the proposed model over the independent LSTM and CNN techniques. Furthermore, the suggested CL-TL-CSO and CL-TL approaches outperformed the other non-transfer techniques irrespective of whether they were deep learning algorithms (i.e., LSTM, CNN, etc.) or shallow-layer network techniques (i.e., ELM and Elman).

Authors in [17] suggested four ML techniques, namely, SVR, ANN, RF and regression trees for wind power forecasting. The findings indicated that using a single metric that takes into account both training time and performance, the SVR might be the optimum choice. Authors in [18] utilized a unique STCM based on CNN-LSTM for ultra-short-term wind power prediction. The efficacy and supremacy of the suggested CNN-LSTM technique were demonstrated by comparing four assessment criteria with LSTM and CNN employed separately. The experiment findings demonstrate that the overall model’s mean MAE, MAPE, RMSE, and NRMSE reduce by 33.77 percent, 30.69 percent, 25.3 percent, and 23.3 percent (compared to CNN), and 12.0 percent, 10.6 percent, 14 percent, and 12.7 percent (compared to LSTM). The suggested STCM for multi-step prediction based on CNN-LSTM completely addressed the spatio-temporal correlation of meteorological parameters across the wind farm and can predict wind farm power more correctly.

Authors in [19] suggested a hybrid wind power projection technique based on ELM and KMPE. The results indicated that the suggested ELM-KMPE strategy outperformed the traditional FFBPNN approach. Nonetheless, because to the fixed-point phase, ELM-KMPE demonstrated a slower estimating speed. As a result, more investigation is necessary to address the computation complexity difficulties. Authors in [20] introduced a parameter optimization mechanism into the framework of back-propagation neural networks (BPNN), where layers are merely piled in depth, to improve training effectiveness. Authors in [21] demonstrated a hybrid technique for predicting wind power production for twenty-four hours in advance. This unique technique is built on CNN with a Radial Basis Function Neural Network (RBFNN). The simulation outcomes show that the suggested technique was more effective than standard methods for estimating wind power 24 h in advance. Authors in [22] introduced a novel effective hybrid prediction model integrating variational mode decomposition (VMD) and mixed Kernel ELM (MKELM) for accurate wind energy forecasting. According to the results, the suggested model produced the best effective predictive results with the lowest SMAPE, MAE and RMSE values. A recent study presented by Alkesaiberi et al. [23] presented a comparative study of wind power prediction using machine learning methods. The models presented in [23–30] describes the algorithms and approaches to predict the wind power based on different evaluation matrices as presented in Tab. 1.

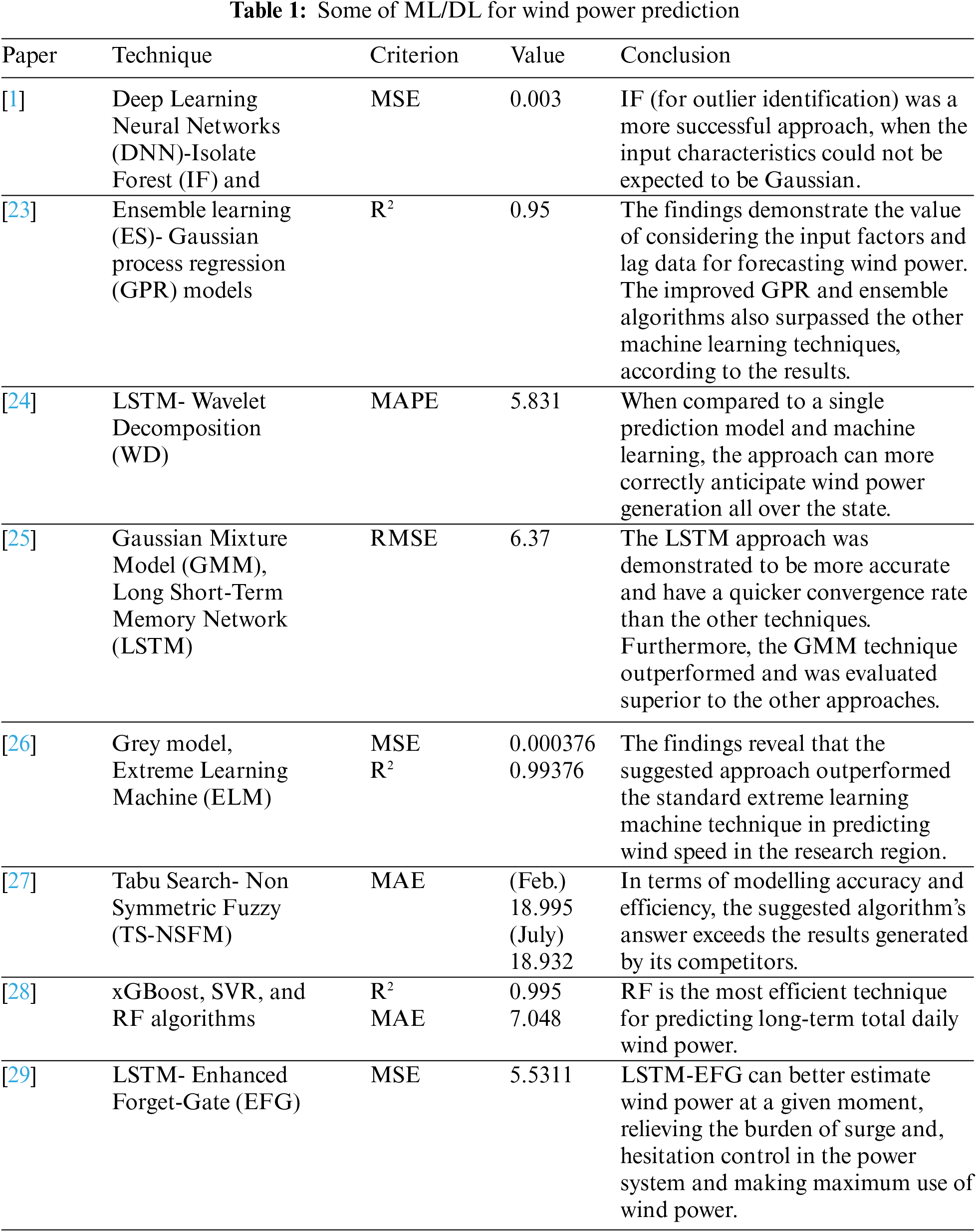
According to the previous table, numerous strategies are routinely employed to forecast wind power, although with limited model enhancement and data preprocessing capabilities. This shortage of experience is a substantial problem for authoritative and consistent wind energy forecasts. As a result, in comparison to the prior research discussed in this article, we suggest an approach to attain the best performance of the wind power prediction system.

3  Proposed Methodology

A Deep Neural Network (DNN) is essentially an ANN with several hidden layers. The approach is believed to be especially useful when working with huge data samples. It is built on a feedforward multilayer network. A backpropagation method is used in the learning phase to change neuron weights in order to decrease training error. The knowledge between layers is transferred through a nonlinear activation function modification. Multiple layers of nonlinearity result in improved feature extraction and info gain [30]. Deep learning techniques are very deep structures based on successive layers of impersonation and abstraction [31]. Fig. 2 presents the deep network architecture of DNN with multiple layers network.

In this work, we utilized DNN architecture with three basic layers which are the input layers that represents the features selected from the applied wind dataset. The hidden layers which include five stacked hidden layers each with five neurons in each layers with an ReLU activation function and Adam optimizer. We utilized 50 epochs as a number of iterations with a patch size 64 and the learning rate 0.0001. The proposed scheme is a hybrid model of type sequential hybrid means the first paradigm is the LSTM that passes its output to the second paradigm SFS-PSO to optimize the results and to boost the evaluation criteria results.

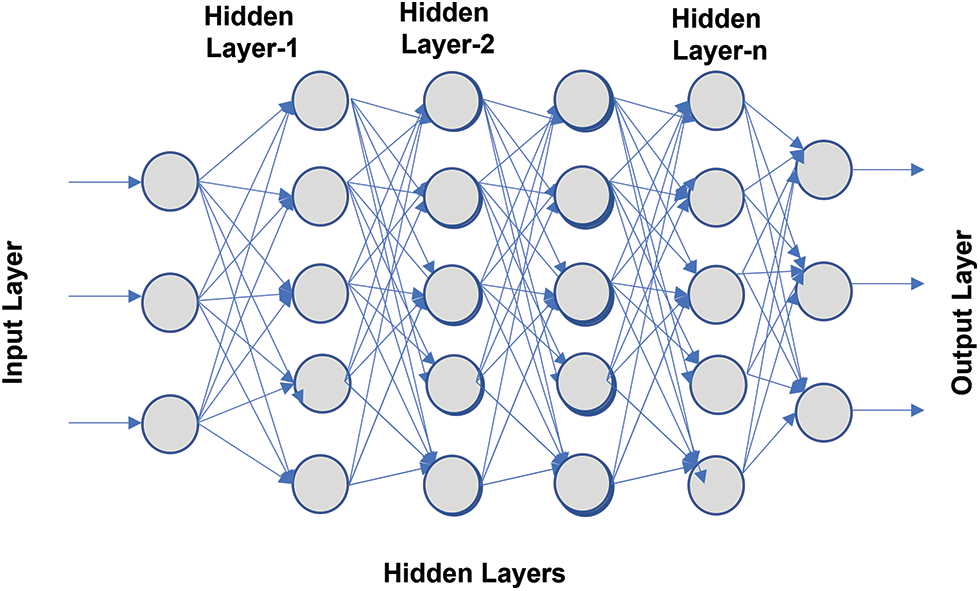
Figure 2: Deep network architecture with multiple layers

3.1 Long Short-Term Memory

Long Short-Term Memory (LSTM) is a type of recursive neural network (RNN) that may learn to depend on input for an extended period of time. Furthermore, it is appropriate for analyzing and anticipating necessary events in time series with relatively lengthy gaps and delays. LSTM has had significant success and is extensively utilized on a variety of conditions [29]. The LSTM presents a memory unit based on RNN that is regulated by input, forgetting gates and output. It may improve the screening, storage, and information flow monitoring under the time feedback procedure, efficiency avoid risk of data loss, and address the gradient absence and explosion issue. The transformation equation is defined as in Eqs. (1) to (5) [29]:

ft=σ(Wf[ht−1;xt]+bf)(1)

it=σ(Wi[ht−1;xt]+bi)(2)

ot=σ(Wo[ht−1;xt]+bo)(3)

st=ft⊙st−1+it⊙tanh⁡(Ws[ht−1;xt]+bs)(4)

ht=ot⊙tanh⁡(st)(5)

where notation [ht−1;xt] is the union of the previously concealed state with the current vector of input. ⊙ represents the elementwise multiplication and σ denotes the logistic function defined elementwise by Eq. (6):

σ(x)=11+e−x(6)

The cell state st is the core innovation of LSTM. In comparison to the rapid shift in the concealed state ht, The cell state can recall a more extensive past. The forget gate ft controls its memory. Through an output gate, the hidden state ht is acquired from st.

3.2 Particle Swarm Optimization

When it comes to the particle swarm optimization (PSO) method, it’s inspired by the way flocks of birds move together [32]. For example, the social behavior of birds may be simulated using the PSO algorithm Changes in velocity are used to guide the movement of swarms in their quest for food. These are the parameters of each particle in the PSO.

•   The fitness function is used to evaluate the particles’ current positions.

•   Last best positions, which store better positions’ values of the particles.

•   Velocity or rate of position change.

•   Position, which indicated a point in the search space.

All particles’ locations and speeds change during the algorithm’s rounds. The following commands are used to change the particle’s location as in Eq. (7).

xt+1=xt+vt+1(7)

where xt+1 is the new particle position, and the updated velocity of each particle vt+1 can be calculated as in Eq. (8):

vt+1=ωvt+C1r1(pt−xt)+C2r2(G−xt)(8)

where ω is the inertia weight, C1 and C2 represent cognition learning factor and the social learning factor. Parameter G is the global best position and r1 and r2 are random numbers in [0; 1].

3.3 Stochastic Fractal Search

An algorithm that uses random fractals as an inspiration for metaheuristic algorithms can be as efficient and accurate as the original fractal technique. To find a solution to a given problem, the Fractal Search (FS) technique follows three basic rules.

1.    The best particles are kept while the others are removed with each new generation.

2.    There are several ways to make and disperse new particles. In the new particles, the original particle energy is shared.

3.    A particle can have electrical potential energy.

Finding fractals in any given object is possible with the use of the Stochastic Fractal Search (SFS), as explained in detail in [33]. The fractal-shaped objects are built using the Diffusion Limited Aggregation (DLA) process. When compared to the original FS approach, the SFS method makes use of diffusion and two distinct types of update processes. This solution BP might be surrounded by the solutions BP1-BP5 in order to arrive at the best potential outcome.

3.4 Diffusion Process

The Gaussian distribution approach is used in the DLA growth process to produce new particles based on the diffusion procedure of SFS. In the diffusion process, a list of walks created by the best solution P→ may be determined as Eq. (9).

P′→=Gaussian(μP→,σ)+(β×P→−β′×V→)(9)

where the updated best solution is denoted by P′→. The values of β and β′ are selected randomly from the range [0; 1]. The point in the group is denoted by V→, whereas the position of the best point is referred to as P→. In addition, μP→ is equal to |P→| and σ is equal to |V→−P→|. A better solution can be found by using the application of SFS into the process of PSO, which is an exploration method based on the algorithm’s diffusion process. The proposed algorithm is based on employing the SFS to improve the exploration of the PSO optimization algorithm. The details of the proposed algorithm are presented in Algorithm 1.

3.5 The Proposed SFS-PSO Algorithm

To improve performance of LSTM network, we proposed a new optimization approach based on PSO and SFS to achieved better balance between the exploration and exploitation of the optimization process, the proposed algorithm employs the SFS technique to boost the performance of the exploitation step. The steps of the proposed algorithm are listed in Algorithm 1, and the balance between the exploration and exploitation is depicted in Fig. 3 depicts. In addition, the flowchart shown in Fig. 4 clarifies the steps of the proposed methodology.

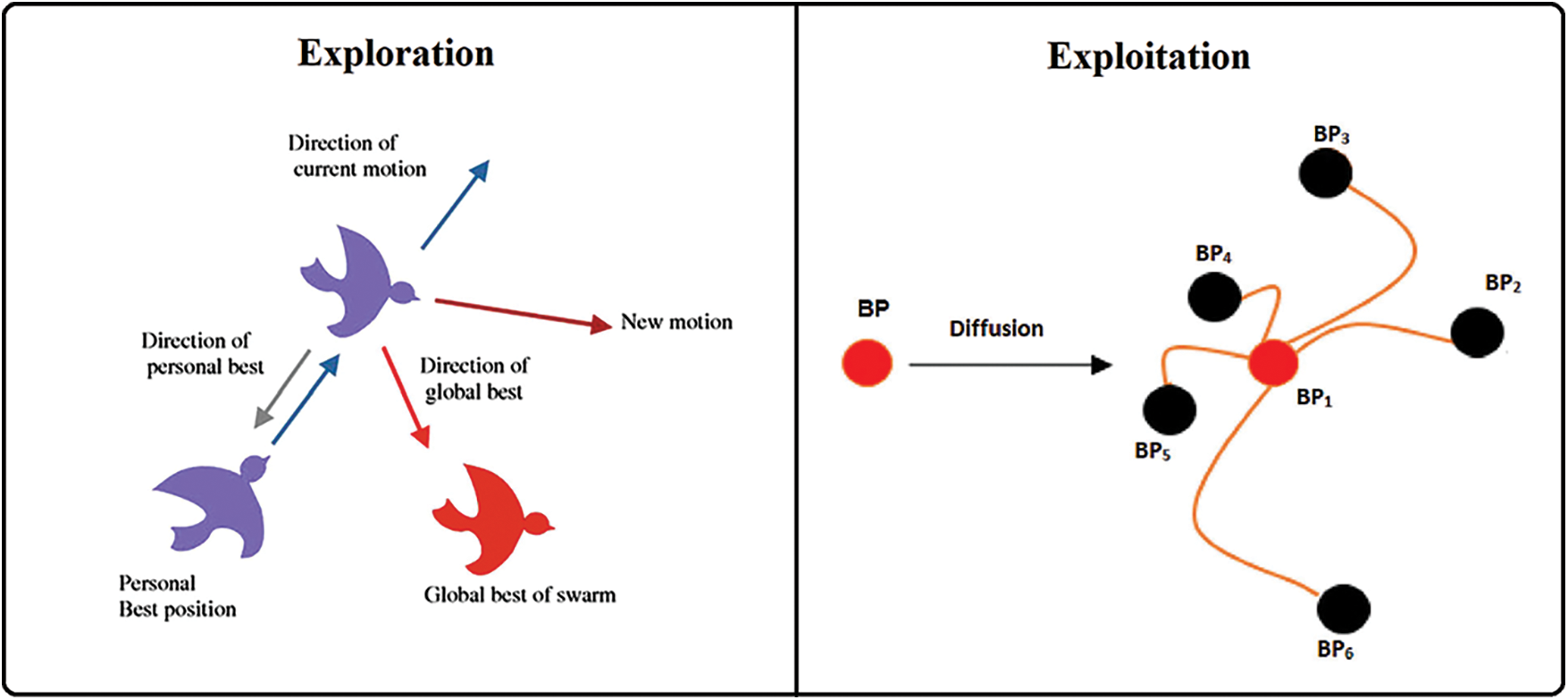
Figure 3: The balance between exploration and exploration tasks of the proposed method

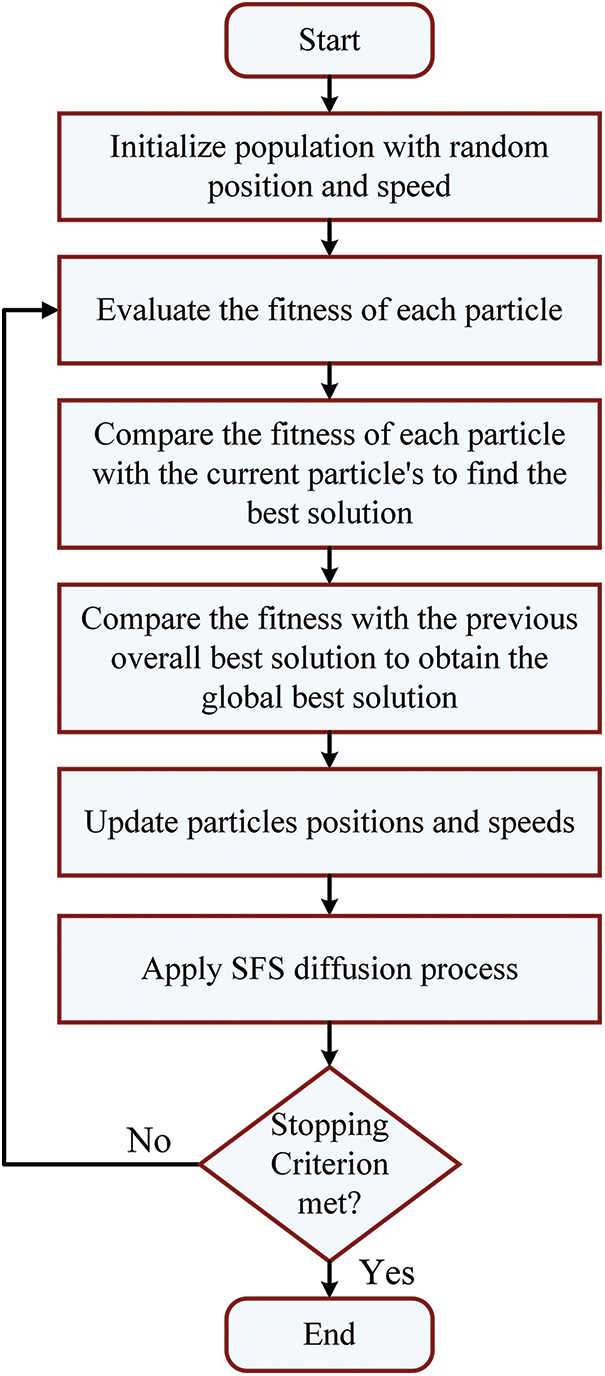
Figure 4: Flowchart of the proposed SFS-PSO optimization algorithm steps

In this paper, we present Exploitation that described as a greedy strategy in which the proposed model use estimated value rather than real value to try to acquire greater rewards. As a result, we use this strategy to make the best decision possible based on current knowledge. Unlike exploitation strategies are more concerned with enhancing their understanding of each action than with receiving more rewards in order to reap long-term gains. Accordingly, this work depends on multi-feature learning model with greater local attention. At the same time, this model might gain more representative global and local properties. To extract more complete global characteristics, global features combine both the middle and final layers [34,35].

4  Results

The results of the conducted experiments on the wind forecasting using the proposed approach along with the traditional baseline models are presented and discussed in this section. The section starts with presenting the employed dataset, followed by presenting the achieved results.

4.1 Dataset

As a case example, the studies use a wind power forecasting dataset to estimate hourly power output at seven wind farms for up to 48 h in advance. On Kaggle, the dataset is called Wind Turbine Scada Dataset linked in https://www.kaggle.com/datasets/berkerisen/wind-turbine-scada-dataset. Fig. 5 shows the correlation matrix of the features of this dataset. In addition, a statistical analysis of the dataset features is presented in Tab. 2, and the histogram of the wind power values is shown in Fig. 6.

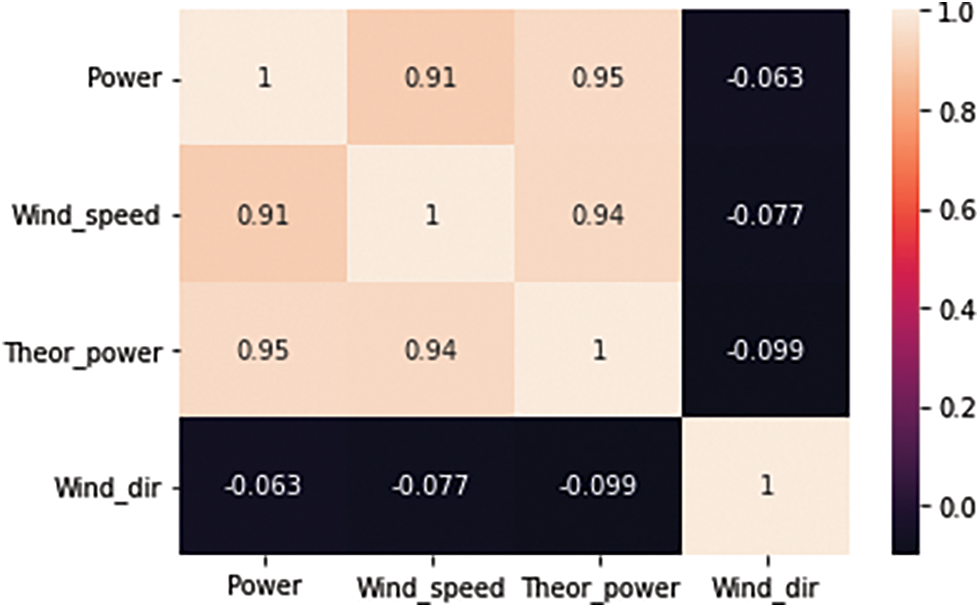
Figure 5: Correlation matrix of the wind dataset features

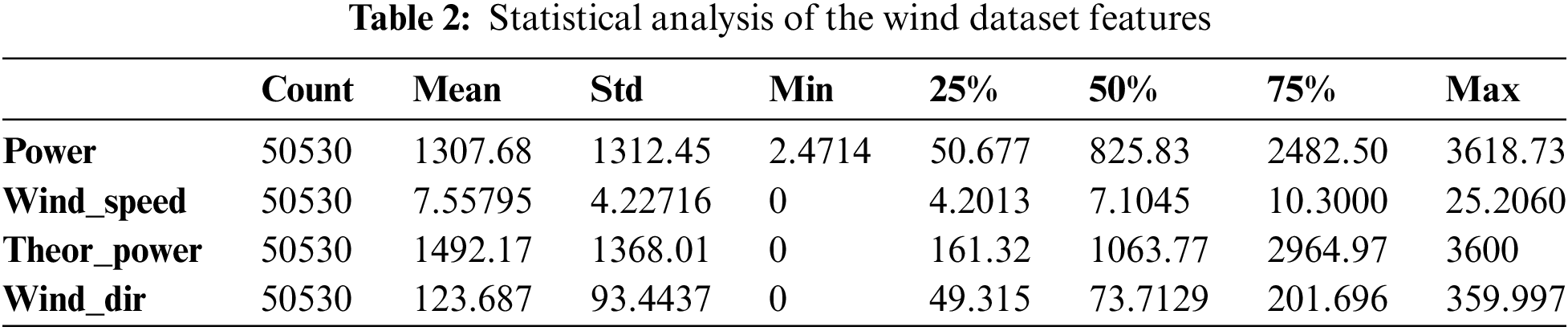
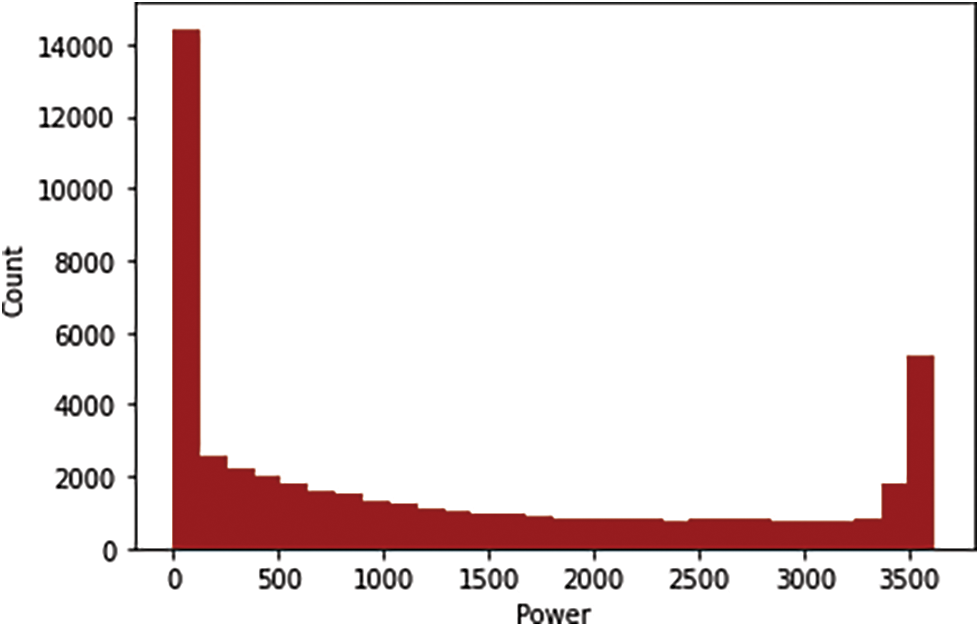
Figure 6: Histogram of the wind power based on the records of the wind dataset

4.2 Evaluation Criteria

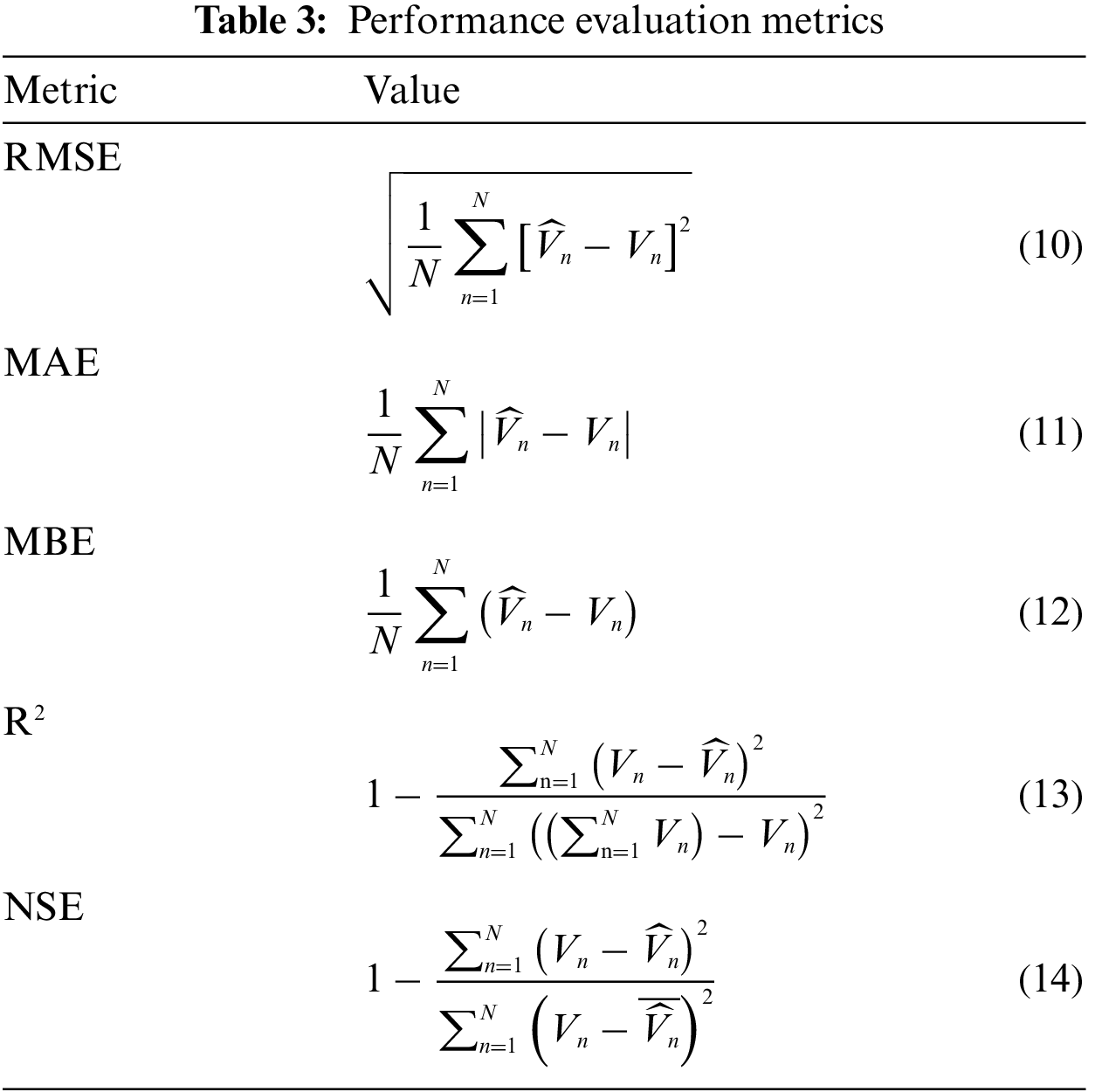
The evaluation of the proposed approach is performed in terms of the metrics presented in Tab. 3. These metrics are Nash Sutcliffe Efficiency (NSE), coefficient of determination (R2), mean bias error (MBE), root mean error (RMSE) and mean absolute error (MAE) where N is the number of observations in the dataset; Vn^ and Vn are the nth predicted and actual wind power values, and Vn^¯ and Vn¯ are the arithmetic means of the estimated and observed values Eqs. (10)–(14).

4.3 Evaluation Results

In this section, the prediction results of the wind power is performed in terms of two experiments. Firstly, the prediction using the proposed optimized LSTM. Secondly, the prediction using a set of baseline models. These models include, deep neural network, K-nearest neighbor, average ensemble model, random forest, bagging regression model, and gradient boosting regression model. The discussion of the achieved results is presented in the next section.

4.3.1 Results Using the Proposed Approach

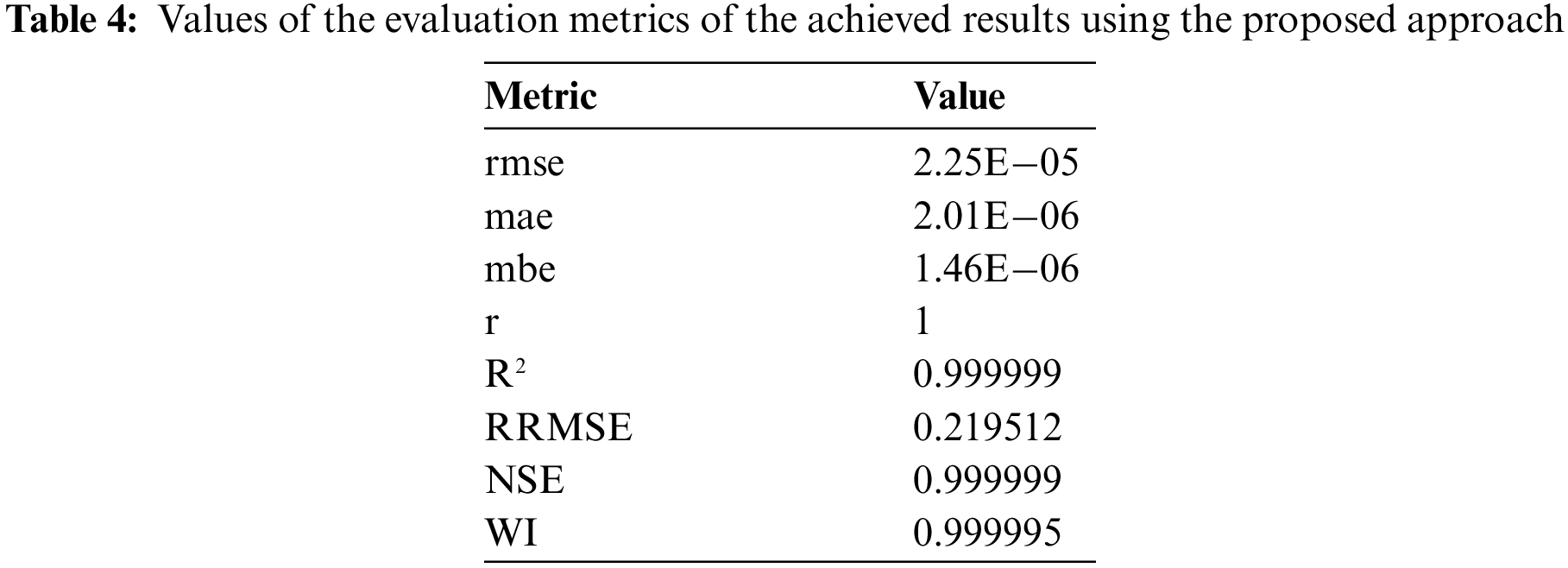
The proposed optimized LSTM is employed to predict the wind power values. Fig. 7 shows the mapping between the predicted and actual wind power values. As shown in the figure, this mapping is fitted to a line which indicated the accurate prediction of the wind power values. The number of samples employed in this experiment is 500 samples. On the other hand, the assessment of the achieved results is performed and the results are listed in Tab. 4.

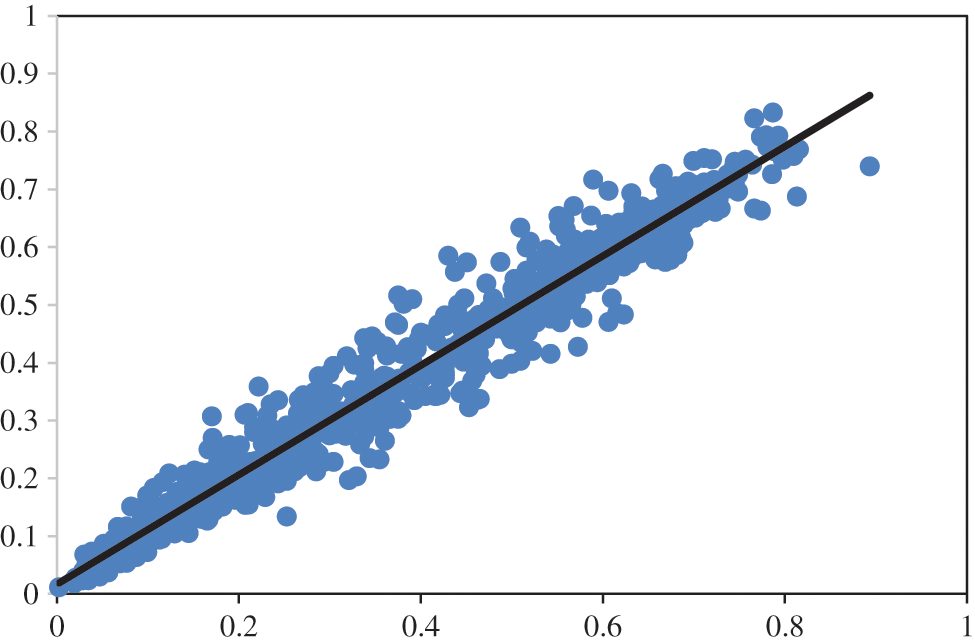
Figure 7: The predicted vs. actual values of wind power values with line fitting

4.3.2 Results Using the Baseline Models

The baseline models included in this experiment are deep neural network, K-nearest neighbor, random forest, bagging regression model, and gradient boosting regression model. The parameters of these models are presented in Tabs. 5–8.

On the other hand, the alignments of the predicted and actual values of the wind power using the five baseline models are shown in Fig. 8. Only 100 points of test samples are employed in this experiment. Although the alignment of the test points in this figure are properly fit a line, this alignment does not perform the same way when the number of points increased. This makes the proposed approach superior as it performs better in case of employing larger set of test points.

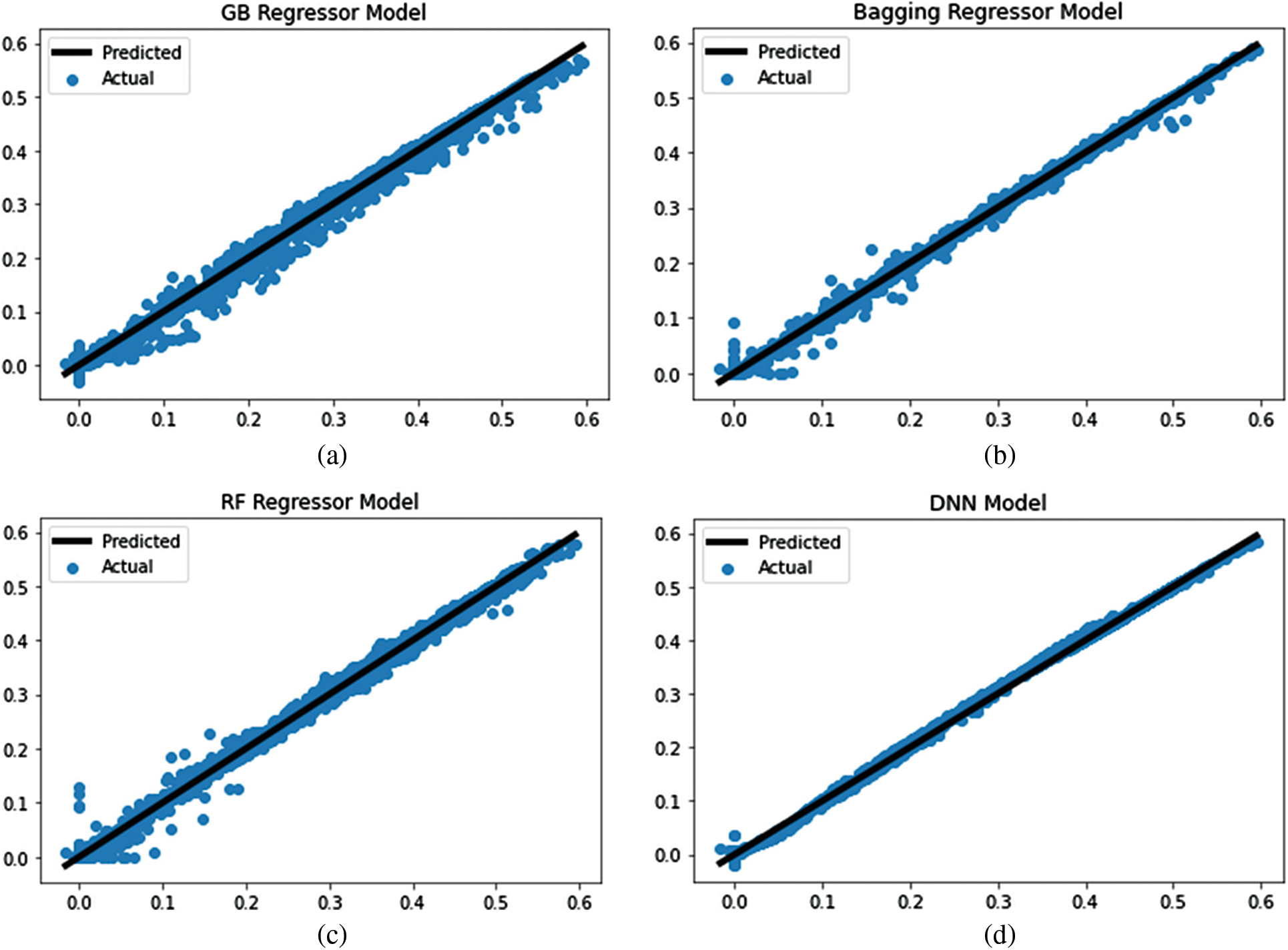
Figure 8: The predicted vs. actual values of wind power values with line fitting

4.3.3 Results Comparison

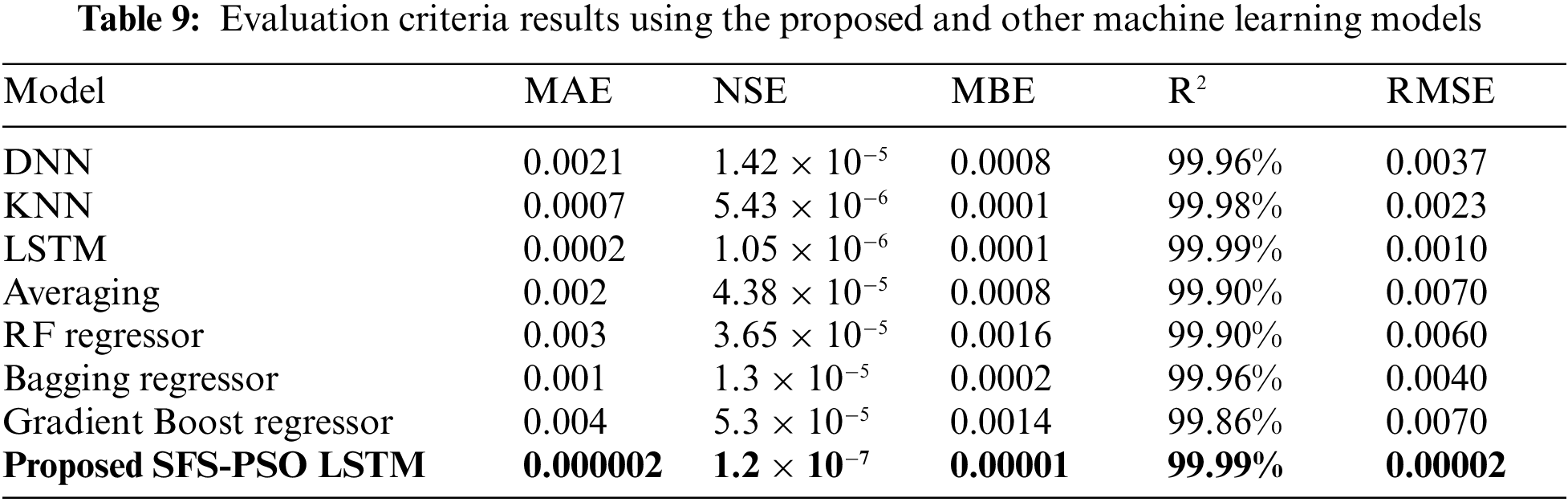
A comparison between the results achieved by the proposed approach and the baseline models is presented in Tab. 9. As presented in the table, the proposed approach could achieve the best results among the models included in the conducted experiments. The MAE of the proposed approach is (0.000002), NSE is (1.2 × 10−7), MBE is (0.00001), R2 is (99.99%), and RMSE is (0.00002).

5  Conclusions

Wind forecasting data is used in this study to test the proposed optimized LSTM model’s efficiency. A new optimization technique is used to optimize the parameters of the LSTM network. To improve the exploration and exploitation capabilities of the PSO optimizer, this optimization strategy utilizes both the PSO optimizer and SFS to generate stochastic groups of agents. Experiments were done to evaluate the suggested approach’s performance and compare it to findings from six other machine learning models to demonstrate its viability. To assess the success of the project, five assessment criteria are used. This approach’s stability and effectiveness were further illustrated with analysis plots derived from the obtained data. It’s clear from the comparisons with other models that the strategy we’ve provided is superior. The future of this study entails testing the suggested technique on different datasets and assessing its applicability to other prediction tasks.

Data Availability: A data availability found in https://www.kaggle.com/datasets/berkerisen/wind-turbine-scada-dataset.

Funding Statement: This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Z. Lin, X. Liu and M. Collu, “Wind power prediction based on high-frequency SCADA data along with isolation forest and deep learning neural networks,” International Journal of Electrical Power & Energy Systems, vol. 118, no. 105835, pp. 1–10, 2020. [Google Scholar]

 2.  T. Ahmad and D. Zhang, “A data-driven deep sequence-to-sequence long-short memory method along with a gated recurrent neural network for wind power forecasting,” Energy, vol. 239, no. 122109, pp. 1–20, 2022. [Google Scholar]

 3.  F. Zhang, P. -C. Li, L. Gao, Y. -Q. Liu and X. -Y. Ren, “Application of autoregressive dynamic adaptive (ARDA) model in real-time wind power forecasting,” Renewable Energy, vol. 169, pp. 129–143, 2021. [Google Scholar]

 4.  S. Hanifi, X. Liu, Z. Lin and S. Lotfian, “A critical review of wind power forecasting methods—past, present and future,” Energies, vol. 13, no. 15, pp. 1–24, 2020. [Google Scholar]

 5.  M. H. Lipu, M. S. Miah, M. A. Hannan, A. Hussain, M. R. Sarker et al., “Artificial intelligence based hybrid forecasting approaches for wind power generation: Progress, challenges and prospects,” IEEE Access, vol. 9, pp. 102460–102489, 2021. [Google Scholar]

 6.  Y. Wang, R. Zou, F. Liu, L. Zhang and Q. Liu, “A review of wind speed and wind power forecasting with deep neural networks,” Applied Energy, vol. 304, no. 117766, pp. 1–24, 2021. [Google Scholar]

 7.  M. Yang, C. Shi and H. Liu, “Day-ahead wind power forecasting based on the clustering of equivalent power curves,” Energy, vol. 218, no. 119515, pp. 1–10, 2021. [Google Scholar]

 8.  H. Yin, Z. Ou, S. Huang and A. Meng, “A cascaded deep learning wind power prediction approach based on a two-layer of mode decomposition,” Energy, vol. 189, no. 116316, pp. 1–11, 2019. [Google Scholar]

 9.  H. -F. Yang and Y. -P. P. Chen, “Representation learning with extreme learning machines and empirical mode decomposition for wind speed forecasting methods,” Artificial Intelligence, vol. 277, no. 103176, pp. 1–10, 2019. [Google Scholar]

10. I. K. Bazionis and P. S. Georgilakis, “Review of deterministic and probabilistic wind power forecasting: Models, methods, and future research,” Electricity, vol. 2, no. 1, pp. 13–47, 2021. [Google Scholar]

11. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

12. Y. Deng, H. Jia, P. Li, X. Tong, X. Qiu et al., “A deep learning methodology based on bidirectional gated recurrent unit for wind power prediction,” in 2019 14th IEEE Conf. on Industrial Electronics and Applications (ICIEA), Xi’an, China, pp. 591–595, 2019. [Google Scholar]

13. C. Yildiz, H. Acikgoz, D. Korkmaz and U. Budak, “An improved residual-based convolutional neural network for very short-term wind power forecasting,” Energy Conversion and Management, vol. 228, no. 113731, pp. 1–15, 2021. [Google Scholar]

14. Z. Sun and M. Zhao, “Short-term wind power forecasting based on VMD decomposition, ConvLSTM networks and error analysis,” IEEE Access, vol. 8, pp. 134422–134434, 2020. [Google Scholar]

15. L. -L. Li, X. Zhao, M. -L. Tseng and R. R. Tan, “Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm,” Journal of Cleaner Production, vol. 242, no. 118447, pp. 1–12, 2020. [Google Scholar]

16. H. Yin, Z. Ou, J. Fu, Y. Cai, S. Chen et al., “A novel transfer learning approach for wind power prediction based on a serio-parallel deep learning architecture,” Energy, vol. 234, no. 121271, pp. 1–16, 2021. [Google Scholar]

17. A. -N. Buturache and S. Stancu, “Wind energy prediction using machine learning,” Low Carbon Economy, vol. 12, no. 1, pp. 1–21, 2021. [Google Scholar]

18. Q. Wu, F. Guan, C. Lv and Y. Huang, “Ultra-short-term multi-step wind power forecasting based on CNN-LSTM,” IET Renewable Power Generation, vol. 15, no. 5, pp. 1019–1029, 2021. [Google Scholar]

19. N. Li, F. He and W. Ma, “Wind power prediction based on extreme learning machine with kernel mean P-power error loss,” Energies, vol. 12, no. 673, pp. 1–19, 2019. [Google Scholar]

20. G. Chen, L. Li, Z. Zhang and S. Li, “Short-term wind speed forecasting with principle-subordinate predictor based on Conv-LSTM and improved BPNN,” IEEE Access, vol. 8, pp. 67955–67973, 2020. [Google Scholar]

21. Y. -Y. Hong and C. L. P. P. Rioflorido, “A hybrid deep learning-based neural network for 24-h ahead wind power forecasting,” Applied Energy, vol. 250, pp. 530–539, 2019. [Google Scholar]

22. V. K. Rayi, S. P. Mishra, J. Naik and P. K. Dash, “Adaptive VMD based optimized deep learning mixed kernel ELM autoencoder for single and multistep wind power forecasting,” Energy, vol. 244, no. 122585, pp. 1–29, 2022. [Google Scholar]

23. A. Alkesaiberi, F. Harrou and Y. Sun, “Efficient wind power prediction using machine learning methods: A comparative study,” Energies, vol. 15, no. 2327, pp. 1–24, 2022. [Google Scholar]

24. B. Liu, S. Zhao, X. Yu, L. Zhang and Q. Wang, “A novel deep learning approach for wind power forecasting based on WD-LSTM model,” Energies, vol. 13, no. 4964, pp. 1–17, 2020. [Google Scholar]

25. J. Zhang, J. Yan, D. Infield, Y. Liu and F. Lien, “Short-term forecasting and uncertainty analysis of wind turbine power based on long short-term memory network and Gaussian mixture model,” Applied Energy, vol. 241, pp. 229–244, 2019. [Google Scholar]

26. M. Qolipour, A. Mostafaeipour, M. Saidi-Mehrabad and H. R. Arabnia, “Prediction of wind speed using a new Grey-extreme learning machine hybrid algorithm: A case study,” Energy & Environment, vol. 30, no. 1, pp. 44–62, 2019. [Google Scholar]

27. D. Karamichailidou, V. Kaloutsa and A. Alexandridis, “Wind turbine power curve modeling using radial basis function neural networks and tabu search,” Renewable Energy, vol. 163, pp. 2137–2152, 2021. [Google Scholar]

28. H. Demolli, A. S. Dokuz, A. Ecemis and M. Gokcek, “Wind power forecasting based on daily wind speed data using machine learning algorithms,” Energy Conversion and Management, vol. 198, no. 111823, pp. 1–12, 2019. [Google Scholar]

29. R. Yu, J. Gao, M. Yu, W. Lu, T. Xu et al., “LSTM-EFG for wind power forecasting based on sequential correlation features,” Future Generation Computer Systems, vol. 93, pp. 33–42, 2019. [Google Scholar]

30. M. Y. Shams, A. Tolba and S. Sarhan, “A vision system for multi-view face recognition,” International Journal of Circuits, Systems, and Signal Processing, vol. 10, no. 1, pp. 455–461, 2017. [Google Scholar]

31. M. Y. Shams, S. Sarhan and A. Tolba, “Adaptive deep learning vector quantisation for multimodal authentication,” Journal of Information Hiding and Multimedia Signal Processing, vol. 8, no. 3, pp. 702–722, 2017. [Google Scholar]

32. R. Bello, Y. Gomez, A. Nowe and M. M. Garcia, “Two-step particle swarm optimization to solve the feature selection problem,” in Proc. of the Int. Conf. of Intelligent Systems and Design Applications, Rio de Janeiro, Brazil, pp. 691–696, 2007. [Google Scholar]

33. E. -S. M. El-Kenawy, M. M. Eid, M. Saber and A. Ibrahim, “MbGWO-SFS: Modified binary grey wolf optimizer based on stochastic fractal search for feature selection,” IEEE Access, vol. 8, no. 1, pp. 107635–107649, 2020. [Google Scholar]

34. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]

35. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]