An Algorithm to Reduce Compression Ratio in Multimedia Applications

1  Introduction

The increasing number of choices for transferring and storing images via the internet has emerged from the continuous growth and advancement of digital apps [1]. Images include a large quantity of data and cover a wide range of applications, including medical imagery, remote sensing, security, video conferencing, facial recognition, satellite communications and the environment and sustainability [2–7]. The visual data is made up of redundant and correlated pixels, which can be reduced using a sophisticated compression algorithm, resulting in smaller storage and transmission bandwidth [8]. The RGB model is widely used in color picture processing. The RGB color space is initially de-correlated with the use of an appropriate color conversion. This color space may contain additional color formats such as YCbCr, YUV, and International Commission on Illumination (CIE) La*b*;. It is desirable to modify the color space because the RGB components are inadequate for compression due to substantial inter-color dependency. The luma and chroma components of YCbCr are divided into image blocks [9]. In [10] the original RGB image is converted to YCbCr color space with discrete wavelet transform (DWT) and discrete cosine transform (DCT) applied to the Cb and Cr portions, respectively. Color spaces RGB, YCbCr, CIE La*b*;, and CIE Luv are examined for facial expression identification using a tensor perceptual color framework, with results favoring CIE La*b*; and CIE Luv in terms of robustness and performance. Clustering is possible in CIE La*b*; because a* and b* components represent the color element and the L component represents the brightness. CIE La*b*; is used for quantitative result evaluation in research aimed at eliminating the radiometric variance encountered in picture mosaicking [11].

Lossy methods can significantly reduce data size if the decompressed data is recovered within the acceptable boundaries set by each application. When opposed to its competing approach, lossy compression, lossless compression is used in situations that need correct retrieval and preservation of sensitive data at the cost of increased data size [9]. Initially Fourier Transform and DCT were preferred for image compression [12]. With time, several new techniques for image compression are offered including different variations of Wavelet Transform (WT) [13,14]. Medical imagery is preferred to be compressed by lossless algorithm for digital imaging and communications in Medicine [15]. Integer wavelet transform (IWT) is used [16] in conjunction with Huffman coding to compress images in area of telemedicine. This approach increases the magnitude of picture bit streams while lowering the signal to noise ratio (SNR). In [17], it describes a Discrete Fourier Transform (DFT) technique for compressing high Pixels Per Inch (PPI) photographs. An effective block-based lossless compression is proposed in [18] employing a Hadamard transformation on an image that has already been decomposed using IWT. While Discrete Cosine Transform (DCT) is widely used for image compression, Quantum DCT (QDCT), as explained in [19], is more efficient in terms of complexity than DCT.

The compression technique in this work is based on three color spaces, that is RGB, CIE La*b*; and YCbCr by applying seven discrete orthogonal transforms, namely Sequency Ordered–Complex Hadamard Transform (SCHT) [20,21], Conjugate Symmetric Sequency-Ordered Complex Hadamard Transform (CS-SCHT) [22], Natural ordered complex Hadamard Transform (NCHT) [23], Unified–Complex Hadamard Transform (UCHT) [24], Discrete Orthogonal--Complex Hadamard Transform (DOT-CHT) [25], Discrete Fourier Transform (DFT) [26] and Discrete Cosine Transform (DCT) [27]. In the RGB paradigm, determining a specific color is challenging. The fundamental advantage of the CIE La*b*; color space is that it is device independent. The findings suggest that the proposed CIE La*b*; algorithm outperforms alternative color spaces in detecting color. The YCbCr color space, unlike RGB, is brightness independent, which is why it performs better. Each obtained RGB image is also converted to YCbCr and CIE La*b*; color space. The different color planes of that image are compressed separately and then concatenated for the final image. The motivation behind this research is that to design and modify the quantization matrix in the transform domain in relation to various color models, as well as to find the optimal discrete orthogonal transform for color image compression. The paper is organized into four sections: an introduction and literature review in Section 1, methodology in Section 2, results and conclusion in Sections 3 and 4, respectively.

2  Methodology

The extended method is developed for lossy color image compression, as previously stated. The compression is proposed and implemented utilizing multiple color spaces RGB, CIE La*b*, and YCbCr in the transform domain, in addition to numerous discrete orthogonal transformations (DOTs) such as SCHT, CS-SCHT, NCHT, UCHT, DOT-CHT, DFT, and DCT. According to the color model, the original image is passed via numerous color planes. For other models, the original RGB image is first converted into YCbCr and CIE La*b*. Before changing the image, all of the planes are split into R, G, B, L, a*, b*, Y, Cb and Cr with respect to the color model, as shown in Fig. 1. In terms of color space, the 8 × 8 DOT(s) are applied to each color plane. Lossy compression is achieved after thresholding and quantization, and a compressed image is received from the encoder. To restore the original image seen in Fig. 2, the decoder repeats the same inverse step. With respect to the various DOTs, Eqs. (1)–(3) present the different color planes into the transform domain (s).

Ψr,L,Y(k1,k2)=1NM∑n1N∑n2MξR,L,Y(n1,n2)H N(1)

Ψg, a*, Cb(k1,k2)=1NM∑n1N∑n2MξG, a*, Cb(n1,n2)H N(2)

Ψb, b*, Cr(k1,k2)=1NM∑n1N∑n2MξB, b*, Cr(n1,n2)H N(3)

where Ψr(k1,k2), Ψg(k1,k2), Ψb(k1,k2), ΨL(k1,k2), Ψa(k1,k2), Ψb(k1,k2), ΨY(k1,k2), ΨCb(k1,k2) and ΨCr(k1,k2) are the individually transformed planes in respective color space and DOTs. ξR(n1,n2), ξG(n1,n2), ξB(n1,n2), ξL(n1,n2), ξa∗(n1,n2), ξb∗(n1,n2), ξY(n1,n2), ξCb(n1,n2) and ξCr(n1,n2) are spatial domain color planes of respective color space with N and M number of rows and columns. H N is the 8 × 8 different DOT(s) matrix to transform the color image into the transform domain. The three color spaces are applied and discussed below:

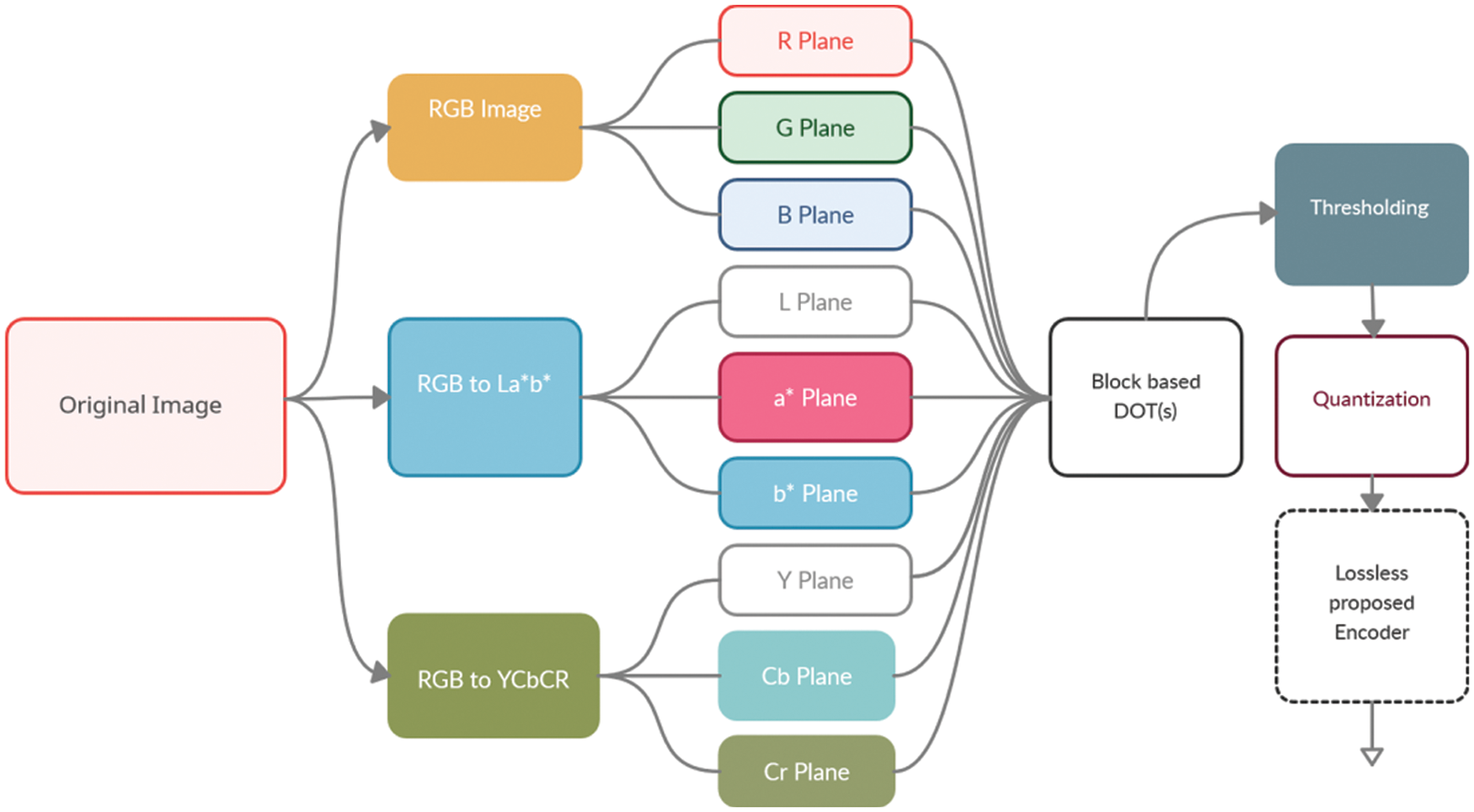
Figure 1: Encoding process for compression

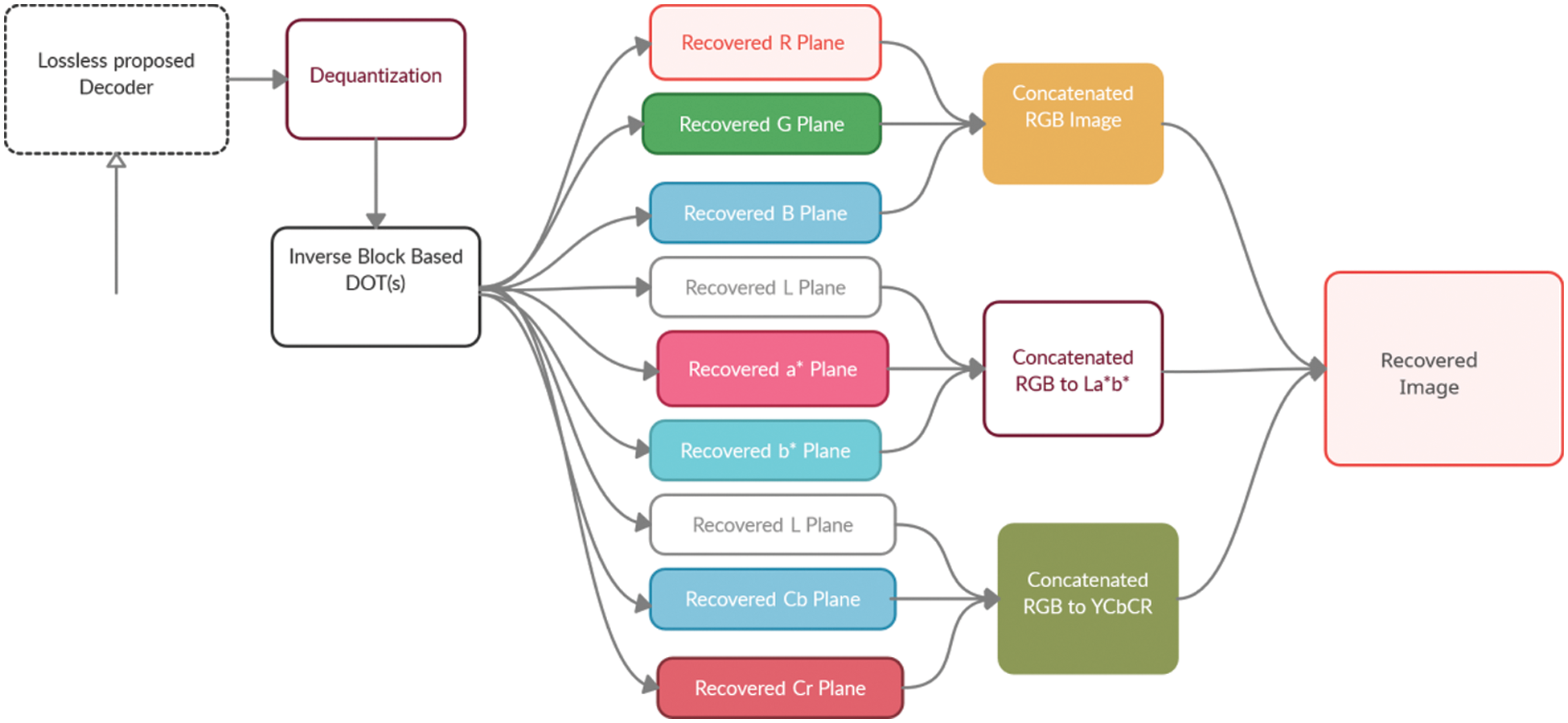
Figure 2: Decoding process for the lossy compression

2.1 RGB Color Space

This color space is a display-oriented additive color model. Colors change depending on the color coordinates. On the basis of channel or plane, color picture compression is performed on each pixel of the image. As a result, color details and sharpness are diminished, potentially resulting in the loss of residual information in the form of tiny color details.

2.2 RGB to CIE La*b*; Transformation

After converting from one color space to another, compression is done on several planes to ensure that the color is lost as little as possible. The image is transformed from RGB to CIE La*b*; transformation before applying the DOT(s). Converting RGB to XYZ coordinates is required for CIELa*b*; [9,28]:

XYZ=[0.4124530.3575800.1804230.2126710.7151600.0721690.0193340.1191930.950227][RGB](4)

The CIELa*b*; coordinates are extracted from XYZ as below:

L∗=116f(YYn)−16(5)

a∗=500(f(XXn)−f(YYn))(6)

b∗=200(f(YYn)−f(ZZn))(7)

2.3 RGB to YCbCr Transformation

It has been observed that the YCbCr provides a better compression ratio without dropping the information [9]. The RGB image is converted in to the YCbCr before applying the DOT(s):

[YCbCr]=[0.2990.5870.144−0.16875−0.331260.50.5−0.41869−0.08131][RGB]Invese↔[RGB]=[101.4021−0.34413−0.7141411.7720][YCbCr](8)

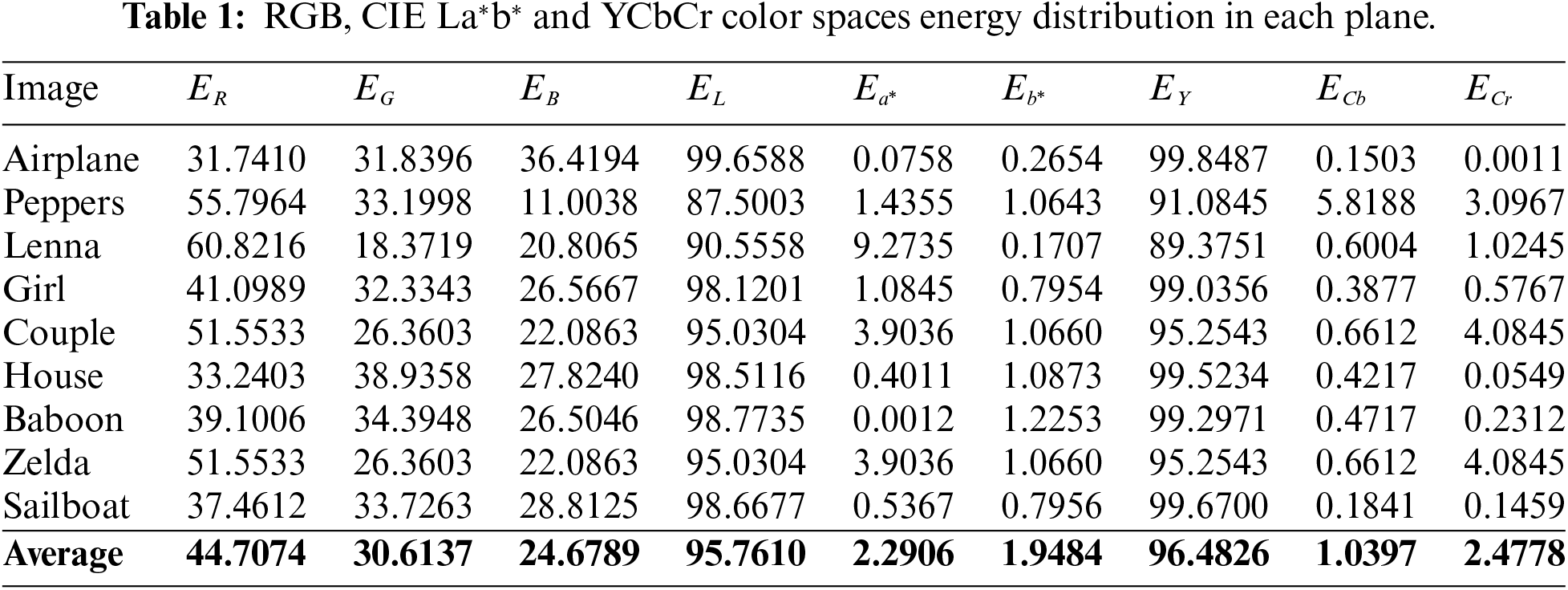
The energy of each plane of the three color spaces are expressed below:

ER,G,B=(∑n=0N∑m=0MRn,m2 or Gn,m2 or Bn,m2ETotal_RGB)×100(9)

EL,a*,b*=(∑n=0N∑m=0MLn,m2 or an,m2 or bn,m2ETotal_Lab)×100(10)

EY,Cb,Cr=(∑n=0N∑m=0MYn,m2 or Cbn,m2 or Crn,m2ETotal_YCbCr)×100(11)

Total energy is defined as below:

ETotal=(∑n=0N∑m=0MP1n,m2)+(∑n=0N∑m=0MP2n,m2)+(∑n=0N∑m=0MP3n,m2)(12)

The color planes of each color space are P1, P2 and P3. In Tab. 1, energy distribution of each plane is shown. The energy distribution confirms that color space conversion from RGB to CIELa*b* and YCbCr is required to achieve concrete results, whether for isolated or combined images (as an average).

2.4 Proposed Quantization

The quantization matrix determines the compressed image quality (Qm). To provide the needed compressed image quality, the standard Qm is adjusted. The human eye is more sensitive to the brightness component of a color image than the chroma component, according to research. As a result, increasing the operating Qm reduces the image chrominance effect while maintaining overall quality.

In the suggested and designed algorithm, a standard JPEG Qm is a primary model and modified using Eq. (13):

FQm=∑n=0N∑m=0M((∑m=0MR(k,m)) Qm(n,m)P Max((∑m=0MR(k,m)))(13)

In a modified quantization matrix is FQm, the sum of the column vector of the transformed plane is ∑m=0MR(k,m), P is a crisp parameter that varies from 1 to 25 to maintain the quality of the image [29]. If P is less than 1, the image quality deteriorate therefore it is never equal to zero. Fig. 3 shows the process of the modified quantization matrix.

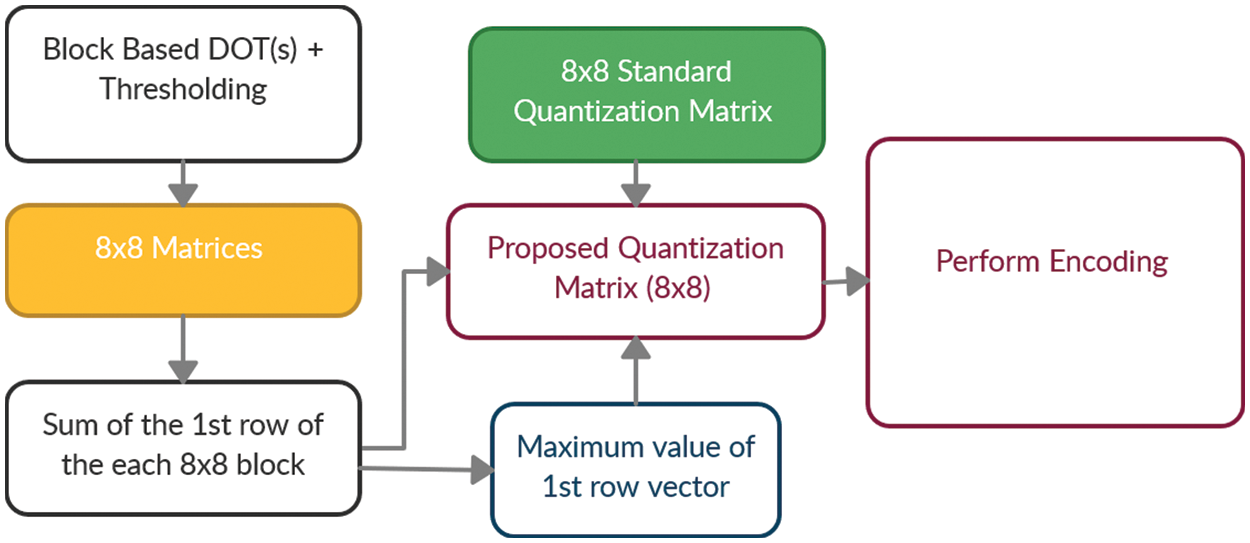
Figure 3: Proposed quantization matrix

2.5 Block Based DOT(s)

The color planes are split for the appropriate color space, and each plane is transformed in 8 × 8 blocks with respect to the transformation matrix and quantized with the appropriate DOT(s), such as (SCHT, CSSCHT, NCHT, UCHT, DOTCHT, DFT, and DCT), and new coefficients for each DOT are obtained. Similarly, decompression is performed, and the compressed picture is received at the decoder side.

3  Experimental Results and Comparison

The standardized test images “Airplane, Baboon, Couple, Girl, House, Lena, Peppers, and Sailboat” are used to test the improved quantization matrix in the frequency domain, as shown in Fig. 4. Different DOT(s) are applied such as SCHT, CS-SCHT, NCHT, UCHT, DOTCHT, DFT and DCT in numerous color spaces are applied such as RGB, CIE La*b*;, and YCbCr. In the frequency domain, several metrics such as PSNR, SNR, Compression ratio, BPP, SI and file size are analyzed to determine compression quality and efficiency. The performance of the modified quantization matrix that is applied during compression for the various DOTs is shown in Tabs. 2–8. The 8 × 8 block size is applied with respect to the quantization matrix after preparatory processes of color domain conversion for the various color spaces. Experiments are performed with different “P” values (P = 1, 5, 10, 15, 20, 25). Fig. 5 presents the qualitative analysis of the compression comparison for the DOTs with P = 1 for all the test images. Fig. 6 shows the measurable outcomes of the PSNR for the “airplane” image using DOTs and color spaces.

Figure 4: Original images: Airplane, baboon, couple, girl, house, lena, peppers and sailboat respectively

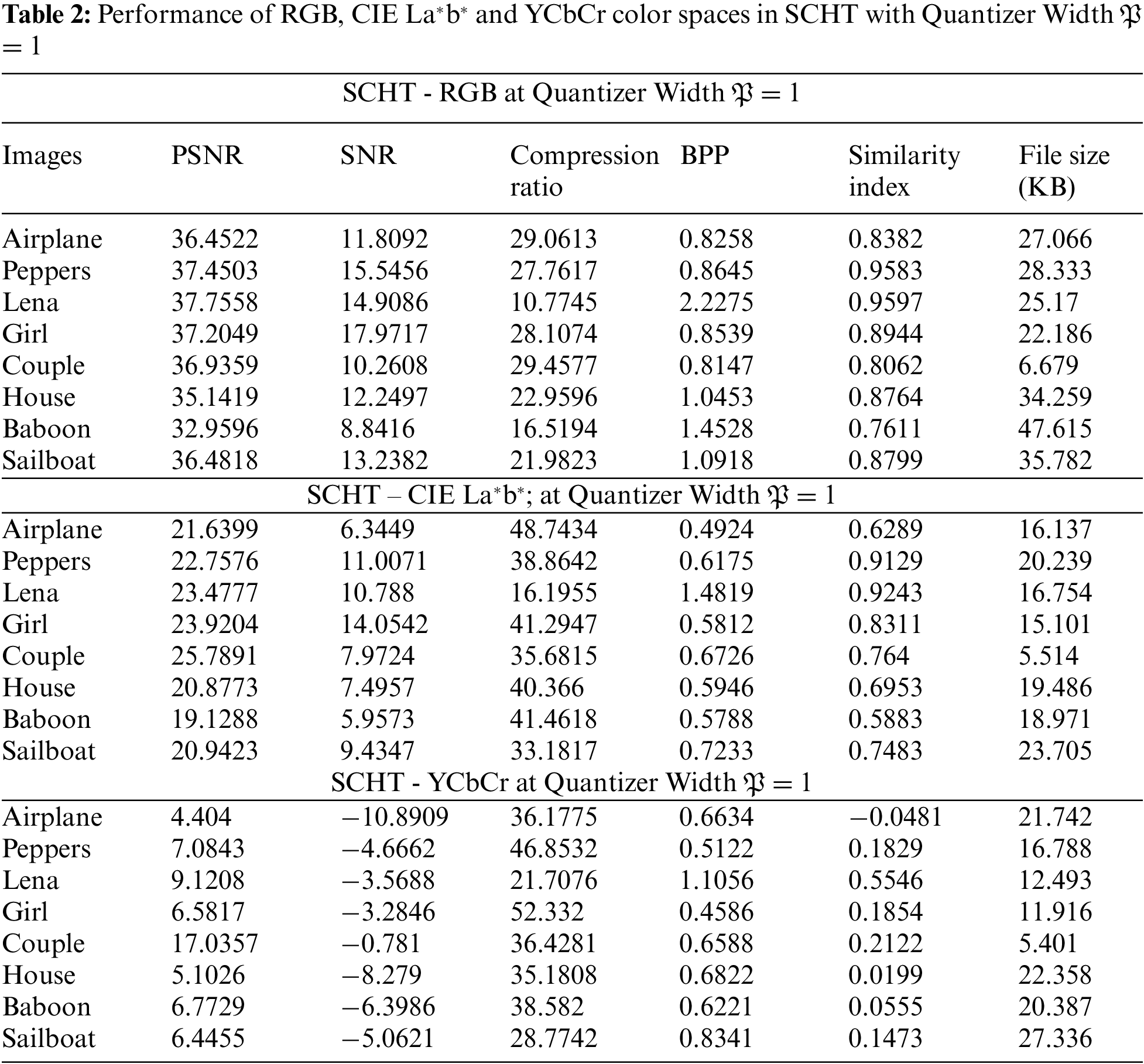
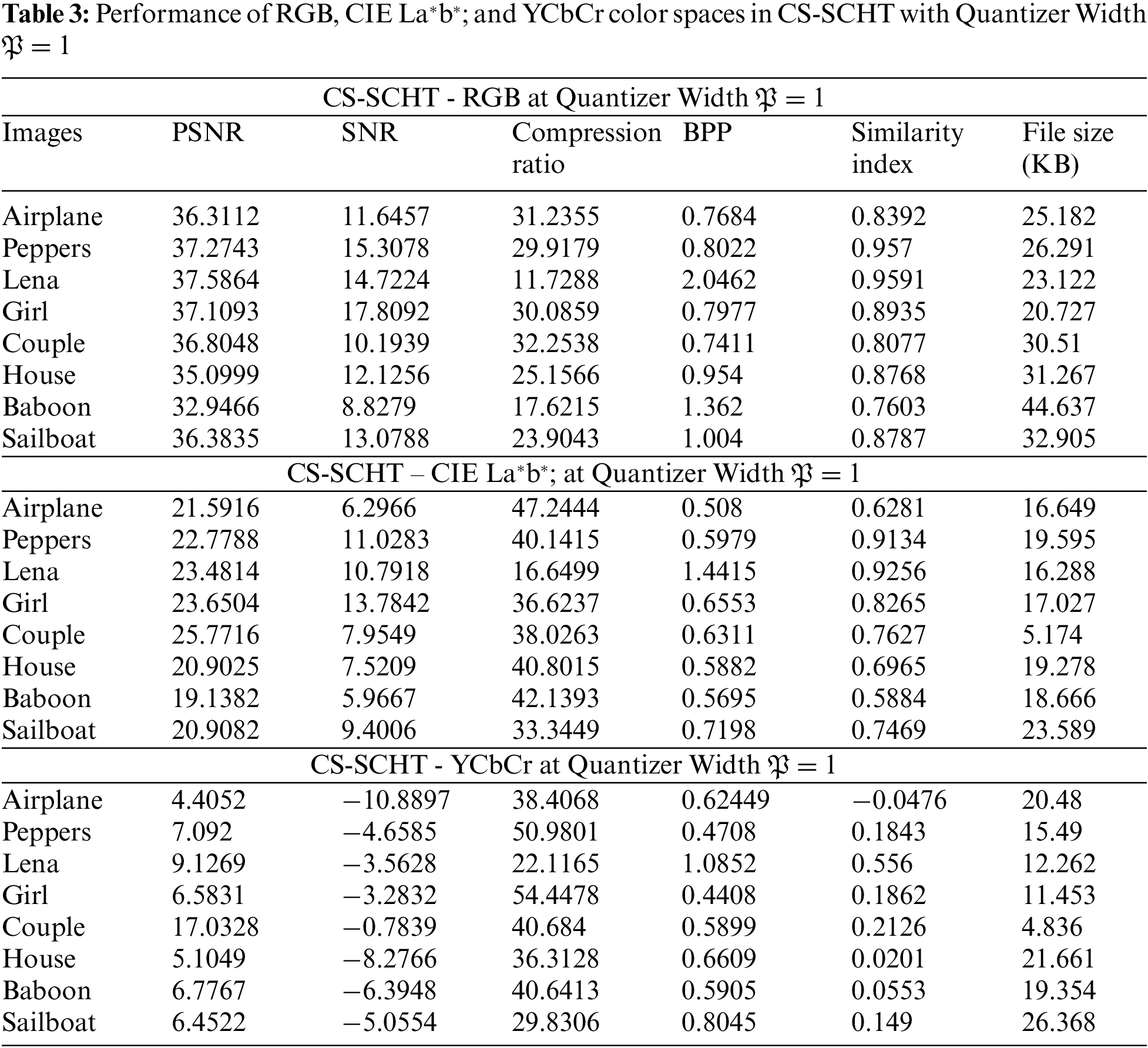
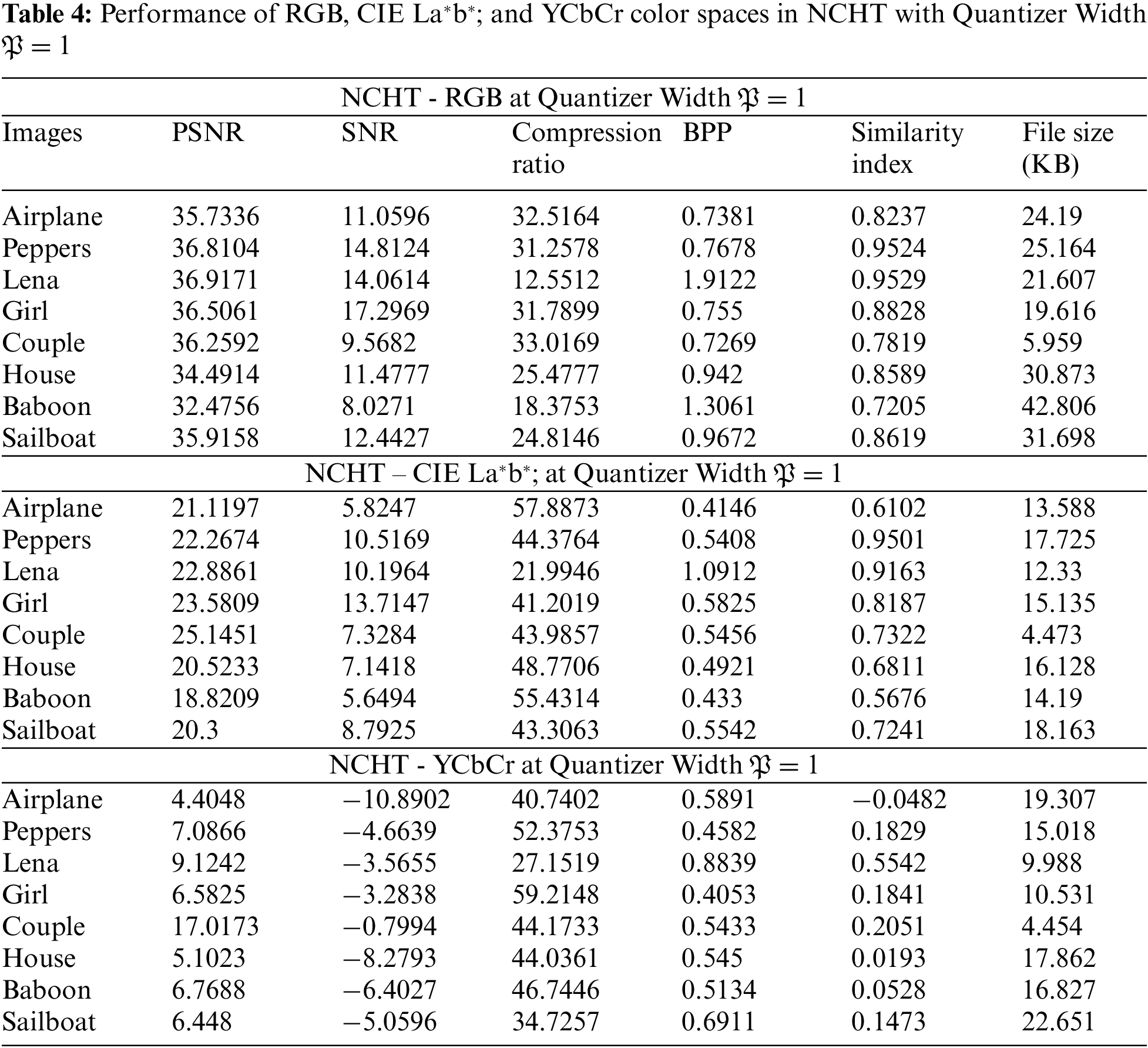
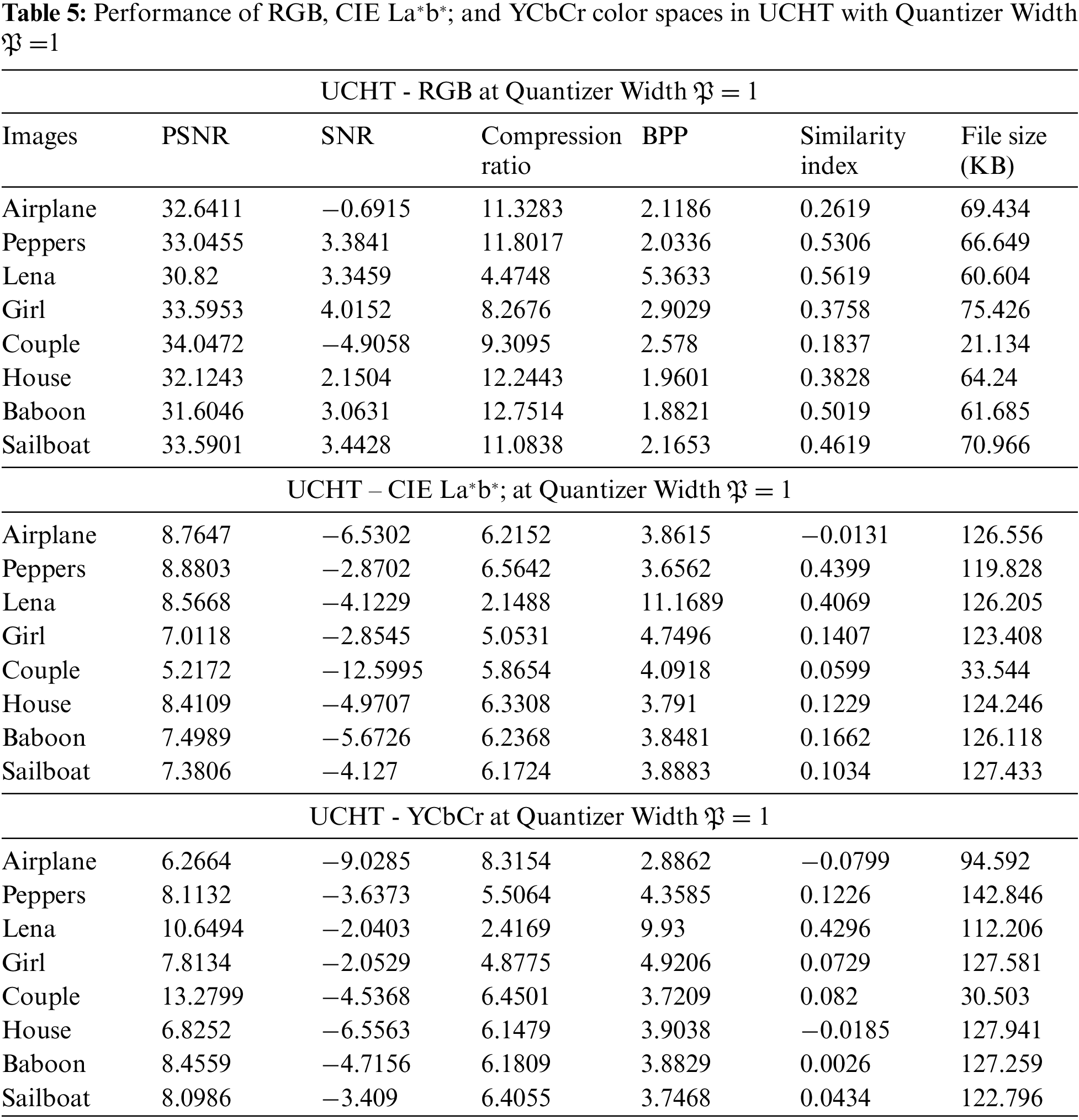
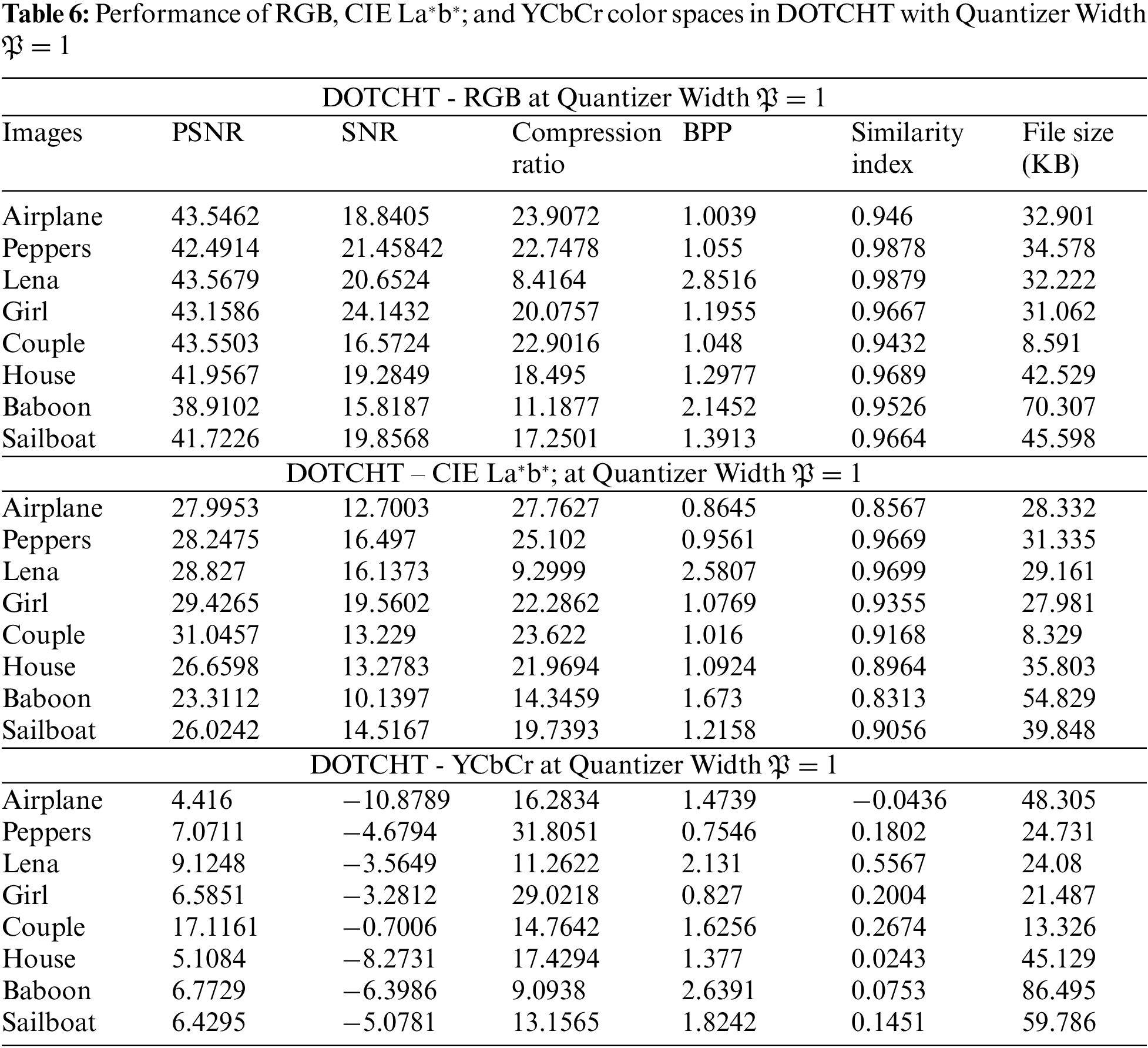
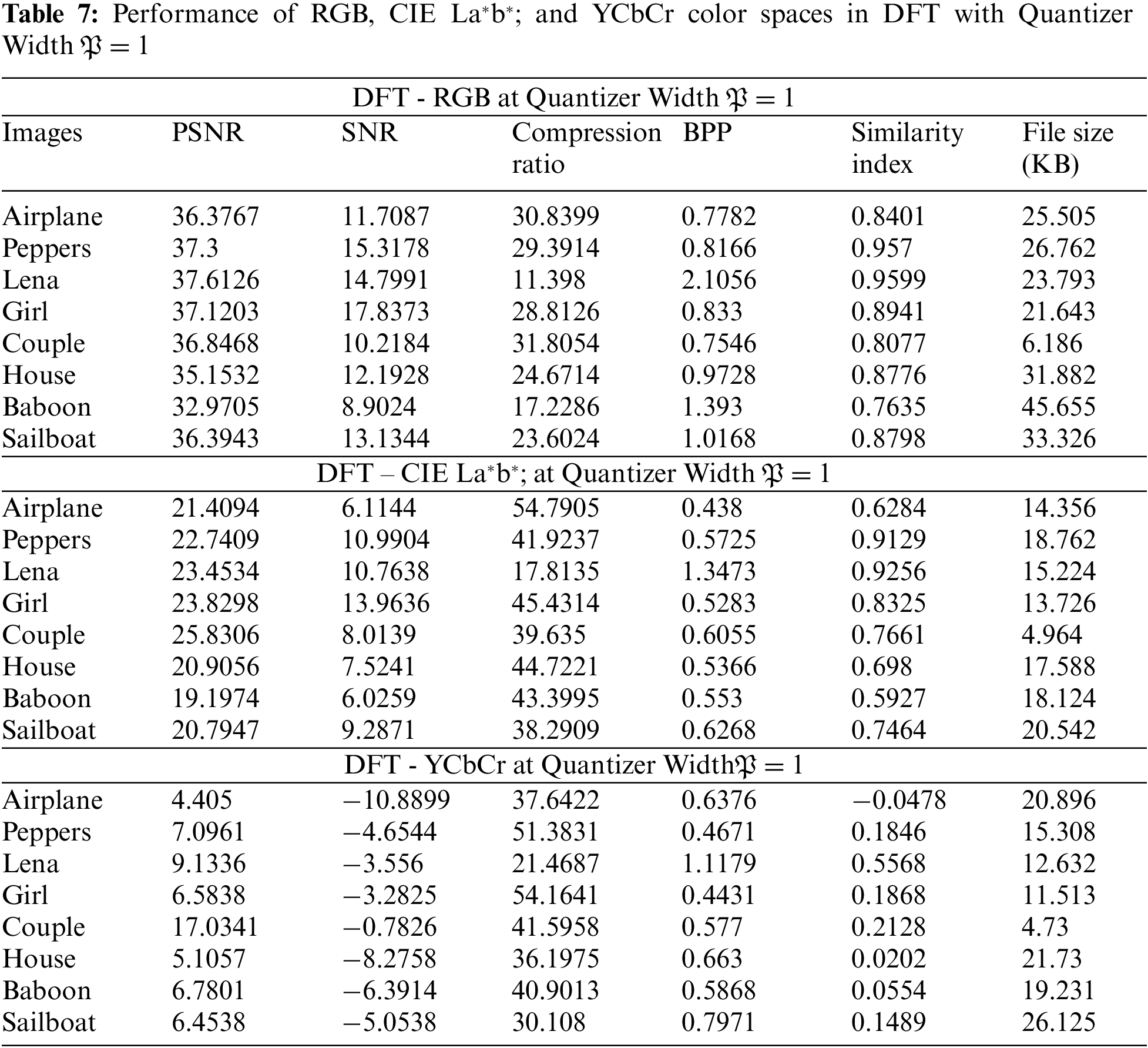
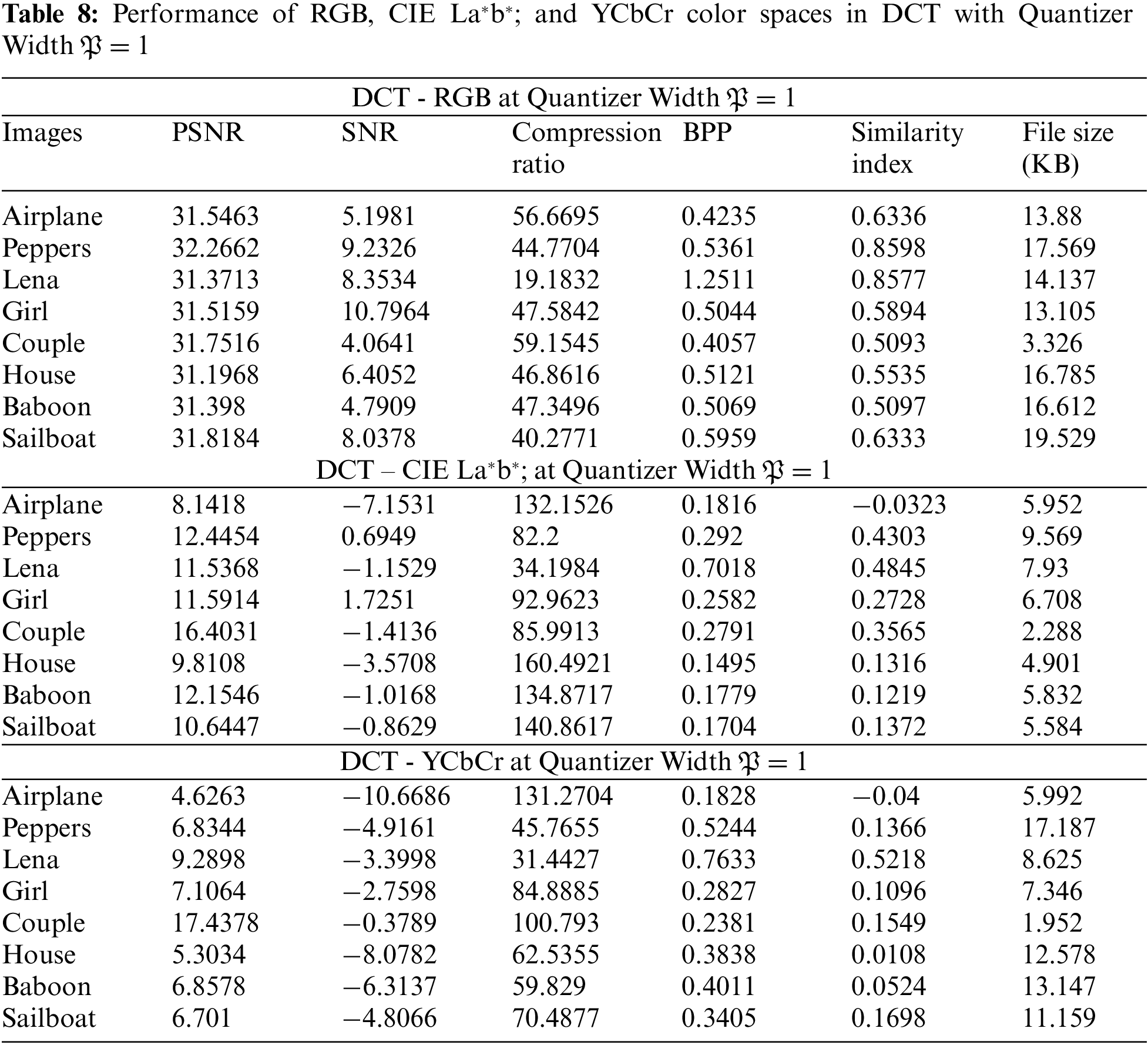
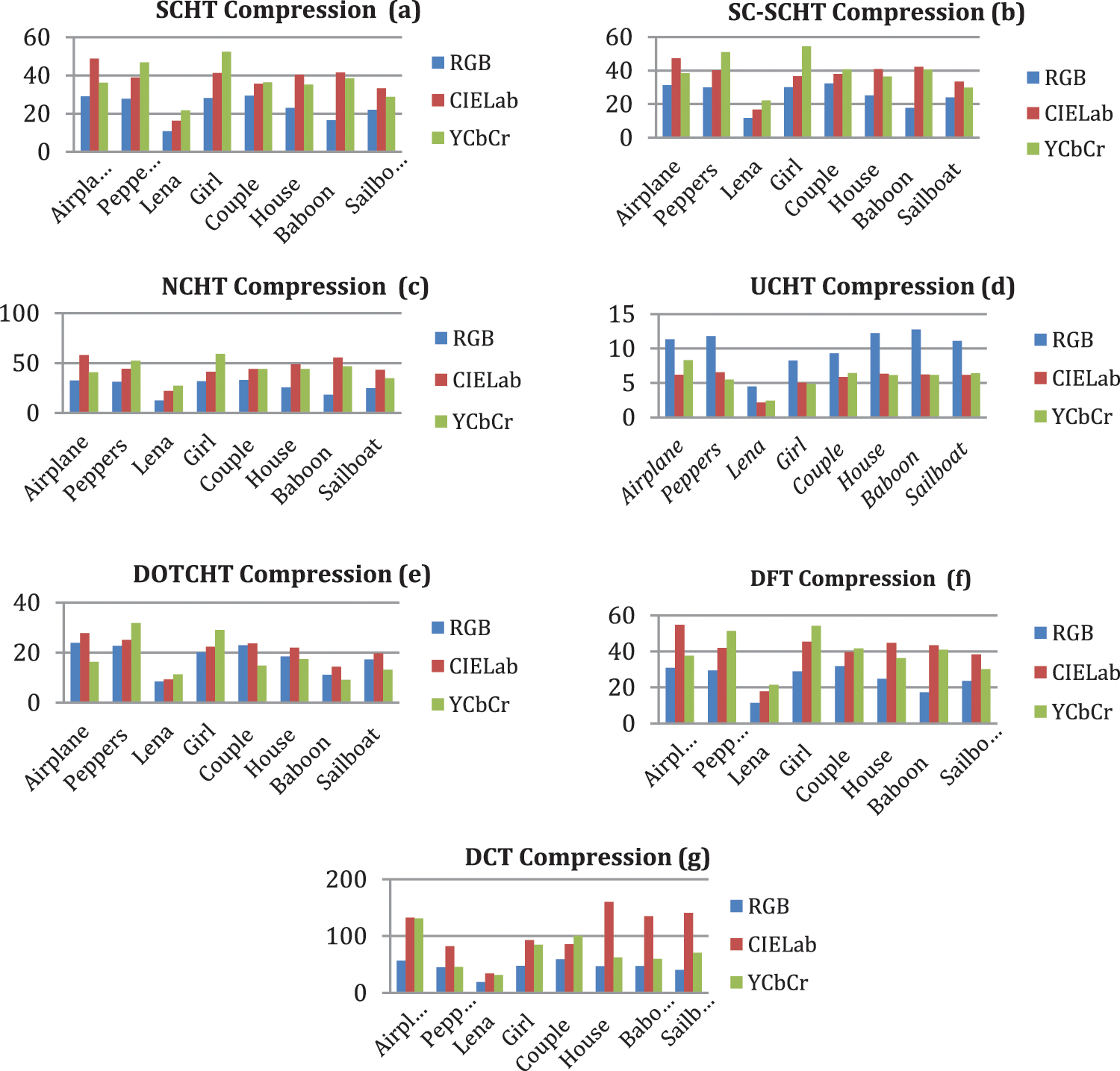
Figure 5: Compression ratio is graphically is presented for RGB, CIE La*b*; and YCbCr color models using (a) SCHT, (b) CS-SCHT, (c) NCHT, (d) UCHT, (e) DOTCHT, (f) DFT and (g) DCT

Figure 6: Peak to signal noise ratio at P = 1 of airplane image for all DOT(s) in different color spaces

Average PSNR of all DOTs shown in Fig. 7 illustrates the better performance of SCHT, CS-SCHT, DOTCHT and DFT against the NCHT, UCHT, and DCT for RGB, in CIE La*b*; UCHT and DCT have less quality outcomes as compared to other DOTs whereas in YCbCr color space all DOTs provides almost similar performance.

SCHT RGB and CIE La*b*;: It has been observed that by varying the value of P from 1 to 25 PSNR increases along with file size but the compression ratio decreases and BPP also increases whereas in YCbCr PSNR is almost constant. Tab. 2 demonstrates the results of all images with P = 1.

CS-SCHT RGB and CIE La*b*;: In different experiments, by varying the values of “P” in increasing order, the simulation results illustrate that the CS-SCHT in RGB and CIELa*b*; color space PSNR, BPP and file size increase with the value of P and compression decreases. However, it is found that PSNR is almost equal for YCbCr.

NCHT RGB and CIE La*b*;: For this variant of Complex Hadamard Transform, it is observed in a number of experiments that the PSNR, BPP, SNR and file size is increased with increasing the value of P for the quantization matrix but the compression ratio decreases slowly from 32.5 to 22.2 by the varying value of P from 1 to 25 respectively. Though for YCbCr color space, PSNR is varied very slightly for the second digit after the decimal, SNR observed with negative values and file size is increased from 19.3 to 73.3 Kb for P= 1 and 25 respectively. Tab. 4 demonstrates the results of all different images.

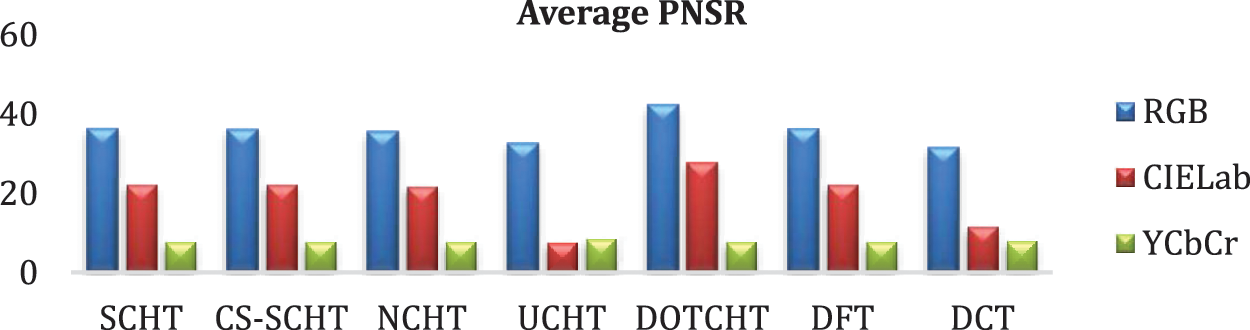
Figure 7: Average peak to signal noise ratio at quantizer width (P) = 1 for all DOT(s) in different color spaces

UCHT RGB and CIE La*b*;: For various experimentations, by modifying the quantization matrix at different values of “P” in increasing order, the simulation results illustrate that the UCHT in RGB and CIELa*b*; color space PSNR, BPP and file size increases but compression ratio decreases. SNR in CIE La*b*; shows negative values at lower value of P and positive at higher values.

Contrariwise, it is observed that PSNR is an almost same in the YCbCr color domain and SNR is in negative. Tab. 5 presents the results of different parameters for compression using the UCHT.

DOTCHT RGB and CIE La*b*;: Results of DOTCHT in different experiments proves that PSNR, SNR, BPP and file size increases and more or less similarity index shows the same results, but the compression ratio decreases at increasing order of “P”. However, in experimental simulations, changing the value of P improves the visual quality. Tab. 6 summarises the qualitative findings.

DFT RGB and CIE La*b*;: It has been observed that different performing parameters of DFT (PSNR, SNR, CR, and SI) possess similarity with SCHT and CS-SCHT due to their similar structure of transformation matrix [29]. Whereas file size of DFT, SCHT, and CS-SCHT [25.2, 27, and 25.2 Kb] to [36.3, 36.1, and 36 Kb] is respectively varied from P: [1 to 25]. DFT’s performance is shown Tab. 7, and the findings can be compared to Tabs. 2 and 3. Fig. 8 depicts these transforms for various test color pictures, CR, and file size.

Figure 8: Comparison of airplane image for DFT, SCHT and CSSCHT at quantizer width (P) = 1 in RGB color space

DCT RGB and CIE La*b*;: DCT performance improves in different experiments. By varying the values of “P” in increasing order, the simulation results illustrate that the DCT in RGB and CIELa*b*; color space comprises of smaller values of PSNR, SNR, BPP and file size while the compression decreases gradually. However, it is found that PSNR is almost constant for YCbCr.

Fig. 9 shows the difference in bits per pixel and similarity of index during compression with SCHT, CSSCHT, DFT, and DCT in different color planes (a, b and c). Fig. 9d depicts DCT’s compression ratio performance in comparison to the other DOTs for an aeroplane image.

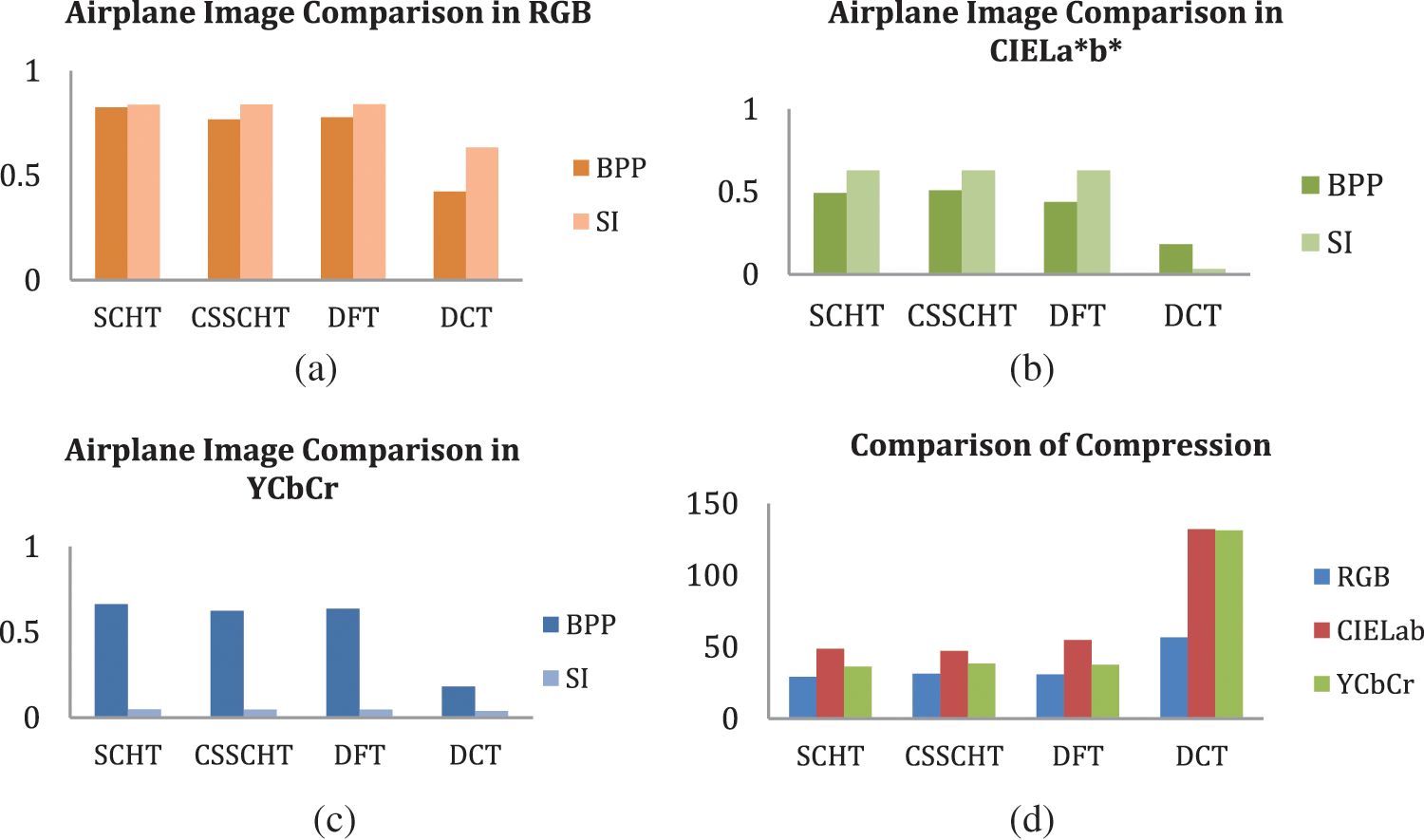
Figure 9: Comparison of airplane image for SCHT, CSSCHT, DFT and DCT: (a) RGB. (b) CIE La*b*;. (c) YCbCr. (d) Comparison of airplane image for SCHT, CSSCHT, DFT and DCT in different color spaces

The performance of DCT in color domain compression study is shown in Tab. 8. Fig. 10 depicts the compressed image quality for DOT(s) in various color spaces. In comparison to other color spaces, the RGB color space has been found to deliver a higher visual quality.

All DOT(s) except the DOTCHT show color artifacts in CIE La*b*;, however the UCHT shows blocky artefacts all across the image. The image quality is not improved by YCbCr since the color information degrades the compressed image. At P = 1, the image quality of DCT and UCHT compressed images is quite low. The SCHT, CSSCHT, DOTCHT, DFT, and DCT provide higher image quality in the RGB domain for different values of the P for the updated quantization matrix, though the DOTCHT provides superior results in all color domains at P = 1. The image quality is altered by adjusting the value of the P.

Figure 10: Compressed images of sailboat using DOT(s) in different color spaces

4  Conclusion

In this paper, the qualitative and quantitative analysis is presented in detail. The modified quantization matrix has been applied to several DOT(s) in RGB, YCbCr, and CIE La*b*; color spaces in this research work. This work is based on lossy image compression and is offered for static color images. The quantization procedure determines the compressed data’s quality features. The photos are converted from RGB to CIE La*b*; and YCbCr color spaces before being used. In the transform domain, the color planes are encoded using the proposed quantization matrix. The standard quantization matrix is updated with the corresponding image block to increase the compressed image’s efficiency and quality. The thresholding, quantization, de-quantization, inverse Complex Hadamard Transform, CIE Lab, and YCbCr to RGB conversion are among the seven discrete orthogonal transforms performed, which include five variants of the Complex Hadamard Transform, Discrete Fourier Transform, and Discrete Cosine Transform. Peak to signal noise ratio, signal to noise ratio, image similarity index, and compression ratio are used to assess the quality of compressed images. The compressed image quality of each DOT(s) is examined in detail and it has been discovered that the DOTCHT image quality improves when the quantization matrix width is increased. The visual quality of DFT compressed images is comparable to SCHT and CSSCHT. At reduced quantization widths, DCT does not perform better. The compressed image quality degrades when UCHT and NCHT are used. DOTs are playing an increasingly essential role in multimedia applications and advanced devices, helping to cut costs and increase efficiency for multi-purpose needs. We altered the quantization matrix and devised a new adaptive compression technique for color images, lowering the compression ratio and potentially assisting a variety of multimedia applications. In recent years, it has been seen that a variety of online software’s have been utilized to connect for meetings, lectures, seminars, and workshops where text, audio, photos, documents, and videos were used for discussion or study purposes due to COVID 19. Because such data requires a large amount of bandwidth, we need approaches that compress these data requirements for faster and more efficient data transfer.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. K. Sardar and A. Adhikari, “A new lossless secret color image sharing scheme with small shadow size,” Journal of Visual Communication and Image Representation, vol. 68, pp. 102768, 2020. [Google Scholar]

 2.  X. Zeng, S. Tong, Y. Lu, L. Xu and Z. Huang, “Adaptive medical image deep color perception algorithm,” IEEE Access, vol. 8, pp. 56559–56571, 2020. [Google Scholar]

 3.  S. Mahajan and A. K. Pandit, “Hybrid method to supervise feature selection using signal processing and complex algebra techniques,” Multimedia Tools and Applications, vol. 5, no. 4, pp. 537, 2021. [Google Scholar]

 4.  M. Yang and A. Sowmya, “An underwater color image quality evaluation metric,” IEEE Transactions on Image Processing, vol. 24, no. 12, pp. 6062–6071, 2015. [Google Scholar]

 5.  S. Mahajan and A. K. Pandit, “Image segmentation and optimization techniques: A short overview,” Medicon Engineering Themes, vol. 2, no. 2, pp. 47–49, 2022. [Google Scholar]

 6.  X. R. Zhang, H. L. Wu, W. Sun, A. G. Song and S. K. Jha, “A fast and accurate vascular tissue simulation model based on point primitive method,” Intelligent Automation & Soft Computing, vol. 27, no. 3, pp. 873–889, 2021. [Google Scholar]

 7.  X. R. Zhang, W. Z. Zhang, W. Sun, H. L. Wu, A. G. Song et al., “A real-time cutting model based on finite element and order reduction,” Computer Systems Science and Engineering, vol. 43, no. 1, pp. 1–15, 2022. [Google Scholar]

 8.  C. Zhang and X. He, “Image compression by learning to minimize the total error,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 23, no. 4, pp. 565–576, 2013. [Google Scholar]

 9.  F. Douak, R. Benzid and N. Benoudjit, “Color image compression algorithm based on the DCT transform combined to an adaptive block scanning,” AEU International Journal of Electronics and Communications, vol. 65, no. 1, pp. 16–26, 2011. [Google Scholar]

10. Y. G. Yang, L. Zou, Y. H. Zhou and W. M. Shi, “Visually meaningful encryption for color images by using Qi hyper-chaotic system and singular value decomposition in YCbCr color space,” Optik, vol. 213, pp. 164422, 2020. [Google Scholar]

11. Y. Zhang, L. Yu, M. Sun and X. Zhu, “A mixed radiometric normalization method for mosaicking of high-resolution satellite imagery,” IEEE Transactions on Geoscience and Remote Sensing, vol. 55, no. 5, pp. 2972–2984, 2017. [Google Scholar]

12. G. K. Wallace, “The JPEG still picture compression standard,” IEEE Transactions on Consumer Electronics, vol. 38, no. 1, pp. xviii–xxxiv, 1992. [Google Scholar]

13. C. Wu, J. Chang, C. Quan, X. Zhang and Y. Zhang, “The optical image compression and encryption method based on Fresnel diffraction and discrete wavelet transform,” Results in Optics, vol. 1, pp. 100021, 2020. [Google Scholar]

14. S. H. Farghaly and S. M. Ismail, “Floating-point discrete wavelet transform-based image compression on FPGA,” AEU International Journal of Electronics and Communications, vol. 124, pp. 153363, 2020. [Google Scholar]

15. Y. Hou, Z. Ren, Y. Tao and W. Chen, “Learning-based parameter prediction for quality control in three-dimensional medical image compression,” Frontiers of Information Technology & Electronic Engineering, vol. 22, no. 9, pp. 1169–1178, 2021. [Google Scholar]

16. S. T. Ahmed and S. Sankar, “Investigative protocol design of layer optimized image compression in telemedicine environment,” Procedia Computer Science, vol. 167, pp. 2617–2622, 2020. [Google Scholar]

17. S. Yuan and J. Hu, “Research on image compression technology based on Huffman coding,” Journal of Visual Communication and Image Representation, vol. 59, pp. 33–38, 2019. [Google Scholar]

18. D. Venugopal, S. Mohan and S. Raja, “An efficient block based lossless compression of medical images,” Optik, vol. 127, no. 2, pp. 754–758, 2016. [Google Scholar]

19. C. Y. Pang, R. G. Zhou, B. Q. Hu, W. Hu and A. El-Rafei, “Signal and image compression using quantum discrete cosine transform,” Information Sciences, vol. 473, pp. 121–141, 2019. [Google Scholar]

20. A. Aung, B. P. Ng and S. Rahardja, “Sequency-ordered complex Hadamard transform: Properties, computational complexity and cpplications,” IEEE Transactions on Signal Processing, vol. 56, no. 8, pp. 3562–3571, 2008. [Google Scholar]

21. D. Jabeen, G. Monir and F. Azim, “Sequency domain signal processing using complex Hadamard transform,” Circuits, Systems, and Signal Processing, vol. 35, no. 5, pp. 1783–1793, 2016. [Google Scholar]

22. A. Aung, B. P. Ng and S. Rahardja, “Conjugate symmetric sequency-ordered complex Hadamard transform,” IEEE Transactions on Signal Processing, vol. 57, no. 7, pp. 2582–2593, 2009. [Google Scholar]

23. A. Aung and B. P. Ng, “Natural-ordered complex Hadamard transform,” Signal Processing, vol. 90, no. 3, pp. 874–879, 2010. [Google Scholar]

24. S. Rahardja and B. J. Falkowski, “Family of unified complex Hadamard transforms,” IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, vol. 46, no. 8, pp. 1094–1100, 1999. [Google Scholar]

25. S. Pei, C. Wen and J. Ding, “Conjugate symmetric discrete orthogonal transform,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 61, no. 4, pp. 284–288, 2014. [Google Scholar]

26. J. G. Proakis and D. G. Manolakis, Digital Signal Processing: Principles, Algorithms, and Applications, 4th ed., Hoboken: Prentice-Hall, 2007. [Google Scholar]

27. K. R. Rao, D. H. Ochoa and S. Shreyanka, “3 The discrete cosine and sine transforms,” in JPEG Series. Denmark: River Publishers, pp. 49–65, 2021. [Google Scholar]

28. C. Connolly and T. Fleiss, “A study of efficiency and accuracy in the transformation from RGB to CIELAB color space,” IEEE Transactions on Image Processing, vol. 6, no. 7, pp. 1046–1048, 1997. [Google Scholar]

29. A. A. Siddique, M. T. Qadri and Z. Mohy-Ud-Din, “Exhaustive crisp parameter modification in quantization table for effective image compression,” Mehran University Research Journal of Engineering and Technology, vol. 39, no. 2, pp. 279–286, 2020. [Google Scholar]