Optimization Task Scheduling Using Cooperation Search Algorithm for Heterogeneous Cloud Computing Systems

1  Introduction

The cloud computing model emerged with the growth of the Internet and the services that the Internet provides to its users. The cloud model is based on distributed computing and consists of different virtual computers that can be interconnected and dynamic to form computing resources. The vacant resources should be used globally to increase the utilization and gain of the resources by increasing the economic efficiency of these resources. The cloud model best serves this. The primary goal of the cloud computing concept is to enable users to share data and resources. It is a platform to provide applications and services to its users. There are three forms of cloud computing: platform as a service (paas), software as a service (saas), and infrastructure as a service (iaas) [1]. These services are available to users on a pay-on-demand basis and share servers, computing resources, applications, networks, and data storage. The licenced software is delivered to the user on a subscription basis for the services in a saas service. These services may be accessed from any device using a web browser. In paas, users can create their services using the available cloud services and then publish those services on their devices. In iaas, the organizational infrastructure for clients is available online. To use this, the consumer does not need to comprehend the internal nature of the infrastructure [1]. Instead of buying the entire infrastructure for business requirements, which the customer takes as basic rent when there are no more infrastructure requirements, the customer uses the amount paid for the services. In the last year, the number of cloud users has increased, so the volume of tasks you need to manage by default for this task is required for scheduling [1]. To solve the problem of scheduling tasks better, we have proposed a novel efficient approach based on the cooperation search algorithm called the Efficient Cooperation Search Algorithm (ECSA) to minimize the makespan of the user requests on the resources. In the cooperation search algorithm, the representation of a vector is a continuous value, so we use two methods to convert the continuous value to a discrete value. We assess our algorithm’s performance by running it through three cases with varying numbers of tasks.

The following is the paper’s structure: Section 2 contains the notations. Related work for problems of scheduling tasks is given in Section 3. The problem description is given in Section 4. Section 5 shows the cooperation search algorithm. Section 6 describes the ECSA approach. The results were obtained by applying the ECSA and compared with the other results and discussion presented in Section 7. Section 8 concludes and offers future work.

2  Notations

TG represents the graph of tasks

Tasi represents the task i

Prosi represents the processor i

NMP represents the processor’s number

NMT represents the task’s number

C(Tasi, Tasj) The communication cost between Tasi and Tasj

Start_Time(Tasi, Prosj) represents the task’s start time i on a processor Prosj

Finish_Time(Tasi, Prosj) represents the task’s finish time i on a processor Prosj

Ready_Time(Prosi) represents the processor’s ready time i

LT represents a list of jobs arranged in directed acyclic graph topological order

Data_Arrive(Tasi, Prosj) represents the time of data arrival of task i to processor j

3  Related Work

In terms of cloud computing, scheduling tasks directly influences resource utilization and operational expenses. Many metaheuristic approaches and variants for optimizing scheduling have been created to boost the efficiency of task executions in the cloud. This study [2] introduces the Whale Optimization Algorithm (WOA) for scheduling tasks in the cloud using a multiobjective improvement model, intending to increase the cloud system performance with limited resources for computing. Based on that assumption, an improved method called Improved Whale Optimization Algorithm (IWC) for scheduling tasks in the cloud was created to boost the whale optimization algorithm-based method’s best solution search capability. The algorithm aims to Improve convergence speed and accuracy and increase the resource utilization cost.

Cloud computing is a relatively new paradigm for exploiting distant resources for computing; It is also becoming a more robust and popular technology that enables on-demand resource allocation and release in near real-time. Scheduling tasks are crucial in cloud computing and are one of the most challenging things to master in this field. As a result, a strong and effective scheduling system is necessary to better resource utilization. An excellent algorithm for scheduling tasks can improve the quality of service, overall performance, and end-user experience. As the number of available tasks grows, so does the complexity of the problem, resulting in a huge search space. To offer a technique capable of finding a near-optimal solution for a multiobjective scheduling task issue in a cloud computing environment while also reducing search time. The authors provide the hybridized bat algorithm, a swarm-intelligence-based technique for multiobjective task scheduling [3]. The algorithm aims to utilize makespan, cost, and Hyervolume indicator.

The most critical need in a cloud computing environment is scheduling tasks since it is vital to the overall functioning of cloud computing facilities. In cloud computing, scheduling tasks implies allocating the possible resources for the work to be executed while considering dependability, time, scalability, cost, makespan, throughput, resource consumption, availability, etc. The suggested approach takes reliability and availability into account. Because of the difficulties of achieving these criteria, most scheduling methods do not incorporate cloud computing ecosystem stability and availability. A mathematical model for cloud computing that uses mutation of load balancing and a particle swarm optimization based allocation and schedule that considers the time of transmission, time of the round trip, reliability, time of execution, load balancing, makespan, cost of transmission, and between virtual machines and tasks is presented [4]. It can contribute to the dependability of the cloud computing environment by considering the availability of resources and rescheduling tasks that fail to allocate them.

Several advantages are provided by central cloud facilities based on virtual computers, including reduced costs of scheduling and improved service accessibility and availability. The cloud computing strategy is viable because of the combination of security measures and online services. The feature spaces of the source and destination domains differ in task transfer. This problem is exacerbated by network traffic, which causes data transmission delays and prevents some vital operations from being completed on time. This work introduces a hybrid multi-verse optimizer with a genetic algorithm as a practical optimization approach for job scheduling. The suggested algorithm is intended to improve the performance of the tasks transported over the cloud network based on the workload of resources in the cloud. It is required to give suitable decisions of transfer to reschedule the transfer tasks in the cloud based on the efficiency weight of the acquired jobs. The suggested technique considers a variety of cloud resource attributes, including throughput, capacity, number of virtual machines, number and size of tasks, and speed [5]. The algorithm aims to optimize the transfer time of large cloud tasks, which reflects its effectiveness.

Cloud computing is a type of on-demand Internet-based computing widely used by both working and non-working individuals throughout the world. One of the essential applications utilized by cloud service providers and end-users is task scheduling. The task scheduler’s main challenge is to locate the best resource for the given input job. A hybrid electro search combined with a genetic algorithm is proposed [6] to optimize scheduling task behaviour by considering load balancing, makespan, multi-cloud cost, and resource usage criteria. The proposed solution leveraged the benefits of both an electrical search algorithm and a genetic algorithm. The genetic algorithm gives the best solutions within the local optimum, whereas the electro-search method delivers the best solutions within the global optimal. The algorithm aims to decrease makespan, cost, and response time.

The scheduling task is essential to improving the performance of collaborative and distributed e-science and e-business applications at scale. This typical application includes multiple communication tasks that are performed on virtual machines. The primary objective of any scheduling method is to reduce the extent of the configuration, which reflects the exit task completion time. Focusing on downsizing for allocating or scheduling multiple tasks across heterogeneous virtual machines, in this paper [7] a model based on the Crow Search Algorithm (CSA) was proposed and the main objective of this model is to reduce the makespan.

Scheduling tasks is the primary issue in cloud computing, which reduces the system’s performance. It’s an effective method to organize the user’s requirements and achieve multiple goals. An efficient scheduling task algorithm is required to improve the system’s performance. A Genetic Algorithm (GA) has been described for task assignment and execution. The algorithm aims to decrease the execution cost and makespan of tasks and increase resource utilization [8].

4  Problem Description

During this work, the task scheduling model is defined as distributed Number of Tasks (NMT) tasks to be implemented on Number of Processors (NMP) processors. The processors may be different in general. Task Graph (TG) may be mapped to describe the problem structure. TG is a Directed Acyclic Graph (DAG) made up of NMT tasks: Tas1, Tas2, Tas3,… Tasn. Every node in the graph is termed a task. A task is assumed to be a set of instructions that must be implemented sequentially by an assigned processor. A task (node) might have pre-demanded data (inputs) before implementation. When all the inputs are received, the task can be triggered to be implemented. These inputs are expected to be delivered after some other tasks end their implementation, as these tasks evaluate them. We call this relying on task dependency. If a task is dependent on other tasks’ data, then we consider that task as the parent of the task, and the task is their child. A task with no parents is called an entry task, and a task with no children is called an exit task [9]. The execution time of a task is what we call the computation cost. Whenever the computation cost of a task Tasi is denoted by weight (Tasi, Prosj), the graph additionally has directed edges representing a partial order among the tasks. The partial order introduces a precedence-constrained DAG and implies that if (Tasi → Tasj), then Tasj is a child, which means it cannot start until its parent Tasi finishes. The weight on edge represents the communication cost between the tasks and is denoted by C(Tasi, Tasj); the communication cost is considered only if Tasi and Tasj are assigned to different processors; otherwise, it’s calculated to be zero. In that case, Tasi and Tasj are assigned to the same processor. If a node Tasi is assigned to processor Prosj, the task’s start time and finish time are denoted by Start_Time(Tasi, Prosj) and Finish_Time(Tasi, Prosj), respectively. After scheduling the tasks, the makespan is defined as the max {Finish_Time(Tasi, Prosj)} across all processors. The task scheduling problem is to find a schedule for the tasks in the processors such that the makespan is decreased over possible schedules, where the task dependency constraints are preserved. Task dependency constraints state that any task can’t start until all parents have finished. Assume that Prosj is the processor and that the Kpath parent task Task of task Tasi, is scheduled. The Data_Arrive of Tasi at processor Prosj is the time at which the per-demanded data for the task execution becomes available. This is defined in [9] by the following:

1(1)

Start_Time(Tasi,Prosj)=max{Ready_Time(Prosj),Data_Arrive(Tasi,Prosj)}(2)

Finish_Time(Tasi,Prosj)=Start_Time(Tasi,Prosj)+weight(Tasi,Prosj)(3)

Ready_Time(Prosj)=Finish_Time(Tasi,Prosj)(4)

Makespan=max{Finish_Time(Tasi,Prosj)}wherei=1,2,3…NMT(5)

5  Cooperation Search Algorithm

The specifics of the Cooperation Search Algorithm (CSA) approach [10] are provided in this part to provide a unique additional tool for global optimization problems: The cooperative team behaviours in current organizations are explained first, followed by the search concept of the CSA approach. The following are some examples of frequent restricted minimization optimization problems:

ming(y)y=[y1,….,yj,…..,yJ]∈RJ

Such\; thatggee(y)≤0ee=1,2,3,…..,EE(6)

hhg(y)=0g=1,2,3,…..,\; G

yj\; _≤\; yj≤yj¯j=1,2,3,…..,J

where g(x) denotes the J-dimensional solution’s objective value. yj denotes the jth variable in solution y, yj¯ and yj\; _ are the upper and lower bounds of the jth variable, respectively. The number of possible decision factors is denoted by the letter J. The inequality constraint is ggee(y). The gth equality constraint is expressed as hhg(y). The variables G and EE represent the number of equality and inequality constraints, respectively.

5.1 Insights from Teamwork Behaviour in Modern Businesses

In recent years, all types of businesses have played an increasingly essential part in economic and social growth. Cooperative team conduct is critical to one company’s normal functioning. The boards of supervisors and directors, the chairman, and the staff are four different positions frequently used in the corporate cooperation process. The board of directors, which comprises shareholders who have been chosen to represent them, oversees the company’s business operations and administers the productive duties inside. In other words, the board of directors oversees all of the company’s affairs and transactions. The board of supervisors is tasked with supervising the executive directors and promoting the interests of the shareholders [10]. In contrast, the boards of supervisors and directors can’t participate in the firm’s corporate decision-making process and can’t represent the organization externally. As an executive elected by the board of directors, the chairman is primarily responsible for the company’s scientific activities. Furthermore, as the firm’s spokesman, the chairman frequently has significant, if not decisive, influence over the company to ensure smooth and orderly operations before reaching a consensus on board decisions. The staff is required to participate in specific tasks under the direction of the board of directors, which typically has the authority to select members of the boards of supervisors and directors. It is generally recognized that human people are one of the essential components in increasing productivity, implying that growing staff strength is a critical aspect of the company’s scientific development. In order to achieve this aim, it is vital to assist individual staff members in gaining as much information as possible. In general, a group of leaders on the boards of supervisors and directors and a chairperson can all impact staff knowledge at the same time. Because of their role as team leaders, the chairman on duty frequently has the most power. At the same time, members of the boards of supervisors and directors supply ample information to minimize or even eliminate potential mistakes. After some time, each staff member is urged to contemplate self-improvement methods and given the option to assume the position of their superior leaders once their performance has improved. In other words, the chairman and the members of the board of directors and supervisors can be dynamically updated to boost the company’s market competitiveness. It has been discovered that there are close connections among members of various social statuses; underperforming leaders or staff might be replaced by promising young people, while ordinary staff has the opportunity to improve their knowledge and advance their job positions through hard work. As a result, the firm can continue to operate to achieve sustainable development [10].

5.2 The CSA Method’s Search Principle

In CSA, the optimization process of the target problem is viewed as the development of an enterprise; each solution is viewed as a staff member, while a group of staff members forms an enterprise team; the value of the fitness of the problem is equal to the performance per staff member; the board of supervisors is made up of personal best-known solutions; the board of directors is made up of the external archive set (M global best-known solutions found by far); the chairman on duty is rando. The population may then gradually develop high-quality solutions by replicating team cooperation behaviours in the modern industry by employing three evolutionary operators: The team communication operator is used to assist employees in capturing useful leaders’ knowledge; The operator for reflective learning is used to increase the staff’s overall strength by drawing lessons from the past. The internal competition operator improves the top solutions’ work experiences and leadership vision. Following that, the technical elements of the CSA technique are as follows [10]:

The team-building phase: The equation determines all team members at random Eq. (7). After evaluating all solutions’ performances, Mϵ[1,I] solutions for leaders will be picked from the original swarm to create the external elite set.

yi,jk=O(yj_,yj¯),wherei\; ∈[1,I],\; j\; ∈[1,J],\; k=1(7)

where I is the current swarm’s number of solutions. The jth value of the ith solution during the kth cycle is represented by yi,jk. O (Lower Bound (LOB), Upper Bound (UPB)) is a function that generates a random number with a uniform distribution in the range [LOB, UPB] [10].

The operator of team communication: Each staff member may learn new messages by sharing information with the chairman and the board of supervisors and directors. As shown in Eq. (8), the team communication process consists of the chairman’s knowledge W, E the board of directors’ collective knowledge, and the collective knowledge Z from the board of supervisors. The chairman is picked randomly from the board of directors to replicate the rotating mechanism. In contrast, all supervisors and directors’ board members are assigned identical positions in calculating E and Z [10].

qi,jk+1=\; yi,jk+\; Wi,jk+\; Ei,jk+Zi,jk,where i∈[1,I],\; j∈[1,J],\; k∈[1,K](8)

Wi,jk=log⁡(1O(0,1)).(globestinde,jk−\; yi,jk)(9)

Ei,jk=α.O(0,1).[1M∑m=1Mglobestm,jk−\; yi,jk](10)

Zi,jk=β.O(0,1).[1I∑i=1Iperbesti,jk−\; yi,jk](11)

qi,jk+1 denotes the jth value of the ith group solution during the (k + 1)th cycle. The jth value of the ith personal best-known solution during the kth cycle is given by perbesti,jk. The jth value of the indeth global best-known solution from the beginning of the kth cycle is represented by globestinde,\; jk. The index inde is chosen at random from the set of {1, 2,…, M}. Wi,jk represents the information obtained from the chairman, who was randomly picked from the external elite group. Ei,jk and Zi,jk represent the average knowledge acquired from M global best-known solutions discovered by far and I personal best-known solutions, respectively. α and β are the learning coefficients used to alter the influence degrees of Ei,jk and Zi,jk, respectively [10].

The operator of reflective learning: Aside from learning from the leader’s solutions, the staff may also receive new information by summarising their own experience in the other way, as seen below [10]:

li,jk+1={hi,jk+1if(qi,jk+1≥\; zj)si,jk+1if(qi,jk+1<\; zj),where\; i∈[1,\; I],\; j\; ∈[1,\; J],\; k\; ∈[1,K](12)

hi,jk+1={O(yj¯+yj_−\; qi,jk+1,\; zj)if(|qi,jk+1−zj|<O(0,1).|yj¯−yj_|)O(yj_,yj¯+yj_−\; qi,jk+1)otherwise(13)

si,jk+1={O(zj,yj¯+yj_−\; qi,jk+1)if(|qi,jk+1−zj|<O(0,1).|yj¯−yj_|)O(yj¯+yj_−\; qi,jk+1,yj¯)otherwise(14)

zj=12.(yj¯+yj_)(15)

li,jk+1 denotes the jth value of the ith reflective solution during the (k + 1)th cycle.

The operator of internal competition: The team steadily improves its competitiveness in the market by ensuring that all employees with superior performance are always retained, as shown below [10]:

yi,jk+1={qi,jk+1if(G(qik+1)≤G(lik+1))li,jk+1if(G(qik+1)>G(lik+1)),where i∈[1,\; I],\; j\; ∈[1,\; J],\; k\; ∈[1,K](16)

G(y) denotes the value of fitness of the solution y. In order to implement multiple physical constraints, Eq. (17) is used to modify all the variables in y to the feasible zone. Then the penalty functions approach in Eq. (18) is used to achieve the fitness value G (y) by combining the value of constraint violation with the objective value g (y). Then, all constraints are well fulfilled for feasible solutions, resulting in the original objective value being equal to a fitness value; for infeasible alternatives, the constraint violation value becomes positive, resulting in a fitness value more significant than the objective value. As a result, the swarm may be directed to a practical search region [10].

yj=max{min{yj¯,\; yj},yj_}(17)

G(y)=g(y)+∑ee=1EEzee1.max{ggee(y),0}+∑g=1Gzg2.|hhg(y)|(18)

where yj is the jth value to be evaluated from the solution y. The eeth inequality constraint penalty coefficient is denoted by zee1. For the gth inequality constraint, the penalty coefficient is zg2.

6  The Proposed Algorithm

We can see that the representation of a vector is a continuous value; therefore, we will apply the Smallest Position Value (SPV) rule [11] and the Largest Position Value (LPV) rule [12], as well as the modulus function with the number of processors and increasing the value by 1, as shown in Fig. 1.

Figure 1: An example of the proposed schedule

Where the tasks Tas1 and Tas3 are scheduled into processor 1. The tasks Tas2, Tas6, and Tas7 are scheduled into processor 2. The tasks Tas4 and Tas5 are scheduled into processor 3, as shown in Fig. 2.

Figure 2: The proposed schedule

We can see as shown above that Algorithm 1 is used to compute the makespan by taking the schedule after converting it by Algorithm 2, which detects the method that is used to convert the continuous value to a discrete value by generating a random number, the number maybe 1 or 2. The proposed algorithm uses the operation of a cooperation search algorithm to find the best solution for the makespan. We can see that the value of speedup, efficiency, and throughput depends on the makespan. The smaller the makespan, the higher the speedup, efficiency, and throughput.

7  Evaluation of the ECSA

In this part, we demonstrate the ECSA’s efficacy by applying it to three cases. The first case is of three heterogeneous processors and eleven tasks. The second case consists of three heterogeneous processors and ten tasks. The third one consists of a different number of tasks and processors. ECSA was implemented as a system by MATLAB 2016. We set the initial values of the parameters initial population = 100, α=0.10,β=0.15, max of iteration = 100.

Speedup is the ratio between the results obtained by assigning all tasks to a processor that gives the minimum makespan and the results obtained by executing tasks in parallel. It is calculated as shown in Eq. (19) [7].

Speedup=minprosj(∑Tasiweighti,j\; makespan)(19)

Efficiency is the ratio between the obtained speedup results and the total number of processors used. It is calculated as shown in Eq. (20) [7].

Efficiency=SpeedupNMP(20)

Throughput: The value of the throughput metric can be defined as the number of tasks executed per unit of time. It is calculated as shown in Eq. (21) [13].

Throughput=NMTmakespan(21)

7.1 Case 1

In this case, the tasks {Tas0, Tas1, Tas2, Tas3, Tas4, Tas5, Tas6, Tas7, Tas8, Tas9, Tas10} will be executed on three heterogeneous processors {Pros1, Pros2, Pros3}. The cost of executing each task on different processors is shown in Tab. 1 [14]. The schedule obtained by ECSA and other algorithms is shown in Tab. 2. The results obtained by the proposed ECSA are compared with those obtained by the Genetic Algorithm (GA) [8], and New Genetic Algorithm (NGA) [14]. The task priority of ECSA {Tas0, Tas2, Tas3, Tas4, Tas1, Tas6, Tas8, Tas7, Tas5, Tas9, Tas10}, task priority of NGA {Tas0, Tas4, Tas3, Tas2, Tas8, Tas1, Tas6, Tas5, Tas7, Tas9, Tas10}, GA {Tas0, Tas2, Tas6, Tas4, Tas1, Tas3, Tas8, Tas7, Tas5, Tas9, Tas10}. Figs. 3–6 represent the results obtained by the ECSA, NGA, and GA in terms of makespan, speedup, efficiency, and throughput.

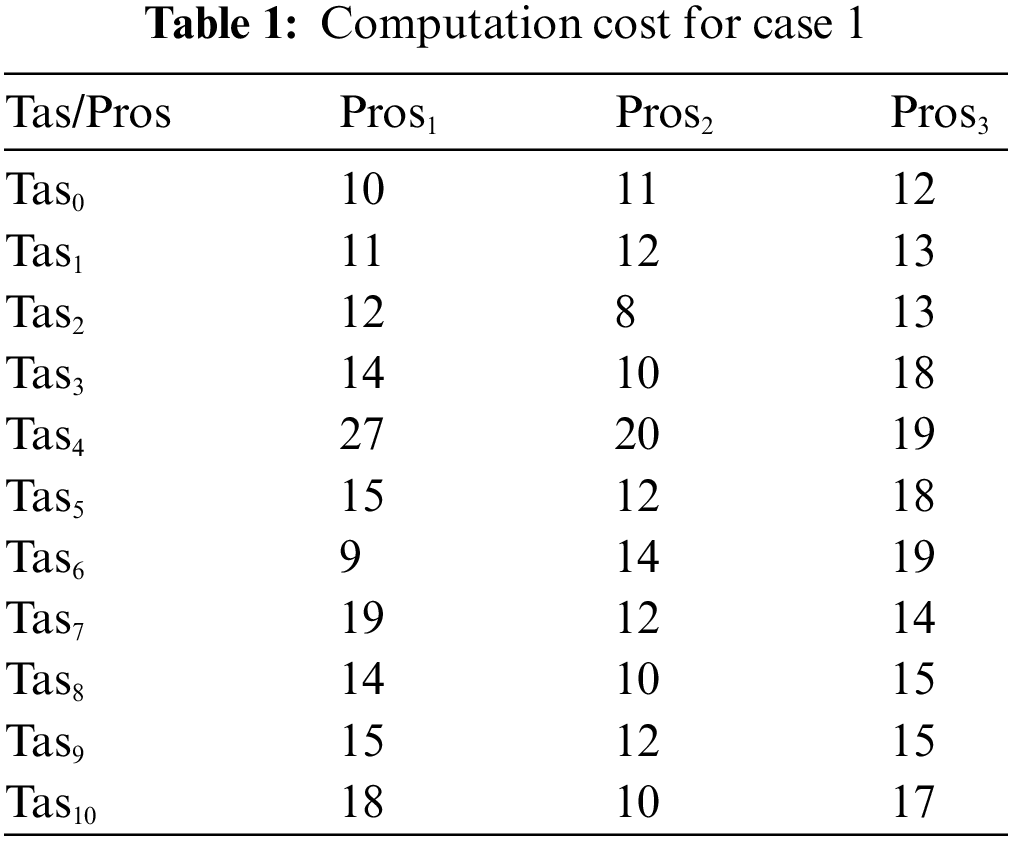
Figure 3: Comparison of makespan for case 1

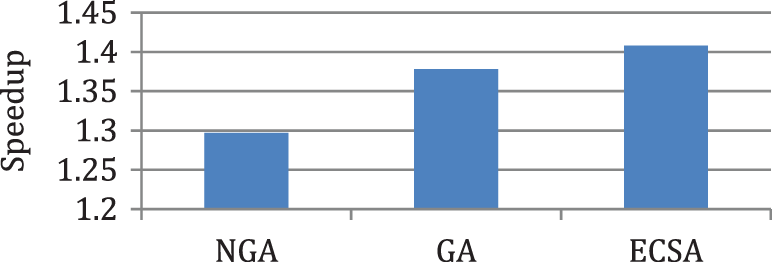
Figure 4: Comparison of speedup for case 1

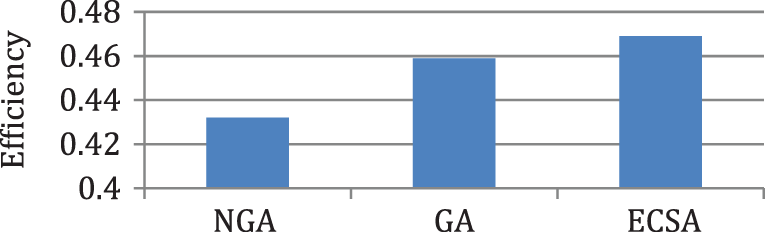
Figure 5: Comparison of efficiency for case 1

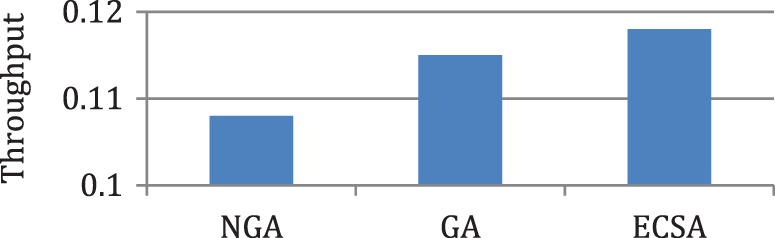
Figure 6: Comparison of throughput for case 1

7.2 Case 2

In this case, the tasks {Tas1, Tas2, Tas3, Tas4, Tas5, Tas6, Tas7, Tas8, Tas9, Tas10} are executed on three heterogeneous processors {Pros1, Pros2, Pros3}. The cost of executing each task on different processors is shown in Tab. 3, [9]. The schedule obtained by ECSA and other algorithms is shown in Tab. 4. The results obtained by the ECSA are compared with those obtained by the Whale Optimization Algorithm (WOA) [15]. Gravitational Search Algorithm (GSA) [16], and Hybrid Heuristic and Genetic (HHG) [17]. The task priority of ECSA {Tas1, Tas6, Tas4, Tas5, Tas2, Tas3, Tas8, Tas9, Tas7, Tas10}, task priority of WOA {Tas1, Tas3, Tas5, Tas2, Tas4, Tas6, Tas7, Tas8, Tas9, Tas10}, task priority of GSA {Tas1, Tas3, Tas2, Tas6, Tas4, Tas5, Tas7, Tas8, Tas9, Tas10}, task priority of HHG {Tas1, Tas2, Tas6, Tas3, Tas4, Tas5, Tas8, Tas7, Tas9, Tas10}. Figs. 7–10 represent the results obtained by the ECSA, WOA, GSA, and HHG in terms of makespan, speedup, efficiency, and throughput.

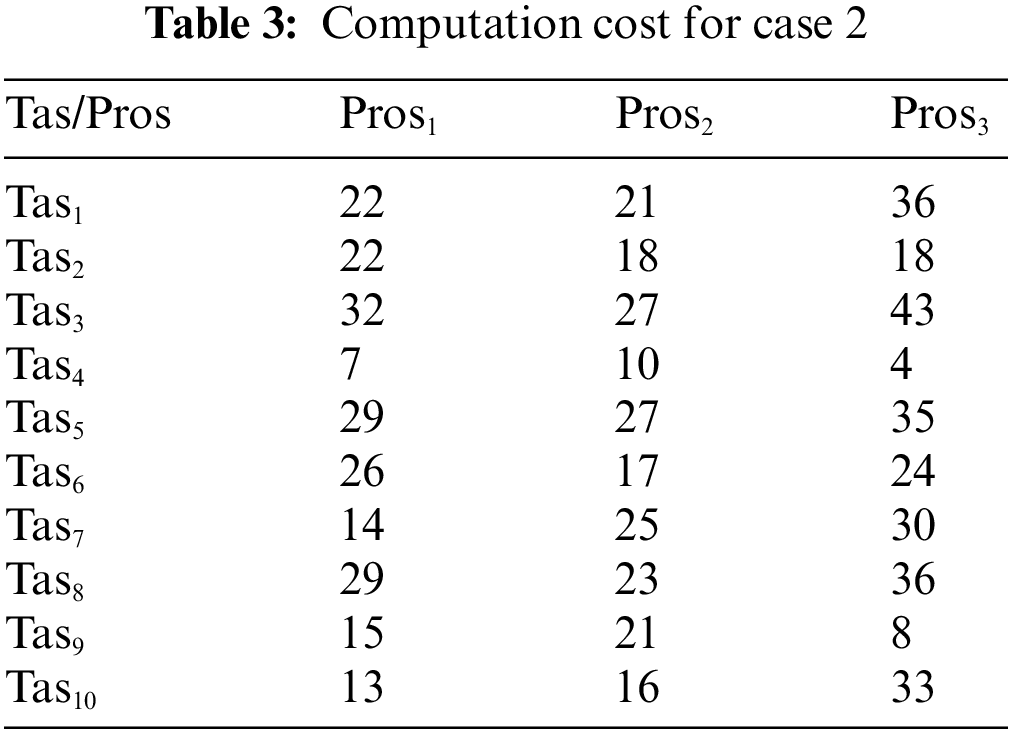
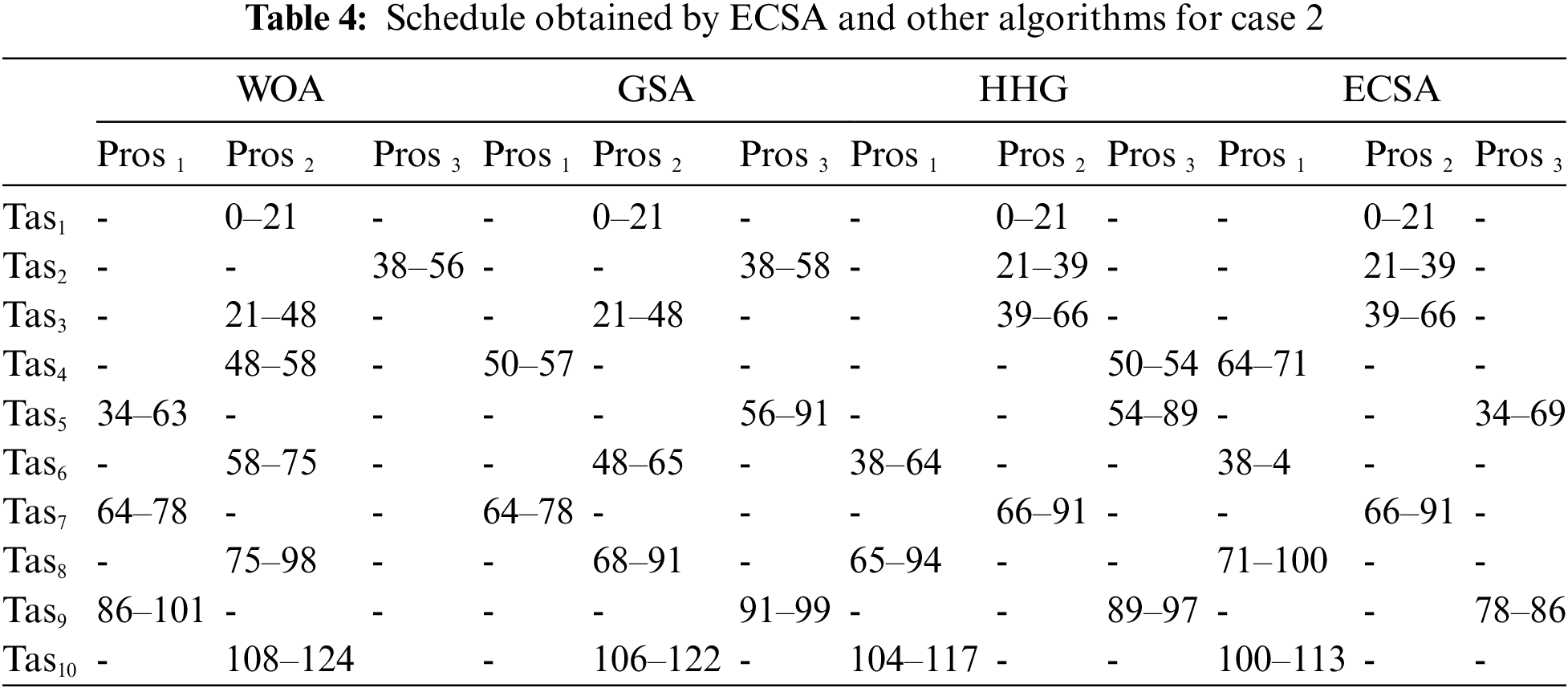
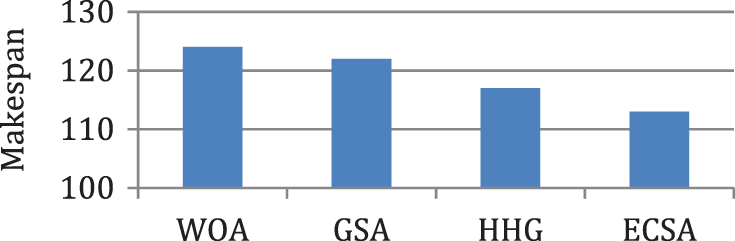
Figure 7: Comparison of makespan for case 2

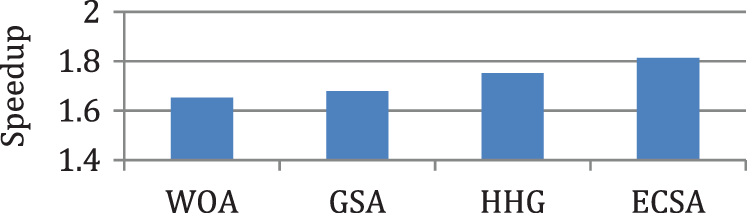
Figure 8: Comparison of speedup for case 2

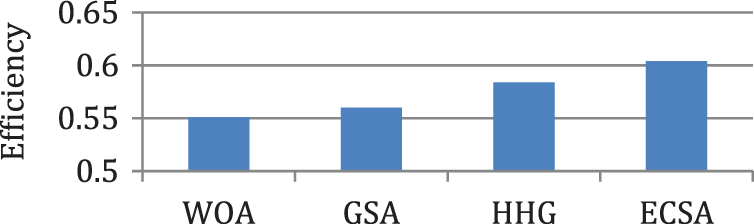
Figure 9: Comparison of efficiency for case 2

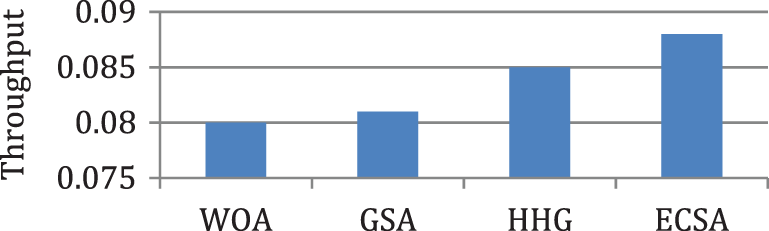
Figure 10: Comparison of throughput for case 2

7.3 Case 3

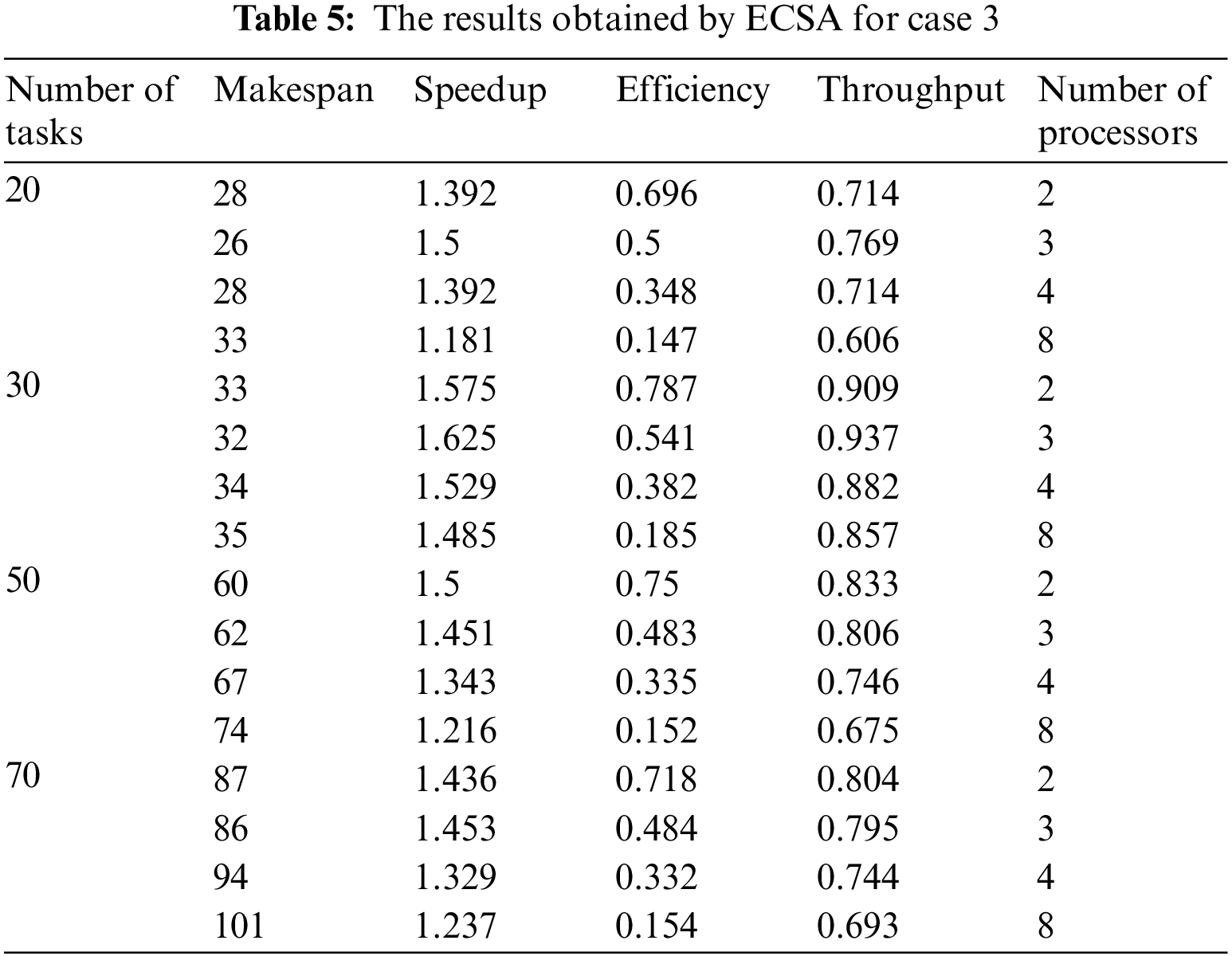
To analyze the behavior of the ECSA, we consider four cases with M = 2, 3, 4, and 8 processors. The number of tasks is 20, 30, 50, and 70 tasks in the first, second, third, and fourth cases (N = 20, 30, 50, and 70). The communication cost between the tasks and the computation cost of each task on different processors are randomly generated from 1 to 20, and 1 to 5, respectively. We run our proposed algorithm one more time. The results obtained by the proposed algorithm are shown in Tab. 5.

7.4 Discussion

According to the results in Figs. 3–6, it is found that the makespan of the ECSA is reduced by (7.9%) and (2.1%) about NGA and GA respectively. The speedup of the ECSA is improved by (8.5%) and (2.1%) for NGA and GA respectively. The efficiency of the ECSA is improved by (8.5%) and (2.1%) for NGA and GA respectively. The throughput of the ECSA is improved by (9.2%) and (2.6%) about NGA and GA respectively. According to the results in Figs. 7–10, it is found that the makespan of the ECSA is reduced by (8.8%), (7.7%), (3.4%) about WOA, GSA, HHG, respectively. The speedup of the ECSA is improved by (9.7%), (7.9%), and (3.5%) about WOA, GSA, and HHG, respectively. The efficiency of the ECSA is improved by (9.6%), (7.8%), and (3.4%) about WOA, GSA, and HHG, respectively. The throughput of the ECSA is improved by (10%), (8.6%), and (3.5%) about WOA, GSA, and HHG, respectively.

8  Conclusion and Future Work

To get near-optimal results for the problem of scheduling tasks in a cloud computing environment, efficient strategies for the optimal mapping of the tasks are required. In this research, we propose a novel efficient approach based on the cooperation search algorithm called the Efficient Cooperation Search Algorithm (ECSA) to solve the problem of scheduling tasks in a cloud computing environment. The system is made up of a limited number of fully connected heterogeneous processors. The comparison of the algorithm has been made against the algorithms in terms of makespan, speedup, efficiency, and throughput. The comparative analysis explains that the proposed algorithm performance is significantly better in all cases, it reduces the makespan by (7.9%), (2.1%), (8.8%), (7.7%), (3.4%) about New Genetic Algorithm (NGA), Genetic Algorithm (GA), Whale Optimization Algorithm (WOA), Gravitational Search Algorithm (GSA), and Hybrid Heuristic and Genetic (HHG) respectively according to makespan. In our future work, we will develop an efficient coronavirus herd immunity optimizer algorithm for optimizing scheduling tasks in cloud computing.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Dubey, M. Kumar and S. C. Sharma, “Modified HEFT algorithm for task scheduling in cloud environment,” Procedia Computer Science, vol. 125, pp. 725–732, 2018. [Google Scholar]

 2.  X. Chen, L. Cheng, C. Liu, Q. Liu, J. Liu et al., “A woa-based optimization approach for task scheduling in cloud computing systems,” IEEE Systems Journal, vol. 14, no. 3, pp. 3117–3128, 2020. [Google Scholar]

 3.  T. Bezdan, M. Zivkovic, E. Tuba, I. Strumberger, N. Bacanin et al., “Multiobjective task scheduling in cloud computing environment by hybridized bat algorithm,” Journal of Intelligent & Fuzzy Systems, vol. 42, no. 1, pp. 411–423, 2022. [Google Scholar]

 4.  A. I. Awad, N. A. El-Hefnawy and H. M. Abdel_kader, “Enhanced particle swarm optimization for task scheduling in cloud computing environments,” Procedia Computer Science, vol. 65, pp. 920–929, 2015. [Google Scholar]

 5.  L. Abualigah and M. Alkhrabsheh, “Amended hybrid multi-verse optimizer with genetic algorithm for solving task scheduling problem in cloud computing,” Journal of Supercomputing, vol. 78, no. 1, pp. 740–765, 2022. [Google Scholar]

 6.  S. Velliangiri, P. Karthikeyan, V. M. Arul Xavier and D. Baswaraj, “Hybrid electro search with genetic algorithm for task scheduling in cloud computing,” Ain Shams Engineering Journal, vol. 12, no. 1, pp. 631–639, 2021. [Google Scholar]

 7.  A. Mishra, M. N. Sahoo and A. Satpathy, “H3CSA: A makespan aware task scheduling technique for cloud environments,” Transactions on Emerging Telecommunications Technologies, vol. 32, no. 10, pp. 1–20, 2021. [Google Scholar]

 8.  A. Y. Hamed and M. H. Alkinani, “Task scheduling optimization in cloud computing based on genetic algorithms,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3289–3301, 2021. [Google Scholar]

 9.  A. Younes, A. BenSalah, T. Farag, F. A. Alghamdi and U. A. Badawi, “Task scheduling algorithm for heterogeneous multi processing computing systems,” Journal of Theoretical and Applied Information Technology, vol. 97, no. 12, pp. 3477–3487, 2019. [Google Scholar]

10. Z. -K. Feng, W. -J. Niu and S. Liu, “Cooperation search algorithm: A novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems,” Applied Soft Computing Journal, vol. 98, pp. 1–27, 2021. [Google Scholar]

11. I. Dubey and M. Gupta, “Uniform mutation and SPV rule based optimized PSO algorithm for TSP problem,” in Proc. of the 4th Int. Conf. on Electronics and Communication Systems, Coimbatore, India, pp. 168–172, 2017. [Google Scholar]

12. L. Wang, Q. Pan and F. M. Tasgetiren, “A hybrid harmony search algorithm for the blocking permutation flow shop scheduling problem,” Computers & Industrial Engineering, vol. 61, no. 1, pp. 76–83, 2011. [Google Scholar]

13. S. Nabi, M. Ibrahim and J. M. Jimenez, “DRALBA: Dynamic and resource aware load balanced scheduling approach for cloud computing,” IEEE Access, vol. 9, pp. 61283–61297, 2020. [Google Scholar]

14. B. Keshanchi, A. Souri and N. Navimipour, “An improved genetic algorithm for task scheduling in the cloud environments using the priority queues: Formal verification, simulation, and statistical testing,” Journal of Systems and Software, vol. 124, pp. 1–21, 2017. [Google Scholar]

15. S. R. Thennarasu, M. Selvam and K. Srihari, “A new whale optimizer for workflow scheduling in cloud computing environment,” Journal of Ambient Intelligence Humanized Computing, vol. 12, no. 3, pp. 3807–3814, 2020. [Google Scholar]

16. T. Biswas, P. Kuila, A. K. Ray and M. Sarkar, “Gravitational search algorithm based novel workflow scheduling for heterogeneous computing systems,” Simulation Modelling Practice and Theory, vol. 96, pp. 1–21, 2019. [Google Scholar]

17. M. Sulaiman, Z. Halim, M. Lebbah, M. Waqas and S. Tu, “An evolutionary computing-based efficient hybrid task scheduling approach for heterogeneous computing environment,” Journal of Grid Computing, vol. 19, no. 1, pp. 1–31, 2021. [Google Scholar]