Metaheuristics-based Clustering with Routing Technique for Lifetime Maximization in Vehicular Networks

1  Introduction

The Vehicular Ad hoc Networks (VANETs) are regarded in the subsection of the conventional structure of the Mobile Adhoc Network system (MANETs) [1]. The important character of VANET indicates the telecommunication nodes mention the vehicles which were granted with critical ‘on-board unit’ apparatus, transportable in limited roads or lanes, and interacting with one another for swapping messages via the Vehicle to Vehicle (V2V) protocol of transmission, that describes the extent amongst the vehicles and standard roadside accessible points [2]. This extent explanation further inculcates the wireless network and mobile substructure, in those cases where V2V form of information transfer is done [3]. Even though there comes numerous resemblance among VANETs and MANETs, the particular features of the vehicle motion models cause VANETs to have higher difficulties and issues [4]. For example, the higher mobility of vehicles creates recurrent differences in the network topology in VANETs, paving the way to have complications in routing table maintenance and worst node connectivity [5]. The vehicle could just move in a single direction and might be met with emergency accidents or traffic jams, such situations would make the transmission position among vehicle nodes to be very complex. Over several decades, several authors make much effort and contributing to the model of routing protocol for VANETs and suggested distinct routing methods [6]. Few are categorized into broadcast-related, topology-related, position-related, infrastructure-related, and cluster-related. By comparing, location-related routing denotes a hopeful scheme in vehicular circumstances as it assists geographical location data of every vehicle to provide routing [7]. Whenever a source node initiates to transmit packets towards the destination node, the route path cannot be fixed due to the relay node is computed from the position information of itself, neighbors, and the destination. Nodes do not sustain the routing table and it does not accomplish the global path amongst destination and source [8]. This routing scheme could implement recurrent frequent topology variations in a better way. But, such location-oriented routing protocols contain some restrictions. The node’s connectivity is not considered in the routing method that is amplified in insufficient cases.

For addressing such issue, numerous new routing methods were suggested. Few utilize Road Side Units (RSU) for making statistics on the road situations, like road connectivity traffic volume, and so on. In general terms, the prevailing routing schemes are divided into a couple of groups depending on their route-finding procedure and substructure [9]. But every group has particular restrictions in several aspects. Particularly, linear routing schemes or the non-hierarchical executions degrade in very dense network systems in relation to transmission and computational cost. Therefore, cluster related routing protocols are presented to optimal manage vehicles to groups depending on their similarity, targeting to minimize the computational overhead through choosing a maximum sum of clusters [10]. Distinct protocols leverage several variables for the selection of cluster head (CH) and cluster members in the literature, like velocity, travel time, ID, link reliability, route confidence level, degree of neighbors connectivity, average link lifetime, propagation delay, average relative velocity, total quantity of vehicles to pursue, and so on.

This paper presents an enhanced metaheuristics based clustering with multihop routing technique for lifetime maximization (EMCMHR-LM) in VANET. The presented EMCMHR-LM model involves the procedure of arranging clusters, cluster head (CH) selection, and route selection appropriate for VANETs. The presented EMCMHR-LM model uses slime moldoptimization based clustering (SMO-C) technique to group the vehicles into clusters. Besides, an enhanced wild horse optimization based multihop routing (EWHO-MHR) protocol by the optimization of network parameters. The presented EMCMHR-LM model is simulated using Network Simulator (NS3) tool.

2  Related Works

ChandrenMuniyandi et al. [11] presented an enhanced harmony search optimization (EHSO) system which assumes the outline of the OLSR variables by pairing 2 phases, a course for optimization take place by the EHSO methodology depends on implanting 2 famous selection techniques in its storage, like, tournament selection roulette and wheel selection. In [12], a hybrid clustering system is suggested that complies with the context related geographic related clustering techniques. The hybrid clustering minimizes the traffic and controls overhead in the networks. Secondly, the destination aware routing protocol is suggested for inter clustering routing that enhances the complete packet delivery ratio and minimizes the endwise postponement. In [13], a clustering routing protocol, termed QMM-VANET, that assumes Quality of Service (QoS) needs, the distrust value variables, and mobility restraints, is suggested. This protocol indicates a dependable and standard cluster and rises the durability and connectedness at the time of transmissions. Javadpour et al. [14] decrease the impacts of unexpected issues on the best track for replacing the broken link or path. A QoSR having Particle Swarm Optimization (QoSR-PSO) is utilized in this work to enhance QoSs in vehicular ad hoc network systems. By shaping the attitude of a set of particles, particle swarm optimization methods discover the superior feasible resolution to the issues. Ardakani [15] developed a cluster related routing protocol for VANET using an innovative addressing scheme in that every node receives an address respective to their mobility paradigm. Hamming distance approach is utilized after making the separation of the network in an address centric mode. Sangeetha et al. [16] suggested an unclear genetic optimization approach for VANETs. The node clustering, base station movement, and cluster head selection is depends on unclear sense. Moreover, genetic method is utilized for finding the superior feasible routing route.

The researchers in [17] suggested a cluster related method for enhancing data communication. In this algorithm, an original technique is recommended for selecting the CH. The CH selection method is carried out in 3 stages, initial stage is normal CH selection, next stage is cluster leaving and final stage is cluster merging. Afterward selecting the CH, the routing path must be accomplished on the basis of the link quality that can be measured with the help of the link life period. In [18], a hierarchical method was devised for managing huge VANETs by offering superior mobility management. The creation of manifold overlay clusters from huge VANETs leveraging k-means method is main feature of this technique. Moreover, an addressing infrastructure was launched by 2 data registers.

3  The Proposed Model

In this study, a new EMCMHR-LM model was enhanced to resolve scalability issues and increase lifetime of VANET. The presented EMCMHR-LM model involves the procedure of arranging clusters, CH selection, and route selection appropriate for VANETs. At the initial stage, the presented EMCMHR-LM model uses SMO-C technique to group the vehicles into clusters. In addition, the WHO-MHR protocol has been developed by the optimization of network parameters. Fig. 1 depicts the overall process of EMCMHR-LM technique.

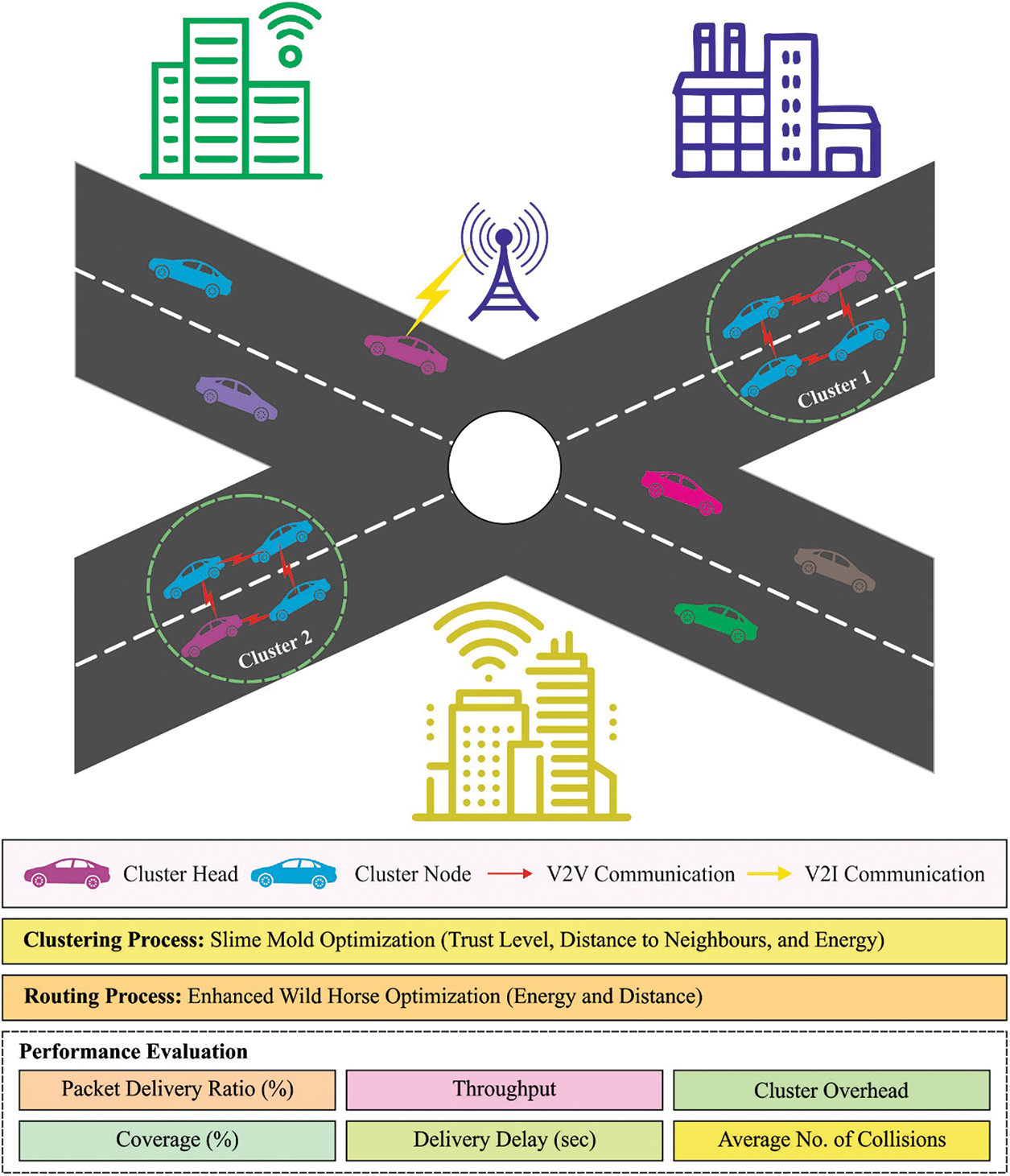
Figure 1: Overall process of EMCMHR-LM technique

3.1 Overview of SMO Algorithm

The SMO algorithm has been developed depending upon the oscillation mode of slime mould in nature. Consider N slime mould is existing in the searching space with lower boundary (LB) and upper boundary (UB). Next, i-th slime moulds located in d-th dimension are formulated by Xi=(xi1,xi2,…,xid),∀i∈[1,N], and fitness (odor) of i-th slime is characterized by f(Xi),∀i=[1,N]. Hence, the fitness and position of N slime mould at t time is formulated by using Eq. (1):

X(t)=[x11x12⋯x1dx21x22⋯x2d⋮⋮⋮⋮xN1xN2⋯xNd]=[X1X2⋮XN](1)

f(X)=[f(X1),f(X2),…,f(XN)](2)

The location of slime mould for the second iteration (t+1) in SMO algorithm can be upgraded as follows [19]:

Xi(t+1)={ XLB(t)+Vb(W⋅XA(t)−XB(t))r1≥δ and r2<piVc⋅Xi(t)r1≥δ and r2≥pi,rand⋅ (UB---LB)+LBr1<δ                                         ∀i∈[ 1,N ]  (3)

In Eq. (3), The local optimal individual for the existing iteration is represented as XLB, randomly pooled slime mould from current population is denoted by XA and XB, Windicates the weight factor, Vb and Vc denotes the arbitrary velocity. The r1 and r2 are the two arbitrary values lie within [0,1]. δrepresent the probability of slime mould that initialized to an arbitrary searching position that is set to 0.03, piindicates the thresholding value of i-th slime moulds that assist in choosing the slime mould location with the optimal individuals as follows:

pi=tanh|f(Xi)−fGB|,∀i∈[1,N](4)

In Eq. (4), f(Xi)represent the fitness value of i-th slime moulds Xi, and the global optimal fitness value fGB is assessed by the following equation of the global optimal location XGB.

fGB=f(XGB)(5)

Next, the weight W for N slime moulds in an existing iteration t can be described by the Eq. (6):

W(SortIndf(i))={1+rand⋅log⁡(fLB−f(Xi)fLB−fLW+1)1≤i≤N21---rand.log⁡(fLB−f(Xi)fLB−fLW+1)N2<i≤N(6)

Let rand be an arbitrary value lies within [0,1],fLB indicates the local best fitness and the local worst fitness value is fLW. The fLB and fLW is defined from the fitness value f. For a minimization problem, sort the fitness value in ascending order as:

[Sortf,SortIndf]=sort(f)(7)

The local best individual XLB and local best fitness fLB are extracted by:

fLB=f(Sortf(1))(8)

XLB=X(SortIndf(1))(9)

The local worst fitness fLW is extracted by:

fLW=f(Sortf(N))(10)

The Vb and Vc indicates the arbitrary velocity selected from the uniform distribution [−b,b] and [−c,c]. The b and c for the iteration t are selected by:

b=arctanh(−(tT)+1)(11)

c=1−tT(12)

where the maximal iteration refers to T.

3.2 Process Involved in SMO-C Technique

The SMO-C algorithm obtains a fitness function using three input variables namely energy for CH selection, trust level, and distance to neighbors.

Distance to neighbor: It is applicable for selecting CH with minimal distance amongst neighboring nodes. In the intra-cluster transmission technique, energy consumption of sensors to CH transmission. After the neighbor node distance is minimized, subsequently the energy of intracluster transmission is minimalized correspondingly.

Objective 1: Minimize

f1=∑j=1m1lj(∑i=1ljdis(CHj,si))(13)

Trust factor (TF): Initially, each node is specified that TF is one. The TF value is reduced through anomalous prediction method while the node process the abnormal tasks and such nodes are named malicious nodes.

Objective 2: Maximize

f2=∑j=1m1m(TFj)(14)

Energy: It is amount of energy expended as CH to RE of CH. When a CH consumes less energy as sensing, process, and also transmission process with high RE is gathered of low energy ratio. Therefore, lower as energy ratio, the CH selection develops further feasible.

Objective 3: Minimize

f3=∑j=1mEc(CHj)ER(CHj)(15)

In the proposed SMO-C method, it is crucial for decreasing the linear integration of objective function. Thus, the possible energy function of SMO-C algorithm is implemented by:

MinimizePotientialenergyfunction=α1×f1+α2×f2+α3×f3(16)

Here α1+α2+α3=1,α2≥(α1+α3).Also0<f1,f2,f3<1.

3.3 Steps Involved in EWHO-MHR Technique

In this study, the EWHO-MHR technique has been introduced to select optimal routes [20,21]. The WHO method is a Meta-heuristic swarm-based approach stimulated by the social behavior of horses [20], namely mating, grazing, domination, and leadership hierarchy. The WHO approach comprises five discrete steps, as follows: when G groups and N individuals exist, the number of leaders is G and the number of non-leaders (foals and mares) is N−G. The proportion of stallions is determined as PS, that is G/N. As previously mentioned, most foals spent a lifetime grazing nearby their group. To simulate the grazing stage, we consider that the stallion location existed in the grazing area center. To enable other individuals to move, the following formula is used. Fig. 2 depicts the flowchart of WHO technique.

XG,ji=2Zcos⁡(2πRZ)×(StallionG,j−XG,ji)+StallionG,j(17)

In Eq. (17), position of the i-th group member and stallion in the j-th group can be represented as XG,ji and StallionG,j, correspondingly, Rrefers to random number that lies within the range of [−2, 2], and Z indicates an adoptive variable calculated as follows:

P=R→1<TDR,IDX=(P==0),Z=R2ΘIDX+R→3Θ(∼IDX)(18)

Let P be a vector comprising 0 and 1, and their dimension equivalents to the dimensional problem, R→1 and R→3 represent arbitrary vector ranges from 0 and 1, and R2 denotes a random number ranging from 0 and 1. TDR signifies a linear diminishing variable calculated as follows.

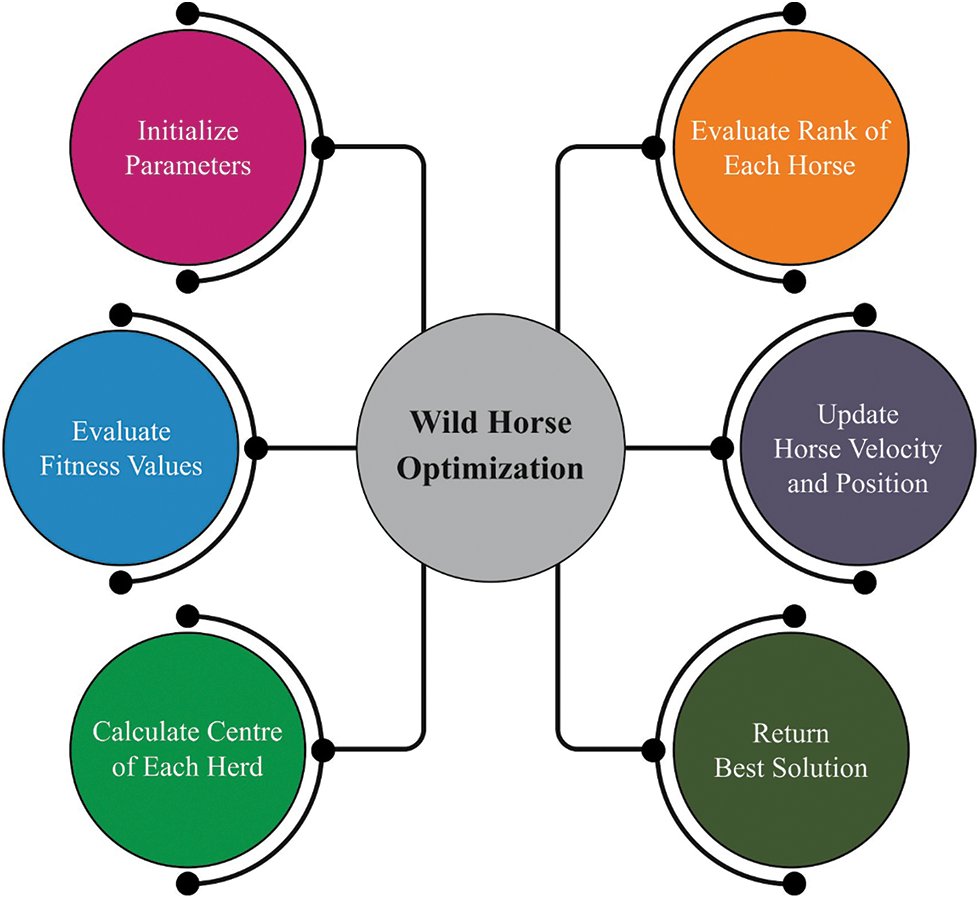
Figure 2: Flowchart of WHO technique

TDR=1−tT(19)

In Eq. (19) tand T denote the present and maximal iterations, correspondingly. As previously mentioned, the unique behavior of horses compared to other animals is splitting foals from the original group prior to the mating and reaching puberty. The following formula is used to simulate the behavior of mating between horses:

XG,kp=Crossover(XG,i′qXG,jz),i≠j≠k,q=z=end(20)

Crossover=Mean

In Eq. (20), the position of horse p in group can be represented by kXG,kp, i.e., formed by position of horse z in group j and horse q in group i. In the simple WHO, the possibility of crossover is fixed as a constant called PC. The group leader (stallion) leads other group members to a convenient location (waterhole). Also, Group leader (stallion) competes for the waterhole, which leads the dominant group to use the waterhole initially. To simulate this behavior, the following formula is used:

Stallion¯G,j={2Zcos⁡(2πRZ)×(WH−StallionG,j)+WHifrand>0.52Zcos⁡(2πRZ)×(WH−StallionG,j)−WHifrand≤0.5(21)

In Eq. (21), the candidate position and the current leadership position in the jth group are denoted as Stallion¯G,j and StallionG,j, correspondingly, WH stands for the location of waterhole. In the beginning, leaders are designated in a random fashion. Next, leaders are designated on the basis of fitness value. The following formula is used to simulate the exchange between leader positions and other individuals:

StallionG,j={XG,ji,iff(XG,ji)<f(StallionG,j)StallionG,i,iff(XG,ji)≥f(StallionG,j)(22)

In Eq. (22), the fitness values of foal and stallion are characterized by f(XG,ji) and f(StallionG,j), correspondingly. The dynamic weight approach makes use of EWHO algorithm and is beneficial to finding a global optimum solution once they are brought into algorithm [21]. Consequently, to assist the stallion to find the best waterhole, a dynamic weight is added to the waterhole in the initial formulation of Eq. (21). In the following, the modified formula and weight are measured:

w={wmin+(wmax−wmin)×f(t)i−f(t)minf(t)avg−f(t)min,iff(t)i≤f(t)avgwmax,iff(t)i>f(t)avg(23)

Stallion¯G,j=2Zcos⁡(2πRZ)×(WH−StallionG,j)+w×WH(24)

From the above equations, the upper and lower boundary values are denoted as wmin and wmax correspondingly, the fitness value of the current stallion at t-th iteration is indicated byf(t)i, the average fitness value of each stallion is denoted asf(t)avg, and the minimum fitness value of the population is represented as f(t)min.

In order to define a set of routes utilizing the EWHO-MHR model, the given function is applied to define the subsequent hop to Base Station (BS) as follows:

f(x)={i,for which|(ik−Xifj)| is minimum,∀i1≤i≤k(25)

The aim is to define a set of routes in CH to BS using an Fitness Function (FF) comprising 2 variables such as distance and energy. At first, the Residual Energy (RE) of next-hop node is established and the nodes with the highest energy are provided as relay nodes. For data transmission, the source node transmits to relay node that further transfer to BS through inter CH. Hence, the node with greater RE is provided as next-hop node. The f1 initial sub-objectives are provided as follows:

f1=ECH(26)

In Eq. (22), Euclidean distance can be employed to determine the distance between CH to BS. The reduction of energy dissipation is based largely on the broadcasting distance. By using a minimal distance, the energy is retained considerable. When the distance is enhanced, additional amount of energy is consumed. Consequently, the nodes with lower distances are desired for a relay node. Therefore, the next sub-objectives using distance is f2 can be formulated by:

f2=1∑i=1mdis(CHi,NH)+dis(NH,BS)(27)

The abovementioned sub-objectives are regarded as to FF as given under where α1 and α2 represent the weight allotted for each sub-objective.

Fitness=α1(f1)+α2(f2),where∑i=12αi=1αiε(0,1);(28)

4  Experimental Validation

The proposed model is simulated using NS3 tool. The performance validation of the EMCMHR-LM model is tested using distinct aspects. Tab. 1 and Fig. 3 report a detailed packet delivery ratio (PDR) examination of the EMCMHR-LM model with recent models under varying vehicle counts [22–24]. The experimental values implied that the EMCMHR-LM model has resulted in maximum PDR values. For instance, with 50 vehicles per km2, the EMCMHR-LM model has obtained increased PDR of 20.90% whereas DACRS, CBCLR, AODV-CV, CBR, and DBR models have obtained reduced PDR of 14.69%, 14%, 16.30%, 14.46%, and 10.78% respectively. Meanwhile, with 75 vehicles per km2, the EMCMHR-LM model has reached maximum PDR of 59.56% whereas DACRS, CBCLR, AODV-CV, CBR, and DBR models have accomplished minimal PDR of 56.11%, 50.82%, 37.93%, 30.34%, and 28.73% respectively.

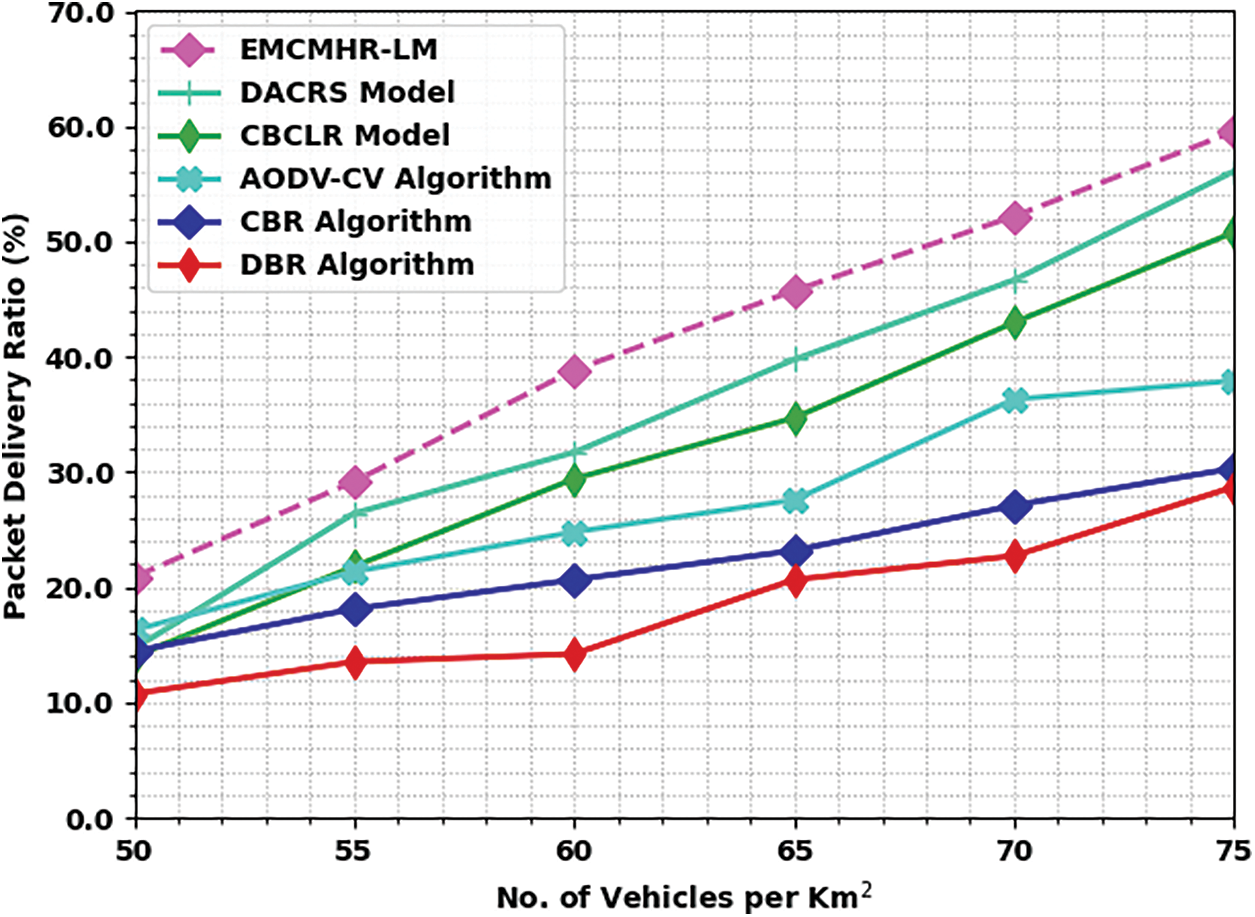
Figure 3: PDR analysis of EMCMHR-LM technique under varying vehicle count

Tab. 2 and Fig. 4 define a detailed throughput (THPT) inspection of the EMCMHR-LM approach with recent models under varying vehicle counts. The experimental values implied that the EMCMHR-LM system has resulted in maximal THPT values. For instance, with 50 vehicles per km2, the EMCMHR-LM algorithm has obtained higher THPT of 32 whereas DACRS, CBCLR, AODV-CV, CBR, and DBR systems have obtained decreased THPT of 30, 27, 25, 27, and 23 correspondingly. In the meantime, with 75 vehicles per km2, the EMCMHR-LM algorithm has reached maximal THPT of 188 whereas DACRS, CBCLR, AODV-CV, CBR, and DBR methodologies have accomplished minimal THPT of 178, 169, 141, 121, and 112 correspondingly.

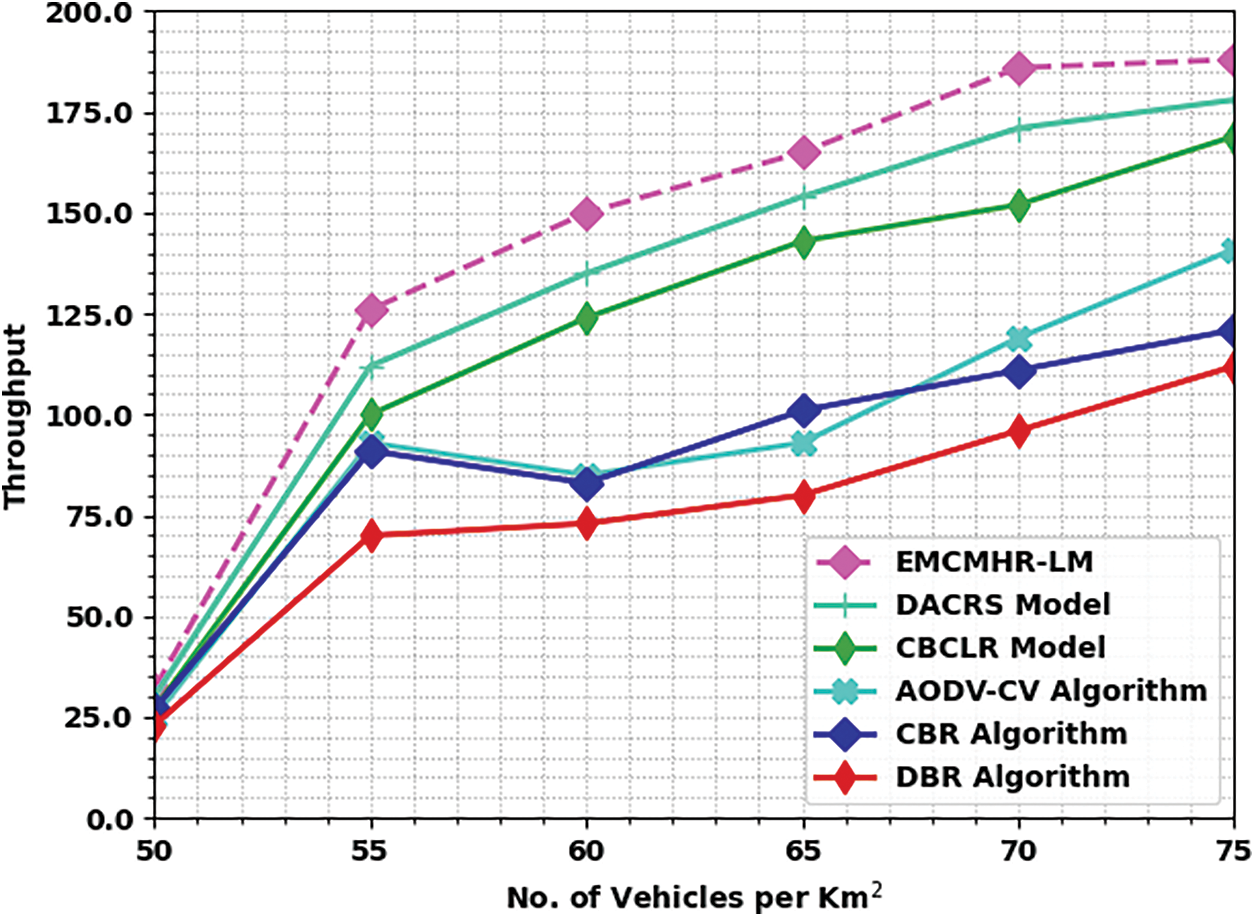
Figure 4: Throughput analysis of EMCMHR-LM algorithm under varying vehicle count

A detailed cluster overhead (COH) inspection of the EMCMHR-LM model with recent models is made in Tab. 3 and Fig. 5. The experimental outcomes portrayed that the EMCMHR-LM model has obtained lower COH over other models. For instance, with 50 vehicles per km2, the EMCMHR-LM model has resulted in least COH of 13 whereas DACRS, CBCLR, AODV-CV, CBR, and DBR models have demonstrated increased COH of 22, 26, 31, 31, and 45 respectively.

Figure 5: COH analysis of EMCMHR-LM algorithm under varying vehicle count

Also, with 75 vehicles per km2, the EMCMHR-LM system has resulted in least COH of 77 whereas DACRS, CBCLR, AODV-CV, CBR, and DBR techniques have outperformed higher COH of 109, 132, 140, 152, and 210 correspondingly. Tab. 4 and Fig. 6 determines a detailed coverage examination of the EMCMHR-LM approach with recent methods under varying vehicle count. The experimental values referred that the EMCMHR-LM method has resulted in higher coverage values. For instance, with 50 vehicles per km2, the EMCMHR-LM methodology has obtained increased coverage of 28.74% whereas DACRS, CBCLR, AODV-CV, CBR, and DBR systems have obtained decreased coverage of 21.39%, 19.55%, 15.87%, 15.87%, and 8.52% correspondingly. Besides, with 75 vehicles per km2, the EMCMHR-LM algorithm has reached increased coverage of 93.43% whereas DACRS, CBCLR, AODV-CV, CBR, and DBR approaches have accomplished minimal coverage of 89.02%, 80.94%, 82.41%, 70.28%, and 60.72% correspondingly.

Figure 6: Coverage analysis of EMCMHR-LM technique under varying vehicle count

A detailed delivery delay (DD) analysis of the EMCMHR-LM technique with recent methods is made in Tab. 5 and Fig. 7. The experimental outcomes outperformed that the EMCMHR-LM approach has obtained lower DD over other methods. For instance, with 50 vehicles per km2, the EMCMHR-LM approach has resulted in minimal DD of 15 s whereas DACRS, CBCLR, AODV-CV, CBR, and DBR algorithms have demonstrated superior DD of 19, 21, 17, 19 and 22 s correspondingly. Besides, with 75 vehicles per km2, the EMCMHR-LM algorithm has resulted in lower DD of 15 s whereas DACRS, CBCLR, AODV-CV, CBR, and DBR models have depicted higher DD of 19, 21, 17, 19 and 22 s correspondingly.

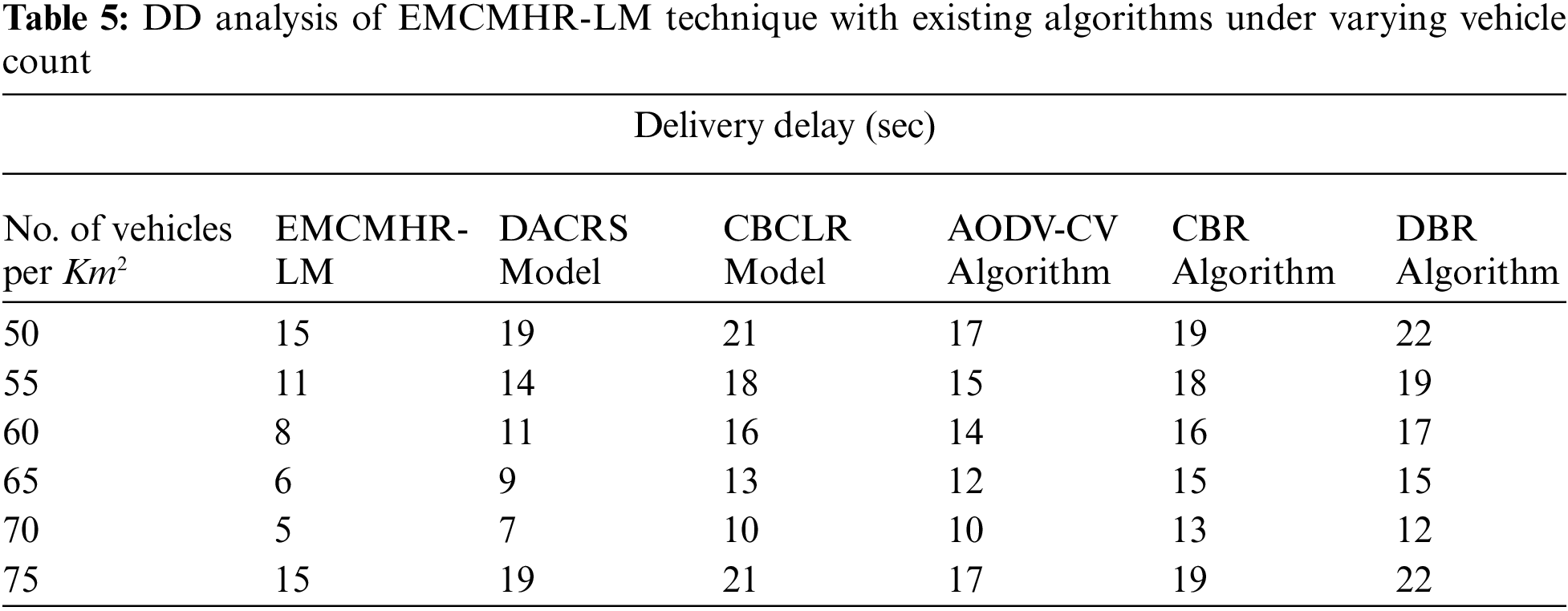
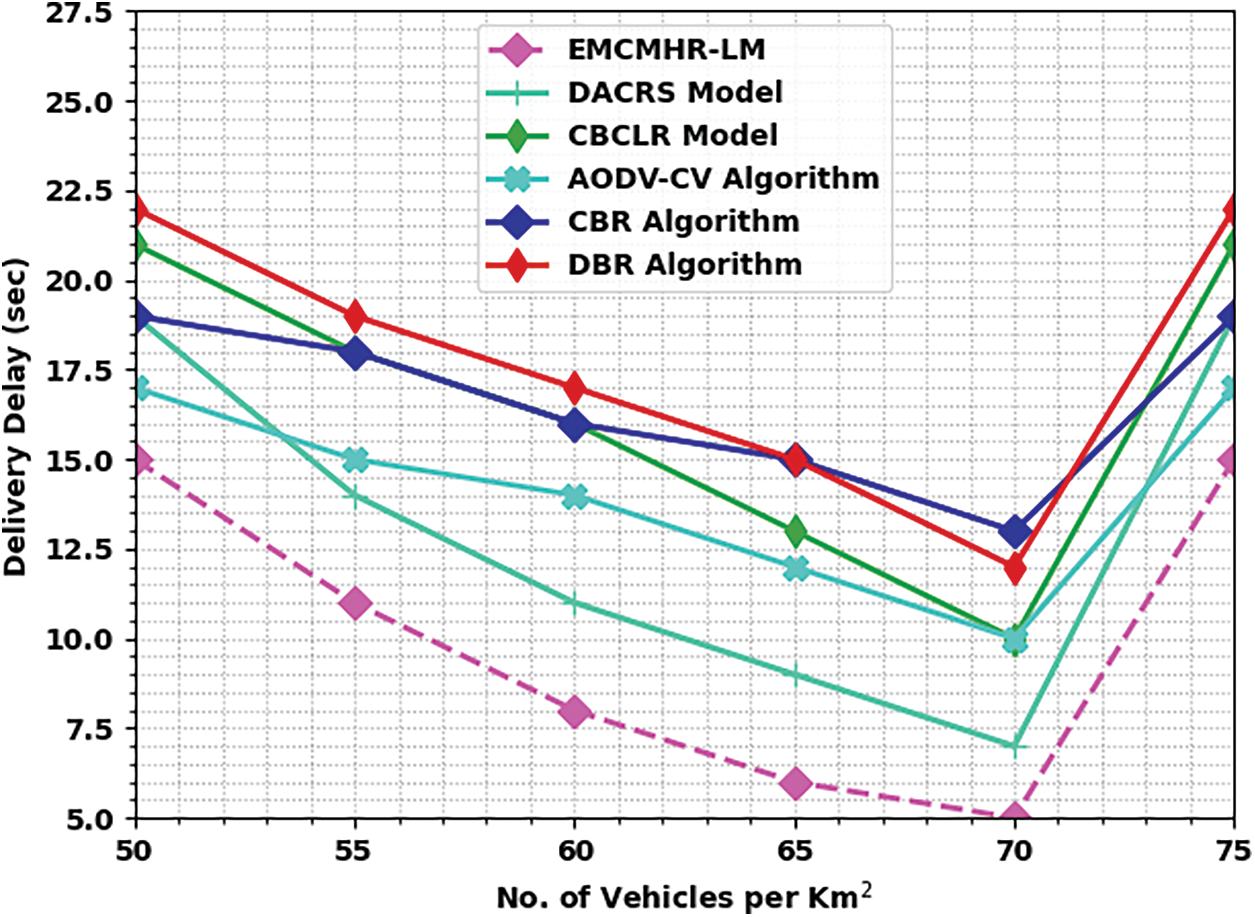
Figure 7: DD analysis of EMCMHR-LM algorithm under varying vehicle count

A detailed average number of collisions (ANOC) investigation of the EMCMHR-LM methodology with recent methods is made in Tab. 6 and Fig. 8. The experimental outcomes exhibited that the EMCMHR-LM model has obtained lesser ANOC over other models.

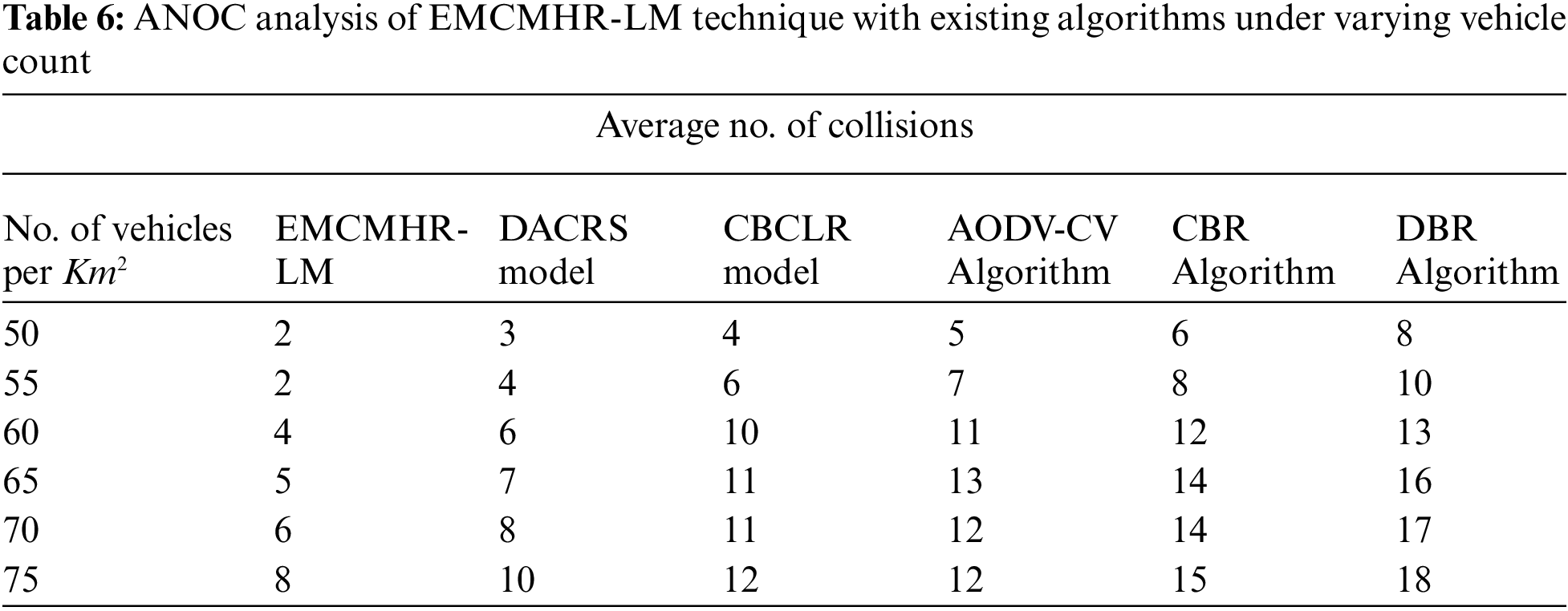
Figure 8: ANOC analysis of EMCMHR-LM technique under varying vehicle count

For instance, with 50 vehicles per km2, the EMCMHR-LM technique has resulted in minimal ANOC of 2 whereas DACRS, CBCLR, AODV-CV, CBR, and DBR systems have demonstrated increased ANOC of 3, 4, 5, 6, and 8 respectively. Followed by, with 75 vehicles per km2, the EMCMHR-LM approach has resulted in minimum ANOC of 8 whereas DACRS, CBCLR, AODV-CV, CBR, and DBR algorithms have depicted superior ANOC of 10, 12, 12, 15, and 18 correspondingly. From the detailed experimental analysis, it is apparent that the EMCMHR-LM model has shown better results than other models.

5  Conclusion

In this study, a new EMCMHR-LM model was enhanced to resolve scalability issues and increase lifetime of VANET. The presented EMCMHR-LM model involves the procedure of arranging clusters, CH selection, and route selection appropriate for VANETs. At the initial stage, the presented EMCMHR-LM model uses SMO-C technique to group the vehicles into clusters. In addition, the EWHO-MHR protocol has been developed by the optimization of network parameters. The presented EMCMHR-LM model is simulated using NS3 tool and the simulation outcomes reported the advanced performance of the proposed EMCMHR-LM technique over the other models. Thus, the EMCMHR-LM model can be utilized for effectual network performance in VANET. In future, privacy preserving blockchain enabled secure data transmission protocol can be designed for VANET.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Elhoseny and K. Shankar, “Energy efficient optimal routing for communication in VANETs via clustering model,” in Proc. Emerging Technologies for Connected Internet of Vehicles and Intelligent Transportation System Networks, Switzerland, Springer, Cham, pp. 1–14, 2020. [Google Scholar]

 2.  B. Singh, P. Kavitha, R. Regin, K. Praghash, S. Sujatha et al., “Optimized node clustering based on received signal strength with particle ordered-filter routing used in VANET,” Webology, vol. 17, no. 2, pp. 1–12, 2020. [Google Scholar]

 3.  Z. Khan, P. Fan, S. Fang and F. Abbas, “An unsupervised cluster-based VANET-oriented evolving graph (CVoEG) model and associated reliable routing scheme,” IEEE Transactions on Intelligent Transportation Systems, vol. 20, no. 10, pp. 3844–3859, 2019. [Google Scholar]

 4.  W. Qi, B. Landfeldt, Q. Song, L. Guo and A. Jamalipour, “Traffic differentiated clustering routing in DSRC and C-V2X hybrid vehicular networks,” IEEE Transactions on Vehicular Technology, vol. 69, no. 7, pp. 7723–7734, 2020. [Google Scholar]

 5.  R. Kaur, R. K. Ramachandran, R. Doss and L. Pan, “The importance of selecting clustering parameters in VANETs: A survey,” Computer Science Review, vol. 40, pp. 100392, 2021. [Google Scholar]

 6.  S. Yogarayan, S. F. A. Razak, A. Azman, M. F. A. Abdullah, S. Z. Ibrahim et al., “A review of routing protocols for vehicular ad-hoc networks (VANETs),” in Proc. 8th Int. Conf. on Information and Communication Technology (ICoICT), IEEE, Yogyakarta, Indonesia, pp. 1–7, 2020. [Google Scholar]

 7.  U. A. Khan and S. S. Lee, “Multi-layer problems and solutions in VANETs: A review,” Electronics, vol. 8, no. 2, pp. 204, 2019. [Google Scholar]

 8.  A. Katiyar, D. Singh and R. S. Yadav, “State-of-the-art approach to clustering protocols in VANET: A survey,” Wireless Networks, vol. 26, no. 7, pp. 5307–5336, 2020. [Google Scholar]

 9.  K. Kandali, L. Bennis and H. Bennis, “A new hybrid routing protocol using a modified K-means clustering algorithm and continuous hopfield network for VANET,” IEEE Access, vol. 9, pp. 47169–47183, 2021. [Google Scholar]

10. J. Cheng, G. Yuan, M. Zhou, S. Gao, Z. Huang et al., “A Connectivity-prediction-based dynamic clustering model for VANET in an urban scene,” IEEE Internet of Things Journal, vol. 7, no. 9, pp. 8410–8418, 2020. [Google Scholar]

11. R. Chandren Muniyandi, M. K. Hasan, M. R. Hammoodi and A. Maroosi, “An improved harmony search algorithm for proactive routing protocol in VANET,” Journal of Advanced Transportation, vol. 2021, pp. 1–14, 2021. [Google Scholar]

12. K. Aravindhan and C. Dhas, “Destination-aware context-based routing protocol with hybrid soft computing cluster algorithm for VANET,” Soft Computing, vol. 23, no. 8, pp. 2499–2507, 2019. [Google Scholar]

13. H. Fatemidokht and M. K. Rafsanjani, “QMM-VANET: An efficient clustering algorithm based on QoS and monitoring of malicious vehicles in vehicular ad hoc networks,” Journal of Systems and Software, vol. 165, pp. 110561, 2020. [Google Scholar]

14. A. Javadpour, S. Rezaei, A. K. Sangaiah, A. Slowik and S. Mahmoodi Khaniabadi, “Enhancement in quality of routing service using metaheuristic PSO algorithm in VANET networks,” Soft Computing, Early Access, pp. 1–12, 2021. [Google Scholar]

15. S. P. Ardakani, “ACR: A cluster-based routing protocol for VANET,” International Journal of Wireless & Mobile Networks (IJWMN), vol. 10, no. 2, pp. 39–53, 2018. [Google Scholar]

16. M. Sangeetha, T. Vijayan, N. A. Unnikrishnan, G. Kalanandhini and R. N. Shaw, “Genetic fuzzy based VANET routing algorithm for better efficiency,” in Proc. Int. Conf. on Electrical and Electronics Engineering, Springer, Singapore, pp. 669–677, 2022. [Google Scholar]

17. V. G. Krishnan and N. S. Ram, “A novel approach to select cluster head and optimising the data transmission in VANET,” International Journal of Advanced Intelligence Paradigms, vol. 21, no. 3–4, pp. 235–246, 2022. [Google Scholar]

18. P. K. Pandey, V. Kansal and A. Swaroop, “OCSR: Overlapped cluster-based scalable routing approach for vehicular ad hoc networks (VANETs),” Wireless Communications and Mobile Computing, vol. 2022, pp. 1–18, 2022. [Google Scholar]

19. R. Zheng, H. Jia, L. Abualigah, Q. Liu and S. Wang, “Deep ensemble of slime mold algorithm and arithmetic optimization algorithm for global optimization,” Processes, vol. 9, no. 10, pp. 1774, 2021. [Google Scholar]

20. I. Naruei and F. Keynia, “Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems,” Engineering with Computers, Early Access, pp. 1–32, 2021. [Google Scholar]

21. R. Zheng, A. G. Hussien, H. M. Jia, L. Abualigah, S. Wang et al., “An improved wild horse optimizer for solving optimization problems,” Mathematics, vol. 10, no. 8, pp. 1311–1324, 2022. [Google Scholar]

22. B. Elira, K. P. Keerthana and K. Balaji, “Clustering scheme and destination aware context based routing protocol for VANET,” International Journal of Intelligent Networks, vol. 2, pp. 148–155, 2021. [Google Scholar]

23. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

24. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A Multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]