Submit

Login Login

Register Register

Home/ Journals/ CMC/ Vol.74, No.1, 2023/ 10.32604/cmc.2023.031871

Table of Content

iconOpen Access

ARTICLE

Stochastic Investigations for the Fractional Vector-Host Diseased Based Saturated Function of Treatment Model

Thongchai Botmart1, Qusain Hiader2, Zulqurnain Sabir3, Muhammad Asif Zahoor Raja4, Wajaree Weera1,*

1 Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand
2 Department of Mathematics, University of Gujrat, Gujrat, 50700, Pakistan
3 Department of Mathematics and Statistics, Hazara University, Mansehra, 21120, Pakistan
4 Future Technology Research Center, National Yunlin University of Science and Technology, 123 University Road, Section 3, Douliou, 64002, Yunlin, Taiwan

* Corresponding Author: Wajaree Weera. Email: email

Computers, Materials & Continua 2023, 74(1), 559-573. https://doi.org/10.32604/cmc.2023.031871

Received 28 April 2022; Accepted 20 June 2022; Issue published 22 September 2022

Abstract

The goal of this research is to introduce the simulation studies of the vector-host disease nonlinear system (VHDNS) along with the numerical treatment of artificial neural networks (ANNs) techniques supported by Levenberg-Marquardt backpropagation (LMQBP), known as ANNs-LMQBP. This mechanism is physically appropriate, where the number of infected people is increasing along with the limited health services. Furthermore, the biological effects have fading memories and exhibit transition behavior. Initially, the model is developed by considering the two and three categories for the humans and the vector species. The VHDNS is constructed with five classes, susceptible humans , infected humans , recovered humans , infected vectors , and susceptible vector based system of the fractional-order nonlinear ordinary differential equations. To solve the number of variations of the VHDNS, the numerical simulations are performed using the stochastic ANNs-LMQBP. The achieved numerical solutions for solving the VHDNS using the stochastic ANNs-LMQBP have been described for training, verifying, and testing data to decrease the mean square error (MSE). An extensive analysis is provided using the correlation studies, MSE, error histograms (EHs), state transitions (STs), and regression to observe the accuracy, efficiency, expertise, and aptitude of the computing ANNs-LMQBP.

Keywords

1  Introduction

Human illnesses due to infectious pathogenic organisms are referred to the vector-borne diseases (VBDs), such as parasitic infections, viruses, and bacteria. Pathogens are transferred between humans or in some cases, from animals to humans via vectors. Mosquitoes, flies, insects, ticks, and snails carrying pests are the most common vectors. The VBDs are typically found in tropical and subtropical areas, particularly in such areas, where safe drinking water and sanitary are limited. The VBDs are changeable and measured as a dangerous disease, accounting for around 700,000 deaths because of vector-borne pathogenic illnesses, like leishmaniasis, dengue, schistosomiasis, Trypanosoma, cryptosporidiosis, yellow kind of fever, and trichinosis [1]. Based on the reports of WHO, 231 million declared variants of malaria were enlisted four centuries ago, culminating in 416000 causalities, whereas 228 million people were directly affected by malaria in 2018, which tends to result in 405000 causalities [2]. From 2015 to 16, the Zika epidemic was the susceptible to more than 360000 individuals in various states across the United States [3]. Ross [4] pioneered mathematical analysis of vector-borne diseases by developing the two differential systems for transferring the susceptible densities and afflicted vectors (mosquitoes) as well as hosts (people) to present the fundamental consideration of malaria spread dynamics. The basic model of Ross has been extended by Macdonald [5], who developed the concept of elementary reproduction number, which is described as a secondary case formed by an affected individual. Many researchers have expanded the Ross–Macdonald model to contain the additional features of [6–12]. The modeling system shows the alterations to label the dynamic behavior of secondary vector-borne pathogens, including Chagas disease based on the [13–16].

The computational mathematics approach based on infectious diseases has considered a valuable tool to predict the disease transmission behavior along with the prevention plans for the effective diseases. These models can help with public health preparation and response. To investigate the dynamic behavior based on the numerous vector-host communicable viruses, several fractional order systems using the standard nonlinear dynamical systems have been investigated to develop a time-dependent transmitting model for analyzing the dynamic nature of VBD [17]. Khan et al. [18] investigated the dynamic Leptospirosis disease behavior like a saturated estimated occurrence. The dictating tactics and their efficiency for the dengue co-infection system are provided [19] as well as similar kind of mathematical model for diarrhea and malaria co-infection is studied in [20]. The dynamic nature of dengue infection along with the regulator strategies in Pakistan, is presented in [21,22].

The fractional calculus study is assumed to be a general form of traditional calculus and applied as a powertool tool to develop the epidemic systems. In the recent literature, the analytical solutions formulated with fractional operators have a higher level of precision and perfectly match the real statics [23–27]. Currently, the focus of the researchers based on the fractional calculus is Caputo derivatives [28], Caputo-Fabrizio [29], and Atangana-Baleanu-Caputo (ABC) [30]. Based on the fractional order, the ABC operator is to model the actual systems of communicable diseases along with its numerous characteristics [31–37]. The spreading diseases of numerous vector-host designs form a mathematical model, like dengue [38], schistosomiasis [39], zoonotic instinctive leptospirosis [40], Zika [41], and West Nile virus [42]. Furthermore, the authors considered the linear care function on the disease of vector-host communications, which is physiologically unsuitable in circumstances, where the infected grow, and the society lacks adequate health resources. As a result, in this paper, the saturated action features have been used in the vector-host system [43–45]. The purpose of this research is to present the simulation studies of the fractional-order (FO) vector-host disease nonlinear system (VHDNS) along with the numerical treatment of the artificial neural networks (ANNs) techniques supported by Levenberg-Marquardt backpropagation (LMQBP), known as ANNs-LMQBP.

The paper is organized as follows: Section 2 represents the fractional vector host disease system. Section 3 shows the stochastic novel features. Section 4 indicates the proposed procedures based on the ANNs-LVMBP method. Section 5 provides the results, and discussion and the last Section shows the concluding remarks.

2  Fraction Order Vector-Host Disease Differential System

In this section, the dynamic nature of the vector-host disease is presented by indicating the total population of humans Nh(t) and further subdivision is into three distinct classes, namely susceptible humans Sh(t), afflicted humans Ih(t), and healed humans Rh(t) at any time t, so Nh(t)=Ih+Sh+Rh. The enrollment of individuals at a rate of ζh increases the number of individuals of susceptible humans. It is reduced by effective contact with Shγ1Ih1+χ1Ih, where χ1 represents the disease interaction rate among susceptible human to afflicted vector and γ1 is the concentration constant. The natural death rate is ηh and the effective contact rate is Shγ1Ih1+χ1Ih, which generates in the community of infected humans. The natural deaths ηh, the disease associated death rate εh, and κωIh1+νωIh. It seems to be that when I or ω is very small, the diagnosis function coincides with a near-zero value, and when I is very vast, the diagnosis function reaches a finite value limit. Using such a function (treatment) will normally represent the epidemic system, so that it can be included in the evaluation of the present work. The term κν is determined by the maximum supply of healthcare possessions per unit of time, whereas 11+νωIh represents the converse consequences of the infected persons who are delayed for therapies and have a significant effect on virus spread; for more information, see [18]. The people in the recoverable class are produced by the treatment function κωIh1+νωIh, while ηh decreases due to natural death. This variation can be represented by the differential equation and the VHDNS model is mathematically signified as [46]:

{dSh(t)dt=−ζh+Shγ1Ih1+χ1Ih−ηhSh,S0=k1,dIh(t)dt=Shγ1Ih1+χ1Ih−ηhIh−εhIh−κωIh1+νωIh,I0=k2,dRh(t)dt=κωIh1+νωIh−ηhRh.R0=k3.(1)

The vector society is denoted by Nv, and it is separated into two subclasses: Sv susceptible vector and Iv afflicted vector. As a result, Nv=Iv+Sv. The susceptible vector sequence is created by the birth rate v, which is reduced by the contact rate λSvIv1+ρIv and normal death rate v. The contact rate λSvIv1+ρIv generates the afflicted populations, while the natural fatality rate ηv decreases it. This discussion leads to the following differential equation:

{dSv(t)dt=−ζv+λSvIv1+ρIv−ηvSv,S0=k4,dIv(t)dt=λSvIv1+ρIv−ηvSv.I0=k5,(2)

where k1,k2,k3,k4, and k5 be the initial conditions of Eqs. (1) and (2). After combining these two equations, the SIRSI system is obtained as:

{dτSh(t)dtτ=ζh−Shγ1Ih1+χ1Ih−ηhSh,S0=k1,dτIh(t)dtτ=Shγ1Ih1+χ1Ih−ηhIh−εhIh−κωIh1+νωIh,I0=k2,dτRh(t)dtτ=κωIh1+νωIh−ηhRh,R0=k3,dτSv(t)dtτ=ζv−λSvIv1+ρIv−ηvSv,S0=k4,dτIv(t)dtτ=λSvIv1+ρIv−ηvSv.I0=k5.(3)

This system, τ shows the FO derivative of the SIRSI model. In Eq. (3), FO-SIRSI system parameters are denoted by small Greek and English characters. Each model parameter has a particular value, calculated using the actual information given in [46]. Fig. 1 illustrates the visual effects of every phase of the epidemic.

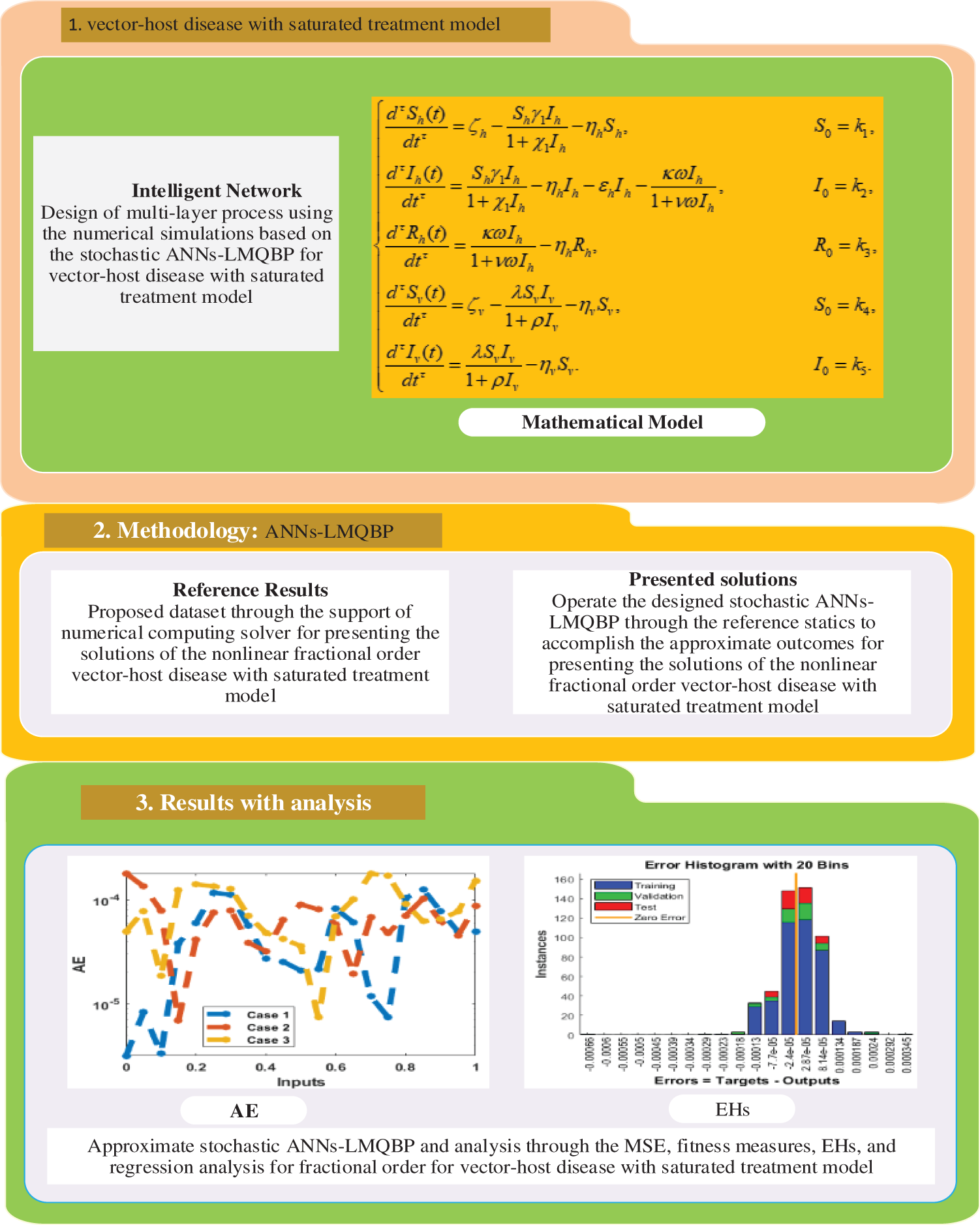
images

Figure 1: Workflow-based fractional-order derivative of the mathematical VHDNS model using the ANNs-LVMBP method

3  Novel Stochastic Solvers Features

The numerical measures through the ANNs-LMQBP are proposed for solving the FO-SIRSI system. The stochastic solvers have been exploited using local and global search efficiencies based on the complicated, singular, and stiff models [47–49]. Few more schemes of the stochastic schemes are third-order nonlinear singular models [50], and fractional-order singular models [51–54]. In this study, the solutions of the fraction order VHDNS based on the SIRSI have been proposed using the ANNs-LMQBP. Recently, stochastic solvers have been presented to solve the fractional dynamical models. Few of them are dynamical nonlinear susceptible infected and quarantine differential model [55], immune-chemotherapeutic treatment for breast cancer [56], nonlinear prey-predator system [57], SIDARTHE COVID-19 pandemic differential model [58], Bagley–Torvik mathematical model [59] and seventh order singular system [60]. It is found that the time FO derivatives have been applied to different conditions in various applications. The FO derivative represents the framework based on remembrance [61]. Few novel features of the ANNs-LMQBP are presented as:

• A preliminary design of its FO-VHDNS is presented based on the nonlinear mathematical form of the SIRSI effects.

• The solutions of the FO-VHDNS system using the nonlinear mathematical form of the SIRSI model have never been presented through the stochastic solvers.

• The numerical stochastic measures based on the ANNs-LMQBP have been presented for the FO-VHDNS using the nonlinear mathematical form of the SIRSI.

• The comparisons of the obtained results through ANNs-LMQBP have been presented with the reference (Adams–Bashforth–Moulton) solutions to authenticate the excellence of stochastic computing solvers.

• The absolute error (AE) in good measures has been achieved for the FO-VHDNS using the nonlinear mathematical form of the SIRSI.

• The reliability and consistency of the developed ANNs-LMQBP for solving the FO-VHDNS system are validated by using the regression, STs, MSE, EHs, and similarity performances

4  Proposed Procedures: ANNs-LVMBP Method

The ANNs-LVMBP scheme is provided in two steps to solve the FO-VHDNS system using the nonlinear mathematical form of the SIRSI model. First the basic procedures of the ANNs-LVMBP operator performances are introduced along with the designed structure of the FO-VHDNS system using the nonlinear mathematical form of the SIRSI model.

Fig. 1 shows the multi-layer performances of the optimization using the stochastic ANNs-LVMBP. The ANNs-LVMBP procedures are assembled in MATLAB through the ‘nftool’ process, with data chosen as 74% for training, 12% for testing, and 14% for authorization.

5  Results and Discussions

The numerical results with three FO-SIRSI cases using the ANNs-LVMBP method are drawn in this section. These cases have been presented by using the variations of the FO to solve the model using the stochastic schemes.

Case 1: Consider the FO-SIRSI model by taking the τ=0.5, ζh=0.0002, γ1=0.000044, χ1=0.003, ηh=0.00020, v=0.4, εh=0.002, κ=0.1, ζv=0.008, λ=0.007, ρ=0.002, ηv=0.2, S0=0.01, I0=0.01, R0=0.01, ω=0.1, S0=0.01and I0=0.01 is given as:

{d0.5Sh(t)dt0.5=0.0002−0.000044ShIh1+0.003Ih−0.00020ShS0=0.01,d0.5Ih(t)dt0.5=0.000044ShIh1+0.003Ih−0.0022Ih−0.01Ih1+0.04IhI0=0.01,d0.5Rh(t)dt0.5=0.01Ih1+0.04Ih−0.00020RhR0=0.01,d0.5Sv(t)dt0.5=0.008−0.007SvIv1+0.002Iv−0.2SvS0=0.01,d0.5Iv(t)dt0.5=0.007SvIv1+0.002Iv−0.2SvI0=0.01.(4)

Case 2: Consider the FO-SIRSI model by taking the τ=0.6, ζh=0.0002, γ1=0.000044, χ1=0.003, ηh=0.00020, v=0.4, εh=0.002, κ=0.1, ζv=0.008, λ=0.007, ρ=0.002, ηv=0.2, S0=0.01, I0=0.01, R0=0.01, ω=0.1, S0=0.01and I0=0.01 is presented as:

{d0.6Sh(t)dt0.6=0.0002−0.000044ShIh1+0.003Ih−0.00020ShS0=0.01,d0.6Ih(t)dt0.6=0.000044ShIh1+0.003Ih−0.00020Ih−0.002Ih−0.01Ih1+0.04IhI0=0.01,d0.6Rh(t)dt0.6=0.01Ih1+0.04Ih−0.00020RhR0=0.01,d0.6Sv(t)dt0.6=0.008−0.007SvIv1+0.002Iv−0.2SvS0=0.01,d0.6Iv(t)dt0.6=0.007SvIv1+0.002Iv−0.2SvI0=0.01.(5)

Case 3: Consider the FO-SIRSI model by taking the τ=0.7, ζh=0.0002, γ1=0.000044, χ1=0.003, ηh=0.00020, v=0.4, εh=0.002, κ=0.1, ζv=0.008, λ=0.007, ρ=0.002, ηv=0.2, S0=0.01, I0=0.01, R0=0.01, ω=0.1, S0=0.01and I0=0.01 is described as:

{d0.7Sh(t)dt0.7=0.0002−0.000044ShIh1+0.003Ih−0.00020ShS0=0.01,d0.7Ih(t)dt0.7=0.000044ShIh1+0.003Ih−0.00020Ih−0.002Ih−0.01Ih1+0.04IhI0=0.01,d0.7Rh(t)dt0.7=0.01Ih1+0.04Ih−0.00020RhR0=0.01,d0.7Sv(t)dt0.7=0.008−0.007SvIv1+0.002Iv−0.2SvS0=0.01,d0.7Iv(t)dt0.7=0.007SvIv1+0.002Iv−0.2SvI0=0.01.(6)

The numerical representations of the FO mathematical bone disease model are discussed using the ANNs-LVMBP method with 15 neurons along with the data selection is chosen as 74%, 12% and 14%, for training, certification, and testing. The structure of the input, hidden, and output neurons are depicted in Fig. 2.

images

Figure 2: Designed ANNs-LVMBP method for VHDNS

The plots are using the ANNs-LVMBP method for the VHDNS model based on the FO-SIRSI are shown in Figs. 3–5. The graphical visualizations are illustrated in Figs. 3 and 4 to investigate the STs best measures. The MSE and STs for training, ideal curves, and confirmation are produced in Fig. 3 to solve the FO-SIRSI system. On behalf of these accomplishments based on the FO-SIRSI are provided at epochs 6, 6, and 6, the derived values are 9.9334e−09, 6.5823e−09, and 8.6883e−09, respectively. The curve values are also provided in Fig. 3 for the VHDNS model based on the FO-SIRSI. These cure performances have been provided as 2.6797e−08 for Case 1, 1.6746e−08 for Case 2, and 3.6855e−08 for Case 3. These visualization tools show the convergence of recommended ANNs-LVMBP for the VHDNS model based on the FO-SIRSI. Fig. 4 shows the results and EHs performances of the FO system. The EHs for cases 1, 2, and 3 are predicted as −2.4e−05, −1.8e−05 and −2.8e−05. The convergence of the model using the complexity, MSE, training, verification, generations, and testing is provided in Tab. 1.

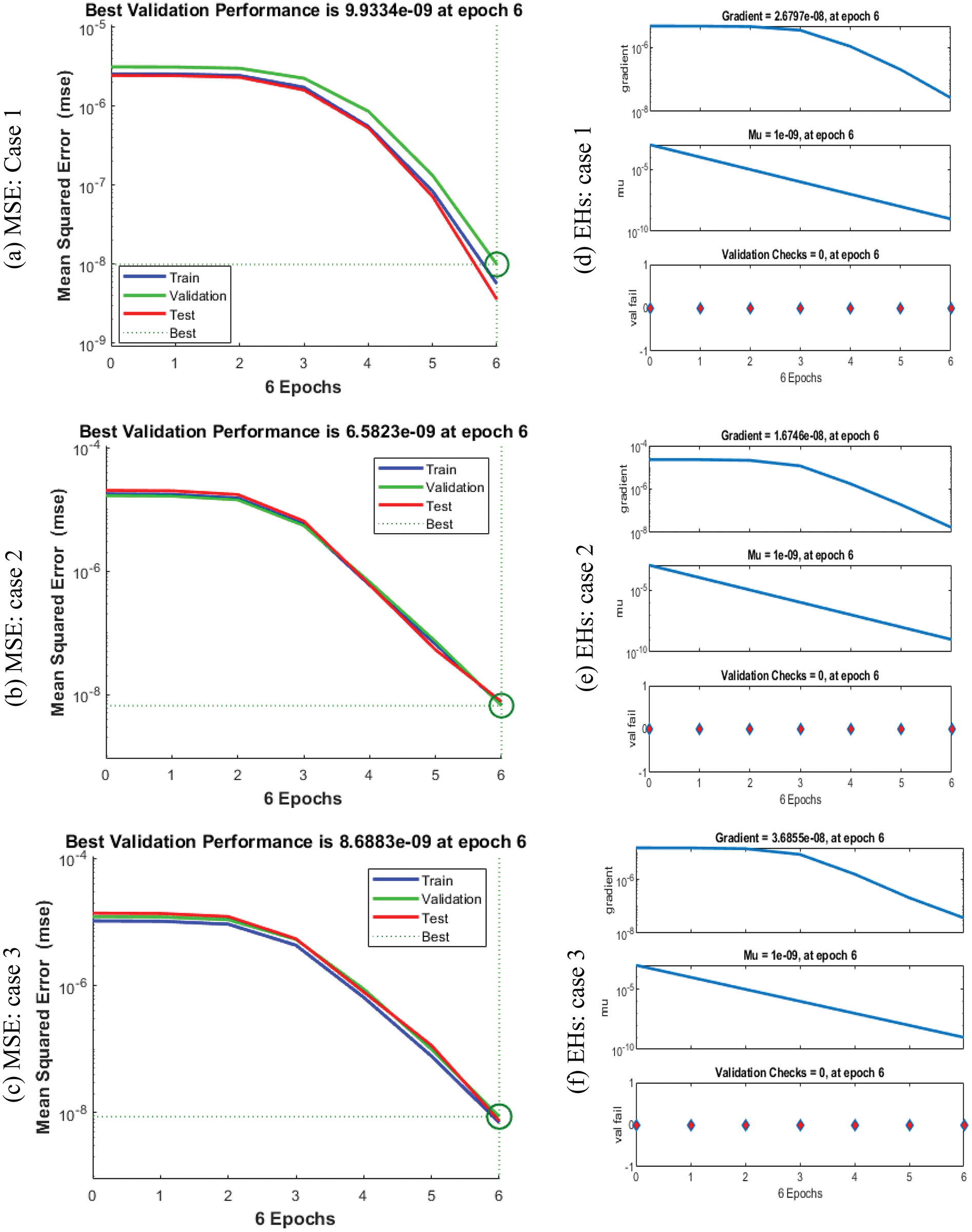
images

Figure 3: MSE and STs performances for the fractional order system

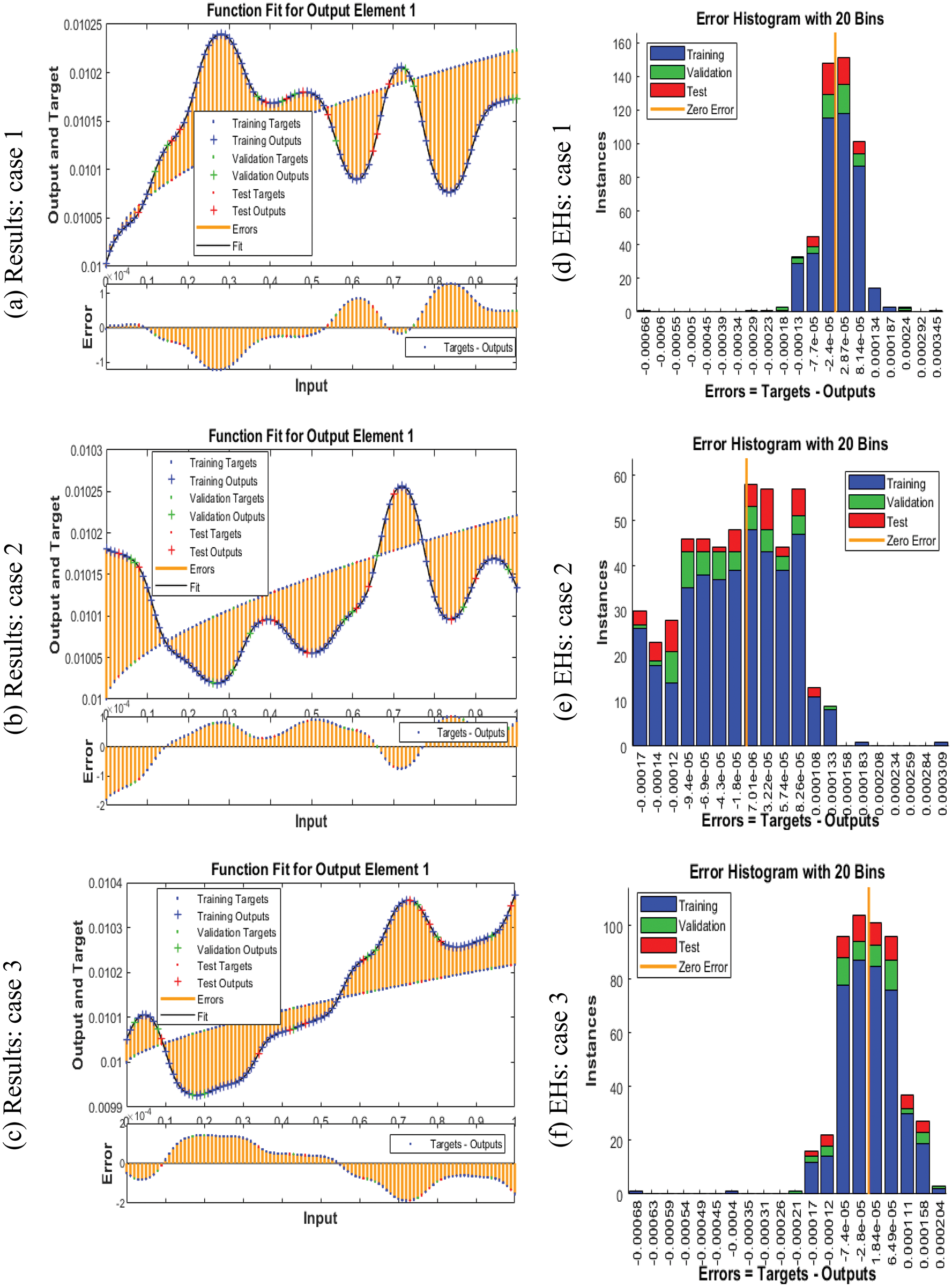
images

Figure 4: Results and EHs performances for the fractional order system

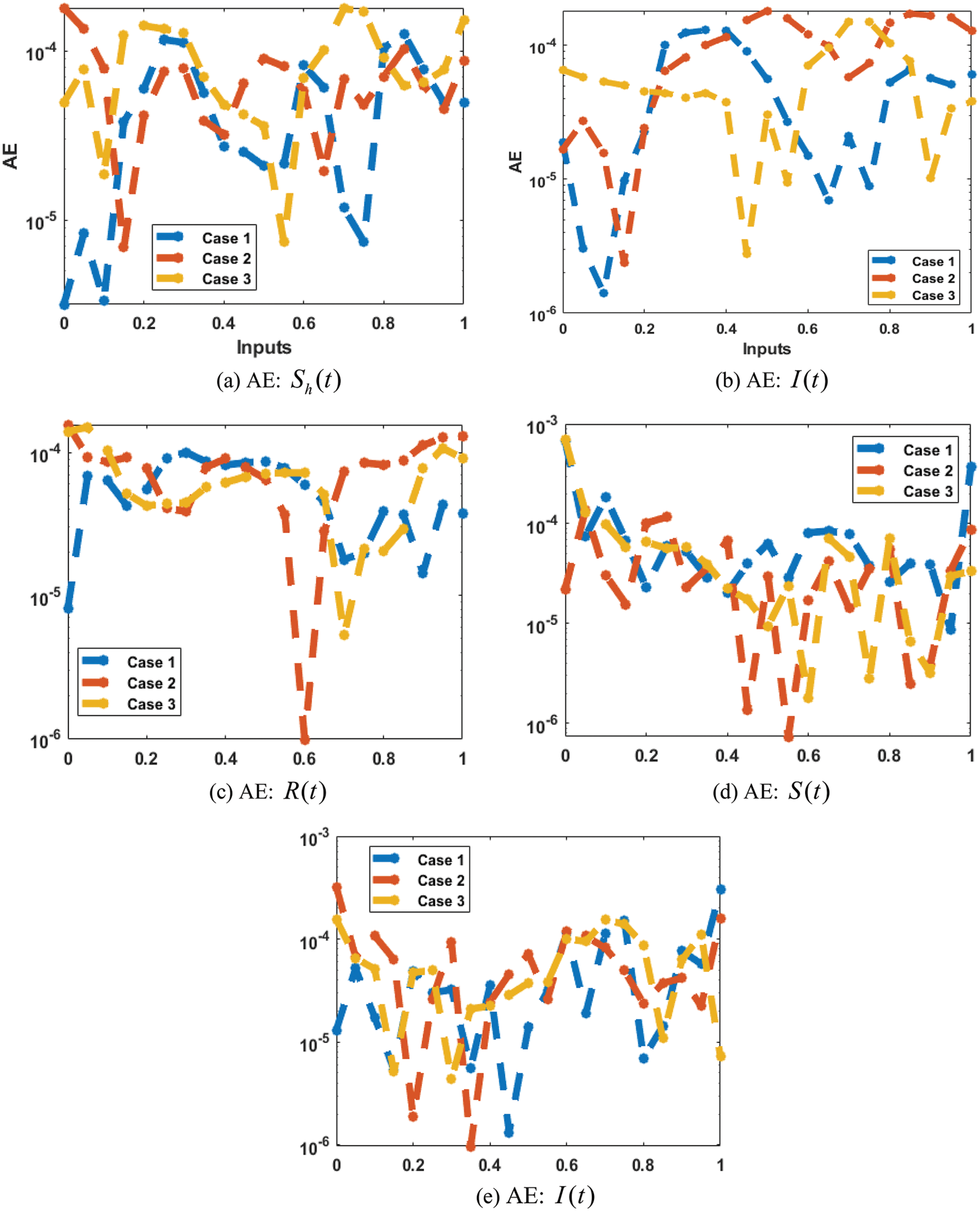
images

Figure 5: AE for the performances for the fractional order system

images

Fig. 5 presents the AE for the VHDNS model based on the nonlinear FO-SIRSI mathematical system. The AE based on the Sh(t) dynamics are calculated as 10−04−10−05, 10−04−10−06and 10−05−10−06 for the corresponding cases of the FO-SIRSI model. The AE is based on the Ih(t), Rh, Sv(t)and Iv(t).

6  Conclusions

This study aims to perform the simulations of the vector-host disease nonlinear system using the numerical artificial neural networks scheme along with the support of Levenberg-Marquardt backpropagation. The vector-host disease nonlinear system depends upon five dynamics: susceptible humans Sh(t), infected humans Ih(t), recovered humans Rh(t), infected vectors Iv(t) and susceptible vectors Sv(t). The vector-host disease nonlinear system is generalized into the fractional-order derivative to find more realistic solutions and the calculations have been performed using the SNNs-LMQBP. The correctness of the FO-VHDNS is observed using the comparison performances of the obtained and the reference solutions. This study has taken fifteen neurons and the data selection is 74%, 12% and 14%, for training, certification, and testing. The scheme’s exactness is achieved by achieving suitable AE measures for each dynamic of the FO-VHDNS. The AE based on each dynamic of the FO-SIRSI model is calculated as 10−05−10−06. Moreover, correlation studies, MSE, EHs, STs and regression have been achieved to observe the accuracy, efficiency, expertise, and aptitude of the computing SNNs-LMQBP. In upcoming studies, the proposed numerical procedure has been used to find the solutions for the fluid mechanic’s systems, nonlinear systems, omics studies, lonngren-wave, and data security networks [62–66].

Funding Statement: This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

  1. D. Otranto, F. Dantas-Torres and E. B. Breitschwerdt, “Managing canine vector-borne diseases of zoonotic concern: Part one,” Trends Parasitol, vol. 25, pp. 157–163, 2009.
  2. World Health Organization (WHO“Malaria,” 202 [Online]. Available: https://www.who.int/news-room/fact-sheets/detail/malaria.
  3. K. L. Koenig, A. Almadhyan and M. J. Burns, “Identify-isolate inform: A tool for initial detection and management of zika virus patients in the emergency department,” Western Journal of Emergency Medicine, vol. 17, no. 3, pp. 238–244, 2016.
  4. J. O. Zavaleta and P. A. Rossignol, “Community-level analysis of risk of vector-borne disease,” Transactions of the Royal Society of Tropical Medicine and Hygiene, vol. 98, no. 10, pp. 610–618, 200
  5. G. Macdonald, “Epidemiological basis of malaria control,” Bulletin of the World Health Organization,” vol. 15, no. ( 3–5,pp. 613, 1956.
  6. Z. S. Wong, J. Zhou and Q. Zhang, “Artificial intelligence for infectious disease big data analytics,” Infection, Disease & Health, vol. 24, no. 1, pp. 44–48, 2019.
  7. A. Rahman and M. A. Kuddus, “Cost-effective modeling of the transmission dynamics of malaria: A case study in Bangladesh,” Communications in Statistics: Case Studies, Data Analysis and Applications, vol. 6, no. 2, pp. 270–286, 2020.
  8. N. Chitnis, J. M. Cushing and J. M. Hyman, “Bifurcation analysis of a mathematical model for malaria transmission,” SIAM Journal on Applied Mathematics, vol. 67, pp. 24–45, 2006.
  9. D. Gao and S. Ruan, “A multi-patch malaria model with logistic growth populations,” SIAM Journal on Applied Mathematics, vol. 72, pp. 819–841, 2012.
  10. J. C. Koella, “On the use of mathematical models of malaria transmission,” Acta Tropica, vol. 49, no. 1, pp. 1–25, 1991.
  11. D. Rigling and S. Prospero, “Cryphonectria parasitica, the causal agent of chestnut blight: Invasion history, population biology and disease control,” Molecular Plant Pathology, vol. 19, no. 1, pp. 7–20, 2018.
  12. D. L. Smith and F. E. McKenzie, “Statics and dynamics of malaria infection in anopheles mosquitoes,” Malaria Journal, vol. 3, no. 1, pp. 1–14, 2004.
  13. J. X. Velasco-Hernández, “A model for chagas disease involving transmission by vectors and blood transfusion,” Theoretical Population Biology, vol. 46, no. 1, pp. 1–31, 1994.
  14. C. Vargas-De-León, “Global analysis of a delayed vector-bias model for malaria transmission with incubation period in mosquitoes,” Mathematical Biosciences & Engineering, vol. 9, no. 1, pp. 165–174, 2012.
  15. C. Dye, “The logic of visceral leishmaniasis control,” The American Journal of Tropical Medicine and Hygiene, vol. 55, no. 2, pp. 125–130, 1996.
  16. C. Bowman, A. B. Gumel, P. van den Drissche, J. Wu and H. Zhu, “Mathematical model for assessing control strategies against west Nile virus,” Bulletin of Mathematical Biology, vol. 67, no. 5, pp. 1107–1133, 2005.
  17. T. Sardar and B. Saha, “Mathematical analysis of a power-law form time dependent vector-borne disease transmission model,” Mathematical Biosciences, vol. 288, pp. 109–123, 20
  18. M. A. Khan, S. F. Saddiq, S. Islam, I. Khan and S. Shafie, “Dynamic behavior of leptospirosis disease with saturated incidence rate,” International Journal of Applied and Computational Mathematics, vol. 2, no. 4, pp. 435–452, 2016.
  19. K. O. Okosun, “Optimal control analysis of malaria schistosomiasis co-infection dynamics,” Mathematical Biosciences & Engineering, vol. 14, no. 2, pp. 377–405, 2016.
  20. F. Agusto and M. Khan, “Optimal control strategies for dengue transmission in Pakistan,” Mathematical Biosciences, vol. 305, pp. 102–121, 2018.
  21. L. M. Cai, X. Z. Li, B. Fang and S. Ruan, “Global properties of vector–host disease models with time delays,” Journal of Mathematical Biology, vol. 74, no. 6, pp. 1397–1423, 2017.
  22. Z. Sabir, M. Umar, G. M. Shah, H. A. Wahab and Y. G. Sánchez, “Competency of neural networks for the numerical treatment of nonlinear host-vector-predator model,” Computational and Mathematical Methods in Medicine, vol. 2021, pp. 1–13, 2021.
  23. M. A. Khan, S. Ullah and M. Farooq, “A new fractional model for tuberculosis with relapse via atangana–Baleanu derivative,” Chaos, Solitons & Fractals, vol. 116, pp. 227–238, 2018.
  24. S. Ullah, M. A. Khan and M. Farooq, “A fractional model for the dynamics of tuberculosis virus,” Chaos, Solitons & Fractals, vol. 116, pp. 63–71, 2018.
  25. H. W. Berhe, S. Qureshi and A. A. Shaikh, “Deterministic modelling of dysentery diarrhea epidemic under fractional caputo differential operator via real statistical analysis,” Chaos, Solitons & Fractals, vol. 131, pp. 109536, 2020.
  26. S. Qureshi, “Monotonically decreasing behavior of measles epidemic well captured by Atangana–Baleanu–Caputo fractional operator under real measles data of Pakistan,” Chaos, Solitons & Fractals, vol. 131, pp. 109478, 2020.
  27. Y. Luchko, “Fractional derivatives and the fundamental theorem of fractional calculus,” Fractional Calculus and Applied Analysis, vol. 23, no. 4, pp. 939–966, 2020.
  28. N. H. Aljahdaly, R. P. Agarwal, R. Shah and T. Botmart, “Analysis of the time fractional-order coupled burgers equations with non-singular kernel operators,” Mathematics, vol. 9, no. 18, pp. 1–24, 2021.
  29. A. Atangana and D. Baleanu, “New fractional derivatives with nonlocal and non-singular kernel theory and application to heat transfer model,” The Journal Thermal Science, vol. 20, no. 2, pp. 1–8, 2015.
  30. M. A. Khan and A. Atangana, “Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative,” Alexandria Engineering Journal, vol. 59, no. 4, pp. 2379–2389, 2020.
  31. K. M. Owolabi and E. Pindza, “Modeling and simulation of nonlinear dynamical system in the frame of nonlocal and nonsingular derivatives,” Chaos, Solitons & Fractals, vol. 127, pp. 146–157, 2019.
  32. K. M. Owolabi and A. Atangana, “Mathematical analysis and computational experiments for an epidemic system with nonlocal and nonsingular derivative,” Chaos, Solitons & Fractals, vol. 126, pp. 41–49, 2019.
  33. S. A. A. Shah, M. A. Khan, M. Farooq, S. Ullah and E. O. Alzahrani, “A fractional order model for hepatitis B virus with treatment via Atangana–Baleanu derivative,” Physica A: Statistical Mechanics and Its Applications, vol. 538, pp. 122636, 2020.
  34. S. Ullah, M. A. Khan and M. Farooq, “Modeling and analysis of the fractional HBV model with Atangana-Baleanu derivative,” The European Physical Journal Plus, vol. 133, no. 8, pp. 1–18, 2018.
  35. S. Ullah, M. A. Khan, M. Farooq and E. O. Alzahrani, “A fractional model for the dynamics of tuberculosis (TB) using Atangana-Baleanu derivative,” Discrete & Continuous Dynamical Systems-S, vol. 13, no. 3, pp. 937–956, 2020.
  36. K. Shah, F. Jarad and T. Abdeljawad, “On a nonlinear fractional order model of dengue fever disease under caputo-fabrizio derivative,” Alexandria Engineering Journal, vol. 59, no. 4, pp. 2305–2313, 2020.
  37. K. Muhammad Altaf and A. Atangana, “Dynamics of ebola disease in the framework of different fractional derivatives,” Entropy, vol. 21, no. 3, pp. 1–32, 2019.
  38. R. Jan, M. A. Khan, P. Kumam and P. Thounthong, “Modeling the transmission of dengue infection through fractional derivatives,” Chaos, Solitons & Fractals, vol. 127, pp. 189–216, 2019.
  39. D. Kumar, J. Singh, M. Al Qurashi and D. Baleanu, “A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying,” Advances in Difference Equations, vol. 2019, no. 1, pp. 1–19, 2019.
  40. M. A. Khan, O. Kolebaje, A. Yildirim, S. Ullah, P. Kumam et al., “Fractional investigations of zoonotic visceral leishmaniasis disease with singular and non-singular kernel,” The European Physical Journal Plus, vol. 134, no. 10, pp. 1–29, 2019.
  41. M. A. Khan, S. Ullah and M. Farhan, “The dynamics of zika virus with caputo fractional derivative,” AIMS Mathematics, vol. 4, pp. 134–146, 2019.
  42. N. Sweilam, O. M. Saad and D. Mohamed, “Fractional optimal control in transmission dynamics of west Nile virus model with state and control time delay: A numerical approach,” Advances in Difference Equations, vol. 2019, no. 1, pp. 1–25, 2019.
  43. D. Okuonghae, “Backward bifurcation of an epidemiological model with saturated incidence, isolation and treatment functions,” Qualitative Theory of Dynamical Systems, vol. 18, no. 2, pp. 413–440, 2019.
  44. L. Zhou and M. Fan, “Dynamics of an SIR epidemic model with limited medical resources revisited,” Nonlinear Analysis: Real World Applications, vol. 13, no. 1, pp. 312–324, 2012.
  45. I. M. Wangari and L. Stone, “Analysis of a heroin epidemic model with saturated treatment function,” Journal of Applied Mathematics, vol. 2017, pp. 1–21, 2017.
  46. M. A. Khan, N. Iqba, Y. Khan and E. Alzahrani, “A biological mathematical model of vector-host disease with saturated treatment function and optimal control strategies,” Mathematical Biosciences and Engineering, vol. 17, no. 4, pp. 3972–3997, 2020.
  47. Z. Sabir, M. A. Z. Raja, A. S. Alnahdi, M. B. Jeelani and M. A. Abdelkawy, “Numerical investigations of the nonlinear smoke model using the gudermannian neural networks,” Mathematical Biosciences and Engineering, vol. 19, no. 1, pp. 351–370, 2022.
  48. Z. Sabir, H. A. Wahab, S. Javeed and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 1–14, 2021.
  49. Z. Sabir, K. Nisar, M. A. Z. Raja, A. A. B. A. Ibrahim, J. J. P. C. Rodrigues et al., “Design of morlet wavelet neural network for solving the higher order singular nonlinear differential equations,” Alexandria Engineering Journal, vol. 60, no. 6, pp. 5935–5947, 2021.
  50. Z. Sabir, J. L. Guirao and T. Saeed, “Solving a novel designed second order nonlinear lane–Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, pp. 1–12, 2021.
  51. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Meyer wavelet neural networks to solve a novel design of fractional order pantograph lane-emden differential model,” Chaos, Solitons & Fractals, vol. 152, pp. 1–14, 2021.
  52. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. F. Aguilar, “FMNEICS: Fractional meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order lane–Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020.
  53. Z. Sabir, M. A. Z. Raja, M. Umar, M. Shoaib and D. Baleanu, “FMNSICS: Fractional meyer neuro-swarm intelligent computing solver for nonlinear fractional lane–Emden systems,” Neural Computing and Applications, vol. 34, no. 6, pp. 4193–4206, 2022.
  54. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A novel design of fractional meyer wavelet neural networks with application to the nonlinear singular fractional lane-Emden systems,” Alexandria Engineering Journal, vol. 60, no. 2, pp. 2641–2659, 2021.
  55. T. Botmart, Z. Sabir, M. A. Z. Raja, W. Weera, R. Sadat et al., “A numerical study of the fractional order dynamical nonlinear susceptible infected and quarantine differential model using the stochastic numerical approach,” Fractal and Fractional, vol. 6, no. 3, pp. 1–13, 2022.
  56. Z. Sabir, M. Munawar, M. A. Abdelkawy, M. A. Z. Raja, C. Ünlü et al., “Numerical investigations of the fractional-order mathematical model underlying immune-chemotherapeutic treatment for breast cancer using the neural networks,” Fractal and Fractional, vol. 6, no. 4, pp. 1–16, 2022.
  57. Z. Sabir, T. Botmart, M. A. Z. Raja and W. Weera, “An advanced computing scheme for the numerical investigations of an infection-based fractional-order nonlinear prey-predator system,” Plos One, vol. 17, no. 3, pp. 1–13, 2022.
  58. A. N. Akkilic, Z. Sabir, M. A. Z. Raja and H. Bulut, “Numerical treatment on the new fractional-order SIDARTHE COVID-19 pandemic differential model via neural networks,” The European Physical Journal Plus, vol. 137, no. 3, pp. 1–14, 2022.
  59. J. L. Guirao, Z. Sabir, M. A. Z. Raja and D. Baleanu, “Design of neuro-swarming computational solver for the fractional bagley–Torvik mathematical model,” The European Physical Journal Plus, vol. 137, no. 2, pp. 1–15, 2022.
  60. J. L. Guirao, Z. Sabir and T. Saeed, “Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model,” Mathematical Problems in Engineering, vol. 2020, pp. 1–9, 2020.
  61. K. Vajravelu, S. Sreenadh and R. Saravana, “Influence of velocity slip and temperature jump conditions on the peristaltic flow of a jeffrey fluid in contact with a newtonian fluid,” Applied Mathematics and Nonlinear Sciences, vol. 2, no. 2, pp. 429–442, 2017.
  62. M. S. M. Selvi and L. Rajendran, “Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 351–364, 2019.
  63. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, pp. 1–13, 2021.
  64. M. Gürbüz and Ç. Yıldız, “Some new inequalities for convex functions via riemann-liouville fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 537–544, 2021.
  65. T. Saeed, Z. Sabir, M. S. Alhodaly, H. H. Alsulami and Y. G. Sánchez, “An advanced heuristic approach for a nonlinear mathematical based medical smoking model,” Results in Physics, vol. 32, pp. 1–13, 2022.
  66. Y. G. Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, pp. 1–9, 2020.

Cite This Article

T. Botmart, Q. Hiader, Z. Sabir, M. A. Z. Raja and W. Weera, "Stochastic investigations for the fractional vector-host diseased based saturated function of treatment model," Computers, Materials & Continua, vol. 74, no.1, pp. 559–573, 2023. https://doi.org/10.32604/cmc.2023.031871


cc This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 749

    View

  • 563

    Download

  • 1

    Like

Related articles

Copyright© 2024 Tech Science Press
© 1997-2024 TSP (Henderson, USA) unless otherwise stated

Share Link