SP-DSTS-MIMO Scheme-Aided H.266 for Reliable High Data Rate Mobile Video Communication

1  Introduction

Shannon identified the channel behavior of a noisy channel to show the upper limit of data rates to be achieved on some specific channel [1]. This theorem predicts the highest data rate and specifies the bound on error-free information to be achieved on specific bandwidth over a noisy communication channel upon the addition of redundant bits to the transmitted messages. Source encoder is embedded in the systems to effectively deal with the noisy channel constraints while immersing the unpalatable vulnerability of transmission errors to the bit-stream. A noisy channel allows us to transmit limited information over an allocated bandwidth. Therefore, the source compression standard is required to transmit more contents within an allocated bitstream. Data integrity is another important parameter that ensures that the data needs to be delivered accurately to its intended user. Attenuation, shadowing, fading and multi-user interference are the major factors that causes time-varying and location varying channel conditions. There are numerous techniques i.e., diversity techniques, Forward Error Correction (FEC), interleaving, fast power control, Multiple-Input Multiple-Output (MIMO) systems and broadband access are used to overcome the variation in channel condition [2–7]. Some amount of errors may be tolerated for low-delay applications due to the noisy communication channel. Considering the practical scenario, Joint Source Channel Decoding (JSCD) gets significant research interest due to providing the lowest possible Bit Error Rate (BER) on realistic channels [8–10]. The series of JSCD schemes operated on residual redundancy as a prime source for error protection in the coded video bitstream [11,12]. To cope with the noisy behavior of wireless channels, Data Partitioning (DP) for error-resilient is compensated in Advance Video Coding (AVC). Each stream is divided into three different stream layers in DP and have their own importance and set of parameters. Several error-resilient schemes exist but with the trade-off increasing computational complexity and reducing compression efficiency [13]. Similarly, motivated by concatenated codes, the authors in [9] proposed Iterative Source and Channel Decoding (ISCD) for improving the error robustness features in digital systems by manipulating residual and artificial redundancy. The extent of achievement in the number of profitable iterations is determined by Extrinsic Information Transfer (EXIT) chart analysis [14]. In [9], the error-correcting or concealment capabilities of ISCD are evaluated by the EXIT Chart. In [15], the authors show the EXIT chart as a versatile tool for designing different serial concatenated codes. The source coding part in ISCD extracts the spectral coefficient from the multimedia contents (audio or video signal). Natural residual redundancy remains in the spectral coefficient after passing from the source codec in the form of non-uniform distribution. Residual redundancy is the source of performance manipulated at the receiver side to overcome transmission errors. Furthermore, a soft input decoder based on exploiting the residual redundancy in compressed bits and on the A-Posteriori Probability (APP) of each symbol was presented in [9]. In [10] Irregular-Variable length coding (IVLC) is presented which endow its performance to near capacity joint source coding. Cordless video telephony and interactive cellular use burst by burst adoptive transceivers and a principles scheme is designed in [16]. Sphere Packing modulation aided Differential Space Time Spreading (SP-DSTS) is briefly presented in [3–5]. An iterative Belief Propagation aided convolutional neural network (BP-CNN) architecture is presented in [17]. The deployment of 5G and 6G wireless communication is underway and the wireless research community is taking a higher interest in providing novel solutions. For this purpose, the authors in [18] discussed the evolution of mobile generation from the earlier First Generation (1G) mobile communication to the latest Fifth Generation (5G) and Sixth Generation (6G) by comparing the challenges and features. The future wireless communication will be transformative and will revolutionize the evolution from “connected things” to “connected intelligence” promising a very higher data transmission up to 1 Tera bits per second (Tb/s), very high energy efficiency with the support of enabling battery-free Internet of Things (IoT) devices, low latency, and utilizing broad frequency bands [19]. In [20], provides an overview and outlook on the architecture, modeling, design, and performance of massively distributed antenna systems (DAS) with nonideal optical fronthauls. In [21], the authors provides an overview and outlook on the application of sparse code multiple access (SCMA) for 6G wireless communication systems, which is an emerging disruptive non-orthogonal multiple access (NOMA) scheme for the enabling of massive connectivity. Moreover, the authors propose to use SCMA to support massively distributed access systems (MDASs) in 6G for faster, more scalable, more reliable, and more efficient massive access. Highest Efficient Video Coding (HEVC) is the source compression standard which is specially designed for providing parallel processing, coding gain, and error resilience efficiency. The main target of the HEVC development was to reduce the bitrate up to 50% with the same quality as the existing standards. On the other hand, Versatile Video Coding (VVC) is finalized in September 2020 providing significantly greater compression efficiency compared to Highly Efficient Video Coding (HEVC) [22–24]. The novelty of the propose work is providing bandwidth-efficient communication, the latest source encoding standard VVC and HEVC is used as a compression standard while SP-DSTS as a MIMO scheme for providing reliable higher data rate video communication. It is a challenging task implementing this research architecture to transmit a highly compressed packets of HEVC & VVC encoding standard over a correlated Rayleigh fading channel. The error rate on Rayleigh fading channel model cannot be much reduced by simply increasing transmission power or increasing the allocation of bandwidth as it is contrary to requirements of the next generation systems. As, a single bit in error from the highly compressed stream may affect the correct decoding of a number of frames. Therefore, a clever and intelligent system is designed in the propose work in order to get the attained the reliability along with providing a highly compressed bitstream. Moreover, a Belief Propagation aided Convolutional Neural Network (BP-CNN) architecture is included to find the results of the proposed on the said architecture with the transmission of a video sequence. In order to find the effect of the interesting neural network in stochastic channel noise estimation, the results of the proposed work is further compared with the same system utilizing H.265 source encoding standard and BP-CNN architecture at the decoding side. The motivation and contributions of the proposed research is itemized as given below:

•   To the best of our knowledge, this is the first scheme which transmits the video sequences compressed by VVC video encoded standard using SP-DSTS encoder and analyzed the received video sequence from the wireless network using objective and subjective performance metrics.

•   Turbo codes achieve the ultimate theoretical limits and can be used to implement real-time high energy efficient low latency transceivers with enabling high-speed data transmission and exploiting transmitter diversity gain, advanced modulations, self-concatenated, and differential codes to meet the required quality of service demand.

•   The results of convolutional codes with the source encoding standard VVC have been compared to the same system when H.265 and H.266 source encoder is utilized.

•   The objective and subjective video quality performance of the proposed is measured with AVC, HEVC and VVC. From the subjective video quality, it can visualized that HEVC preserved a large number of frames to the receiving end and frame dropout rate is too low. The same fact can be visualized for VVC video coding standard. Moreover, VVC maintaining a good PSNR values for all the frames even for a lower Eb/N0 value as well. It is clearly shown that the system with VVC conserved a large number of frames at the receiving side with high quality.

•   Moreover, the performance of BP-CNN is compared with the bench marker system using H.265 as a source encoding standard while transmitting the Akiyo video sequence.

The overall structure of the proposed work has been organized as follows. Section 2 briefly presents the preliminaries and system design criteria for the proposed work. Section 3 presents different parameters of the utilized channel codes. The system model has been presented in Section 4. Simulation results of the proposed work are given in Section 5. Finally, a conclusion of the proposed work is presented in Section 6.

2  Preliminaries & System Design Criteria

The model between two parties comprises sender, receiver, message, channel and the underlying protocol. The protocol is a set of rules on which both the parties agree for specifying different layers and their functionalities to provide an application-oriented communication. The communication channel adds an unwanted signal to the original signal when the signal passes through the channel. Decoding the received signal requires modeling the behavior of a noise signal. In the case of Rayleigh fading or multipath channels, a statistical model is used for specifying the behavior of the channel. It is since there exists randomness in the location of the object and due to the multipath channel. The transmitting antennas, transmit a signal to the receiver while the signal at the decoding side does not remain the original signal but is received as a sum of different replicas i.e., reflected, scattered and diffracted versions received from walls, trees and buildings. In the absence of line of sight and if I versions of the original signal exist, then the received signal is the sum of I components with the Gaussian noise as follows [25]:

r(t)=∑i=1Paicos⁡(2πfct+ϕi)+η(t)(1)

where ai represents amplitude, fc represents carrier frequency, while ϕi represents the phase of the corresponding component and η(t) represents the Gaussian noise. Furthermore,

r(t)=cos⁡(2πfct)∑i=11aicos⁡(ϕi)−sin⁡(2πfct)∑i=1Taisin⁡(ϕi)+η(t)(2)

The above equation represents a summation of the term ∑i=1Iaicos⁡(ϕi) and ∑i=1Iaisin⁡(ϕi) i.e., the replicas of I random variables. Rayleigh random variable X can be defined as the square root of independent and identically distributed Gaussian random variables X1 and X2 each having zero mean and two degrees of freedom [25].

X=X12+X22(3)

Probability Distribution Function (PDF) of (X) is as given below:

P(X)={Xσ2e−X22σ2X>00otherwise(4)

In Eq. (4), the σ2 represents the variance of X1 and X2 while 2σ2 represents the sum of variances of X1 and X2. The mean and variance of a variable X is given by the following equation.

E[X]=σπ2(5)

VAR[X]=(2−π2)σ2(6)

The Cumulative Distributive Function (CDF) of X can be achieved by integrating the PDF and is represented as follows:

F[X]={1−e−X22σ2X>00 otherwise (7)

Shadowing effect on the original signal is generated due to objects and large block such as building in the communication model channel. It can be modelled with the lognormal distribution (Y) such as given below:

Y=ln⁡S∨S=eY(8)

Then the PDF of S is given as:

P(S)={12πσ2Se−(ln⁡S−m)22σ2X≥00 otherwise(9)

Where m and σ represents the mean and variance respectively.

E[ X ]=em+σ22 (10)

VAR[ X ]=e2m+σ2(σ2−1)(11)

3  Channel Codes Performance Parameters

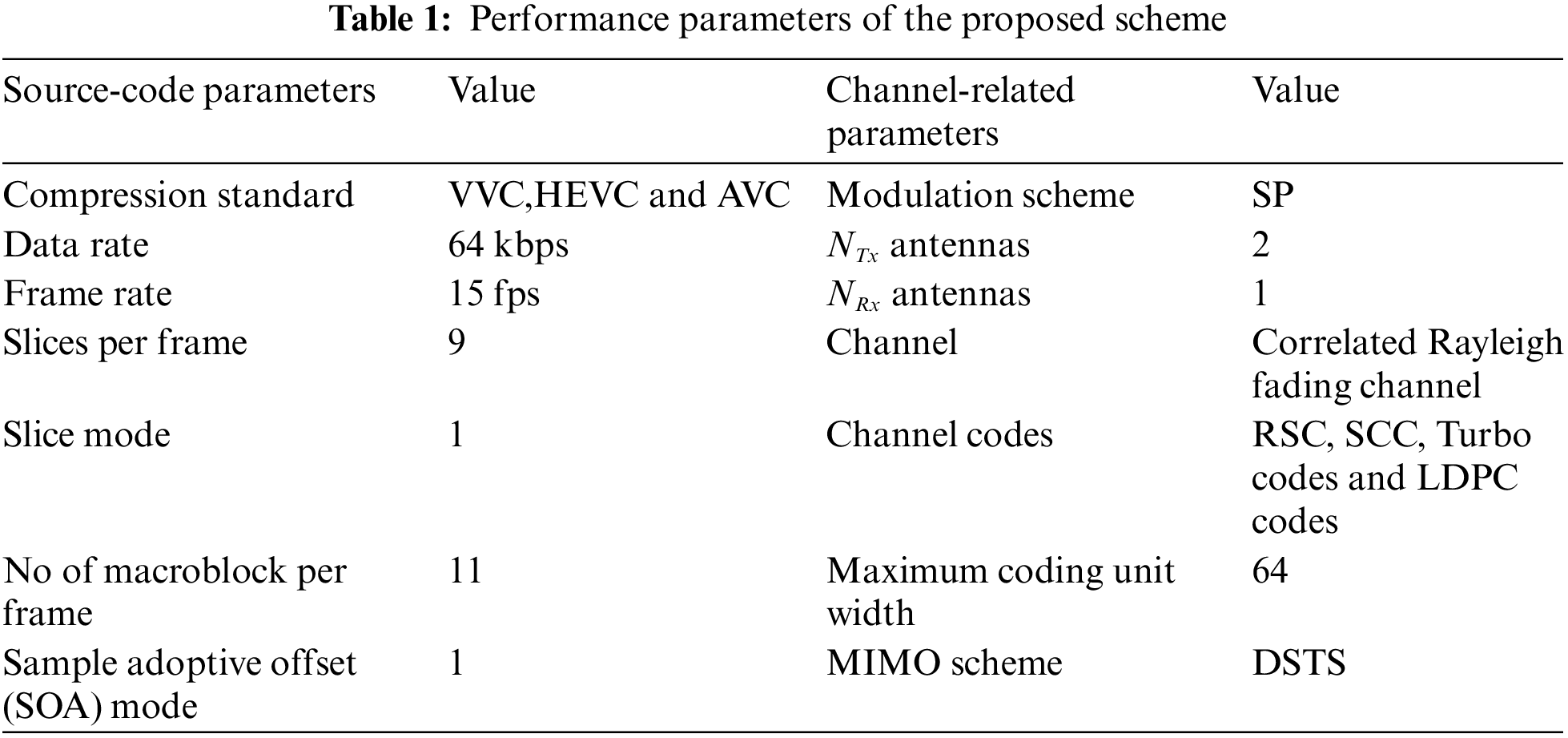
The proposed work compares three different channel codes to provide high data rate reliable video communication over a communication channel with aid of H.265 and H.266 source encoding standards and a BP-CNN architecture for H.265 compressed video decoding. The primary channel code in term of tremendous performance and ease of implementation is Recursive Systematic Convolutional (RSC) codes. The convolutional codes characteristic can be obtained with the following generator polynomial equation having constraint length v as in [13].

G(i)(D)=g0(i)+g1(i)D+g2(i)D2…g(v−1)(i)D(v−1)(12)

The input polynomial expression of convolutional codes is given with the following equation.

Un′(D)=u0′+u1′D+…un′Dn(13)

The output can be obtained as will the following equation for input bitstream.

Y(i)(D)=G(i)(D)⋅Un′(D)(14)

=Y0(i)+Y1(i)D+Y2(i)D2+…..+Yv+n−1(i)Dv+n−1(15)

Convolutional codes take k input bits and output n bits while the output depends on the generator polynomial function. The characteristic of convolutional codes can be drawn with the help of a state machine diagram where the next state generally corresponds to the current state as well as the input infiltrate to the encoder. From Fig. 1, the design example can be explained as, let the generator polynomials is G1=(1,1,1) and G2=(1,1,0). The initial state is represented in the state diagram while for an initial state 00, the next state will be the same as the current state if 0 is input to the encoder. The input and output are represented in the state diagram as 0/00 (input/output). Similarly, for input 1, the next state is 10 from the current state while providing output 11 and can be expressed as 1/11. All the states and corresponding output can be obtained from the state diagram accordingly. Code rate is the primarily parameter for comparing the performance of different channel codes which is the ratio between the input k bits to that of the output n bits at a corresponding instance of time, i.e., can be expressed as with the following equation.

Rc=kn(16)

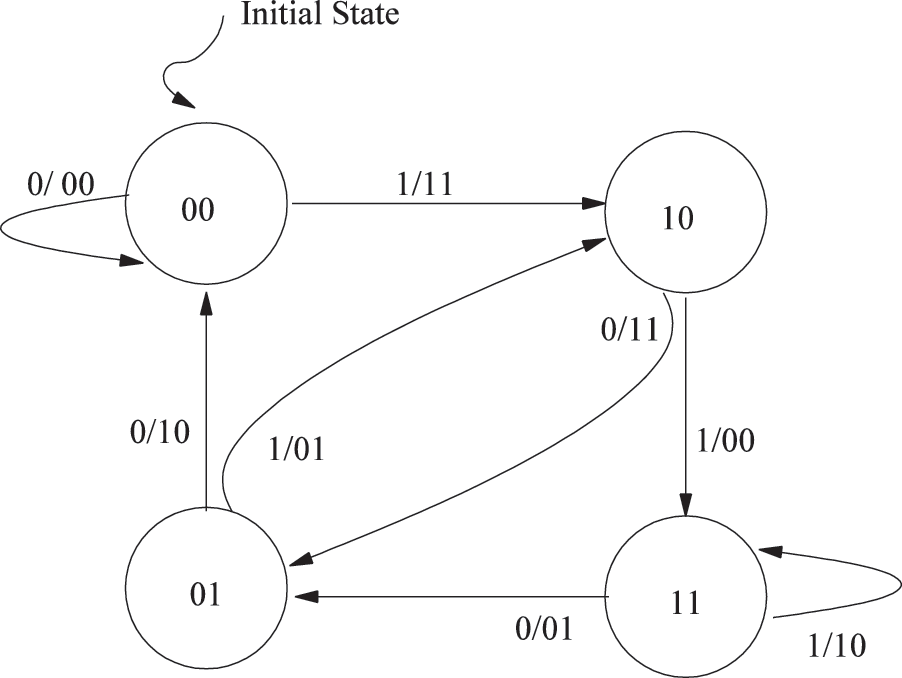
Figure 1: State machine diagram of convolutional coding

Traditionally, as the number of output bits n is generally always greater than the number of input bits therefore, the ratio results in a code rate of less than 1. The unit of RSC codes is bits/transmission and represents the symbols that are transmitted in each individual instance of time. The number of symbols L i.e., M-ary symbols transmitted per codeword can be expressed as with the following equation. In Eq. (17), the length of the codeword is represented with n while the constellation size is represented with M.

L=nlog2⁡M(17)

The transmission rate (R) can be expressed as with the following equation. Eq. (18) represents the transmission time for transmitting k information bits when the symbol duration is Ts.

R=kLTs(18)

The transmission rate can be further derived by putting the values of L from Eq. (17) in Eq. (18) and be expressed as with the following equation.

R=k∗log2⁡Mn∗Ts(19)

R=Rclog2⁡MTsbps(20)

Spectral bitrate (r) or bandwidth efficiency is the ratio between the encoding scheme bitrate to that of the bandwidth utilized and can be obtained with the following equation.

r=R(bps)W(Hz)(21)

The efficiency of the transmitting system can be measured in terms of the spectral bitrate. The signal with utilizing bandwidth W must be decoded at the receiving end if the sampling rate is not less than 2 W per second. The following equation represents the degree of freedom with duration T and bandwidth W.

N=2WT(22)

The threshold bandwidth requirements for a transmission can be expressed as with the following equation.

W=NTs(23)

Putting the value of Ts

W=RN2RClog2⁡Mbits/sec(24)

With the passage of time and advancements in communication, the concept of turbo codes is widely accepted and matured [25]. Such powerful class of codes merely operates by the deployment of an interleaver between two Recursive Systematic Convolutional (RSC) encoders in a parallel fashion. The constituent RSC encoders may be operating on the same or different architectures and rates. These codes find extensive applications in the scenarios of low Bit-Error-Rate (BER) missions without any additional specific power requirements. The advent of turbo codes has paved the direction for the researchers in designing efficient codes that can be decoded with the least complexity as well [26]. These demanding codes approaching the Shannon's theoretical limit are based on the RSC codes for achieving the near-limit capacity as highlighted in the pioneering work of Shannon. The schematics of a turbo encoder and decoder is given in Figs. 2 and 3. The code puncturing techniques and multiplexing are mostly helpful in achieving the desired rate for the scheme. Turbo codes produces randomness in coding due to the presence of interleaver between the member encoders. Convolutional coding lacks interleaver. Turbo codes are recursive, systematic, and with parallel structure whereas convolutional codes are non-recursive and non-systematic. For the decoding of Turbo codes, a clever approach based on divide-and-conquer is processed. It is worth mentioning that the constituent decoders rely on the sharing of mutual information between each other. Mutual information (I) and entropy are two correlated terminologies that are commonly used where information sharing is the primarily resource of performance. Mutual information is the amount of information one variable have about other while the self-information of a random variable is called entropy.

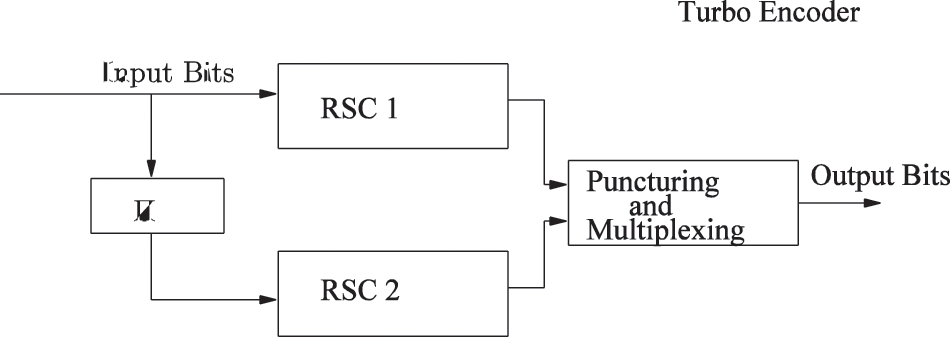
Figure 2: Turbo encoder

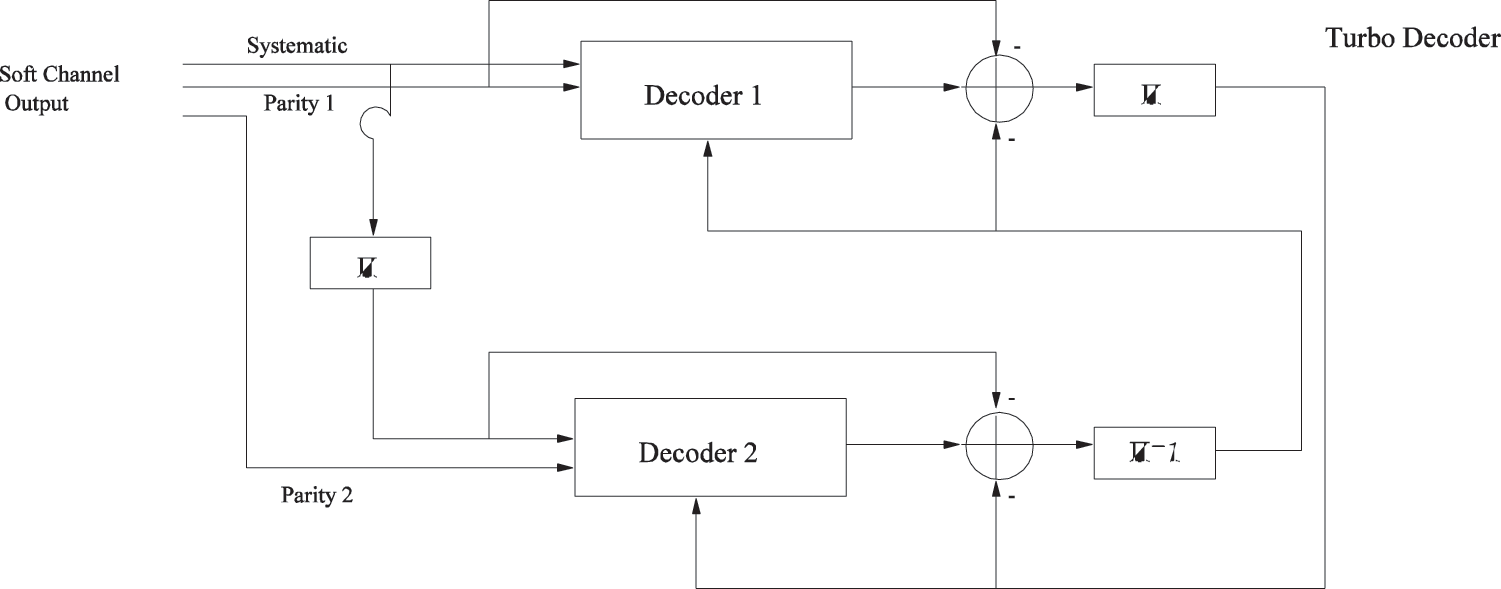
Figure 3: Turbo decoder

Mutual information is also called relative entropy where it represents the distance between two probability distributions. For a transmitted symbol Y and with the channel output Z, the mutual information can be expressed as with the following equation [15,16].

I(Y1;Z)=1NA⋅∑n=1NA∫−∞+∞p(z∣Y1=an)×ldp(z∣Y1=an)p(z)dz(25)

With conditional probability density function (PDF)

p(z∣Y1=an)=12πσ⋅exp⁡[−(z−an)22σ2](26)

p(z)=1NA∑n=1NAp(z∣Y1=an)(27)

These decoders accept Soft-Input (SI) to yield Soft-Output (SO) [27]. Mostly, the stream of information that is iteratively shared between the decoders is in the form of Logarithmic Likelihood ratio (LLR). The input LLRs accepted by the SISO decoder is processed to increase the reliability about the transmitted data, using the concept of redundancy [28]. The output LLR from the SISO is expressed by the equation.

Lout (d)=Linput (d)+E(d)(28)

The alphabet L stands for the LLR, corresponding to the appropriate subscript and E(d) is the extrinsic information of bit d. The block diagram of the turbo decoder is given in Fig. 2. In the decoding process, LLRs are appropriately interleaved and deinterleaved to continue the process of iterations. The main issue of convergence is solved primarily with this iterative behavior. The negative feedback governs for the stability of the overall decoding process. After several iterations, both decoders succeed in achieving the stability and convergence. Another interesting class is the Self-Concatenated Convolutional Coding (SCC) which is based on a very much simpler approach. As in the case of turbo codes, although a performance of near capacity was achieved, but it involves two RSC encoders and separate decoders as well. Keeping in view the complexity of turbo codes, a much simpler approach is offered by the SCC scheme [29]. It involves only a single RSC encoder and a single decoder. The block diagram is depicted in Fig. 4. The decoding side is divided into component decoders for the sake deployment of iterative decoding. The process of iterations continues and one component decoder feeds on the second rendering improvements in the knowledge of decoders [30]. The mathematical equation governing the overall code rate R for the SCCC based on R1 and R2 is given by Eq. (29) where R1 is the rate of the RSC encoder used whereas R2 is the puncturing rate used in the SCC scheme [31].

R=R1(2∗R2)(29)

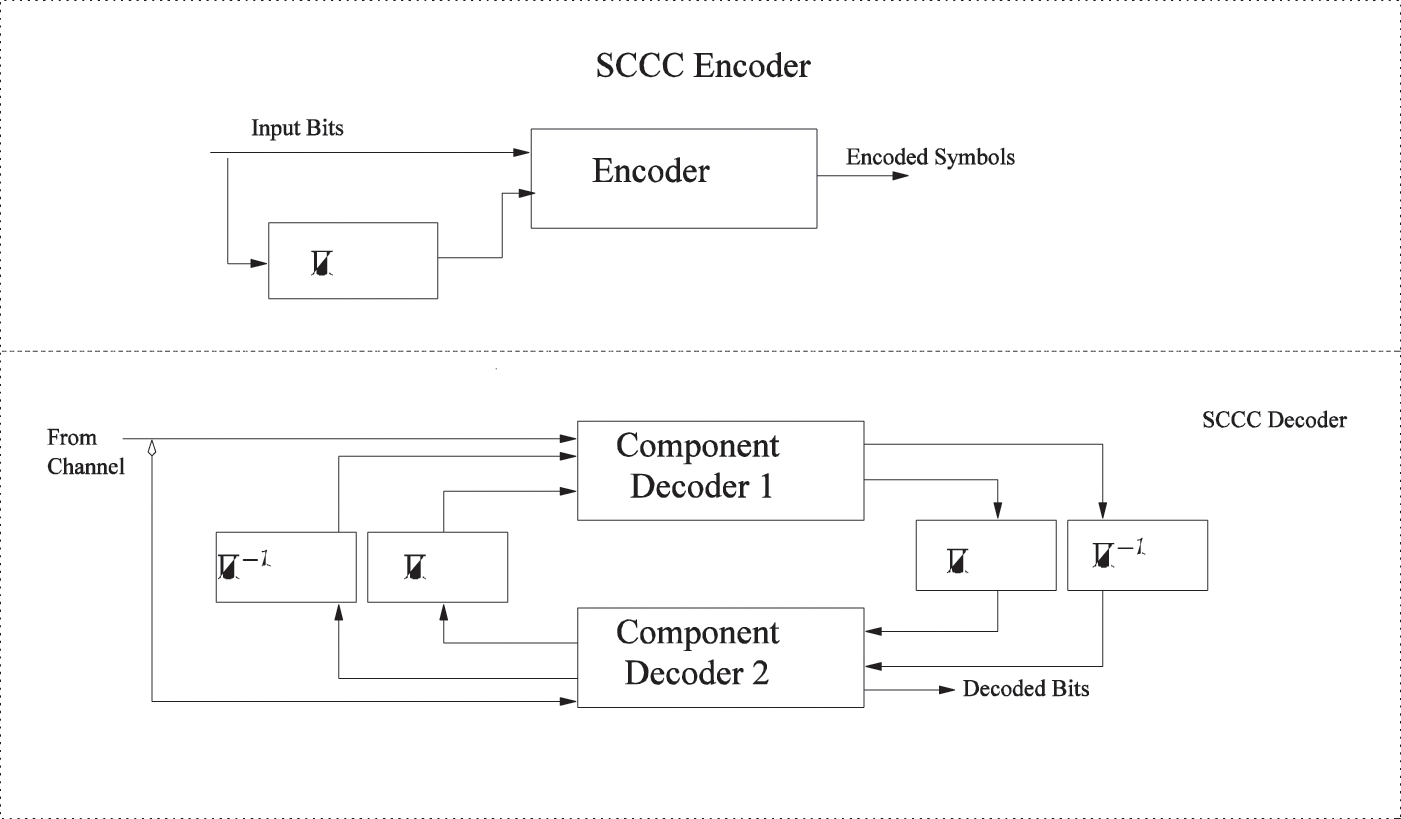
Figure 4: Self-concatenated convolutional codes encoder and decoder

4  Proposed System Model

The performance of the proposed is analyzed using H.266 and H. 265 source encoding aided a BP-CNN architecture at the decoding side refer to Fig. 5. Initially, a Standard Definition or High Definition video is provided at the input of the latest H.266 and H.265 source encoding standard as shown in Fig. 5. The performance parameters for the proposed word is given in Tab. 1. H.266 is the latest source compression standard with 50% compression efficiency compared to H.265. H.266 and H.265 generates a compressed bitstream x which are then presented to the channel encoder. The channel encoder adds redundant bits to the bitstream and results in a stream of u. Shannon information theory presented messages and signals as a function of space and the modulation process is a mapping from one space into another. Therefore, the bitstream is then forwarded to a SP modulation block where a symbol s is generated from the constellation points. The symbol is then forwarded to DSTS block which results in differential encoded symbols y1 and y2. The differential symbols are then transmitted over a channel which adds a noise η to the signal. The error rate on Rayleigh fading channel model cannot be much reduced by simply increasing transmission power or increasing the allocation of bandwidth as it is contrary to requirements of the next generation systems. An iterative BP-CNN architecture is presented in [17]. The proposed work uses the BP-CNN architecture for noise estimation from the H.265 encoded video sequence at the receiver side. The symbol y is received from the channel where it is first presented to DSTS decoder. The DSTS decoded symbol s is then presented to SP Demodulation results in symbol. The symbol u is then further presented to BP-CNN. Finally, a resultant bitstream x^ is provided to the H.266 and H. 265 source decoder where a resultant video stream is reconstructed and different performance parameters has been computed.

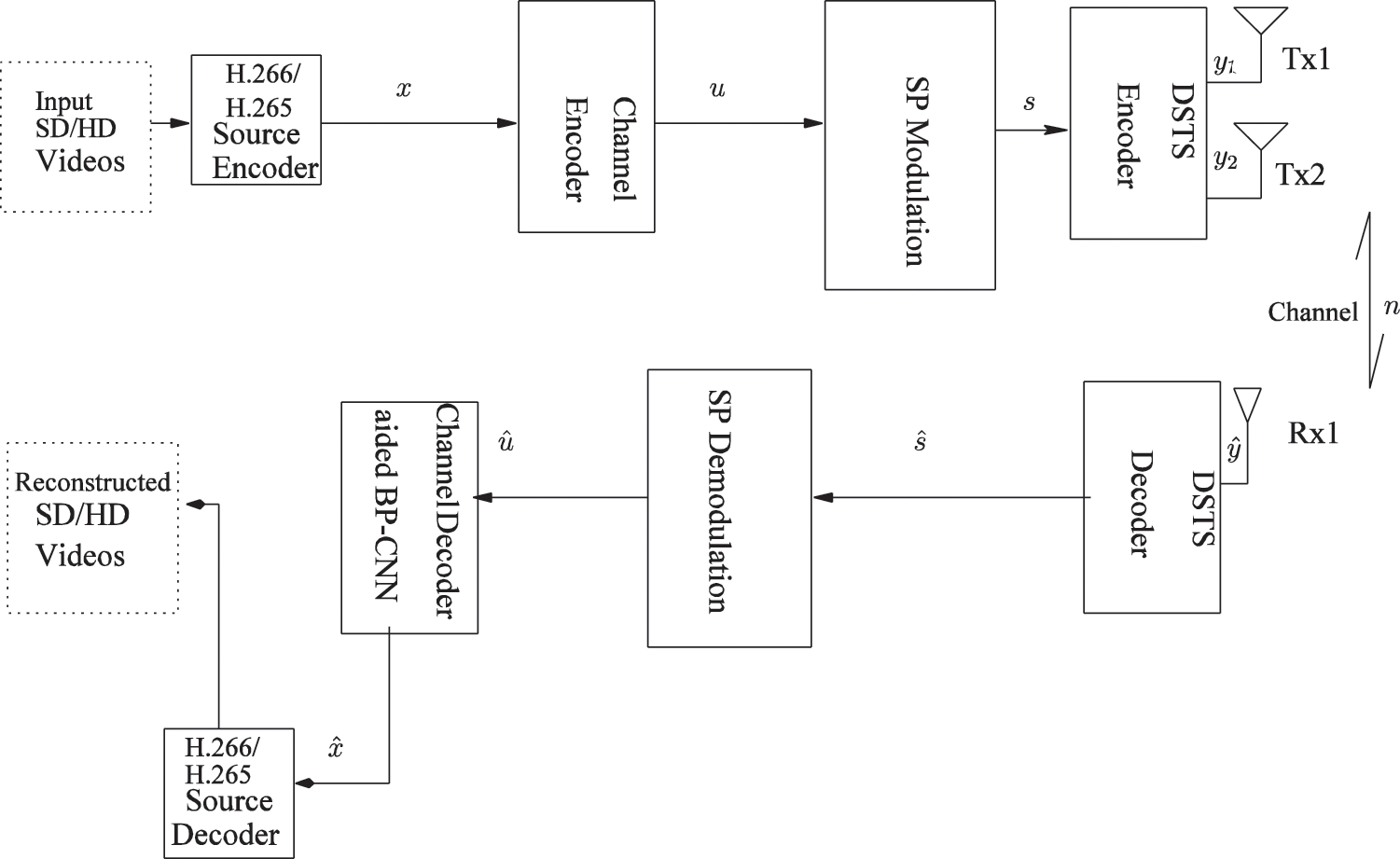
Figure 5: Convolutional codes using H.265 aided CNN at the decoding

5  Simulation Results

Objective quality of the proposed has been drawn on the performance parametric. BER and PSNR curve is plotted for visualizing the performance of the proposed system for objective video quality assessment. The proposed system is utilizing VVC and HEVC as a source encoder while convolutional, turbo, and self-concatenated convolutional codes as a channel encoder. There are two versions of the currently released VVC standard. One is VVCSoftware_VTM_master and the other one is VVenc-master. VVCSoftware takes much time in encoding while VVenc-master is the faster version. The compression efficiency of VVC over HEVC is given in Tab. 2.

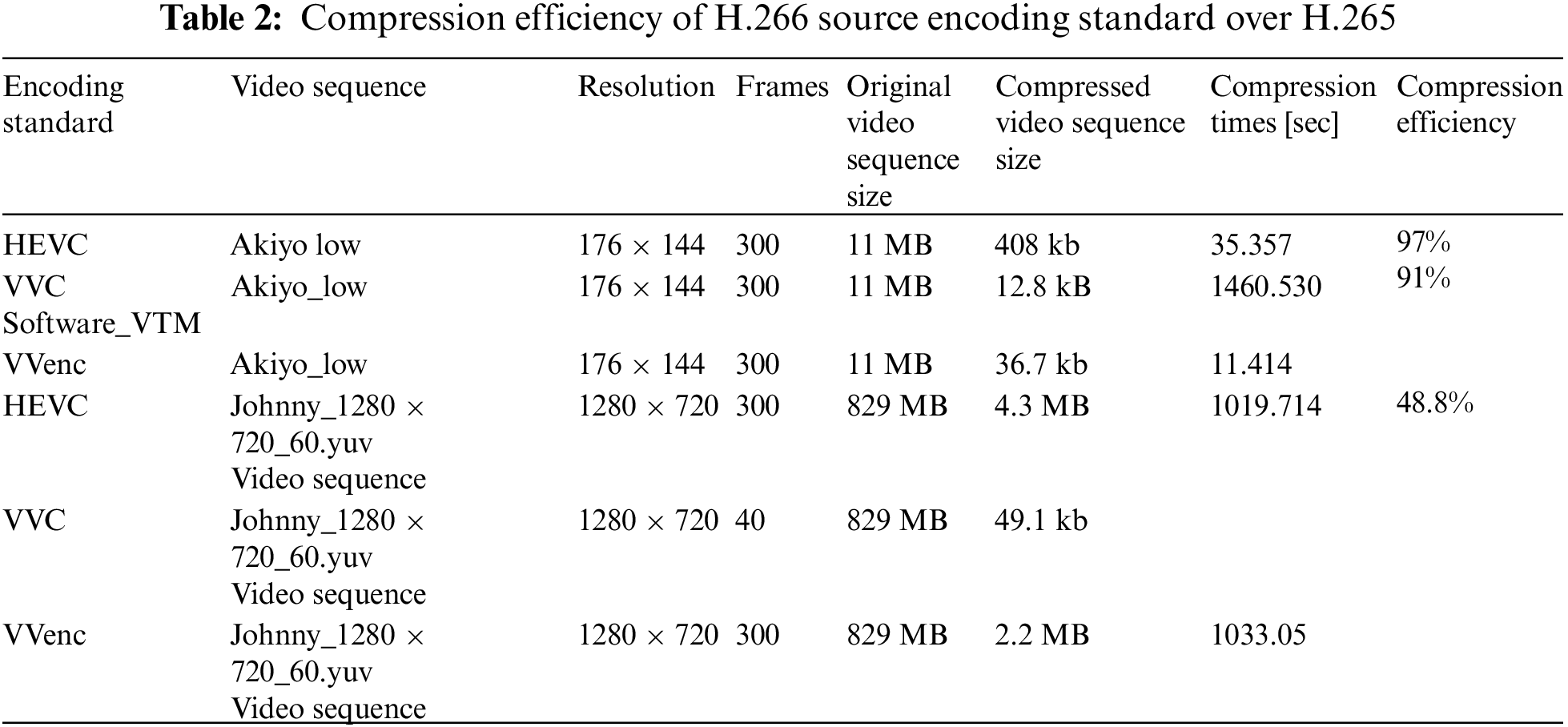
From the given results in Tab. 2, VVC outperform over 97% compared to HEVC for a low resolution video sequence while for high resolution video sequence, VVC outperform on about 48.8% compared to HEVC encoding standard. Moreover, a BP-CNN architecture is included to find the results of the proposed on the said architecture with the transmission of a video sequence. The proposed system is using the same code rates for all the three channel codes and utilizing Akiyo video sequence for transmission over the system. The video bitstream is also transmitted on the system aiding the BP-CNN architecture at the decoding side. To perform a fair analysis, there must be some performance parameters for comparison. There are two approaches that are mainly utilized for comparing the system results i.e., Objective and Subjective analysis. The proposed work is evaluated on objective performance parameters which is BER and PSNR. The simulation results is plotted by varying different values of Eb/N0 dB having a constant code rate of 1/3 by transmitting bitstream.

As the value of Eb/N0 dB increases the BER decreases and within limited time, BER of Turbo codes approaches to zero as shown in Fig. 6. Turbo codes on the developed system is also compared with the convolutional codes and self concatenated convolutional codes. Convolutional codes is performing better relative to SCC codes in terms of BER in the developed system. Turbo codes and Convolutional codes achieved a perfect knowledge about the channel state information and a steady jump to lower BER value has been visualized. An Eb/N0 of 1.5 dB gain is achieved in turbo codes compared to convolutional codes at on approximate BER value of 10−5 while convolutional codes gain an Eb/N0 of 3.2 dB compared to SCC. In order to find the effect of the interesting neural network in stochastic channel noise estimation, the results of the proposed work is further compared with the same system utilizing H.265 source encoding standard and BP-CNN architecture at the decoding side. BER vs. Eb/N0 dB curve is plotted in Fig. 7 while transmitting a compressed video sequence. The BER is decreases with increasing the Eb/N0 dB values refer to Fig. 7. The channel codes when applying a BP-CNN architecture at the decoding side achieved a perfect knowledge about the channel stochastic noise estimation and a steady jump to lower BER value has been observed. A gain of 0.8 Eb/N0 dB is achieved compared to the bench marker system. The Eb/N0 vs. PSNR curve is plotted for H.266, H.265 and H.264 source encoding standard considering convolutional codes as a channel code as shown in Fig. 8. PSNR is increasing with varying Eb/N0 values in dB. AVC performance is better for a lower Eb/N0 but the performance reduces for higher values. It is clear from the results that the convolutional codes with the latest H.266 outperform with the PSNR gain of 6 dB on about 3 dB Eb/N0 compared to H.265 while H.265 outperform with about 5.5 dB PSNR gain compared to H.264. Subjective Video quality for the considered AVC, HEVC, and VVC standard has been given in Fig. 9 while the validation for each corresponding frame is provided Tab. 3.

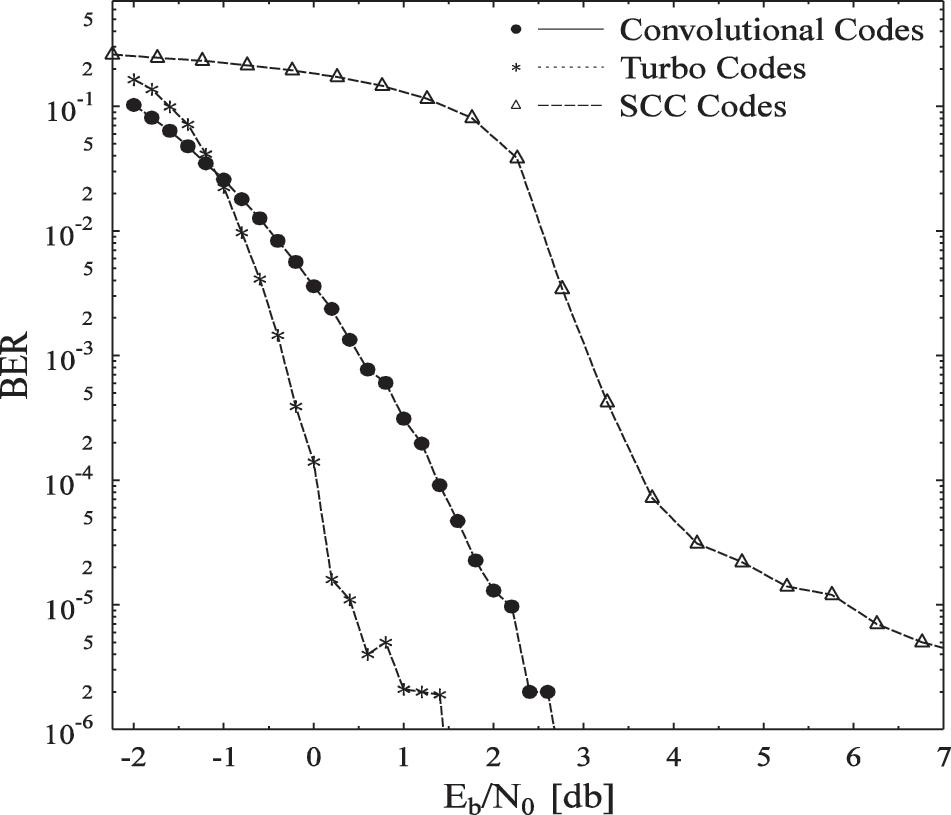
Figure 6: BER vs. Eb/N0 comparison of convolutional, turbo and self concatenated codes

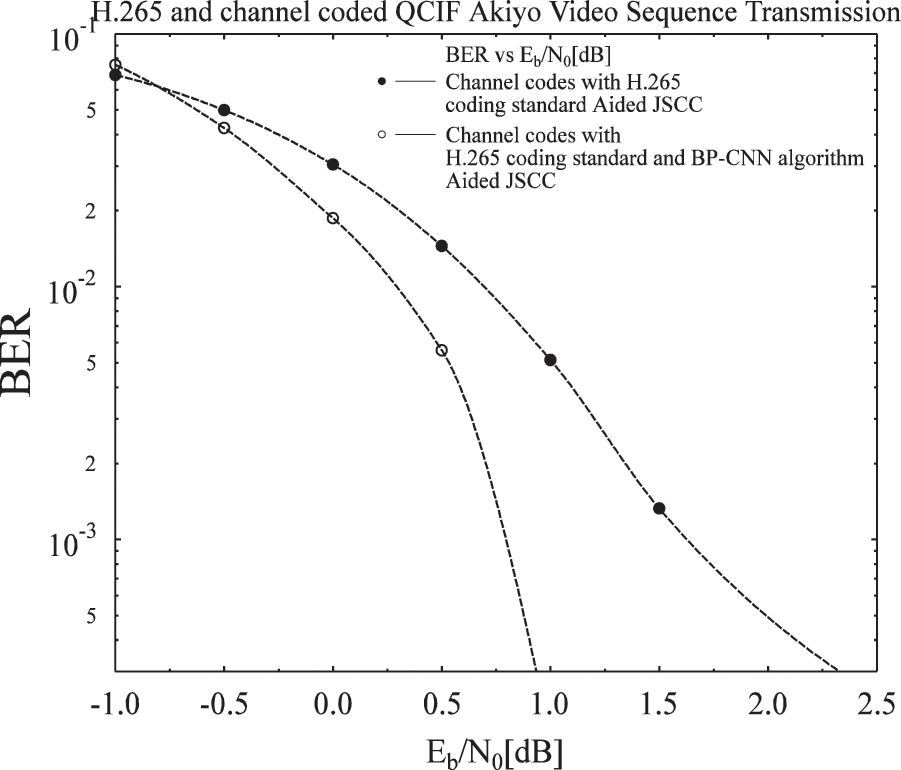
Figure 7: Channel codes utilizing CNN and HEVC

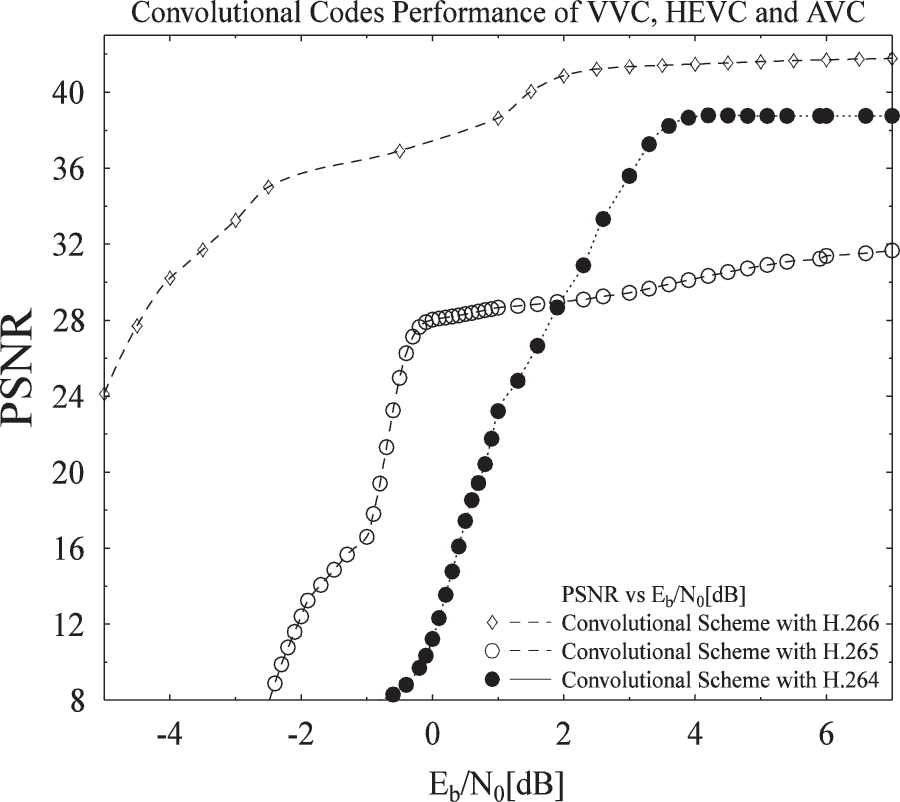
Figure 8: Eb/N0 vs. PSNR for H.264, H.265, and H.266

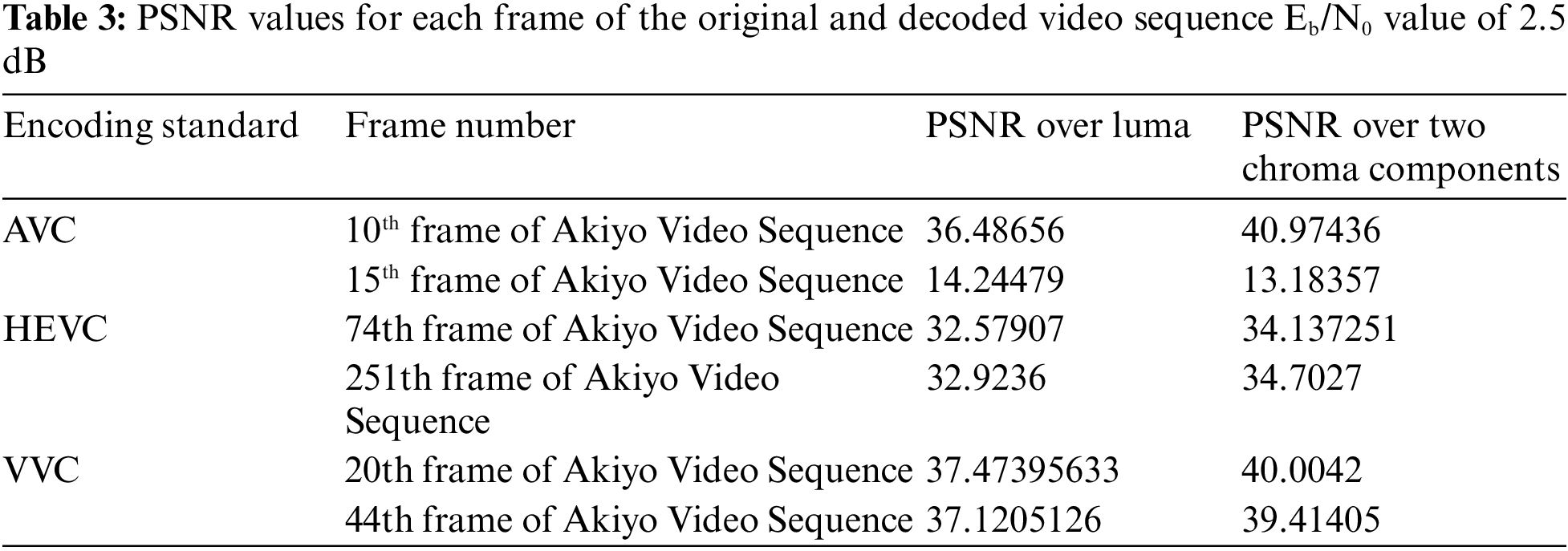
Figure 9: Subjective video performance of AVC, HEVC, and VVC using the proposed model

From the subjective video quality of the proposed work, it can be clearly observed that AVC perform better for a lower frame index i.e., 10th frame but afterwards drops the remaining frames as from Figs. 9a and 9d. For HEVC, an about 300 number of frames are transmitted and received all the frames with a given PSNR value in Tab. 3. The HEVC subjective results for a frame number of 74th and 251th is given in Figs. 9b and 9e, correspondingly. It is clear that HEVC preserved a large number of frames to the receiving end and frame dropout rate is too low. The same fact can be visualized for VVC video coding standard. The frame number 20th and 44th is given in Figs. 9c and 9f. VVC maintaining about a constant PSNR for all the frame for a lower Eb/N0 value as well.

6  Conclusion

This article is comparing the architecture, performance and the design of three extensively used channel codes utilizing the latest source encoder VVC, HEVC and VVC. Moreover, a BP-CNN architecture is added at the decoding side for attaining lower BER compared to the benchmarked. We proceed by comparing their block structures to distinguish among the said codes. Further, after simulating the codes for their performance on accounts of the BER, it is conclusively accepted that the turbo codes exceed the others in performance by considerable amount. Turbo codes outperform with an Eb/N0 dB gain of 1.5 dB compared to convolutional codes while convolutional codes defeats SCC with an average Eb/N0 gain of 3.2 dB. The PSNR results of convolutional codes with the source coding standard of H.266 is plotted against convolutional codes with HEVC/H.265 and it was concluded VVC outperform with about 6 dB PSNR gain at Eb/N0 of 3 dB. From the subjective video quality assessment, it is concluded that HEVC and VVC preserved a higher number of frames at the receiving end while the frame dropout rate is too low. Subjective Furthermore, BP-CNN based system produces an Eb/N0 gain of 0.8 dB compared to the bench marker system while transmitting the HEVC compressed video sequence.

Acknowledgement: The financial support of NCBC-UETP, under the auspices of Higher Education Commission, Pakistan is gratefully acknowledged.

Funding Statement: This article was supported by the Ministry of Education of the Czech Republic (Project No. SP2022/18 and No. SP2022/5) and by the European Regional Development Fund in the Research Centre of Advanced Mechatronic Systems project, project number CZ.02.1.01/0.0/0.0/16 019/0000867 within the Operational Programme Research, Development, and Education.

Conflicts of Interest: The authors declare that there is no conflict of interest regarding the publication of this paper.

References

 1.  C. E. Shannon, “A mathematical theory of communication,” Bell System Technical Journal, vol. 27, no. 3, pp. 379–423, 1948. [Google Scholar]

 2.  A. Hero, B. Ma and O. Michel, “Imaging applications of stochastic minimal graphs,” Proceedings 2001 Int. Conf. on Image Processing (Cat. No. 01CH37205), vol. 3, pp. 573–576, 2001. [Google Scholar]

 3.  N. Minallah, K. Ullah, J. Frnda, L. Hasan and J. Nedoma, “On the performance of video resolution, motion and dynamism in transmission using near-capacity transceiver for wireless communication,” Entropy, vol. 23, no. 5, pp. 562–586, 2021. [Google Scholar]

 4.  N. Minallah, K. Ullah, J. Frnda, K. Cengiz and M. A. Javed, “Transmitter diversity gain technique aided irregular channel coding for mobile video transmission,” Entropy, vol. 23, no. 2, pp. 235–256, 2021. [Google Scholar]

 5.  A. Khalil, N. Minallah, I. Ahmed, K. Ullah, J. Frnda et al., “Robust mobile video transmission using DSTS-SP via three-stage iterative joint source-channel decoding,” Human Centric Computing and Information Sciences, vol. 11, no. 42, pp. 343–359, 2021. [Google Scholar]

 6.  N. Minallah, M. F. U. Butt, I. U. Khan, I. Ahmed, K. S. Khattak et al., “Analysis of near-capacity iterative decoding schemes for wireless communication using EXIT charts,” IEEE Access, vol. 8, pp. 124424–124436, 2020. [Google Scholar]

 7.  N. Minallah, I. Ahmed, M. Ijaz, A. S. Khan, L. Hasan et al., “On the performance of self-concatenated coding for wireless mobile video transmission using DSTS-SP-assisted smart antenna system,” Wireless Communications and Mobile Computing, vol. 5, no. 11, pp. 1530–8669, 2021. [Google Scholar]

 8.  A. Guyader, E. Fabre, C. Guillemot and M. Robert, “Joint source channel turbo decoding of entropy-coded sources,” IEEE Journal on Selected Areas in Communications, vol. 19, no. 9, pp. 1680–1696, 2001. [Google Scholar]

 9.  J. Kliewer and R. Thobaben, “Iterative joint source-channel decoding of variable-length codes using residual source redundancy,” IEEE Transactions on Wireless Communications, vol. 4, no. 3, pp. 919–929, 2005. [Google Scholar]

10. R. G. Maunder, J. Wang, S. X. Ng, L. Yang and L. Hanzo, “On the performance and complexity of irregular variable length codes for near-capacity joint source and channel coding,” IEEE Transactions on Wireless Communications, vol. 7, no. 4, pp. 1338–1347, 2008. [Google Scholar]

11. T. Fingscheidt and P. Vary, “Softbit speech decoding: A new approach to error concealment,” IEEE Transactions on Speech and Audio Processing, vol. 9, no. 3, pp. 240–251, 2001. [Google Scholar]

12. M. Adrat and P. Vary, “Iterative source-channel decoding: Improved system design using exit charts,” EURASIP Journal on Applied Signal Processing, vol. 2005, pp. 928–941, 2005. [Google Scholar]

13. J. Ostermann, J. Bormans, P. List, D. Marpe, M. Narroschke et al., “Video coding with h. 264/avc: tools, performance, and complexity,” IEEE Circuits and Systems Magazine, vol. 4, no. 1, pp. 7–28, 2004. [Google Scholar]

14. J. Hagenauer, “The exit chart-introduction to extrinsic information transfer in iterative processing,” in 2004 12th European Signal Processing Conf., IEEE, pp. 1541–1548, 2004. [Google Scholar]

15. S. T. Brink, “Designing iterative decoding schemes with the extrinsic information transfer chart,” AEU Int. J. Electron Commun., vol. 54, no. 6, pp. 389–398, 2000. [Google Scholar]

16. L. Hanzo, P. Cherriman and E. Kuan, “Interactive cellular and cordless video telephony: State-of-the-art system design principles and expected performance,” Proceedings of the IEEE, vol. 88, no. 9, pp. 1388–1413, 2000. [Google Scholar]

17. F. Liang, C. Shen and F. Wu, “An iterative bp-cnn architecture for channel decoding,” IEEE Journal of Selected Topics in Signal Processing, vol. 12, no. 1, pp. 144–159, 2018. [Google Scholar]

18. A. U. Gawas, “An overview on evolution of mobile wireless communication networks: 1G-6G,” International Journal on Recent and Innovation Trends in Computing and Communication, vol. 3, no. 5, pp. 3130–3133, 2015. [Google Scholar]

19. L. Khaled, W. Chen, Y. Shi, J. Zhang and Y. A. Zhang, “The roadmap to 6G: AI empowered wireless networks,” IEEE Communications Magazine, vol. 57, no. 8, pp. 84–90, 2019. [Google Scholar]

20. Y. Lisu, J. Wu, A. Zhou, E. Larsson and P. Fan, “Massively distributed antenna systems with nonideal optical fiber fronthauls: A promising technology for 6G wireless communication systems,” IEEE Vehicular Technology Magazine, vol. 15, no. 4, pp. 43–51, 2020. [Google Scholar]

21. L. Yu, L. Zilong, W. Miaowen, C. Donghong, D. Shuping et al., “Sparse code multiple access for 6G wireless communication networks: Recent advances and future directions,” IEEE Communications Standards Magazine, vol. 5, no. 2, pp. 92–99, 2021. [Google Scholar]

22. M. Viitanen, J. Sainio, A. Mercat, A. Lemmetti and J. Vanne, “From HEVC to VVC: The first development steps of a practical intra video encoder,” IEEE Transactions on Consumer Electronics, vol. 68, no. 2, pp. 139–148, 2022. [Google Scholar]

23. B. Bross, Y. Wang, Y. Ye, S. Liu, J. Chen et al., “Overview of the versatile video coding (VVC) standard and its applications,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 31, no. 10, pp. 3736–3764, 2021. [Google Scholar]

24. X. Zhao, S. Kim, Y. Zhao, H. E. Egilmez, M. Koo et al., “Transform coding in the VVC Standard,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 31, no. 10, pp. 3878–3890, 2021. [Google Scholar]

25. J. G. Proakis and M. Salehi, Digital Communications. vol. 4. New York: McGrawhill, 2001. [Google Scholar]

26. C. Urrea, J. Kern and R. L. Escobar, “Design of an interleaver with criteria to improve the performance of turbo codes in short block lengths,” Wireless Networks, vol. 28, no. 90, pp. 1428–1429, 2022. [Google Scholar]

27. L. A. Perisoara and R. Stoian, “The decision reliability of map, logmap, max-log-map and sova algorithms for turbo codes,” International Journal of Communications, vol. 2, no. 1, pp. 65–74, 2008. [Google Scholar]

28. C. Berrou, R. Pyndiah, P. Adde, C. Douillard and R. L. Bidan, “An overview of turbo codes and their applications,” in The European Conf. on Wireless Technology,, IEEE, pp. 1–9, 2005. [Google Scholar]

29. S. X. Ng, M. F. U. Butt and L. Hanzo, “On the union bounds of self-concatenated convolutional codes,” IEEE Signal Processing Letters, vol. 16, no. 9, pp. 754–757, 2009. [Google Scholar]

30. M. F. U. Butt, S. X. Ng and L. Hanzo, “Self-concatenated code design and its application in power-efficient cooperative communications,” IEEE Communications Surveys & Tutorials, vol. 14, no. 3, pp. 858–883, 2011. [Google Scholar]

31. M. F. U. Butt, “Self-concatenated coding for wireless communication systems,” PhD thesis, University of Southampton, 2010. [Google Scholar]