 Open Access
Open Access
ARTICLE
Privacy Data Management Mechanism Based on Blockchain and Federated Learning
1 Engineering Research Center of Digital Forensics of Ministry of Education, School of Computer, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2 Zhengde Polytechnic, Nanjing, 211106, China
3 Xi’an University of Posts & Telecommunications, Xi’an, 710061, China
4 Department of Cyber Security at VaporVM, Abu Dhabi, 999041, United Arab Emirates
* Corresponding Author: Xiaowan Wang. Email:
Computers, Materials & Continua 2023, 74(1), 37-53. https://doi.org/10.32604/cmc.2023.028843
Received 19 February 2022; Accepted 19 April 2022; Issue published 22 September 2022
Abstract
Due to the extensive use of various intelligent terminals and the popularity of network social tools, a large amount of data in the field of medical emerged. How to manage these massive data safely and reliably has become an important challenge for the medical network community. This paper proposes a data management framework of medical network community based on Consortium Blockchain (CB) and Federated learning (FL), which realizes the data security sharing between medical institutions and research institutions. Under this framework, the data security sharing mechanism of medical network community based on smart contract and the data privacy protection mechanism based on FL and alliance chain are designed to ensure the security of data and the privacy of important data in medical network community, respectively. An intelligent contract system based on Keyed-Homomorphic Public Key (KH-PKE) Encryption scheme is designed, so that medical data can be saved in the CB in the form of ciphertext, and the automatic sharing of data is realized. Zero knowledge mechanism is used to ensure the correctness of shared data. Moreover, the zero-knowledge mechanism introduces the dynamic group signature mechanism of chosen ciphertext attack (CCA) anonymity, which makes the scheme more efficient in computing and communication cost. In the end of this paper, the performance of the scheme is analyzed from both asymptotic and practical aspects. Through experimental comparative analysis, the scheme proposed in this paper is more effective and feasible.Keywords
With the accelerating process of digitization of medical systems in various countries, medical data shows an exponential upward trend [1]. Therefore, the fields of public medical management, online patient access and medical data management have become the research topics in academic and medical circles. The Internet has largely improved the traditional pattern of medical interrogation, thus forming a medical network community dominated by patients, research institutions and medical institutions. The community is conducive to alleviating the contradiction between patients and society. Different measures taken by relevant industries in various countries have proved this situation to a certain extent. In Estonia [2], a digital medical infrastructure was created to form a healthy community network of citizens and health care stakeholders (providers, insurance companies, etc.). Through this way, it is of great significance to study the reform of medical model under the new situation. The recent 2019 New Coronavirus (also known as 2019-nCoV and COVID-2019) pandemic also demonstrated the necessity to establish a medical network community. Through the management of patient medical data in various countries, research institutions can conduct data visual analysis based on big data [3], and provide government and other-decision-making institutions with real-time research and judgment and make these institutions able to predict the epidemic situation, which greatly reduces the momentum of public panic about the epidemic situation [4].
In the medical network community, the patient’s personal information data and condition information will be recorded to form big data [5]. Big data has been applied in many fields and plays a particularly critical role in the decision-making process of many hospital institutions [6]. For the security needs of data management, medical institutions have the responsibility to take confidentiality measures for patients’ private data [7,8]. If being leaked, this information may be biased. FL keeps all sensitive data in the local organization to which the data belongs, which makes it possible to combine fragmented medical data sources with privacy protection. Although the training method of FL exchanging model parameters without exchanging specific data can effectively protect users’ privacy, FL still faces some security risks. In the training process of FL model, though the local original data of each user will not be disclosed, but it still have limitation that if there are ‘dishonest’, ‘honest and curious’ servers or malicious clients, the user’s local data information may still be deduced from the updated model parameters, that is, reasoning attack, poisoning attack and attack of Generative Adversarial Networks (GAN) and other types of attacks [9]. Therefore, the privacy protection ability of important data under FL environment is insufficient.
Security and privacy of data management are priorities [10]. In order to make up for the lack of privacy protection of important data in FL, we use KH-PKE scheme to hide patient data information and data sources. At the same time, FL algorithms can reduce the frequency of data communication and reduce the risk of exposing patient data. Therefore, when considering data security, we use the smart contract system based on the above-mentioned KH-PKE solution instead of the joint server to realize that medical data can be uploaded to the CB and realize the automatic sharing of medical data. In each round of federation, smart contracts collect data from medical and research institutions and return aggregated parameters for all parties to automatically update the Machine Learning model. In view of the openness and distributed execution of smart contracts, all parties can also verify the correct execution of the steps in an open manner at any time. The goal is to construct a zero-knowledge proof scheme for lightweight devices under FL without excessively increasing the scale of proof, so as to realize medical data management. It hides the addresses of the sender and receiver to achieve anonymity and privacy protection. In non-interactive zero knowledge (NIZK), the dynamic group signature scheme based on CCA anonymity we used makes the NIZK scheme more secure and efficient in computing and communication cost. In the end, we combined theory and practice to analyze, and simulated and implemented the program on a personal computer.
We organize the rest of this article as follows. The second section introduces the related work, and the third section mainly constructs the data security management framework of medical network community based on CB and FL. The fourth section mainly introduces the data security sharing mechanism of medical network community based on smart contract. The fifth section mainly constructs the data privacy protection mechanism based on FL and CB and compares it with the previous schemes. The sixth section is the conclusions of this paper.
2.1 Data Management in Consortium Blockchain
The ideal medical data management scheme should meet the following basic requirements, namely security and privacy protection [11], data access [12], access control and unified standards [13]. Therefore, the scheme proposed in this paper should meet the following requirements.
1. Security and privacy protection: no one may illegally use medical data. The program should be able to ensure that the data resists illegal attacks.
2. Data access: after obtaining the authorization, the research institution can view all relevant medical records, and the research institution can access the previous medical information under the authorization of the medical institution.
3. Access control: only medical institutions can manage patient data, that is, no one can obtain historical data without the consent of the medical institution.
4. Unified standards: unified data management standards should be adopted in the model to balance the overall stability of the system.
2.2 Data Management in the Consortium Blockchain with Federated Learning
The powerful, robust, flexible and secure functions of FL data cognition is helpful to solve the problem of the reliability, security, privacy protection of CB data management and optimize the storage data cost of blockchain data sharing.
Providing a trusted mechanism for all participants of FL through blockchain. The parameters of the FL model can be stored in the blockchain to ensure its security and reliability. FL has the characteristics of distributed intelligence and data privacy protection. It combines with the CB to complement each other’s advantages and improve the overall security of the system.
Some researchers use blockchain as a secure distributed ledger, which provides a potential solution for cross system management of medical information. Li et al. [14] constructed a privacy data storage protocol based on elliptic curve using ring signature to ensure data security and user identity privacy in blockchain applications. Omar et al. [15] proposed a patient-centered medical data management system medical chain, which realized privacy protection based on blockchain. Liu et al. [16] proposed a privacy protection electronic medical records management scheme based on blockchain. The original data is stored in the cloud environment, and the data index is retained in the CB to reduce the risk of disclosure [17]. However, the above scheme is not suitable for the confidentiality and constantly updated data requirements in our system.
3 Data Security Management Framework of Medical Network Community
3.1 Privacy Data Protection in Federated Learning
In the process of FL model training, the user’s local data information may still be deduced from the updated model parameters by reasoning attack, and may also be subject to poisoning attack, and attack of GAN and other types of attacks. At the same time, FL does not detect and verify the participants. Malicious participants may attack and destroy the FL training process by providing false model parameters, resulting in training failure. Therefore, the privacy protection ability of important data in FL is insufficient.
In the medical network community, data security is the premise of medical big data management. FL’s common privacy protection technologies, such as secure multi-party computing and differential privacy, are not enough to ensure data security [18,19]. At the same time, if privacy data was leaked, it would cause serious harm to patients. However, the development trend of medical big data is sharing and opening. Therefore, we should strengthen the ability of privacy protection in FL on the premise of ensuring the effective sharing of training data among participants, so as to give full play to the value of data management.
In order to make up for the lack of privacy protection of important data in FL, a zero-knowledge proof scheme suitable for lightweight devices is constructed to realize medical data management. In NIZK scheme, CCA anonymous dynamic group signature mechanism [20] is more secure and efficient in computing and communication cost. The signature mechanism can be used in the CB to provide unlinkability and anonymity, so as to improve the ability of data management and privacy protection in the medical CB. At the same time, in order to consider the security of private data, a smart contract system for the safe sharing of medical data is constructed based on the KH-PKE scheme to realize that the medical data hidden and stored in medical institutions and research institutions are stored on the CB for automatic data sharing operation to meet the needs of more High privacy requirements.
3.2 Medical Network Community Based on Consortium Blockchain and Federated Learning
Consortium Blockchain network: as a part of the blockchain [21], the CB has more advantages in efficiency and flexibility than the public blockchain, and can provide better privacy protection. It uses the distributed and tamper proof characteristics of blockchain to realize the secure storage and sharing of medical and health data and reduce the management cost. as shown in Fig. 1.
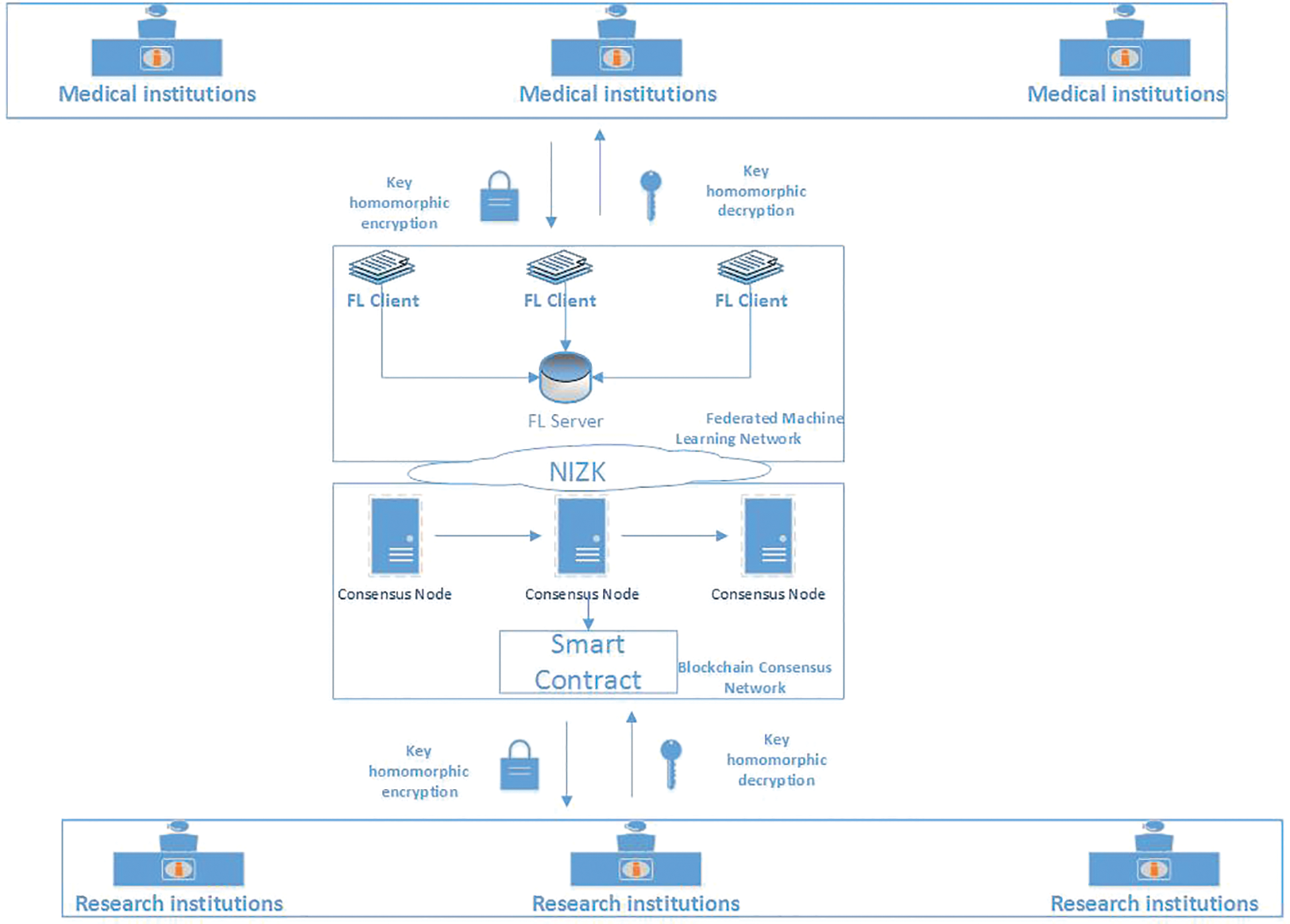
Figure 1: Medical network community framework based on Consortium Blockchain and Federated learning
Federated learning network: providing a trusted mechanism for all participants of federated learning through CB. On an artificial neural network predictive model (ANN) [22], use weight parameters and biases to train medical data and upload the trained data to a smart contract for data sharing. Keeping medical data on the blockchain throughout the data sharing environment. At the same time, the global model is stored and shared using the blockchain, thus avoiding a potential single point of failure on a central server.
Entity: including research institutions and medical institutions. The mechanism of KH-PKE scheme is used to directly store ciphertext and perform some calculations on the FL and blockchain. There is no need to make any change to the FL and CB itself, so as to provide confidentiality and privacy protection in the process of data management between research institutions and medical institutions.
4 Data Security Sharing Mechanism of Medical Network Community
CB can provide technical support for the security protocol and training method of FL algorithm. After the data of medical institutions are encrypted by the mechanism of KH-PKE scheme, the local model parameters are calculated by FL. Finally, upload the data to the smart contract, aggregate different data information and return the results. At the same time, smart contracts can also resist poisoning attacks and improve the security of private data.
In the medical network community, in order to consider the security of private data, public key encryption schemes are usually used to hide medical data. However, the fact that homomorphic public key encryption schemes are vulnerable to (adaptive) ciphertext selection attacks has been ignored to some extent. Theoretically, the adversary sends a homomorphic evaluation challenge ciphertext to the decryption oracle, and can immediately destroy the security. Therefore, we use the KH-PKE scheme to hide medical privacy data to meet higher privacy requirements. Homomorphic encryption scheme can only achieve indistinguishable encryptions under chosen plaintext attack security. Our KH-PKE scheme evaluates the secret key by controlling the homomorphic operation function and achieves stronger security than indistinguishable encryptions under chosen ciphertext attack(IND-CCA1) and is as close to indistinguishable encryptions under adaptive chosen ciphertext attack(IND-CCA2) as possible. Then, the structure is described under the secure under the decision linear(DLIN) assumption, and its security proof is given.
Definition 1 (KH-PKE): let M be a message space and ⊙ be a binary operation on M. We require that for all
Gen:The secret key generation algorithm takes the security parameter
Enc:The encryption algorithm takes
Dec:The decryption algorithm takes
Eval:The evaluation algorithm adopts
So far, the above KH-PKE scheme does not realize the homomorphic attribute, but the homomorphic function is reflected in the correctness defined below. Let
Definition 2 (correctness). For all
Definition 3 (KH-CCA Security). a KH-PKE scheme is considered to meet KH-CCA security if for any PPT adversary A:
It can be ignored in
• Evaluate oracle
• Homomorphic key disclosures oracle
• Decryption prophecy
• Lemma 1. Under the DLIN assumption , the above KH-PKE scheme meets the IND-CCA1 security.
Proof. Suppose that the effective adversary A destroys the KH-KHE scheme in the sense of KH-CCA with a non-negligible probability poly(n) and gives a tuple
Algorithm
Select
When A sends ciphertext C as the decryption query, B forwards C as the decryption query of B.
Sampling
If
Otherwise, returns 0.
• If
• If
Therefore, the probability of B distinguishes the distributions
In the medical network community environment, assuming that A and B want to share medical data, they will publish a medical data sharing information on the medical CB, which is basically written as follows. The medical data ciphertext t of medical institution A is shared with research institution B, then σ is t’s signature. Then, the consortium chain first verifies whether the signature is correct, that is, whether there is medical data t in A. If so, the data sharing operation will be carried out and the behavior will be published on the CB, otherwise the behavior will be ignored. as shown in Fig. 2.

Figure 2: Data security sharing of medical network community based on smart contract
In the above data sharing process, we can all know the medical data t shared from A to B (that is, the privacy of the shared medical data t is not guaranteed). Therefore, in Section 5, this paper introduces a data privacy protection scheme based on FL and CB, which is used to prove the security of medical data t under data sharing operation.
5 Data Privacy Protection Mechanism Based on Federated Learning and Blockchain
This section constructs an efficient NIZK scheme. The scheme first constructs a Σ-Protocols [23], and then use the Fiat-Shamir heuristic method to construct the NIZK protocol in the FL environment. Finally, the NIZK scheme for complete lightweight devices is obtained by using the set member proof protocol. At the same time, CCA anonymous dynamic group signature mechanism is introduced, which greatly improves the time efficiency of generating proof. The signature mechanism is more secure and efficient in computing and communication cost under the data security management framework of medical network community [24], based on CB and FL. At the same time, the NIZK scheme is used to realize the security sharing of medical data, and verify the correctness of medical data under the sharing operation on the smart contract. Below, we will construct the design details of a zero-knowledge proof scheme suitable for FL.
NIZK parameters have certifier A and verifier B. Suppose the plaintext space is
Setup. Generate a bilinear group [25]
That is,
Run
That is
Therefore, the integer signature value
After receiving the group signature, the verifier returns
• Partylnitial. For example, when the medical data
• Private key:
• Public key:
• Encrypted data:
According to the rules of sharing smart contract of medical data security, in the data sharing scenario, we explain how to construct a data sharing sentence
Assume that P and V are the prover and verifier, respectively. Fiat-Shamir heuristic [26] converts the Σ-protocol into NIZK parameters: After calculating a from P, the challenge c = H(a) is obtained. Among them, H is a random oracle. Finally, calculate z and send the proof
The proof language L defining the P is as follows:
The data sharing sentence
A)
B)
C)
D)
E)
F)
Proof generation by P.
Certifier A takes PP as the public input and generates the NIZK proof of the above statement using private input
Proof of formula (A-F) through Σ-protocols. Formula (E) can be proved by the value range in [27,28]. Randomly select samples
Finally, A sends proof
The verifier V calculates c after receiving the proof π. Using the public input
Theorem 1. Assuming DLIN, q-Strong Diffie-Hellman(q-SDH) assumptions, Σ-protocols is a NIZK demonstration with perfect completeness, perfect zero knowledge and computational reliability in oracle model. In addition, complete zero knowledge is established in the standard common random stringmodel.
Proof. The following describes our proof conclusion.
Perfect Completeness. This property can be directly verified.
Soundness. It is assumed that the CCA anonymous dynamic group signature based on q-SDH assumptions is unforgeable, and its reliability is proved under the random oracle model. If the PUSH-PULL traffic(PPT) certifier
Then, construct the extractor Ext:
Verifier information can be extracted by calculation (for
Under the condition of extracting the prover, if
Perfect zero knowledge. Construct a simulated Sim to prove the proposition

Figure 3: Simulator for new NIZK parameters
The parameters are divided into 3 parts:
For clarity and convenience, we express the simulation parameters as
Set
In the argument of simulation, under the same conditions, the given value
The Fiat-Shamir heuristic algorithm is applied to the Σ-protocols to build NIZK, so as to achieve perfect zero-knowledge. At the same time, the reliability of the construction is proven in the model.
Set the set of
Under the condition of
where
Set
Combining (22) and (25), We conclude that for any inconsistent PPT adversary
(perfect) get zero knowledge property. The next step is to verify the correctness of NIZK scheme. Instead of verifying
by calculating
In the formula above, only two pairing calculations are calculated, which is more efficient than ((1),(2)). Meanwhile, ((1),(2))⇒ (29): after replacing all values
(29)⇒ ((1),(2)): Consider formula (29):
If
1)
2) There are some
That is, the probability is negative because
Overall, the overwhelming probability is
In this section, the NIZK scheme is compared with the existing zero-knowledge succinct non-interactive argument of knowledge(ZKSNARK), Hyrax and Bulletproofs. The specific comparison results are shown in Fig. 4. As shown in Fig. 4, compared with other work, our NIZK scheme will significantly improve the running time of the prover. In the actual comparison, we can see that our scheme is more than twice as fast as the Bulletproofs scheme in proving its running time. Compared with Hyrax and ZKSNARK, our prover also has advantages in running time. In the running time of the verifier, our scheme also optimizes the verification time efficiency of the verifier, which is significantly different from other schemes and reduces the data communication cost.
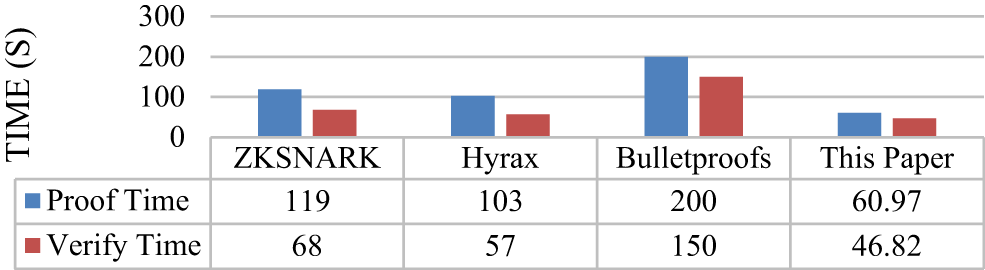
Figure 4: Comparison between NIZK scheme and existing zero knowledge proof(ZKP) system
Subsequently, the computational complexity of NIZK scheme is compared with the existing ZKSNARK, Hyrax and Bulletproofs schemes in theory and practice. This paper uses Python programming language to run experiments on Windows (Window 7, 64-bit), and uses Inter (R) Core (TM) i7-3687CPU with 2.10 and 8 GB RAM. However, the verifiers of ZKSNARK, Hyrax and Bulletproofs are memory intensive, so they are evaluated on a server with 100 GB memory and 322.80 GHz memory. The specific comparison results are shown in Tab. 1. Where C is the size of the circuit with depth

In order to verify the effectiveness of the overall scheme, this paper cites the medical dataset of the National Institutes of Health in the United States to evaluate the scheme. Firstly, we trained 60 epochs in the ensemble environment and used the ANN model to evaluate the results of the ensemble model training each epoch, as shown in Fig. 5. The experimental results show the fact that the original data has an impact on the accuracy of the model and the fact that it is beneficial to the training dataset under different circumstances.

Figure 5: Experiments 10 times to verify the accuracy of medical data
Secondly, in order to test the accuracy of the medical dataset in the CB and FL environment. The 10 participating institutions were simulated to assign the dataset in a random fashion. In this environment, 3 experimental results were randomly selected. The results show that the FL environment (black line) is significantly lower than the accuracy of the medical dataset in the consortium chain and FL environment (red line). Finally, using the ANN model can protect the medical data of the participating parties from attacks in the context of this paper. as shown in Fig. 6.
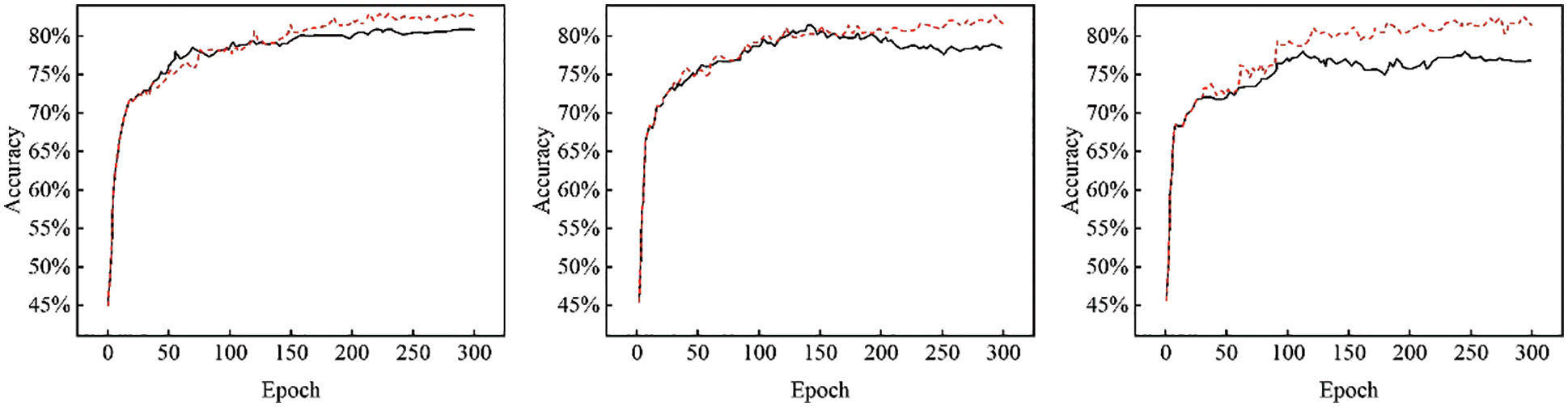
Figure 6: Results accuracy of the three participating institutions in the consortium chain and Federated learning environment
This paper presents a data management framework of medical network community based on CB and FL. An intelligent contract system based on KH-PKE scheme is designed to ensure the security of important data in medical network community. This paper also designs a NIZK scheme suitable for lightweight devices, and introduces CCA anonymous dynamic group signature, which greatly improves the time efficiency of generating proof and realizes the privacy protection of important data.
Funding Statement: This work is supported by the NSFC (No. 62072249). Yongjun Ren received the grant and the URLs to sponsors’ websites is https://www.nsfc.gov.cn/.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]
2. S. Balasubramanian, V. Shukla, J. S. Sethi, N. Islam and R. Saloum, “A readiness assessment framework for blockchain adoption: A healthcare case study,” Technological Forecasting and Social Change, vol. 165, no. 1, pp. 120536, 2021. [Google Scholar]
3. Y. J. Ren, Y. Leng, Y. P. Cheng and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]
4. C. P. Ge, Z. Liu, J. Y. Xia and L. M. Fang, “Revocable identity-based broadcast proxy re-encryption for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1214–1226, 2021. [Google Scholar]
5. T. Li, Y. Ren and J. Xia, “Blockchain queuing model with non-preemptive limited-priority,” Intelligent Automation & Soft Computing, vol. 26, no. 5, pp. 1111–1122, 2020. [Google Scholar]
6. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
7. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “A verifiable and fair attribute-based proxy re-encryption scheme for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 7, pp. 1–12, 2021. [Google Scholar]
8. Y. Ren, K. Zhu, Y. Q. Gao, J. Y. Xia, S. Zhou et al., “Long-term preservation of electronic record based on digital continuity in smart cities,” Computers, Materials & Continua, vol. 66, no. 3, pp. 3271–3287, 2021. [Google Scholar]
9. J. Wang, H. Han, H. Li, S. He, P. K. Sharma et al., “Multiple strategies differential privacy on sparse tensor factorization for network traffic analysis in 5G,” IEEE Transactions on Industrial Informatics, vol. 18, no. 3, pp. 1939–1948, 2022. [Google Scholar]
10. Y. J. Ren, Y. Leng, J. Qi, K. S. Pradip, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, no. 3, pp. 304–313, 2021. [Google Scholar]
11. C. P. Ge, W. Susilo, J. Baek, Z. Liu, J. Y. Xia et al., “Revocable attribute-based encryption with data integrity in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 8, pp. 1–12, 2021. [Google Scholar]
12. Y. Ren, F. J. Zhu, S. P. Kumar, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]
13. C. P. Ge, W. Susilo, Z. Liu, J. Y. Xia, L. M. Fang et al., “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 6, pp. 2787–2800, 2021. [Google Scholar]
14. X. F. Li, Y. R. Mei, J. Gong, F. Xiang and Z. X. Sun, “A blockchain privacy protection scheme based on ring signature,” IEEE Access, vol. 8, pp. 76765–76772, 2020. [Google Scholar]
15. A. A. Omar, M. S. Rahman, A. Basu and S. Kiyomoto, “Medibchain: A blockchain based privacy preserving platform for healthcare data,” in Int. Conf. on Security, Privacy and Anonymity in Computation, Communication and Storage, Canton, CAN, CHN, pp. 534–543, 2017. [Google Scholar]
16. J. W. Liu, X. L. Li, L. Ye, H. L. Zhang, X. J. Du et al., “BPDS: A blockchain based privacy-preserving data sharing for electronic medical records,” in 2018 IEEE Global Communications Conf. (GLOBECOM), Abu Dhabi, United Arab Emirates, pp. 1–6, 2018. [Google Scholar]
17. Y. Ren, J. Qi, Y. P. Liu, J. Wang and G. Kim, “Integrity verification mechanism of sensor data based on bilinear map accumulator,” ACM Transactions on Internet Technology, vol. 21, no. 1, pp. 1–20, 2021. [Google Scholar]
18. L. M. Fang, M. H. Li, Z. Liu, C. T. Lin, S. L. Ji et al., “A secure and authenticated mobile payment protocol against off-site attack strategy,” IEEE Transactions on Dependable and Secure Computing, vol. 21, no. 2, pp. 1–12, 2021. [Google Scholar]
19. J. Wang, C. Y. Jin, Q. Tang, N. X. Xiong and G. Srivastava, “Intelligent ubiquitous network accessibility for wireless-powered MEC in UAV-assisted B5G,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 4, pp. 2801–2813, 2021. [Google Scholar]
20. X. H. Yue, M. J. Sun, X. B. Wang, H. Shao and Y. He, “An efficient dynamic group signatures scheme with CCA-anonymity in standard model,” in Int. Symp. on Cyberspace Safety and Security, Canton, CAN, CHN, pp. 205–219, 2019. [Google Scholar]
21. Y. J. Ren, F. Zhu, J. Wang, P. Sharma and U. Ghosh, “Novel vote scheme for decision-making feedback based on blockchain in internet of vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 1639–1648, 2022. [Google Scholar]
22. J. S. Almeida, “Predictive non-linear modeling of complex data by artificial neural networks,” Current Opinion in Biotechnology, vol. 13, no. 1, pp. 72–76, 2002. [Google Scholar]
23. S. Ma, Y. Deng, D. He, J. Zhang and X. Xie, “An efficient NIZK scheme for privacy-preserving transactions over account-model blockchain,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 2, pp. 641–651, 2021. [Google Scholar]
24. L. Ren, J. Hu, M. Li, L. Zhang and J. Xia, “Structured graded lung rehabilitation for children with mechanical ventilation,” Computer Systems Science & Engineering, vol. 40, no. 1, pp. 139–150, 2022. [Google Scholar]
25. D. Boneh, B. Lynn and H. Shacham, “Short signatures from the Weil pairing,” Journal of Cryptology, vol. 17, no. 4, pp. 297–319, 2004. [Google Scholar]
26. A. Fiat and A. Shamir, “How to prove yourself: Practical solutions to identification and signature problems,” in Conf. on the Theory and Application of Cryptographic Techniques, Berlin, Germany, pp. 186–194, 1986. [Google Scholar]
27. J. Camenisch, R. Chaabouni and A. Shelat, “Efficient protocols for set membership and range proofs,” in Int. Conf. on the Theory and Application of Cryptology and Information Security, Berlin, Germany, pp. 234–252, 2008. [Google Scholar]
28. T. Li, W. D. Xu, L. N. Wang, N. P. Li, Y. J. Ren et al., “An integrated artificial neural network-based precipitation revision model,” KSII Transactions on Internet and Information Systems, vol. 15, no. 5, pp. 1690–1707, 2021. [Google Scholar]
29. R. S. Wahby, I. Tzialla, A. Shelat, J. Thaler, M. Walfish et al., “Doubly-efficient zksnarks without trusted setup,” in 2018 IEEE Symp. on Security and Privacy (SP), London, LON, United Kingdom, pp. 926–943, 2018. [Google Scholar]
30. B. Bünz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille et al., “Bulletproofs: Short proofs for confidential transactions and more,” in 2018 IEEE Symp. on Security and Privacy (SP), London, LON, United Kingdom, pp. 315–334, 2018. [Google Scholar]
31. E. Ben-Sasson, I. Bentov and Y. Horesh, “Scalable, transparent, and post-quantum secure computational integrity,” IACR Cryptol. ePrint Archive, vol. 2018, no. 46, 2018. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools