Employment Quality Evaluation Model Based on Hybrid Intelligent Algorithm

1  Introduction

With the continuous increase of employment, the employment pressure is increasing. There are often hundreds of job competing, so employment is facing great pressure. For a university, the employment quality is not only an important goal of the development of higher education, but also an important index to measure the talent training goal of colleges and universities [1]. The evaluation of employment quality can evaluate the change trend of employment quality and formulate corresponding talent training plans [2]. Therefore, the evaluation of employment quality of colleges and universities has become an important topic in the current research of colleges and universities. The traditional employment quality evaluation is mainly carried out through some expert experience [3–5]. Due to the simplification of expert information and certain limitations of knowledge, it is unable to describe the information of employment quality, which makes the deviation of employment quality evaluation large [6]. At the same time, the employment quality evaluation results of experts are blind. Then the employment quality evaluation technology based on qualitative analysis technology appeared, but because the change of employment quality is very complex, and the qualitative analysis technology can only describe the change of employment quality as a whole, the interpretation of the evaluation results of employment quality is relatively poor [7]. In recent years, with the research and development of artificial intelligence technology and machine learning theory, many scholars have introduced them into the research of employment quality, and proposed fuzzy C-means algorithm (FCM) and artificial neural network employment quality evaluation model, These algorithms can obtain better evaluation results of employment quality than qualitative analysis technology and expert experience [8]. However, in the actual evaluation, because the employment quality is related to many factors, these models can not well consider the influence of objective and human factors of employment quality, and the model evaluation is difficult to realize the accurate evaluation of employment quality network.To solve the problem of College Students’ employment quality, we must establish a complete and scientific evaluation model of College Students’ employment quality. Therefore, the design of College Students’ employment quality evaluation model has become an important research topic.

Based on the current research on employment quality evaluation and combined with the actual needs of employment quality evaluation, this paper puts forward Grey Relational Analysis (GRA) and employment quality evaluation module (GRA-FCM) of FCM clustering algorithm [9,10]. This model combines GRA with FCM clustering analysis algorithm, and processes the employment quality evaluation indexes through GRA algorithm, FCM clustering analysis algorithm is used to establish the employment quality evaluation model, and compared with other employment quality evaluation models, the employment quality evaluation model in this paper has great advantages, the accuracy of employment quality evaluation results is high, and can meet the development requirements of modern employment quality evaluation.

2  Design of Employment Quality Evaluation Index System

The construction of employment quality model is to analyze some factors affecting its change, find the change law of employment quality, and estimate and evaluate the future change trend of employment quality. The quality of employment is related to a variety of factors, including external factors, objective factors and subjective influence. These factors are expressed as indicators in the evaluation of employment quality. Therefore, it is necessary to establish an index system in the Fig. 1 that can describe the change characteristics of employment quality. According to the principles of diversification, comprehensiveness and easy data collection, the employment quality evaluation index system which are represented by x1∼x11 respectively [11–14].

Figure 1: Evaluation index system of employment quality

3  GRA-FCM Employment Quality Evaluation Model

3.1 GRA Algorithm Determines the Weight of Employment Quality Evaluation Index

GRA algorithm is a multivariable processing technology, which can describe the relationship between variables and the system. For the employment quality evaluation problem in this paper, it is to find the correlation between the evaluation index and the employment quality evaluation [15]. GRA algorithm is used to analyze the employment quality evaluation indicators, establish the corresponding statistical data of employment quality evaluation indicators, and convert them into geometric curves [16]. The closer the geometric curves are, the greater the correlation degree of employment quality evaluation indicators is [17]. The weight determination process of employment quality evaluation index based on GRA algorithm is as follows:

(1) Select the reference sequence of the employment quality evaluation index combination according to the employment quality evaluation objectives.

X0={x0(1),x0(2),⋅⋅⋅,x0(n)}(1)

In which, n represents the number of evaluation indicators.

(2) Collect employment quality evaluation index data as the samples.

(X1,X2,⋯,Xm)=[x1(1)x2(1)⋯xm(1)x1(1)x2(2)⋯xm(2)⋮⋮⋱⋮x1(n)x2(n)⋯xm(n)](2)

In which, m represents the number of employment quality evaluation samples; Xi={xi(1),xi(2),⋯,xi(n)}T.

(3) Because the dimensions of the employment quality evaluation indicators are different, the index values vary greatly in the order of magnitude, which will affect the efficiency of employment quality evaluation [18]. Therefore, in order to improve the efficiency of employment quality evaluation, this paper uses the extreme value method of Eq. (3) to deal with the employment quality evaluation indicators dimensionless, and the dimensionless results are shown in Eq. (4).

xl′(h)=xl(h)−xminxmax−xmin(3)

(x1′,x2′,⋯,xm′)=[x1′(1)x2′(1)⋯xm′(1)x1′(2)x2′(2)⋯xm′(2)⋮⋮⋱⋮x1′(n)x2′(n)⋯xm′(n)](4)

(4) Calculate the reference sequence of employment quality evaluation index combination and compare the maximum and minimum values of absolute difference, and obtain the grey correlation coefficient as follows:

εl(h)=min|X0(h)−Xl(h)|+ρ⋅max|X0(h)−X(h)||X0(h)−X1(h)|+ρ⋅max|X0(h)−X1(h)|(5)

In which, ρ is the resolution coefficient.

(5) Calculate the comprehensive relevance value of the employment quality evaluation index.

rl=1n∑h=1nεl(h)(6)

(6) Sort the employment quality evaluation indicators according to the comprehensive correlation value, remove some indicators with relatively small comprehensive correlation value, reduce the number of employment quality evaluation indicators and reduce the complexity of employment quality evaluation.

GRA algorithm is used to determine the weight of employment quality evaluation index, as shown in Fig. 2. As can be seen from Fig. 2, different indicators have different impact on the evaluation results of employment quality. Therefore, some indicators with weight less than 0.4 are deleted, and the remaining 7 employment quality evaluation indicators are left.

Figure 2: Weights of employment quality evaluation indicators

3.2 Establishment of Employment Quality Evaluation Model by FCM Algorithm

3.2.1 FCM Algorithm

Mean clustering algorithm is a data classification method, which divides different data into multiple types. However, mean clustering algorithm has some limitations [18–21]. Some scholars introduced fuzzy theory and produced FCM algorithm on the basis of mean clustering algorithm. The basic working idea is: first classify the objective function, then design certain fuzzy rules, calculate the distance between all samples and the cluster center, and finally determine the attribution category of each sample according to the distance [22–27].

The employment quality evaluation sample set is X={x1,x2,⋯,xn}, n represents the number of employment quality evaluation samples; the k employment quality evaluation sample is xk={x1,x2,⋯,xkp}, p represents the number of employment quality evaluation indicators. The employment quality is divided into C grades, that is, there are C clustering centers, which can be expressed as V={V1,V2,…,VC}, then the membership matrix can be obtained as U=[uik]c×v. It meets the following conditions:

uik∈[0,1],1≤i≤C,1≤k≤n(7)

∑i=1cuik=1,1≤k≤n(8)

In which, uik represents the membership degree of the kth employment quality evaluation sample belonging to the ith grade.

The objective function is defined as follows:

J(U,V)=∑i=1c∑k=1n(uik)m‖xk−vi‖(9)

In which, m is the fuzzy weighted index; vi represents the ith cluster center.

3.2.2 Steps of Establishing Employment Quality Evaluation Model by FCM Algorithm

(1) The grade of the employment quality evaluation result is C, the initialization cluster center of the employment quality evaluation is V0, the number of iterations is t=0, and the iteration stop threshold is set to ε.

(2) Calculate the membership of the employment quality evaluation sample according to Eq. (10):

uij=∑k=1c‖xi−vj‖2m−1/‖xi−vk‖2m−1(10)

(3) Update the cluster center as follows:

vi=∑j=1nuijmxj/∑j=1nuijm(11)

(4) If ‖V(k+1)−Vk‖<ε, the cluster center is obtained, the employment quality evaluation model is established according to the cluster center. Otherwise, k=k+1 and return to step (2) to continue the iteration.

3.3 Employment Quality Evaluation Steps of GRA-FCM Algorithm

(1) Establish an employment quality evaluation index system and collect corresponding employment quality evaluation index data.

(2) The grade of employment quality is divided. This paper is divided into five grades: excellent, good, medium, qualified and unqualified, which are described by 1~5 respectively.

(3) Analyze the employment quality evaluation index data by experts, determine the corresponding employment quality level, and establish the sample data of employment quality level evaluation.

(4) Use GRA algorithm to determine the weight of employment quality evaluation indicators, set a certain threshold, and remove the indicators whose weight is less than the threshold.

(5) Process the sample data of employment quality grade evaluation according to the important indicators retained by GRA algorithm to obtain the learning sample set.

(6) According to the learning sample set, the employment quality evaluation model is established by using FCM algorithm.

(7) For the sample data without knowing the employment quality level, the established employment quality evaluation model is used for analysis to obtain the corresponding level.

4  Simulation Test

4.1 Data Source of Test Environment and Employment Quality Evaluation

In order to analyze the advantages of GRA-FCM’s employment quality evaluation, the employment quality evaluation model of GRA algorithm and the employment quality evaluation model of FCM algorithm are selected for comparative experiments. The specific configuration of the test environment is: Basic frequency of CPU is higher than 3.2 GHz; Memory is greater than 16 GB; Hard disk is greater than 250 GB; Network card is greater than 100 MB; Operating system is Windows system; The programming environment is based on the Python language [28,29].

Collect the historical data of employment quality as the test object. The employment quality evaluation results adopt the 100 point system to normalize the employment quality and make them in the range of 0~1. A total of 500 historical data of employment quality are obtained. The normalized data are shown in Tab. 1.

4.2 Results and Analysis

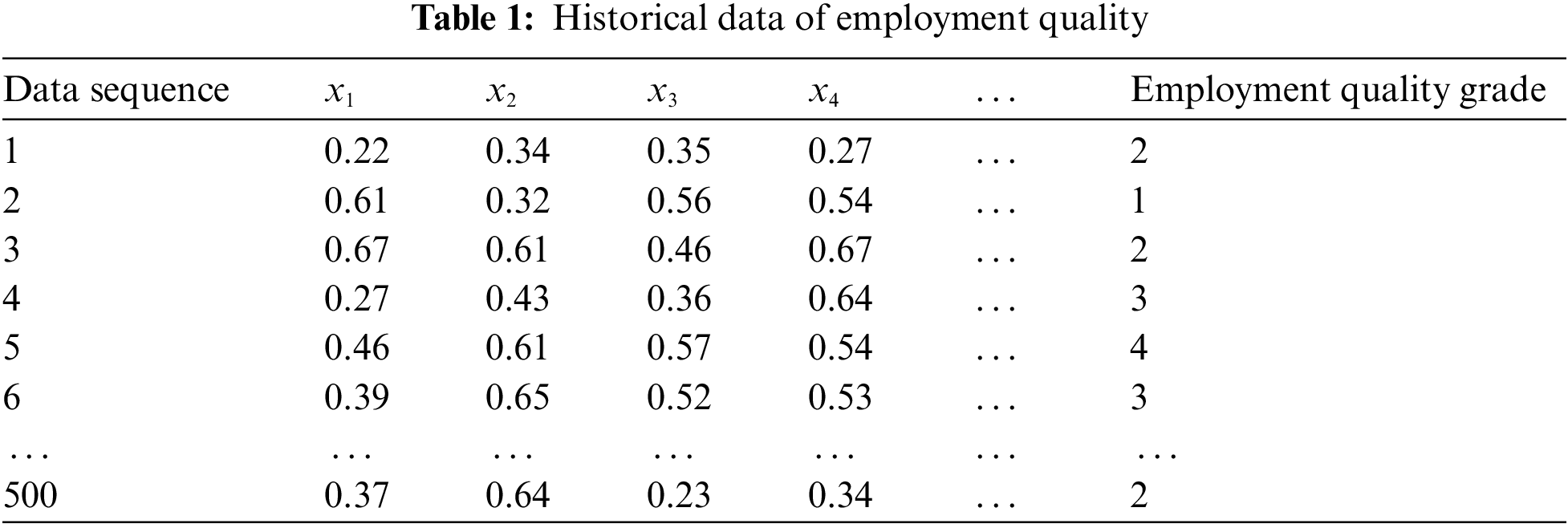
Five test experiments were conducted to reflect the fairness of the employment quality test. For each test, 100 samples were randomly selected from Tab. 1 to form the employment quality test sample set, and the other 400 samples formed the training sample set of employment quality. GRA-FCM, GRA algorithm and FCM algorithm were used to learn the training sample set of employment quality, Establish the employment quality evaluation model, evaluate the test sample set of employment quality, and count the employment quality evaluation accuracy of each experiment. The results are shown in Fig. 3.

Figure 3: Comparison of evaluation accuracy of employment quality of different models

By analyzing the accuracy of employment quality evaluation in Fig. 3, the following conclusions can be drawn:

(1) The accuracy of employment quality evaluation of GRA algorithm and FCM algorithm is lower than 85%, and the error of employment quality evaluation in practical application is required to be controlled within 10%, so they can not meet the actual requirements. This is because GRA algorithm and FCM algorithm can only describe the change characteristics of employment quality from one aspect, and can not accurately describe the change characteristics of employment quality, resulting in employment quality the evaluation error is large.

(2) Compared with GRA and FCM algorithms, GRA - FCM improves the accuracy of employment quality evaluation, significantly suppresses the error of employment quality evaluation, and controls the error of employment quality evaluation within the scope of practical application. This is because GRA-FCM makes use of the advantages of GRA and FCM algorithms, realizes the complementary advantages of GRA and FCM algorithms, and can better reflect the change characteristics of employment quality required by errors, It overcomes the disadvantages of the current employment quality evaluation model, and the comparative test results verify the superiority of GRA-FCM’s employment quality evaluation.

The employment quality evaluation training and testing time of 5 test experiments were counted. The average value between is shown in Tab. 2.

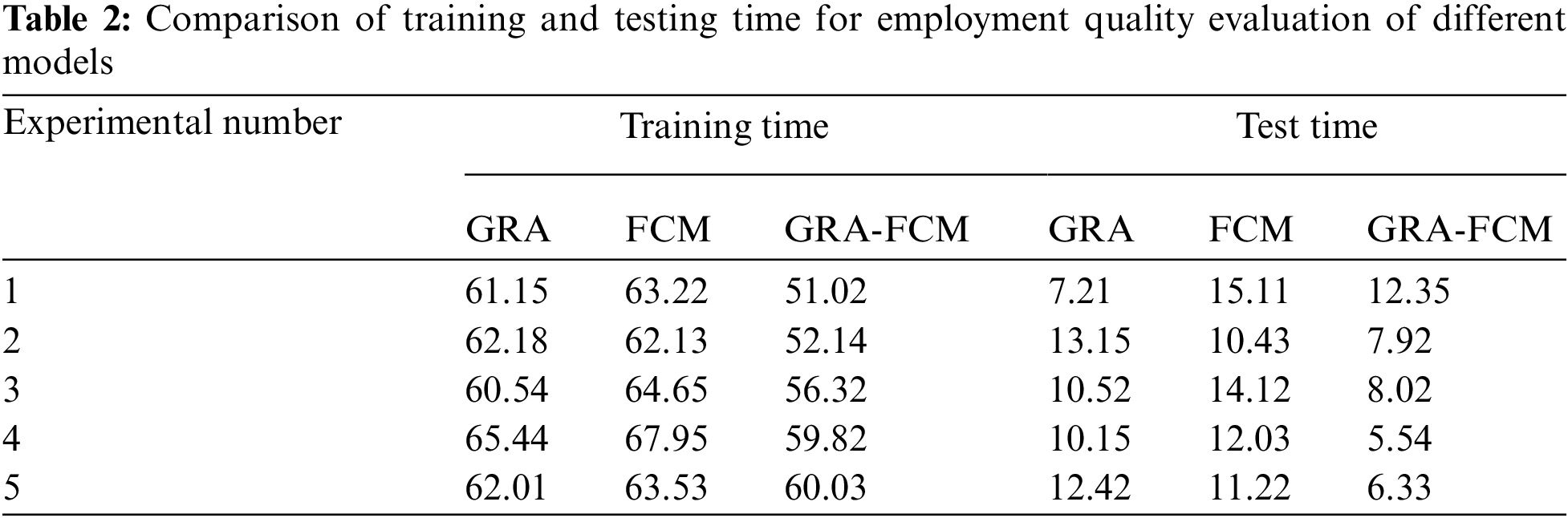
It can be seen from Tab. 2 that regardless of the training and testing time of employment quality evaluation, the employment quality evaluation time of GRA-FCM is significantly shorter than that of GRA and FCM algorithms, which can meet the requirements of the development of modern employment quality evaluation to online.

5  Conclusion

College Students’ employment is the focus and focus of current colleges and universities,so the employment quality evaluation has become its key core issue. The employment quality is related to many factors. Different evaluation methods have different emphasis on employment evaluation. There are some problems of long evaluation time and low evaluation accuracy in employment quality evaluation, so this study proposes an employment quality evaluation model based on GRA - FCM algorithm. The test and simulation show that the model can well overcome the problems of large error and low reliability in the traditional employment quality evaluation model, and can control the error accuracy within 6%, and can well meet the requirements of employment quality evaluation of modern vocational education. It can provide online information for employment management and government employment quality supervision, and realize real-time and dynamic grasp of the universities and colleges employment quality,and can better serve students and achieve high-quality and accurate employment.

Acknowledgement: Thank the team members for their hard work, the scientific research platform provided by the University, and the strong support from the government funds.

Funding Statement: This work was supported by the project of science and technology of Henan province under Grant No. 222102240024 and 202102210269, and the Key Scientific Research projects in Colleges and Universities in Henan Grant No. 22A460013 and No. 22B413004.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Li, Q. Wu and W. Zhang, “Water resources security evaluation model based on grey relational analysis and analytic network process: A case study of guizhou province,” Journal of Water Process Engineering, vol. 37, no. 10, pp. 160–166, 2020. [Google Scholar]

 2.  R. Qiu, J. Pan and J. Zhao, “Evaluation of ELINT system effectiveness based on grey relational optimization algorithm,” Journal of Physics Conference Series, vol. 1, no. 16, pp. 628–630, 2020. [Google Scholar]

 3.  L. Yang and N. Xie, “Evaluation of provincial integration degree of ‘internet + industry’ based on matrix grey relational analysis Case of China 2014-2016,” Grey Systems: Theory and Application, vol. 9, no. 1, pp. 31–44, 2019. [Google Scholar]

 4.  D. H. Liu, J. H. Li and Y. Peng, “Comprehensive evaluation of sintering basic characteristics of iron ore based on grey relational analysis,” Journal of Iron and Steel Research, International, vol. 12, no. 1, pp. 432–440, 2019. [Google Scholar]

 5.  Y. U. Zhuo and L. Meng, “Comprehensive evaluation of P2P lending platform development based on entropy method and grey relational analysis,” Jilin Normal University Journal, vol. 12, no. 3, pp. 68–72, 2019. [Google Scholar]

 6.  H. Wang, G. Jia and R. Wei, “Decision making method of University Asset Allocation based on deng’s grey relational analysis,” Journal of Physics: Conference Series, vol. 3, no. 46, pp. 4–8, 2021. [Google Scholar]

 7.  L. J. Zhang, L. M. Zhou, L. Ning and J. Chen, “Research on the “five high” employment quality evaluation system of college graduates based on AHP--Taking Lanzhou Petrochemical Vocational and Technical University as an example,” Modern Information Technology, vol. 9, no. 5, pp. 134–137, 2021. [Google Scholar]

 8.  X. K. Meng and S. S. Xu, “Evaluation model of college students’ employment quality based on grey correlation analysis and deep learning,” Modern Electronic Technology, vol. 44, no. 3, pp. 100–104, 2021. [Google Scholar]

 9.  L. Ling and K. Wu, “Research on micro employment quality of graduate students majoring in graphic information based on BOD evaluation model--Taking n University as an example,” Information Science, vol. 38, no. 11, pp. 142–147, 2020. [Google Scholar]

10. J. Li and J. X. Xu, “Construction and application of graduate employment quality evaluation model,” Regional Governance, vol. 4, no. 36, pp. 163–165, 2019. [Google Scholar]

11. S. N. Qiu, “Research on employment quality evaluation of college graduates based on grey correlation analysis,” North China University of Water Resources and Hydropower, vol. 3, no. 1, pp. 64–70, 2019. [Google Scholar]

12. Y. L. Liu, X. L. Huang, D. Jin and H. M. Zhang, “The assessment of traffic accident risk based on grey relational analysis and fuzzy comprehensive evaluation method,” Natural Hazards, vol. 88, no. 3, pp. 1409–1422, 2017. [Google Scholar]

13. P. Wang, D. H. Zhang, B. Chen, S. Li and G. H. Ma, “Multi process scheme evaluation based on fuzzy comprehensive evaluation and grey correlation analysis,” Journal of Aerospace Power, vol. 27, no. 9, pp. 2075–2085, 2012. [Google Scholar]

14. B. O. P. Soepangkat, R. Norcahyo, P. Rupajati, M. K. Effendi and H. C. K. Agustin, “Multi-objective optimization in wire-EDM process using grey relational analysis method (GRA) and backpropagation neural network-genetic algorithm (BPNN-GA) methods,” Multidiscipline Modeling in Materials and Structures, vol. 15, no. 5, pp. 1016–1034, 2019. [Google Scholar]

15. Y. Sheng, J. Zhang, W. Tan, J. Wu, H. Lin et al., “Application of grey model and neural network in financial revenue forecast,” Computers, Materials & Continua, vol. 69, no. 3, pp. 4043–4059, 2021. [Google Scholar]

16. K. Balaji, M. S. Kumar and N. Yuvaraj, “Multi objective taguchi grey relational analysis and krill herd algorithm approaches to investigate the parametric optimization in abrasive water jet drilling of stainless steel,” Applied Soft Computing, vol. 102, no. 12, pp. 70–75, 2021. [Google Scholar]

17. M. Premkumar, P. Jangir, B. S. Kumar, M. A. Alqudah and K. S. Nisar, “Multi-objective grey wolf optimization algorithm for solving real-world bldc motor design problem,” Computers, Materials & Continua, vol. 70, no. 2, pp. 2435–2452, 2022. [Google Scholar]

18. J. X. Zhou and Y. S. Huang, “Research on evaluation model of employment quality of college graduates,” School Party Construction and Ideological Education, vol. 2, no. 1, pp. 88–90, 2018. [Google Scholar]

19. Y. Z. Tian, “Construction of college talent training quality index system based on CIPP model,” Journal of Three Gorges University, vol. 39, no. 2, pp. 175–177, 2017. [Google Scholar]

20. X. M. Zhao, K. Meng, X. Gao, H. Y. Wu, L. F. Kong et al., “Establishment of employment quality evaluation model for college graduates and horizontal and vertical comparative study,” Journal of Heilongjiang Bayi Agricultural Reclamation University, vol. 29, no. 5, pp. 111–119, 2017. [Google Scholar]

21. A. M. Abdullah, H. Rezk, A. Elbloye, M. K. Hassan and A. F. Mohamed, “Grey wolf optimizer-based fractional mppt for thermoelectric generator,” Intelligent Automation & Soft Computing, vol. 29, no. 3, pp. 729–740, 2021. [Google Scholar]

22. C. Jana, G. Muhiuddin and M. Pal, “Multiple-attribute decision-making problems based on SVTNH methods,” Journal of Ambient Intelligence and Humanized Computing, vol. 11, no. 2, pp. 3717–3733, 2020. [Google Scholar]

23. W. W. Kong, C. Y. Lu and C. M. Niu, “Application Research of employment quality measurement model based on principal component analysis,” Journal of Wuhan University of Technology (Information and Management Engineering Edition), vol. 38, no. 3, pp. 377–381, 2016. [Google Scholar]

24. R. Fessi, H. Rezk and S. Bouallègue, “Grey wolf optimization based tuning of terminal sliding mode controllers for a quadrotor,” Computers, Materials & Continua, vol. 68, no. 2, pp. 2265–2282, 2021. [Google Scholar]

25. Y. H. Wu, Y. B. Wang and Y. Z. Shi, “Evaluation model of employment quality of college graduates based on analytic hierarchy process,” Journal of Bengbu University, vol. 3, no. 2, pp. 24–28, 2014. [Google Scholar]

26. W. Sung and S. Hsiao, “Employing a fuzzy approach for monitoring fish pond culture environment,” Intelligent Automation & Soft Computing, vol. 31, no. 2, pp. 987–1006, 2022. [Google Scholar]

27. Z. Y. Li, “Research on tracking and evaluation system of graduates in Higher Vocational Colleges,” Wireless Internet Technology, vol. 1, no. 4, pp. 179–182, 2014. [Google Scholar]

28. G. Shahzadi, G. Muhiuddin, M. Butt and A. Ashraf, “Hamacher interactive hybrid weighted averaging operators under fermatean fuzzy numbers,” Journal of Mathematics, vol. 2021, no. 3, pp. 1–17, 2021. [Google Scholar]

29. P. B. Dhandapani, D. Baleanu, J. Thippan and V. Sivakumar, “New fuzzy fractional epidemic model involving death population,” Computer Systems Science and Engineering, vol. 37, no. 3, pp. 331–346, 2021. [Google Scholar]