Deep Learning-Based Program-Wide Binary Code Similarity for Smart Contracts

1  Introduction

As one of the most successful applications of blockchain technology, smart contracts enable people make agreements while minimizing trusts, which are deployed in various decentralized applications [1]. However, many critical security vulnerabilities within smart contracts on Ethereum platform have caused huge financial losses to users [2]. Hence, the security analysis of smart contract has become a new trending of academic research [3–6]. Binary code similarity analysis (BCSA) quantitatively measures the similarities between two or more pieces of binary code, which has been widely adopted in diverse security applications such as plagiarism detection [7], malware detection [8], and vulnerability discovery [9]. Comparing binary code is especially fundamental for smart contracts where the contract source code is not available. For instance, only about 2 percent of the top 1.5 million smart contracts deployed on the blockchain disclose the source code on the Ethereum browser Etherscan [10].

Conventional BCSA approaches mainly aimed at detecting the similarity between binary functions [11], such as raw feature-based bug search [12], but they are unable to deal with the opcode reordering issue caused by different compilations. Recently, graph embedding-based methods are proposed to solve BCSA since machine learning has shown great success that lead to promising results in program analysis [13].

Despite the surging research interest in BCSA, it is significantly challenging to perform new research in smart contract for several reasons:(1) high reusability of smart contracts, which disenable existing methods directly employed on the smart contract binary code. (2) Prior works mostly focus on solving the BCSA issues at the token or function level, which is less applicable for the desired scenarios in smart contracts.

To solve the above problem, this paper proposes a neural network-based binary similarity detection on smart contract. We construct the binary code of smart contract as a program-wide Control Flow Graph (CFG) and employ graph neural networks to learn the contract representation. Particularly, we explore the improved GCN and MPNN models to capture the semantic information and the program-wide control flow information with temporal orders, leading to encouraging results of binary similarity detection in smart contract.

In conclusion, we summarize our contributions as follows:

•   We propose an end-to-end method based on graph neural network to solve the program-wide binary code similarity detection in smart contracts.

•   We propose a temporal graph neural network to learn the contract representation for similarity detection, which explicitly capture both the semantic and the temporal information to generate graph embeddings.

•   We conduct extensive experiments on two real-world smart contract datasets, and the results demonstrate our approach outperforms state-of-the-art methods on both accuracy and efficiency.

2  Related Work

In this section, we will briefly discuss the related work focusing on code similarity, which have been widely applied for bug search, plagiarism detection and vulnerability discovery [14].

For learning-based bug search approach [15], many researchers have worked on the problem of raw feature-based bug search in binaries, and made great progress in this direction. In general, they rely on various raw features extracted directly from binaries for code similarity matching. N-grams or N-perms [16] are two early approaches which adopt the binary sequence or mnemonic code matching without understanding the semantics of code, so they cannot solve the opcode reordering issue caused by different compilations. To further improve accuracy, the tracelet-based approach [17] captures execution sequences as features for code similarity checking, which solve the problem of opcode changes. Tree Edit Distance Based Equational Matching (TEDEM) [18] captures semantics using the expression tree for each basic block. However, the opcode and register names are different across architectures, so these two approaches are not suitable for finding bugs across architectures. The graph embedding used in graph analysis has two different meanings. The first one is to embed the nodes of a graph. This means finding a map from the nodes to a vector space, so that the structural information of the graph is preserved. In recent years, more and more works have adopted deep learning-based method to process large-scale graph datasets.

Another research line of graph embedding explored in this paper is to learn vectors that represent the entire graph, from tradition image processing [19–22] to program analysis [23]. Inspired by this, more researchers apply machine learning methods to handle tasks such as protein design and graph analysis [24]. Currently, the kernel method is a technology widely used to process structured data such as sequences and graphs.

The key to the kernel method is a carefully designed kernel function (a positive semi-definite function between a pair of nodes). For example, [25] counts specific subtree patterns in a graph; [26] counts the appearance of subgraph with specific sizes, where different structures will be counted in a process named Weisfeiler-Lehman (WL) algorithm. However, the kernels in these methods are fixed before learning, so the embedding space may suffer large dimensions. To overcome this problem, we explore graph neural network-based methods to learn both graph structure of smart contract CFGs and semantic information by extracting contract features.

3  Problem Statement

Problem formulation. Presented with a pair of smart contract binary codes, we focus on designing a fully automated approach that can identify binary similarity at the program level. That is, the label y^ for each smart contract binary pair, denoted by SP, where y^ = 1 represents contracts in SP are similar at a certain degree while y^ = 0 denotes the pair are not similar contracts. In this paper, we focus on two types of smart contracts.

Ethereum smart contract. Ethereum is an open-source public blockchain platform with smart contract functions. It provides decentralized Ethernet virtual machines to handle point-to-point contracts through its special cryptocurrency. Ethereum’s smart contract is not a common contract in reality, but an application executed by Ethereum virtual machine. These applications can be used to implement certain predetermined rules. In current releases of Ethereum, the smart contract code is executed on the Ethereum Virtual Machine (EVM). Developers can write smart contracts using Solidity, a high-level programming language [27], which are then compiled into EVM bytecode. For example, the smart contract named Owned in Fig. 1 provides a function for transferring ownership. After compilation, the contract is converted from the source code to its bytecode format. Then the binary code of smart contract is constructed as a program-wide CFG generated by Octopus [28], a security analysis tool translating bytecode into assembly representation and control flow graphs, in which the contract graph is represented by block nodes and edges referring to the jump relationship among blocks.

Figure 1: An example of Ethereum source code, bytecode and CFG

EOS smart contract. Enterprise Operation System (EOS) platform [29] is an open source public blockchain platform that focuses on the scalability of transaction speed. WebAssembly (WASM) [30] is a binary instruction format for a stack-based virtual machine, being adopted by the EOS blockchain platform for better efficiency and reliability. As shown in Fig. 2, the source code of a EOS smart contract is compiled into WASM bytecode for execution within the WASM Virtual Machine (VM). And the Application Binary Interfaces (ABIs) describe the public interfaces of the smart contract to interact with. Every EOS smart contract must provide an apply function as the entrance function to handle actions. For example, the transfer function of a smart contract is usually used to handle transfer actions related to the contract [31]. The apply function utilizes the receiver, code, and action input parameters as filters to map the actions to the corresponding functions [32].

4  Our Method

Method overview. The overall workflow of the method includes three stages: (1) graph generation phase, in which the graph representation is constructed from each targeted smart contract bytecode. (2) graph embedding phase, in which two improved neural networks MPNN and GCN are used to aggregate the information of each node in CFGs and learn a high-level embedding for each contract graph. (3) Similarity comparison phase calculates the consistent distance between the two embeddings to identify the similarity of each given contract pair.

4.1 Graph Generation

Our work mainly focuses on the binary code of smart contract and compares the similarity of the two binary contracts. To this end, we adopt Octopus (the classic security analysis framework of smart contracts) to deal with smart contracts in bytecode format on Ethereum and WASM format on EOS. Although there are many differences between the binary code of smart contract on Ethereum and EOS platforms, the graph representation generated by Octopus is relatively similar when dealing with these two binary codes. In the phase of graph generation, we collect block nodes and edges to construct smart contract CFGs, where the node set contains all basic blocks consisted of the instruction set. The edge set denotes the jump relationships among blocks. Then, we use word2vec to convert the block nodes into vector representation.

Figure 2: An example of EOS source code, bytecode and CFG

Figure 3: Overall structure of our improved model

4.2 Embedding Network

Our graph embedding network is inspired from the classic graph neural networks GCN and MPNN. Given a graph pair as p=<g,g′> where g=<V,E>, V and E are the sets of blocks and edges respectively. The embedding network will compute a p dimensional feature uv for each block v∈V and then the embedding vector ug of g will be computed as an aggregation of these block embeddings.

4.2.1 Improved GCN

GCN proposes to apply convolutional neural networks to graph-structured data, which develops a layer-wise propagation network as:

Xl+1=σ(D−12^A^D−12^XlWl)(1)

where A^ = A + I is the adjacency matrix (A) enhanced with self-loops (I), Xl is the feature matrix of layer l, and Wl is a trainable weight matrix. In the equation, the diagonal node degree matrix D^ is used to normalize A^.

When the node vector is output from the hidden layer, it is equivalent to encoding the nodes. Let hiT be the final hidden state of the ith nodes. We may generate the graph representation g^ by

g^=∑i=1|V|hiT(2)

where |V| denotes the number of major nodes.

4.2.2 Improved MPNN

MPNN consists of a message propagation phase and a readout phase. In the message propagation phase, MPNN passes information along the edges successively by following their temporal order. Then, MPNN computes a label for the entire graph G by using a readout function, which aggregates the final states of all nodes in G.

Formally, a contract graph is expressed by G = {V, E}, where V consists of all major nodes and E contains all edges. Denote E = {e1, e2,…, eN }, where ek represents the k-th temporal edge.

Message propagation phase. Messages are passed along the edges, one edge per time step. At time step 0, the hidden state hi0 for each node Vi is initialized with the feature of Vi. At time step k, message flows through the kth temporal edge ek and updates the hidden state of Vek, namely the end node of ek. Particularly, message mk is computed basing on hsk, the hidden state of the starting node of ek, and the edge type tk:

xk=hsk⊕tk(3)

mk=Wkxk+bk(4)

where ⊕ denotes concatenation operation, matrix Wk and bias vector b are network parameters. The original message xk contains information from the starting node of ek and edge ek itself, which are then transformed into a vector embedding using Wk and b.

After receiving the message, the end node of ek updates its hidden state hek by aggregating information from the incoming message and its previous state. Formally, hek is updated according to:

h^ek=tanh(Umk+Zhek+b1)(5)

hek′=softmax(Rh^ek+b2)(6)

where U,Z,R are matrices, while b1 and b2 are bias vectors.

Readout phase. After successively traversing all the edges in G, MPNN computes the graph embedding for G by reading out the final hidden states of all nodes. Let hiT be the final hidden state of the ith node, we may generate the graph embedding g^ by

g^=∑i=1|V|f(hiT)(7)

where f is a mapping function, e.g., a neural network, and |V| denotes the number of graph nodes.

4.3 Similarity Comparison

We use Siamese architecture to implement the same two graph embedded network. The Siamese architectures is a popular network architecture among tasks that involve finding similarity between two comparable things, which has been adopted by existing BCSA methods with good results [33]. Each graph embedding network will take a CFG as its input and output the embedded graph g^.The final output of Siamese architecture is the cosine distance of these two embedded contracts. In addition, the two embedding networks share the same parameter set. Therefore, during the training, the two networks remain same. Given a graph pair p=<g,g′>, with ground truth pairing information y∈{1,−1}, where y = 1 indicates that g and g′ are similar, otherwise y = −1.

y^=Sim(g^,g^′)=cos⁡(g^,g^′)=<g^,g^′>||g^||⋅||g^′||(8)

where g^ is the graph embedding representation generated by the improved GCN and MPNN.

At the same time, to train the model parameters for the above models, we will optimize the following objective function as follows:

min∑i=1K(Sim(gi,gi′)−yi)2(9)

We can optimize the objective of Expression (9) with stochastic gradient descent. The gradients of the parameters are calculated recursively according to the graph topology. In the end, once the Siamese network can achieve a good performance, the training process terminates.

5  Experiments

5.1 Experimental Settings

Datasets. Extensive experiments are conducted on two datasets of real-world binary contracts collected from the Ethereum and EOS platforms. Particularly, we collected the source code files of 44096 Ethereum smart contracts [24], which roughly contain 230452 independent smart contracts. After compilation, disassembly and de duplication, there are 3250 distinct contracts in the Ethereum dataset. For EOS, we collected 3881 real-world smart contracts [34]. After deduplication, there are 2306 contract binaries left in the EOS dataset. Then, we construct a series of similar contract pairs tagged as positive samples and a certain of dissimilar contract pairs tagged as negative samples for each distinct contract.

Compared methods. We compare our proposed approaches (improved GCN and MPNN) with a traditional graph matching method and two deep learning method. The traditional graph matching methods is WL [35], which calculates the structural similarity of two graphs based on subtree. The two deep learning methods are Density-Based Spatial Clustering of Application with Noise (DBSCAN) [36] and Gemini [33]. DBSCAN is a density-based spatial clustering algorithm while Gemini is a neural network-based method, which uses Structure2vec to compute the graph embedding of CFGs and identify whether the binary codes of two traditional high-level programs are similar. For the neural network-based methods, we randomly pick 80% contracts from each dataset as the training set while the remaining are utilized for the test set.

Metrics. In the comparison, classic metrics for BCSA such as accuracy, recall, precision, and F1 score are all involved. Particularly, the results of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) are used to compute the above metrics. The true values represent the number of correctly predicted results, which can be either true positive or true negative. The false values indicate that our model gives the wrong output.

The precision metric describes the ratio of truly positive values to all positive predictions. This indicates the reliability of the classifier’s positive prediction. The recall metric shows the proportion of actual positives that are correctly classified. The formulas to compute these two metrics are given below:

Precision=TPTP+FP(10)

Recall=TPTP+FN(11)

The F1 score metric is commonly used in information retrieval and it quantifies the overall decision accuracy using precision and recall. The F1 score is defined as the harmonic mean of the precision and recall:

F1=2∗Precision∗RecallPrecision+Recall(12)

Notice that, the best and the worst value of the F1 score is 1 and 0, respectively. The F1 score can be calculated for each class label or globally. In our evaluation, we use the weighted F1 score where the per-class F1 scores are weighted by the number of samples from that class.

Finally, the accuracy metric describes the effectiveness of our methods, which represents the correct proportion of all samples:

Accuracy=TP+TNTP+TN+FP+FN(13)

5.2 Results Analysis

Performance comparison in terms of the above metric is shown in Tab. 1, where we compare the proposed method (i.e., improved GCN and MPNN models) with existing approaches on the collected datasets. Meanwhile, we illustrate the effectiveness of our models by evaluating their ROCs in Figs. 4 and 5. Smart contracts on Ethereum and EOS are so different in instruction and size that we elaborately discuss the experimental results respectively.

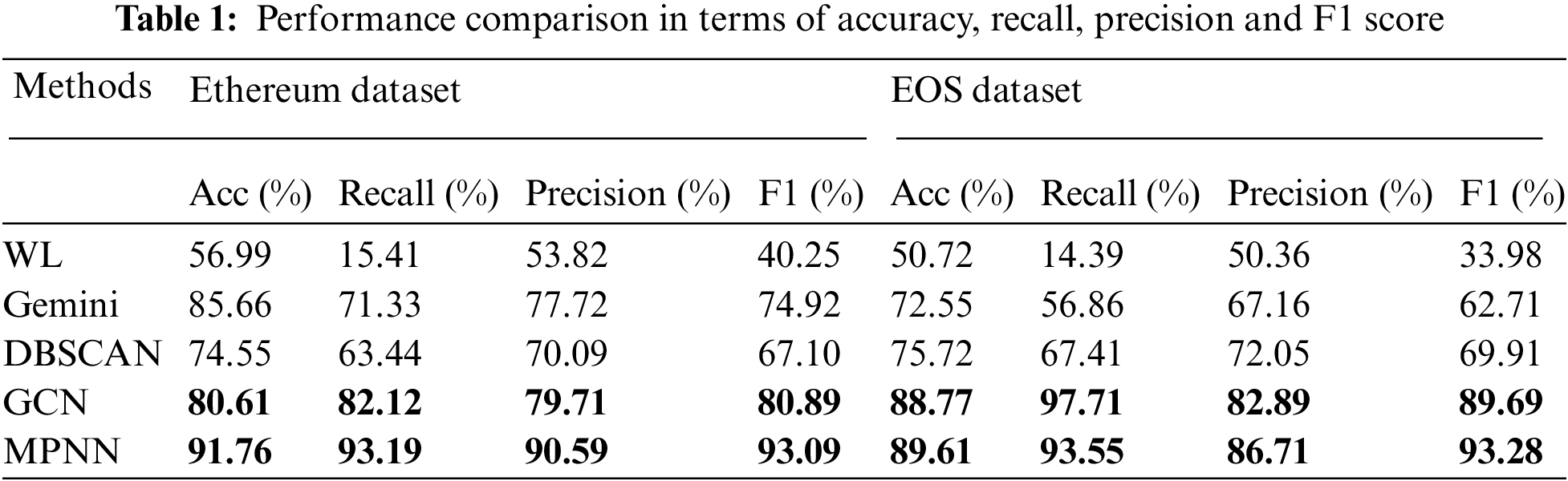
Figure 4: ROC analysis for GCN, MPNN on Ethereum dataset

Figure 5: ROC analysis for GCN, MPNN on EOS dataset

5.2.1 Comparison on Ethereum Dataset

Firstly, we compare the improved GCN and MPNN methods with WL, DBSCAN and Gemini in the similarity detection of Ethereum binary contracts. Tab. 1 shows the performance of different methods via the metric accuracy, recall, accuracy and F1 score.

From the quantitative results in Tab. 1, we have the following observations. Firstly, it confirms that the traditional method has not achieved satisfied accuracy in the similarity detection. For example, the accuracy of WL is 56.45%. Second, the improved MPNN method has achieved great improvement over the traditional method. More specifically, MPNN achieves an accuracy of 91.76%. Compared with the traditional method, the accuracy has been increased by 35.31%. Third, the improved GCN also obtains better results than the traditional method. The empirical results prove that the application of graph neural network to binary contract similarity detection has great potential. We further study the traditional similarity detection tool to explore the reason behind these observations. WL heavily relies on graphic structure while ignoring the semantic information within blocks, leading to its low accuracy and other metrics.

To verify if the proposed neural network-based methods can successfully detect the similarity of Ethereum smart contracts, we compare our method with the well-known deep learning method in BCSA, i.e., Gemini. Experimental results show that the performance of Gemini is better than the traditional method WL, the clustering method DBSCAN and the improved GCN. This informs that only considering both graphical information and semantic information can outperform in similarity detection. In the meanwhile, we want to emphasize that the improved MPNN model achieves the high scores in all four indicators, since more messages passed by edges contribute to the final embeddings of contract CFGs. ROCs shown in Fig. 4 also illustrate the effectiveness of our two proposed model, the larger the ROC area, the stronger the similarity detection ability.

5.2.2 Comparison on EOS Dataset

We list comparison results of the binary similarity detection of EOS contracts in Tab. 1. It indicates that static method fails to identify contract similarity when processing complex smart contracts, where the accuracy rate is only about 50%. However, our methods are able to deal with complex programs, though the results of MPNN do not change much but GCN’s are significantly improved. This confirms that GCN is relatively good at processing complex graph information. The reason is that when MPNN and GCN learn a given contract CFG, they take the semantic information of each node into consideration. Then this information will be transmitted to neighboring nodes along with the edge message between nodes, and finally obtain a complete graph representation of the CFG that is more capable of expressing the complex contracts.

Compared to the neural network methods, the ability dealing with complex programs of Gemini is significantly reduced, while the performance of DBSCAN is not influenced by the program complexity. At the same time, two improved models we propose outperform than these two methods, especially when solving the BSCA problem in terms of binary contracts. This is because Gemini deals with traditional high-level languages, but smart contracts and traditional high-level languages have huge differences in functionality and implementation. It also can be observed from Fig. 5 where our models have achieved promising ROCs.

5.3 Case Study

The goal of our proposed graph neural network models is to better understand and identify the similarity of the given smart contract binary code pair. As illustrated in Fig. 3, we elaborate the proposed workflow with an example of two similar smart contract, which are generated by the same smart contract with different compiler versions.

Understanding binary code is a difficult problem, so we firstly generate graph representations, i.e., CFGs, of these two binary contracts shown in Fig. 6. Basic blocks of different instruction sets are modeled as nodes and control flow relationship between nodes are modeled as edges in CFGs. To clearly show the dissimilar parts of these contract graphs, we use ‘…’ to represent the similar blocks in the CFGs and add the serial number to identify different blocks. Then we utilize word2vec to convert the block nodes into vector representation and feed to the next graph embedding network. In the graph embedding phase, we exploit the proposed graph neural network (e.g., the well trained CGN or MPNN model) to encode the input graph representation into a high-level embedding. In other words, each graph embedding network will take a CFG as its input and output the graph embeddings. Lastly, we use the cosine distance of these two embeddings to detect whether the pair of smart contracts is similar or not. In this case, the detection result is similar, which proves the accuracy of our proposed method in the similarity detection.

Figure 6: Example CFGs of a similar smart contract pair

From the Fig. 6, we can see both the graph structure of CFGs and the instruction sets of basic blocks have a certain difference between the contract pair. For example, Block1, block10, and block38 with some stack operation instructions like DUP1, POP, have little effect on instruction analysis. In contrast, there are more useful instructions in block10. By learning the graph features, i.e., the semantic information of these blocks and the graph structure of the binary contract pair, our proposed model can correctly determine that the given binary files of contract pair are similar.

6  Conclusion

In this paper, we proposed a deep learning-based scheme for program-wide binary code similarity of smart contracts, in which improved GCN and MPNN models are exploited for similarity detection of two given binary contracts. We used control-flow graph (CFG) to represent binary code of smart contract, and then graph neural network is adopted to generate the graph embedding. We then employed the Siamese Network for integrating two identical graph neural networks to calculate the similarity between two contract encodings. As far as we concerned, this is the first work that apply the similarity detection method to the binary contracts. For the model training, we built two real-world datasets from two well-known blockchain platforms, i.e., Ethereum and EOS respectively, containing 49,725 binary smart contracts in total. Compared with the state-of-art methods, we have achieved promising results on the accuracy of similarity detection. Evaluation results show that our method outperforms three state-of-the-art methods by achieving a great improvement up to 6.1% and 17.06% in accuracy. We believe that this is also an important step to continue to study the task of binary code similarity of smart contract.

Funding Statement: This work is supported by the Basic Research Program (No. JCKY2019210B029) and Network threat depth analysis software (KY10800210013).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Hu, Z. Zhang, J. Liu, Y. Liu, J. Yin et al., “A comprehensive survey on smart contract construction and execution: Paradigms, tools, and systems,” Patterns, vol. 2, no. 2, pp. 100179, 2021. [Google Scholar]

 2.  N. Atzei, M. Bartoletti and T. Cimoli, “A survey of attacks on Ethereum smart contracts (SoK),” in Int. Conf. on Principles of Security and Trust, Heidelberg, Berlin, pp. 164–186, 2017. [Google Scholar]

 3.  J. Huang, S. Han, W. You, W. Shi, B. Liang et al., “Hunting vulnerable smart contracts via graph embedding based bytecode matching,” IEEE Transactions on Information Forensics and Security, vol. 16, pp. 2144–2156, 2021. [Google Scholar]

 4.  B. Jiang, Y. Liu and W. K. Chan, “ContractFuzzer: Fuzzing smart contracts for vulnerability detection,” in 2018 33rd IEEE/ACM Int. Conf. on Automated Software Engineering (ASE), Montpellier, France, pp. 259–269, 2018. [Google Scholar]

 5.  Z. Liu, P. Qian, X. Wang, Y. Zhuang, L. Qiu et al., “Combining graph neural networks with expert knowledge for smart contract vulnerability detection,” IEEE Transactions on Knowledge and Data Engineering, Early Access, vol. 2021, pp. 1, 2021. https://doi.org/10.1109/TKDE.2021.3095196. [Google Scholar]

 6.  L. Luu, D. H. Chu, H. Olickel, P. Saxena and A. Hobor, “Making smart contracts smarter,” in Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security, Vienna, Austria, pp. 254–269, 2016. [Google Scholar]

 7.  J. Jang, D. Brumley and S. Venkataraman, “Bitshred: Feature hashing malware for scalable triage and semantic analysis,” in Proc. of the 18-th ACM Conf. on Computer and Communications Security, Chicago, Illinois, USA, pp. 309–320, 2011. [Google Scholar]

 8.  L. Luo, J. Ming, D. Wu, P. Liu and S. Zhu, “Semantics-based obfuscation-resilient binary code similarity comparison with applications to software plagiarism detection,” in Proc. of the 22nd Int. Symp. on Foundations of Software Engineering, Hong Kong, China, pp. 389–400, 2014. [Google Scholar]

 9.  X. Meng, B. P. Miller and K. S. Jun, “Identifying multiple authors in a binary program,” in Proc. of the 22nd European Symp. on Research in Computer Security, Oslo, Norway, pp. 286–304, 2017. [Google Scholar]

10. Etherscan, “The Ethereum block explorer,” 2021. [Online]. Available: https://etherscan.io/. [Google Scholar]

11. Q. Feng, R. Zhou, C. Xu, Y. Cheng, B. Testa et al., “Scalable graph-based bug search for firmware images,” in Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security, Vienna, Austria, pp. 480–491, 2016. [Google Scholar]

12. F. Zuo, X. Li, P. Young, L. Luo, Q. Zeng et al., “Neural machine translation inspired binary code similarity comparison beyond function pairs,” in Proc. of the 2019 Network and Distributed System Security Symp., San Diego, California, USA, pp. 1–15, 2019. [Google Scholar]

13. Z. Feng, D. Guo, D. Tang, N. Duan, X. Feng et al., “Codebert: A pre-trained model for programming and natural languages,” in Findings of the Association for Computational Linguistics: EMNLP 2020, Online, pp. 1536–1547, 2020. [Google Scholar]

14. J. Kivinen, A. J. Smola and R. C. Williamson, “Online learning with kernels,” IEEE Transactions on Signal Processing, vol. 52, no. 8, pp. 2165–2176, 2004. [Google Scholar]

15. Q. Feng, R. Zhou, C. Xu, Y. Cheng, B. Testa et al., “Scalable graph-based bug search for firmware images,” in ACM Conf. on Computer and Communications Security (CCS’16), Vienna, Austria, pp. 480–491, 2016. [Google Scholar]

16. W. M. Khoo, A. Mycroft and R. Anderson, “Rendezvous: A search engine for binary code,” in 2013 10th Working Conf. on Mining Software Repositories (MSR), San Francisco, CA, USA, pp. 329–338, 2013. [Google Scholar]

17. Y. David and E. Yahav, “Tracelet-based code search in executables,” in Proc. of the 35th ACM SIGPLAN Conf. on Programming Language Design and Implementation, New York, NY, 49, pp. 349–360, 2014. [Google Scholar]

18. J. Pewny, F. Schuster, L. Bernhard, T. Holz and C. Rossow, “Leveraging semantic signatures for bug search in binary programs,” in Proc. of the 30th Annual Computer Security Applications Conf., New Orleans, Louisiana, USA, pp. 406–415, 2014. [Google Scholar]

19. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

20. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

21. W. Sun, G. Z. Dai, X. R. Zhang, X. Z. He and X. Chen, “TBE-Net: A three-branch embedding network with part-aware ability and feature complementary learning for vehicle re-identification,” IEEE Transactions on Intelligent Transportation Systems, pp. 1–13, 2021. https://doi.org/10.1109/TITS.2021.3130403. [Google Scholar]

22. W. Sun, L. Dai, X. R. Zhang, P. S. Chang and X. Z. He, “RSOD: Real-time small object detection algorithm in UAV-based traffic monitoring,” Applied Intelligence, vol. 92, no. 6, pp. 1–16, 2021. [Google Scholar]

23. Y. Zhuang, Z. Liu, P. Qian, Q. Liu, X. Wang et al., “Smart contract vulnerability detection using graph neural network,” in IJCAI 2020, YoKohama, Japan, pp. 3283–3290, 2020. [Google Scholar]

24. B. Zhang, H. Ling, P. Li, Q. Wang, Y. Shi et al., “Multi-head attention graph network for few shot learning,” Computers, Materials & Continua, vol. 68, no. 2, pp. 1505–1517, 2021. [Google Scholar]

25. J. Ramon and T. Gärtner, “Expressivity versus efficiency of graph kernels,” in Proc. of the First Int. Workshop on Mining Graphs, Trees and Sequences, Cavtat-Dubrovnik, Croatia, pp. 65–74, 2003. [Google Scholar]

26. N. Shervashidze, P. Schweitzer, E. J. Leeuwen, K. Mehlhorn and K. M. Borgwardt, “Weisfeiler-lehman graph kernels,” Journal of Machine Learning Research, vol. 12, no. 9, pp. 2539–2561, 2011. [Google Scholar]

27. Solidity, 2021. [Online]. Available: https://solidity.readthedocs.io/en/v0.6.4/. [Google Scholar]

28. M. Angelo and G. Salzer, “A survey of tools for analyzing ethereum smart contracts,” in Proc. of the 2019 IEEE Int. Conf. on Decentralized Applications and Infrastructures (DAPPCON), Berlin, German, pp. 69–78, 2019. [Google Scholar]

29. EOSIO, 2021. [Online]. Available: https://eos.io/build-on-eosio/eosio-cdt/. [Google Scholar]

30. WebAssembly, 2021. [Online]. Available: https://webassembly.org/. [Google Scholar]

31. Transfer function of EOSIO smart contracts, 2021. [Online]. Available: https://developers.eos.io. [Google Scholar]

32. EOSIO ABI macro and apply, 2021. [Online]. Available: https://developers.eos.io/eosiocpp/v1.2.0/docs/abi. [Google Scholar]

33. X. Xu, C. Liu, Q. Feng, H. Yin, L. Song et al., “Neural network-based graph embedding for cross-platform binary code similarity detection,” in Proc. of the 2017 ACM SIGSAC Conf. on Computer and Communications Security, Dallas, Texas, USA, pp. 363–376, 2017. [Google Scholar]

34. Y. Huang, B. Jiang and W. Chan, “EOSFuzzer: Fuzzing EOSIO smart contracts for vulnerability detection,” in 12th Asia-Pacific Symp. on Internetware (Internetware’20), New York, USA, Association for Computing Machinery, pp. 99–109, 2020. [Google Scholar]

35. M. Sugiyama, M. E. Ghisu, F. Llinares-López and K. Borgwardt, “Graphkernels: R and Python packages for graph comparison,” Bioinformatics, vol. 34, no. 3, pp. 530–532, 2018. [Google Scholar]

36. F. G. Yasar and G. Ulutagay, “Challenges and possible solutions to density-based clustering,” in 2016 IEEE 8th Int. Conf. on Intelligent Systems, Sofia, Bulgaria, pp. 492–498, 2016. [Google Scholar]