Computers, Materials & Continua DOI:10.32604/cmc.2022.031626
Article

The Impact of Check Bits on the Performance of Bloom Filter

Rehan Ullah Khan1, Ali Mustafa Qamar2,*, Suliman A. Alsuhibany2 and Mohammed Alsuhaibani2

1Department of Information Technology, College of Computer, Qassim University, Buraydah, Saudi Arabia
2Department of Computer Science, College of Computer, Qassim University, Buraydah, Saudi Arabia
*Corresponding Author: Ali Mustafa Qamar. Email: al.khan@qu.edu.sa
Received: 22 April 2022; Accepted: 07 June 2022

Abstract: Bloom filter (BF) is a space-and-time efficient probabilistic technique that helps answer membership queries. However, BF faces several issues. The problems with traditional BF are generally two. Firstly, a large number of false positives can return wrong content when the data is queried. Secondly, the large size of BF is a bottleneck in the speed of querying and thus uses large memory. In order to solve the above two issues, in this article, we propose the check bits concept. From the implementation perspective, in the check bits approach, before saving the content value in the BF, we obtain the binary representation of the content value. Then, we take some bits of the content value, we call these the check bits. These bits are stored in a separate array such that they point to the same location as the BF. Finally, the content value (data) is stored in the BF based on the hash function values. Before retrieval of data from BF, the reverse process of the steps ensures that even if the same hash functions output has been generated for the content, the check bits make sure that the retrieval does not depend on the hash output alone. This thus helps in the reduction of false positives. In the experimental evaluation, we are able to reduce more than 50% of false positives. In our proposed approach, the false positives can still occur, however, false positives can only occur if the hash functions and check bits generate the same value for a particular content. The chances of such scenarios are less, therefore, we get a reduction of approximately more than 50% false positives in all cases. We believe that the proposed approach adds to the state of the art and opens new directions as such.

Keywords: Bloom filter; big data; network processing; optimization; check bits

1  Introduction

The exponentially growing usage of social media networks, online newspapers, and mobile applications, among many other platforms, has led to an unprecedented era of massive volumes of data generated daily. As a result, various techniques are developed to collect structured and unstructured data as part of what is referred to nowadays as big data [1].

A variety of applications can be found in big data, such as social networks and healthcare. A comprehensive study of indexing technologies for big data was recently done by Abdullahi et al. [2], which indicated that handling big data successfully and efficiently is challenging. Due to an exponential increase in the variety of cyberattacks, this challenge has played a pivotal role not just in indexing and membership queries, but likewise in big data security analytics [3]. Big data security analytics differentiate themselves by being able to correlate events across space and time, in addition to deeply examining and analyzing the network’s packets.

Accordingly, different techniques have been proposed and utilized in the field of big data security analytics. Bloom Filter (BF), developed by Bloom in 1970 [4], is a space-and-time efficient probabilistic data structure. In particular, the BF is generally known as a dense data structure that helps membership queries [5]. The enrichment of employing BF in terms of space-saving, locating, and saving time typically dominates a potential false positives’ poor rate that might appear in membership queries. This directly impacts the main characteristics of big data security analytics, which are scale, performance, and analytical flexibility.

A previously proposed work by Alsuhibany [6] has conducted an extensive experiment on using BF for big data security analysis. However, the False Positive Rate (FPR) growth was demonstrated. In the false positive case, a yes result is returned when the element is not a member of a given set. As such, the performance of the whole data analytics process can be negatively affected. Therefore, this paper proposes various techniques based on check bits to reduce the false-positive rate for the BF. The evaluation of the proposed methods gave quite promising results and helped reduce FPR by more than 80% in some cases.

The rest of the paper is organized as follows: Section 2 discusses the background and related works. Section 3 presents the proposed methodology, while the experiments and results are provided in Section 4. The paper is concluded in Section 5, along with the provision of some future directions.

2  Related Work

A bloom filter (BF) is a dense data structure that helps membership queries [5]. The enrichment of employing BF in terms of space-saving, locating, and saving time commonly overshadows a potential false-positive poor rate that might appear in membership queries. The core idea of the standard bloom filter (SBF) is to allocate a bit vector, B, of m bits that are initially assigned zeros, and then a pre-defined k number of independent hash functions, h1,h2,…,hk are adopted with a range {0,…,1−m} for each. The bits’ location of an element to be added, s, into the bit vector B are made as one such as B[h1(s)]=…=B[hk(s)]=1 to complete the element addition [7].

It is worth mentioning that some bits might be turned into one numerous times because some bits might be shared among the added elements. As such, bits at the location h1(s),…,hk(s) are checked to query using the BF whether a particular element, s, is a member of the BF or not. When the values of all checked bits are one, then the element in question is a member in B; otherwise, it is not. Nevertheless, the checked bits might be one, but the element s is not a member in B, in which case this probability is known as the false positive.

In false positive, a yes result is returned when the element is not actually in the filter. On the other side, it is not possible in BF to get a false negative, that is, getting ‘no’ when the element in question indeed exists in the filter. The false-positive probability can be computed as shown in Eq. (1).

f≈(1−(1−1m)kn)k≈(1−e−knm)k(1)

where f is the false positive rate (FPR), m is the storage size, and k is the computation time. There exists a tradeoff between m, k, and f such that f can be minimized by setting k=ln⁡2mn and f becomes fmin=(12)k≈(0.6185)mn. As such, f decreases as m increases in proportion to n [8].

Various types of BFs have been classified grounded on the application. However, because the work presented in this paper centers on introducing the concept of check bits and applying the BF in the network security domain, we only assess some types of BF, such as (i) standard BF (SBF), (ii) compressed (ComBF), (iii) dynamic (DBF), (iv) generalized (GBF), (v) hierarchical (HBF), (vi) space-code BF (SCBF), and their involvement in the network security field.

In SBF, which this paper utilizes to introduce the concept of check bits, the element set S:f=S→[0,1] membership function is stored [9]. With SBF, arbitrary functions can be encoded to associate values with a subset of the elements. While their efficient use of storage is maintained, such arbitrary functions can be generalized with dynamic updates though the functions remain unaffected.

ComBF [10] introduces a transmission size z alongside three main factors, k, m, and n. The idea behind this transmission size is that the data size must be sent over the network, which turns out to be significant in saving the bandwidth but with higher memory requirements cost. As highlighted previously, the SBF is only applicable with static (unchangeable over time) and known-size sets. To address this limitation, a DBF was introduced by Guo et al. [11], in which a dynamic set A with an active n × m bit matrix is created. The DBF initially starts with activating an SBF, followed by activating a new SBF only when the FPR starts growing. Once the new SBF is activated, the old one is switched to the new one. All other filters (old ones) are then deactivated, and only the last activated filter is maintained active.

SBF lacks the upper bound of the FPR, which is a lack of achieving 100% FPR, which might cause a security issue. The GBF was thus proposed by Laufer et al. [12] to tackle this issue with an upper bound on the FPR probability by setting the bits of the filter and resetting the bits by hash functions. GBF reports a robust performance for security purposes.

Instead of only using a single level of the probabilistic array, HBF uses two levels of arrays to lookup and map files inside a group of metadata servers [13]. The first array signifies the distribution of the metadata server to reduce the memory overhead considerably, while the second array caches a partial distribution information metadata server. HBF demonstrates an efficient and improved performance and scalability of the file system.

Kumar et al. [14] later introduced SCBF to approximate the measurement of per-flow traffic. Precisely, SCBF approximates using several SBFs the representation of a multiset for answering queries, such as whether an element x is an element of a multiset or not.

It is worth highlighting the involvement of the BF types mentioned earlier in the network security domain from the perspective of authentication, firewalling, anomaly detection, trace backing, node replication detection, anonymous routing and privacy-preserving, string matching, and SYN flooding addressing [6].

The SBF involves and is applicable in all of the aforementioned network security perspectives, which justifies utilizing it with the proposed check Bits approach in this paper. Nevertheless, ComBF, GBF, HBF, and SCBF are involved with trace backing alone, and similarly, DBF involvement is solely on node replication detection.

Alsuhibany [6] has introduced big data security analysis using BF. In particular, the counting BF with a smaller dataset was presented to test such a space-and-time efficient probabilistic technique with big data security analysis. However, such a concept was only evaluated with a small dataset using counting BF to prove the concept. Recently, potential vulnerabilities to cryptanalysis attacks are associated with BF’s encoded values. For example, an efficient simulated attack was conducted on BFs and reported success with re-identifying sensitive attribute values [15]. The efficient attack is later carried out on an actual database based on the BF construction principle of hashing elements of sets into the positions of bits. This process can effectively re-identify sensitive encoded values independently of the encoding function. Therefore, Christen et al. [15] proposed Hashing BF method seeking to utilize a single base hash function and some modulo operations to reduce the expenses caused by hash functions while maintaining a similar FPR.

For identifying the repeatedly co-occurring positions of bits in the BF set, Christen et al. [16] have similarly proposed a frequent item mining attack method. This attack method has the ability to re-identify the sensitive encoded values, despite the uniqueness of the encoded item set in the database. A study by Lu et al. [17] has later introduced an enhancement of BF called Ultra-Fast BF (UFBF), following the approach of the Single Instruction Multiple Data (SIMD) processor. UFBF mainly focuses on an efficient membership checking process with a bit-test process in parallel and encoding the bit information in a small block.

Patgiri et al. [18] analyzed the role of BF in big data research. They discussed fingerprint BF, a specific BF to match a fingerprint with stored fingerprints. Furthermore, they presented a Multidimensional BF that uses 2D, 3D, or even higher dimensional BF arrays. A BF is not suitable for exact query requirements e.g., real-time systems. Reviriego et al. [19] proposed one memory access BF that avoids false positives for repeated elements for various queries. The approach was tested in networking applications and an FPR of less than 5% was achieved while using as little as four bits per element. Another survey related to BF variants for different domains was conducted by Abdennebi et al. [20]. They discussed one hashing BF, which only uses a single function. Only some of the BF, such as Cuckoo BF, Counting BF, DBF, and High-dimensional BF allow deletions. Wu et al. [21] came up with an interesting idea of Elastic BF which offers deletion as well as expansion without increasing the FPR and avoiding the reduced query speed. They introduced Elastic fingerprints which absorb and release bits during compression and expansion.

To the best of our knowledge, none of the aforementioned related work has principally focused on addressing the issue of the increasing FPR. Hence, the work presented in this paper introduces a novel approach based on check bits, as a false positive reduction approach, as detailed in the next section.

3  Proposed Methodology

This section gives an overview of the proposed methodology. More specifically, we offer a novel method to reduce the false positive rate of the bloom filter. In particular, the proposed algorithm is based on the concept of using multiple check bits. The input element to the BF, which can be in textual or numeric form, is converted to binary format. Later, all the bits are added together to generate a number in decimal form. This is followed by converting the number once again to the binary form.

After getting the binary number, we devise various techniques to reduce the number of false positives. For our approach, the check bit offset is fixed to 1. It means that the increment of bits for taking check bits from the bits’ sample is 1. In case the check bits’ offset is more than one, there is a higher chance of getting out of the bits’ array (beyond 0 and beyond the maximum size) of the content bits. Moreover, we set the number of hash functions to three. With initial experiments, we found three hash functions to be optimal. Then, we varied different parameters, such as the check bits’ position (e.g., middle or at the left of the bits) and their number and bloom filter size. Fig. 1 shows the flowchart of the proposed method to reduce the false positives.

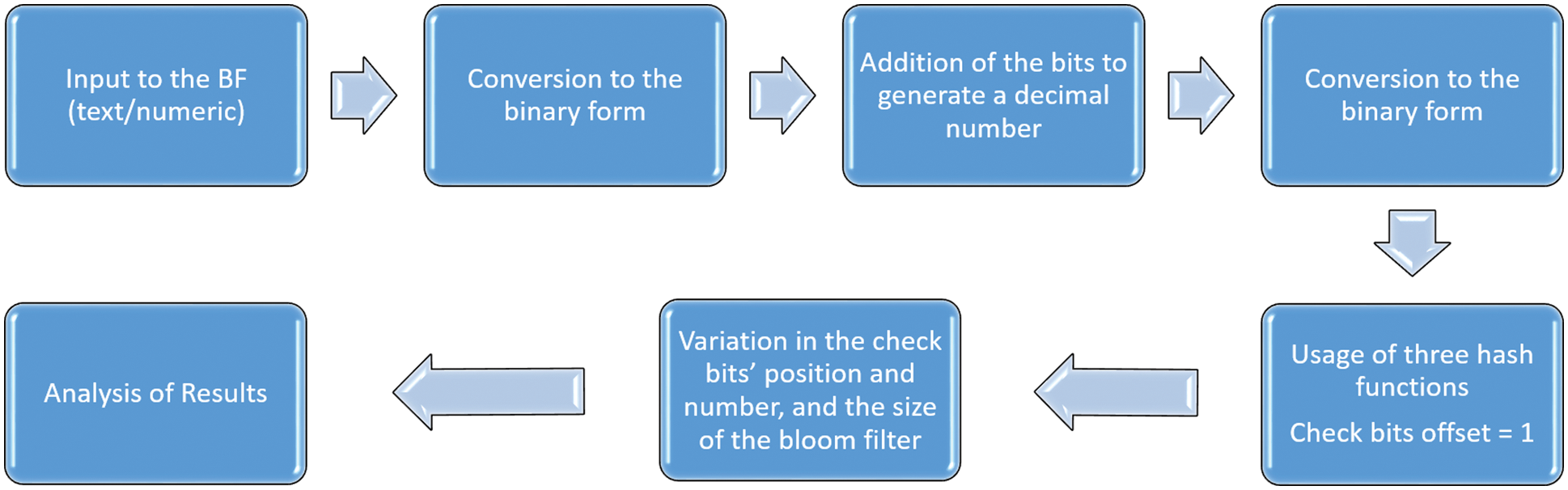
Figure 1: Flowchart of the proposed false positive reduction approaches

The stepwise implementation of the proposed algorithm in the form of Pseudo-Code is provided in Algorithm 1.

4  Experiments and Results

This section describes the experimental evaluation of the effect of the check bits.

4.1 Variation in the Number of Check Bits

Tab. 1 represents the constant parameters used for the first set of experiments. For these experiments, the check bit offset is fixed to 1. It means that the increment of bits for taking check bits from the bits’ sample is 1. The size of the bloom filter is kept at 500. We keep this size to analyze the influence of the check bits optimally. A large number can be used; however, the false positives can already be reduced without check bits by significantly increasing the bloom filter size. Therefore, we choose 500 to be the optimal size of the bloom filter for the tested dataset. Tab. 1 shows that three hash functions are used for the first set of experiments. With initial experiments, we found three hash functions to be optimal. For extracting the position of check bits, we start from the middle of the bits and increment by 1 for extracting the check bits.

Fig. 2 shows the first set of experiments and depicts the performance analysis of the number of check bits enabled/disabled. The x-axis indicates the number of check bits used. Y-axis shows the number of false-positive entries. The blue color shows the number of false positive for the corresponding check bits enabled. Similarly, the red bars show the performance when the check bits are disabled. For example, ‘2’ on the x-axis represent the check bits used while creating a bloom filter.

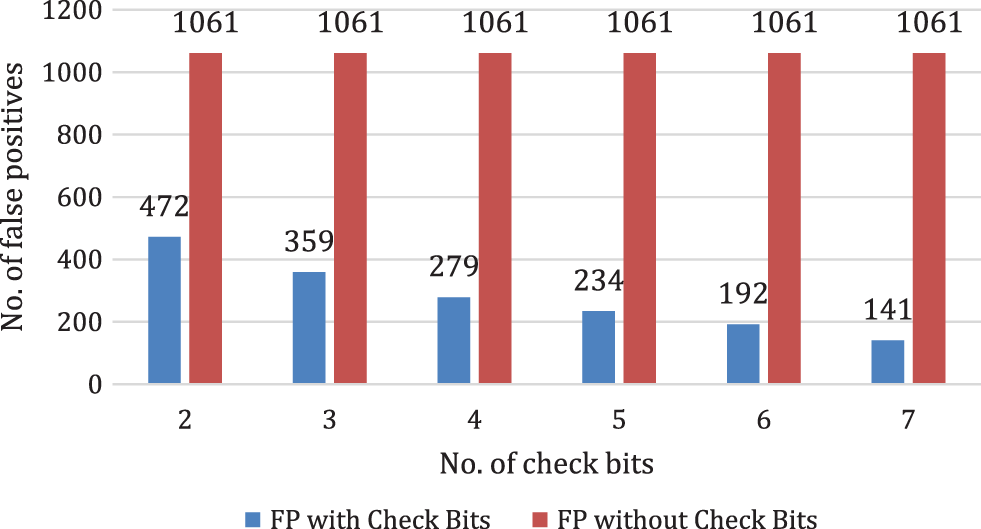
Figure 2: Check bits and their role in the false-positive reduction (check bits computed from the middle)

As seen in Fig. 2, for two check bits, the number of false positives without check bits is 1061. For being enabled, we get 472 false positives. For two check bits, we get 55.51% reductions. We got 359 false positives for three check bits when check bits were enabled, thus providing a 66.16% improvement in the number of false positives. Similarly, as the number of check bits increases, more and more reduction in the number of false positives is observed. 86.71% reduction is seen when the number of check bits is increased to 7.

4.2 Effect of the Position of Check Bits on the False Positives

The constant parameters for the second set of experiments are shown in Tab. 2. The check bit offset is kept as one, and three hash functions are used, just like in the first set of experiments. Moreover, the bloom filter size is fixed at 500, like in the first set of experiments. However, for extracting the position of check bits, we start from the leftmost bit and increment by 1 each time.

Fig. 3 shows the impact of this approach on the number of false positives. A gradual reduction in the number of false positives is observed as the number of check bits is increased from 2 to 7, where the check bits are computed from the left. The number of false positives without any check bits remained at 1061, just like the first set of experiments. 55.42% reduction in false positives is observed as two check bits are used. This increased to a 67.20% reduction as the number of check bits was incremented by 1. The maximum reduction is observed for seven check bits (82.66% reduction).

Figure 3: Check bits and their role in the reduction of false positives (check bits computed from the left)

4.3 Impact of Bloom Filter Size vs. Check Bits

Tab. 3 depicts the set of constant parameters used for the third set of experiments. In this set, the number of check bits is kept constant at 2. Similarly, the check bit offset is fixed as one, and three hash functions are used just like the first two sets of experiments. For extracting the position of the check bits, we still start from the middle of the bits.

The bloom filter size is increased from 500 to 3000 (six times increase), as shown in Fig. 4. The role of the size of the bloom filter on the number of false positives could be easily observed. Increasing and decreasing trends are seen for the number of false positives without using any check bits. As the bloom filter size is increased from 500 to 600, the false positives are increased from 1061 to 1125, representing an increase of 6.03%. On the other hand, the number of false positives decreased to 958 as the bloom filter size is further increased to 700, showing a reduction of 14.84%. The minimum number of false positives is observed for a bloom filter of size 2000. Increasing the size of the filter further to 3000 does not help further reduce the number of false positives. On the other hand, the number of false positives while using two check bits is 472.

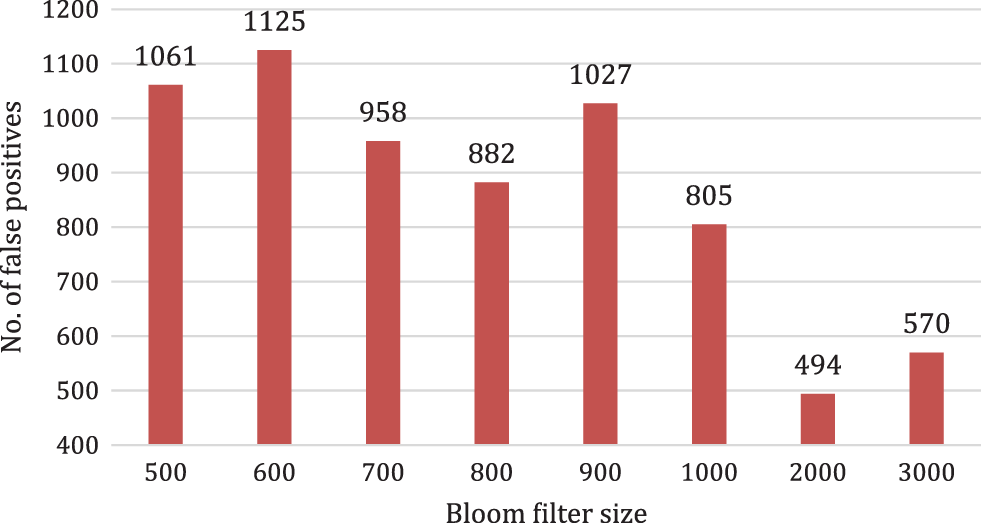
Figure 4: The role of the size of the bloom filter on the false positives

5  Conclusion and Future Work

This paper presented various techniques based on check bits to reduce the false-positive rate observed in a bloom filter. The bloom filter is a space-and-time efficient method designed to satisfy membership queries. We discussed techniques based on the positioning of the check bits, such as in the middle or on the left side. The proposed method got promising results and helped reduce the check bits up to more than 80% in some cases. Lastly, the impact of the bloom filter size on the number of false positives is also observed.

One of our future works is to evaluate the proposed false positive rate reduction method using a large dataset in different scenarios. Moreover, it might be interesting to apply the proposed method to the Cuckoo filter, which is somehow related to the bloom filter.

Funding Statement: The authors would like to thank the chair of Prince Faisal bin Mishaal Al Saud for Artificial Intelligent research for funding this research work through the project number QU-CPFAI-2-7-4. Also would like to extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education, and the Deanship of Scientific Research, Qassim University, for their support of this research.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Gani, A. Siddiqa, S. Shamshirband and F. Hanum, “A survey on indexing techniques for big data: Taxonomy and performance evaluation,” Knowledge and Information Systems, vol. 46, no. 2, pp. 241–284, 2016. [Google Scholar]

 2.  A. U. Abdullahi, R. Ahmad and N. M. Zakaria, “Indexing in big data mining and analytics,” in Machine Learning and Data Mining for Emerging Trend in Cyber Dynamics: Theories and Applications, Cham: Springer, pp. 123–143, 2021. [Google Scholar]

 3.  M. M. Alani, “Big data in cybersecurity: A survey of applications and future trends,” Journal of Reliable Intelligent Environments, vol. 7, no. 2, pp. 85–114, 2021. [Google Scholar]

 4.  B. Bloom, “Space/time trade-offs in hash coding with allowable errors,” Communications of the ACM, vol. 13, no. 7, pp. 422–426, 1970. [Google Scholar]

 5.  M. Gomez-Barrero, C. Rathgeb, G. Li, R. Ramachandra, J. Galbally et al., “Multi-biometric template protection based on bloom filters,” Information Fusion, vol. 42, no. 3, pp. 37–50, 2018. [Google Scholar]

 6.  S. A. Alsuhibany, “A space-and-time efficient technique for big data security analytics,” in Proc. of 4th Saudi Int. Conf. on Information Technology (Big Data Analysis) (KACSTIT), Riyadh, Saudi Arabia, pp. 1–6, 2016. [Google Scholar]

 7.  F. Grandi, “On the analysis of bloom filters,” Information Processing Letters, vol. 129, no. 7, pp. 35–39, 2018. [Google Scholar]

 8.  J. Yan and P. L. Cho, “Enhancing collaborative spam detection with bloom filters,” in Proc. of the 22nd Annual Computer Security Applications Conf. (ACSAC'06), Miami Beach, FL, USA, pp. 414–428, 2006. [Google Scholar]

 9.  B. Chazelle, J. Kilian, R. Rubinfeld and A. Tal, “The Bloomier filter: An efficient data structure for static support lookup tables,” in Proc. of the Fifteenth Annual ACM-SIAM Symp. on Discrete Algorithms (SODA), Portland, Oregon, USA, pp. 30–39, 2014. [Google Scholar]

10. M. Mitzenmacher, “Compressed Bloom filters,” IEEE/ACM Transactions on Networking, vol. 10, no. 5, pp. 604–612, 2002. [Google Scholar]

11. D. Guo, J. Wu, H. Chen and X. Luo, “Theory and network applications of dynamic bloom filters,” in Proc. of IEEE INFOCOM, 2006 25th IEEE Int. Conf. on Computer Communications, Barcelona, Spain, pp. 1–12, 2006. [Google Scholar]

12. R. P. Laufer, P. B. Velloso and O. C. M. B. Duarte, “Generalized bloom filters. Electrical engineering program,” COPPE/UFRJ, Tech. Rep. GTA-05-43. Vancouver, 2005. [Online]. Available: https://www.gta.ufrj.br/ftp/gta/TechReports/LVD05d.pdf. [Google Scholar]

13. Y. Zhu, H. Jiang and J. Wang, “Hierarchical bloom filter arrays (HBAA novel, scalable metadata management system for large cluster-based storage,” in Proc. of 2004 IEEE Int. Conf. on Cluster Computing, San Diego, CA, USA, pp. 165–174, 2004. [Google Scholar]

14. A. Kumar, J. Xu and J. Wang, “Space-code bloom filter for efficient per-flow traffic measurement,” IEEE Journal on Selected Areas in Communications, vol. 24, no. 12, pp. 2327–2339, 2006. [Google Scholar]

15. P. Christen, R. Schnell, D. Vatsalan and T. Ranbaduge, “Efficient cryptanalysis of bloom filters for privacy-preserving record linkage,” in Proc. of Pacific-Asia Conf. on Knowledge Discovery and Data Mining (PAKDD), Jeju, Republic of Korea, pp. 628–640, 2017. [Google Scholar]

16. P. Christen, A. Vidanage, T. Ranbaduge and R. Schnell, “Pattern-mining based cryptanalysis of bloom filters for privacy-preserving record linkage,” in Proc. of Pacific-Asia Conf. on Knowledge Discovery and Data Mining (PAKDD), Melbourne, VIC, Australia, pp. 530–542, 2018. [Google Scholar]

17. J. Lu, Y. Wan, Y. Li, C. Zhang, H. Dai et al., “Ultra-Fast bloom filters using SIMD techniques,” IEEE Transactions on Parallel and Distributed Systems, vol. 30, no. 4, pp. 953–964, 2019. [Google Scholar]

18. R. Patrgiri, S. Nayak and S. K. Borgohain, “Role of bloom filter in big data research: A survey,” International Journal of Advanced Computer Science and Applications, vol. 9, no. 11, pp. 655–661, 2018. [Google Scholar]

19. P. Reviriego, A. Sánchez-Macián, O. Rottenstreich and D. Larrabeiti, “Adaptive one memory access bloom filters,” IEEE Transactions on Network and Service Management, Early Access, vol. 19, no. 2, pp. 848–859, 2022. [Google Scholar]

20. A. Abdennebi and K. Kaya, “A bloom filter survey: Variants for different domain applications,” arXiv preprint, arXiv: 2106.12189, pp. 1–30, 2021. [Google Scholar]

21. Y. Wu, J. He, S. Yan, J. Wu, T. Yang et al., “Elastic bloom filter: Deletable and expandable filter using elastic fingerprints,” IEEE Transactions on Computers, vol. 71, no. 4, pp. 984–991, 2022. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.