Computers, Materials & Continua DOI:10.32604/cmc.2022.031580
Article

Optimal FOPID Controllers for LFC Including Renewables by Bald Eagle Optimizer

Ahmed M. Agwa1, Mohamed Abdeen2 and Shaaban M. Shaaban1,3,*

1Department of Electrical Engineering, College of Engineering, Northern Border University, Arar, 1321, Saudi Arabia
2Electrical Engineering Department, Faculty of Engineering, Al-Azhar University, Cairo, 11651, Egypt
3Department of Engineering Basic Science, Faculty of Engineering, Menoufia University, Shebin El-Kom, 32511, Egypt
*Corresponding Author: Shaaban M. Shaaban. Email: shabaan27@gmail.com
Received: 21 April 2022; Accepted: 07 June 2022

Abstract: In this study, a bald eagle optimizer (BEO) is used to get optimal parameters of the fractional-order proportional–integral–derivative (FOPID) controller for load frequency control (LFC). Since BEO takes only a very short time in finding the optimal solution, it is selected for designing the FOPID controller that improves the system stability and maintains the frequency within a satisfactory range at different loads. Simulations and demonstrations are carried out using MATLAB-R2020b. The performance of the BEO-FOPID controller is evaluated using a two-zone interlinked power system at different loads and under uncertainty of wind and solar energies. The robustness of the BEO-FOPID controller is examined by testing its performance under varying system time constants. The results obtained by the BEO-FOPID controller are compared with those obtained by BEO-PID and PID controllers based on recent metaheuristics optimization algorithms, namely the sine–cosine approach, Jaya approach, grey wolf optimizer, genetic algorithm, bacteria foraging optimizer, and equilibrium optimization algorithm. The results confirm that the BEO-FOPID controller obtains the finest result, with the lowest frequency deviation. The results also confirm that the BEO-FOPID controller is stable and robust at different loads, under varying system time constants, and under uncertainty of wind and solar energies.

Keywords: Fractional order PID control; load frequency control; renewable energy; bald eagle optimizer

1  Introduction

Frequency stability is one of the most dynamic problems with adverse influences on the entire system [1,2]. Frequency is inversely proportional to the load. With increasing or decreasing load, the rotor speed decreases or increases, and therefore the frequency decreases or increases [3,4]. A load frequency control (LFC) is designed to maintain the frequency of each zone within the scheduled range under any load conditions [5,6]. A well-designed LFC stabilizes the system, as the frequency is very close to the set value under various disturbances [7]. Researchers have proposed several techniques to support system frequency stability such as robust control [8–10], decentralized control [7,11,12], variable structure control [13,14], and proportional–integral–derivative (PID) controller based on optimization methods [15–17]. Among these, optimization techniques are quite promising due to their simplicity, effectiveness, and dispense with additional controller. In [1], the cuckoo search algorithm was suggested to identify the finest gains of the PI controller. In [15], the authors used Harris hawks optimizer (HHO) for tuning the PI controller for system frequency support and the results demonstrated that HHO is better than other methods. In [16], the authors utilized genetic algorithm (GA) to select the optimal gains of the PID controller for enhancing the system frequency. In [17], the bat algorithm was applied to tune the PI controller to regulate the system frequency. In [18], a teaching learning-based optimizer was utilized for optimizing the gains of the two-degree-freedom PID controller. In [19], a modified ant colony optimization algorithm was presented to obtain the appropriate values of the fuzzy PID controller. In [20], the symbiotic organisms search algorithm was introduced to optimally extract the PID gains of automatic generation control. In [21,22], the bacterial foraging optimizer (BFO) was implemented to fine-tune the PID controller parameters. Multiple techniques were utilized to obtain the ideal settings of PID controllers such as GA [23], grey wolf optimizer (GWO) [24], sine–cosine approach (SCA) [25], Jaya approach [26], equilibrium optimization algorithm (EOA) [27], improved Rao algorithm [28], the linear–quadratic–Gaussian technique [29]. The optimized fractional-order PID (FOPID) controller for LFC possesses excellent disturbance rejection capability and high robustness during system parameter variations [30–33]. The optimum parameters of the FOPID were determined using the manta ray foraging optimizer [34], hunger games search optimizer [35], flower pollination algorithm [36], and chaos game optimizer [37].

Despite this succinct literature representation, the No Free Lunch Theorem steers us that the identification of the controller parameters is probably improved using modern optimization approaches. Hence, in this study, we proposed a bald eagle optimizer (BEO) algorithm—a meta-heuristic optimization technique—to design the FOPID controller for system frequency support. The BEO was created in 2020 [38] where the results confirmed that the BEO performance is better than that of other approaches. Afterward, the BEO has been used in many engineering fields to solve optimization problems. In [39], an effective management plan of energy for the economic utilization of a microgrid based on the BEO algorithm was proposed and the results proved that the BEO achieved the minimum cost and the highest efficiency when compared with other optimizers. In [40,41], the BEO was positively employed to obtain the photovoltaic parameters. This study contributed to the following:

•   The recent BEO is implemented to obtain the optimal gains of FOPID for enhancing the system frequency.

•   The gotten results using the BEO are compared with the results based on SCA, Jaya, GWO, GA, BFO, and EOA algorithms in order to confirm its robustness.

•   The supremacy of the FOPID over the PID controller is demonstrated.

•   The performance of BEO-FOPID is validated under step load perturbation and random load variation.

•   The impact of both system parameters and sources of renewable energy (RE) on the performance of the BEO-FOPID controller is investigated.

The remnant of the article is laid out as follows: system modeling is introduced in the second section. BEO is explained in the third section. The objective function (FunObj) is formulated in the fourth section. The control strategy is shown in the fifth section. Simulation results and discussion are produced in the sixth section. The conclusion is drawn in the seventh section.

2  System Modeling

Fig. 1 shows the MATLAB/Simulink model of a two-zone interlinked power system of the non-reheat thermal plan. The power rating of each zone is 2000 MW, with the nominal load being 1000 MW. This model was adopted in many studies for the design and analysis of LFC of interlinked zones [15,22–27]. The load disturbances (ΔPd1), tie-line power error (ΔPt), and the controller’s output (ΔPref) are the inputs of each zone. On the other hand, the generator frequency deviation (Δf) and zone control errors (ZCEs) are the outputs of each zone. Tab. 1 lists the parameters of the investigated power system.

Figure 1: MATLAB/Simulink model of a two-zone power system without controllers

3  BEO

BEO is an algorithm that follows the same manner of bald eagles in their hunting [38]. There are three phases in BEO. An eagle chooses the area with the greatest amount of food in the first phase (selecting space). The eagle looks for food in the selected region during the second phase (searching in space). In the third phase, the eagle swoops to discover the finest hunting location using the position that obtained in the second phase [39].

3.1 Selection Phase

During this phase, new positions will be created using the following equation:

Lk,new=Lbest+γ⋅(Lmean−Lk)⋅r(1)

where Lk,new is the updated position, Lbest refers to the search space that bald eagles are exploring, dependent on the location they discovered throughout their prior search, r is the number whose value randomly ranges from 0 to 1, γ controls the changes of location via taking a number between 1.5 and 2, and Lmean is the mean location [40].

3.2 Searching Phase

Once the best search space Lbest is determined by the algorithm, then it updates the location of the eagles within that space. During this phase, the eagle position is updated using the following formula:

Lk,new=Lk+y(k)⋅(Lk−Lk+1)+x(k)⋅(Lk−Lmean)(2)

where x and y are the coordinates of direction for the kth point, which are written as

x(k)=xr(k)max(|xr|),y(k)=yr(k)max(|yr|)(3)

x(k)=xr(k)max(|xr|),y(k)=yr(k)max(|yr|)(4)

ϑ(k)=∝⋅π⋅rand,r(k)=ϑ(k)⋅Q⋅rand(5)

where ∝ is a parameter, ranging from 5 to 10, which determines the intersection point search in the center, and the number of cycles is determined by the parameter Q, which has a value among 0.5 and 2 [38].

3.3 Swooping Phase

In this phase, eagles move from the finest available position toward the target prey. This manner is mathematically illustrated as following [41]:

Lk,new=rand⋅Lbest+x1(k)⋅(Li−c1⋅Lmean)+y1(k)⋅(Li−c2.Lbest)(6)

where c1 and c2 range from 1 to 2 and x1 and y1 are the coordinates of direction given as:

x1(k)=xr(k)max(|xr|),y1(k)=yr(k)max(|yr|)(7)

xr(k)=r(k)⋅sinh⁡(ϑ(k)),yr(k)=r(k)⋅cosh⁡(ϑ(k))(8)

ϑ(k)=∝⋅π⋅rand,r(k)=ϑ(k)(9)

Fig. 2 reveals the flowchart of BEO steps.

Figure 2: The flowchart of BEO steps

4  The FunObj Formularization

The main targets of LFC are to take the frequency back to its rated value as speedily as possible and lessen the oscillations of Pt among the contiguous control zones throughout load perturbations. The peak undershoots (PeUn), settling time (tsett), and steady-state error are the descriptions of ∆f and ∆Pt in the time-domain study to be enhanced. It was discovered that the finest criterion for all stated descriptions is the integral-time-absolute errors (ITAE) of f and Pt, so FunObj is suggested to minimize the ITAE [22–27]:

FunObj=minimize(ITAE)=minimize(∫0tsimut⋅{|Δf1|+|Δf2|+|ΔPt|}⋅dt)(10)

where tsimu is the time of the simulation. The constraints subjugate the gains of the PID controller inside the lower and upper limits and FunObj is correspondingly subjugated.

5  The Proposed Controller

Fig. 3 reveals the proposed FOPID controller, which is written mathematically as:

Figure 3: MATLAB/Simulink model of the two-zone power system with FOPID controllers

u(t)=Kpe(t)+KiDt−λe(t)+KdDtµe(t)(11)

e(t)=ΔPt(t)+BiΔfi(t)(12)

where u(t) represents the control signal, Kp, Ki, and Kd are the gains of proportional, integral, and derivative components, respectively, λ and μ are the orders of integral and derivative, respectively, ΔPt is the tie-line power error, and e(t) is the error signal.

6  Simulation Results and Discussions

The effectiveness and robustness of the BEO-FOPID controller are validated by comparing it with some previous controllers at increasing load, disturbed random loading (DRL), and under uncertainty of wind and solar energies. The impact of system parameters Tge, Tgo, and Tt on the performance of the BEO-FOPID controller is also investigated.

Our results have been acquired using MATLAB-R2020b under Windows 10 running on a laptop with an Intel Core i7−1065G7 CPU at 1.3 GHz (8 CPUs) with 16 GB of RAM.

The values of BEO parameters are determined as suggested in [38], namely c1=2, c2=2, γ=2, ∝=10, and Q=1.5, which are in the recommended ranges as illustrated in Section 3.

6.1 Case 1: System Performance Under Increasing Load

In this section, a 10% step load perturbation is implemented in zone 1. Tab. 2 lists the controllers parameters constraints that are the same utilized in the compared algorithm that exists in [22–27] for fairly comparing among optimizers. The parameters of the PID and FOPID controllers based-BEO algorithm are listed in Tab. 3. Fig. 4 reveals that the FOPID controller-based BEO is better than PID controller-based BEO for enhancing the system frequency. Fig. 5 shows that the BEO-FOPID controller has faster convergence when compared to the BEO-PID controller, where it can achieve the lowest ITAE after 20 iterations.

Figure 4: System responses of the BEO-FOPID and BEO-PID controllers

Figure 5: Convergence of ITAE under case 1

Fig. 6 reveals comparisons between the system responses of the BEO-FOPID controller with those of other controllers to demonstrate its effectiveness. The BEO-FOPID controller owns the finest performance, whereas the PeUn and tsett have the least values. Thus, the time for frequency to arrive at its steady state is very short. The GA-PID and PFO-PI controllers cannot effectively improve the system dynamic response, where they consume a long time to drive the frequency to its steady state and result in high PeUn.

Figure 6: System responses of the BEO-FOPID controller compared to PID controllers based on other optimization algorithms

Tab. 4 summarizes a comparison between the previous different controllers and the BEO-FOPID controller, where ITAE, PeUn, tsett, the particles population (Np), and the number of iterations (Nm) are given. The results reveal that the smallest value of ITAE, PeUn, tsett, and algorithm parameters are obtained by the BEO-FOPID controller, indicating its supremacy for LFC.

6.2 Case 2: System Performance Under DRL

To validate conclusively the implementation of the BEO-FOPID controller for system frequency support, a random load whose value ranges from 0% to 10% of the rated load is created, as revealed in Fig. 7. The proposed controller quickly regulates the frequency, where Δf1, Δf2, and ΔPt recovered to zero regardless of the percentage of increasing or decreasing the load, as shown in Fig. 7. The results prove the effectiveness and robustness of the BEO-FOPID controller for enhancing the frequency under different loads.

Figure 7: Deviations of tie-line power and frequencies under DRL

6.3 Case 3: System Performance Under Variation of System Time Constants

In this section, we investigate the performance of the BEO-FOPID controller when the system parameters Tge, Tgo, and Tt are changed by ±50% and a 10% step load perturbation is simultaneously implemented to zone 1, as indicated in Figs. 8–10.

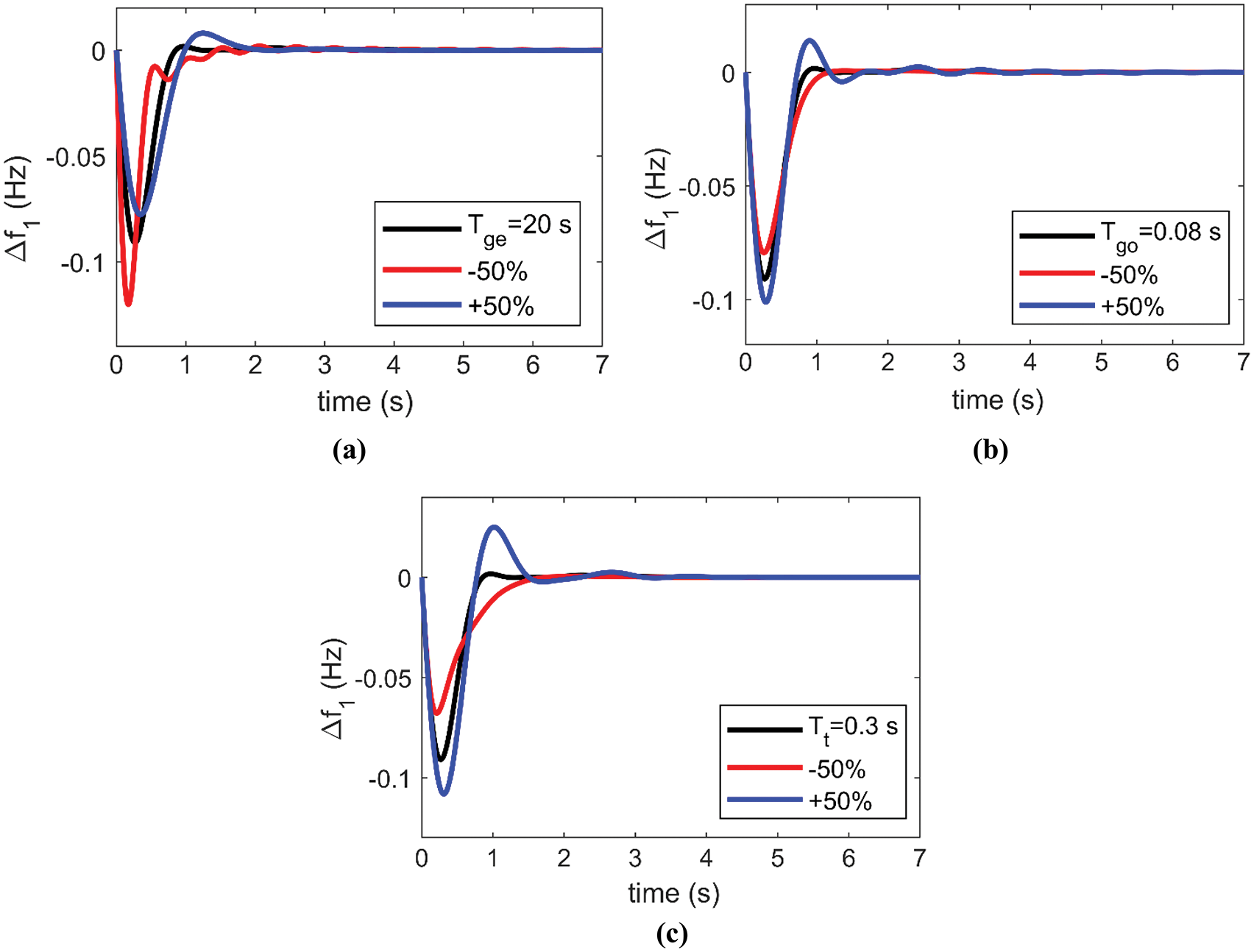
Figure 8: Resultant deviation in zone 1 frequency under 10% increase in zone 1 loading with +50% and −50% change in the rated value of (a) Tge, (b) Tgo, and (c) Tt

Figure 9: Resultant deviation in zone 2 frequency under 10% increase in zone 1 loading with +50% and −50% change in the rated value of (a) Tge, (b) Tgo, and (c) Tt

Figure 10: Resultant deviation in tie-line power under 10% increase in zone 1 loading with +50% and −50% change in the rated value of (a) Tge, (b) Tgo, and (c) Tt

From Figs. 8–10, we conclude the following:

1.    The decrease in Tge and the increase in Tgo harm the system stability where the system includes more oscillation, as shown in Figs. 8a and 8b, 9a and 9b, and 10a and 10b, respectively.

2.    The increase in Tt leads to larger values of PeUn and tsett of Δf1, Δf2, and ΔPt, as shown in Figs. 8c, 9c and 10c, respectively.

3.    ∆f1 has less tsett, where the frequency reaches its nominal value after 1.8 s at most. On the other hand, ∆f2 and ∆Pt have greater tsett, where frequency returns to its nominal value after 7 and 4 s at most, respectively.

The BEO-FOPID controller maintains the system frequency within its predefined range even under varying system time constants.

6.4 Case 4: System Performance Under Uncertainty of Wind and Solar Energies

The wind farm chosen for this study, involves 100 wind turbines (WTs; G52/850-GAMESA model [42]), each with an 850 kW rated capacity, that is, the total capacity is 85 MW (0.0425 p.u.). The wind energy is linked just after zone 1 thermal turbine shown in Fig. 4. Fig. 11a reveals the employed daily wind speed (υ) which fluctuates randomly and accordingly the output power (PWT) because it relies on wind speed as depicted in the following equation [43]:

Figure 11: One-day measurements of (a) wind speed and (b) solar radiation

PWT={00≤υ≤υc−i orυ≥υc−oaυ3+bPWTratedυc−i≤υ≤υnPWTratedυn≤υ≤υc−o(13)

where

a=PWTratedυn3−υc−i3(14)

b=υc−iυn3−υc−i3(15)

where υc-i, υc-o, and υn are the cut-in, cut-out, and rated speeds of the WT, respectively. The small-capacity wind generators are modeled by a huge-capacity generator whose transfer function (TFWTG) is written as:

TFWTG=10.3s+1(16)

The wind farm is not contributing to basic frequency control as we suppose the wind generators are running at the maximum power point tracking (MPPT) [20].

The PV array (KC200GT-Kyocera model) we studied has 200 kW rated power at standard test conditions (STCs), that is, radiation (G) of 1000 W/m2 and ambient temperature (Tamb) of 25°C. One hundred PV arrays are parallelly linked to supply 20 MW (0.01 p.u.) at STCs. The PV energy is linked just after zone 1 thermal turbine shown in Fig. 4. The daily solar irradiation is shown in Fig. 11b. The produced power of PV (PPV) is mainly proportional to G and weakly inversely proportional to Tamb as described in Eq. (17) [15,44].

PPV=GGSTC⋅PPVrated⋅ηMPPT(1−0.005⋅(Tamb−25))(17)

Here, Tamb is supposed to be constant at 25°C, so PPV is proportional to G only. In this article, the efficiency of MPPT systems of PV (ηMPPT) is supposed to be 98%. The transfer functions of the inverter (TFinv) and interconnection device (TFi_c) are written in Eqs. (18) and (19), respectively.

TFinv=10.04s+1(18)

TFi_c=10.004s+1(19)

Fig. 12 shows the system performance under the uncertainty of wind and solar energies. The BEO-FOPID controller supports the system frequency, improves the system stability well, and achieves fewer frequencies deviations and settling times.

Figure 12: System responses of the BEO-FOPID controller under 10% increase in zone 1 loading with renewable energies

7  Conclusions

In this study, we have suggested using BEO for tuning the FOPID controllers to support system frequency. The objective function has minimized the deviations of frequencies and tie-line power. A two-zone interlinked power system has been utilized to confirm the efficacy of the BEO-FOPID controller for LFC. Compared with other methods, the FOPID controller based on BEO has performed well for supporting system frequency when the load in zone 1 increased by 10% of the rated load. Furthermore, the BEO-FOPID controller is effective when loading in zone 1 disturbed randomly from 0% to 10% of the rated load. We also investigated the impact of variation of the system time constants by −50% and +50% with simultaneous load increase by 10% on the system performance. The results have proved that these time constants variations harm the system stability while the BEO-FOPID controller has retained its ability to maintain the system frequency at its set value. Moreover, the uncertainty of wind and solar energies has been also investigated where the simulation results have confirmed the capability of the BEO-FOPID controller for supporting the system frequency.

Acknowledgement: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number “IF_2020_NBU_434”.

Funding Statement : This research was funded by the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia through the project number “IF_2020_NBU_434”.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Tomsovic, D. E. Bakken, V. Venkatasubramanian and A. Bose, “Designing the next generation of real-time control, communication, and computations for large power systems,” Proceedings of the IEEE, vol. 93, no. 5, pp. 965–979, 2005. [Google Scholar]

 2.  P. Kundur, Power system stability and control, 1st ed., NY, USA: McGraw-Hill, 1994. [Google Scholar]

 3.  A. J. Wood and B. F. Wollenberg, Power generation operation and control, 2nd ed., NY, USA: John Wiley and Sons, 1996. [Google Scholar]

 4.  P. Kumar Ibraheem and D. P. Kothari, “Recent philosophies of automatic generation control strategies in power systems,” IEEE Transaction of Power Systems, vol. 20, pp. 346–357, 2005. [Google Scholar]

 5.  A. J. Wood, B. F. Wollenberg and G. B. Sheblé, Power generation, operation and control, 3rd ed., NY, USA: John Wiley & Sons, 2013. [Google Scholar]

 6.  A. Abdelaziz and E. S. Ali, “Cuckoo search algorithm-based load frequency controller design for nonlinear interconnected power system,” International Journal of Electrical Power & Energy Systems, vol. 73, pp. 632–643, 2015. [Google Scholar]

 7.  A. Yazdizadeh, M. H. Ramezani and E. Hamedrahmat, “Decentralized load frequency control using a new robust optimal MISO PID controller,” International Journal of Electrical Power & Energy Systems, vol. 35, no. 1, pp. 57–65, 2012. [Google Scholar]

 8.  R. A. Maher, I. A. Mohammed and I. K. Ibraheem, “Polynomial based H∞ robust governor for load frequency control in steam turbine power systems,” International Journal of Electrical Power & Energy Systems, vol. 57, pp. 311–317, 2014. [Google Scholar]

 9.  C. Peng, J. Zhang and H. Yan, “Adaptive event-triggering H∞ load frequency control for network-based power systems,” IEEE Transactions on Industrial Electronics, vol. 65, no. 2, pp. 1685–1694, 2017. [Google Scholar]

10. J. Liu, Y. Gu, L. Zha, Y. Liu and J. Cao, “Event-triggered H∞ load frequency control for multiarea power systems under hybrid cyber attacks,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 8, pp. 1665–1678, 2019. [Google Scholar]

11. Y. Zhang and T. Yang, “Decentralized switching control strategy for load frequency control in multi-area power systems with time delay and packet losses,” IEEE Access, vol. 8, pp. 15838–15850, 2020. [Google Scholar]

12. P. Chen, S. Liu, D. Zhang and L. Yu, “Adaptive event-triggered decentralized dynamic output feedback control for load frequency regulation of power systems with communication delays,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, in press. https://doi.org/10.1109/TSMC.2021.3129783. [Google Scholar]

13. M. Shouran, F. Anayi and M. Packianather, “The bees algorithm tuned sliding mode control for load frequency control in two-area power system,” Energies, vol. 14, no. 18, pp. 5701, 2021. [Google Scholar]

14. S. Prasad, S. Purwar and N. Kishor, “Load frequency regulation using observer based non-linear sliding mode control,” International Journal of Electrical Power & Energy Systems, vol. 104, no. 1, pp. 178–193, 2019. [Google Scholar]

15. D. Yousri, T. S. Babu and A. Fathy, “Recent methodology-based Harris hawks optimizer for designing load frequency control incorporated in multi-interconnected renewable energy plants,” Sustainable Energy, Grids and Networks, vol. 22, pp. 100352, 2020. [Google Scholar]

16. D. Kler, V. Kumar and K. P. Rana, “Optimal integral minus proportional derivative controller design by evolutionary algorithm for thermal-renewable energy-hybrid power systems,” IET Renewable Power Generation, vol. 13, no. 11, pp. 2000–2012, 2019. [Google Scholar]

17. S. Abd-Elazim and E. Ali, “Load frequency controller design via bat algorithm for nonlinear interconnected power system,” International Journal of Electrical Power & Energy Systems, vol. 77, no. 2, pp. 166–177, 2016. [Google Scholar]

18. R. K. Sahu, S. Panda, U. K. Rout and D. K. Sahoo, “Teaching learning-based optimization algorithm for automatic generation control of power system using 2-DOF PID controller,” International Journal of Electrical Power & Energy Systems, vol. 77, no. 4, pp. 287–301, 2016. [Google Scholar]

19. G. Chen, Z. Li, Z. Zhang and S. Li, “An improved ACO algorithm optimized fuzzy PID controller for load frequency control in multi area interconnected power systems,” IEEE Access, vol. 8, pp. 6429–6447, 2019. [Google Scholar]

20. H. M. Hasanien and A. A. El-Fergany, “Symbiotic organisms search algorithm for automatic generation control of interconnected power systems including wind farms,” IET Generation, Transmission & Distribution, vol. 11, no. 7, pp. 1692–1700, 2017. [Google Scholar]

21. E. Ali and S. Abd-Elazim, “BFOA based design of PID controller for two area load frequency control with nonlinearities,” International Journal of Electrical Power & Energy Systems, vol. 51, no. 1, pp. 224–231, 2013. [Google Scholar]

22. E. S. Ali and S. M. Abd-Elazim, “Bacteria foraging optimization algorithm-based load frequency controller for interconnected power system,” International Journal of Electrical Power & Energy Systems, vol. 33, no. 3, pp. 633–638, 2011. [Google Scholar]

23. S. Panda and N. K. Yegireddy, “Automatic generation control of multi-area power system using multi-objective non-dominated sorting genetic algorithm-II,” International Journal of Electrical Power & Energy Systems, vol. 53, pp. 54–63, 2013. [Google Scholar]

24. D. Guha, P. K. Roy, S. J. S. Banerjee and E. Computation, “Load frequency control of interconnected power system using grey wolf optimization,” Swarm and Evolutionary Computation, vol. 27, no. 1, pp. 97–115, 2016. [Google Scholar]

25. S. Mishra, S. Gupta and A. Yadav, “Design and application of controller based on sine-cosine algorithm for load frequency control of power system,” in Int. Conf. on Intelligent Systems Design and Applications (ISDA 2018), Vellore, India, Springer, 941, pp. 301–311, 2018. [Google Scholar]

26. S. P. Singh, T. Prakash, V. Singh and M. G. Babu, “Analytic hierarchy process based automatic generation control of multi-area interconnected power system using Jaya algorithm,” Engineering Applications of Artificial Intelligence, vol. 60, pp. 35–44, 2017. [Google Scholar]

27. A. M. Agwa, “Equilibrium optimization algorithm for automatic generation control of interconnected power systems,” Przegląd Elektrotechniczny, vol. 96, no. 9, pp. 143–149, 2020. [Google Scholar]

28. M. Khamies, G. Magdy, A. Selim and S. Kamel, “An improved Rao algorithm for frequency stability enhancement of nonlinear power system interconnected by AC/DC links with high renewables penetration,” Neural Computing and Applications, vol. 34, no. 4, pp. 2883–2911, 2022. [Google Scholar]

29. M. Khamies, G. Magdy, M. Ebeed and S. Kamel, “A robust PID controller based on linear quadratic gaussian approach for improving frequency stability of power systems considering renewables,” ISA Transactions, vol. 117, no. 12, pp. 118–138, 2021. [Google Scholar]

30. S. Sondhi and Y. V. Hote, “Fractional order PID controller for load frequency control,” Energy Conversion and Management, vol. 85, pp. 343–353, 2014. [Google Scholar]

31. S. Kumar and M. N. Anwar, “Fractional order PID controller design for load frequency control in parallel control structure,” in 54th Int. Universities Power Engineering Conf. (UPEC), Bucharest, Romania, pp. 1–6, 2019. [Google Scholar]

32. A. Kumar and S. Pan, “Design of fractional order PID controller for load frequency control system with communication delay,” ISA Transactions, in press. https://doi.org/10.1016/j.isatra.2021.12.033. [Google Scholar]

33. A. Saba, “Fractional order PID controller for minimizing frequency deviation in a single and multi-area power system with GRC, GDB and time delay,” Journal of Robotics and Control (JRC), vol. 3, no. 1, pp. 32–47, 2022. [Google Scholar]

34. E. A. Mohamed, E. M. Ahmed, A. Elmelegi, M. Aly, O. Elbaksawi et al., “An optimized hybrid fractional order controller for frequency regulation in multi-area power systems,” IEEE Access, vol. 8, pp. 213899–213915, 2020. [Google Scholar]

35. A. Fathy, D. Yousri, H. Rezk, S. B. Thanikanti and H. M. Hasanien, “A robust fractional-order PID controller based load frequency control using modified hunger games search optimizer,” Energies, vol. 15, no. 1, pp. 361, 2022. [Google Scholar]

36. T. Niyomsat and D. Puangdownreong, “Fractional-order PID controller design optimization for load frequency control via flower pollination algorithm,” in Proc. of the 2019 2nd Artificial Intelligence and Cloud Computing Conf. (AICCC 2019), New York, USA, Association for Computing Machinery, pp. 197–202, 2019. [Google Scholar]

37. M. Barakat, “Novel chaos game optimization tuned-fractional-order PID fractional-order PI controller for load-frequency control of interconnected power systems,” Protection and Control of Modern Power Systems, vol. 7, no. 1, pp. 16, 2022. [Google Scholar]

38. H. Alsattar, A. Zaidan and B. Zaidan, “Novel meta-heuristic bald eagle search optimisation algorithm,” Artificial Intelligence Review, vol. 53, no. 3, pp. 2237–2264, 2020. [Google Scholar]

39. S. Ferahtia, H. Rezk, M. A. Abdelkareem and A. Olabi, “Optimal techno-economic energy management strategy for building’s microgrids based bald eagle search optimization algorithm,” Applied Energy, vol. 306, no. 2, pp. 118069, 2022. [Google Scholar]

40. A. Ramadan, S. Kamel, M. H. Hassan, T. Khurshaid and C. Rahmann, “An improved bald eagle search algorithm for parameter estimation of different photovoltaic models,” Processes, vol. 9, no. 7, pp. 1127, 2021. [Google Scholar]

41. N. F. Nicaire, P. N. Steve, N. E. Salome and A. O. Grégroire, “Parameter estimation of the photovoltaic system using bald eagle search (BES) algorithm,” International Journal of Photoenergy, vol. 2021, pp. 1–20, 2021. [Google Scholar]

42. https://www.thewindpower.net/turbine_en_42_gamesa_g52-850.php. Accessed on 13-1-2022. [Google Scholar]

43. S. Sanajaoba and E. Fernandez, “Maiden application of cuckoo search algorithm for optimal sizing of a remote hybrid renewable energy system,” Renewable Energy, vol. 96, no. 7, pp. 1–10, 2016. [Google Scholar]

44. K. Nosrati, H. R. Mansouri and H. Saboori, “Fractional-order PID controller design of frequency deviation in a hybrid renewable energy generation and storage system,” CIRED-Open Access Proceedings Journal, vol. 2017, no. 1, pp. 1148–1152, 2017. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.