Computers, Materials & Continua DOI:10.32604/cmc.2022.031417
Article

Generalization of Advanced Encryption Standard Based on Field of Any Characteristic

Nabilah Abughazalah1, Majid Khan2,*, Noor Munir2, Ammar S. Alanazi3 and Iqtadar Hussain4,5

1Department of Mathematical Sciences, College of Science, Princess Nourah Bint Abdulrahman University, P.O.Box 84428, Riyadh 11671, Saudi Arabia
2Department of Applied Mathematics & Statistics, Institute of Space Technology, Islamabad, Pakistan
3King Abdulaziz City for Science and Technology, Riyadh, Saudi Arabia
4Mathematics Program, Department of Mathematics, Statistics and Physics, College of Arts and Sciences, Qatar University, 2713, Doha, Qatar
5Statistical Consulting Unit, College of Arts and Science, Qatar University, Doha, Qatar
*Corresponding Author: Majid Khan. Email: mk.cfd1@gmail.com
Received: 17 April 2022; Accepted: 15 June 2022

Abstract: Nowadays most communications are done by utilizing digital transmission mechanisms. The security of this digital information transmitted through different communication systems is quite important. The secrecy of digital data is one of the burning topics of the digitally developed world. There exist many traditional algorithms in the literature to provide methods for robust communication. The most important and recent modern block cipher named the advanced encryption standard (AES) is one of the extensively utilized encryption schemes with binary based. AES is a succession of four fundamental steps: round key, sub-byte, shift row, and mix column. In this work, we will provide an innovative methodology for extending the AES in a Galois field with any characteristic p. All four steps in the fundamental process with binary characteristics will be adjusted because of the new enhancement. By applying double affine transformations, we have enhanced the number of options in our suggested substitution boxes. The reconstruction of the nonlinear confusion component and encryption structure provides robustness in the generalized AES. The increase in the keyspace due to the Galois field generalization implies that we have improved additional confusion abilities and broadened the current notions. The implementation of the proposed structure of AES for image, audio, and video encryption will provide high security for secure communication.

Keywords: AES; generalized AES; binary field; ternary function

1  Introduction

It is critical to keep secret multimedia material out of the hands of unauthorized parties. Content, music, still images, liveliness, and video are all examples of the interactive media material. Multimedia security is used to protect these compounds. This is done using cryptographic techniques. These plans foster communication security, robbery, and refugee protection. Encryption is made more difficult by image size [1]. Typically, a typical photograph is of a large scale. Encryption of large amounts of mixed media data will be difficult if a standard encryption technique is used [2]. Due to the large amount of data that must be encrypted, we need to use techniques that demand a minimal amount of computation [3]. Privacy of data is also concerned with the authentication of the source [4,5]. Authentication is provided by some hashing and signature schemes [6,7]. Many encryption structures are protected by digital signature schemes [8]. Numerous studies show the importance of digital signature implementation [9–11]. Digital signatures work on the structure of the asymmetric encryption phenomenon [12]. In comparison to asymmetric key algorithms, private key methods are computationally less genuine. Asymmetric key algorithms are often thousands of times quicker than public-key algorithms [13]. Symmetric key encryption methods provide a more acceptable approach to scrambling interactive media content [14]. It is because of this that the AES symmetric key encryption approach is so fast [15]. In the literature, several novel AES enhancements have been presented [16–19]. In the symmetric block cipher family, the AES is one of the most important, with a key of 128 bits. Typically, the total round in AES is determined by one of three sizes of the secret key utilized in several variations: 128 bits, 192 bits, and 256 bits (10, 12 & 14). A new extension of current AES structures on any characteristic Galois field is our major goal here. Brute-force assaults on encrypted data have been bolstered by the removal of the field of generic prime features [20]. We have added two examples for ternary and quinary finite fields [21,22].

There are four sections in this research article. The basic notions are discussed in segment 2. The suggested scheme along with examples is now discussed in Section 3. Lastly, we have concluded the section.

2  Mathematical Concepts

2.1 Galois Field

A Galois field is a finite field with finite order. The Galois field has an order of prime or an exponent of prime, GF(pn), as p is prime and represents the field’s characteristic and n denotes a positive integer. It is described as:

GF(pn)={a0+a1x+a2x2+…+an−1xn−1,ai∈Zp∀i∈[0,n−1]}.(1)

Now we describe the structure of GF(32). Consider f(x)=x2+2x+2 be a primitive irreducible polynomial for GF(32). Consider α be the solution of this polynomial thus

f(α)=0,(2)

α2+2α+2=0,(3)

α2=−2α−2,(4)

As in GF(32), 3α+3=0 therefore we can write it as,

α2=−2α−2+3α+3=α+1,α3=2α+1,α4=2,α5=2α,α6=2α+2,α7=α+2,α8=1.(5)

GF(32)={0,1,α,α2,α3,α4,α5,α6,α7}={0,1,α,α+1,2α+1,2,2α,2α+2,α+2}.(6)

The elements of GF(32) represents the extension field of polynomials with maximum degree one, whose coefficients belongs to Z3.

2.2 Ternary Logic

There are three sets of assertions or propositions that we will refer to as ternary logic {0,1,2}. To designate this collection, we’ll use the set Z3. It is possible to determine the value of the r proposition by using the map μ:η→Z3, as shown below.

μ(r)={1if ris true 0if ris either true,or false2if ris false(7)

Consider, if μ(r)=1, then it is true according to the rules of binary logic, and if μ(r)=1, then it is true according to the rules of ternary logic. The same is true for the false value. Alternatively, analogous factors are created for binary logic, which we avoid μ by having μ(r)=r. Over η, we describe the subsequent fundamental operations:

•   Implication → (if…then)

•   Negation ∼ (not)

•   Conjunction ∧ (and)

•   Disjunction ∨ (or)

The system η satisfies closure law for the above operations, by this assumption, we can suppose that if r,s∈η then r∨s∈η,∼r∈η,r∧s∈η, and r→s∈η. Additionally, the proposition in ternary logic is not derived from the other three fundamental operations such as we accomplish in binary logic.

The outcomes in Tab. 1 are ∼r,r∨s,r∧s and r→s differ in their input r and s. The conjunction and implication equivalency operation are also shown in Tab. 1. Another way to think of these fundamental processes is as functions. The unary operator negation is a function described as h:Z3→Z3 and a binary operator can be defined as h:Z32→Z3. Commonly, we can identify a ternary logic function as mappings h:Z3n→Z3.

Unary functions are defined as those in which there is only one solution, and this is the case when n is equal to one. There are 331=27 possible solutions, each of which has its own unique set of functions h(r). All 27 of these functions are also referred to as modal functions. The binary function h(r,s) has 332=19683 possible outcomes when n is 2 (see Tab. 2).

By utilizing this process, we can calculate 333=7625597484987 various functions of several functions. Usually, there exist 33n several ternary functions h(r1,r2,…,rn) for n variables.

2.3 S-box Used in AES

An affine transformation S:GF(2)n→GF(2)n known as a substitution box or S-box is defined by the combination of three functions [7].

S=G∘L∘M,(8)

where L is the linear transformation, M is the inverse transformation, and G is the affine transformation, which can be stated mathematically as follows:

M(a)={a−1a≠0,0a=0,(9)

L(a)=Ba,(10)

G(a)=a⊕3b.

As a result, S-box structure is described as

S(a)=G(L(M(a)))=G(L(a−1))=G(Ba−1)=Ba−1⊕b,(11)

This is the required structure for the S-Box design created on GF(p)n.

2.4 Proposed S-box

S-box is the main non-linear component of the block cipher, which increase the confusion in the algorithm, therefore it must be strong and highly resistant to cryptanalytic attacks. Here we define a new approach to constructing a strong Substitution box. We define a map S:GF(p)n→GF(p)n by

S(x)=A2.I(A1x⊕b1)⊕b2,(12)

where A1,A2 are linear invertible matrices, b1,b2 are column matrices, I is the inverse transformation, and ⊕ is rit-wise addition operation under modp.

2.5 Advanced Encryption Standard

In the context of symmetric algorithms, AES is referred to as a “block cipher.” Commercial systems, such as Microsoft’s Windows, use it regularly (IPsec, the internet Skype, the IEEE 802.11i, and TLS). AES is referred to as AES-128, AES-192, or AES-256 depending on the size of the key employed in the encryption of the information being protected. Depending on the size of the key, the data matrix has 10, 12, or 14 rounds. m(x)=x8+x4+x3+x+1 is an irreducible polynomial in a finite Galois field of degree 8. The finite Galois field of degree 8 is utilized in the construction of S-box, Sub-byte transformation, and mix column transformation.

3  Generalization of AES on Ternary Logic Function and Double Affine Transformation

Other than binary qualities, we’ve mostly made use of the extension field in this section. To begin, we must expand the block cipher’s nonlinear S-box component to include features 3 and 5, as well as shift row, mix column, and round key. Here we define AES on the plaintext and key of 8-rits with two rounds of encryption, but in general, we can use the desired length of key and plaintext. The round of encryption can also be increased. The working strides of the proposed generalized AES are shown in Fig. 1.

Figure 1: Working strides of proposed generalized AES

3.1 Structure of S-box Created on GF(32) and Double Affine Transformation Proposed S-box

A substitution box can be constructed by using the map S:GF(3)2→GF(3)2 therefore we can write it as

S(x)=A2.I(A1x⊕3b1)⊕3b2,(13)

where I represents the inverse transformation and the symbol ⊕3 is rit-wise addition under modulo 3. Now consider the matrices for this expression be

A1=[0211],b2=[11],

A2=[0121],b2=[02].

The S-box changes to the following value when input values are inserted into the expression (see Tab. 3):

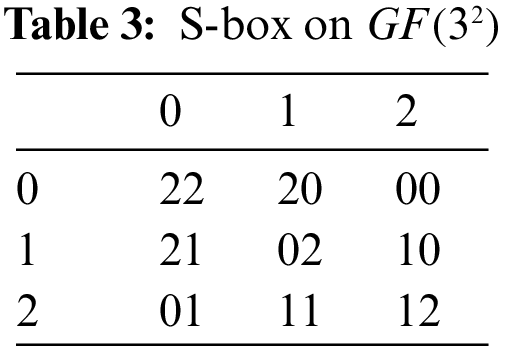
The inverse S-box, as shown in the Tab. 4, can be obtained by applying the inverse transformation.

3.2 Proposed AES on GF(32)

Suppose the plaintext of 8-rits be

P=01211020.

Now we divide this 8-rits plaintext into 4 parts, each consisting of 2-rits

P0=01,P1=21,P2=10,P3=20.

The following matrix can be used to represent the simple text:

P=[01102120].

Assume the key be of equal length as plaintext i.e., 8-rits

K0=10112022.

The following is a matrix representation of the key:

K0=[10201122].

First, we add a key matrix in the plaintext matrix

A1=P+K0,

A1=[01102120]⊕3[10201122],A1=[11000212].

Round 1

Sub-byte Transformation

The first step is to do the sub-byte conversion to each element of the matrix A1 and we get

B1=[02220010].

Shift Row

After shifting the components in the matrix B1 using the shift row, we get

C1=[00112120].

Mix Column

Consider a matrix for the mix column’s operation.

X=[1102].

By successively multiplying the X matrix by the C1 matrix’s columns, we arrive to

[d0d1]=[1102][0210]=[1220],

[d0d2]=[1102][2200]=[2200].

In the end, when we combine these two columns into a single matrix, we obtain

D1=[12222000].

Key Generation

By using the recent key K0 we can construct a new key K1 by using the following procedure

w0=k0,w1=k1,w2=k2,w3=k3.

w4=w0⊕3Nibblesub.(w3)⊕3rcon(1),w5=w1⊕3w4,w6=w2⊕3w5,w7=w2⊕3w6,

w4=10⊕3Nibblesub.(22)⊕301=20,w5=11⊕320=01,w6=20⊕301=21,w7=22⊕321=10.

Therefore, the key becomes

K1=[20210110].

Key Addition

By adding the key K1 in the matrix D1, we get

E1=D1⊕3K1,=[12222000]⊕3[20210110],E2=[21022000].

Round 2

Sub-byte transformation

We obtain the following as the matrix E1 has been sub-byte transformed:

B2=[00211121].

Shift Row

Shift row is applied to the matrix B2

C2=[00212111].

Mix Column

There is no mix column in the last round

Key Generation

The following procedure can be used to produce the key:

w8=w0⊕3Nibblesub.(w7)⊕3rcon(1),w9=w5⊕3w8,w10=w6⊕3w9,w11=w7⊕3w10.

w8=20⊕3Nibblesub.(10)⊕310=10,w9=01⊕321=22,w10=21⊕322=10,w11=10⊕310=20.

Therefore, the key becomes

K2=[21102220].

Key Addition

E2=C2⊕3K2,=[00212111]⊕3[21100120],E2=[21011001].

The encrypted message is E2=21100101.

Decryption

The encrypted data can be decrypted by utilizing the reverse process of encryption.

Round 1

Key subtraction

For decryption, the key matrix K2 is subtracted from the encrypted matrix E2 and each element is subtracted from other rit-wise under mod3.

C2=E2−K2=[21011001]−[21102220],C2=[00212111].

Inverse Shift Row

After key subtraction inverse shift row is applied to the matrix C2

B2=[00211121].

Inverse Sub-byte Transformation

After applying inverse shift row, inverse sub-byte transformation is applied by using inverse S-box

E1=[02102110].

Round 2

Key Subtraction

Now we subtract the key of round 2 i.e., K1

D1=E1−K1=[02102110]−[20210110],D1=[12222000].

Inverse Mix Column

In the inverse mix column, we take the inverse of the matrix

X=[1102],X−1=[1102].

After multiplying the columns of the matrix D1 with the matrix X−1 one by one we get

[c0c1]=[1102][1220]=[0210],[c0c1]=[1102][2200]=[2200].

After putting these columns together in a matrix,

C1=[02221000].

Inverse Shift Row

After utilizing the inverse shift row on the matrix, which is obtained after the inverse mix column, C1

B1=[02220010].

Inverse Sub-byte Transformation

After utilizing inverse Sub-byte transformation by using inverse S-box, we get

A1=[11000212].

Key Subtraction

Finally, we subtract the initial key from the matrix A1, and we get

P=A1−K0,=[11000212]−[10201122],P=[01102120].

Finally, the recovered message is P=01211020.

3.3 Construction of S-box GF(52) Based on Double Affine Transformation

A substitution box can be constructed by using the map S:GF(5)2→GF(5)2 therefore we can write it as

S(x)=A2.I(A1x⊕5b1)⊕5b2,

where I represents the inverse transformation and the symbol ⊕5 is rit-wise addition under mod5.

Now consider the matrices for this expression be

A2=[2401],b2=[12],

A2=[3111],b2=[04].

As a result, we acquire output values by adding input values into the above formula, the required S-box is given in Tab. 5.

The inverse S-box is shown below in Tab. 6.

3.4 AES Based on GF(52)

Consider the plaintext of 8-rits be

P=01423143.

Now we divide this 8-rits plaintext into 4 parts, each consisting of 2-rits

P0=01,P1=42,P2=31,P3=43.

The following is a matrix representation of the plain text

P=[01314243].

Assume the key be of equal length as plaintext i.e., 8-rits

K0=40231330.

Using the matrix form, the key may be expressed as follows:

K0=[40132330].

First, we add a key matrix in the plaintext matrix

A1=P⊕5K0,

A1=[01314243]⊕5[40132330],A1=[41441023].

Round 1

Sub-byte Transformation

Initially, we utilize the S-box transformation to all components of the matrix A1 and we obtain

B1=[43331342].

Shift Row

After employing the shift row to the components of the matrix B1 we obtain

C1=[43334213].

Mix Column

Consider a matrix for the mix column’s operation.

X=[1402].

This is the result of multiplying each column of the matrix C1 with X one by one

[d0d1]=[1402][4342]=[0134],

[d2d3]=[1402][3313]=[2021].

Combining these two columns into one matrix yields the following result:

D1=[01203421].

Key Generation

By using the recent key K0 we can construct a new key K1 by using the following procedure

w0=k0,w1=k1,w2=k2,w3=k3.

w4=w0⊕5Nibblesub.(w3)⊕5rcon(1),w5=w1⊕5w4,w6=w2⊕5w5,w7=w2⊕5w6,

w4=10⊕5Nibblesub.(22)⊕501=20,w5=11⊕520=01,w6=20⊕501=21,w7=22⊕521=10.

Therefore, the key becomes

K1=[21322412].

Key Addition

By adding the key K1 in the matrix D1, we get

E1=D1⊕5K1,=[01203421]⊕5[01322412],E2=[02020333].

Round 2

Sub-byte transformation

We obtain the following as the matrix E1 has been sub-byte transformed:

B2=[32321123].

Shift Row

By implementing shift row on the matrix B2

C2=[32322311].

Mix Column

In the last round, there is no mix column.

Key Generation

Keys can be produced in the following way:

w8=w0⊕5Nibblesub.(w7)⊕5rcon(1),w9=w5⊕5w8,w10=w6⊕5w9,w11=w7⊕5w10.

w8=01⊕5Nibblesub.(12)⊕510=12,w9=24⊕512=31,w10=32⊕531=13,w11=12⊕513=20.

Therefore, the key becomes

K2=[12133120].

Key Addition

E2=C2⊕5K2,=[32322311]⊕5[12133120],E2=[44400431].

The encrypted message is E2=21100101.

Decryption

The encrypted text can be decrypted by utilizing the reverse process of encryption.

Round 1

Key Subtraction

For decryption, the key matrix K2 is subtracted from the encrypted matrix E2 and each element is subtracted from other rit-wise under mod5.

C2=E2−K2=[44400431]−[12133120],C2=[32322311].

Inverse Shift Row

After key subtraction inverse shift row is applied to the matrix C2

B2=[32321123].

Inverse Sub-byte Transformation

After applying inverse shift row, inverse sub-byte transformation is applied by using inverse S-box

E1=[02020333].

Round 2

Key subtraction

Now we subtract the key of round 2 i.e., K1

D1=E1−K1=[02020333]−[01322412],D1=[01203421].

Inverse Mix Column

In the inverse mix column, we take the inverse of the matrix

X=[1402],X−1=[1303].

After multiplying the columns of the matrix D1 with the matrix X−1 one by one we get

[c0c1]=[1303][0134]=[4342],[c2c3]=[1303][2021]=[3313].

After combining these columns in one matrix

C1=[43334213].

Inverse Shift Row

After utilizing the inverse shift row on the matrix, which is obtained after the inverse mix column, C1

B1=[43331342].

Inverse Sub-byte Transformation

After employing inverse Sub-byte transformation by using inverse S-box, we get

A1=[41441023].

Key Subtraction

Finally, we subtract the initial key from the matrix A1 , and we get

P=A1−K0,=[41441023]−[40131130],P=[01314243].

Finally, the recovered message is P=01423143.

4  Conclusion

In this paper, we have defined a generalization of AES which gives better results to increase the security of the algorithm. This modifies AES as a complex mathematical structure which is utilizing the composition of two affine nonlinear functions instead of one affine Boolean function as in the case of standard AES. Moreover, the use of different characteristics other than the binary is one of the thought-provoking problems of cryptography. As a result, brute force attacks fail on the modified AES due to increasing the number of possibilities to find the key. The use of ternary and quinary characteristic finite field is yet not used in the development of AES structure. We have utilized ternary and quinary characteristic fields to design a new mathematical foundation for modified AES. The implementation of the generalized AES on hardware is one of the challenging problems for future interests. The designed structure can be utilized for audio and video encryption as well.

Acknowledgement: This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R87), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R87), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. M. Shtewi, “An efficient modified advanced encryption standard (MAES) adapted for image cryptosystems,” International Journal of Computer Science and Network Security, vol. 10, pp. 226–2232, 2010. [Google Scholar]

 2.  S. Lian, “Quasi-commutative watermarking and encryption for secure media content distribution,” Multimedia Tools and Applications, vol. 43, pp. 91–107, 2009. [Google Scholar]

 3.  K. Gu, W. J. Jia and J. M. Zhang, “Identity-based multi-proxy signature scheme in the standard model,” Fundamenta Informaticae, vol. 150, no. 2, pp. 179–210, 2017. [Google Scholar]

 4.  K. Gu, W. J. Jia, G. J. Wang and S. Wen, “Efficient and secure attribute-based signature for monotone predicates,” Acta Informatica, vol. 54, no. 5, pp. 521–541, 2017. [Google Scholar]

 5.  K. Gu, K. M. Wang and L. L. Yang, “Traceable attribute-based signature,” Journal of Information Security and Applications, vol. 49, pp. 102400, 2019. [Google Scholar]

 6.  K. Gu, W. J. Jia and C. L. Jiang, “Efficient identity-based proxy signature in the standard model,” the Computer Journal, vol. 58, no. 4, pp. 792–807, 2015. [Google Scholar]

 7.  K. Gu, L. H. Yang, Y. Wang and S. Wen, “Traceable identity-based group signature,” RAIRO-Theoretical Informatics and Applications, vol. 50, no. 3, pp. 193–226, 2016. [Google Scholar]

 8.  K. Gu, Y. Wang and S. Wen, “Traceable threshold proxy signature,” Journal of Information Science & Engineering, vol. 33, no. 1, pp. 63–79, 2017. [Google Scholar]

 9.  Z. Xu, C. Xu, J. Xu and X. Meng, “A computationally efficient authentication and key agreement scheme for multi-server switching in WBAN,” International Journal of Sensor Networks, vol. 35, no. 3, pp. 143–160, 2021. [Google Scholar]

10. L. Y. Xiang, X. B. Shen, J. H. Qin and W. Hao, “Discrete multi-graph hashing for large-scale visual search,” Neural Processing Letters, vol. 49, no. 3, pp. 1055–1069, 2019. [Google Scholar]

11. M. A. R. Khan and M. K. Jain, “Feature point detection for repacked android apps,” Intelligent Automation & Soft Computing, vol. 26, no. 6, pp. 1359–1373, 2020. [Google Scholar]

12. N. B. A. Ghani Binti, M. Ahmad, Z. Mahmoud and R. M. Mehmood, “A pursuit of sustainable privacy protection in big data environment by an optimized clustered-purpose based algorithm,” Intelligent Automation & Soft Computing, vol. 26, no. 6, pp. 1217–1231, 2020. [Google Scholar]

13. S. Heron, “Advanced encryption standard (AES),” Network Security, vol. 2009, no. 12, pp. 8–12, 2009. [Google Scholar]

14. F. B. Muhaya, “Modified AES using chaotic key generator for satellite imagery encryption,” Emerging Intelligent Computing Technology and Applications, vol. 5754, pp. 1014–1024, 2009. [Google Scholar]

15. G. N. Krishnamurthy and V. Ramaswamy, “Making AES stronger: AES with key dependent S-box,” International Journal of Computer Science and Network Security, vol. 8, pp. 388–398, 2008. [Google Scholar]

16. P. Kawle, A. Hiwase, G. Bagde, E. Tekam and R. Kalbande, “Modified advanced encryption standard,” International Journal of Soft Computing and Engineering, vol. 4, pp. 21–23, 2014. [Google Scholar]

17. M. Khan, T. Shah and S. I. Batool, “A new approach for image encryption and watermarking based on substitution box over the classes of chain rings,” Multimedia Tools and Applications, vol. 76, pp. 24027–24062, 2017. [Google Scholar]

18. M. Khan and T. Shah, “Construction and applications of chaotic S-boxes in image encryption,” Neural Comput & Applic, vol. 27, pp. 677–685, 2016. [Google Scholar]

19. M. Khan, T. Shah and S. I. Batool, “A new implementations of chaotic S-boxes in CAPTCHA,” Signal, Image and Video Processing, vol. 10, pp. 293–300, 2016. [Google Scholar]

20. A. Belazi, M. Khan, A. A. Abd El-Latif and S. Belghith, “Efficient cryptosystem approaches: S-boxes and permutation substitution-based encryption,” Nonlinear Dynamics, vol. 87, pp. 337–361, 2017. [Google Scholar]

21. K. N. Vijeyakumar, V. Sumathy, M. G. Devi, S. Tamilselvan and R. R. Nair, “Design of hardware efficient high speed multiplier using modified ternary logic,” Procedia Engineering, vol. 38, pp. 2186–219, 2012. [Google Scholar]

22. M. Mukaidono, “Regular ternary logic functions; ternary logic functions suitable for treating ambiguity,” IEEE Transactions on Computers, vol. 35, pp. 179–183, 1986. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.