| Computers, Materials & Continua DOI:10.32604/cmc.2022.030906 |  |
| Article |
Enhanced Heap-Based Optimizer Algorithm for Solving Team Formation Problem
1Faculty of Science, Suez Canal University, Ismailia, Egypt
2Faculty of Computers and Artificial Intelligence, Helwan University, Helwan, Egypt
3Faculty of Computers and Artificial Intelligence, Benha University, Benha 13518, Egypt
4Faculty of Computer Studies, Arab Open University, Cairo, Egypt
*Corresponding Author: Mustafa Abdul Salam. Emails: mustafa.abdo@fci.bu.edu.eg, mustafa.abdo@aou.edu.eg
Received: 05 April 2022; Accepted: 29 May 2022
Abstract: Team Formation (TF) is considered one of the most significant problems in computer science and optimization. TF is defined as forming the best team of experts in a social network to complete a task with least cost. Many real-world problems, such as task assignment, vehicle routing, nurse scheduling, resource allocation, and airline crew scheduling, are based on the TF problem. TF has been shown to be a Nondeterministic Polynomial time (NP) problem, and high-dimensional problem with several local optima that can be solved using efficient approximation algorithms. This paper proposes two improved swarm-based algorithms for solving team formation problem. The first algorithm, entitled Hybrid Heap-Based Optimizer with Simulated Annealing Algorithm (HBOSA), uses a single crossover operator to improve the performance of a standard heap-based optimizer (HBO) algorithm. It also employs the simulated annealing (SA) approach to improve model convergence and avoid local minima trapping. The second algorithm is the Chaotic Heap-based Optimizer Algorithm (CHBO). CHBO aids in the discovery of new solutions in the search space by directing particles to different regions of the search space. During HBO’s optimization process, a logistic chaotic map is used. The performance of the two proposed algorithms (HBOSA) and (CHBO) is evaluated using thirteen benchmark functions and tested in solving the TF problem with varying number of experts and skills. Furthermore, the proposed algorithms were compared to well-known optimization algorithms such as the Heap-Based Optimizer (HBO), Developed Simulated Annealing (DSA), Particle Swarm Optimization (PSO), Grey Wolf Optimization (GWO), and Genetic Algorithm (GA). Finally, the proposed algorithms were applied to a real-world benchmark dataset known as the Internet Movie Database (IMDB). The simulation results revealed that the proposed algorithms outperformed the compared algorithms in terms of efficiency and performance, with fast convergence to the global minimum.
Keywords: Team formation problem; optimization problem; genetic algorithm; heap-based optimizer; simulated annealing; hybridization method; chaotic local search
Team-Forming (TF) has sparked a lot of interest in several fields. TF is considered an NP-hard problem, and the complexity increases with the size of the problem [1]. As a result, manually solving the problem is difficult, if not impossible. In the corporate world, project teams are critical work frameworks. When a company formulates new projects, it breaks them down into smaller jobs and assigns each of its employees to complete one job or a group of them according to the need. And accomplishing each assignment will require a wide range of abilities. Because the number of abilities required to execute a task far exceeds the number of skills acquired by a single worker, which also violates the rules of fair use of human resources, employees are recruited in groups to complete each task. This is a simplified explanation for Team-Formation problem. To solve the TF problem, a team of experts who can combine all the necessary expertise and interact effectively with one another to accomplish a particular mission will be assembled. There are several advantages to using a team strategy in the workplace, since a group can perform more efficiently than individuals attempting to solve problems. Working in a group allows members of the group to collaborate and think creatively. Group brainstorming will aid the team in coming up with new ideas and gaining a deeper understanding of the problem. Since team members are often required to collaborate to achieve the highest degree of productivity and efficiency, it is critical to ensure that collaboration is successful.
The success of these teams is largely determined by the individuals that make up the project team. As a result, the project team’s selection is critical to the project’s progress. Selecting the right team members to complete a project within a specified deadline can be interpreted as an important issue. The expertise of team members is also an important issue. Choosing a good leader for the role of team manager and making capable staff cooperate as team members is the key to success in an enterprising institution’s business activities [2]. Important aspects that determine the success of a project include the efficiency of teamwork and communication among these people as a team through social networking. The presence of social connections is often a good indicator of effective collaboration. Team productivity is strongly influenced by the health of the social relationships among group members. So, the idea of team formation is a very powerful and successful idea, especially when using social networks, but we can notice that forming the right team on social networks is a non-trivial problem. The TF problem is also a practical one, which is related to many real-life applications such as task assignment problems, scheduling problems, and community-based question answering and project development in social networks. The equitable distribution of work among team members is also an important matter that must be considered to ensure that there is no workload on one member without the other. Most other research depends on solving one aspect, either discussing how to minimize the communication cost or balancing the workload, but this paper addresses all these aspects, and suggests efficient methods that address all these requirements. The suggested methods form teams that always satisfy the required skills, provide approximation guarantees with respect to team communication overhead, and are online-competitive with respect to load balancing. Experiments performed on random data sets and collaboration networks among film actors (IMDB), confirm that suggested methods are successful compared to the other compared methods.
In this paper, two new algorithms are proposed to solve the team formation problem. They are based on the heap-based optimizer algorithm (HBO). The first is the hybrid Heap-Based Optimizer and Simulated Annealing algorithm (HBOSA), and the second is the Chaotic Heap-based optimizer algorithm (CHBO). The introduced algorithms are evaluated against several algorithms, including PSO, GA, GWO, DSA, and the standard HBO. The introduced algorithms are tested using a set of known benchmark functions and a random dataset for TF problems. The experimental results illustrate that CHBO and HBOSA achieve lower costs compared with other techniques.
When applying the proposed algorithm to the IMDB dataset, the results showed that the proposed algorithm can achieve the lowest communication cost and is superior to other algorithms, but notice that this cost is equal to zero, which means that only one expert will do the task. And this contradicts the concept of the team and the equitable distribution of tasks to team members without placing the burden on one of them alone, which made us focus on balancing the workload of team members to guarantee the best results.
Another contribution is applying the workload concept, to distribute the tasks evenly among team members. This constraint must apply in solving the team formation problem to minimize the workload among team members and minimize the communication cost between them. Most of the previous work has either focused on minimizing communication costs or balancing the workload.
The remainder of the paper is laid out as follows. The description of the team formation problem is illustrated in Section 3. Section 4 describes the suggested methods used for solving the problem. The proposed algorithm’s experimental findings are shown in Section 5. Finally, Section 6 brings the work to a close and identifies areas for potential research.
In recent years Artificial Intelligence (AI) is considered the most complicated and amazing invention-creation of humanity yet. Although it is growing rapidly, it is still largely unexplored. AI has many fields, the most popular fields in the recent period are neural networks [3–7], and data science which includes the Team formation problem as one of the most popular problems in data science.
TF problem is an approximation problem [8]. Using non-deterministic and approximate algorithms helps in exploring the search space to come up with a good approximation of the common solution to such problems as in [9] and [10]. A limited amount of research has been done on meta-heuristic algorithms, which are characterized as search strategies that guide the search process. [11] used the Variable Neighborhood Search algorithm to solve the multiple team formation problem, that is, find multiple different teams solving multiple tasks while considering each team’s minimal cost.
One of the proposed algorithms introduced in this paper is a hybridization of two well-experienced algorithms: the HBO and the improved Simulated Annealing algorithms. The idea of hybridization increases the efficiency of the algorithm and increases the speed of reaching the best solution. The hybridization concept is a very successful method since it assists in achieving wide exploration and deep exploitation. This idea has been the subject of numerous studies in various fields [12–15].
On the other hand, there is an issue with the team formation problem discussed in this work, which is workload. The idea is to how to create an efficient team of users that meets the requirements of a project and the chosen team members, ensuring that no user is overburdened by the assignment and that no user is assigned tasks that are beyond her/his capacity [16]. In [17], the researchers deal with the problem as a multi-objective problem, their aim is to find an ideal team who can get the job done while keeping project management and personnel costs to a minimum. Since multi-objective is an area of mathematics used in multiple criterion decision-making, it deals with optimization issues involving two or more objective functions that must be optimized at the same time [18,19]. This assumption makes the problem even more difficult, as we have multi-objective that must be dealt with.
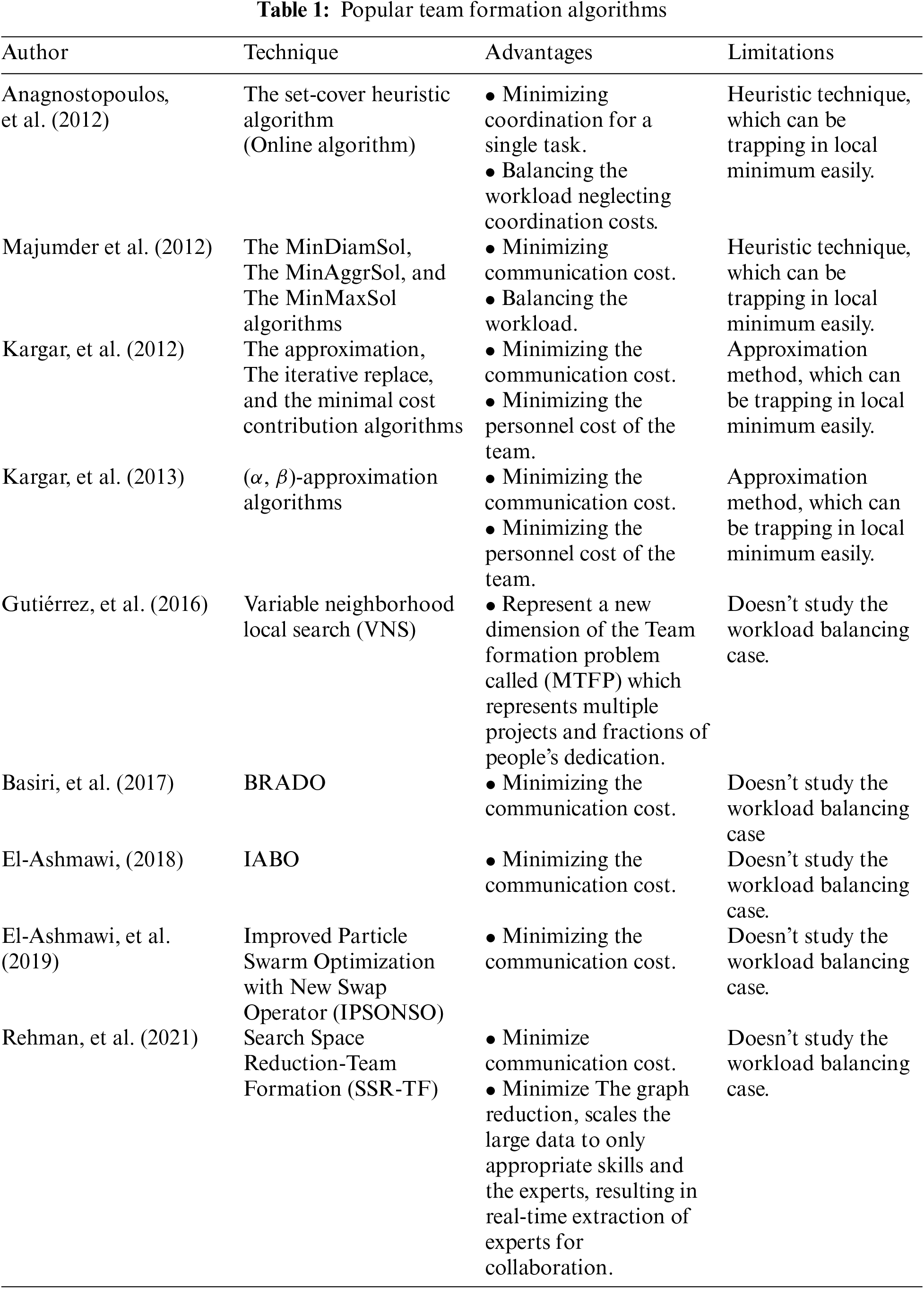
Last year, different researchers solved this problem using swarm intelligence algorithms, as in [20,21], which are the Brain Drain optimization algorithm (BRADO) and ant colony optimization used to solve the same problem. In [22] in 2018, the author suggested an improved African Buffalo (IABO) algorithm for the social network team formation problems. To obtain better teams that cover all the skills, the IABO algorithm is combined with a discrete crossover operator and a swap sequence. The author attempted again in early 2019 to solve the TF issue using particle swarm optimization (PSO) using the same old swap operator [23] their goals were to find a joint team of users who could be able to finish the job while keeping communication costs to a minimum among team members. In [24], the author focused on a different concept, graph reduction, which scales the large data to only appropriate skills and the experts, resulting in the real-time extraction of experts for collaboration. Popular and major contributions to team formation (TF) in literature are given in Tab. 1.
3 Team Formation Problem Definition
TF problem can be expressed as a task S, where
Since communication cost
Swarm intelligence (SI) techniques are one of the most important and promising subfields of artificial intelligence. They are nature-inspired techniques that have proved their efficiency in recent years to solve real-world optimization problems due to their simplicity, robustness, and adaptive nature toward hard problems. These techniques iteratively conserve information of search space and find the global optimum solution through continuous interaction of search agents. SI includes multiple optimization techniques used to solve NP-hard problems for which traditional methods are not effective [25]. This paper suggested two enhanced Heap based optimizer algorithms. Also, a set of algorithms will be created and modified using different strategies to suit the problem being addressed, and then the results will be compared to see which strategy is better. The compared algorithms are the Particle Swarm Algorithm (PSO), which is defined obviously in [26], Genetic algorithm (GA) [27], Grey wolf algorithm (GWO) defined in [28,29], Simulated annealing (SA) defined in [30], and Heap-based optimizer (HBO) [31]. These algorithms were chosen because they are regarded the most well-known for solving hard optimization problems.
4.1 Heap Based Optimizer Algorithm (HBO)
The major processes of the HBO algorithm will be discussed here. It was created in 2020 [31] by Qamar Askari and Mehreen Saeed as a version of the Meta-Heuristic inspired by some human social behavior. HBO has been used more than once to solve different problems, and it has proven its efficiency in solving problems, including [32,33]. HBO is utilizing Corporate Rank Hierarchy (CRH) as a template because human interaction is visible in organizations where personnel are grouped into a hierarchy known as an organizational chart, which groups the people who work together to achieve a common goal. This has resulted in the development of hierarchical structures within businesses to help individuals become more successful at allocating tasks and managing work. The mathematical model of HBO is separated into three major categories: the first category is the relationship between subordinates and their immediate supervisor, the second category is the relationship between colleagues, and the last is the employees’ self-contribution. The major processes of the standard HBO algorithm are described in more detail below.
1) Parameters setting: identify the generic parameters of problem, such as number of search agent (N), variables number (D), maximum iterations number (T), and ranges of the design variables (
2) Initialize population: usually selected randomly between the lower and upper bounds defined for each variable these bounds are set based on the problem natural. The population at generation T defined as:
3) Design and perform CRH: uses a heap data structure to mimic the CRH, which allows grouping solutions in a hierarchy based on their fitness and utilizing the arrangement in the algorithm’s position updating process in a very particular way. CRH is accomplished using a 3-ary heap since it can be accomplished faster and better using an array because of its completeness feature. Based on the formula.
• Their exist at maximum 3 children at any node, the child j for node i can be formulated mathematically.
• The depth of any node can be formulated mathematically with the following formula
• Any node at the level of node i is known as node i’s colleagues. This function returns the index of any randomly chosen colleague of node I, computed using any random number in the range.
• Algorithm 1 below describes how a heap is built and how to search upward in the heap for nodes and swap them to an appropriate location to preserve the heap property, since (heap. value) saving the indications of the search agents in our population and (heap. key) saving the fitness value for the related search agent.
4) Updating search agent positions: the position can be updated through three concepts. First, mimic the relationship between subordinates and their immediate supervisor. The second concept is to mimic the relationship between colleagues, and the last is to mimic employees’ self-contribution. To balance the exploration and exploitation stages, these concepts can be combined into the following equation: Search agents constantly change their positions to find the best solution.

This idea is inspired by Genetic Algorithms, especially the crossover operation, which is considered the most important operation in GA. There are different types of genetic crossover. A single point crossover was chosen in this research, in which a random point on the parent chromosomes was chosen. All genes beyond that point on the chromosomes are swapped between the two parent chromosomes. The Single Point Crossover can have a high chance of producing a good offspring with more simplicity than the others, because unlike the others, not all skills will be in the offspring and some skills will be there more than once. Using the single-point crossover [34] to solve a TF problem can produce one or more offspring from the chosen parents. Apply this process by selecting a random point Z in the parents between the first gene and the last gene. The two parents are swamping all the genes between point Z and the last gene.
4.3 Devolved Simulated Annealing Algorithm (DSA).
Kirkpatrick et al. introduced Simulated Annealing (SA) as an efficient stochastic search method in 1983 [31], and V. Cerny independently presented the method in 1985 [35]. It is a function optimization algorithm that moves uphill and downhill, whereas traditional algorithms only move downhill. As a result, it can break free from local optima and aim for the global optimum with a high probability of success by taking uphill steps in the search space. The simulated annealing algorithm can be used to solve a wide range of optimization problems, such as neural network training, image processing, code design, economic problems, continuous optimization problems, scheduling problems, and parallel machines, due to its simplicity and performance [36]. This paper suggested new Developed SA algorithm (DSA). Its steps are shown in the following subsection. This modification is applied by using the mutation operation from the Differential Evaluation (DE) algorithm [37] to generate the new state solution to ensure the randomness of the new solution and that it is more suitable for team formation problem. The general operations of DSA algorithm for team formation problem are illustrated as follow
1) The algorithm begins with the best solution obtained from the HBO algorithm and then produces new states for the problem at random selection from the obtained solution, calculating the cost function in the process.
2) The annealing simulation begins with a high imaginary temperature.
3) In the current population, a new state is selected by applying the differential evaluation’s mutation operations to old individuals, resulting in the mutated vector.
• which randomly select three solution vectors (
4) Calculate the difference between the current and the new cost functions, if it is less than zero, the cost is lower, then accept this new state.
• As a result, the system is forced to a state that corresponds to a local or possibly global minimum. There are several local minima in most big optimization problems, and the optimization algorithms are frequently stuck in one
5) To avoid getting stuck in a local minimum, accept the increase in the cost function with a certain probability,
6) Repeat this step until the equilibrium condition is satisfied, and then decrease the temperature and repeat the steps until the stopping criteria is satisfied.
One of the most current search methods is chaos optimization. Although swarm intelligent algorithms depend on randomness in the way they are built to search through the search space and increase the exploration ability in the search process, however, it may sometimes fail to reach the optimal solution to avoid this shortcoming. Recently, chaos-based randomization methods have been used. They help to discover new solutions in the search space by moving particles towards different regions in the search space. The main concept is to use chaos parameters and variables to form a solution space. The chaotic features are ergodicity, regularity, and stochastic qualities, which are used to find the global optimum, increase the convergence rate, and increase the algorithm’s ability to avoid trapping in local minima [39]. All these advantages can dramatically boost the performance of evolutionary algorithms. There are many chaotic maps used for enhancing meta-heuristic algorithms, such as logistic, singer, tent, piecewise, and sinusoidal. The chaotic map’s efficiency varies according to the problem. In this work, a logistic map is adopted to obtain chaotic sets, as it is the most well-known map. Logistic map is defined as follows.
where
4.5 The Enhanced Heap-Based Optimizer Algorithms for Solving Optimization Problems and the Team Formation Problem.
This paper suggests two methods to enhance the Heap-based optimizer algorithms: Hybrid Heap-based Optimizer and Simulated Annealing Algorithms (HBOSA), and Chaotic Heap-based Optimizer and Simulated Annealing Algorithms (CHBO), discussed in more detail in the following subsections.
4.5.1 Hybrid Heap-Based Optimizer and Simulated Annealing Algorithms (HBOSA)
Two suggestions have been invoked in HBOSA. The first one is using single point crossover to improve and develop the HBO update process. A new state is selected by applying the single point crossover operations to the old solution. After the HBO algorithm has finished and got the best solution, the DSA algorithm starts the search from the best solution obtained from HBO. The DSA algorithm is able to exploit research around the best solution and make a jump to avoid falling into local minima which increases the diversity of the search. Our two suggested strategies in HBOSA can improve the performance of the algorithm and help it obtain a promising solution in a reasonable time. The main components of our suggested algorithm, HBOSA, are shown in Algorithm 3, which represents the structure of the suggested algorithm, HBOSA.
1) At the beginning, put the value of the initial parameter.
2) Generate the initial population, where the population in the benchmark function is generated randomly between the lower and upper bounds of the function, and the population in the team formation problem is generated from the IMDB data set. An example is illustrated in Fig. 1, since any solution is an array list of size 1 × 3, where the first needed skill is (History), the second one is (Thriller), and the third skill is (Comedy). Fig. 1 represents the possible values for each index of a solution.
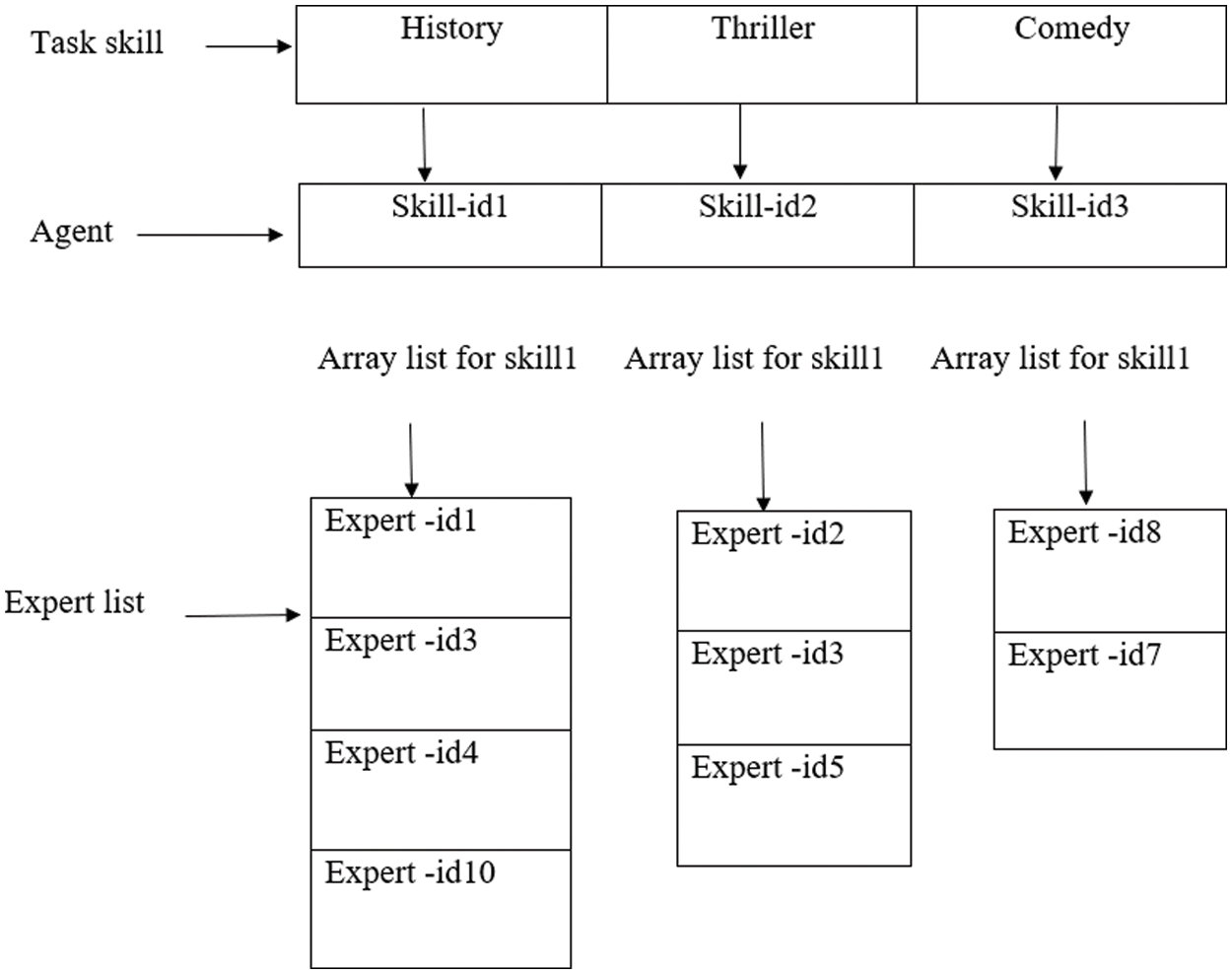
Figure 1: Search agent representation for team formation problem
3) Evaluate the fitness function for each solution in the population.
4) The following steps are repeated until the termination criteria is satisfied.
5) Apply the Happify (
6) Select the global best solution
7) The single-point crossover operator is used to produce a new solution by combining the current solution and
8) Updating search agent positions using Eq. (11).
9) Evaluate the fitness function, in the problem using Eq. (1). The best solution and best function value are selected.
10) Apply the DSA algorithm to the best solution to avoid trapping in local minima.
11) The overall best solution is obtained.

4.5.2 Chaotic Heap-Based Optimizers Algorithms (CHBO)
In this subsection, the random variables used for updating the HBO position are replaced with chaotic variables. As updating HBO position influences the optimal solution and convergence rate, by using the chaotic sequence generated from chaotic maps, such a combination of chaos and HBO is defined as “CHBO”. In this paper, a Logistic chaotic map is used for the optimization process. This map can significantly improve the performance and convergence rate of HBO. The CHBO approach combined with chaotic sequences is described in Eq. (12).
where
Optimization algorithms must be capable of exploring the search space to discover favorable areas and exploiting these areas to obtain the best solution. CHBO, and HBOSA algorithms requires a balance between exploration and exploitation. In this section attempted to evaluate their behavior and performance. The proposed algorithms were experimented on a set of benchmark functions, a simple example model of the problem, and then tested using the IMDB dataset. The results of the experiment clarified that the suggested algorithm is an auspicious algorithm able to find the best solution at the lowest cost. Numerical Experiment to perform a wide exploration and deep exploitation during the search process.
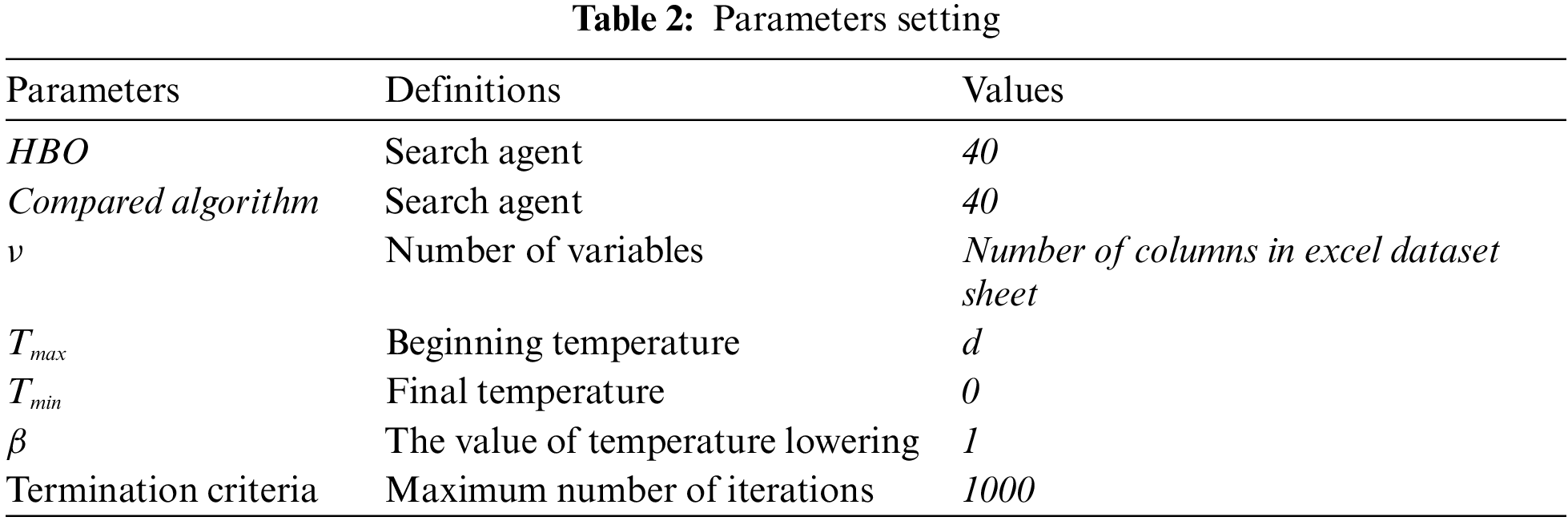
CHBO and HBOSA algorithms were programmed in Python. The results were compared against the following algorithms (HBO, DSA, GA, GWO, and PSO) using a set Benchmark Function and with a random dataset and an IMDB dataset. The general efficiency of our suggested algorithms and their ability to converge to optimality are investigated using different experiments. But in the first summary, the setting parameters of the HBOSA, and CHBO algorithms are as follows: the compared algorithm parameter taken from its original paper, and the chaotic sequence parameter defined in Subsection 4.4
HBOSA parameters are outlined with their allocated values as shown in Tab. 2. These values are determined using several numerical experiments to stabilize them or based on a commonly used setting in the literature.
5.2 Benchmark Function Set and Compared Algorithms
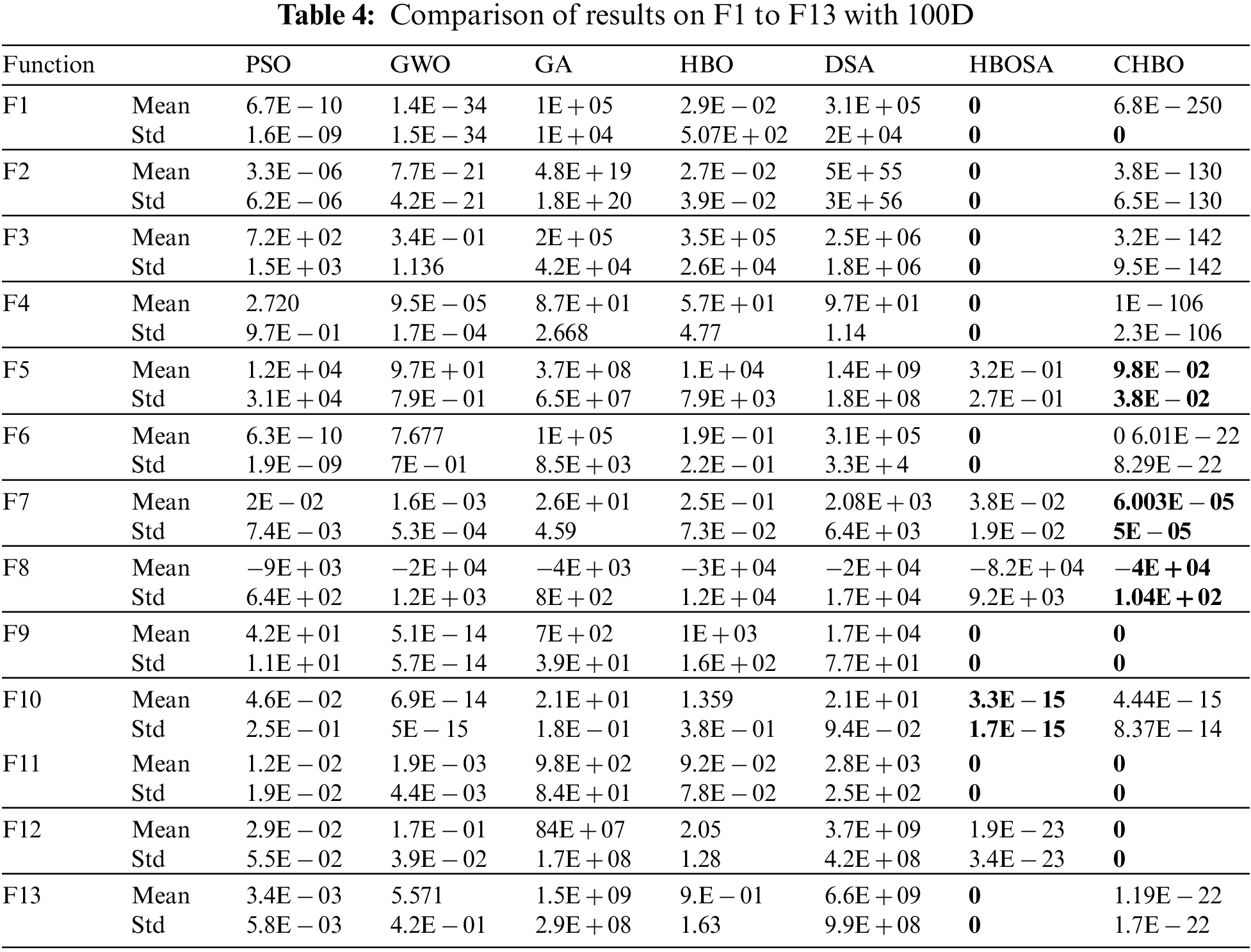
To measure the performance of the HBOSA, and CHBO suggested algorithms, a set of well-known benchmark functions are employed for testing. This set of benchmark functions includes unimodal functions and multimodal functions. The selected set of benchmark functions includes 7 unimodal functions (F1–F7). Which have a single global optimal solution using this benchmark function to evaluate the local exploitation capability of the suggested algorithms. Also using six multimodal functions (F8–F13) that have multiple local optimal solutions besides the global optimal solution. These functions are used to test the global exploration capability and local optimal avoidance capability of the suggested algorithm. Tab. 3 reveals the mathematical formulas and characteristics of these functions. The benchmark functions are scalable at dimensions (D = 100). 30 runs were performed for each function. The average (Mean) and standard deviations (Std) of function values over 30 independent runs for D = 100 dimensions are reported in Tab. 4. The value of the function evaluation is used as the main termination criteria. The results of these experiments have shown that the proposed versions called CHBO and HBOSA have achieved the best results in terms of Mean and Std, and they are returning a solution with a good fitness value within the prescribed number of iterations. In Tab. 4 can notice that the HBOSA algorithm reaches an optimal value in most cases (F1, F2FF3, F4, F6, F8, F9, F10, F11, F113), but it seems to encounter some difficulties while optimizing (F5, F7, F12), but this failure can be solved by increasing the number of iterations, and CHBO is very close to optimal value in most cases, and it can obtain the optimal value in (F1, F6, F8, F9, F11). From this experiment, can show that the suggested algorithms are promising algorithms and can outperform other compared algorithms.

5.3 Comparison Between HBO, DSA, PSO, GA, GWO, and Proposed HBOSA, CHBO on Random Dataset
The performance of the suggested algorithms and other comparison algorithms is investigated in a random data set by generating a random data set consisting of 40 experts. The results apply to a variety of skill sets.
To verify the efficiency of the proposed algorithm, it is first compared with the compared algorithms that have been discussed previously using a random dataset. Tab. 5 summarizes the results, these results of 30 random runs, including the minimum (Min), maximum (Max), average (Mean), and standard deviation (Std). The best results are shown in bold font. Tab. 5 outperform the others. Furthermore, the fitness values obtained by HBOSA, and CHBO as shown in Tab. 5, are always superior to those obtained by other algorithms, demonstrating their ability to escape local optima. Other algorithms, on the other hand, can easily be stuck or trapped in local optima.
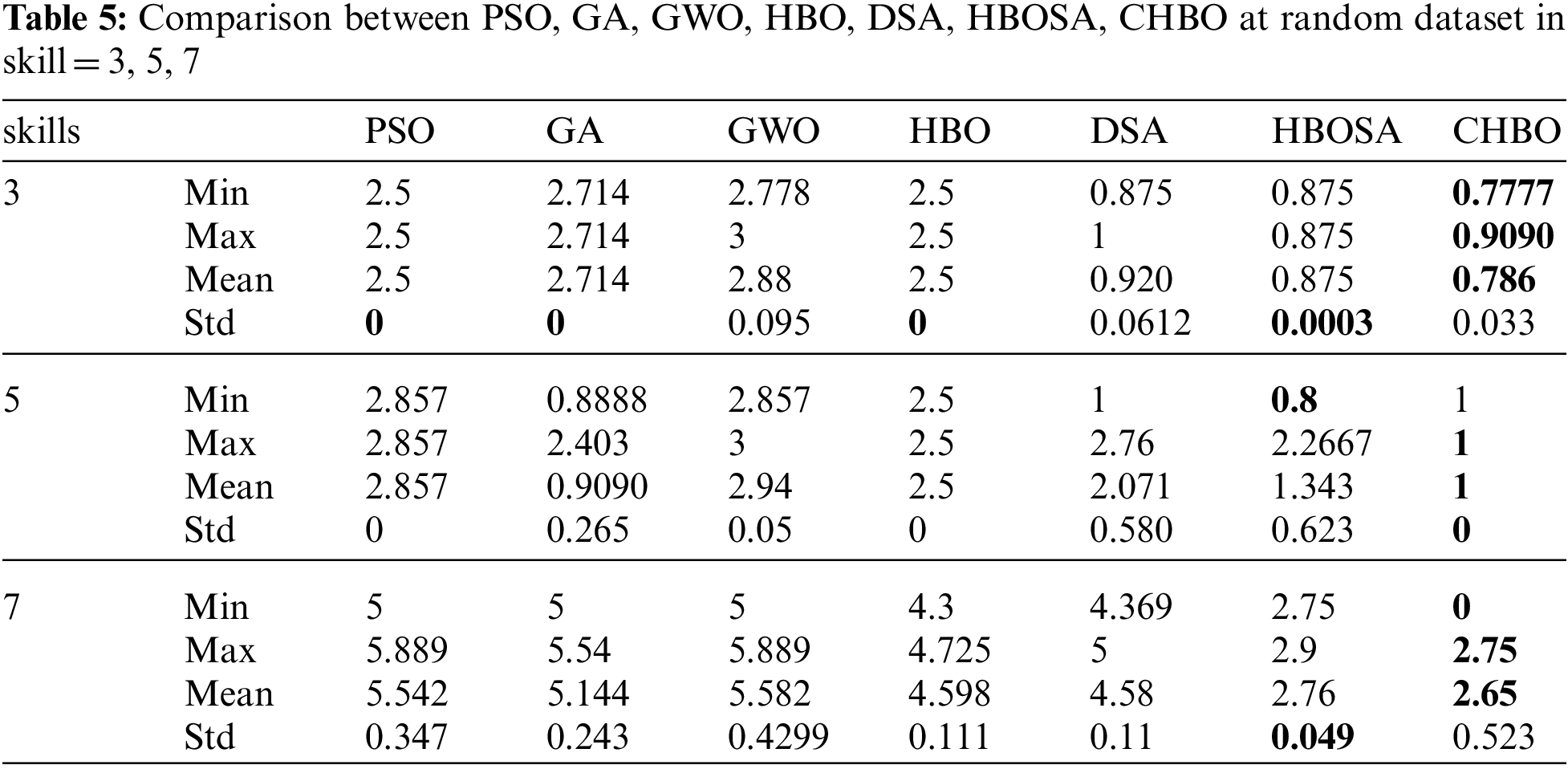
IMDB datasets are used here as a real-life dataset to extract the connective and expertise data. The suggested algorithms are tested on IMDB dataset to mimic reality, which has been extracted from IMDb XML. IMDb (Internet Movie Database) is an online database that includes cast, production crew, and personal biographies, story summaries, trivia, ratings, and critical criticism for films, television shows, home videos, video games, and streaming content online. In this research, using the data set to include actors and the characters or roles they played in different movies. Appling the suggested algorithms and the other comparison algorithms in this dataset to record the performance of the suggested methods to find teams able to solve the task. Apply a set of experiments with a different number of skills and experts. From the IMBD data set, construct the collaborative social network from randomly selected 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100 experts, and choose 3, 5, and 7 skills to perform tasks. Test each one separately with ten groups of experts. Our experiment clarified that the suggested methods (HBOSA, and CHBO) can find teams with least communication costs calculated using Eqs. (1), (2), and compose teams of experts at an efficient running time.
5.5 Comparison Between HBO, SA, PSO, GA, GWO, and Proposed HBOSA, CHBO on IMDB Dataset
In this subsection, the convergence of the suggested methods is examined, compared with HBO, SA, PSO, GA, and GWO. Using the IMDB dataset with various experts and skills numbers. The results at a number of skills = 5 are shown in Fig. 2, which represents the convergence curve for the seven algorithms, and it clarifies that HBOSA, and CHBO outperform the other algorithms.
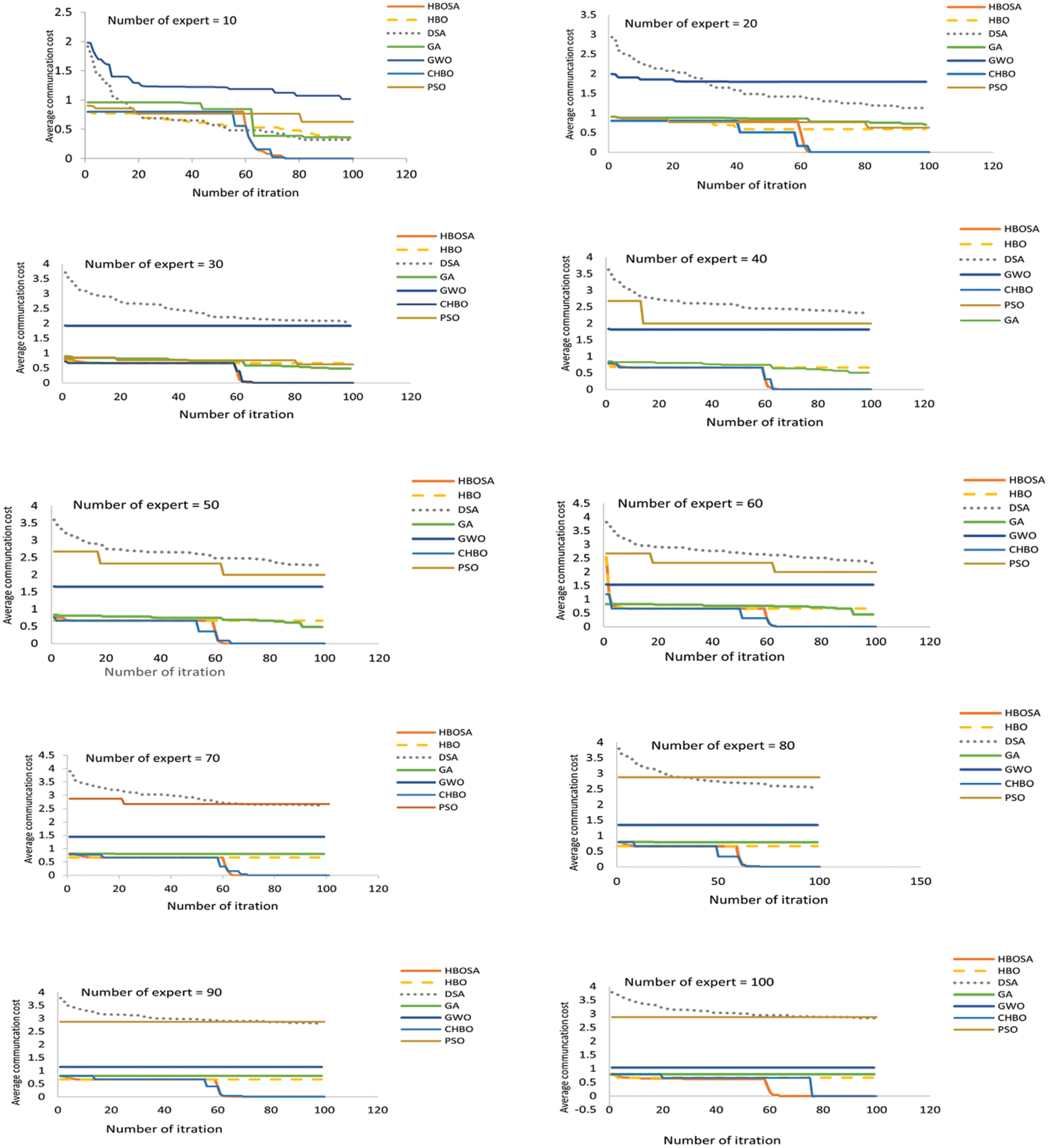
Figure 2: Comparison between HBOSA, CHBO, HBO, DSA, PSO, GA, GWO on IMBD dataset at number of skills 5
Throughout the search process, the suggested methods are successful in working in an equivalent manner in the exploration and exploitation processes, overall iteration number. They also outperformed all other algorithms in convergence in all 10 experiments and obtained the best communication cost in most cases, as shown in Fig. 2. As a result, when HBOSA, and CHBO convergence were compared to other algorithms, they found that while the number of iterations increases, the convergence rate becomes more rapid. Furthermore, as shown by the convergence curves in Fig. 2, the suggested methods solve premature convergence better than other algorithms by balancing exploration and exploitation as well as improving population diversity. The efficiency of the HBOSA algorithm is due to two modifications to the original HBO algorithm, one of which is the use of the hyper strategy of the SA algorithm after applying SA improvement. This improvement helped in diversifying the results, which increased the SA algorithm’s ability to escape from local minimum. And the efficiency of the CHBO algorithm is due to the chaotic sequence generated by iterating a logistic map. According to Fig. 2, the suggested methods are more capable of exploring and exploiting search space than other optimization algorithms. This shows HBOSA’s, and CHBO’s superior abilities to achieve solution diversity as compared to other algorithms. Finally, this result confirmed that the suggested algorithms outperform other algorithms in terms of discovery. Also can observe from the results that the algorithms are auspicious and powerful, and they can find the best or near-best solution within an acceptable time frame.
Although these results showed the success of our algorithms in obtaining the optimal solution, this solution is not the best at all, as it guarantees that the algorithms reach the best solution that gives them the lowest cost without looking at any other restrictions, including fairness in distributing work to users. Without loading the work on one without the other, this is what made us think of finding a solution that considers these constraints, and this is what will be discussed in the following section.
5.6 Applying Load Balancing Constraint in Team Formation Problem
Previously, constructed algorithms which provably convergence to optimal solution to TF problem and tested them by using the real dataset IMDB. These algorithms are appropriate to solve the team formation problems with a low communication cost. The objective is to form teams to deal with an influx of assignments that are unknown ahead of time. Each activity necessitates a set of skills that members of the gathered team must possess. Each team should have a low coordination cost, which means they should be well-connected according to the underlying social network, but this allocation should be fair in the sense that no one should be unfairly singled out or overloaded with work. During this part, a several concerns about the applicability of the suggested strategies are addressed. To create an optimization algorithm that addresses multi-criteria objectives, trying to minimize the maximum load on each team member while keeping in mind that the team members must include all the skills demanded by the assignment at the lowest cost, which is considered another contribution in this paper.
Studying how to assemble an efficient group of experts, which will include the project’s requirements. That is, by knowing all the skills of each expert can assemble an appropriate team of experts. Also, must ensure that the team members that are chosen to work on the project meet the load balance. And make sure that no one is overloaded with work and that no job is assigned to an expert who is unable to complete or handle it. This is called the equitable distribution of work.
During this experiment, the workload balance constraint is applied to ensure that the workload does not exceed a certain limitation. For example, if the task needs three skills, there is a condition that each expert in the team has only one single task, and in the case of needing five or seven skills, then every expert in the team has no more than two tasks.
In this section, the HBOSA, and CHBO algorithms are compared with HBO, DSA, PSO, GA, and GWO using various numbers of skills and various numbers of experts for the IMBD dataset. Tab. 6 represented the average communication cost for the seven algorithms at three different skills (3, 5, 7) and various numbers of experts (10, 20, 30, 40, 50, 100).
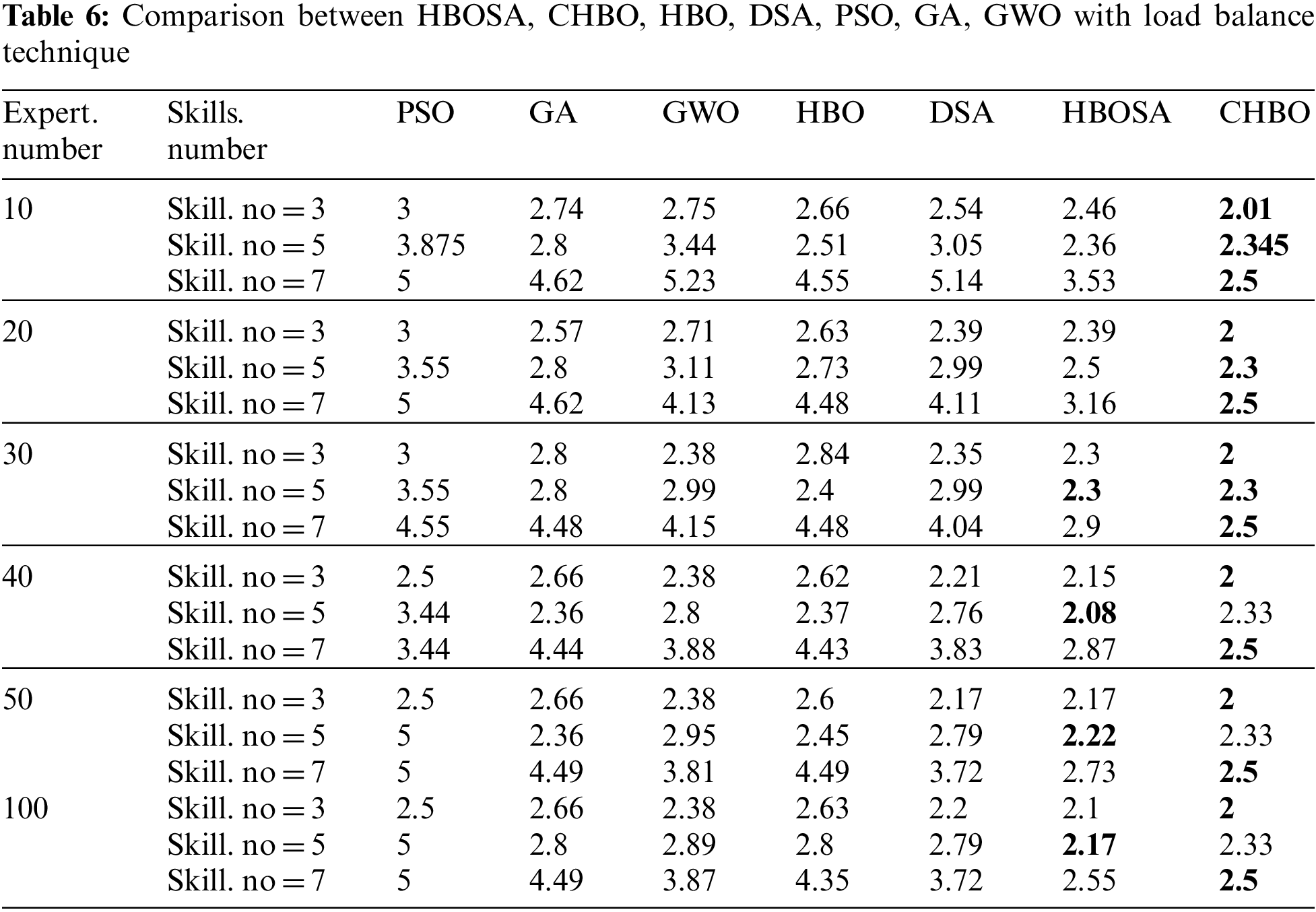
The result in Tab. 6, shows that the CHBO algorithm outperform other algorithms when the number of skills equals seven, also it outperforms HBOSA algorithm. When the number of skills equals five the HBOSA is outperform PSO, GA, GWO, and HBO algorithms and outperform CHBO at expert number equal 30, 40, 50, 100. It can be concluded from this experiment that the suggested algorithms can obtain the optimal team with minimum communication cost, and they in general, have the best performance than the other compered algorithms which stack in local optimum.
To estimate the performance of the suggested algorithms applying a validation test T test is used to detect a statistically significant difference between the suggested algorithm HBOSA and the compared algorithms (HBO, SA, PSO, GA, and GWO), show in Tab. 7. And the CHBO with the compared algorithms (HBO, SA, PSO, GA, and GWO) in Tab. 8.
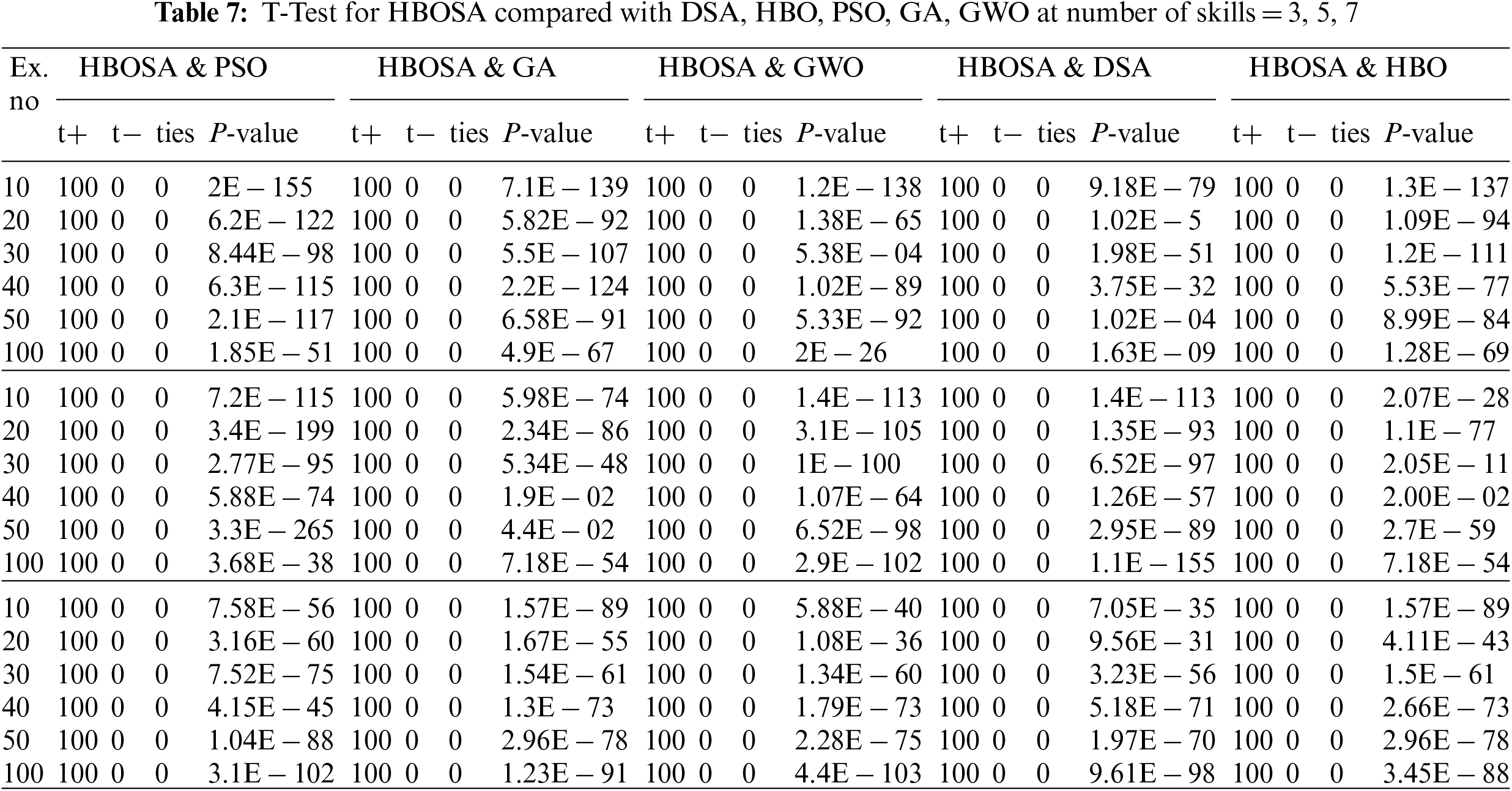
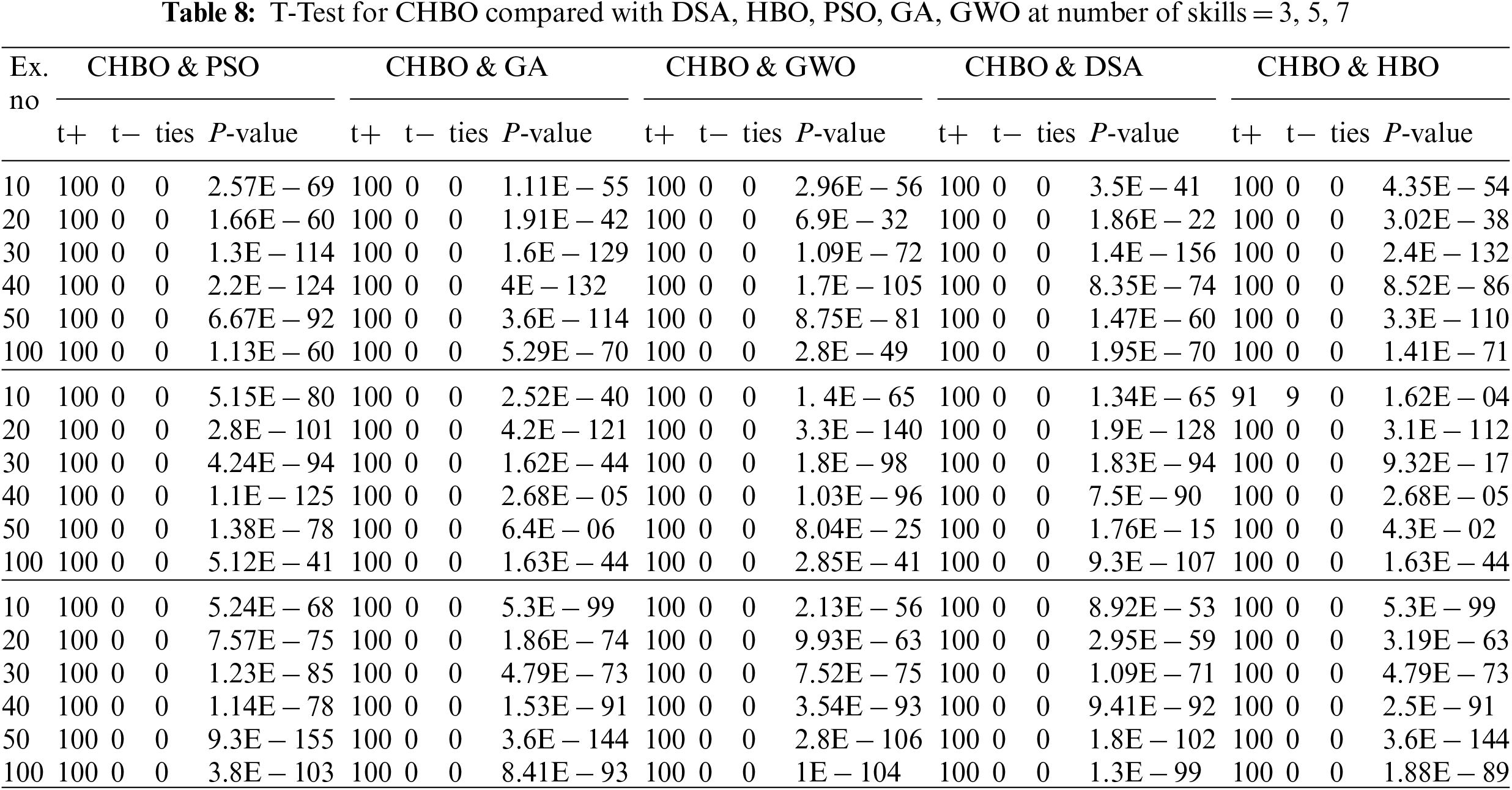
The T-test, which was devised by William Sealy Gosset in 1908, is one of several types of statistical tests used to test hypotheses and show whether the results of the experiment are significant. The T-test is considered the best test for a similar or dependent group of data [41]. Applying this test to determine if the means of two groups differ significantly or not by comparing the average (mean) of our suggested algorithms HBOSA and CHBO with other compared algorithms Tab. 7 shows the results of comparing the means of HBOSA vs. HBO, means of HBOSA vs. SA, means of HBOSA vs. PSO, means of HBOSA vs. GA, and means of HBOSA vs. GWO at skills (3, 5, 7). Also, Tab. 8 shows the results of comparing the means of CHBO vs. HBO, means of CHBO vs. SA, means of CHBO vs. PSO, means of CHBO vs. GA, and means of CHBO vs. GWO at skills (3, 5, 7), applying this test using an excel program.
The T-test for two samples is shown in Tabs. 7 and 8. The term p-value, or probability value, refers to a statistically significant event in which the proposed algorithm outperforms the compared algorithm. Where a P-Value is less than the alpha level selected, 0.05 is statistically significant, since the lowest the P-Value, the stronger the evidence. The result of the T-test demonstrates that there is statistically significant between the compared algorithms.
Another test to measure the performance of each of the algorithms is to measure the success and failure times and the equality of each algorithm during the 30 trials (run numbers) by using the sign excel function, Tabs. 7 and 8 present the test results for three samples selected at a number of skills = 3, 5, 7. No. T+ refers to the number of positive trials where the suggested algorithms HBOSA and CHBO are outperforms against the other algorithms, No. T− represents the number of negative trials where the suggested algorithm fails to precede against the other algorithms, and No. ties are the number of equal trials for the two algorithms. The T-test proves that there is a statistical difference in performance between the suggested algorithms and the other algorithms. It can be concluded that this test’s success proves that the suggested algorithms have the best performance ever.
Team formation problems are the process of finding a group of users who interact effectively with each other to carry out a specific task using their skills. This research suggested two algorithms to solve the team formation problem. The first one is a hybrid heap-based optimizer (HBO) and a simulated annealing algorithm (HBOSA). The HBO is incorporated with a developed simulated annealing algorithm (DSA) to enhance the performance of standard HBO. To avoid being trapped in local minima, DSA is applied to the best solution obtained from the HBO algorithm. The second proposed algorithm is the chaotic heap-based optimizer algorithm (CHBO) with a logistic chaotic map, which is used in the updating process of solutions. A set of experiments were applied to test the performance of the suggested algorithms. Firstly, a set of well-known benchmark functions were used to evaluate the suggested algorithms’ performance against a standard one and some well-known optimizers. Secondly, a random dataset and a real-life IMBD dataset were used to evaluate the proposed algorithms. The suggested algorithms were compared with five other algorithms. These algorithms are, namely, the particle swarm algorithm (PSO), the grey wolf algorithm (GWO), the genetic algorithm (GA), the devolved simulated annealing algorithm (DSA), and the standard heap-based optimizer (HBO). Experimental results showed that the proposed HBOSA and CHBO algorithms improved the capability and efficacy of the classical HBO algorithm. Also, the ability of proposed algorithms to select the best solution with the least communication outperformed all compared algorithms. CHBO algorithm has proven its superiority over all the comparison algorithms due to its use of the logistic map, which increases its ability to explore the search space. The efficiency of the proposed algorithms was evaluated by applying the validation test, the T-test, and the post hoc T-test. The experimental results showed that the proposed algorithms outperformed the compared methods in the speed of convergence to reach the optimal solution in the speed of convergence to reach the optimal solution with the least communication cost without stacking in the local optimum. A parallel version of the proposed algorithms will be developed and applied to different real-world applications in the future. Also, in future work, there will be a series of research that considers the problem in various forms, including considering it as a multi-objective problem, solving the Multi-Team Formation problem, and discussing different study cases and different team formation applications such as nurse scheduling problems, Task Assignment problems.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. T. Lappas, K. Liu and E. Terzi, “Finding a team of experts in social networks,” in Proc. of the 15th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Paris, France, pp. 467–476, 2009. [Google Scholar]
2. H. Wi, S. Oh, J. Mun and M. Jung, “A team formation model based on knowledge and collaboration,” Expert Systems with Applications, vol. 36, no. 5, pp. 9121–9134, 2009. [Google Scholar]
3. M. J. Ebadi, A. Hosseini and M. M. Hosseini, “A projection type steepest descent neural network for solving a class of nonsmooth optimization problems,” Neurocomputing, vol. 235, pp. 164–181, 2017. [Google Scholar]
4. F. Heydarpour, E. Abbasi, M. J. Ebadi and S. M. Karbassi, “Solving an optimal control problem of cancer treatment by artificial neural networks,” International Journal of Interactive Multimedia & Artificial Intelligence, vol. 6, no. 4, pp. 18--25, 2020. [Google Scholar]
5. N. Jamali, A. Sadegheih, M. M. Lotfi, L. C. Wood and M. J. Ebadi, “Estimating the depth of anesthesia during the induction by a novel adaptive neuro-fuzzy inference system: A case study,” Neural Processing Letters, vol. 53, no. 1, pp. 131–175, 2021. [Google Scholar]
6. S. Fouladi, M. J. Ebadi, A. A. Safaei, M. Y. Bajuri and A. Ahmadian, “Efficient deep neural networks for classification of COVID-19 based on CT images: Virtualization via software defined radio,” Computer Communications, vol. 176, pp. 234–248, 2021. [Google Scholar]
7. A. Haq, U. M. Modibbo, A. Ahmed and I. Ali, “Mathematical modeling of sustainable development goals of India agenda 2030: A Neutrosophic programming approach,” Environment, Development and Sustainability, vol. 1, pp. 1–28, 2021. [Google Scholar]
8. A. Anagnostopoulos, L. Becchetti, C. Castillo, A. Gionis and S. Leonardi, “Online team formation in social networks,” in Proc. of the 21st Int. Conf. on World Wide Web, New York, NY, USA, pp. 839–848, 2012. [Google Scholar]
9. M. Kargar, A. An and M. Zihayat, “Efficient bi-objective team formation in social networks,” in Joint European Conf. on Machine Learning and Knowledge Discovery in Databases, Springer, Bristol, UK, pp. 483–498, 2012. [Google Scholar]
10. M. Kargar, M. Zihayat and A. An, “Finding affordable and collaborative teams from a network of experts,” in Proc. of the 2013 SIAM Int. Conf. on Data Mining, Austin, Texas, USA, pp. 587–595, 2013. [Google Scholar]
11. J. H. Gutiérrez, C. A. Astudillo, P. Ballesteros-Pérez, D. Mora-Melia and A. Candia-Vejer, “The multiple team formation problem using sociometry,” Computers & Operations Research, vol. 75, pp. 150–162, 2016. [Google Scholar]
12. A. A. Hafez, A. Y. Abdelaziz, M. A. Hendy and A. F. Ali, “Optimal sizing of off-line microgrid via hybrid multi-objective simulated annealing particle swarm optimizer,” Computers & Electrical Engineering, vol. 94, pp. 107294, 2021. [Google Scholar]
13. F. Alkhateeb and B. H. Abed-Alguni, “A hybrid cuckoo search and simulated annealing algorithm,” Journal of Intelligent Systems, vol. 28, no. 4, pp. 683–698, 2019. [Google Scholar]
14. A. R. Hedar and M. Fukushima, “Hybrid simulated annealing and direct search method for nonlinear unconstrained global optimization,” Optimization Methods and Software, vol. 17, no. 5, pp. 891–912, 2002. [Google Scholar]
15. A. M. Turhan and B. Bilgen, “A hybrid fix-and-optimize and simulated annealing approaches for nurse rostering problem,” Computers & Industrial Engineering, vol. 145, pp. 106531, 2020. [Google Scholar]
16. A. Majumder, S. Datta and K. V. M. Naidu, “Capacitated team formation problem on social networks,” in Proc. of the 18th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, New York, NY, USA, pp. 1005–1013, 2012. [Google Scholar]
17. M. Kargar, A. An and M. Zihayat, “Efficient bi-objective team formation in social networks,” in Joint European Conf. on Machine Learning and Knowledge Discovery in Databases, Berlin, Heidelberg, Springer, pp. 483–498, 2012. [Google Scholar]
18. M. F. Khan, A. Haq, A. Ahmed and I. Ali, “Multiobjective multi-product production planning problem using intuitionistic and neutrosophic fuzzy programming,” IEEE Access, vol. 9, pp. 37466–37486, 2021. [Google Scholar]
19. S. Gupta, A. Haq, I. Ali and B. Sarkar, “Significance of multi-objective optimization in logistics problem for multi-product supply chain network under the intuitionistic fuzzy environment,” Complex & Intelligent Systems, vol. 7, no. 4, pp. 2119–2139, 2021. [Google Scholar]
20. J. Basiri, F. Taghiyareh and A. Ghorbani, “Collaborative team formation using brain drain optimization: A practical and effective solution,” World Wide Web, vol. 20, no. 6, pp. 1385–1407, 2017. [Google Scholar]
21. C. Eichmann and C. Mueller, “Team formation based on nature-inspired swarm intelligence,” Journal of Software, vol. 10, no. 3, pp. 344–354, 2015. [Google Scholar]
22. W. H. El-Ashmaw, “An improved african buffalo optimization algorithm for collaborative team formation in social network,” Int. J. Inf. Technol. Comput. Sci., vol. 10, pp. 16–29, 2018. [Google Scholar]
23. W. H. El-Ashmawi, A. F. Ali and M. A. Tawhid, “An improved particle swarm optimization with a new swap operator for team formation problem,” Journal of Industrial Engineering International, vol. 15, no. 1, pp. 53–71, 2019. [Google Scholar]
24. M. Z. Rehman, K. Z. Zamli, M. Almutairi, H. Chiroma, M. Aamir et al., “A novel state space reduction algorithm for team formation in social networks,” PloS One, vol. 16, no. 12, pp. 259786, 2021. [Google Scholar]
25. A. Sharma, J. K. Pandey and M. Ram, “Swarm Intelligence: Foundation, Principles, and Engineering Applications,” CRC Press, Boca Raton, 2022. [Google Scholar]
26. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN’95-Int. Conf. on Neural Networks, IEEE, Perth, WA, Australia, vol. 4, pp. 1942–1948, 1995. [Google Scholar]
27. J. H. Holland, “Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence,” MIT Press, 55 Hayward St., Cambridge, MA, United States, 1992. [Google Scholar]
28. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]
29. H. Joshi and S. Arora, “Enhanced grey wolf optimization algorithm for global optimization,” Fundamenta Informaticae, vol. 153, no. 3, pp. 235–264, 2017. [Google Scholar]
30. S. Kirkpatrick, C. D. Gelatt Jr and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar]
31. Q. Askari, M. Saeed and I. Younas, “Heap-based optimizer inspired by corporate rank hierarchy for global optimization,” Expert Systems with Applications, vol. 161, pp. 113702, 2020. [Google Scholar]
32. S. K. Elsayed, S. Kamel, A. Selim and M. Ahmed, “An improved heap-based optimizer for optimal reactive power dispatch,” IEEE Access, vol. 9, pp. 58319–58336, 2021. [Google Scholar]
33. M. Abdel-Basset, R. Mohamed, M. Elhoseny, R. K. Chakrabortty and M. J. Ryan, “An efficient heap-based optimization algorithm for parameters identification of proton exchange membrane fuel cells model: Analysis and case studies,” International Journal of Hydrogen Energy, vol. 46, no. 21, pp. 11908–11925, 2021. [Google Scholar]
34. S. Katoch, S. S. Chauhan and V. Kumar, “A review on genetic algorithm: Past, present, and future,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 8091–8126, 2021. [Google Scholar]
35. V. Černý, “Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm,” Journal of Optimization Theory and Applications, vol. 45, no. 1, pp. 41–51, 1985. [Google Scholar]
36. J. Zhang, M. Ohsaki and Z. Li, “Optimization of large-scale transmission tower using simulated annealing,” in Proceedings of IASS Annual Symposia, International Association for Shell and Spatial Structures (IASS), Hamburg, Germany, vol. 2017, no. 16, pp. 1–8, 2017. [Google Scholar]
37. R. Storn and K. Price, “Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, no. 4, pp. 341–359, 1997. [Google Scholar]
38. J. Brest and M. S. Maučec, “Self-adaptive differential evolution algorithm using population size reduction and three strategies,” Soft Computing, vol. 15, no. 11, pp. 2157–2174, 2011. [Google Scholar]
39. G. I. Sayed, A. E. Hassanien and A. T. Azar, “Feature selection via a novel chaotic crow search algorithm,” Neural Computing and Applications, vol. 31, no. 1, pp. 171–188, 2019. [Google Scholar]
40. D. P. Feldman, Chaos and Fractals: An Elementary Introduction, Oxford University Press, Oxford Scholarship Online, 2012. [Google Scholar]
41. B. Gerald, “A brief review of independent, dependent and one sample t-test,” International Journal of Applied Mathematics and Theoretical Physics, vol. 4, no. 2, pp. 50–54, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |