| Computers, Materials & Continua DOI:10.32604/cmc.2022.030399 |  |
| Article |
Chaotic Krill Herd with Deep Transfer Learning-Based Biometric Iris Recognition System
1Department of Computer Science, Faculty of Information Technology, Al-Hussein Bin Talal University Ma’an, 71111, Jordan
2MIS Department, College of Business Administration, University of Business and Technology, Jeddah, 21448, Saudi Arabia
*Corresponding Author: Bassam A. Y. Alqaralleh. Email: b.alqaralleh@ubt.edu.sa
Received: 25 March 2022; Accepted: 07 June 2022
Abstract: Biometric verification has become essential to authenticate the individuals in public and private places. Among several biometrics, iris has peculiar features and its working mechanism is complex in nature. The recent developments in Machine Learning and Deep Learning approaches enable the development of effective iris recognition models. With this motivation, the current study introduces a novel Chaotic Krill Herd with Deep Transfer Learning Based Biometric Iris Recognition System (CKHDTL-BIRS). The presented CKHDTL-BIRS model intends to recognize and classify iris images as a part of biometric verification. To achieve this, CKHDTL-BIRS model initially performs Median Filtering (MF)-based preprocessing and segmentation for iris localization. In addition, MobileNet model is also utilized to generate a set of useful feature vectors. Moreover, Stacked Sparse Autoencoder (SSAE) approach is applied for classification. At last, CKH algorithm is exploited for optimization of the parameters involved in SSAE technique. The proposed CKHDTL-BIRS model was experimentally validated using benchmark dataset and the outcomes were examined under several aspects. The comparison study results established the enhanced performance of CKHDTL-BIRS technique over recent approaches.
Keywords: Biometric verification; iris recognition; deep learning; parameter tuning; machine learning
Security sciences have started leveraging interesting elements for the past few years to ensure secure admission to confined places since it has become a crucial issue. The rising interest upon effective security confirmation frameworks has boosted the development of verification frameworks that are safer and highly proficient [1,2]. Conventional ways to deal with Iris Detection (ID), for example, utilization of a key or secret phrase is unacceptable in selected applications. This is due to the fact that these techniques can undoubtedly be neglected, taken, or broken. To conquer these shortcomings, the mechanization of distinguishing proof frameworks is applied with the help of biometric methods [3]. The requirement for dependable and secure frameworks has prompted the rise of physiological and social models in biometric frameworks. Iris Recognition System (IRS) framework is highly effective in nature and it is a solid framework to check the reality [4]. It can be enclosed by means of a design in such a way that it can influence an individual’s wellbeing. Further, it can be implemented through a painless gadget [5]. As a result, some futuristic organizations that deal with security have already started anticipating the fate of IRS, because of its wide applications and capability of innovation.
The primary reason behind considering iris for biometric verification is that it is one of the truly-steady biometric feature that barely changes in the lifetime of human being [6]. Subsequently, iris locale can be successfully constructed and used for recognition or ID [7]. There is enormous scope available for projects that distinguish public and the need for appropriate biometric recognition is progressively conveyed across the globe. Public ID programs are progressively using IRS for better accuracy and dependability to enroll the residents (notwithstanding, the usage of various biometric recognition methods like two-layered face and unique mark recognition framework). IRS is a high-precision confirmation approach whilst its high potentials are yet to be unleashed [8].
IRS is being progressively applied in robotized frameworks especially in security. In this regard, most of the nations started utilizing IRS to enhance security at entry checkpoints such as air terminals and boundaries, at government entities like medical clinics and even in cell phones too [9]. Albeit, a significant number of past works conducted upon IRS accomplish high precision rates. It includes huge pre-processing tasks (counting iris division and unwrapping the first iris into a rectangular region) and utilization of a few hands-tailored highlights. However, this may not be ideal for different iris datasets, collected under different lighting and ecological circumstances. Lately, there has been a great deal of spotlight on creating models to learn the elements together. In line with this, Deep Learning (DL) models have been exceptionally effective in different computer vision tasks [10].
Zhao et al. [11] presented a DL approach based on capsule network structure in IRS. In this infrastructure, the network features are adjusted after which a different routing technique is offered based on dynamic routing between two capsule layers. This is done so to make this approach, a suitable one for IRS. Adamović et al. [12] proposed a novel IRS model based on Machine Learning (ML) approaches. The motivation behind this research belongs to the association between biometric schemes and stylometry as demonstrated in literature. The purposes of the presented technique are to achieve high classification accuracy, remove false acceptance rate, and cancel the probability of recreating iris image in a created template. Ahmadi et al. [13] presented an extravagant IRS approach based on a group of two-dimension Gabor kernel (2-DGK), Step Filtering (SF), and Polynomial Filtering (PF) to extract the features and hybrid Radial Basis Function Neural Network (RBFNN) with Genetic Algorithm (GA) to perform equivalent tasks. In literature [14], the authors examined a novel DL-based model for IRS and attempted to improve the accuracy with the help of basic infrastructure in order to recover the representative feature. It can be assumed that the residual network learns with dilated convolution kernel during the optimization of training method and aggregation of contextual data in iris image. In the study conducted earlier [15], the authors proposed a structure to capture real-time IRS and perform segmentation from video as part of biometric detection model. The method concentrates on image capture, IRS, and segmentation from video frame in a controlled manner. The criteria include border and access control while the people collaborate from different detection procedures.
The current study introduces a novel Chaotic Krill Herd with Deep Transfer Learning Based Biometric Iris Recognition System (CKHDTL-BIRS). The aim of the presented CKHDTL-BIRS model is to recognize and classify iris images for biometric verification. To achieve this, CKHDTL-BIRS model initially performs Median Filtering (MF)-based preprocessing and segmentation for iris localization. In addition, MobileNet model is utilized to generate a set of useful feature vectors. Moreover, Stacked Sparse Autoencoder (SSAE) technique is also applied for classification. At last, CKH algorithm is exploited for the optimization of parameters involved in SSAE technique. The proposed CKHDTL-BIRS model was experimentally validated using benchmark dataset and the outcomes were inspected under several aspects.
Rest of the paper is organized as follows. Section 2 discusses about the proposed model and Section 3 offers the experimental validation. Finally, Section 4 concludes the work.
In this study, a novel CKHDTL-BIRS technique has been developed to recognize and classify iris for biometric verification. Initially, Median Filter-based preprocessing of the data is performed in CKHDTL-BIRS model after which segmentation is performed to localize iris regions. Besides, MobileNet model is utilized to generate a suitable group of feature vectors. Moreover, CKH with SSAE technique is also executed for classification. Fig. 1 illustrates the block diagram of CKHDTL-BIRS technique.
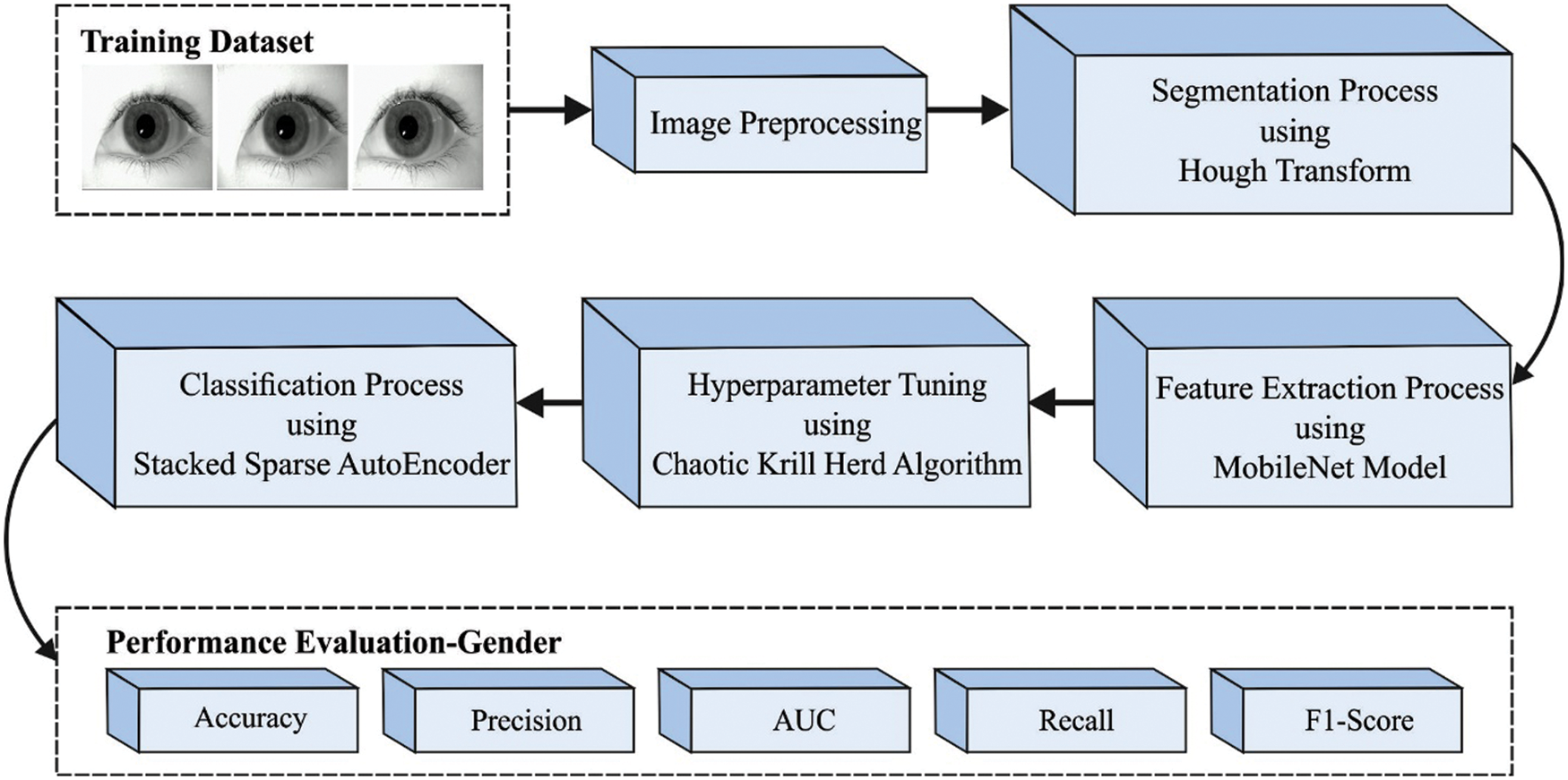
Figure 1: Block diagram of CKHDTL-BIRS technique
At the initial stage, the input image is preprocessed through MF technique to remove the noise. MF approach is determined as a nonlinear signal processing method that depends on existing statistics. The MF outcome is determined to be
whereas
When (1) and (2) are compared, the results demonstrate that the MF function depends upon two objectives such as size of the mask and noise distribution. MF executes noise removal that is significant, if related to average filters. The function of MF is to maximize, once the MF technique is combined with average filter method.
After preprocessing, segmentation is performed to localize iris regions. The outer radius of iris pattern and pupils are localized primarily with Hough Transform (HT) which contains Canny edge detector to generate edge mapping. HT identifies the place of circles and ellipses; it places contour from ‘n’ dimension space by investigating whether it can lie on curve of a detailed shape. An identical approach, using parameterized parabolic arcs, is executed to detect upper as well as lower eyelids. Afterwards, the localized iris segment is altered to fixed-size rectangular images.
At this stage, MobileNet model is utilized to generate a set of useful feature vectors. MobileNet approach is usually employed in image classification process since it requires minimal computation complexity, compared to other DL methods [16]. The feature vector map is of size
The multiplier value is context-oriented and it lies in the interval of 1 to
It integrates depth-wise and point-wise restricted convolutions using depletion parameter which is defined using the parameter
The size of input image is set to be
2.4 SSAE Based Iris Recognition
Once the feature vectors are derived, SSAE model is applied for classification. In image classification, the feature vector is provided to SSAE approach so as to allot appropriate class labels. In comparison with Stacked Autoencoder (SAE), SSAE can be trained with the identification of an optimal parameter
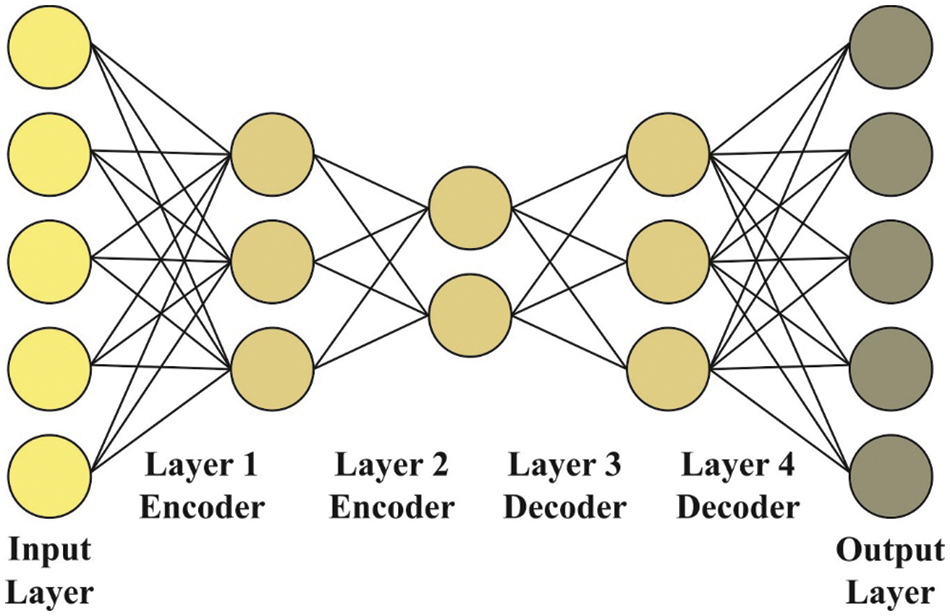
Figure 2: Structure of SSAE
In SSAE technique, all the trained patches
Here,
2.5 CKHA Based Parameter Optimization
In this final stage, CKH algorithm is exploited for optimization of the parameters [18,19] involved in SSAE model. Based on swarm behaviour of krill, Krill Herd (KH) algorithm [20], a metaheuristic optimization approach is utilized to resolve optimization problem. In KH, the place is frequently affected by three actions such as,
• Foraging performance;
• Physical diffusion; and
• Effort affected by another krill
In KHA, Lagrangian process is employed from the present searching space as given below.
whereas
An initial one, and their direction,
The secondary one is calculated through two elements such as food place and previous experiences. In order to achieve
whereas
and
Here,
CKHA approach is the resultant product by incorporating chaotic models such as KHA. In this case, a 1D chaotic map is combined with CKHA method.
The proposed CKHDTL-BIRS model was validated for its performance using CASIA iris image database. The results were investigated under five dissimilar runs. Fig. 3 depicts some of the sample images.
Figure 3: Sample images
Tab. 1 provides the overall recognition performance of MobileNet with SSAE (MN-SSAE) model and CKHDTL-BIRS model. The results imply that CKHDTL-BIRS model yielded improved outcomes over MN-SSAE model.
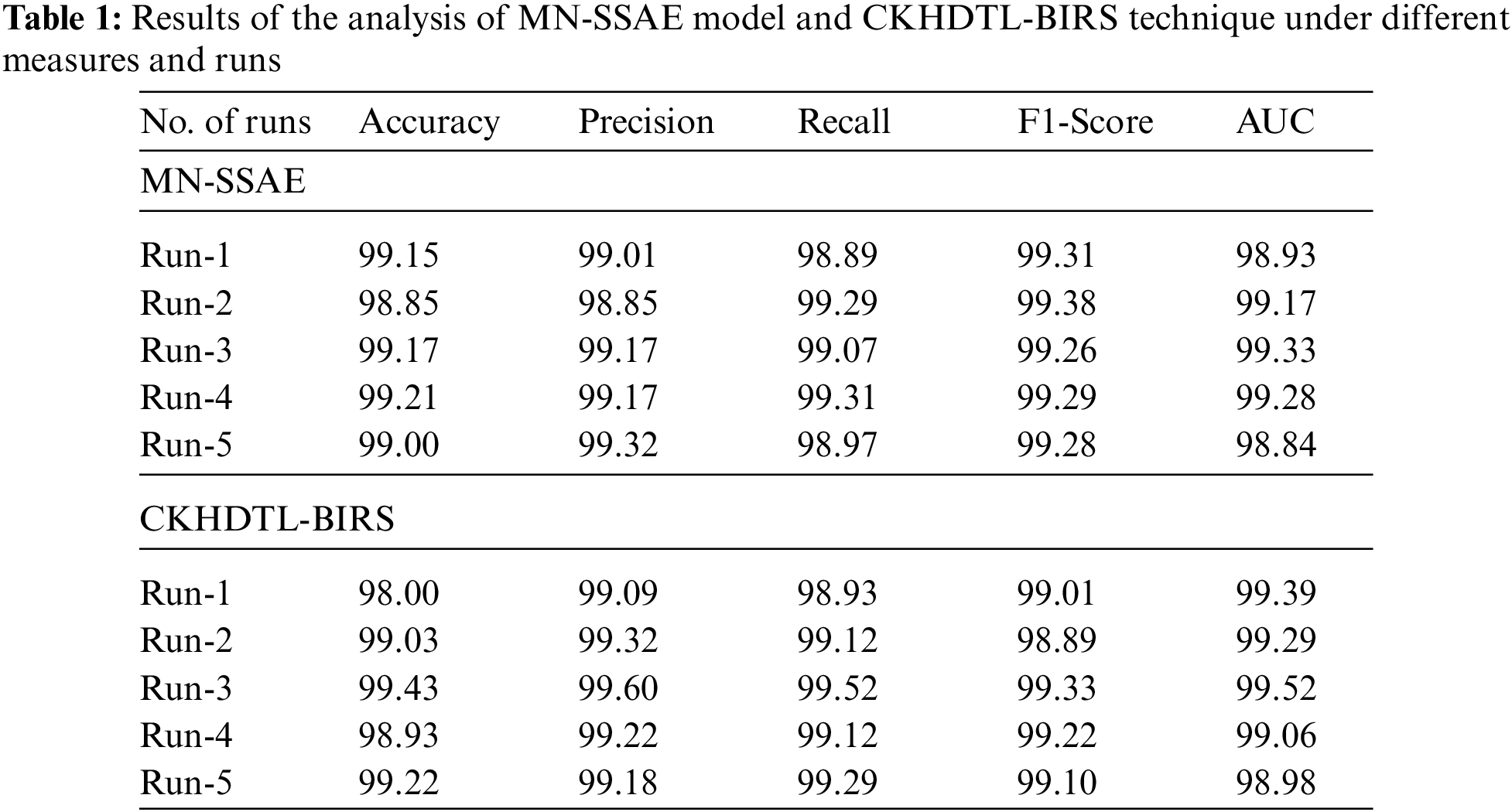
Fig. 4 highlights the IR outcomes of MN-SSAE model in terms of
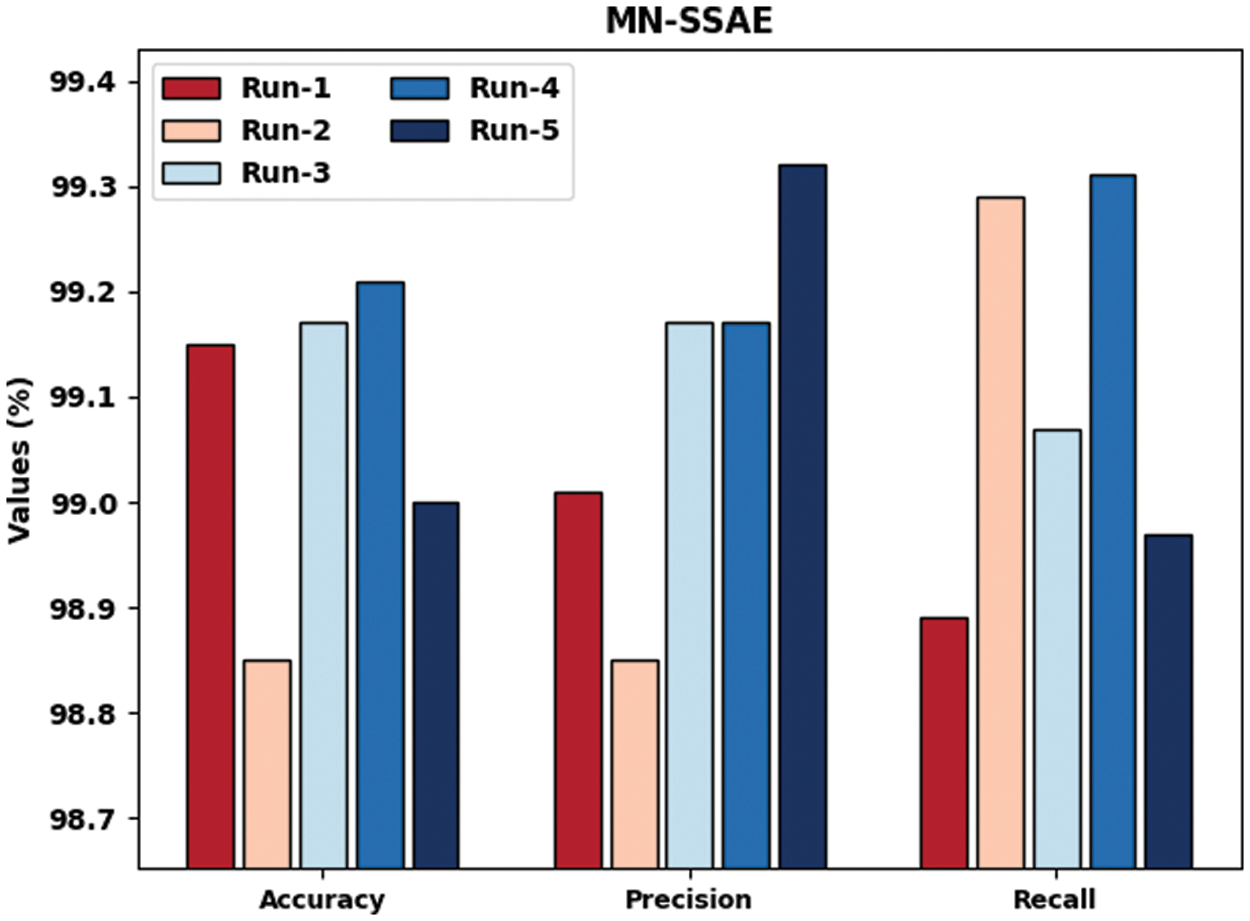
Figure 4: Results of the analysis of MN-SSAE technique under distinct runs
Fig. 5 highlights the IR outcomes of MN-SSAE technique with respect to
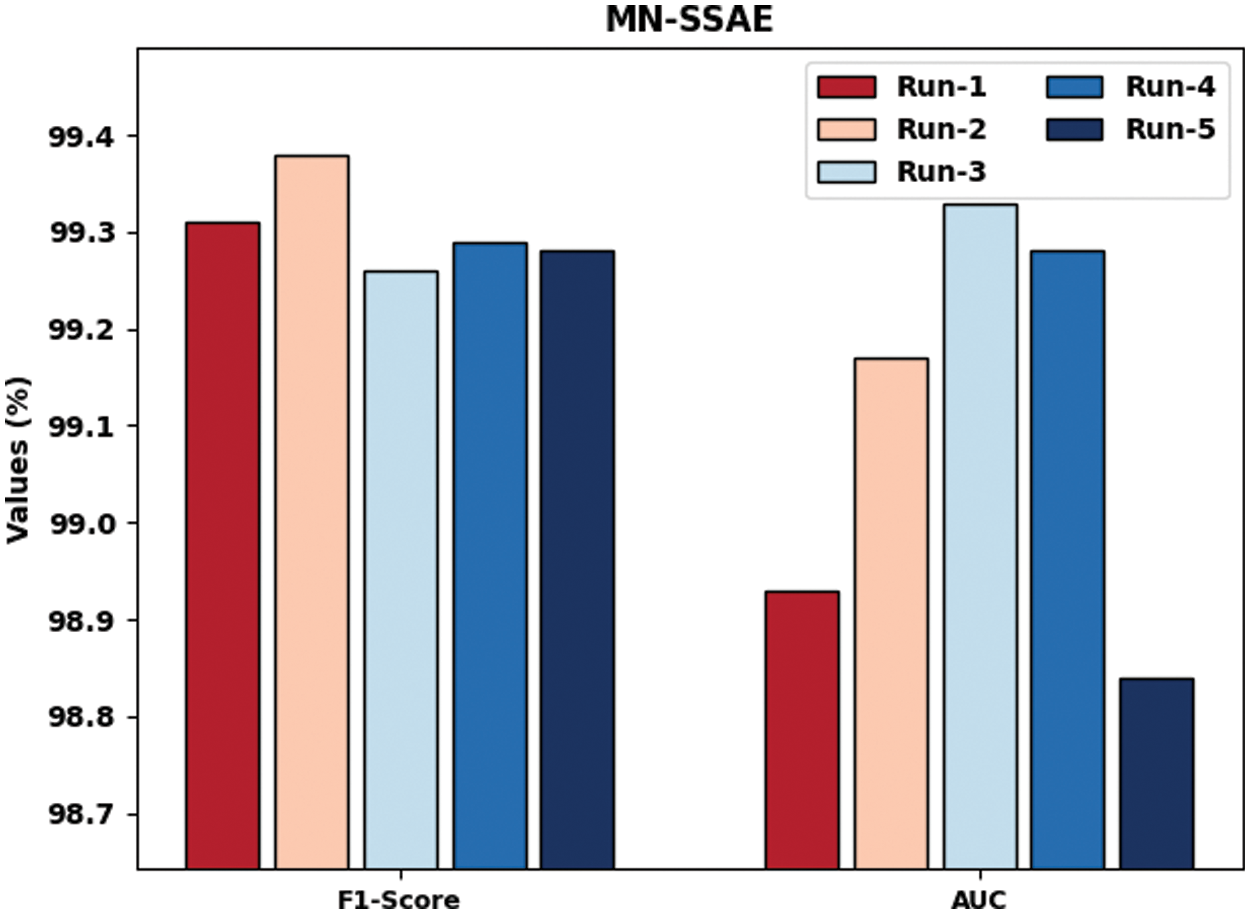
Figure 5:
Fig. 6 examines the IR outcomes of CKHDTL-BIRS approach with respect to
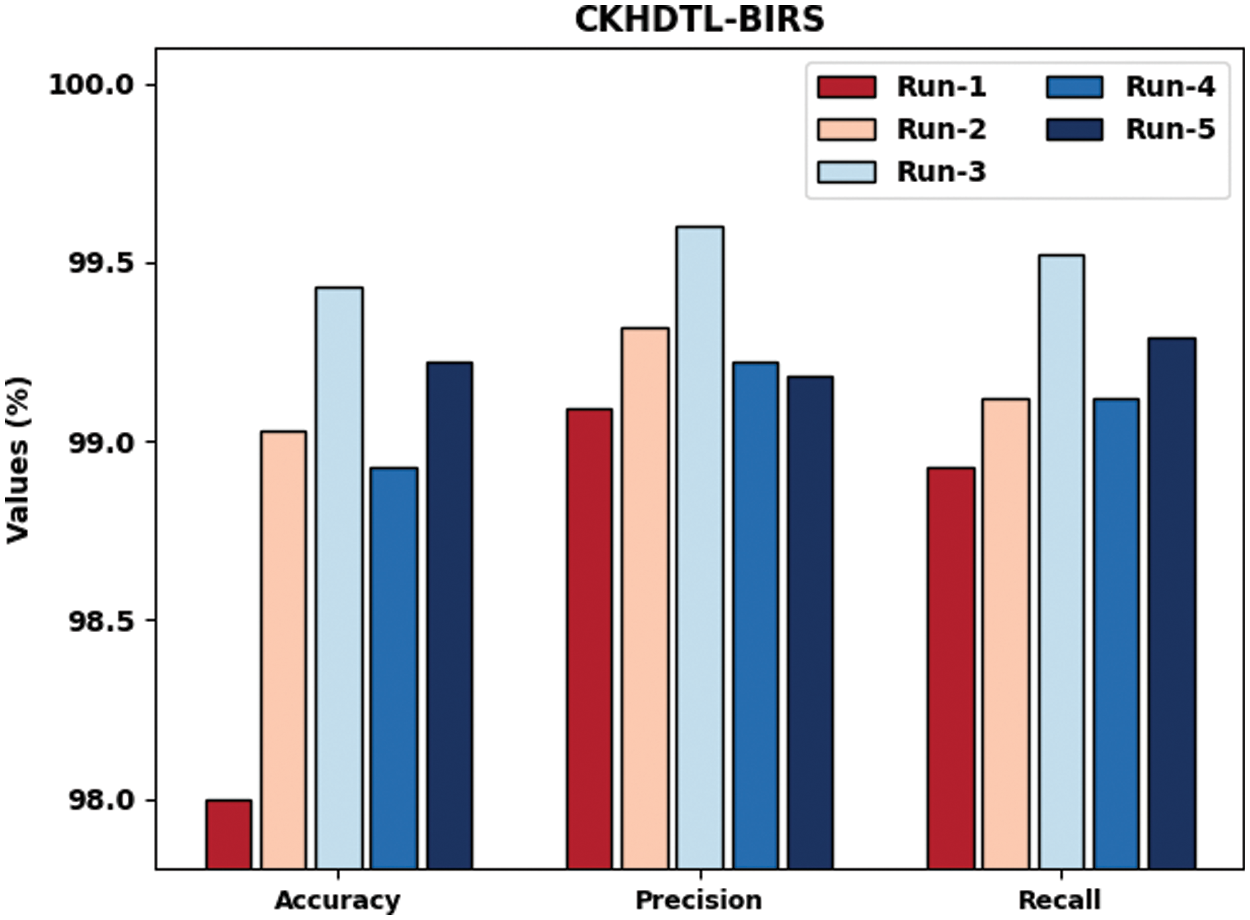
Figure 6: Results of the analysis of CKHDTL-BIRS technique under distinct runs
Fig. 7 demonstrates the IR outcomes achieved by CKHDTL-BIRS system in terms of
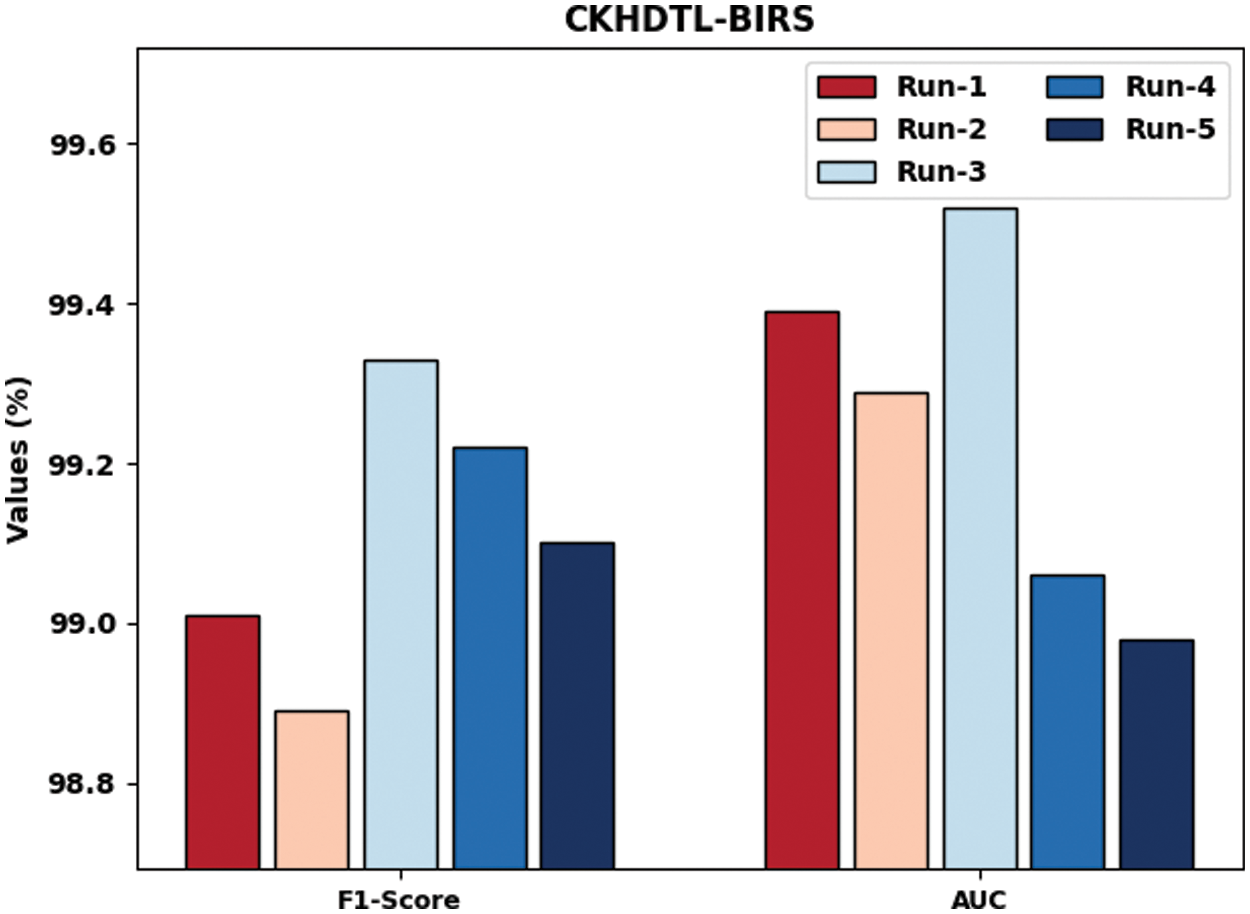
Figure 7:
A brief comparative study was conducted between CKHDTL-BIRS model and the existing models while the results are shown in Tab. 2. Fig. 8 reports the detailed comparative
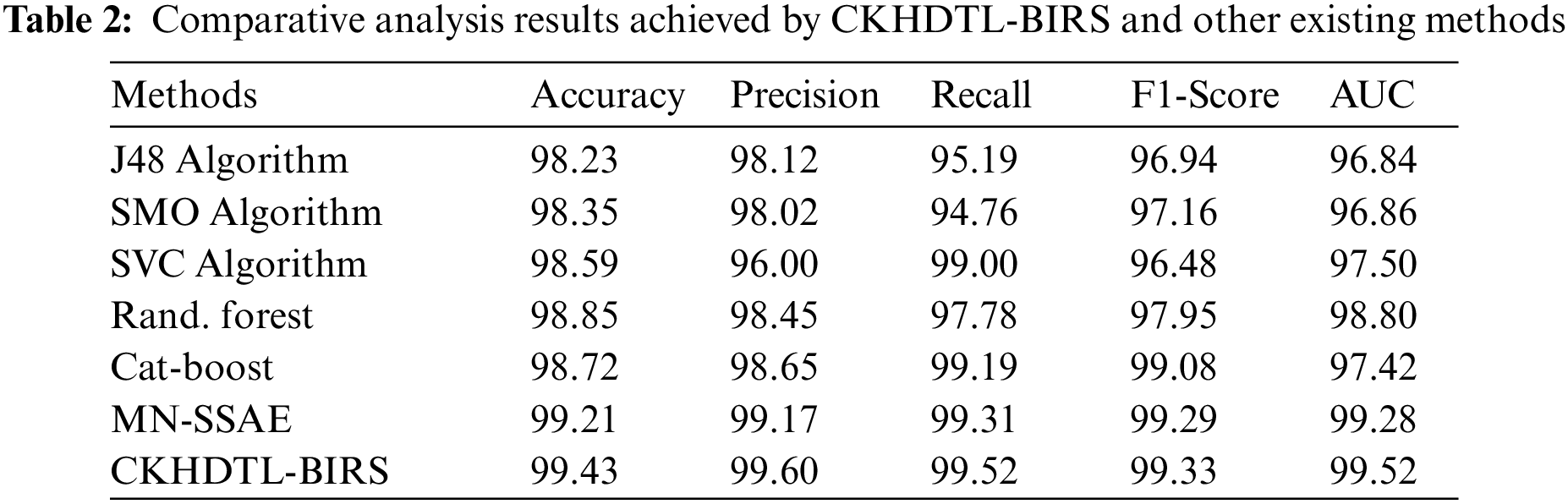
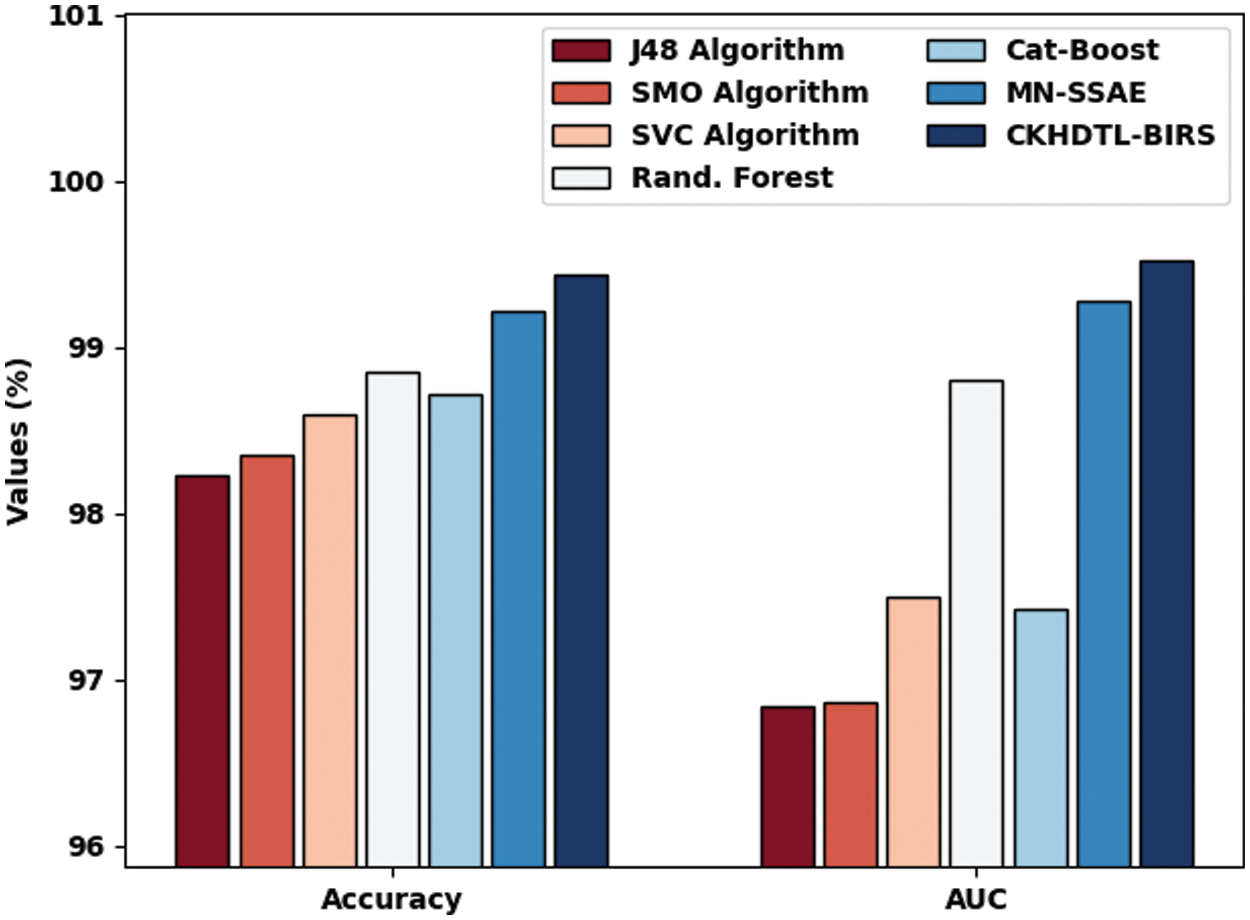
Figure 8:
Fig. 9 portrays the detailed comparative
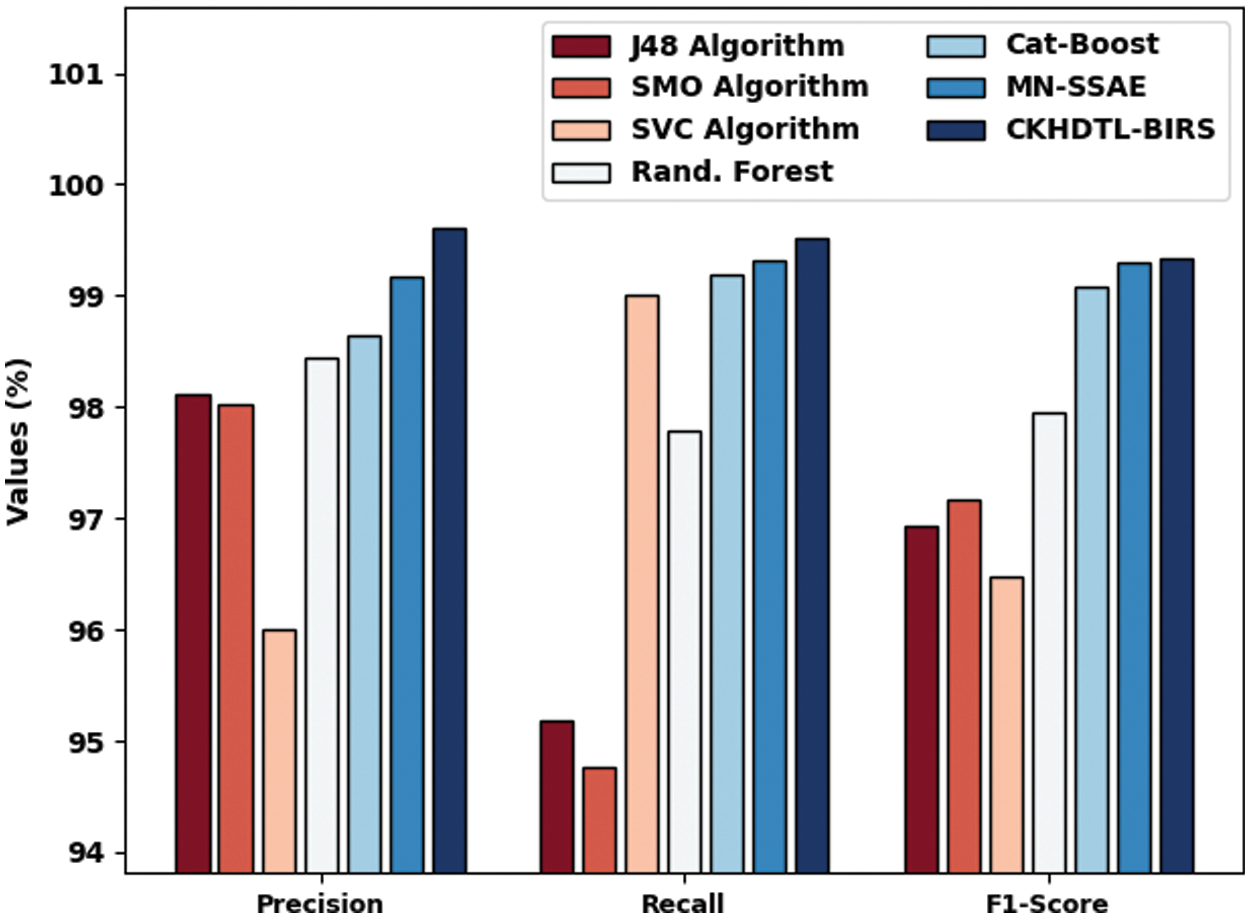
Figure 9: Comparative analysis results of CKHDTL-BIRS and other existing approaches
In this study, a novel CKHDTL-BIRS technique has been developed to recognize and classify iris images for biometric verification. The proposed CKHDTL-BIRS model initially performs MF to preprocess the images after which segmentation process is employed to localize iris regions. Besides, MobileNet model is also utilized to generate a set of useful feature vectors. Moreover, SSAE model is applied for classification. At last, CKH algorithm is exploited for optimization of the parameters involved in SSAE approach. The proposed CKHDTL-BIRS model was experimentally validated using benchmark dataset and the outcomes were examined under several aspects. The comparison study outcomes established the enhanced performance of CKHDTL-BIRS model than the existing algorithms since the proposed model achieved the maximum
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. S. A. Waisy, R. Qahwaji, S. Ipson, S. Al-Fahdawi and T. A. Nagem, “A Multi-biometric iris recognition system based on a deep learning approach,” Pattern Analysis and Applications, vol. 21, no. 3, pp. 783–802, 2018. [Google Scholar]
2. A. Boyd, S. Yadav, T. Swearingen, A. Kuehlkamp, M. Trokielewicz et al., “Post-mortem iris recognition—a survey and assessment of the state of the art,” IEEE Access, vol. 8, pp. 136570–136593, 2020. [Google Scholar]
3. M. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]
4. W. Sun, X. Chen, X. R. Zhang, G. Z. Dai, P. S. Chang et al., “A Multi-feature learning model with enhanced local attention for vehicle re-identification,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3549–3560, 2021. [Google Scholar]
5. V. C. Kagawade and S. A. Angadi, “A new scheme of polar fast Fourier transform code for iris recognition through symbolic modelling approach,” Expert Systems with Applications, vol. 197, pp. 116745, 2022. [Google Scholar]
6. J. R. Malgheet, N. B. Manshor, L. S. Affendey and A. B. A. Halin, “Iris recognition development techniques: A comprehensive review,” Complexity, vol. 2021, pp. 1–32, 2021. [Google Scholar]
7. M. B. Lee, J. K. Kang, H. S. Yoon and K. R. Park, “Enhanced iris recognition method by generative adversarial network-based image reconstruction,” IEEE Access, vol. 9, pp. 10120–10135, 2021. [Google Scholar]
8. Y. Chen, Z. Zeng, H. Gan, Y. Zeng and W. Wu, “Non-segmentation frameworks for accurate and robust iris recognition,” Journal of Electronic Imaging, vol. 30, no. 3, pp. 033002, 2021. [Google Scholar]
9. B. Muthazhagan and S. Sundaramoorthy, “Ameliorated face and iris recognition using deep convolutional networks,” in Machine Intelligence and Big Data Analytics for Cybersecurity Applications, Studies in Computational Intelligence Book Series, Springer, Cham, vol. 919, pp. 277–296, 2021. [Google Scholar]
10. S. Lei, B. Dong, A. Shan, Y. Li, W. Zhang et al., “Attention meta-transfer learning approach for few-shot iris recognition,” Computers & Electrical Engineering, vol. 99, pp. 107848, 2022. [Google Scholar]
11. T. Zhao, Y. Liu, G. Huo and X. Zhu, “A deep learning iris recognition method based on capsule network architecture,” IEEE Access, vol. 7, pp. 49691–49701, 2019. [Google Scholar]
12. S. Adamović, V. Miškovic, N. Maček, M. Milosavljević, M. Šarac et al., “An efficient novel approach for iris recognition based on stylometric features and machine learning techniques,” Future Generation Computer Systems, vol. 107, pp. 144–157, 2020. [Google Scholar]
13. N. Ahmadi, M. Nilashi, S. Samad, T. A. Rashid and H. Ahmadi, “An intelligent method for iris recognition using supervised machine learning techniques,” Optics & Laser Technology, vol. 120, pp. 105701, 2019. [Google Scholar]
14. K. Wang and A. Kumar, “Toward more accurate iris recognition using dilated residual features,” IEEE Transactions on Information Forensics and Security, vol. 14, no. 12, pp. 3233–3245, 2019. [Google Scholar]
15. E. G. Llano and A. M. Gonzalez, “Framework for biometric iris recognition in video, by deep learning and quality assessment of the iris-pupil region,” Journal of Ambient Intelligence and Humanized Computing, pp. 1–13, 2021, Article in press, https://doi.org/10.1007/s12652-021-03525-x. [Google Scholar]
16. Y. Li, H. Huang, Q. Xie, L. Yao and Q. Chen, “Research on a surface defect detection algorithm based on MobileNet-SSD,” Applied Sciences, vol. 8, no. 9, pp. 1678, 2018. [Google Scholar]
17. Y. Qi, C. Shen, D. Wang, J. Shi, X. Jiang et al., “Stacked sparse autoencoder-based deep network for fault diagnosis of rotating machinery,” IEEE Access, vol. 5, pp. 15066–15079, 2017. [Google Scholar]
18. B. A. Y. Alqaralleh, T. Vaiyapuri, V. S. Parvathy, D. Gupta, A. Khanna et al., “Blockchain-assisted secure image transmission and diagnosis model on internet of medical things environment,” Personal and Ubiquitous Computing, 2021, Article in press, https://doi.org/10.1007/s00779-021-01543-2. [Google Scholar]
19. B. A. Y. Alqaralleh, S. N. Mohanty, D. Gupta, A. Khanna, K. Shankar et al., “Reliable multi-object tracking model using deep learning and energy efficient wireless multimedia sensor networks,” IEEE Access, vol. 8, pp. 213426–213436, 2020. [Google Scholar]
20. G. G. Wang, L. Guo, A. H. Gandomi, G. S. Hao and H. Wang, “Chaotic krill herd algorithm,” Information Sciences, vol. 274, pp. 17–34, 2014. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |