Computers, Materials & Continua DOI:10.32604/cmc.2022.030371
Article

A Beamforming Technique Using Rotman Lens Antenna for Wireless Relay Networks

Samer Alabed*, Mohammad Al-Rabayah and Wael Hosny Fouad Aly

College of Engineering and Technology, American University of the Middle East, Kuwait
*Corresponding Author: Samer Alabed. Email: samer.al-abed@aum.edu.kw
Received: 24 March 2022; Accepted: 27 May 2022

Abstract: Rotman lens, which is a radio frequency beam-former that consists of multiple input and multiple output beam ports, can be used in industrial, scientific, and medical applications as a beam steering device. The input ports collect the signals to be propagated through the lens cavity toward the output ports before being transmitted by the antenna arrays to the destination in order to enhance the error performance by optimizing the overall signal to noise ratio (SNR). In this article, a low-cost Rotman lens antenna is designed and deployed to enhance the overall performance of the conventional cooperative communication systems without needing any additional power, extra time or frequency slots. In the suggested system, the smart Rotman lens antennas generate a beam steering in the direction of the destination to maximize the received SNR at the destination by applying the proposed optimal beamforming technique. The suggested optimal beamforming technique enjoys high diversity, as well as, low encoding and decoding complexity. Furthermore, we proved the advantages of our suggested strategy through both theoretical results and simulations using Monte Carlo runs. The Monte Carlo simulations show that the suggested strategy enjoys better error performance compared to the current state-of-the-art distributed multi-antenna strategies. In addition, the bit error rate (BER) curves drawn from the analytical results are closely matching to those drawn from our conducted Monte Carlo simulations.

Keywords: Performance analysis; smart antenna; Rotman lens antenna; multi-antenna systems; wireless relay networks cooperative diversity schemes; digital network coding; relay selection schemes

1  Introduction

In the recent years, several techniques have been proposed in the field of wireless communications to enhance the error performance of the whole system and its achievable throughput [1–6]. A group of these techniques works by increasing or optimizing the transmitted power, while another group is applying powerful forward error detection and correction techniques to increase the achievable gain. Latest techniques are using time, frequency, and space-diversity techniques in order to enhance the total diversity gain [7–12]. In time diversity, the BER performance can be improved by sending the same signal many times in several time periods [13–16]. While, in frequency diversity the error performance is enhanced by sending the same signal many times in several frequency bands. Also, space diversity schemes that are known as multiple input multiple output (MIMO) schemes can be used to enhance the error performance by broadcasting the same signal many times via different transmitting antennas using the same frequency band and time period, leading to the most powerful performance without requiring extra periods or frequency bands [17,18]. Later on, several schemes are suggested to improve both diversity order and coding gain by combining diversity techniques with coding algorithms including but not limited to space-frequency coding (SFC) schemes and space-time coding (STC) schemes [10,13–15]. Furthermore, special diversity techniques using beamforming schemes [11–12,17–19] are used to steer the transmitting antenna beams towards the destination terminal to enhance the BER performance and the throughput by maximizing the received signal to noise ratio (SNR), given that the BER performance of the multi-antenna systems suffer from the multiuser interference and channel impairments [1–9]. In addition, it is very well known that it is difficult to deploy several antennas at the same mobile station due to several limitations. Therefore, cooperative communication systems can be used to overcome this problem by randomly distributing a group of relay nodes between the two communicating parties [5–11,20,21]. Those relay nodes can be used in two modes of operation, either to amplify and forward (AF) the obtained signals or to detect the transmitted symbols before forwarding them to the receiving antennas. However, relay-nodes in wireless relay systems process the obtained signals before transmitting them to the destination terminals by merging the obtained copies of the transmitted signal received via several links to enhance the diversity order and coding gain. These schemes are well known as the spatial-diversity schemes [5–11]. Lately, several improved relaying methods have been introduced to obtain a high diversity and coding gain. For instance, the so called space-time diversity schemes for cooperative communication systems, in which the relay nodes are applying a space-time coding techniques, are found to enhance the performance in terms of BER and achievable data rate [9,13–15,22]. The distributed beamforming techniques, where the relay nodes are capable of forming a beam towards the destination to enhance the achievable SNR, are introduced in [9,11,12,23–25]. More specifically, the authors of [17] proposed a new beamforming approach by combining a single-group multicasting network with orthogonal space-time block coding in order to minimize the total transmitted power while maintaining the quality of service constraints. Article [11] proposed a new non-coherent beam-forming scheme for bi-directional cooperative communication systems where the angles of the obtained signals on the relay nodes are adjusted without needing CSI or training signals. In [24], a non-trivial combination between the differential diversity and the distributed beamforming techniques have been used to develop a simple distributed differential transmit beamforming technique that does not require CSI at any node while providing high BER, optimal end-to-end delay, and low decoding complexity. A bi-directional differential beamforming scheme have been proposed in [9] by utilizing differential phase shift keying modulation at the relay stations to enable beamforming without the knowledge of any instantaneous CSI. On the other hand, more non-beamforming techniques have been proposed without the knowledge of any instantaneous CSI [26–29]. The Rotman lens is a radio frequency (RF) beam-former that has multi-input and multi-output beam ports [30,31]. The input ports collect the RF signals to be propagated through the lens cavity toward the output ports before being transmitted by the antenna arrays [30]. The authors of [32] emphasize on the need to combine the use of Rotman lens with RF switching for superior performance compared to conventional phased arrays. One great advantage of Rotman lens is its capability to generate many beams without the need to physically moving the antenna system [33], therefore, its being widely used in the radar surveillance systems to see targets in multiple directions without changing the orientation of the antenna. Also, in [34] the authors found that using the low-cost Rotman lens in hybrid beamforming systems can achieve a superior performance, exhibit wideband capability compared to the high-cost phase shifters and the small-scale MIMO systems. In this article, a low-cost Rotman lens antenna is utilized in order to enhance the overall performance of the conventional cooperative communication systems without needing any additional power, extra time or frequency slots. In the suggested system, the smart Rotman lens antennas generate a beam steering in the direction of the destination to maximize the received SNR by applying the proposed optimal beamforming technique. The suggested optimal beamforming technique enjoys high diversity order and low encoding and decoding complexity. Furthermore, we proved the advantages of our suggested strategy through both theoretical results and simulations using Monte Carlo runs. The Monte Carlo simulations show that the suggested strategy enjoys better BER performance compared to the current distributed multi-antenna strategies. In addition, the BER curves drawn from the analytical results are closely matching those drawn from our conducted Monte Carlo simulations.

2  System Model

Given that the Rotman lens is considered as a radio-frequency beam former that consists of N input terminals and M output terminals [30]. The received signals at the N input terminals will flow via the Rotman-lens to the M output terminals before reaching the transmitting antennas. The required phase and amplitude distributions can be obtained using the formulas of the optical path length equality by calculating the needed locations of the input and output terminals, and the transmission-line lengths as well. Rotman lens is capable of producing a steering beam of different phases by exciting the corresponding input/output ports, as well as, producing multiple beams by exciting the multiple input/output ports simultaneously. The use of Rotman lens is an efficient way to design low-cost smart antennas as it provides a true time delay leading to a larger spectrum, and a low insertion loss allowing to be easily fabricated at low cost [30].

In our proposed cooperative communication system, a unidirectional network composed of a transmitter T equipped with a single antenna, a receiver D equipped with a single antenna, and smart Rotman lens relay with a group of M receive antennas and N transmit antennas. The transmitter and the relay are equipped each with a Rotman lens in order to focus their beam-forms. As a first step, the transmitter T broadcasts the information toward the array of smart relay node. The smart relay amplifies and forwards (AF) the information toward the terminal node D. One should note here that all the antennas (T, R and D) have limited average transmission powers. In addition, we also denote the channel gains as fr (from T toRr) and gr (from D toRr). The magnitude, the floor formula that rounds in the direction of zero, the Frobenius norm, and the expectation are denoted by |.|, ⌊⋅⌋,||⋅|| andE(.),respectively. Also, Fig. 2 illustrates the implementation of the Rotman lens with M-input ports and N-output ports within the relay node.

Figure 1: System model showing the two communicating parties and the smart relay node

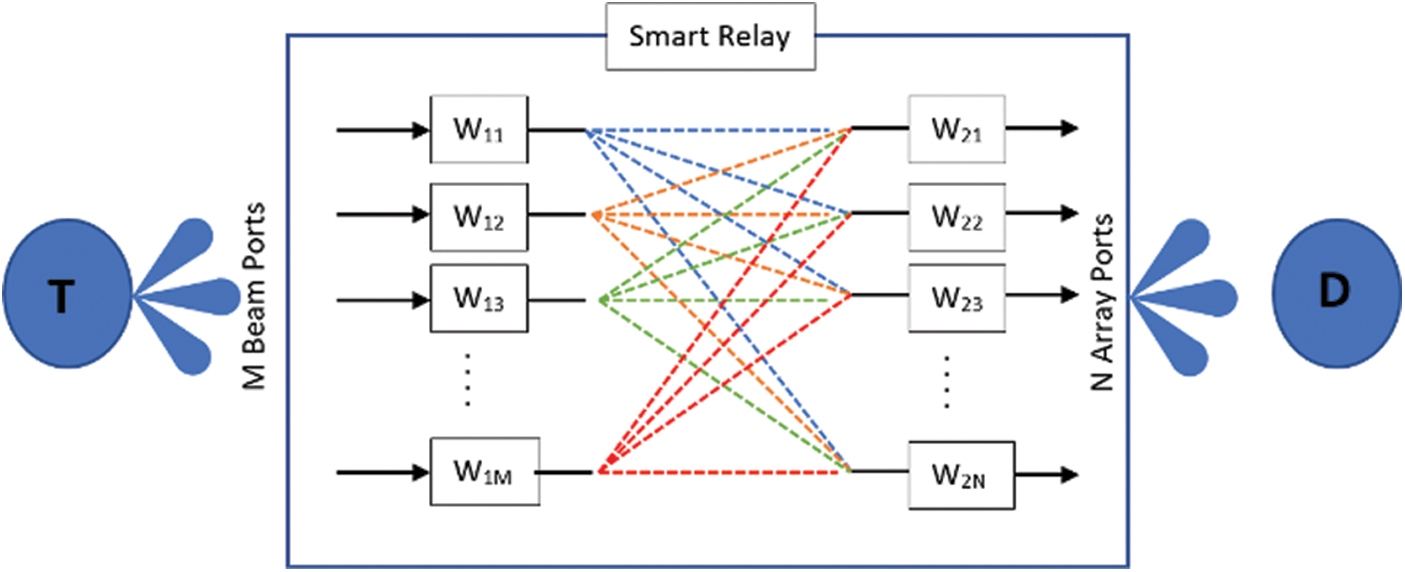
Figure 2: Smart relay Node showing the use of Rotman lens with M-input ports and N-output ports

3  The Proposed Beamforming Technique Using Rotman Lens Antenna

The relationship between the input signal vector and the output signal vector is characterized by the Rotman lens matrix as given in the below equations:

zR=w1w2yR(1)

[z1z2z3⋮zN]=[w21w22w23⋮w2N]×[w11w12w13…w1M]×[y1y2y3⋮yN],(2)

where yR and zR are the vectors representing the input and the output signals respectively, such that

[z1z2z3⋮zN]N×1=[w21w11w21w12w21w13⋯w21w1Mw22w11w22w12w22w13⋯w22w1Mw23w11w23w12w23w13⋯w23w1M⋮⋮⋮⋯⋮w2Nw11w2Nw12w2Nw13⋯w2Nw1M]N×M[y1y2y3⋮yN]M×1,(3)

zR=WRyR=w1w2yR,(4)

where WR is an NxM matrix that represents the links between the input and the output of the Rotman lens [4]. In order to maximize the received signal to noise ratio at the receiver side the above matrix should be optimized. Given that the transmitter T sends the information symbol sT to the relay node with a Rotman lens as per the below equation:

yR=PTfsT+nR,(5)

where sT denotes the transmitted symbol, yR=[y1y2y3…yM]Trepresents the received signal vector at the Rotman lens R, f=[f1f2f3…fM]Trepresents the channel vector between the transmitter and the Rotman lens R, and nR=[n1n2n3…nM]T represents the noise vector at the Rotman lens R and PT is the total power of the transmitter. Noise signals are drawn from a white Gaussian distribution with an average time domain value of zero and varianceσ2. Now, Rotman lens R receives and retransmits the signal toward D after processing it to reduce the overall complexity. The Rotman lens R maximizes the received SNR as all received signals at the destination will be added coherently in-phase. The impact of using the Rotman lens on the received signal can be reflected using the weight vectors w1 andw2, such thatzR=WRyR=w1w2yR. The signal at the receiver side is given in the below equation:

yD=αPRgzR+nD,(6)

where g=[g1g2g3…gN] is the CSI vector between the receiver and the smart Rotman lens antennas, α is scaling factor to control the transmitted power, and nD represents the noise signal at the destination, then:

yD=αPR[g1g2g3…gN][w21w22w23⋮w2N]×[w11w12w13…w1M]×[y1y2y3⋮yN]+nD,(7)

=αPRgw2w1yR+nD,(8)

=αPTPRgw2w1fsT+αPRgw2w1nR+nD,(9)

Here, the signal is represented by the term PTPRgw2w1fs and the noise is represented by the termPRgw2w1nR+nD. Consequently, the received SNR can be written as:

SNR=E{||PRPTgw2w1fsT||2}E{||αPRgw2w1nR+nD||2}.(10)

Given that the Rotman lens is going to adjust the phase shifts of all the received signals to optimize the SNR at the destination. Moreover, we assume that w1i=ejθ1i and w2i=ejθ2i. Then, Eq. (9) can be updated as the following:

yD=(αPRPT∑i=1Mfiejθ1i)(∑i=1Ngiejθ2i,r)sT+αPR(∑i=1Mgiejθ1i)(∑i=1Nejθ2ini)+nD.(11)

Leading to SNR at the receiver side given as:

β=E{||(αPRPT∑i=1Mfiejθ1i)(∑i=1Nejθ2igi)||2}E{||αPR(∑i=1Mgiejθ1i)(∑i=1Nejθ2ini)+nD||2},(12)

where E{|sT|2}=1 and

E{||(∑i=1Mfiejθ1i)(∑i=1Nejθ2igi)||2}≤E{(∑i=1M|fi|2)(∑i=1N|gi|2)}.(13)

Now, in order to maximize β given in (12), Eq. (13) must be hold equal. This can be achieved if:

θ1i=∠fi=fi|fi|,(14)

θ2i=∠gi=gi|gi|.(15)

Also, the power scaling factor α presented in (7) used to ensure an average transmitted power of PR at the Rotman lens can be represented as:

α=PR(PTσf2+σ2),(16)

where σf2 represents the variance of the channel between the transmitter and the Rotman lens antennas and σ2 denotes the noise variance. Substituting (14)–(16) in (12), then the value of SNR can be expressed as:

β=PRPT1||f||2||g||2σ2(PTσf2+PR||g||2+σ2).(17)

Therefore, during the second phase, the received signal can be written as:

yD=αPRPT(∑i=1M|fi|)(∑k=1N|gk|)sT+αPR(∑i=1Mgiejθ1i)(∑i=1Nejθ2ini)+nD,(18)

yD=αPRPT||f||||g||sT+αPR||g||(∑i=1Nejθ2ini)+nD.(19)

Using the maximum likelihood (ML) technique to decode the information at the receiver side as per the below equation:

s~T=arg⁡mins‖yd−αPRPT(||f||2)(||g||2)s‖2.(20)

s~T represents the estimated value of the transmitted symbol. Keeping in mind that in case the user decodes the message received from the direct link, the symbol s~T can be given as:

s~T=arg⁡mins‖yD−αPRPT(‖f‖2)(‖g‖2)s‖2+‖ydl−PTf0s‖2,(21)

Whereydl=PTf0sT+ndl, where f0 represents the direct link between the transmitter and the receiver and ndl is the noise obtained at the receiver through the direct link. It’s worth mentioning here that a linear symbol-wise decoder with a very low decoding complexity can be used to decode the received information symbols.

4  BER Performance Analysis

In this section, using the assumptions presented in Section 2 and without any prior channel knowledge in the whole system, the analytical BER performance of the suggested technique is introduced. For simplicity, we will consider thatM=N=R. Therefore, the conditional BER formula of the differential or conventional strategies for flat fading channels is given by [11,35,36] as follows

Pb(γ)≈122(R+1)π∫−ππf(θ)exp(−α(θ)γ)dθ,(22)

where

f(θ)=b22α(θ)∑r=1R+1(2R+1R)((β−R−βR+2)cos(R(θ+π2))−(β−R+1−βR+1)cos⁡((R+1)(θ+π2))),(23)

α(θ)=b2(1+2βsin⁡(θ)+β2)2.(24)

Here, β=ab is a constant controlled by the modulation order which is depending on the values of a and b, e.g., for BPSK a=10−3, b=2 and for 4-PSK, a=2−2, b=2+2, and γ=γs+∑r=1Rγr where γs and γr represent the SNR of the channel between the transmitter T and the receiver D and the SNR of the indirect channel between T and D through the rth Rotman lens antenna available in the relay node, respectively, where

γr=PRPT|fr|2|gr|2σ2(PTσf2+PR|gr|2+σ2),(25)

γs=PT|f0|22σ2.(26)

Now, the average BER, calculated through finding the average of the conditional formula Pb(γ) expressed by (22) with respect to the random variables using the moment generation function (MGF) technique [11,35,36], can be expressed as

Pb≈122(R+1)π∫−ππf(θ)Mγs(θ)∏r=1RMγr(θ)dθ,(27)

where Mγr(θ) represents the moment generation function (MGF) of the instantaneous SNR γr, given thatr∈{s,1,⋅⋅⋅,R}. With Rayleigh independent fading channels, |fr|2,|gr|2and |f0|2 are independent exponential random variables with parameter1/σf2,1/σg2 and 1/σ02 respectively. Thus, we have

Mγs(θ)=11+K0(θ),(28)

Where K0(θ)=PTα(θ)σ02σ2 and Mγs(θ) represents MGF ofγs. Like (28), Mγr(θ)given in (29) is calculated by integrating with respect to both (exponential) random variables |fr|2 and|gr|2. Thus,

Mγr(θ)=11+Kf[1+A(θ)∫0∞exp⁡(−u/σg2)u+Rr(θ)du],(29)

A(θ)=11+KfPTσf2+σ2σg2PR,(30)

Rr(θ)=PTσf2+σ2PR(1+Kf(θ)),(31)

where Kf(θ)=PTα(θ)σf2σ2. Finally, by substituting (28) and (29) into (27), we end up with a BER expression that involves only double integration. Then, the BER expression in (27) can be upper bounded by the bound in (29). We can see from (31) that Rr(θ) reaches its minimum value when α(θ) attains its maximum at θ=π2 whereα(θ)≤b2(1+β2)2. Therefore, the minimum value of R(θ) is given by

Rr(θ)≥Rr,min=PTσf2+σ2PR[1+PTσf2b2(1+β2)2σ2]−1.(32)

Substituting Rmin(θ) in (27), leads to the BER upper bound as given by

Pb≤122(R+1)π∫−ππf(θ)1+K0(θ)∏r=1R11+Kf(θ)×[1+A(θ)Zr(θ)]dθ,(33)

where Zr,max(θ)=∫0∞exp⁡(−u/σg2)u+Rr,min(θ)du. If a large SNR is considered, i.e., K0≫1 and Kf≫1, 1/(1+Kf)becomes 1/Kf and 1/(1+K0) becomes 1/K0 in (33). For the sake of simplicity, we can also consider that σf2=σ02 , then, the formula expressed in (32) is given by

Pb≤(2σ2PTσf2)R+1×Gr,max(θ),(34)

Gr,max(θ)=122(R+1)π∫−ππf(θ)α(θ)R+1[1+A(θ)Zr,max(θ)]dθ.(35)

Gr,max(θ)and (R + 1) given by (34) and (35) represent the coding gain and diversity order. Therefore, the suggested system with R Rotman lens antennas and direct link between the transmitter and receiver enjoys a diversity order which is equal to (R + 1), i.e., the full diversity order . Like (33), α(θ) is lower bounded by assuming that θ=π2 in (24). Thus,α(θ)≥b2(1−β2)2. Therefore, BER expression given in (34) can be bounded as follows

Pb≥122(R+1)π∫−ππf(θ)1+K0(θ)∏r=1R11+Kf(θ)×[1+A(θ)Zr,min(θ)]dθ,(36)

Zr,min(θ)=∫0∞exp⁡(−u/σg2)u+Rr,max(θ)du,(37)

Rr(θ)≤Rr,max=PTσf2+σ2PR[1+PTσf2b2(1−β2)2σ2]−1.(38)

If a large SNR is considered, i.e., K0≫1 and Kf≫1, 1/(1+Kf)becomes 1/Kf and 1/(1+K0) becomes 1/K0 in (33). For the sake of simplicity, we can also consider that σf2=σ02 , then, the formula expressed in (36) is given by

Pb≥(2σ2PTσf2)R+1×Qr,min(θ),(39)

Qr,min(θ)=122(R+1)π∫−ππf(θ)α(θ)R+1[1+A(θ)Zr,min(θ)]dθ.(40)

5  Results and Discussion

This section presents the analytical and simulated performance results explained before in Section 4. Figs. 3, 4 and 5 show the BER performance of the cooperative communication system shown in Fig. 1 which has a single transmitterT, a single destinationD, with and without considering the direct communication channel between them, as well as, a smart Rotman antennas imbedded at the relay node (R= 1 and 2) performing the AF protocol using one or two bits per channel use (bpcu). In these figures, the proposed technique is compared with the state-of-the-art coherent and non-coherent techniques proposed in [9–14]. In all the simulation figures, Rayleigh flat-fading channels are considered, and the total power used in the whole system is distributed uniformly between the transmitter PT and the smart Rotman relay PR such that PT=PR, and that the whole transmitted power from the smart Rotman relay PR is uniformly distributed on its transmitting antennas. To compare the BER performance of our proposed strategy with the BER performance of the state-of-the art strategies suggested in [9–14] as a function of the total SNR, a Monte Carlo method with 106 iterations is used to draw the curves available in Figs. 3, 4 and 5. Fig. 3 illustrates the BER performance of the proposed strategy assuming there is no direct channel between the transmitter T and the receiverD. Therefore, two Rotman antennas are located at an intermediary relay node (R= 2) performing the AF protocol using one bpcu. In the latter situation, the suggested strategy is compared with the state-of-the-art coherent and non-coherent strategies proposed in [9–14]. Fig. 3 shows that the suggested strategy outperforms all the state-of-the art two-, there-, and four-phase distributed space time coding strategies suggested in [10,13,14], as well as, all the distributed beamforming strategies proposed in [9,11,12]. In Fig. 4, the BER is displayed vs. the SNR. In this figure, the proposed strategy, using two bpcu and two antennas at the smart relay node (R= 2), assuming there is no direct channel between the transmitter T and the receiverD, is compared with the strategies proposed in [9–14]. Fig. 4 shows that the suggested strategies again enjoys a better performance than the current two-, there-, and four-phase distributed space time coding strategies proposed in [10,13,14], as well as, all the distributed beamforming strategies proposed in [9,11,12]. Note that the smart lens antennas can also be improved by modifying the electromagnetic field localization [19,37,38].

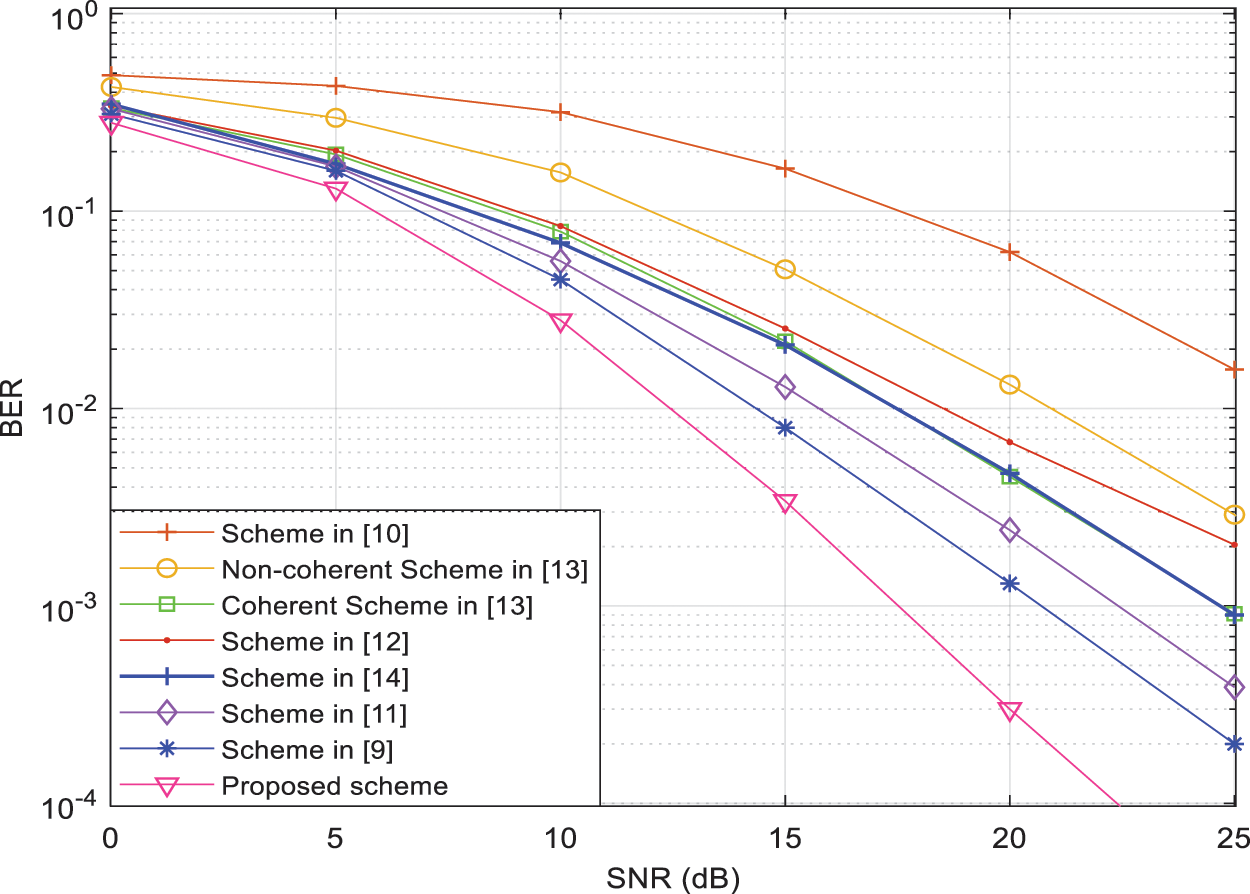
Figure 3: BER vs. SNR for different cooperative diversity strategies using the AF protocol with 1bpcu and R = 2

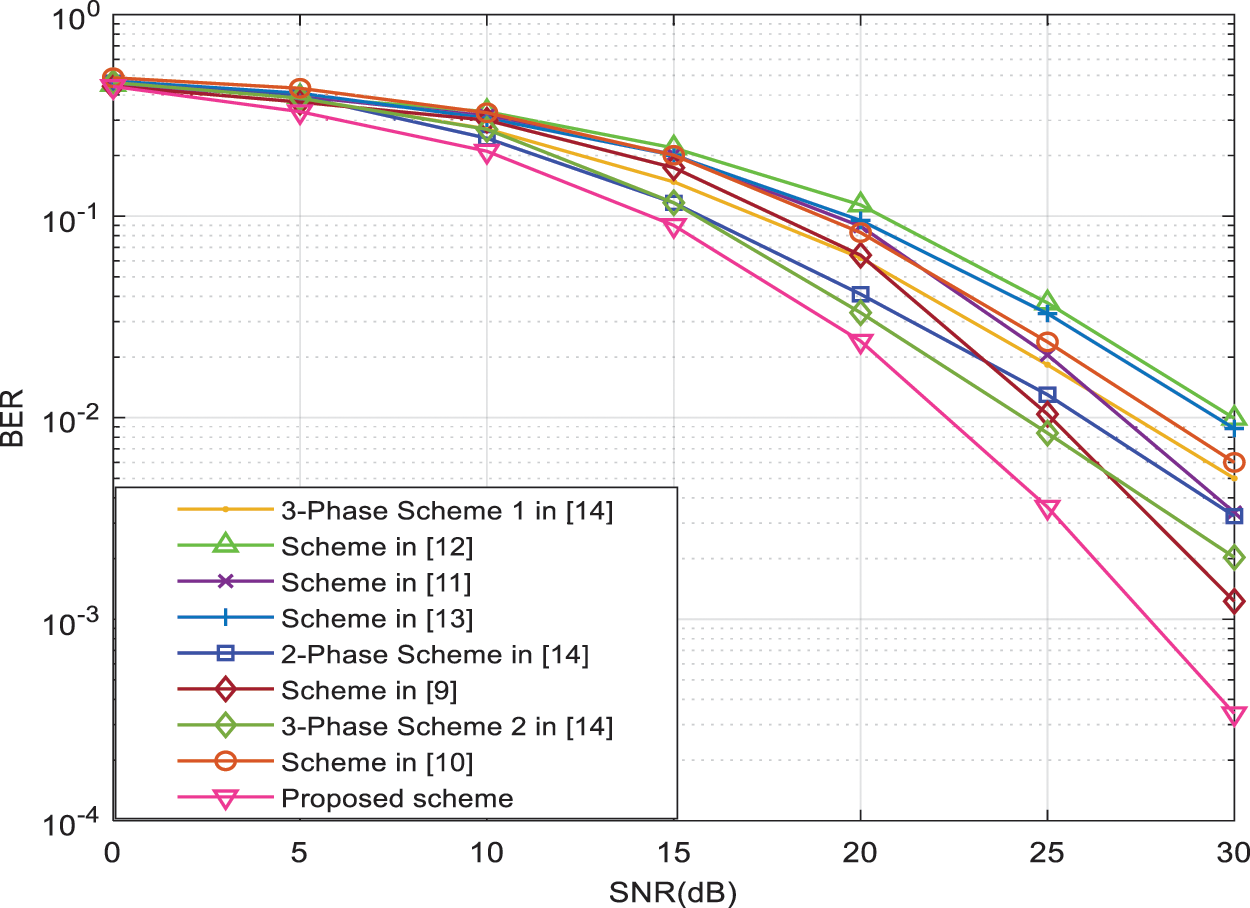
Figure 4: BER vs. SNR for different cooperative diversity strategies using the AF protocol with 2bpcu and R = 2

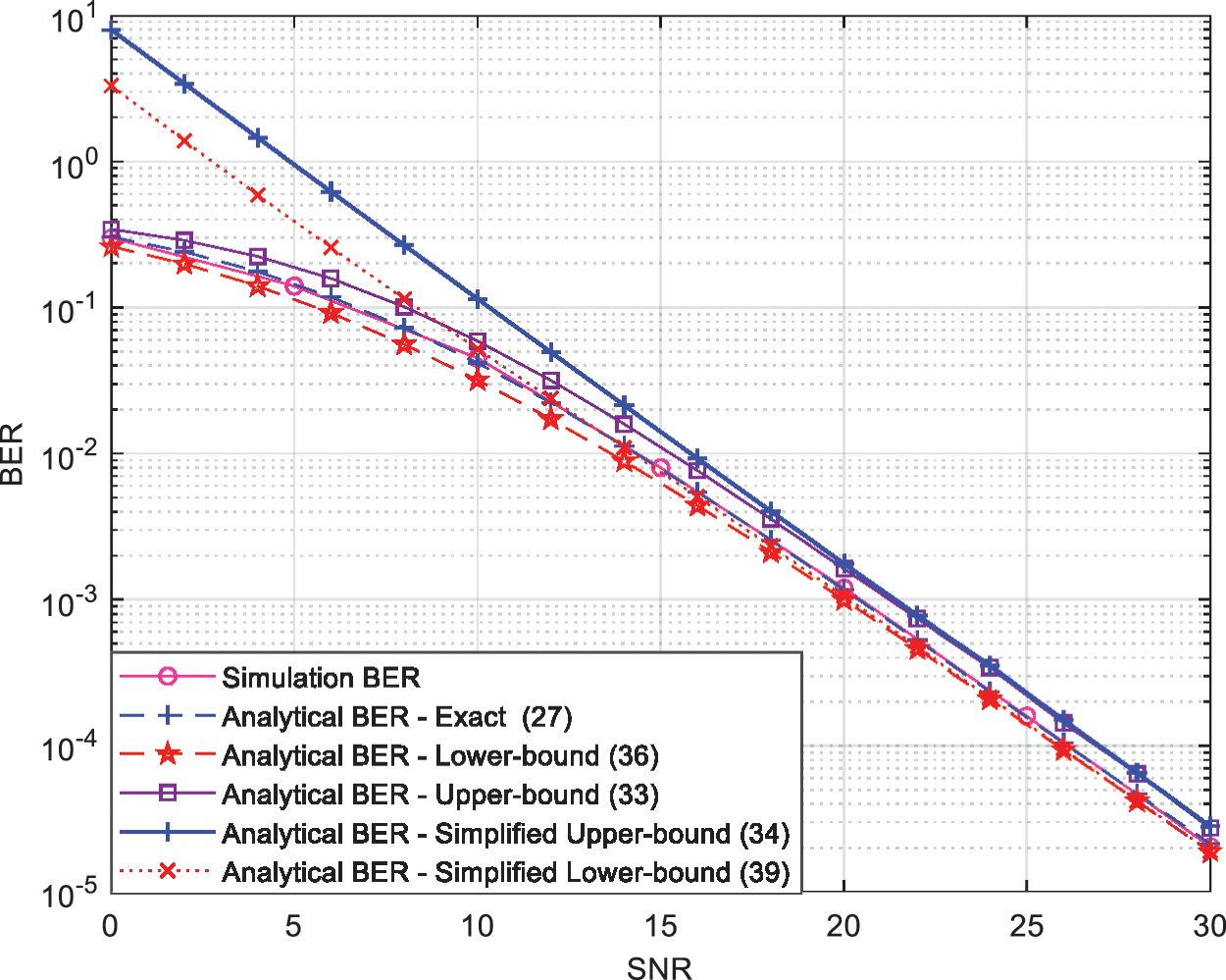
Figure 5: BER vs. SNR using the AF protocol with 4-PSK modulations and R = 1

Fig. 5 considers the scenario when we have a cooperative communication system using only one relay carrying one smart Rotman antenna and a direct channel from the source to destination is considered. Fig. 5 shows the analytical and simulated performance in terms of BER of the suggested technique at the destination using 4-PSK modulation. Moreover, Fig. 5 clearly shows that the performance in terms of BER using Monte Carlo simulation of the suggested strategy matches the analytical performance in terms of BER calculated using the formulas given in Section 4. From Figs. 3, 4 and 5, we can clearly observe that our proposed strategy outperforms all the best-known strategies [9–14].

6  Conclusion

In this article, a low-cost Rotman lens antenna is utilized in order to enhance the performance of the conventional cooperative communication networks without requiring any extra power, or additional time or frequency slots. In the suggested system, the smart Rotman lens antennas form a beam in the direction of the destination to maximize the received SNR at the destination by performing optimal beamforming technique. The suggested optimal beamforming technique enjoys high diversity order and low encoding and decoding complexity. Furthermore, we proved the advantages of our suggested strategy through both theoretical results and simulations using Monte Carlo runs. The Monte Carlo simulations show that the suggested strategy enjoys better BER performance as compared to the current state-of-the-art distributed multi-antenna strategies. In addition, the BER curves drawn from the analytical results are closely matching to those drawn from our conducted Monte Carlo simulations.

Funding Statement: The article has been supported by the College of Engineering and Technology, American University of the Middle East, Kuwait. Homepage: https://www.aum.edu.kw.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present article.

References

 1.  I. Maaz and S. Alabed, “Efficient time reversal strategy for MISO-OFDM systems,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 20, no. 1, pp. 239–247, 2020. [Google Scholar]

 2.  I. Maaz and S. Alabed, “Impact of engineering parameters on performance of relay-assisted wireless network,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 20, no. 1, pp. 248–255, 2020. [Google Scholar]

 3.  S. Alabed, “A computationally efficient detector for MIMO systems,” International Journal of Electrical and Computer Engineering, vol. 9, no. 5, part II, pp. 4138–4146, 2019. [Google Scholar]

 4.  S. Alabed, “Computationally efficient multi-antenna techniques for multi-user two-way wireless relay networks,” International Journal of Electrical and Computer Engineering, vol. 8, no. 3, pp. 1684–1691, 2018. [Google Scholar]

 5.  S. Alabed, I. Maaz and M. Al-Rabayah, “Improved bi-directional three-phase single-relay selection technique for cooperative wireless communications,” Computers, Materials & Continua, vol. 70, no. 1, pp. 999–1015, 2022. [Google Scholar]

 6.  S. Alabed, I. Maaz and M. Al-Rabayah, “Improved two-way double-relay selection technique for cooperative wireless communications,” EURASIP Journal on Wireless Communications and Networking, vol. 2021, no. 57, pp. 1–24, 2021. [Google Scholar]

 7.  S. Alabed, M. Pesavento and A. Klein, “Relay selection based space-time coding for two-way wireless relay networks using digital network coding,” in IEEE ISWCS 2013; the Tenth Int. Symp. on Wireless Communication Systems, Ilmenau, Germany, 27–30 Aug, pp. 1–5, 2013. [Google Scholar]

 8.  S. Alabed, “Performance analysis of bi-directional relay selection strategy for wireless cooperative communications,” EURASIP Journal on Wireless Communications and Networking, vol. 2019, no. 97, pp. 1–11, 2019. [Google Scholar]

 9.  A.Schad, S.Alabed , H.Degenhardt and M.Pesavento, “Bi-directional differential beamforming for multi-antenna relaying,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, pp. 2884–2888, 2015. [Google Scholar]

10. Z. Utkovski, G. Yammine and J. Lindner, “A distributed differential space–time coding scheme for two-way wireless relay networks,” ISIT 2009, pp. 779–783, Seoul, Korea, 2009. [Google Scholar]

11. S. Alabed, “Performance analysis of differential beamforming in decentralized networks,” International Journal of Electrical and Computer Engineering, vol. 8, no. 3, pp. 1692–1700, 2018. [Google Scholar]

12. V. Havary-Nassab, S. Shahbaz Panahi and A. Grami, “Joint transmit receive beamforming for multi-antenna relaying schemes,” IEEE Transactions on Signal Processing, vol. 58, no. 9, pp. 4966–4972, 2009. [Google Scholar]

13. Y. Jing and H. Jafarkhani, “Distributed differential space–time coding in wireless relay networks,” IEEE Transactions on Communications, vol. 56, no. 7, pp. 1092–1100, 2008. [Google Scholar]

14. S. Alabed, M. Pesavento and A. Klein,“ non-coherent distributed space-time coding techniques for two-way wireless relay networks,” EURASIP Special Issue on Sensor Array Processing, vol. 93, no. 12, pp. 3371–3381, 2013. [Google Scholar]

15. S. Alabed, M. Pesavento and A. Gershman, “Distributed differential space–time coding techniques for two-way wireless relay networks,” in Proc. of the Fourth IEEE Int. Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP 11), San Juan, Puerto Rico, pp. 221–224, 2011. [Google Scholar]

16. S. Alabed, “Performance analysis of two-way DF relay selection techniques,” Information & Communications Technology Express,” Elsevier, vol. 2, no. 3, pp. 91–95, 2016. [Google Scholar]

17. X. Wen, K. Law, S. Alabed and M. Pesavento, “Rank-two beamforming for single-group multicasting networks using OSTBC,” in IEEE 7th Sensor Array and Multichannel Signal Processing Workshop, Stevens Institute of Technology, Hoboken, NJ, USA, June 17–20, pp. 65–68, 2012. [Google Scholar]

18. D. Taleb, S. Alabed and M. Pesavento, “Optimal general-rank transmit beamforming technique for multicasting service in modern wireless networks using STTC,” in 19th Int. IEEE/ITG Workshop on Smart Antennas, Ilmenau, Germany, pp. 1–7, 2015. [Google Scholar]

19. S. Alabed, I. Mahariq and M. Salman, “A novel beamforming emulating photonic nanojets for wireless relay networks,” Computers, Materials & Continua, vol. 69, no. 1, pp. 575–588, 2021. [Google Scholar]

20. S. Alabed, I. Maaz and M. Al-Rabayah, “Two-phase bidirectional dual-relay selection strategy for wireless relay networks,” Computers, Materials & Continua, vol. 69, no. 1, pp. 539–553, 2021. [Google Scholar]

21. S. Alabed, I. Maaz and M. Al-Rabayah, “Distributed differential beamforming and power allocation for cooperative communication networks,” International Journal of Electrical and Computer Engineering, vol. 10, no. 6, pp. 5923–5931, 2020. [Google Scholar]

22. K. M. Attiah, K. Seddik and R. H. Gohary, “Differential unitary space-time constellations from spherical codes,” IEEE Wireless Communications Letters, vol. 9, no. 11, pp. 1909–1913, 2020. [Google Scholar]

23. S. Alabed, “Non-coherent distributed beamforming in decentralized two-way relay networks,” IEEE Canada,” Canadian Journal of Electrical and Computer Engineering, vol. 43, no. 4, pp. 305–309, 2020. [Google Scholar]

24. S. Alabed and M. Pesavento, “A simple distributed differential transmit beamforming technique for two-way wireless relay networks,” in In the 16th Int. IEEE/ITG Workshop on Smart Antennas (WSA 2012), Dresden, Germany, pp. 243–247, 2012. [Google Scholar]

25. S. Alabed, J. Paredes and A. Gershman, “A low complexity decoder for quasi-orthogonal space-time block codes,” IEEE Transactions on Wireless Communications, vol. 10, no. 3, pp. 988–994, 2011. [Google Scholar]

26. S. Alabed, J. M. Paredes and A. B. Gershman, “A simple distributed space-time coded strategy for two-way relay channels,” IEEE Transactions on Wireless Communications, vol. 11, no. 4, pp. 1260–1265, 2012. [Google Scholar]

27. S. Alabed, M. Pesavento and A. Klein, “Distributed differential space-time coding for two-way relay networks using analog network coding,” in the 21st European Signal Processing Conf. (EUSIPCO’13), Marrakech, Morocco, pp. 1–5, Sep. 2013. [Google Scholar]

28. J. Zhu, L. Xiao, P. Xiao, A. Quddus, C. He and L. Lu, “Differential STBC-SM scheme for uplink multi-user massive MIMO communications: system design and performance analysis,” IEEE Transactions on Vehicular Technology, vol. 70, no. 10, pp. 10236–10251, 2021. [Google Scholar]

29. J. Zhen, S. Li, J. Zhang and K. M. Wong, “Design of optimal unitary constellation with noncoherent ML receiver,” in IEEE Pacific Rim Conf. on Communications, Computers and Signal Processing, University of Victoria, Victoria, B.C., Canada, pp. 1–5, 2019. [Google Scholar]

30. Q. Luo, S. Gao, W. Liu and C. Gu, Low-cost Smart Antennas, John Wiley & Sons Ltd, Hoboken, New Jersey, U.S., 2019. [Google Scholar]

31. M. A. Hassanien, R. Hahnel and D. Plettemeier, “Wideband rotman lens beamforming technique for 5G wireless applications,” in 2nd Int. Conf. on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, pp. 1–5, 2019. [Google Scholar]

32. H. Tataria, M. Matthaiou, P. J. Smith, G. C. Alexandropoulos and V. F. Fusco, “Uplink interference analysis with RF switching for lens-based millimeter-wave systems,” in 2018 IEEE Int. Conf. on Communications (ICC), Kansas City, MO, USA, pp. 1–7, 2018. [Google Scholar]

33. S. Vashist, M. K. Soni and P. K. Singhal, “A review on the development of rotman lens antenna,” Chinese Journal of Engineering, vol. 2014, pp. 1–9, 2014. [Google Scholar]

34. Y. Gao, M. Khaliel, F. Zheng and T. Kaiser, “Rotman lens based hybrid analog–digital beamforming in massive MIMO systems: Array architectures, beam selection algorithms and experiments,” IEEE Transactions on Vehicular Technology, vol. 66, no. 10, pp. 9134–9148, 2017. [Google Scholar]

35. M. Simon and M. Alouini, “Digital communication over fading channels: A unified approach to performance analysis,” John Wiley & Sons, Inc, Hoboken, New Jersey, U.S., 2002. [Google Scholar]

36. T. Himsoon, W. P. Siriwongpairat, W. Su and K. J. R. Liu, “Differential modulations for multinode cooperative communications,” IEEE Transactions on Signal Processing, vol. 56, no. 7, pp. 2941–2956, 2008. [Google Scholar]

37. I. Mahariq, I. Giden, H. Kurt, O. Minin and I. Minin, “Strong electromagnetic field localization near the surface of hemicylindrical particles,” Optical and Quantum Electronics, vol. 49, no. 12, pp. 1–8, 2017. [Google Scholar]

38. I. Mahariq and H. Kurt, “Strong field enhancement of resonance modes in dielectric microcylinders,” Journal of the Optical Society of America B, vol. 33, no. 4, pp. 656–662, 2016. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.