Computers, Materials & Continua DOI:10.32604/cmc.2022.030246
Article

An Approximation for the Entropy Measuring in the General Structure of SGSP3

Kamel Jebreen1,2,3,*, Muhammad Haroon Aftab4, Mohammad Issa Sowaity5, Zeeshan Saleem Mufti4 and Muhammad Hussain6

1Biostatistics and Clinical Research Department, University Hospital Lariboisière, AP-HP, Universite’ de Paris, Paris, 75010, France
2Department of Mathematics, An-Najah National University, Nablus, P400, Palestine
3Department of Mathematics, Palestine Technical University–Kadoorie, Hebron, P766, Palestine
4Department of Mathematics and Statistics, the University of Lahore, Lahore, 54000, Pakistan
5Department of Mathematics, Palestine Polytechnic University, Hebron, P766, Palestine
6Department of Mathematics, COMSATS University Islamabad, Lahore campus, Lahore, 54000, Pakistan
*Corresponding Author: Kamel Jebreen. Email: Jebreen20@yahoo.com
Received: 22 March 2022; Accepted: 11 May 2022

Abstract: In this article, we calculate various topological invariants such as symmetric division degree index, redefined Zagreb index, VL index, first and second exponential Zagreb index, first and second multiplicative exponential Zagreb indices, symmetric division degree entropy, redefined Zagreb entropy, VL entropy, first and second exponential Zagreb entropies, multiplicative exponential Zagreb entropy. We take the chemical compound named Proanthocyanidins, which is a very useful polyphenol in human’s diet. They are very beneficial for one’s health. These chemical compounds are extracted from grape seeds. They are tremendously anti-inflammatory. A subdivision form of this compound is presented in this article. The compound named subdivided grape seed Proanthocyanidins is abbreviated as SGSP3. This network SGSP3, is converted and modeled into its mathematical graphical formation with the support of the latest mathematical tools. We have also developed many closed formulas for the measurement of entropy for the general chemical structure of the subdivided grape seed Proanthocyanidins network. The achieved outcomes can be correlated with the chemical version of SGSP3 to get a better understanding of its biological as well as physical features.

Keywords: Symmetric division degree; redefined Zagreb; VL index; exponential; multiplicative Zagreb; subdivided grape seed Proanthocyanidins; graphical model; genetics; entropy

1  Introduction

The study of the field of chemical graph theory (CGT) is linked to the discussion and formation of chemical structures using various mathematical tools to grasp the knowledge of their physical and biological activities. We search the mathematical resolutions for the issues and questions raised in molecular chemistry. Shannon developed the basic knowledge of entropy [1–4] in 1948.

The entropies measured for the given graph rely purely on the graph structure and its probability distribution for the node set. In this article, we take and study the general structure of Proanthocyanidins [5], which are chemical in nature and provide colors to different foods, especially fruits and vegetables.

Vukičević and Gašperov invented 148 types of chemical invariants. These are known as “discrete Adriatic indices (DAI)”. The Symmetric division degree index is one of the DAI. Vukičević developed [6,7] this graph invariant and formulated as:

SDD(η´)=∑kl∈E(η´){dkdl+dldk}

In 2013, Ranjini et al. computed again the Zagreb index [8]. They developed the third Zagreb index for the graph η´ and evaluated by:

ReZM(η´)=∑kl∈E(η´){(dk×dl)(dk+dl)}

Recently in 2021, Deepika invented a new invariant named VL index [9,10].

VL(η´)=12∑kl∈E(η´){da+db+4} where,da=dk+dl−2&db=dk×dl−2

VL(η´)=12∑kl∈E(η´){(dk+dl)+(dk×dl)}

Definition 1: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3 denoted by η´, then the first and second exponential Zagreb indices [11–13] are defined by:

EM1(η´)=∑t∈V(η´)edeg(t)2&EM2(η´)=∑kl∈E(η´)edk×dl

Definition 2: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3 denoted by η´, then the first and second multiplicative exponential Zagreb indices are defined by:

E∏1(η´)=∏t∈V(η´)edeg(t)2&E∏2(η´)=∏kl∈E(η´)edk×dl

This paper consists of four sections. In Section 1, we have provided a brief introduction of the importance and history of the topological invariants such as symmetric degree, redefined, VL, first and second exponential and multiplicative exponential topological indices. In Section 2, we have considered the general structure of grape seed Proanthocyanidins in its subdivision form and discussed its construction. We have also introduced some new formulas. While in Sections 3 and 4, we have formulated and discussed some entropy-based formulas such as symmetric division degree entropy, redefined Zagreb entropy, VL entropy, first and second exponential Zagreb entropies and multiplicative exponential Zagreb entropies.

2  Material and Methods

Let η´ be an undirected, connected, finite and simple graph having a set of vertices V′(η´)={v1′,v2′,v3′,…,vn′} and a set of edges vertices E′(η´)={e1′,e2′,e3′,…,eη´′}. Whereas |V′(η´)| and |E′(η´)| depict the cardinality of the graph η´ for all vi′ ∊ V′(η´) and vi′vj′ ∊ E′(η´). We consider the general structure of grape seed Proanthocyanidins network symbolized by GSP3.

To obtain a new structure called a subdivided grape seed Proanthocyanidins network and symbolized as SGSP3, a new vertex at every edge is inserted. The subdivided structure of GSP3 is depicted in Fig. 1. Various topological invariants [14,15] are applied in the comparison of molecular structure with its new mathematical structure to study its properties. The process of computation obeys the following steps.

1.    Consideration of graph: we associate the given molecular structure with the mathematical graph.

2.    Identification of nodes: we identify all different degrees and label them accordingly.

3.    Division of edges: we separate the edges according to the labelled degrees.

4.    Calculation: we obtain the general form after some computations.

We have noticed that two types of edges are attained that are (2, 2) and (2, 3). SGSP3 is illustrated in Fig. 1.

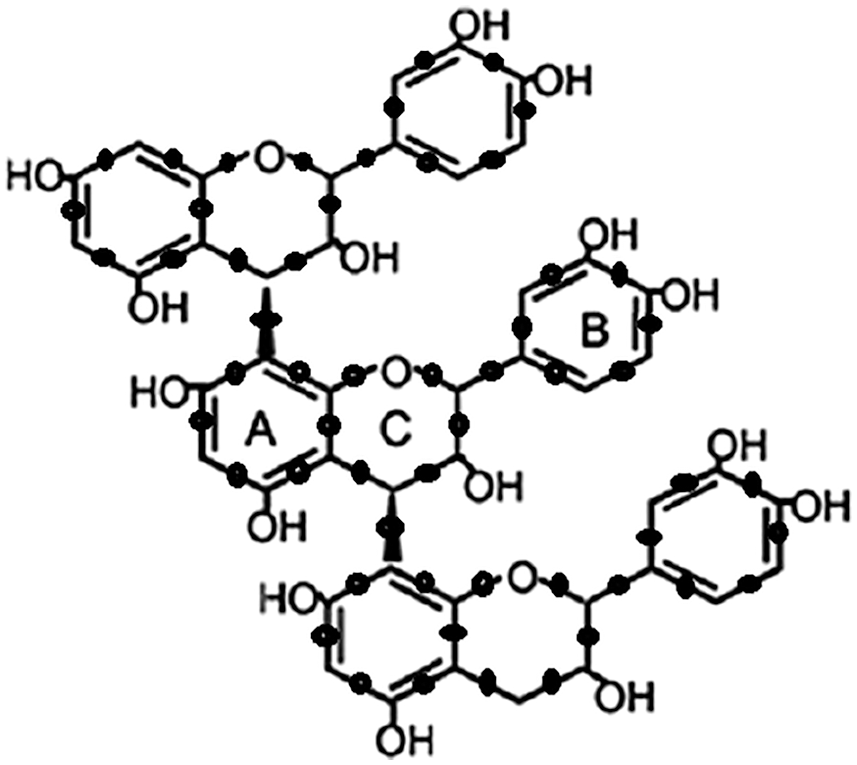
Figure 1: SGSP3

Fig. 1 describes the molecular structure of a subdivided grape seed Proanthocyanidins network.

where, |V(η´)| shows the total number of vertices in η´, |E(η´)| shows the total number of edges in , dt shows the vertices having degrees 2 and 3, |V(dt)| shows the general form of the cardinality of its vertex set consisting of degrees 2 and 3, respectively.

And (dk,dl) for kl∈E(η´) shows the edges having degree 2 at its both ends and edges having degree 2 at its one end and 3 at its other end, |V(dk,dl)| shows the general form of the cardinality of its edge set consisting of degrees 2 and 3.

Proposition 2.1: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its symmetric division degree index is SDD(η´)=79n−5.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1, we obtain

SDD(η´)=∑kl∈E(η´){dkdl+dldk}

SDD(η´)=(20n+4)(2)+(18n−6)136=79n−5.(1)

Proposition 2.2: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its redefined Zagreb index is ReZM(η´)=860n−116.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1, we obtain

ReZM(η´)=∑kl∈E(η´){(dk×dl)(dk+dl)}

ReZM(η´)=(20n+4)(16)+(18n−6)(30)=860n−116.(2)

Proposition 2.3: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its VL index is VL(η´)=179n−17.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1, we obtain

VL(η´)=12∑kl∈E(η´){da+db+4}where,da=dk+dl−2&db=dk×dl−2

VL(η´)=12∑kl∈E(η´){(dk+dl)+(dk×dl)}

VL(η´)=12{(20n+4)(8)+(18n−6)(11)}=179n−17.(3)

Proposition 2.4: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its first and second exponential Zagreb indices are

EM1(η´)=50201n−16152andEM2(η´)=8354n−2202.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1, we obtain

EM1(η´)=∑t∈V(η´)edeg(t)2

EM1(η´)=(29n+1)e4+(6n−2)e9=50201n−16152.(4)

and

EM2(η´)=∑kl∈E(η´)edk×dl

EM2(η´)=(20n+4)e4+(18n−6)e6=8354n−2202.(5)

Proposition 2.5: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its first and second multiplicative exponential Zagreb indices are

E∏1(η´)=e13(12n2+2n−2)andE∏2(η´)=e10(360n2−48n−24).

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1, we obtain

E∏1(η´)=∏t∈V(η´)edeg(t)2

E∏1(η´)=(29n+1)e4×(6n−2)e9=e13(12n2+2n−2).(6)

and

E∏2(η´)=∏kl∈E(η´)edk×dl

E∏2(η´)=(20n+4)e4×(18n−6)e6=e10(360n2−48n−24).(7)

Definition 3: Consider the network GSP3, symbolized by η´, then its degree-based entropy can be calculated as:

ENTSDD(η´)=log(2q)−12q∑i=1m[log⁡(d(ti))d(ti)],

where dtidenotes the vertex degree of node ti.

ENTSDD(η´)=log(76n−4)−1(76n−4)[(29n+1)×log(2)2+(6n−2)×log(3)3]

ENTSDD(η´)=log(76n−4)−26.04n−2.26(76n−4).(8)

3  Discussion and Results

Proanthocyanidins are chemical in nature and are essential polyphenols in human foods. They have many benefits for health. Proanthocyanidins that are obtained from grape seeds are extremely anti-inflammatory. We discuss here its subdivided version. We have studied the chemical network of subdivided grape seed Proanthocyanidins by converting and modeling it into a mathematical graphical form with the help of mathematical tools. New formulas for measuring the entropy [16] of the general molecular structure of the subdivided grape seed Proanthocyanidins network SGSP3 are developed and discussed. The obtained results can be interlinked with the molecular form of SGSP3 to grasp its biological as well as physical features.

Proposition 3.1: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its symmetric division degree entropy is ENTSDD(η´)=log(79n−5)−25.13n−1.9579n−5.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1 and Eq. (1), we obtain

ENTSDD(η´)=log(SDD(η´))−1SDD(η´)∑i=1m∑kl∈Ei(η´)log⁡{dkdl+dldk}{dkdl+dldk}

ENTSDD(η´)=log(79n−5)−179n−5[(20n+4)×log(4)+(18n−6)×log(136)(136)]

ENTSDD(η´)=log(79n−5)−25.13n−1.9579n−5.(9)

Proposition 3.2: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its redefined Zagreb entropy is ENTReZM(η´)=log(860n−116)−[1182.96n−188.81]860n−116.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1 and Eq. (2), we obtain

ENTReZM(η´)=log(ReZM(η´))−1ReZM(η´)∑i=1m∑kl∈Ei(η´)log{(dk×dl)(dk+dl)}{(dk×dl)(dk+dl)}

ENTReZM(η´)=log(860n−116)−[64(5n+1)×log(16)+180(3n−1)×log(30)]860n−116

ENTReZM(η´)=log(860n−116)−[1182.96n−188.81]860n−116.(10)

Proposition 3.3: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its VL entropy is ENTVL(η´)=log(179n−17)−[121.46n−14.79]179n−17.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1 and Eq. (3), we obtain

ENTVL(η´)=log(VL(η´))−1VL(η´)∑i=1m∑kl∈Ei(η´)log{(dk×dl)+(dk+dl)2}{(dk×dl)+(dk+dl)2}

ENTVL(η´)=log(179n−17)−[4(20n+4)×log(4)+112(18n−6)×log(112)]179n−17

ENTVL(η´)=log(179n−17)−[121.46n−14.79]179n−17.(11)

Proposition 3.4: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its first and second exponential Zagreb entropies are

ENTEM1(η´)=log(50201n−16152)−[192783.28n−63249.39]50201n−16152and

ENTEM2(η´)=log(8354n−2202)−[20819.28n−5928.06]8354n−2202.

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1, Eqs. (4) and (5), we obtain

ENTEM1(η´)=log(EM1(η´))−1EM1(η´)∑i=1m∑t∈Vi(η´)log{edeg(t)2}{edeg(t)2}

ENTEM1(η´)=log(50201n−16152)−[e4(29n+1)×log(e4)+e9(6n−2)×log(e9)]50201n−16152

ENTEM1(η´)=log(50201n−16152)−[192783.28n−63249.39]50201n−16152.(12)

and

ENTEM2(η´)=log(EM2(η´))−1EM2(η´)∑i=1m∑kl∈Ei(η´)log{edk×dl}{edk×dl}

ENTEM2(η´)=log(8354n−2202)−[e4(20n+4)×log(e4)+e6(18n−6)×log(e6)]8354n−2202

ENTEM2(η´)=log(8354n−2202)−[20819.28n−5928.06]8354n−2202.(13)

Proposition 3.5: Consider the graph of the subdivided grape seed Proanthocyanidins network SGSP3, then its first and second multiplicative exponential Zagreb entropies are

ENTE∏1(η´)=log(e13(12n2+2n−2))−[522695349.2n2−156207805.5n−6007992.5]e13(12n2+2n−2).

and ENTE∏2(η´)=log(e10(360n2−48n−24))−[35894437.2n2−4785925n−2392962.4]e10(360n2−48n−24).

Proof: Let η´ be the graph of the subdivided grape seed Proanthocyanidins network SGSP3. Then, by Tab.1, Eqs.(6) and (7), we obtain

ENTE∏1⁡(η´)=log(E∏1⁡(η´))−1E∏1⁡(η´)∏i=1m⁡∏t∈Vi(η´)⁡log{edeg(t)2}{edeg(t)2}ENTE∏1⁡(η´)=log(e13(12n2+2n−2))−[e4(29n+1)×log(e4)×e9(6n−2)×log(e9)]e13(12n2+2n−2)=log(e13(12n2+2n−2))−[3003996.26(29n+1)(6n−2)]e13(12n2+2n−2)=log(e13(12n2+2n−2))−[3003996.26(29n+1)(6n−2)]e13(12n2+2n−2)ENTE∏1⁡(η´)=log(e13(12n2+2n−2))−[522695349.2n2−156207805.5n−6007992.5]e13(12n2+2n−2).(14)

and

ENTE∏2( η´)=log(E∏2( η´))−1E∏2( η´) ∏i=1m∏kl ∈ Ei( η´)log{ edk×dl }{ edk×dl }ENTE∏2( η´)=log(e10(360n2−48n−24))−[ e4(20n+4)×log(e4)×e6(18n−6)×log(e6) ]e10(360n2−48n−24)=log(e10(360n2−48n−24))−[ 99706.77(20n+4)(18n−6) ]e10(360n2−48n−24).ENTE∏2( η´)=log(e10(360n2−48n−24))−[ 35894437.2n2−4785925n−2392962.4 ]e10(360n2−48n−24).(15)

4  Conclusion

In this study, a chemical network of subdivided grape seed Proanthocyanidins has been discussed to introduce new prepositions for symmetric division degree entropy, redefined Zagreb entropy, VL entropy, first and second exponential Zagreb entropies, first and second multiplicative exponential Zagreb entropies by using the results of symmetric division degree index, redefined Zagreb index, VL index, first and second exponential Zagreb indices, multiplicative exponential Zagreb indices to understand their physical features. The achieved outcomes can be interlinked with the molecular properties [17] of chemical version of SGSP3 to get a better understanding of its biological features.

Acknowledgement: The authors are grateful to all who supported us in producing this article and for those who contributed to this study but cannot include themselves.

Funding Statement: Under the sponsor of Unité de Recherche Clinique Lariboisière St-Louis (URC) Assistance Publique–Hôpitaux de Paris 200, rue du Fbg Saint-Denis 75010 Paris.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study. And all authors have equally contributed.

References

 1.  S. C. Elwood, “A mathematical theory of communication,” Bell System Technical Journal, vol. 27, no. 3, pp. 79–423, 1948. [Google Scholar]

 2.  W. Y. Raymond, The science of information. In: Information Theory and Network Coding, Information Technology Transmission Processing and Storage. Boston, MA: Springer, pp. 1–4, 2008. [Google Scholar]

 3.  G. Abbas, M. Ibrahim, A. Ahmad, M. Azeem and K. Elahi, “M-polynomials of tetra-cyano-benzene transition metal structure,” Polycyclic Aromatic Compounds, vol. 2021, pp. 1–11, 2021. [Google Scholar]

 4.  S. S. Dragomir and C. J. Goh, “Some bounds on entropy measures in information theory,” Applied Mathematics Letters, vol. 10, no. 3, pp. 23–28, 1997. [Google Scholar]

 5.  M. H. Aftab, M. Rafaqat and M. Hussain, “Topological invariants for the general structure of grape seed Proanthocyanidins,” Punjab University Journal of Mathematics, vol. 54, no. 1, pp. 45–53, 2022. [Google Scholar]

 6.  D. Vukičević and M. Gašperov, “Bond additive modeling 1. Adriatic indice,” Croatica Chemica Acta, vol. 83, pp. 243–260, 2010. [Google Scholar]

 7.  D. Vukičević, “Bond additive modeling 2 mathematical properties of max-min rodeg index,” Croatica Chemica Acta, vol. 54, pp. 261–273, 2010. [Google Scholar]

 8.  P. S. Ranjini, V. Lokesha and A. Usha, “Relation between phenylene and hexagonal squeeze using harmonic index,” International Journal of Graph Theory, vol. 1, pp. 116–121, 2013. [Google Scholar]

 9.  T. Deepika, “VL index and bounds for the tensor products of F-sum graphs,” TWMS Journal of Applied and Engineering Mathematics, vol. 11, no. 2, pp. 374–385, 2021. [Google Scholar]

10. V. Lokesha, Suvarna, A. S. Cevik and I. N. Cangul, “VL reciprocal status index and co-index of graphs,” Journal of Mathematics, vol. 2021, pp. 1–10, 2021. [Google Scholar]

11. J. Rada, “Exponential vertex-degree-based topological indices and discrimination,” MATCH Communications in Mathematical and in Computer Chemistry, vol. 82, pp. 29–41, 2019. [Google Scholar]

12. R. Cruz and J. Rada, “The path and the star as extremal values of vertex-degree-based topological indices among trees,” MATCH Communications in Mathematical and in Computer Chemistry, vol. 82, pp. 715–732, 2019. [Google Scholar]

13. N. Akgunes and B. Aydin, “Introducing new exponential Zagreb indices for graphs,” Journal of Mathematics, vol. 2021, no. 7, pp. 1–13, 2021. [Google Scholar]

14. M. H. Aftab, M. Rafaqat and M. Hussain, “On the computation of topological indices for molecular structures of subdivided Aztec diamonds,” Computational Journal of Combinatorial Mathematics, vol. 2020, no. 2, pp. 13–20, 2021. [Google Scholar]

15. M. H. Aftab, M. Rafaqat, M. Hussain and T. Zia, “On the computation of some topological descriptors to find closed formulas for certain chemical graphs,” Journal of Chemistry, vol. 2021, pp. 1–16, 2021. [Google Scholar]

16. P. Song, H. Ali, M. A. Binyamin, B. Ali and J. B. Liu, “On computation of entropy of Hex-Derived network,” Complexity, vol. 2021, pp. 1–18, Article ID 99935042021. [Google Scholar]

17. H. M. A. Siddiqui, M. A. Arshad, M. F. Nadeem, M. Azeem, A. Haider et al., “Topological properties of supramolecular chain of different complexes of N-Salicylidene-L-Valine,” Polycyclic Aromatic Compounds, vol. 2021, pp. 1–14, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.