Computers, Materials & Continua DOI:10.32604/cmc.2022.029927
Article

Model for Generating Scale-Free Artificial Social Networks Using Small-World Networks

Farhan Amin and Gyu Sang Choi*

Department of Information and Communication Engineering, Yeungnam University, Gyeongsan, 38541, Korea
*Corresponding Author: Gyu Sang Choi. Email: castchoi@ynu.ac.kr
Received: 14 March 2022; Accepted: 14 April 2022

Abstract: The Internet of Things (IoT) has the potential to be applied to social networks due to innovative characteristics and sophisticated solutions that challenge traditional uses. Social network analysis (SNA) is a good example that has recently gained a lot of scientific attention. It has its roots in social and economic research, as well as the evaluation of network science, such as graph theory. Scientists in this area have subverted predefined theories, offering revolutionary ones regarding interconnected networks, and they have highlighted the mystery of six degrees of separation with confirmation of the small-world phenomenon. The motivation of this study is to understand and capture the clustering properties of large networks and social networks. We present a network growth model in this paper and build a scale-free artificial social network with controllable clustering coefficients. The random walk technique is paired with a triangle generating scheme in our proposed model. As a result, the clustering control mechanism and preferential attachment (PA) have been realized. This research builds on the present random walk model. We took numerous measurements for validation, including degree behavior and the measure of clustering decay in terms of node degree, among other things. Finally, we conclude that our suggested random walk model is more efficient and accurate than previous state-of-the-art methods, and hence it could be a viable alternative for societal evolution.

Keywords: Social networks; small-world networks; network generation models; graph theory; random walk; network design; social network analysis

1  Introduction

In recent years, social networks have gained popularity and the attention of researchers working in different fields of science [1]. Social networks offer a combined solution for network growth [2]. A few years ago, a trend in online social networks (OSNs) emerged. The number of OSNs is increasing quickly, and they have become popular in recent years [3].The most popular OSNs are Facebook and Twitter [4,5]. It was estimated that the number of Facebook users exceeded 1.8 billion in 2017 [6,7]. In a typical OSN, many users connect through several links [8]. Typically, the structure of a social network is dynamic because it grows quickly with the addition of new links [9]. These links denote interactions among the users in a network [10]. In these networks, social interaction is a fundamental problem [11]. The growth and evolution of networks is also a problem in network science, especially since networks constantly change over time. In this direction, a lot of research has been done. Plenty of graphical networks have been proposed, and are used for analyzing the structure of social networks. In many cases, the networks such as World Wide Web (WWW) exhibit complex structures. These networks are known as complex networks [12]. Generally, social networks are the same as complex networks and contain many short paths, known as small-world networks [13]. The small world has long been the subject of scientific interest in network growth and evolution. Initially, the small-world phenomenon was proposed by Watts and Strogatz [14]. They have demonstrated that the topology of some social and biological networks is neither completely random nor regular. Hence, they termed an intermediate network a small world [15]. In reality, the small-world phenomenon refers to the principle that all people are linked together by a short chain of acquaintances [16]. For instance, six degrees of separation is the idea that everyone is linked by a chain that is, at most, six people long [16]. For example, Fig. 1 demonstrates the small-world phenomenon. In this example, a group of people in a social network is shown. Given two people, Emma and Lucas, there is a chain of other people such that Emma knows Liam, who knows Noah, who knows Olivia, who also knows Lucas. Suppose that Emma holds a letter and wants to forward this letter to Lucas (the target person). Under the six degrees of separation theory, she forwards it to a neighbor (e.g., Liam). The condition imposed on this network is that each participant can advance the letter only by forwarding it to a single acquaintance. Hence, Emma forwards it to Liam, Liam sends it to Noah, then Noah to Olivia, and finally, it reaches Lucas via Olivia. In this figure, we can observe that short paths (no more than six hops) always exist between all people. This is known as six degrees of separation [14]. Small-world networks comprise three significant properties: (i) degree distribution (ii) clustering coefficients, and (iii) path lengths [17]. The degree of a node in the network is the measure of how many connections the node has. A subgraph of a small world contains many connections between any two nodes, termed a clustering coefficient. Furthermore, in a network, pairs of nodes are linked by at least one short path, called the path length. A lot of researchers have focused on the effect of different aspects of the small world, such as spreading a disease [18,19], the Internet [20], and metabolic networks [21]. These networks share three significant properties [21]. (1) The average path length remains as small as possible; hence, only a few edges are available when two nodes on a graph are to be attached. (2) The average clustering coefficient is large enough to yield a separation of nodes containing common neighbors that are far from each other. (3) The degree distribution of these networks should be scale-free because it follows the power law [22]. Typically, the lack of a scale-free structure for node connectivity is often related to these networks [23]. Social network analysis (SNA) [24], is a process of investigation to study a social structure through graph theory and networks [7]. In a social network [25], it is nearly impossible to obtain the information of all nodes in the network. Typically, SNA is observed in many practical circumstances where a social network is addressed using publicly available interfaces, such as an application programming interface (API) [26]. An API is used to answer a query regarding a target node. In many networks, a public interface is available for analysis of a network. In Fig. 2, a scientist obtains a node ID and a friendship list from a social network using a public API. The self-loop shows the repetition of the scientist’s query. The estimation of structural measures in this network is performed by using the public API. The research on providing public interfaces has received much attention in recent years [27]. To calculate the clustering coefficient of these networks, scientists apply the query to nodes other than the sampled nodes. In fact, in social networks and large scale networks, the estimation of network-based features is difficult because the sizes of these networks are extremely large [28,29]. Also, they contain large datasets that are occasionally unavailable because of privacy concerns [30]. To overcome these issues, authors have proposed several processes, such as the random walk [31]. The random walk is a Markov chain process in which a sequence of nodes is visited using a succession of random steps [31]. Fig. 3 shows the simple process of a random walk in a network. In this figure, the number of nodes in graph G={A,E} is shown in orange. Node A, in blue, indicates the starting point of the random walk and is called the current node. The next step is to identify the neighbors of the current node (i.e., Node B and Node C). In this scenario, the random walk starts a tour from Node A, and after reaching the next node (i.e., Node B), it continues randomly until reaching the final destination (e.g., Node E). In complex networks, the random walk process is used for node selection and is beneficial for the growth of the whole network. In particular, random walks are used to find paths in a network and help determine dissimilarity in neighbors. The pathfinding methods are efficient, and hence, they are widely used in online graphs. The research area in social sciences, marketing, and computer science etc. Usually, in large networks such as social networks, a search engine provides a public interface as a part of the service. The available public interfaces for social networks have been discussed elsewhere [32–34]; also, they are used to estimate the clustering coefficient and the degree distribution. The authors discussed a few studies related to OSNs [33,35]. In these studies, the walkers were used to find the number of persons registered in the network. In practical scenarios, the underlying network may be available only through a public interface. The public interface of most social networks, as shown in Fig. 2, provides the ability to retrieve a list of connections by applying this function iteratively to a random member of the list. By using this, one can easily perform a random walk on that network. Although the public interface allows us to store the social network locally, this practice is considered impractical due to high space/time/communication costs, and it often violates the terms-of-use agreement. In light of this, we proceeded under the following assumptions: (1) we have no prior knowledge about the network, and (2) only external access to the social network is available. The main insight offered in this work is that, under these limitations, the presented random walk algorithm attains accuracy in the estimation of the structural measure of the network. By constructing an artificial social network, this study provides a solution for the growth and evaluation of networks. In this direction, we focused on two network measurements. The first is performed by calculating the node degree distribution, and the second is estimating the clustering coefficient. Both measures are important for understanding the structural properties of a network [3,21]. The degree distribution is important in studying real networks, such as the Internet and social networks. Through the degree distribution, we capture only a small amount of information about a network. However, that information still gives important clues to the structure of the network, such as the number of hubs. Conversely, triadic closure helps find the number of triangles, which helps find the growth of the network. Our objective is to propose a purely local network growth model that makes no use of global sampling across the nodes. To the best of our knowledge, earlier methods used for random walks in social networks have only partially considered the abovementioned properties. In this study, we consider how efficiently global graph properties can be estimated (e.g., the number of links, triangles, and visited nodes) by using a random walk.

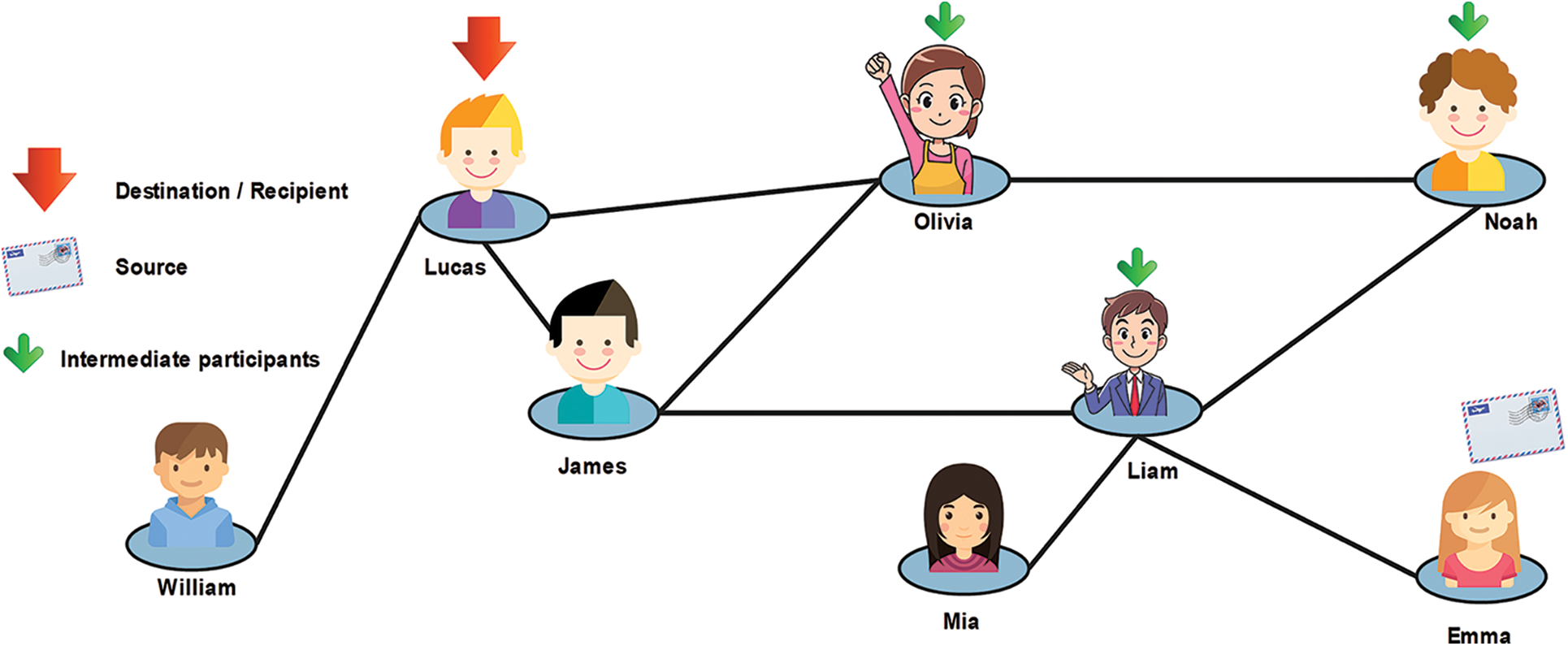
Figure 1: An example of a small-world network

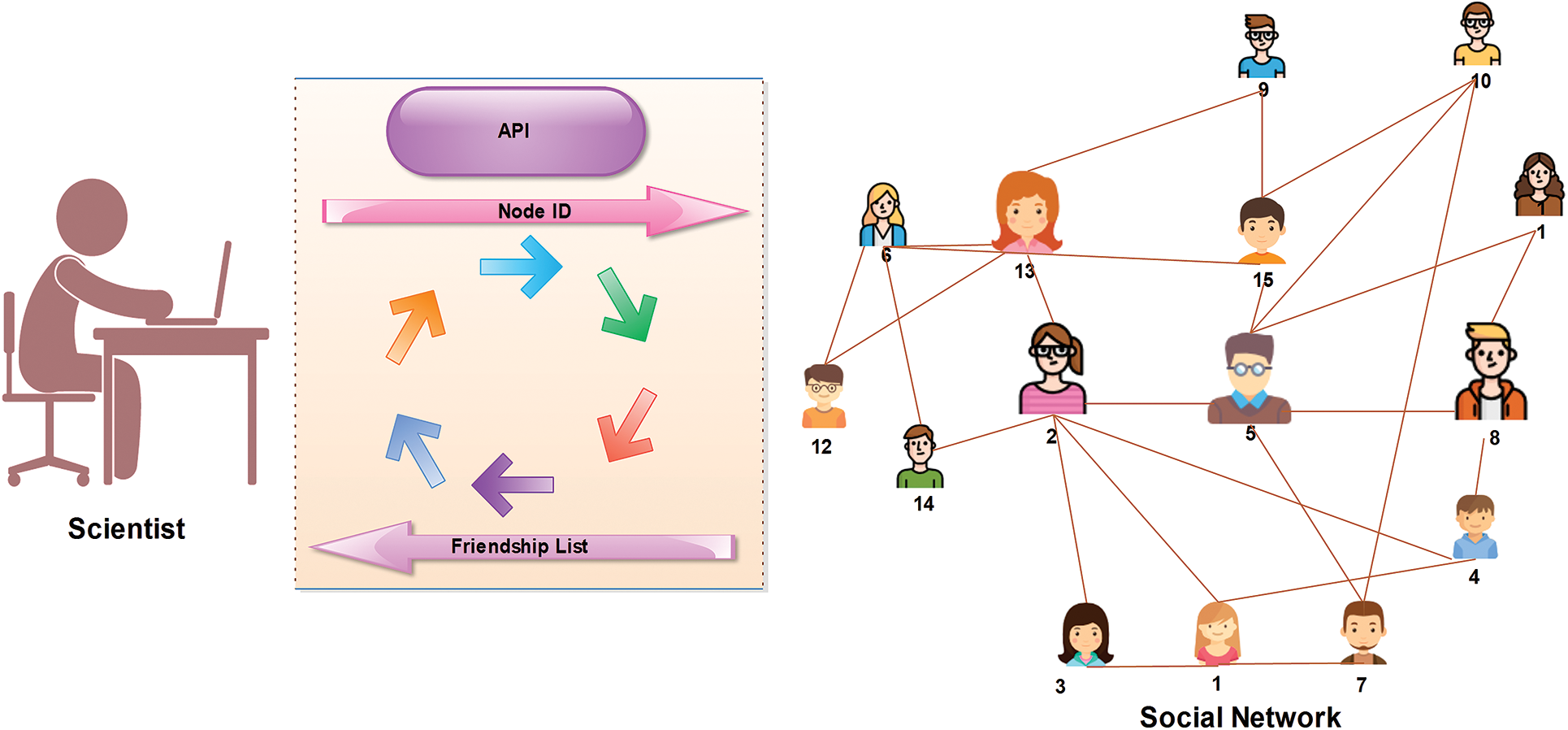
Figure 2: Social network interaction using an API

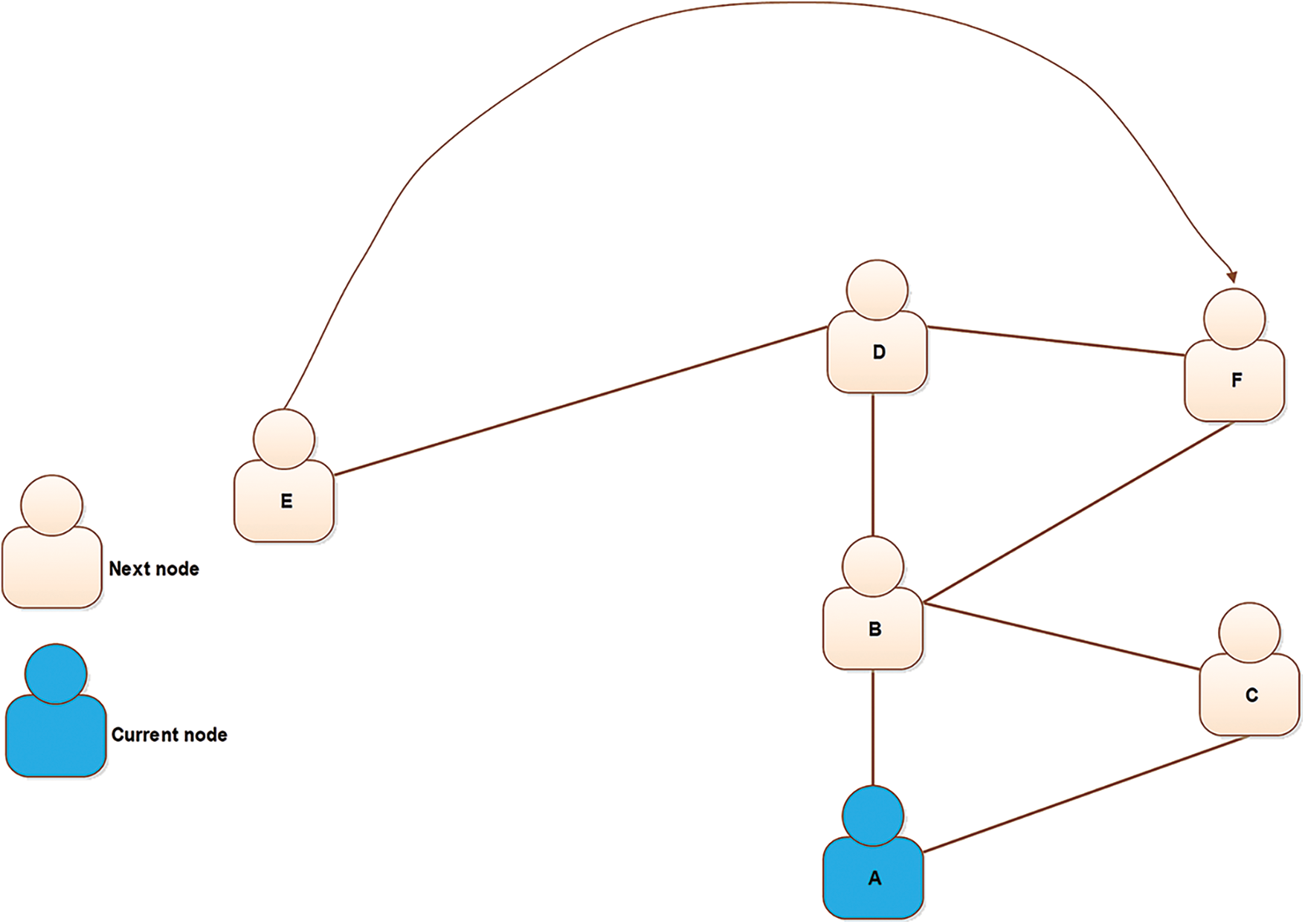
Figure 3: An example of a simple random walk process

1.1 Motivation

The motivation of our study is to capture the basic network properties of large-scale social networks [3,21,36] These networks have larger clustering than the state-of-the-art Barabasi and Albert (BA) model [22]. The artificial social network generation, growth, and evolution of networks is a fundamental problem in network science [2], especially since networks constantly change over time. The random walk process is helpful for the construction of an artificial social network. Therefore, in this study, we discuss the concept of the artificial social network construction model. This growth model reaches toward highly connected nodes and is attained by using a random walk. This study intends to understand the key properties of small-world networks and to enable them to be used for the growth of the network. Several network-generation models have been proposed in the past. These models have both scale-free and small-world properties. For example the author network [37] and the author’s collaboration network [38] etc. In general, randomly generated networks are used to explore the predictions of a theory in the context of a social network. This study is a connection between small-world networks and scale-free networks. More specifically, it is a unifying concept provided in a single model.

1.2 Contributions

The main contributions of this study are given below.

•   We propose a scale-free, artificial social network generation model that is purely local, requiring no global selection of nodes, or any initial network.

•   The random walk model is used to generate artificial networks that incorporate the properties of small-world and scale-free networks, with the additional advantage of having an adjustable clustering coefficient.

•   Using a visual analytics method introduced earlier [38], we demonstrated that there are considerable structural differences between networks that are generated by real-world artificial social networks.

The benefits of this study are given below.

•   It will be helpful to researchers who wish to learn the methods of generating artificial networks.

•   The researchers who want to understand the structural properties of a network.

•   This research is also beneficial for several network mining problems including extrapolation, sampling, model testing, etc.

In Section 2, we discussed standard network measures. Subsequently, we present prior studies on scale-free and small-world networks. we discussed classic random walk models (along with their limitations) and also the problem statement. We discussed our proposed model in Section 3. Section 4 offers detailed experimental results and a discussion related to this study. The conclusion and future work from this study are presented in Section 5.

2  Standard Network Measures and Related Studies

This section is divided into three subsections. In Section 2.1, we discuss classic standard measures in networks. In Section 2.2, we discuss the scale-free and small-world concepts along with their limitations. In Section 2.3, we discuss a few studies related to the classic random walk.

2.1 Standard Network Measures

In this section, we first discuss the standard network measures, and then, we discuss the relationships between these network measures.

2.1.1 Node Degree

Perhaps the most important property of a node in a network is its degree. Node degree illustrates the number of nodes that are directly connected. Generally, nodes may have any whole-numbered degree (including zero, for an isolated node that is not connected to any other). In a network, the degree will be twice the number of edges. In most networks, every edge is usually incident to two different nodes.

2.1.2 Degree Distribution

The degree distribution is how the degrees of the nodes arise across the network, i.e., the number of nodes in a network with degree 1, degree 2, and so forth. In short, any network will have the largest (maximal) and the smallest (minimal) degree. P(k) denotes the fraction of nodes with degree k:

P(deg(v)=k)(1)

which indicates that deg⁡(v), the degree of v, is equal to k. For brevity, it is usually written pk.

2.1.3 Clustering Coefficient

The clustering coefficient is used to measure the grouping, or the triadic closure, in a graph. It is a calculation of the number of triangles in the network. More simply, it is a measure of the extent to which one’s friends are also friends of each other:

Ci=2niki(ki−1)(2)

where Ci is the clustering coefficient of node i, and ki indicates the degree of node ki. The clustering coefficient for a network is defined as

C=∑i=1NCiN(3)

2.1.4 Path Length

The path length (geodesic) is the average distance between two nodes chosen at random. The path length lies in the range between 1 and the diameter. Usually, the path length is a measure of the denseness of the network, in the sense that a short characteristic path denotes a network in which the shortest paths are indeed short. The average path length of graph G can be defined as follows:

G=1n(n−1)∑i−jd(vi,vj)(4)

where vi and vj are any two nodes. In addition, the longest geodesic in a graph is called the diameter of the network. It consists of the largest values for d(vi,vj).

2.2 Concepts of Scale-free and Small-world Networks

We divided this section into three distinct subsections. In Section 2.2.1, we discuss a few studies related to the small-world network. In Section 2.2.2, we discuss two basic concepts: scale-free and PA. In Section 2.2.3, we performed a survey and compare various studies in tabular form.

2.2.1 The Small-world Network

The patterns in several networks, such as the social network [36,39], the technological network, the biological network, and the information network, are explained by complex networks. A random graph is a collection of randomly connected pairs of nodes with a Poisson degree distribution. The only problem with that random model is that it is not completely appropriate for clarifying the behavior of both random and complex networks. Traditionally, a few methods are used by random networks, such as the Erdős-Rényi (ER) model [40]. The ER model is one of the simplest, in which every possible edge is created with the same constant probability. This network starts with isolated nodes (having no edges). It adds an edge between a pair of nodes at a random time. The addition of random edges to a node is based on two parameters; the first is the number of nodes, i.e., n, and the second is the probability, p, that an edge is present. For each edge, n(n−1)2 is the possible number of edges in the network, based on probability p.The best example is the flip of a coin. If we get heads, then it would add an edge to the network; tails, it would not. Also, this is known as the G(n,p) model, where n denotes a node; the associated probability is P(n1……nn). The ER model presents a small-world effect. This effect is defined by two factors: the first is the slow increase of network diameter with the network growth, and the second is the presence of an unexpectedly large number of triangles in the network. The problem with the ER model is that it is a poor indicator of the degree distribution, compared to real-world networks. To minimize the abovementioned properties, Watts and Strogatz (WS) suggested a model named the small-world model [14]. In this model, a regular lattice is constructed, and a pair of nodes can be chosen randomly using shortcuts; subsequently, a connection between nodes is made. Fig. 4 shows the small-world networks generated by the Watts–Strogatz (WS) model. In Fig. 4A, the set of nodes is arranged in the form of a ring, and in Fig. 4B, a ring is constructed with random long-range links, and fewer long-range links are added to the WS network. The suggested cuts in a ring lattice yield the shortest average path length (as random paths), without affecting the local properties, such as high clustering. This is known as a small-world property and can be achieved in any graph with random and long-range links with high local clustering. The WS model was good, but could not have additional properties, such as the discovery of service in large and real networks, and of node degree distribution. It is vastly different from the distribution predicted by the earlier ER model. The inspiring research conducted by Watts and Strogatz were completely focused on small-world networks.

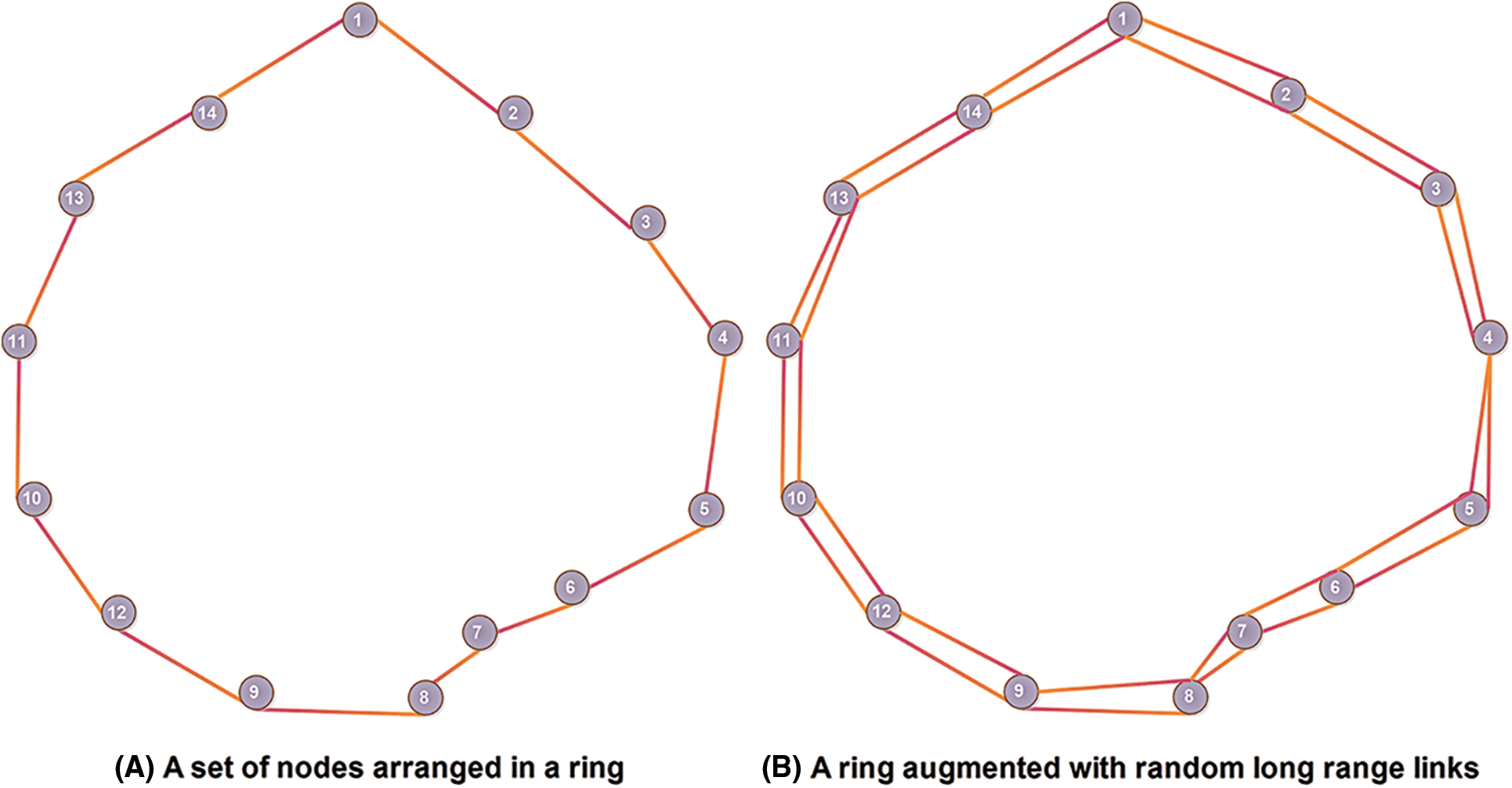
Figure 4: The WS model

2.2.2 Preferential Attachment and the Existence of the Scale-free Network Structure

Saramäki et al. [5], introduced the power law by Barabási et al. [22]. This model is used to find the formation of hubs in a network. In addition, it combines the simple principle of growth and PA. According to the power law, when a new node is added to the network, it is preferentially linked to the nodes already processing a large number of links. The proposed model is based on two fundamental laws. The first is network growth, and the second is PA [5]:

•   In the growth phase, at each timestamp, a new node is added with m links (where m≤m0) that connect the new node to m nodes already in the network.

•   During PA, the attachment preference for a node is only assigned to high-degree nodes.

According to the power law, when a new node is about to join a network, it is preferably linked to the current nodes that constitute a large part of the links in the network. The computed probability, pi, to link a new node to an existing node i depends upon the degree, ki, as follows:

pi=ki∑j=1nki(5)

Fig. 5 illustrates the PA process. In Fig. 5A, the network growth using PA is shown. The network grows by adding a new node in the network. The new node selects a link, as indicated by the black arrow. In Fig. 5B, a new node connects with equal probability to one of the two nodes at the ends of the selected link. In this case, the new node connects to the node at the right end of the selected link. This intuitive method results in the generation of a scale-free network [5]. The BA algorithm uses global information. The BA model was proposed by assuming that in the WWW, new pages link preferentially to the hubs (i.e., very well-known sites such as Google) rather than to pages that hardly anyone knows about. In this model, the authors assumed that every new node has complete information about the whole network, which is not true for large networks and real networks [41]. They did not state completely how PA should be performed. PA typically uses global information on node degrees from the entire network but differs compared with many real networks, such as social networks, the WWW, etc. In addition, the integration of new links in the network is difficult.

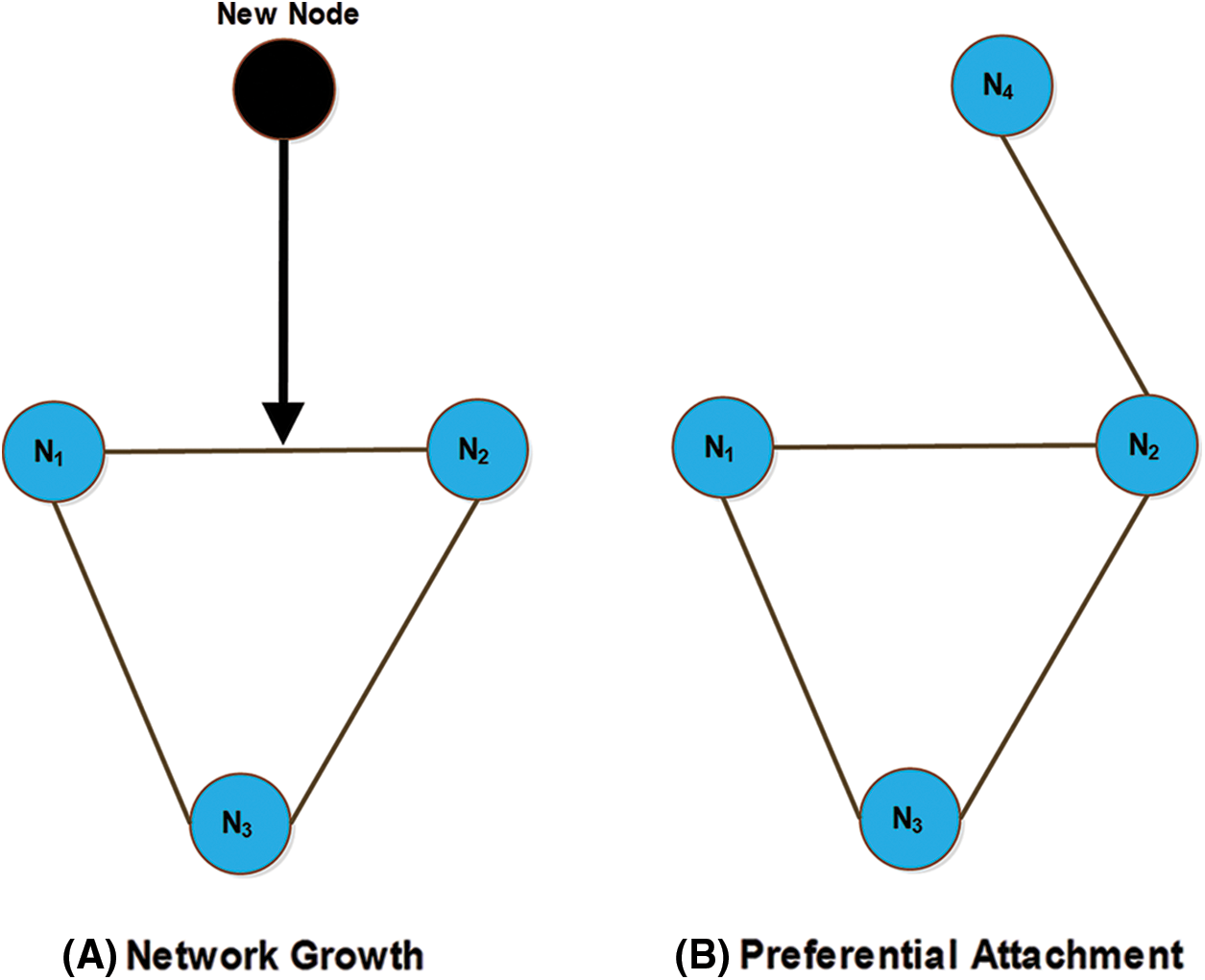
Figure 5: The preferential attachment

2.2.3 Comparison Between Scale-free and Small-world Networks

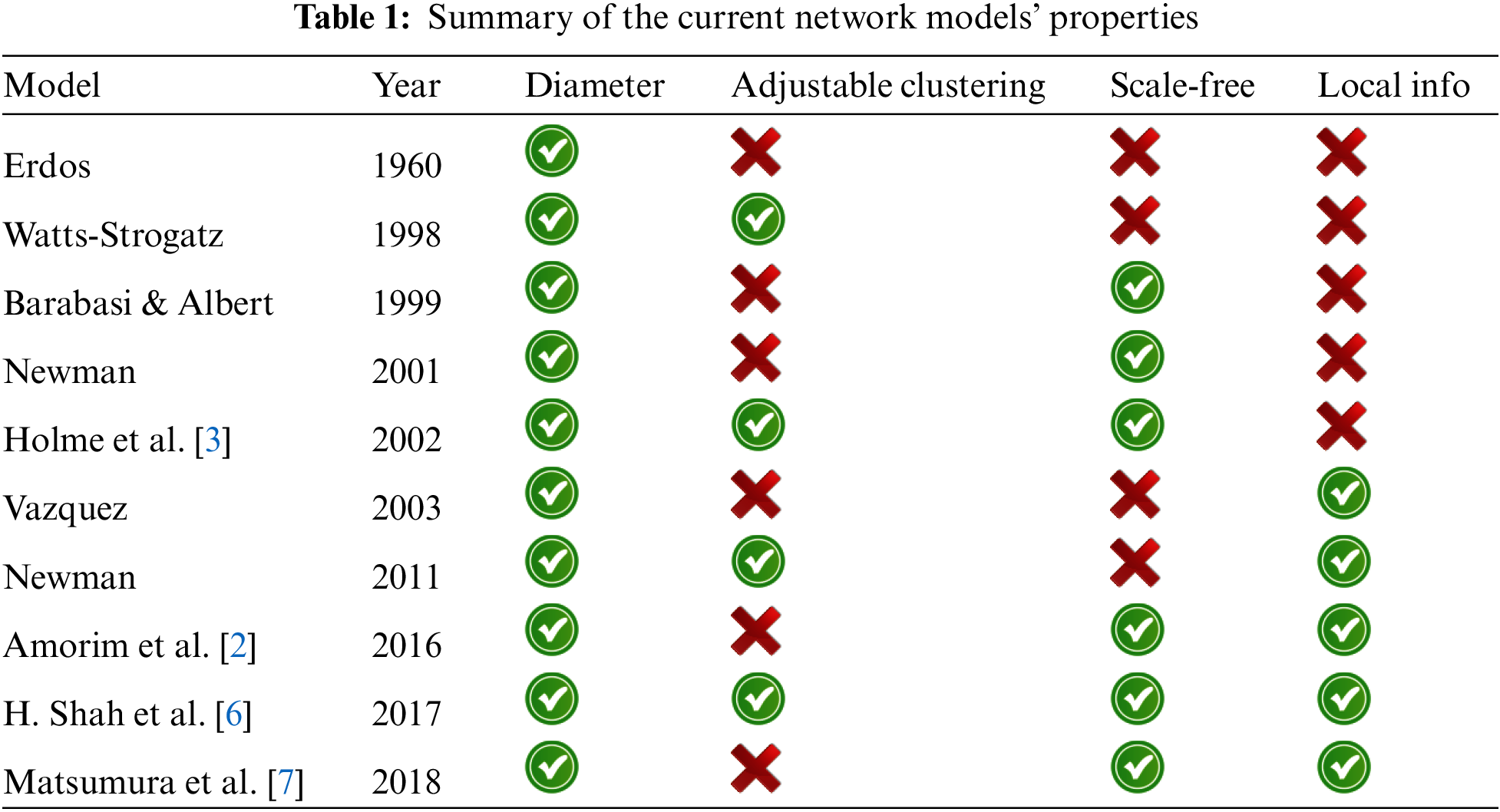
BA model provides the key information for scale-free networks, and the WS model has small-world properties [41]. The WS model exhibits high clustering, but lacks power-law degree distribution, whereas the BA model exhibits the scale-free property but does not possess high clustering. Dorogovtsev and Mendes [42] proposed a simple clustering model for scale-free networks. The addition of new, undirected vertices is made at each stage. However, their model does not describe real networks because they have a fixed average degree. Tab. 1 provides a comparison of different network models, along with the different metrics discussed in the previous section. In this table, we can see which model has a lack of local properties, such as diameter and the clustering coefficient. In this tabular representation, we can easily examine how each model is described. In addition, we can identify which models lack network properties. The objective of this study is to propose a network growth model combining the features of scale-free and small-world networks by using a random walk and producing a network. For that purpose, we modified the BA model by using a random walk method, and our objective is to incorporate a navigable triadic closure. The presence of scale-free structures in many real networks inspired us to write this proposal and further investigate features of real networks, such as short diameters, clustering, and long-tail distribution.

2.3 Classic Random Walk Models and the Problem Statement

In this section, we first discuss a few classic random walk processes, and then, we discuss the problem statement.

2.3.1 Classic Random Walk Models

Generally, in real networks, adding a new node would not require global information about the network. Several studies have been conducted in which local network information is used to spawn scale-free networks without using global information [43,44]. One of these approaches demonstrates how a random walk process is used for the selection of a node that can be attached. This study proves that it can be used for the growth of a network. In [12,5,45], the authors successfully employed different random walk algorithms. A random walk having length L will end up on the node derived from Eq. (6), where the probability of linking to one of two nodes (x to y) is given as seen below, in which ki and Nki are the degrees with the probability given in (1):

px,y={1kivj∈N(ki)Vj0otherwise(6)

where y is the neighbor of x, and x is the out-degree of node y. Transition probability px,y is calculated using a simple random walk (SRW) from [7] and is derived with (6). In the SRW, the authors assumed that the SRW method is used to generate an artificial network. They discussed only the PA procedure, but not the remaining network features, such as the clustering coefficient CC. In [43], the correlation of closing a degree was analyzed under a mean-field hypothesis. The only limitation of this study is that the CC was not considered. Matsumura et al. [7] discussed a crawling-based sampling random walk method for estimating path length in social networks. They offered a solution based on Dijkstra’s algorithm. In that study, a portion of a network for r samples was obtained by time: O(r)3. The only tradeoff observed in this study was the non-existence of an evaluation. Ji et al. [46] discussed Sybil attacks for OSNs. These attacks are used to establish fake accounts in various networks. In those networks, the attacker maintains a massive number of fake accounts, later used for malicious activities. The drawback in that study is the learning of edge weight, in which the labels are augmented for social networks. They had not yet generalized their theoretical analysis to the Markov random field. Most surveyed studies discussed Sybil detection as a problem of supervised learning. The key challenge in the abovementioned approaches is that an attacker and the users in the network can produce similar content, behaviors, and local graph structures. Hence, this renders the method less effective. Cheng et al. [47] proposed two friendship prediction-based models for inferring the friendship circle in a social network. Location entropy and check-in time interval were performed in the first model. In the second model, they used a weighted number for colocation and used the average time interval for the prediction of user relationships. In that study, the authors proposed a noise filtering approach (NFA) for the prediction of links in social networks. The NFA is completely based on considering dissimilar links, such as noise. Among the various studies, the approach of Cheng et al. [47] and Li et al. [48] are closely related.

Katzir et al. [49] suggested the average clustering coefficient of a network using a random walk process. In their proposed algorithm, an SRW algorithm was disseminated slowly over the space in a social network. Their proposed algorithm performed better than other approaches, such as the one in [32]. Iwasaki et al. [50] proposed an algorithm for the estimation of the clustering coefficient in social networks using a sample query. They proposed a non-backtracking random walk (NBRW) [50]. That method is based on the counting of triangles obtained during sampling. They used the NBRW as a public API interface that theoretically displays the information retrieval of a social network. Cohen et al. [51] introduced the concept of reaching highly connected nodes by using random links. A recent study was conducted by H. Shah et al. in [6]. In this study, the authors propose a random walk network growth model using resource constraints. The objective of this model is to be to explain how the real-world network properties were affected by using edge formation like resource constraints. In this model, before starting a random walk, at first, each node that joins the network select a recent node as a seed. The linking of the node is performed based on probability. Later on, it follows the outgoing and the incoming of this seed node and arrived at each node. Every time the new incoming node will decide to link with the same constant linking probability. Then each node either has to decide whether to jump back to the seed node or may follow these incoming and outgoing links. This process is repeated several times. Briefly, this is a local procedure and the linking of a node will be performed without contacting the whole network. The only problem with this method is that they did not discuss the clustering coefficient along with degree distribution. Leskovec et al. [52] discussed the behavior of a graph over a certain time. Their main concern in this paper is to confirm that does the graph changes over a certain time or not. Therefore, they performed a careful analysis using three laws, the densification power law, the community-guided attachment model, and the forest model. In this study, they reported that all of these models behave differently. They observed that most graphs are heavily trailed using in-degree and out degrees. In addition, they have also shrinking by increasing a diameter. Briefly, they discovered a very interesting phenomenon that in a large number of graphs the diameter is changed over the increasing interval of time [53]. Finally, they proposed a new graph generator model based on ‘forest fire’. Their model requires very few parameters such as; the flammability of nodes. They are producing a full range of properties observed in the present and prior studies. Amorim et al. in [2] discussed a scale-free mechanism named No Restart Random walk (NRRW) for the growth of a network using random walk. Initially, their network starts with a single node by using a self-loop. The random walker placed on that node and each walk comprised s number of steps. At each time, new nodes are added to the node, which resides the walker. The walk ends after completing n number of nodes. The proposed model is good but they did not discuss the clustering coefficient in this study. Matsumura et al. [7] discussed a random walk method for estimating the Average path length (APL) in social networks. This crawling-based graph method is suitable for scale-free networks, but in this study, they did not discuss the computation of the clustering coefficient. Saramäki et al. [5], introduced a scale-free network method by adopting PA for local approximation in the network. It is based on BA model; thus, it has three phases: network initialization, growth, and finally, linking. During network initialization, the placement of vertices in the network is performed. In the growth phase, one of the vertices is chosen as a starting point for the walk. Finally, in the linking phase, a new vertex is added to the network, and a link is created between the new vertex and the existing vertices. We observed in this method that when a new node has already been connected to the first chosen node, no triangle is generated. Moreover, we can see that when l=1, a walk continues from the first chosen node to the new node, which results in the generation of a triangle (as we observed in the Holme and Kim [HK] model [3]). Thus, the selected nodes via successive instances of l=1 would add m−1 triangles to the network. This key observation recommends the possibility of implementing a triangle generation–control mechanism by selecting the new starting point for the next walk, proportionally combined with successive instances of l=1. In brief, we performed a careful analysis of previous studies, and our findings are as follows. In earlier methods, no control mechanism was specified; hence, a low-level clustering coefficient is produced. Also, the node distribution in the network is improper [54]. Thus, based on these observations, we are proposing a network growth model based on a random walk and having a dynamic clustering control process.

2.3.2 Problem Statement

In our study, we consider the growth and evolution of networks as a fundamental problem in network science, especially because networks constantly change over time. The random walk process is helpful for the construction and growth of the network. We observed from earlier studies that although triadic closure is helpful for the growth of a network, the incorporation of dynamic triadic closure will produce more powerful and bigger networks. After reviewing several research ideas, our key findings are as follows.

•   The scale-free concept and the power law, including directing rules, are helpful in the growth and the construction of an artificial network.

•   An algorithm is efficient if it uses its local information. The connections are also important in a local network. The introduction of local immunization strategies is effective for the growth of a network.

3  Proposed Model

In this section, we suggest a random walk model for the growth of a network where the clustering coefficient can be estimated and adjusted dynamically. The proposed model is closely related to the recent studies related to growing networks through random walk models by Amorim et al. [2], Matsumura et al. [7], Saramäki et al. [5] and Katzir et al. [49] and Leskovec et al. [52]. These models allow a random walk to take steps before linking a node. The key difference is that we use certain random walk properties that can control the formation of a triangle in the network.

3.1 Basic Preliminaries and Notations

We denote as G=(V,E) an artificial network’s underlying undirected graph, where V={v1,v2,v3,…vn} for the network node-set, and E is the edge set; v=V defines the number of network nodes, and m=E defines the number of edges. In addition, we denote by di the degree of node vi. At each step t, the function f0 produces the probability of distribution, i.e., f(p). We use a Bernoulli distribution. We denote as g a fixed-length graph, and G is a random graph. A random walk on graph G starts at node v. The walk repeatedly moves along an edge to a randomly selected neighbor until V edges have been closed.

3.2 The Proposed Model

There are three basic steps involved in this model.

•   Network initialization: In the first step, network initialization is performed by adding new vertices to the network. One node at a time t is added to the network. Our algorithm takes three parameters: first is the number of vertices, V; second is the m edges (E) to attach from a new node to the existing nodes; third is the construction of an initial seed-connected network with n0 vertices. Therefore, G contains nodes that are well connected as shown in Fig. 6.

Figure 6: Network initialization

•   Network growth and scale-free degree distribution: In this step, the probabilities pi are associated with each node in the network. A Bernoulli distribution, f(p), is assigned to each node. This property ensures that our network follows a scale-free property. Fig. 7 presents the addition of probabilities pi to the current network.

Figure 7: Imposing the bernoulli distribution

•   Linking by random walk: The next step is to select a random node. Thus, node vs is selected as a starting point. Node vs neighbors are identified and marked. The random walk, L>1, starts from node vs. The neighbors of the current node are identified, and the arrived-at node is marked. A new walk from the last marked node is started, which is either a one-step walk or a two-step walk. Finally, one new node is added to the network; we assign the probabilities to the newly joined node and add a link between that node and the existing marked vertices. The proposed model generated by the random walk is shown in Fig. 8. Algorithm 1 shows the step by step network-growing. Initially, one node at a time t is added to the network and a random distribution, f(p), is assigned to each node. Our random walk model requires the construction of an initial seed connected with n0 vertices. We already know this also happens in the original BA model. Our contribution to this new model is the incorporation of an assigned non-zero probability to the initially isolated vertices, based on Eq. (7):

Figure 8: The proposed model

p(k)∼k+a(7)

Hence, in our proposed algorithm we have used the following design parameters: n is the number of nodes, v is the number of edges attached per node, m, and the probability distribution is represented by f(p). Usually, in most growing networks, m allows us to control the average degree, since k=2. We assign p as the probability, pvi. This probability reflects the generic factor declared upon certain distributions, such as f(p). The fraction of nodes is represented by the clustering coefficient (cc) having p(vi)=1, and the remaining nodes, p(pvi)=0. This phenomenon may result in the identification of different community structures of the network. In this study, the probability remains constant during a node’s life, and it will be determined based on the length of the random walk starting from the node. In Fig. 8, at first, a random node named Vs, is chosen as a starting point, and the random walk begins at it. The neighbors of Vs are identified in this step. The walk for L>1 is performed from the node Vs. We assign probability P1 to walk L=1; For a multihop, l=2, it would be 1−p. This random walk model enables us to implement triangle-generation control and select the next-hop nodes. The selection of a link for walk L, where L>1 for a single hop, or L>2 for a second hop, is performed dynamically. Accurate tuning and addition of the number of triangles were implemented using probability p1 for a walk where L=1. If L=2, the probability will be 1−p1.The incorporation of probability and control of a node attribute will facilitate the random walk. In particular, the probability remains the same as that during the node’s life and can be determined by using the length of the random walk. Estimating the network clustering coefficient C [17] is defined as done in [55] and in Eq. (8):

Ci={2eijki(ki−1)0ki≤1ki>1(8)

where Ci indicates the clustering coefficient of node i, and ki indicates the degree of node ki to the neighbors and the number of edges. The clustering coefficient for the entire network is calculated in Eq. (9):

C=1N∑ici(9)

where N represents the number of vertices. In addition, the behavior of our proposed random walk model is the same as the HK model [3]. The HK model exhibits a triad formation with probability Pt=1. In addition, the clustering properties are similar to the Dorogov model [56].

4  Experimental Results and Discussion

In this section, we present our experimental results in detail. We have divided this section into two subsections. At first, we have discussed the preliminaries of the power law, and then we have discussed the achieved experimental results.

4.1 Preliminaries: Generating Power Law

First, we need to define the initial seed and N vertices. This affects the topology of the initial network and the outcome. It is known that this may occur in the original BA model, in which a nonzero probability is initially assigned to the isolated nodes in the network [57]. In many cases, such as in implementation, it is performed by setting a parameter alpha a, in the distribution: i.e., (Discussed in Eq. (7)) p(k)∼k+a; Where the degree of nodes is represented by k0, is equal to the N vertices in the network. It is noteworthy that this value is equal to the a used in the BA model. The network topology is typically based on degree distribution, clustering coefficient, and path length. Typically, a regular lattice exhibits high clustering and a large path length, rather than random networks. Generally, it is observed in random networks have short path lengths and also has low clustering [57]. The regular lattice and random networks fail to explain the features of real networks, such as social networks, citation networks, and movie-actor collaboration networks [57]. Typically, these networks exhibit low-power degree distribution, a short path length, and large clustering [57]. Social networks or real networks can achieve these features by reconstructing a link using a regular network. To do the first walk, we need to construct a regular lattice where the degree k0 is equal to the n0 nodes. If we start a network with the accomplishment of these requirements the performance of our model is affected by the values selected for k0 and n0. A few points are noteworthy before further explanation. The first point is that the value of P is 0, 0.2, or 1, and it may affect the structure of the ring lattice. The second point is that if we change the value of n, it results in some undesirable effects. If we choose n=10 or larger, it produces a fully connected graph where k0=n0−1. It might be possible to produce the deviation from power-law behavior. This effect is shown in Fig. 9 as a result of construction of a completely connected graph. In this figure, a regular graph is shown. However, we are interested in a network growth model rather than a regular network. This graph shows the abnormal behavior of this study.

Figure 9: Visualization of a completely connected random graph

Hence, to address this issue, we have designed a ring lattice with n0=max(10,m), which appears to function properly in many cases. All the results presented below utilized this seed. Moreover, we have used L=7 for the first walk per added node has been used, to avoid dependence on the neighbor’s degree throughout the selection process.

4.2 Results and Discussion

In this section, we have discussed experimental results in terms of degree distribution and triadic closure. We performed a series of experiments using Network X [58]. Network X is a powerful Python package used for the manipulation, creation, and study of the network structure in complex networks. It is used to study large complex networks represented in form of graphs with nodes and edges. Using network X, we can load and store complex networks.

4.2.1 Degree Behavior and the Emergence of Scale-free Structure

The emergence of a scale-free structure during the growing process is discussed in this section. Fig. 10 demonstrates the complementary cumulative distribution function (CCDF) of nodes on a log scale for various values using Saramäki RW (Random walk) [5], No Restart Random Walk (NRRW) [2], and our proposed model. We have calculated this result and got an average of over 100 runs with N=106. The networks are generated using a random walk for l=1. In this figure, we observe that the degree distribution of our proposed random walk model is more linear than both models. This phenomenon is due to the high diameter and the occurrence of high clustering in our proposed model. In this experiment, we used three datasets and performed an extensive series of experiments. A detailed description of datasets is given in Tab. 2. In this table, a comparative summary of various statistics on network-generation models was given. These experiments aimed to find the general shape of the degree distribution by using the CCDF. A graph on a log scale was drawn to examine whether the tail follows the power-law or not. The x-axis represents the maximum number of node neighbors k, while the y-axis represents the degree distributions Pk. In this diagram, we see that because the random walk model completely follows the power law, it is on a straight line. On the other hand, the existing model and the BA model performed nearly equally. The calculated mean degree of the random walk is good, and hence, this behavior and the arrangement of degrees show that our proposed model is efficient and helpful in getting a high clustering. Hence, this result validates that the proposed random walk model behaves like other preferential attachment models [22,52,59].In addition, the proposed random walk model allocates well-organized node degrees, especially if applied on real datasets such as Facebook or Bright kite. Fig. 11 demonstrates the accuracy of growth models by comparing our model with the baseline Harshay shah et al. [6] Random walk (RW) model. In this graph, the line having blue balls indicates our proposed model. On the other hand, the green line indicates the Harshay shah RW model. In this figure, we can see that our model preserves degree distribution compared to the RW model. Therefore, our model outperforms the other in jointly preserving heavy ailed distribution. Tab. 3 demonstrates the description of real datasets that we have used in this experiment. In this table, some statistics of social data sets including edges, nodes, average node degree, and the average clustering coefficient cc are given. Fig. 12 demonstrates the degree distribution using the Bright kite Dataset. In this figure, the vertical red line indicates the Power law proposed by Barabasi et al. in [22]. The blue line indicates the deployment of the node by using our proposed model. We can see that the blue line is very close to the red line and it makes an almost ninety-degree angle. The objective of this experiment is to determine that our proposed model behaves the same as the BA model. The figure proves that the model behaves like a power law (Used by the current model). Similarly, Fig. 13 indicates the nodes distribution using the Facebook data dataset. The number of nodes is very large so the distribution of nodes has more curves. The behavior is quite similar to the earlier graph. These two results prove that our algorithm fits well and the distribution and performs it like power-law models. We have carefully reviewed a very recent random walk model by Amorim et al. named No Restart Random Walk (NRRW) [2]. The authors initially apply a few values to test the behavior of their model. Fig. 14, presents the complementary cumulative distribution of function (CCDF) of a node for various values of pvi in a log scale. In this empirical experiment, we would like to examine the behavior of our proposed model. we can see that when the value of pvi is small the coressponding degree distrbutation behaves differently. Generally, it exhibits a kind of power-law for pvi values. It is noted, that the degree behavior is changed. As the values of probability increases into the medium range, the trends continue, and this distribution to each other. In case we are applying large values, the degree distribution is getting closer and hence the results can’t be distinguishable. A noticeable point when we increasing the value of probability the degrees power-law distribution. Therefore, it suggests the effect of pvi values dominates the dynamics. In addition when the value of p is large then the CCDF shows a power law with the exponent approximately −2. This phenomenon is very similar to the BA model which is based on Preferential attachment (PA). As the coefficient increases, the probability of one-edge nodes increases and the (probabilities of higher-degree nodes decreases.

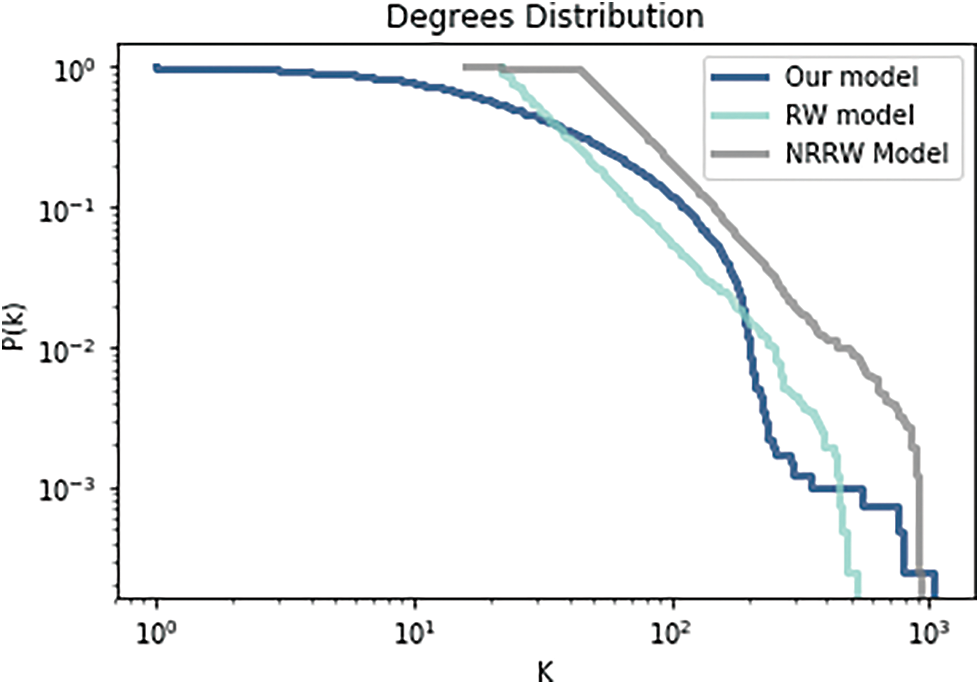
Figure 10: Comparison of degree distribution

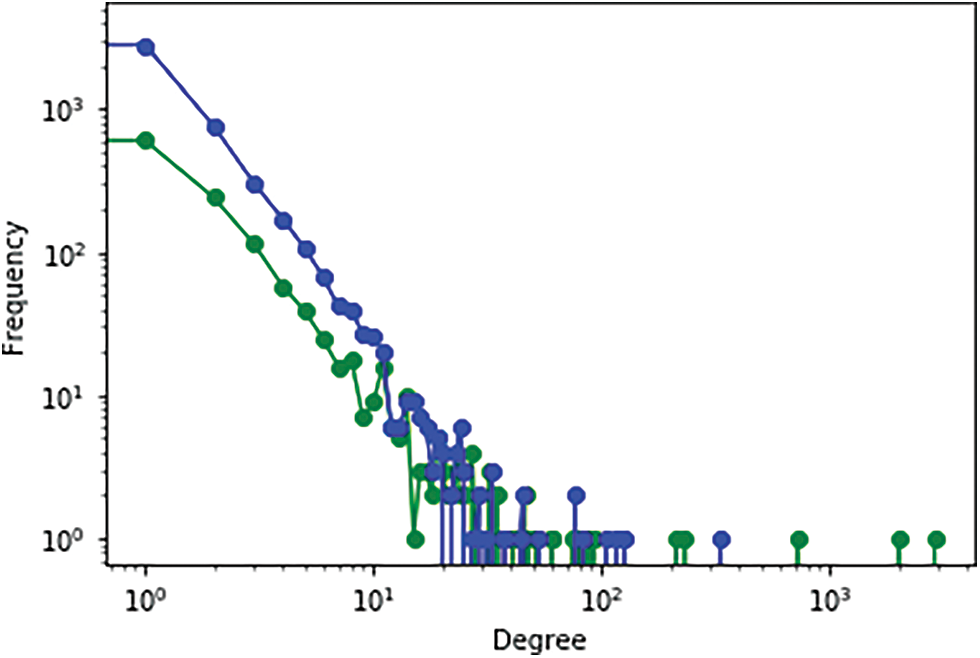
Figure 11: Accuracy of growth models

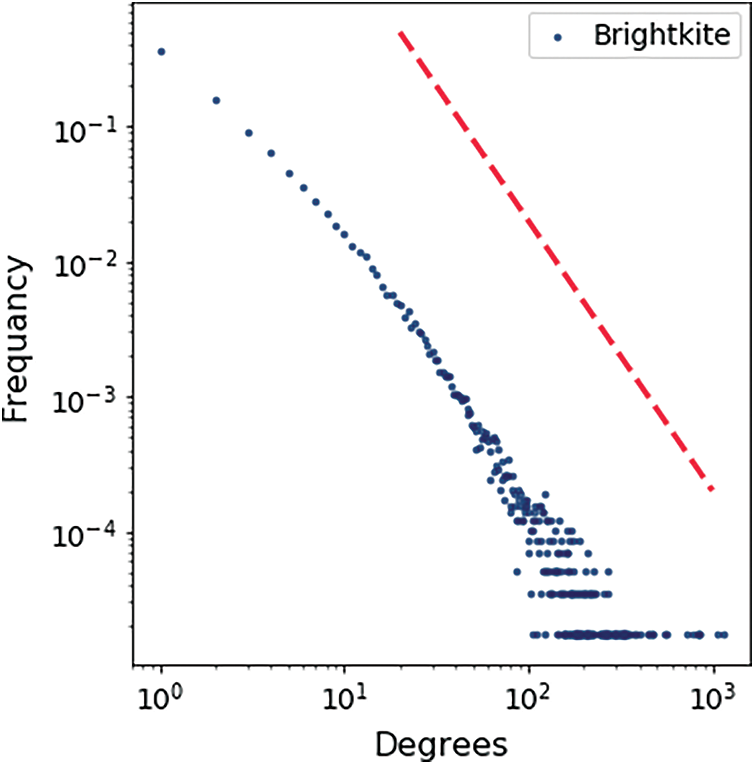
Figure 12: Bright kite

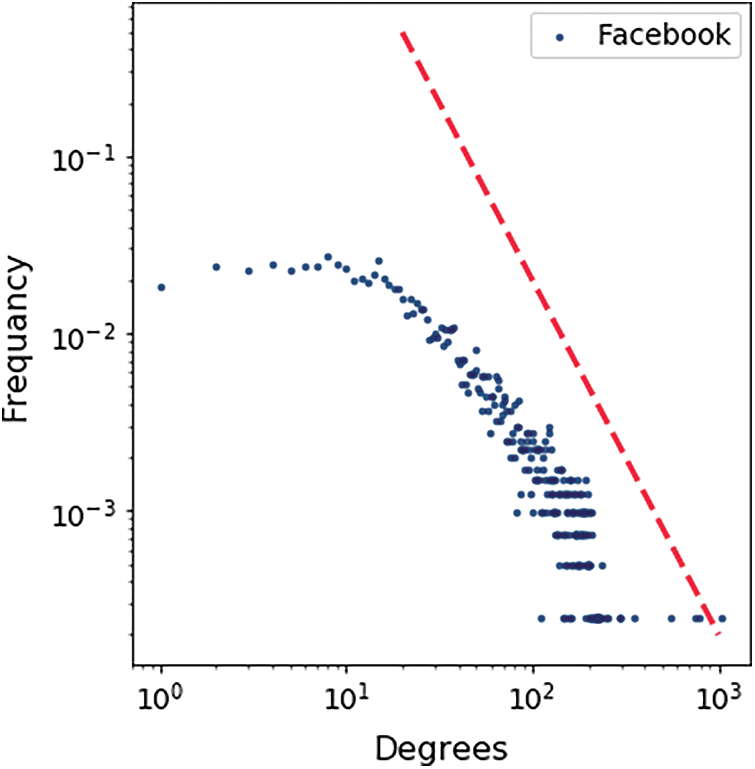
Figure 13: Facebook

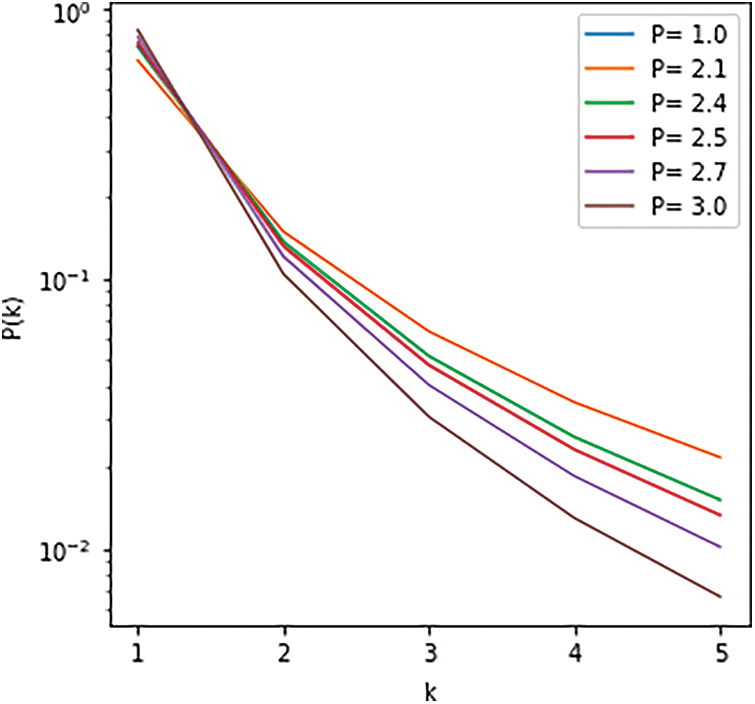
Figure 14: Empirical CCDF

4.2.2 Adjustable Clustering Coefficient Control

We have implemented the clustering coefficient control mechanism by changing the value of probability, i.e., clustering control parameter (cc). A walk for length l in the network is started by selecting a specific point. Fig. 15 presents the implementation of the clustering coefficient control mechanism by using a 2-step walk strategy. The y-axis exhibits the computed clustering coefficient (C) and the x-axis demonstrates the estimated clustering control parameter (CC). The blue point shows the mean clustering coefficient and the red line indicates the standard deviation. In this figure, we easily examine that our proposed model drives a high level of variance for small values of cc.We have tested this experiment 20 times for each value of cc. We adopted a two-step procedure and hence it produced a high value for clustering. we examine that the value of C depends upon the values of CC. The result indicates that triadic closure dependence is based on networks with N=104 (the number of nodes) and m=4 (the number of links). This result proves that the achieved C remains constant for a given value of cc, and hence, the network grows quickly. The results of our proposed random walk model show better results by following a linear relationship and are characterized by C = 0.53864 and CC with R2 = 0.999. We have also performed two experiments to measure the control capability of the clustering coefficient. Fig. 16, presents the empirical results of the first experiment. we have plotted a log-scale graph with the fixed network size, N=1600 to N=50.103. The result can be seen for three values different values of CC. The black color indicates the value of CC=0. The blue color indicates the value of CC=0.5. Finally, the green color indicates the value of C=1.s We can see that applying three different values to our proposed algorithm will produce in getting different clustering coefficients. The lower value of CC indicates the getting of a lower clustering value. Similarly, by increasing the value of CC, we can achieve a higher clustering coefficient. These results prove that our proposed algorithm is efficient in all aspects. In addition, this result validates that controlling the value of the clustering parameter helps in getting a large triadic closure. Similarly, the results of the second experiment are shown in Fig. 17. In this figure, clustering coefficient decay with an average degree is shown. The achieved result indicates that the variation of the maximum clustering coefficient can be generated by our proposed model, especially, when the value of m increases. This result validates that the behavior of the proposed random walk is the same as other recent tunable clustering models such as; [3,60]. Some researchers have proposed the use of an alternative definition of triadic closure since large values of m will bias the degree of clustering correlation in scale-free networks when the standard definition of clustering is employed.

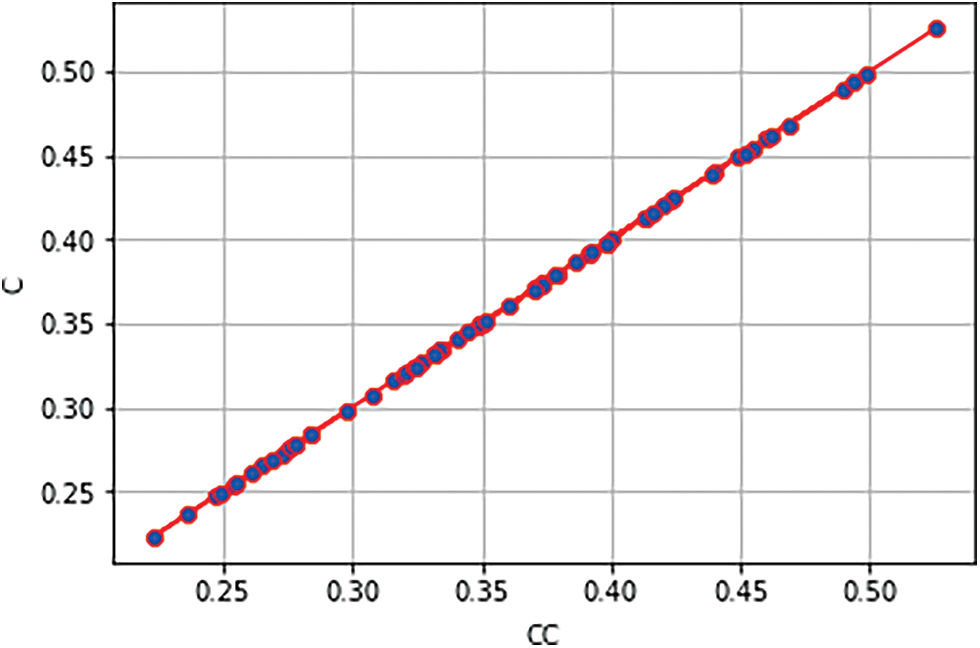
Figure 15: Clustering coefficient control

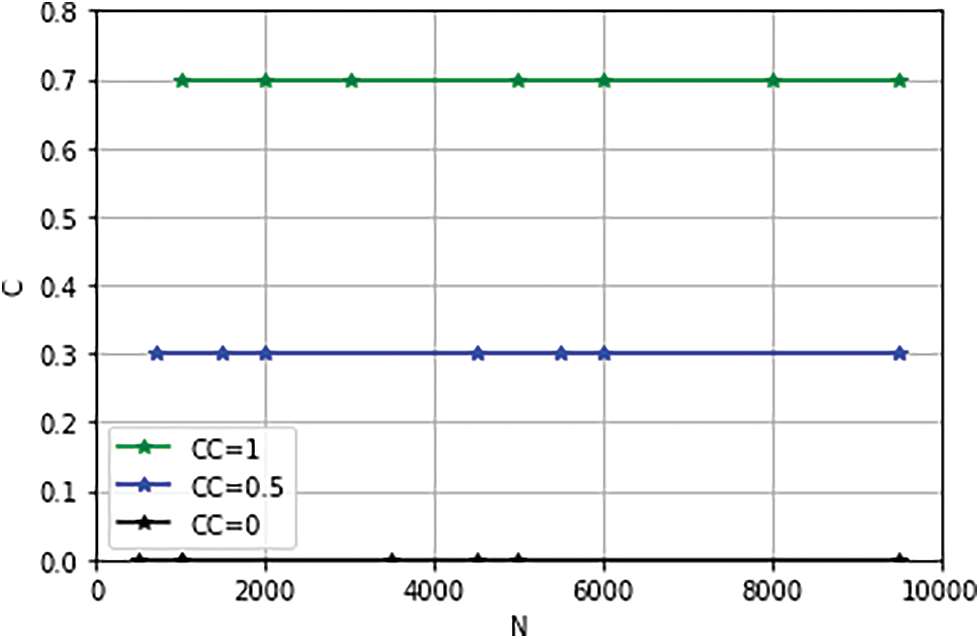
Figure 16: Empirical result of variation in clustering coefficient

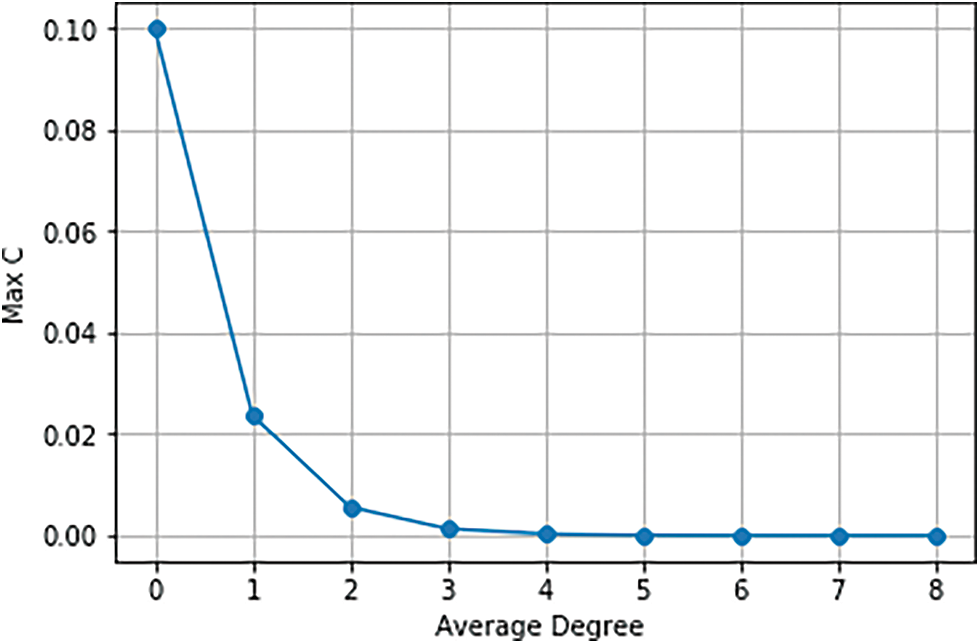
Figure 17: Clustering coefficient decay with average

5  Conclusion and Future Research Directions

We herein define a network growth model that is completely based on the properties of self-organized networks.

Typically, highly clustered and scale-free networks are used. We considered the dependence and growth of networks that are similar to the small-world transition. This phenomenon was observed in many cases of static networks, especially when link rewiring to a regular grid is required. Hence, our study demonstrated a connection between the small-world and scale-free networks. Our proposed random walk model dynamically estimates the clustering coefficient and degree distribution in the network. The proposed random walk model considerably outperformed state-of-the-art methods. We tested our algorithm and concluded that our random walk model is helpful for network growth. Moreover, it is also highly efficient in terms of attaining the node degree and high clustering. Our model is beneficial for several network mining problems including extrapolation, sampling, and model testing. The path length was not discussed, although it is an important property of small-world networks. This will be addressed in future studies.

Acknowledgement: We thank our families and colleagues who provided us with moral support.

Funding Statement: This work was supported in part by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education under Grant NRF-2019R1A2C1006159 and Grant NRF-2021R1A6A1A03039493, and in part by the 2021 Yeungnam University Research Grant.

Conflicts of Interest: The authors declare they have no conflicts of interest regarding the present study.

References

 1.  B. Viswanath, A. Mislove, M. Cha and K. P. Gummadi, “On the evolution of user interaction in facebook,” in Proc. of the ACM Workshop on Online Social Networks, New York,United States, pp. 37–42, 2009. [Google Scholar]

 2.  B. Amorim, D. Figueiredo, G. Iacobelli and G. Neglia, “Growing networks through random walks without restarts,” in Proc. of the 7th Workshop on Complex Networks, Paris, France, pp. 1–13, 2016. [Google Scholar]

 3.  P. Holme and B. J. Kim, “Growing scale-free networks with tunable clustering,” Physical Review, vol. 65, pp. 1–4, 2002. [Google Scholar]

 4.  J. Leskovec and A. Krevl, “SNAP datasets: Stanford large network dataset collection,” in Proc. of the IEEE Tencon, New York, United States, pp. 1–10, 2014. [Google Scholar]

 5.  J. Saramäki and K. Kaski, “Scale-free networks generated by random walkers,” Physica A: Statistical Mechanics and its Applications, vol. 341, no. 24, pp. 80–86, 2004. [Google Scholar]

 6.  H. Shah, S. Kumar and H. Sundaram, “Modeling network growth under resource constraints,” Computing Research Repository (CoRR), vol. 1, pp. 1–11, 2017. [Google Scholar]

 7.  T. Matsumura, K. Iwasaki and K. Shudo, “Average path length estimation of social networks by random walk,” in Proc. of the IEEE Int. Conf. on Big Data and Smart Computing (BigComp), Shanghai, China, pp. 611–614, 2018. [Google Scholar]

 8.  F. Amin, A. Ahmad and G. S. Choi, “Community detection and mining using complex networks tools in social internet of things,” in Proc. of the IEEE Tencon, Jeju, pp. 2086–2091, 2018. [Google Scholar]

 9.  F. Amin and G. S. Choi, “Hotspots analysis using cyber-physical-social system for a smart city,” IEEE Access, vol. 8, pp. 122197–122209, 2020. [Google Scholar]

10. Z. Yu, G. Kening, L. Feng and Y. Ge, “A new method for link prediction using various features in social networks,” in Proc. of the Web Information System and Application Conf., Tianjin, China, pp. 144–147, 2014. [Google Scholar]

11. L. Yao, L. Wang, L. Pan and K. Yao, “Link prediction based on common-neighbors for dynamic social network,” Procedia Computer Science, vol. 83, no. 1, pp. 82–89, 2016. [Google Scholar]

12. A.-L. S. Baraba´si, “Statistical mechanics of complex networks,” Reviews of modern physics, vol. 74, pp. 47–97, 2002. [Google Scholar]

13. F. Amin, A. Ahmad and G. Sang Choi, “Towards trust and friendliness approaches in the social internet of things,” Applied Sciences, vol. 9, no. 1, pp. 1–25, 2019. [Google Scholar]

14. D. J. Watts and S. H. Strogatz, “Collective dynamics of ‘small-world’ networks,” Nature, vol. 393, no. 6684, pp. 440–442, 1998. [Google Scholar]

15. R. Abdul, A. Paul, M. J. Gul and W.-H. Hong, “Exploiting small world problems in a SIoT environment,” Energies, vol. 11, no. 8, pp. 1–18, 2018. [Google Scholar]

16. J. Kleinberg, “The small-world phenomenon: An algorithmic perspective,” in Proc. of the Thirty-Second Annual ACM Symp. on Theory of Computing, Portland Oregon, USA, pp. 163–170, 2000. [Google Scholar]

17. F. Amin, R. Abbasi, A. Rehman and S. G. Choi, “An advanced algorithm for higher network navigation in social internet of things using small-world networks,” Sensors, vol. 19, no. 9, pp. 1–20, 2019. [Google Scholar]

18. C. Moore and M. E. J. Newman, “Epidemics and percolation in small-world networks,” Physical Review E, vol. 61, no. 5, pp. 5678–5682, 2000. [Google Scholar]

19. L. A. N. Amaral, A. Scala, M. Barthélémy and H. E. Stanley, “Classes of small-world networks,” Proceedings of The National Academy of Sciences of The United States of America, vol. 97, no. 21, pp. 11149, 2000. [Google Scholar]

20. R. Albert, H. Jeong and A.-L. Barabási, “Diameter of the world-wide web,” Nature, vol. 401, no. 6749, pp. 130–131, 1999. [Google Scholar]

21. K. Klemm and V. M. Eguíluz, “Growing scale-free networks with small-world behavior,” Physical Review E, vol. 65, no. 5, pp. 1–4, 2002. [Google Scholar]

22. A.-L. Barabási and R. Albert, “Emergence of scaling in random networks,” Science, vol. 286, no. 5439, pp. 509–512, 1999. [Google Scholar]

23. F. Amin and M. Zubair, “Energy-efficient clustering scheme for multihop wireless sensor network (ECMS),” in Proc. of the IEEE Int. Multi Topic Conf., Karachi, Pakistan, pp. 131–136, 2014. [Google Scholar]

24. F. Amin, J.-G. Choi and G. S. Choi, “Community detection based on social Influence in large scale networks,” in Proc. of the Int. Conf. on Advanced Information Networking and Applications (WAINA-2019), Caserta, Italy, pp. 122–137, 2020. [Google Scholar]

25. F. Amin, A. Ahmad and G. Choi, “To study and analyse human behaviours on social networks,” in Proc. of the 4th Annual Int. Conf. on Network and Information Systems for Computers (ICNISC), Wuhan, China, pp. 233–236, 2018. [Google Scholar]

26. M. Gjoka, M. Kurant, C. T. Butts and A. Markopoulou, “Practical recommendations on crawling online social networks,” IEEE Journal on Selected Areas in Communications, vol. 29, no. 9, pp. 1872–1892, 2011. [Google Scholar]

27. L. Katzir and S. J. Hardiman, “Estimating clustering coefficients and size of social networks via random walk,” ACM Trans. Web, vol. 9, no. 4, pp. 1–20, 2015. [Google Scholar]

28. S. Khan, L. Zhu, Z. Zhang, M. A. Rahim and K. Khan, “Attack-resilient TLS certificate transparency,” IEEE Access, vol. 8, pp. 98958–98973, 2020. [Google Scholar]

29. S. Khan, Z. Zhang, L. Zhu and M. Li, “Accountable and transparent TLS certificate management: An alternate public-key infrastructure with verifiable trusted parties,” Security and Communication Networks, vol. 2018, no. 15, pp. 1–17, 2018. [Google Scholar]

30. L. Zhang, H. Jiang, F. Wang and D. Feng, “2-Hopper: Accurately estimate individual and social attributes of social networks with fewer repeats via random walk,” IEEE Access, vol. 7, pp. 139827–139838, 2019. [Google Scholar]

31. S. Bahadori and P. Moradi, “A local random walk method for identifying communities in social networks,” in Proc. of the Artificial Intelligence and Robotics (IRANOPEN), Qazvin, Iran, pp. 177–181, 2017. [Google Scholar]

32. M. Gjoka, M. Kurant, C. T. Butts and A. Markopoulou, “Walking in facebook: A case study of unbiased sampling of OSNs,” in Proc. of the IEEE INFOCOM, San Diego, CA, USA, pp. 1–9, 2010. [Google Scholar]

33. S. J. Hardiman, P. Richmond and S. Hutzler, “Calculating statistics of complex networks through random walks with an application to the on-line social network bebo,” The European Physical Journal, vol. 71, no. 4, pp. 611, 2009. [Google Scholar]

34. B. Ribeiro and D. Towsley, “Estimating and sampling graphs with multidimensional random walks,” in Proc. of the 10th ACM SIGCOMM Conf. on Internet Measurement, New York, United States, pp. 390–403, 2010. [Google Scholar]

35. L. Katzir, E. Liberty and O. Somekh, “Estimating sizes of social networks via biased sampling,” in Proc. of the 20th Int. Conf. on World Wide Web, Bangalore, India, pp. 597–606, 2011. [Google Scholar]

36. A. L. Barabási, H. Jeong, Z. Néda and E. Ravasz, “Evolution of the social network of scientific collaborations,” Physica A: Statistical Mechanics and its Applications, vol. 311, no. 3–4, pp. 590–614, 2002. [Google Scholar]

37. M. E. Newman, “Finding community structure in networks using the eigenvectors of matrices,” Physical Review E, vol. 74, no. 3, pp. 1–22, 2006. [Google Scholar]

38. M. E. Newman, “Mixing patterns in networks,” Physical Review E, vol. 67, no. 2, pp. 1–14, 2003. [Google Scholar]

39. F. Liljeros, C. R. Edling, L. A. N. Amaral and H. E. Stanley, “The web of human sexual contacts,” Nature, vol. 411, no. 6840, pp. 907–908, 2001. [Google Scholar]

40. P. E. A. A. Rényi, “On the evolution of random graphs,” Publication of the Mathematical Institute Of The Hungarian Academy Of Sciences, vol. 3, pp. 17–61, 1960. [Google Scholar]

41. L. F. X. U. Xin-Ping and L. I. Wei, “Growing small-world networks based on a modified BA model,” Chinese Physics Letters, vol. 23, no. 3, pp. 1–11, 2006. [Google Scholar]

42. S. N. Dorogovtsev and J. F. F. Mendes, “Evolution of networks,” Advances in Physics, vol. 51, no. 4, pp. 1079–1187, 2002. [Google Scholar]

43. A. Vázquez, “Growing network with local rules: Preferential attachment, clustering hierarchy, and degree correlations,” Physical Review E, vol. 67, pp. 1–17, 2003. [Google Scholar]

44. S. P. Cornelius, W. L. Kath and A. E. Motter, “Realistic control of network dynamics,” Nature Communications, vol. 4, no. 1, pp. 1–9, 2013. [Google Scholar]

45. T. S. Evans and J. P. Saramäki, “Scale-free networks from self-organization,” Physical Review E, vol. 72, no. 2, pp. 1–6, 2005. [Google Scholar]

46. J. Jia, B. Wang and N. Z. Gong, “Random walk based fake account detection in online social networks,” in Proc. of the 47th Annual IEEE Int. Conf. on Dependable Systems and Networks (DSN), Denver, USA, pp. 273–284, 2017. [Google Scholar]

47. R. Cheng, J. Pang and Y. Zhang, “Inferring friendship from check-in data of location-based social networks,” in Proc. of the IEEE Int. Conf. on Advances in Social Networks Analysis and Mining (ASONAM), New York, United States, pp. 11–19, 2015. [Google Scholar]

48. R.-H. Li, J. Liu, J. X. Yu and H. Chen, “Co-occurrence prediction in a large location-based social network,” Frontiers of Computer Science, vol. 7, no. 2, pp. 185–194, 2013. [Google Scholar]

49. L. Katzir and S. J. Hardiman, “Estimating clustering coefficients and size of social networks via random walk,” Transactions on the Web (TWEB), vol. 9, no. 4, pp. 1–20, 2015. [Google Scholar]

50. K. Iwasaki and K. Shudo, “Estimating the clustering coefficient of a social network by a non-backtracking random walk,” in IEEE Int. Conf. on Big Data and Smart Computing (BigComp), Shanghai, China, pp. 114–118, 2018. [Google Scholar]

51. R. Cohen, S. Havlin and D. ben-Avraham, “Efficient immunization strategies for computer networks and populations,” Physical Review Letters, vol. 91, no. 24, pp. 1–5, 2003. [Google Scholar]

52. J. Leskovec, J. Kleinberg and C. Faloutsos, “Graphs over time: Densification laws, shrinking diameters and possible explanations,” in Proc. of the Eleventh ACM SIGKDD Int. Conf. on Knowledge Discovery in Data Mining, Chicago, USA, 2005. [Google Scholar]

53. Y.-Y. Ahn, S. Han, H. Kwak and S. Moon, “Analysis of topological characteristics of huge online social networking services,” in Proc. of the 16th Int. Conf. on World Wide Web, Banff Alberta, Canada, 2007. [Google Scholar]

54. C. Herrera and P. J. Zufiria, “Generating scale-free networks with adjustable clustering coefficient via random walks,” in IEEE Network Science Workshop, Washington, DC, United States, pp. 4–13, 2011. [Google Scholar]

55. L. D. F. Costa, F. A. Rodrigues, G. Travieso and P. R. Villas Boas, “Characterization of complex networks: A survey of measurements,” Disordered Systems and Neural Networks, vol. 5, pp. 1–84, 2005. [Google Scholar]

56. S. N. Dorogovtsev, J. F. Mendes and A. N. Samukhin, “Size-dependent degree distribution of a scale-free growing network,” Physical Review, vol. 63, pp. 1–10, 2001. [Google Scholar]

57. W. M. Tam, F. C. M. Lau and C. K. Tse, “Construction of scale-free networks with adjustable clustering,” in Proc. of the Int. Symp. on Nonlinear Theory and its Applications, Budapest, Hungary, pp. 3–20, 2008. [Google Scholar]

58. A. Hagberg, P. Swart and D. S. Chult, “Exploring network structure, dynamics, and function using networkX,” in Proc. of the IEEE Conf. on Big Data, San Diego, USA, pp. 1–10, 2008. [Google Scholar]

59. J. Saramäki and K. Kaski, “Scale-free networks generated by random walkers,” Physica A: Statistical Mechanics and its Applications, vol. 341, no. 24, pp. 80–86, 2004. [Google Scholar]

60. M. A. Serrano and M. Boguná, “Tuning clustering in random networks with arbitrary degree distributions,” Physical Review, vol. 72, pp. 1–20, 2005. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.