Computers, Materials & Continua DOI:10.32604/cmc.2022.028394
Article

Controlling Remote Robots Based on Zidan’s Quantum Computing Model

Biswaranjan Panda1, Nitin Kumar Tripathy1, Shibashankar Sahu1, Bikash K. Behera2 and Walaa E. Elhady3,*

1Indian Institute of Science Education and Research, Berhampur, 760005, India
2Bikash’s Quantum (OPC) Private Limited, Balindi, Mohanpur, 741246, West Bengal, India
3Faculty of Computers and Information Technology, The National Egyptian E-Learning University, Cairo, Egypt
*Corresponding Author: Walaa E. Elhady. Email: welhady@eelu.edu.eg
Received: 09 February 2022; Accepted: 22 March 2022

Abstract: In this paper, we propose a novel algorithm based on Zidan’s quantum computing model for remotely controlling the direction of a quantum-controlled mobile robot equipped with n-movements. The proposed algorithm is based on the measurement of concurrence value for the different movements of the robot. Consider a faraway robot that moves in the deep space (e.g., moves toward a galaxy), and it is required to control the direction of this robot from a ground station by some person Alice. She sends an unknown qubit α |0⟩ + β |1⟩ via the teleportation protocol to the robot. Then, the proposed algorithm decodes the received unknown qubit into an angle θ, that determines the motion direction of the robot, based on the concurrence value. The proposed algorithm has been tested for four and eight movements. Two simulators have been tested; IBM Quantum composer and IBM’s system, The two simulators achieved the same result approximately. The motion of any part of the robot is considered, if it has a pre-existing sensor system and a locomotive system,. We can use this technique in many places like in space robots (16 directions). The results show that the proposed technique can be easily used for a huge number of movements. However, increasing the number of movements of the robot will increase the number of qubits.

Keywords: Quantum neural network; competitive learning; swap test; quantum robots

1  Introduction

A robot is a computerized machine that can perform a variety of complex tasks [1]. The programming used for robots running in the different applications may use artificial intelligence [2–4]. Artificial intelligence refers to a computer system’s ability to function in a way that is similar to human intelligence [5,6]. Artificial intelligence could be thought of in the same way that one would when training a machine to act like a person. Capek coined the term “robot” in 1920 at Rossum’s Universal Robots. This was the first time a computerized machine was labeled as such. Robots have been employed in a variety of ways since then. They have appeared in a variety of shapes and sizes [7–9], and they have been recruited for medical research, the military, and space programs. As we entered the twenty-first century, technology continued to advance. A new type of robot is being explored and studied, namely, the quantum robot [7]. The quantum robot is a concept that combines quantum computing and robotics. . Quantum computing is the use of quantum states to perform calculations while quantum robots are essentially complicated quantum systems. They are mobile systems that interact with their surroundings and have quantum computers on board [10–13], and they are operational through the coordination of several programs. Quantum searching and reinforcement learning algorithms are examples of such programs.

As they apply quantum effects to their environments as they perform tasks, quantum robots get increasingly entangled [14,15]. Because of the convolution in quantum computing, quantum robots are expected to be faster, more error-free, and more capable of multitasking at a higher level than normal robots [16–18]. In other domains of research, such as military research, quantum robots may one day be able to provide more accurate medical diagnoses and finer data interpretation. They may also be able to peer into the suitable environments on other worlds as part of a space program or detect the changes in the electromagnetic field. They may also be able to assist us in detecting early warnings of calamities more effectively [19,20].

Teleportation protocol of unknown qubits was first proposed theoretically by Bennett et al. [21] and was realized experimentally later [15]. Then many researchers proposed additional protocols to teleport multiple qubits [22]. Recently, the teleportation of the quantum gate was proposed by Chou et al. [23]. However, the teleportation of a multivariate boolean function is still an open research problem. Zidan’s model [24] is one of the most significant quantum computing models that is used to solve several quantum computing problems [25,26]. In this paper, we propose a novel algorithm based on Zidan’s quantum computing model to control the direction of a quantum-controlled mobile robot remotely. Then, the proposed algorithm is verified by simulating it on IBM’s quantum computer with high fidelity.

The paper is organized as follows: Section 2 explains the problem statement. Section 3 shows the teleportation protocol and Zidan’s quantum computing model which are both used in this paper. Section 4 shows the proposed quantum-controlled mobile robot remotely algorithm. Section 5 shows the experiment’s setup and results. Section 6 discusses obtained results. Section 7 concludes the main findings of the paper.

2  Problem Statement

Suppose that we have a robot that is moving using classical algorithm and is controlled by quantum computer such that:

Given: A quantum-controlled robot that moves in space and is controlled remotely from the terrestrial station via a quantum channel.

Goal: Controlling the direction of the robot’s motion remotely by some person, called Alice, via quantum teleportation.

3  Methodology

3.1 Quantum Teleportation

Quantum states can be teleported [27] but cannot be perfectly replicated according to the no-cloning theorem [28]. In this protocol, a replica of the information contained in the state of a particle is described by the state |ϵ〉 = α |0⟩ + β |1⟩ can be transferred into the state of another particle using a classical communication channel and purely non-classical Einstein-Podolsky- Rosen (EPR) correlations. In the sense that the information of the first particle is lost, and transferred exactly to another particle regardless of the vast distance in between. Teleportation is performed via two main processes: encoding and decoding conducted by a sender and a receiver respectively. Alice and Bob are a sender and a receiver respectively, both of them have a particle of two fully entangled pairs of the bell state as:

|∅AB⟩=|0A0B⟩+|1A1B⟩2(1)

Encoding operation is conducted, as follows: first, Alice applies a CNOT-gate between |ϵ⟩ and |ϕA⟩ as a control qubit and target qubit, respectively, where CNOT |ϵ, ϕA⟩ = |ϵ, (ϵ + ϕA) mod 2⟩, second: she applies Hadamard gate on |ϵ⟩. At this time, the state of the total system is as follows:

|δ⟩=[|00⟩(α|0⟩+β|1⟩)+|01⟩(α|1⟩+β|0⟩)+|10⟩(α|0⟩−β|1⟩)+|11⟩(α|1⟩−β|0⟩)]/2.(2)

Finally, Alice measures the first and the second qubits, and then sends the resultant to Bob via two classical bits messages through a classical communication channel. In the decoding operation, if Bob receives msg = 00 from Alice, then he applies I, which is a 2 × 2 identity gate. However, he applies X gate, X = |0⟩⟨1| + |1⟩⟨0| if he receives msg = 01. On the other hand, if msg = 10, then he applies Z gate, Z = |0⟩⟨0| + |1⟩⟨1|. Finally, he applies X followed by Z if msg = 11. Fig. 1. shows that the blocking TE is equivalent to the circuit model of both encoding and decoding operations. This diagram is a circuit diagram of quantum teleportation.

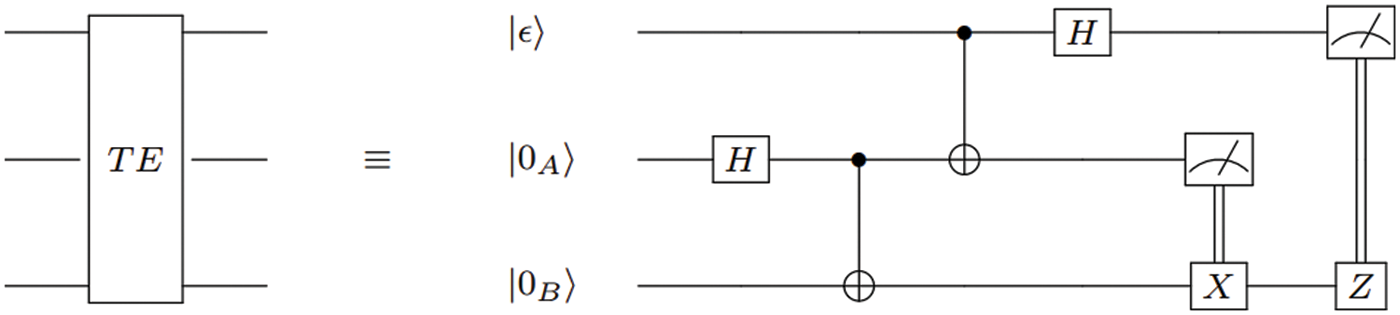
Figure 1: T.E. block diagram is equivalent to the circuit model of teleportation protocol

The right part of Fig. 1. exhibits the circuit model of the teleportation protocol proposed by Bennett et al. [21]. In this circuit, time is moving from left to right when the Hadamard gate followed by a CNOT-gate is applied on the qubit |0A⟩ and the qubit |0B⟩, then the Bell state is shared between Alice and Bob, respectively. Consequently, the application of CNOT-gate followed by the H gate on the first and second qubits shows the encoding operation performed by Alice. Finally, the effect of X and Z gates reveals the decoding operation when Bob receives a two-bit classical message msg.

3.2 Zidan’s Model of Quantum Computing

Quantum computing can be performed via one of five models [17]. One of these models is called Zidan’s model [24], this model utilizes the concurrence measure, which measures the degree of entanglement, to perform computations via quantum computers. The main operation of this model is depicted in Fig. 2. In this figure, for n Boolean variables, that is given through an oracle Uf. The model adds 2 ancillary qubits to the quantum system. As a result, the operator acts on the n + 2 qubits system, and having indices n + 1 and n + 2, are taken as g and h respectively. All the first n qubits may be in an unknown superposition state or the state of the n qubits initialized at the time of running of an algorithm. That is according to the nature of the given quantum problem. In this model, the problem is solved by applying the Uf on the first n + 1 qubits. As a result, the state of qubit |g⟩ is attained by applying the oracle Uf. Then as seen in Fig. 3 Mz operator is applied on |g⟩ and |h⟩. Here the Mz operator performs two operations. The first one is entanglement creation and the other is entanglement measurement. In the first operation, the Mz operator entangles the 2 auxiliary qubits |g⟩ and |h⟩ based on the state of the qubit |g⟩. In the second operation, the Mz operator measures the concurrence value C between |gh⟩ by device D. The preparation of the Mz operator and its functions are explained according to the two Zidan’s theorems [24].

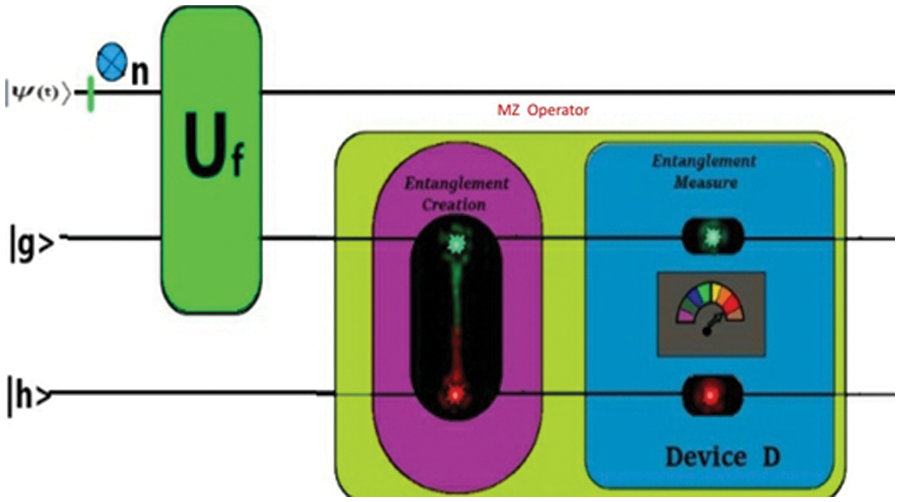
Figure 2: The basic operations of Zidan’s model

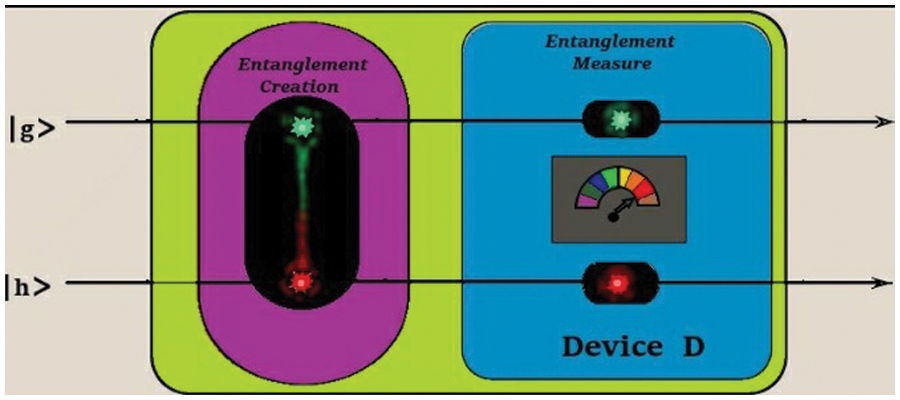
Figure 3: The two operations of Mz operator

3.2.1 Theorem 1 [24]

Let a quantum system of two qubits |ψ⟩, its state is defined as [24]:

|ψ⟩=e1|00⟩+e4|11⟩(3)

The quantum circuit is shown in Fig. 4 can be used to measure the concurrence value C between these 2 qubits as follows:

C=2P0011,or,C=2P1100,or,C=2(P0011+P1100)(4)

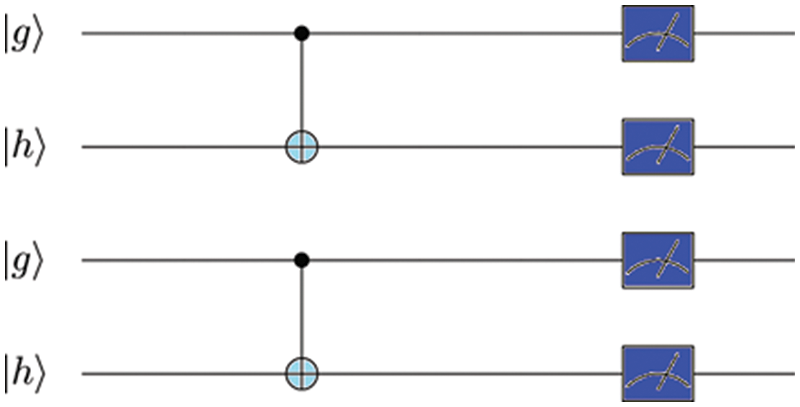
Figure 4: The diagram shows the circuit model of Mz operator

Here P0011 and P1100 are the success probabilities for obtaining the state |0011⟩ and |1100⟩.

3.2.2 Theorem 2 [24]

Suppose an unknown qubit is defined as follows: |g⟩ = e1|0⟩ + e4|1⟩, where e1, e4∈ R+. Then the quantum circuit of the operator Mz can be used to recognize the state of the unknown qubit |g⟩ with arbitrary accuracy in polynomial time as follows:

(a)  If P1111 > P0000, then the state of the qubit |g⟩ is as follows:

|g⟩=e1|0⟩+e4|1⟩=s0N|0⟩+s1N|1⟩(5)

s0=N2(1−1−C2),ands1=N2(1+1−C2)(6)

(b)  If P0000 ≥ P1111, then the state of the qubit |g⟩ is as follows:

s0=N2(1+1−C2),ands1=N2(1−1−C2)(7)

Here z0, z1 and N ∈ R+,

|e1|2+|e4|2=s0N+s1N=1(8)

, N = z0 + z1, N is a predefined number, and C is estimated by Eq. (4).

So, as Theorem 1 shows the quantum circuit of the operator Mz, while Theorem 2 explains that this operator can be used to discriminate non-orthogonal qubits in the form |g⟩ = e1|0⟩ + e4|1⟩. Zidan’s model was used in quantum computing and quantum machine learning algorithms [16,25,26].

4  The Proposed Quantum Robot Algorithm

Here, we explain the steps of the algorithm that enables Alice, in a terrestrial station, to control the direction of the robot that moves in the space via a quantum channel.

Step 1. If Alice needs to change the motion of a space robot, then she teleports two independent replicas of a qubit in the state:

|q1⟩⊗|ψ0⟩=|q2⟩=(α|0⟩+β|1⟩)⊗(α|0⟩+β|1⟩),(9)

Step 2. Robot: attaches two extra qubits to the two received qubits |d1⟩ = |d2⟩ = |0⟩.

Step 3. Robot: Applies Mz operator on the four qubits, then it estimates P0000, P0011, P1100, and P1111, which are the probabilities of the states |0000⟩, |0011⟩, |1100⟩, and |1111⟩, respectively,

C=2(P0011+P1100).(10)

(i)   If the angle θ of the robot is calculated by the following equations: if P0000 ≥ P1111 then

∝ = 1+C+1−C2,β=1+C−1−C2,(11)

(ii)   If P1111 > P0000, then

∝ = 1+C−1−c2,β=1+C+1−C2(12)

Then, the direction θ of the robot is defined by the angle θ according to Eq. (9).

θ=2tan−1(βα)(13)

5  Performance Analysis of the Proposed Algorithm

In-In this section, the proposed algorithm is analyzed in detail. In the first step, Alice teleports to the robot a qubit that in the form |Ψ⟩ = α |0⟩ + β |1⟩ to tell the robot its direction, θ. After the robot receives two copies of the teleported qubit from Alice, it attaches an extra qubit |d1⟩ = |d2⟩ = |0⟩. So, the state of the system is:

|ψ1⟩=(|q1⟩⊗|d1⟩)⊗(|q2⟩⊗|d2⟩)=(α|00⟩+β|10⟩)⊗(α|00⟩+β|10⟩),(14)

In step 3, the Robot applies the Mz operator on the four qubits, so that the state of the quantum before the measurement process of the operator Mz is as follows:

|ψ2⟩=Mz|ψ1⟩=measure(CNOT⊗CNOT)|ψ1⟩=measure(α2|0000⟩+αβ|0011⟩+βα|1100⟩+β2|1111⟩),(15)

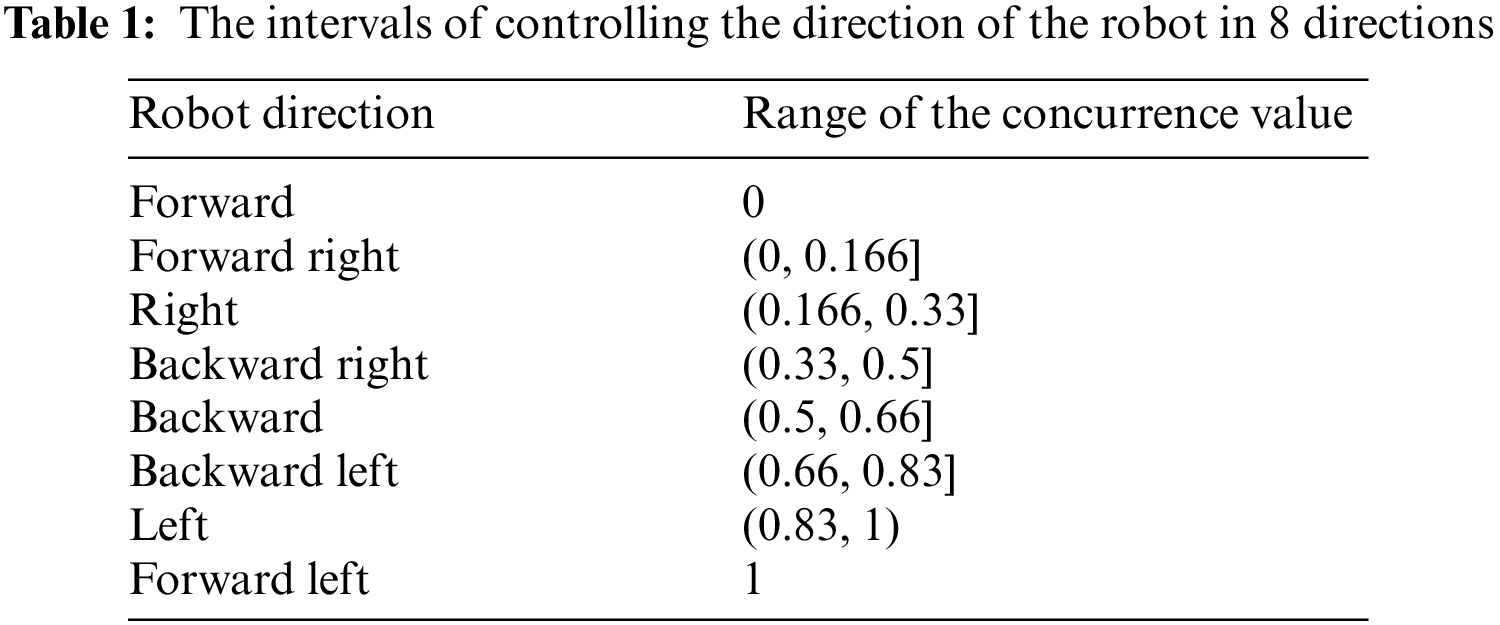
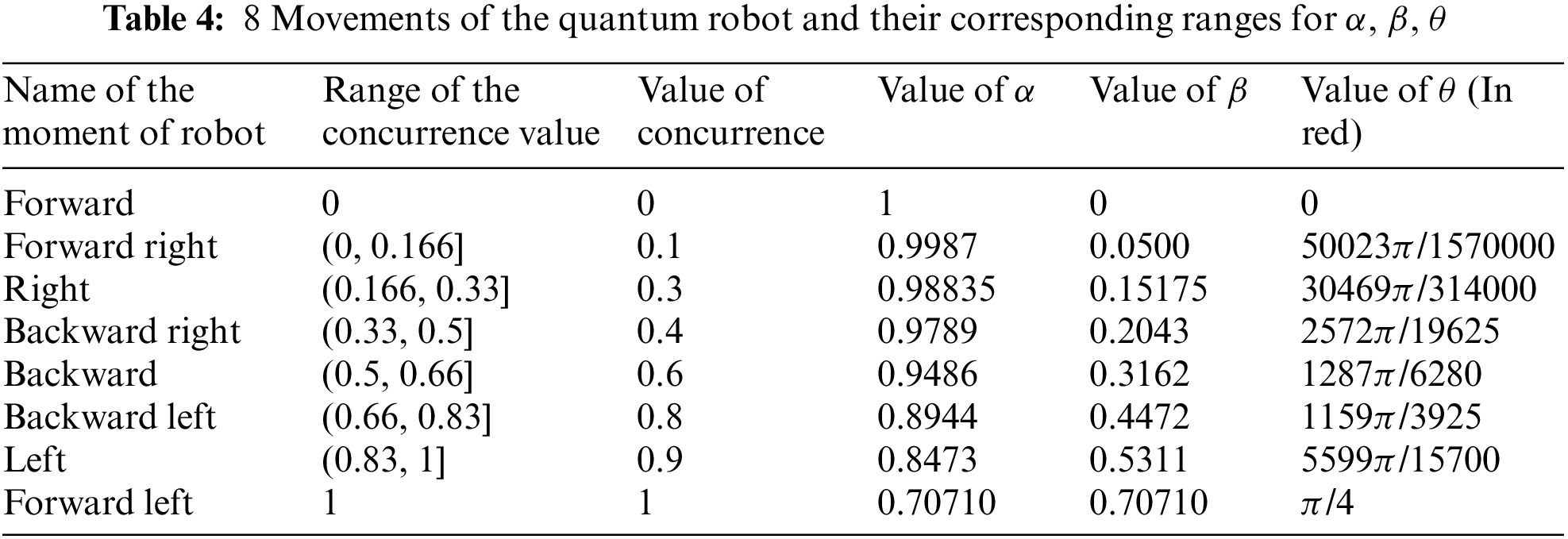
then it estimates P0011, P0011, P1100, and P1111, which are the probabilities of the states |0000⟩, |0011⟩, |1100⟩, and |1111⟩, respectively. So, the concurrence value is C = [2(P0011 + P1100)]0.5 [29]. The idea of the proposed algorithm that controls robot direction is based on Zidan’s model such that the concurrence value C is used to redirect the actuators of the robot. The concurrence value C varies in interval C∈ [0, 1]. This interval of the concurrence C is divided equally to represent 8 possible values of the robot directions namely, right, left, forward, backward right, backward left, forward right, forward left, and backward such that the angle θ as shown in Tab. 1. This angle of the robot direction is determined via the values of α and β that describes the state of the two actuators of the robot as follows:

|ψ⟩=α|00⟩+β|11⟩(16)

Owing back to Theorems 1–2, we can prove the following lemma. Lemma: For an unknown qubit |g⟩ = α|00⟩ + β|11⟩, where α, β ∈ R+, the amplitudes α, and β can be estimated based on the concurrence value C as follows:

If P0000  ≥ P1111 then

α=1+C+1−C2,β=1+C−1−C2,(17)

If P1111 > P0000, then

α=1+C−1−C2,β=1+C+1−C2(18)

Proof: For an unknown quantum state is given as

|ψ⟩=α|00⟩+β|11⟩.(19)

We know that the concurrence value is

C=2|αβ|(20)

where

|α|2+|β|2=1:ifα,β∈R+.(21)

Thus, Eq. (21) can be written as follows:

α2+β2+2αβ−2αβ=1(22)

(α+β)2−2αβ=1(23)

By using Eq. (23) we get

(α+β)−C=1(α+β)2=1+C (α+β)=±1+C(24)

Here negative sign is rejected because α, β ∈ R+. So Eq. (11) will be:

α+β=1+C(25)

Again, Eq. (21) can be written as follows:

α2+β2−2αβ+αβ=1,(α−β)+2αβ=1.(26)

By using Eq. (20) we get:

(α−β)2+C=1.(27)

Therefore,

(α−β)=±1−C(28)

Now if α ≥ β, then Eq. (28) will be:

α−β=1−C(29)

If α < β , then Eq. (28) will be:

α−β=−1−C(30)

By summing Eq. (20) and Eq. (22), we get:

∝ = 1+C+1−C2(31)

For α ≥ β, Now again summing Eq. (20) and Eq. (23), we get:

∝=1+C−1−C2(32)

Now subtracting from Eq. (20) to Eq. (22), we get:

β=1+C−1−C2(33)

Again, by subtracting from Eq. (20) to Eq. (23), we get:

β=1+C+1−C2(34)

Since |ψ⟩=α|0⟩+β|1⟩=cos(θ2)|0⟩+sin(θ2)|1⟩, where α, and β are real.

This implies that tan (θ/2) = (β/α). Thus, θ is calculated as in Eq. (13).

Here we discuss the experimental part and the results. Fig. 5 shows the general circuit diagram of the concurrence value measurement. In this circuit diagram, we put the values of θ for different movements of the robot. Here, in U gate we put the values of θ from the Tabs. 2 and 3.

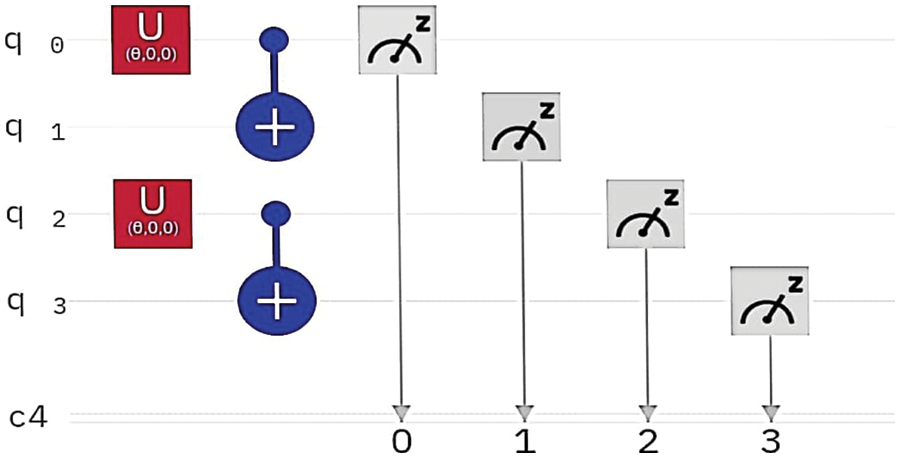
Figure 5: This is a general circuit diagram of the concurrence value measurement

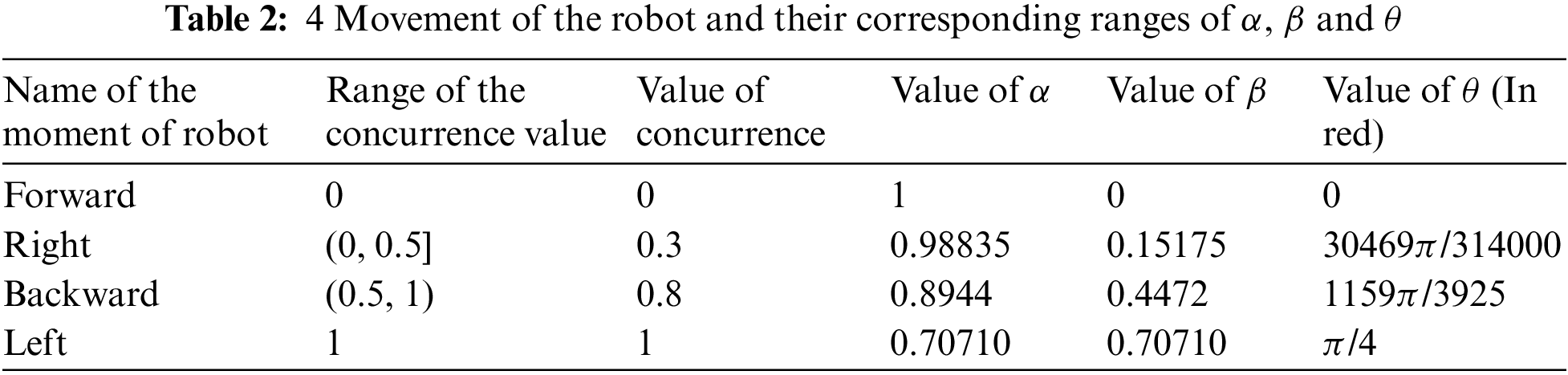
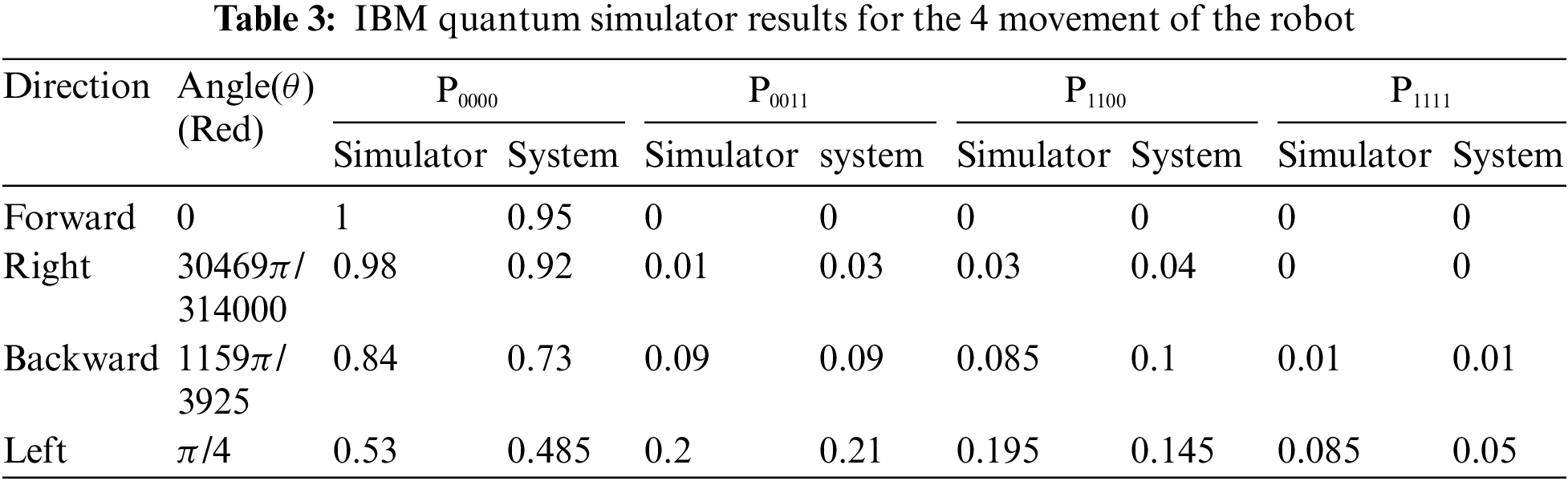
Tab. 2 points to the theoretically calculated values of α, β, and θ. These all values are used in the experimental section. The experimental results are in Tab. 3. Four movements of the robot are written in the table and their corresponding θ values also. We put the four values of θ, which are in Tab. 2, in the circuit for the experiment. And using the circuit model of Zidan’s model, four construct circuits are constructed according to the general circuit diagram in Fig. 5. We run the circuits in the IBM Quantum composer. In Tab. 3, we put the all results that we get after running the circuits in IBM Quantum composer in the simulator. Again, we run the circuit in IBM’s system. Both results are given in tab.3. These two IBM simulators and systems give approximately the same result as given in Tab. 3.

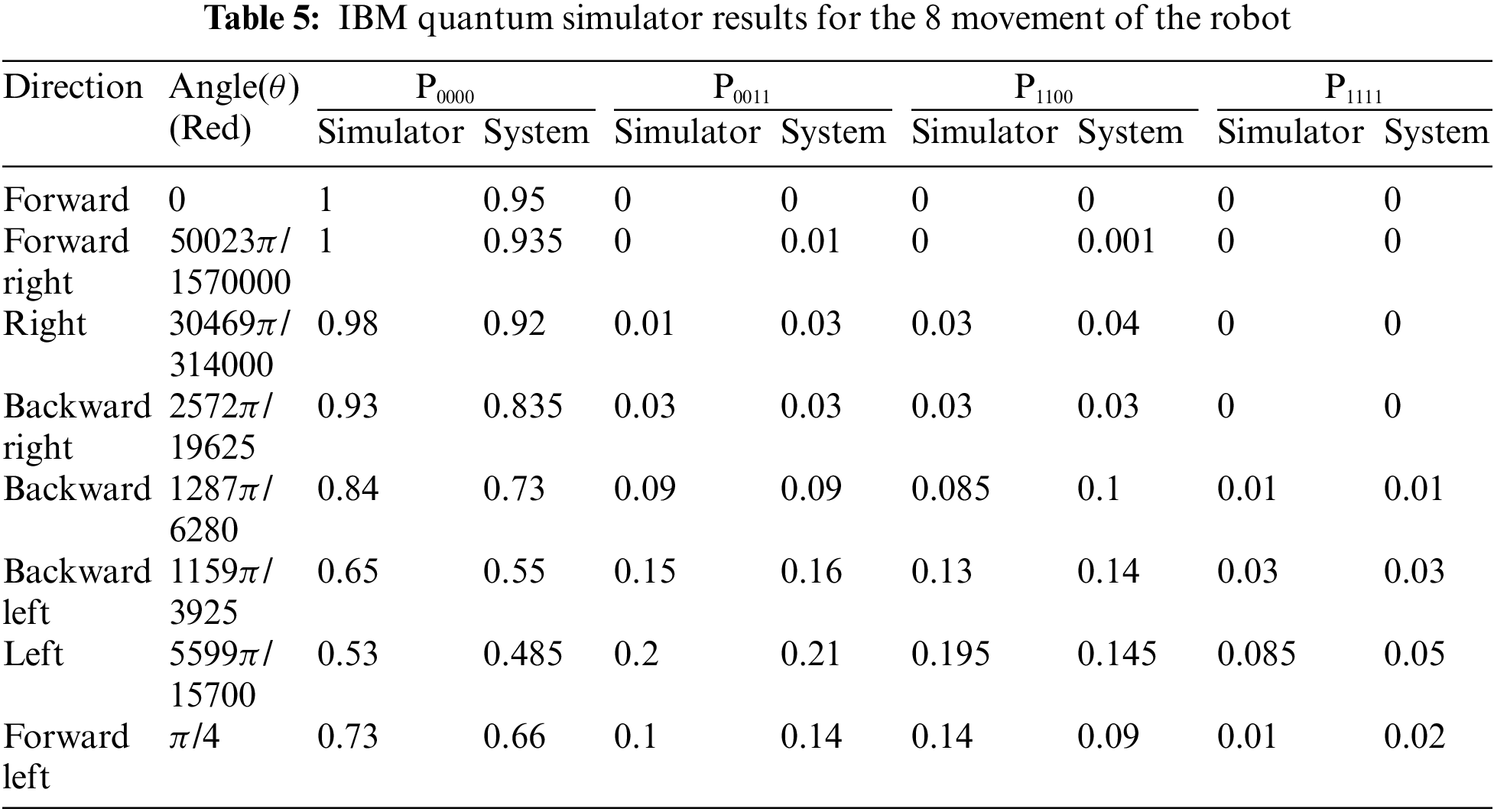
In the following section, we perform the eight movements for the robot. In Tab. 4 we give all the eight values of α, β, and θ. Theoretically, by using the lemma, we calculate the eight values of θ. These values of θ are used in circuits. Again, we develop the circuits based on the circuit of the Zidan model [24]. We run all circuits in the IBM Quantum simulator. The corresponding results are given in Tab. 5. Here also we run the circuits in both IBM simulator and the system. We give the data in Tab. 5. Here also in both cases, the results are approximately the same as given in Tab. 5.

6  Discussion

The main motivation of this paper is to control a robot using quantum computing principles. It is clear from the above experiments that, we use the idea of the measurement of concurrence value for different movements of the robot. The algorithm, which is based on the concurrence value measurement, based on Zidan’s quantum computing model is used to calculate the concurrence value (C) which varies in the interval [0, 1] i.e., 0 ≤ C ≤ 1. Now we have to define α, β, and θ for n intervals. For n number of θ. We can construct n circuits to control the robot for its n number of corresponding movements by using the n number of values of θ and Zidan’s circuit model. Here we have given two examples for the motion of the robot in four movements and eight movements. similarly, one can take the motion of any part of the robot if it has pre-existing sensor system and a locomotive system. We can use this technique in several applications such as space robots (16 directions). For maritime research, we can use quantumly controlled robots to explore deep sea life. In travel and leisure industry, robots can be used to replace human workers; these robots can be controlled by this technique. The same application can be seen in the retails sector. The novel technique of quantum-controlling robots has a myriad of applications and can easily lead to a large number of movements with ease. The only limitation of this approach is that the number of movements is directly proportional to the number of qubits. That is to say if the number of required moves increases, the number of required qubits to perform the task also increases.

7  Conclusion

This paper set out to use basic quantum effects, and show that quantum robots are more sensitive towards examining their environment, and are more committed to performing a specific task. We proposed a lemma which came from theorem 2 of a novel quantum computing model based on the degree of entanglement, through which we can easily calculate the α and β value which is used to calculate θ. The θ value was used to construct the Uf gate, and eventually we could get the concurrence value. Additionally, the Uf gate has various applications in different quantum computing models. By applying the lemma one can able to avoid the tedious calculations in the way to construct the Uf gate. Here we proposed an algorithm to control a robot having n-movements by quantum computing principle. In the foreseeable future, these robots could work as attendants janitors or logistics personnel in restaurants, bars, shopping malls, etc. One could easily use the concept of space exploration in which the robot was able to gather information of celestial data like noise and images. The quantum-controlled robot might be a submarine that can explore beyond the reach of what mankind was able to explore using classical concepts.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. A. Salichs and L. Moreno, “Navigation of mobile robots: Open questions,” Robotica, vol. 18, no. 2, pp. 227–234, 2000. [Google Scholar]

 2.  G. N. DeSouza and A. C. Kak, “Vision for mobile robot navigation: A survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 24, pp. 237–267, 2002. [Google Scholar]

 3.  F. A. Harandia, V. Derhamia and F. Jamshidib, “A new feature selection method based on task environments for controlling robots,” Applied Soft Computing, vol. 85, pp. 105812, 2019. [Google Scholar]

 4.  S. Hashima, K. Hatano, H. Kasban and E. M. Mohamed, “Wi-fi assisted contextual multi-armed bandit for neighbor discovery and selection in millimeter wave device to device communications,” Sensors, vol. 21, no. 2835, pp. 1–19, 2021. [Google Scholar]

 5.  H. Kasban and S. Nassar, “An efficient approach for forgery detection in digital images using hilbert–Huang transform,” Applied Soft Computing, vol. 97, no. A, pp. 106728, 2020. [Google Scholar]

 6.  E. M. Mohamed, S. Hashima, K. Hatano, H. Kasban and M. Rihan, “Millimeter-wave concurrent beamforming: A multi-player multi-armed bandit approach,” Computers, Materials & Continua, vol. 65, no. 3, pp. 1987–2007, 2020. [Google Scholar]

 7.  D. Dong, C. Chen, C. Zhang and Z. Chen, “Quantum robot: Structure, algorithms and applications,” Robotica, vol. 24, no. 4, pp. 513–521. 2006. [Google Scholar]

 8.  R. Farkh, H. Marouani, K. Al Jaloud, S. Alhuwaimel, M. T. Quasim et al., “Intelligent autonomous-robot control for medical applications,” Computers, Materials & Continua, vol. 68, no. 2, pp. 2189–2203, 2021. [Google Scholar]

 9.  S. V. Ulyanov, S. Watanabe, V. S. Ulyanov, K. Yamafuji, L. V. Litvintseva et al., “Soft computing for the intelligent robust control of a robotic unicycle with a new physical measure for mechanical controllability,” Soft Computing, vol. 2, pp. 73–88, 1998. [Google Scholar]

10. H. Y. Huang, M. Broughton, M. Mohseni, R. Babbush, S. Boixo et al., “Power of data in quantum machine learning,” Nature Communications, vol. 12, pp. 2631, 2021. [Google Scholar]

11. D. L. Deng, “Machine learning detection of bell nonlocality in quantum many-body systems,” Physical Review Letters, vol. 120, pp. 240402, 2018. [Google Scholar]

12. M. Zidan, A. H. Abdel-Aty, A. Khalil, M. Abdel-Aty and H. Eleuch, “A novel efficient quantum random access memory,” IEEE Access, vol. 12, pp. 151775–151780, 2021. [Google Scholar]

13. H. Kasban and S. Hashima, “Adaptive radiographic image compression technique using hierarchical vector quantization and huffman encoding,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, pp. 2855–2867, 2019. [Google Scholar]

14. Y. H. Luo, H. S. Zhong, M. Erhard, X. L. Wang, L. C. Peng et al., “Quantum teleportation in high dimensions,” Physical Review Letters, vol. 123, pp. 70505, 2019. [Google Scholar]

15. S. Podoshvedov, “Efficient quantum teleportation of unknown qubit based on DV-CV interaction mechanism,” Entropy, vol. 21, pp. 150, 2019. [Google Scholar]

16. M. Zidan, H. Eleuch and M. Abdel-Aty, “Non-classical computing problems: Toward novel type of quantum computing problems,” Results in Physics, vol. 21, pp. 103536, 2021. [Google Scholar]

17. Y. R. Li, D. H. Jiang and X. Q. Liang, “A novel quantum anonymous ranking protocol,” Quantum Inf Process, vol. 20, pp. 342, 2021. [Google Scholar]

18. W. Hu, R. G. Zhou, X. Li, P. Fan and C. Tan, “A novel dynamic quantum secret sharing in high-dimensional quantum system,” Quantum Inf Process, vol. 20, pp. 159, 2021. [Google Scholar]

19. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

20. X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

21. C. H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres et al., “Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels,” Physical Review Letters, vol. 70, pp. 1895, 1993. [Google Scholar]

22. G. Gordon and G. Rigolin, “Generalized teleportation protocol,” Physical Review A, vol. 73, pp. 042309, 2006. [Google Scholar]

23. K. S. Chou, J. Z. Blumoff, C. S. Wang, P. C. Reinhold, C. J. Axline et al., “Deterministic teleportation of a quantum gate between two logical qubits,” Nature, vol. 561, pp. 368–373, 2018. [Google Scholar]

24. M. Zidan, “A novel quantum computing model based on entanglement degree,” Modern Physics Letters, vol. 34, pp. 2050401, 2021. [Google Scholar]

25. A. H. AbdelAty, H. Kadry, M. Zidan, Y. Al-Sbou, E. A. Zanaty et al., “A quantum classification algorithm for classification incomplete patterns based on entanglement measure,” Journal of Intelligent & Fuzzy Systems, vol. 38, no. 3, pp. 2809–2816, 2020. [Google Scholar]

26. M. Zidan, A. -H. Abdel-Aty, D. M. Nguyen, A. S. A. Mohamed, Y. Al-Sbou et al., “A quantum algorithm based on entanglement measure for classifying boolean multivariate function into novel hidden classes,” Results in Physics, vol. 15, pp. 102549, 2019. [Google Scholar]

27. J. G. Ren, P. Xu and J. W. Pan, “Ground-to-satellite quantum teleportation,” Nature, vol. 549, pp. 70–73, 2017. [Google Scholar]

28. W. K. Wootters and W. H. Zurek, “A single quantum cannot be cloned,” Nature, vol. 299, pp. 802–803, 1982. [Google Scholar]

29. W. Liu, Q. Wu, J. Shen, J. Zhao, M. Zidan et al., “An optimized quantum minimum searching algorithm with sure-success probability and its experiment simulation with Cirq,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, pp. 10425–10434, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.