| Computers, Materials & Continua DOI:10.32604/cmc.2022.028046 |  |
| Article |
Trustworthy Explainable Recommendation Framework for Relevancy
Department of Computer Science, University of Engineering and Technology, Lahore, 54000, Pakistan
*Corresponding Author: Saba Sana. Email: sab_s_g@hotmail.com
Received: 01 February 2022; Accepted: 09 May 2022
Abstract: Explainable recommendation systems deal with the problem of ‘Why’. Besides providing the user with the recommendation, it is also explained why such an object is being recommended. It helps to improve trustworthiness, effectiveness, efficiency, persuasiveness, and user satisfaction towards the system. To recommend the relevant information with an explanation to the user is required. Existing systems provide the top-k recommendation options to the user based on ratings and reviews about the required object but unable to explain the matched-attribute-based recommendation to the user. A framework is proposed to fetch the most specific information that matches the user requirements based on Formal Concept Analysis (FCA). The ranking quality of the recommendation list for the proposed system is evaluated quantitatively with Normalized Discounted Cumulative Gain (NDCG)@k, which is better than the existing systems. Explanation is provided qualitatively by considering trustworthiness criterion i.e., among the seven explainability evaluation criteria, and its metric satisfies the results of proposed method. This framework can be enhanced to accommodate for more effectiveness and trustworthiness.
Keywords: Explainable recommendation; data analysis; formal concept analysis (FCA) approach
Explainable recommendation helps with the development of methods to pitch in searching data and generating a quality recommendation. Besides, it tops it up with an explanation of recommended items which enhances the transparency, trustworthiness, and effectiveness of the system. In explainable recommendation, different methods such as neural networks, domain knowledge graph [1], improved knowledge graph attention network [2], knowledge graphs [3], matrix factorization [4], Multi-domain Matrix Factorization (MF) recommendation systems, and Restricted Boltzmann Machines (RBM) [5], and collaborative filtering [6] have been used in recommending the relevant results based on the user query with an explanation. One of those methods is Formal Concept Analysis (FCA), a mathematical approach for analyzing the given data and creating hierarchies i.e., concept lattice, based on sub-concept super-concept manner [7]. FCA provides an efficient way of data analysis and helps in creating a meaningful relationship among objects and attributes present in the data for information retrieval [8].
To retrieve relevant, precise and explainable summary of information from knowledge sources for trustworthy recommendation to user is required. The work addresses the problem of surplus information by targeting the summarized version of source data and delivers end user with the most relevant information he requires [4]. State-of-the-art explainable recommendation methods [3,6] use diverse approaches towards finding the relevant information to be recommended. However, there is a need to apply different data analysis methods to explain the recommended data to users by improving the accuracy and efficiency of the recommendation system. Rigorous evaluation of different existing explainable recommendation systems has shown that for relevant information extraction, FCA was the choice in recent past to traverse the concept lattice generated for user profile [9]. It is also the method to explain the amazon items based on their ratings [9]. However, the need is to have the user’s required attribute-based explanation for the recommended object to enhance the accuracy and effectiveness of the explainable recommendation system [9].
Targeting at improving the accuracy, usefulness, and quality of explainable recommendation, an explainable recommendation framework is proposed by using the mathematical approach of data analysis method i.e., formal concept analysis (FCA). In research studies, it is found that FCA is helpful in providing information structure of the recommendation system and this information further helps in explaining it to the system’s end user.
The real dataset is used for the implementation of the proposed way of formal concept analysis method. Both text and ontological resources are used to determine the most relevant concepts of the concerned domain. Natural language helps to understand the query and Information Retrieval (IR) coupled with Machine Learning based approaches to retrieve documents from multiple sources and summarized them according to the most relevant concepts extracted through FCA.
In the present research work, the FCA approach is being used by exploring more about its other sub-methods i.e., infimum and supremum of the formal concepts generated. The idea is to utilize this method for specific concept retrieval against the user query. As infimum of the formal concepts is the most specific concept among them, and supremum is the most generalized concept [7]. In recommending the specific formal concept to the user in response to a query, the attributes-based explanation is provided. Attributes based explanation is about explaining the matched and required attributes combination.
The explanation for recommendation is evaluated by qualitative and quantitative methods. As the explainable recommendation is good in improving the trustworthiness, scrutability, persuasiveness, transparency, effectiveness, and satisfaction of recommendation systems [10], the research work is evaluated through a qualitative approach by considering one of these factors, i.e., trustworthiness. Quantitative evaluation is done by measuring the ranking quality of the recommendation list through Normalized Discounted Cumulative Gain (NDCG) @k.
Application areas of this research include Explainable Recommendation and Search (EARS), data mining, knowledge management, machine learning and information retrieval. Users of recommendation systems actually interact with the backend knowledge bases of recommenders, to get the required relevant knowledge from the sources that are attached with the system. These knowledge bases comprising ontological data or random text documents are the essential resources for researchers to carry on their research experiments. The methods and techniques implemented in this research will assist the recommendation system users to get the most relevant knowledge of their required domain by using the textual and knowledge base sources in the form of precise and trustworthy summarized explanations.
2.1 Explainable Recommendation
Explainable recommendation and search promote the development of methods for searching data and generating a quality based recommendation. In addition to that, it explains the recommended item for enhancing the transparency, trustworthiness, and effectiveness of the system [3]. In the literature, some explainable recommender models have been proposed for improving the recommendation accuracy and performance, prediction accuracy and scalability, and to overcome the new user cold-start problem [5].
In [3], Rose had explained the Knowledge graphs and Neural Networks for explainable recommendation systems. In this research, knowledge graphs are used to enhance the recommendation accuracy by presenting the ranked list of entities as an explanation.
In [4], Zhang had worked on Matrix Factorization for discussing Data Explainability, Model Explainability, and Economic Explainability. The explanation is given here in the form of an abstract summary. RS performance is evaluated by Bordered Block Diagonal Form (BBDF) matrices, prediction accuracy, and scalability. In [5] has touched the area of Explainable Recommendations and search (EARS) by using Multi-domain Matrix Factorization (MF) recommendation systems and Restricted Boltzmann Machines (RBM)). The researcher has overcome the new user cold-start problem using different measures i.e., Bilgic & Mooney’s measure of the quality of an explanation through explainability matrix, Mean Average Precision (MAP), Area Under Curve (AUC) for RS evaluation [5] . In literature [11–13], has given a detailed overview in a survey about explainable recommendation system, in which these knowledge-based explainable recommendation systems are referenced. In recent research work [9], FCA has been used by traversing the concept lattice generated for user-profiles and giving explanations about the amazon items based on their ratings. They have defined different types of explanations based on item-style, property-style, and dependency style.
2.2 FCA and Infimum-Supremum Concepts
FCA is a mathematical framework of data analysis that determines conceptual organizations among data [14]. In analyzing the data, FCA explores the meaningful information consisting of objects and attributes. FCA receives a single input of data i.e., a combination of objects and attributes. After processing, it outlays two outputs i.e., Concept Lattice and attributes implications. Some of the important definitions used in the proposed framework are described below.
Formal Context, Concepts, and Lattice overview in FCA
Definition 1: A Formal Context (P, M, I) consists of two sets P and M, and a binary relation I
Definition 2: A set (A, B) is a Formal Concept of (P, M, I) iff
where
A′ = set of all attributes accessed by all the objects from A
B′ = set of all objects accessing all the attributes from B
Set A is called the extent of the formal concept (A, B), and set B is called an intent [7].
Formal Concepts as Maximal Rectangles
(A, B) is a formal concept of (P, M, I) iff (A, B) is a maximal rectangle in (P, M, I). Let suppose
So, in any context, the maximal rectangles covering all the objects sharing the same attributes are the formal concepts of the context [13,14].
Definition 3: Let suppose
The set of all formal concepts of (P, M, I), ordered by this relation, is denoted by β (P, M, I) and is called the Concept Lattice of the formal context (P, M, I) [7].
Infimum and Supremum of Formal Concepts
Definition 4: For any two formal concepts
• Infimum (greatest common sub-concept, Inf/meet/∧) of
• Supremum (least common super-concept, sup/join/ ⋁) of
3 Framework for Explainable Recommendation System (Infimum-based Formal Concept Analysis Explainable Recommendation (IFCAER))
Given the methods used in state-of-the-art explainable recommendation models, the proposed framework for explainable recommendation is particularly focused on the Infimum-based FCA method and the proposed explanation approach is matched-attributes based. To improve the accuracy, and usefulness of explainable RS and to make it specifically relevant for the end-user, this research work has proposed an Explainable Recommendation Framework by using the mathematical approach of data analysis i.e., Infimum-based Formal Concept Analysis Explainable Recommendation (IFCAER). Here is the algorithm of an Explainable Recommendation Framework followed by the flowchart shown in Fig. 1 i.e., describing the whole processing of the Explainable Recommendation System.
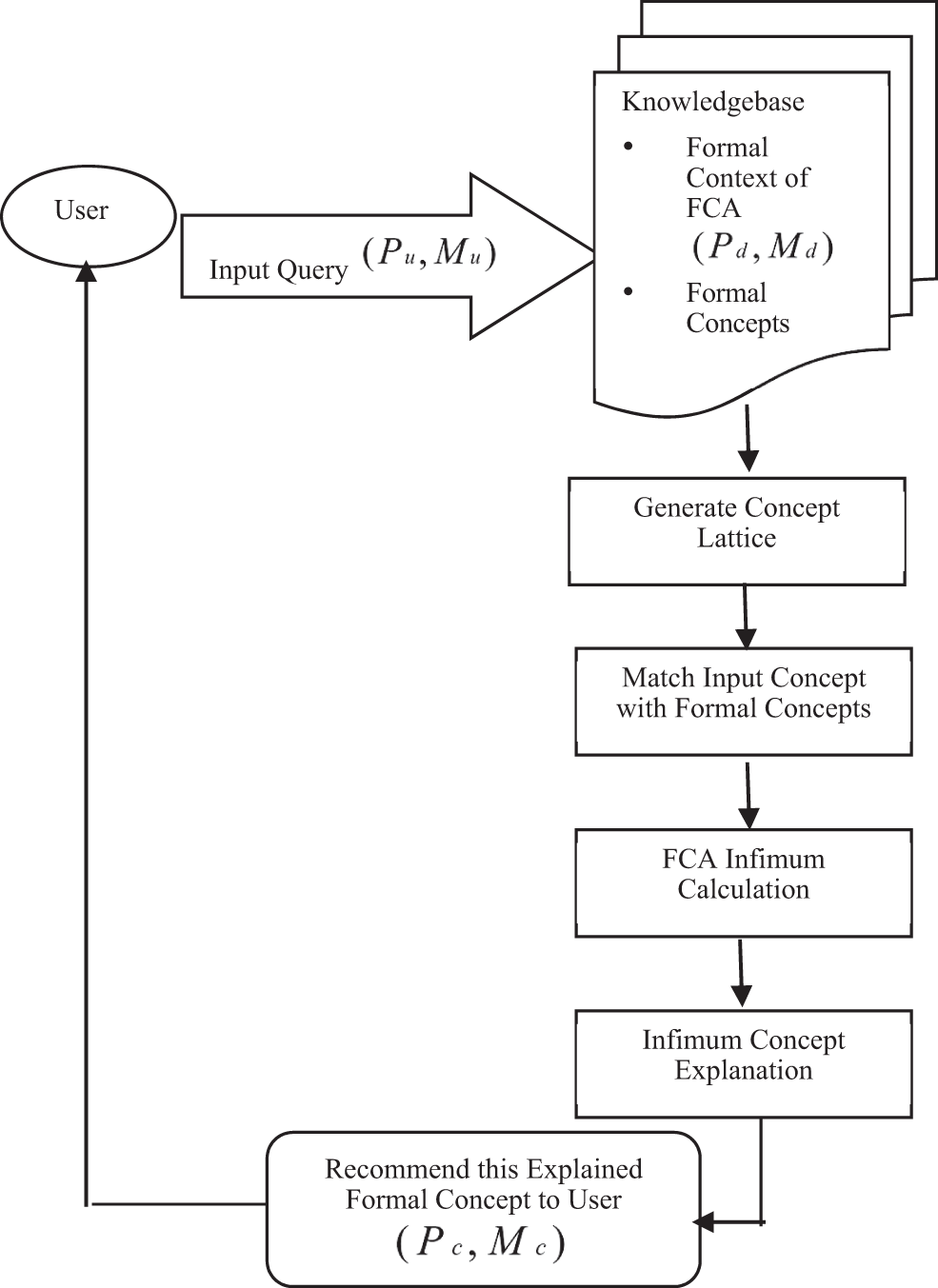
Figure 1: Flowchart of the explainable recommendation framework based on infimum-FCA
Input:
Dataset:
➔ Construct Concept Lattice of formal concepts
➔ Matching Input concept with FCA Context
While (
[Match Concepts (Input
[Relevance Array [RA] = Matched formal concepts/maximal rectangles
[
[return RA;
]
➔ Implement Infimum Method
(check Formal Concepts Array FC[RA] in Lattice == Infimum || Supremum)
Do {(Compare (FC[i] && FC[i + 1])
(traverser lattice)
If FC[i] == Infimum;
{ PUSH (FC[i]) on STACK
Else
PUSH (FC[i + 1]) on STACK }
}
WHILE (Lattice last level);
Return TOP of STACK for recommendation; // FC
➔ Attributes based Explainable Recommendation to User
Output:
For relevant concept extraction through the proposed algorithm i.e., based on Infimum-FCA, the symbolic representations of the users, objects, attributes, and their relationship with each other, are given below in Tab. 1:

3.3 Working of IFCAER Framework
The proposed framework works as in the following steps:
• Input Query
• Knowledgebase Manipulation
• Generate Concept Lattice
• Matching Input Data with Formal Concepts
• FCA Infimum Calculation
• Explainable Recommendation to User
The explainable recommendation system interacts with the user to get the information about the required product/object along with its attributes to recommend back relevant products. The Input query is taken to find out the required object and its attributes. User’s requirements or preferences are identified (through interactive UI) in the form of required object and its attributes or it could be the combination of objects and their attributes i.e., (required object/data, required attributes of an object)
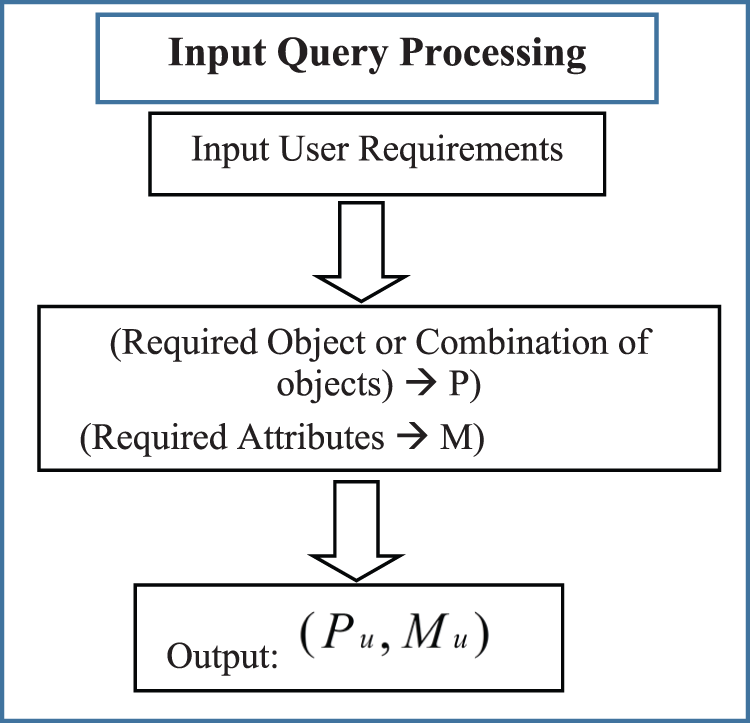
Figure 2: Flowchart of the processing of input query
3.3.2 Knowledgebase Manipulation
According to Definition 1 mentioned above, Formal Context (P, M, I) consists of two sets P and M, and a binary relation I ⊆ P × M. The elements of P are called the objects, and M corresponds to the attributes of (P, M, I). If p ∈ P and m ∈ M are in relation I, write (p, m) ∈ I or p I M and read this as “object p has attribute M”. At the beginning of the algorithm, FCA context is the dataset having objects and attributes. A set
where,
First, FCA context creator software i.e., FcaBedrock [4], is applied on the real dataset of objects and attributes i.e., .csv file, to create the context file. In context file creation through FcaBedrock software, .csv data file is converted into the formal context form i.e., .cxt file. Then this context file is edited in the FCART tool i.e., context editor [4] for specific information handling. The flowchart of this process is explained in Fig. 3.
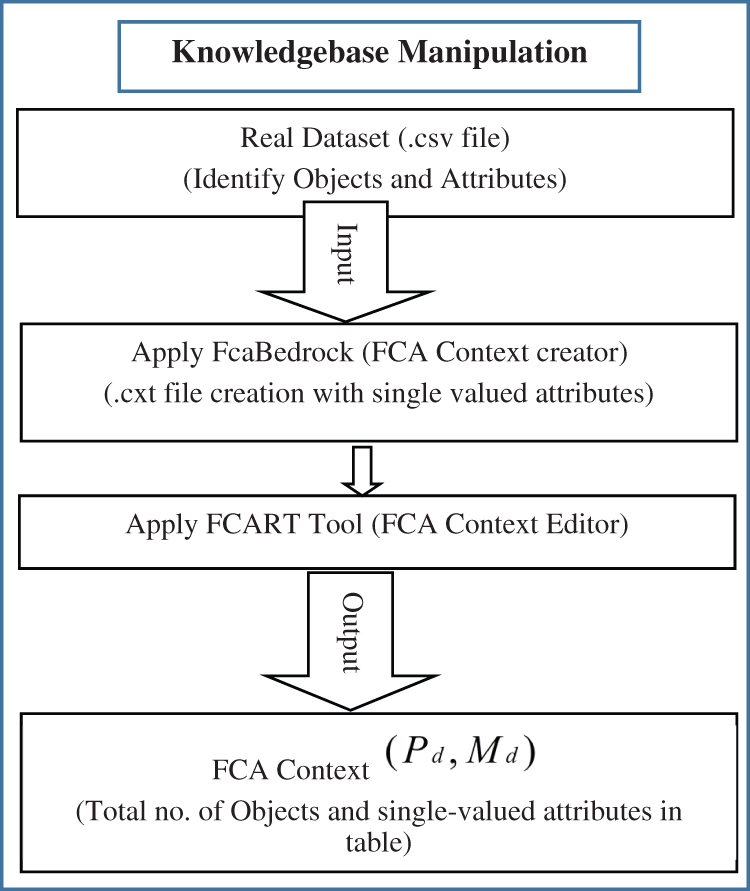
Figure 3: Flowchart of the knowledgebase manipulation
3.3.3 Generate Concept Lattice
Maximal rectangles/Formal concepts are retrieved from the FCA formal context and concept lattice is generated through FCA context editor and lattice generation tool i.e., FCART. Now let say,
where in
The set of all formal concepts of (P, M, I) are ordered by this relation, to make the concept lattice i.e., β (P, M, I). Concept Lattice of formal concepts is generated here. The flowchart of this process is shown in Fig. 4.
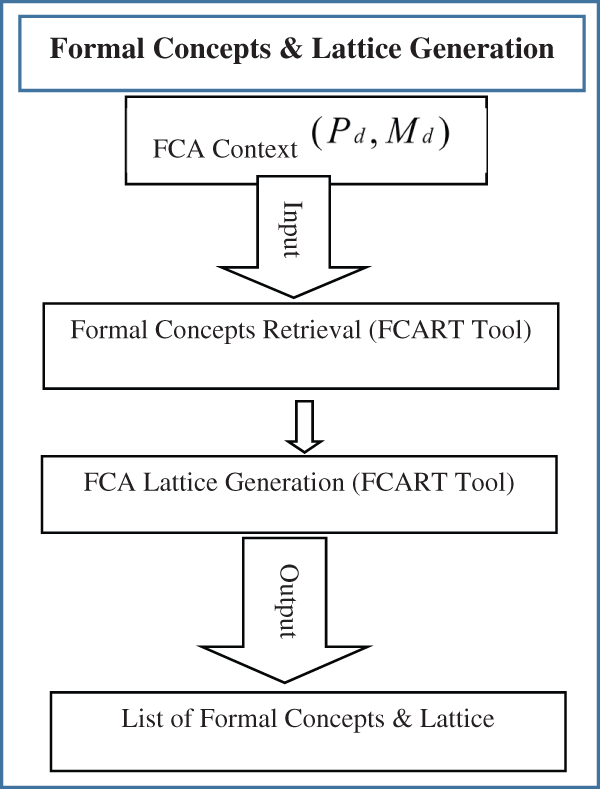
Figure 4: Flowchart of generating formal concepts & concept lattice
3.3.4 Matching Input Data with Formal Concepts
In this step, the concept of input data is matched with the knowledge base i.e., the formal context of the available dataset and its extracted formal concepts. It means input
In any context, the maximal rectangles covering all the objects sharing the same attributes are the formal concepts of the context. The Relevance Array (RA) is constructed side by side to store the matched pair of formal concepts/maximal rectangles from the context. This array provides the top-k recommendation options to the user as per his requirements mentioned in the query. The flowchart of this process is described in Fig. 5.
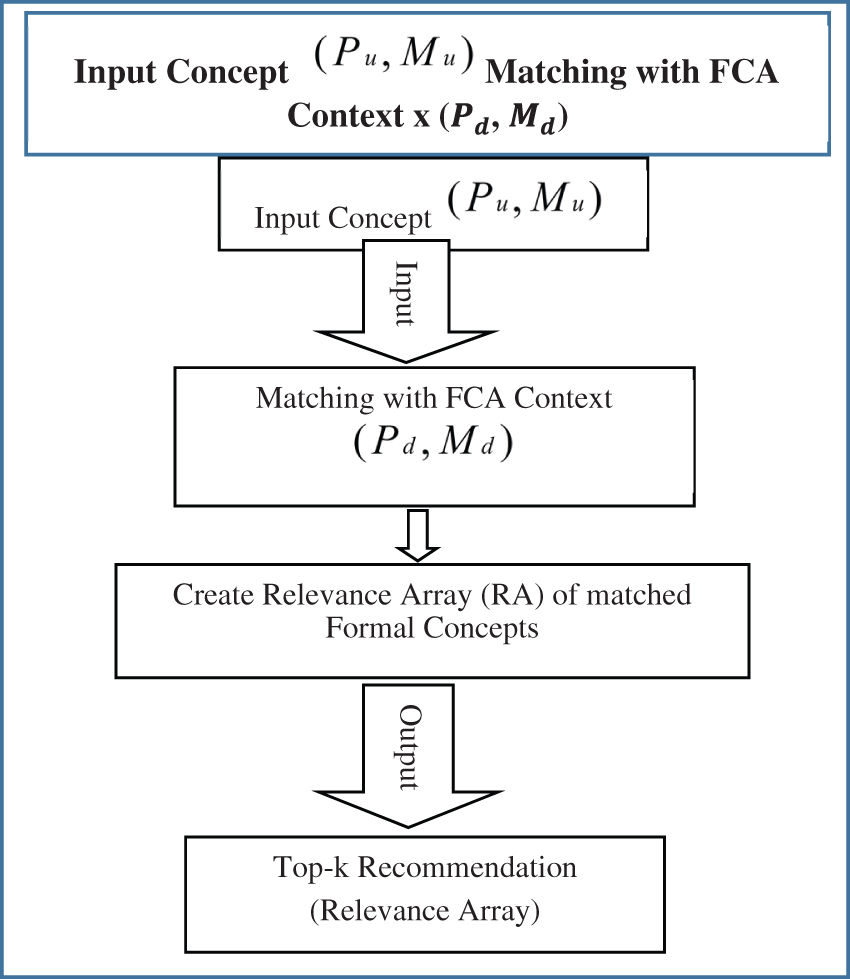
Figure 5: Flowchart of matching input data with formal concepts
To further move on in specifying the matched results with user query, matched formal concepts are extracted and compared with each other for finding out the infimum of the formal concept among all. In formal concepts, the infimum is considered as the Greatest Common Sub-concept (Greatest Lower Bound) and it is represented through conjunction or intersection or meet of the concepts. It is determined by traversing through the concept-lattice and comparing formal concepts with each other. The flowchart of this process is given in Fig. 6.

Figure 6: Flowchart of calculating FCA infimum
By considering definition 4, for any two formal concepts
The symbol ‘∧’ denotes the infimum, and compares the two formal concepts where they meet together. This process is applied on all pairs of matched formal concepts in lattice to find out the most specific and relevant concept required by the user i.e., the Infimum of the formal concepts. So, if formal concepts (
3.3.6 Explainable Recommendation to User
Explanations are given by considering the general to specific case relationship among all matched concepts through traversing concept lattice. Traversing the concept lattice in descending order, it is found that if more specific the formal concept is, the more it is appropriate for recommendation to the user. As maximum matched/common attributes are present in the most specific formal concept i.e., Infimum. The flowchart of this process is shown in Fig. 7.
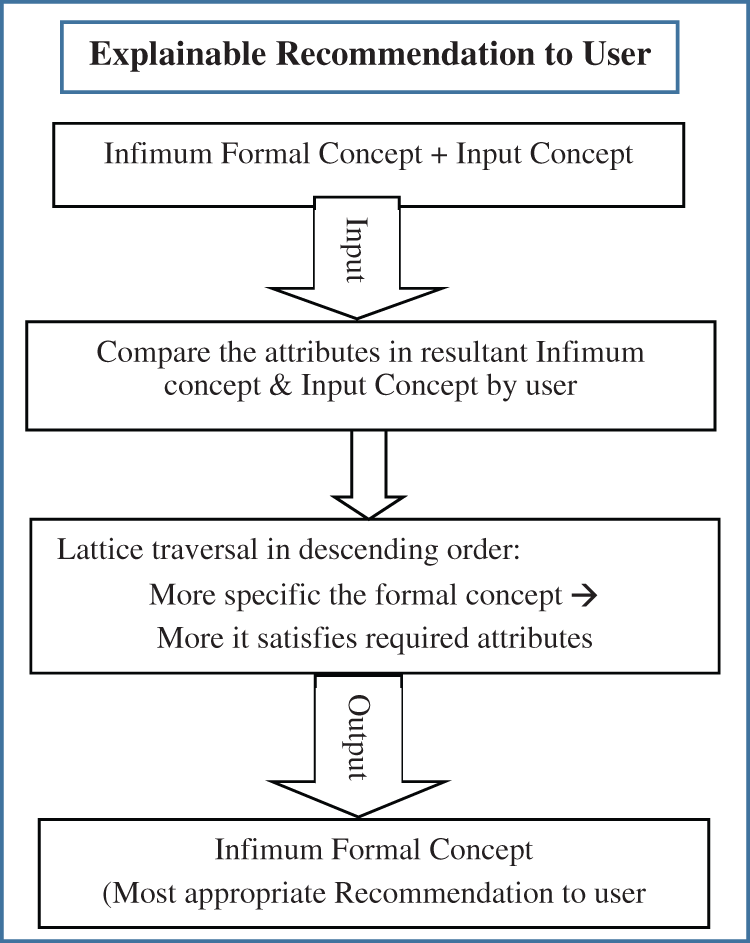
Figure 7: Flowchart of explainable recommendation to user
3.4 Trustworthiness-based Recommendation
As explainable recommendation is good in improving the trustworthiness, persuasiveness, transparency, effectiveness, and satisfaction of recommendation systems. In explaining recommendation, the trust parameter of user is targeted [15]. By gaining the trust of user means that you are able to enhance the confidence level of user towards system. That’s why trust is assumed to be one of the criteria of good explainable recommendation. This research work is based on attribute-style explanation, so the trustworthiness is evaluated w.r.t attributes. As many attributes of the required object are matched from the dataset, the more this object is trustworthy to be recommended towards user. Trust factor can be calculated for any single user by the newly proposed metric explained below.
Trustworthiness Metric
It is the ratio between the total matched attributes in the formal concept and the total no. of attributes required by the user in input concept as shown in Eq. (8):
Whereas, (
T = Trustworthiness
For the recommendation of relevant information with explanation, the proposed framework IFCAER is implemented step-by-step on a real dataset in the first section. Then, to evaluate the performance and effectiveness of an IFCAER, a ranking measure is applied and results are presented in the second section.
4.1 IFCAER Model Implementation on Real Dataset
4.1.1 Knowledgebase Manipulation
Dataset
Yelp dataset is used for exploratory analysis in data manipulation. A part of it is used for evaluation to show the results properly. Following is the description of the dataset, where names of Automobiles are taken as objects and their properties as attributes. Some FCA tools are used for context creation and lattice generation [16].
4.1.2 Create Context File and Generate Concept Lattice
First FCA context creator software i.e., FcaBedrock [8], is applied to the dataset to create the context file. Fig. 8 shows the context file creation through FcaBedrock software, where the .csv data file is converted into the formal context form. Formal Concepts Retrieval from Context file through FCART Tool is done through FCART context editor i.e., shown in Fig. 9. Tab. 2 shows the symbolic representations of attributes and objects, taken from the context file.

Figure 8: Yelp dataset .csv data file conversion through FcaBedrock

Figure 9: FCART context editor
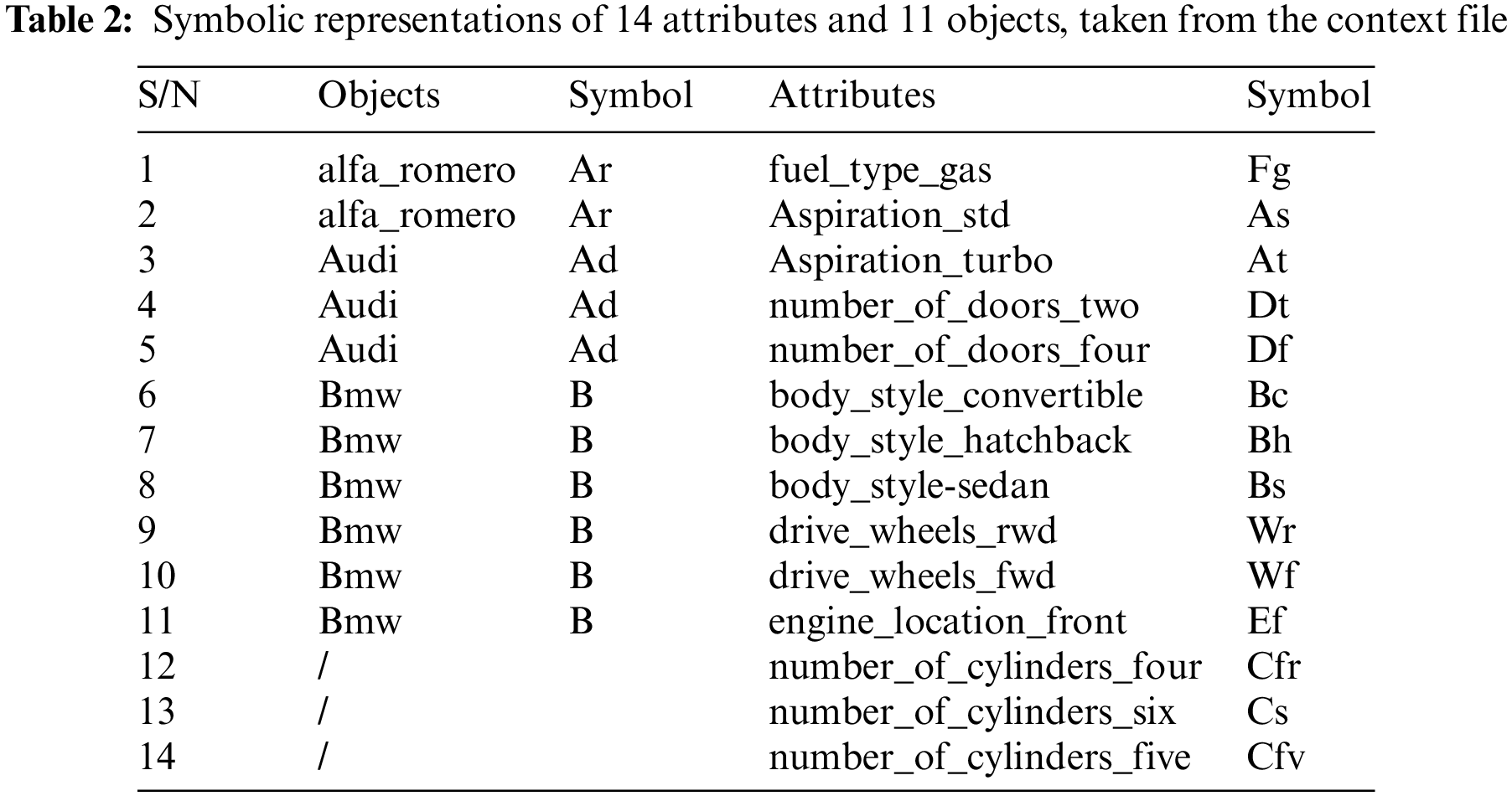
4.1.3 FCA Lattice Generation (FCART Tool) & List of Formal Concepts
Maximal rectangles/Formal concepts are retrieved from the FCA formal context and concept lattice is generated through FCA lattice generation tools i.e., FCART in Fig. 10. Total no. of formal concepts/maximal rectangles generated through FCART tool is shown in Fig. 11.
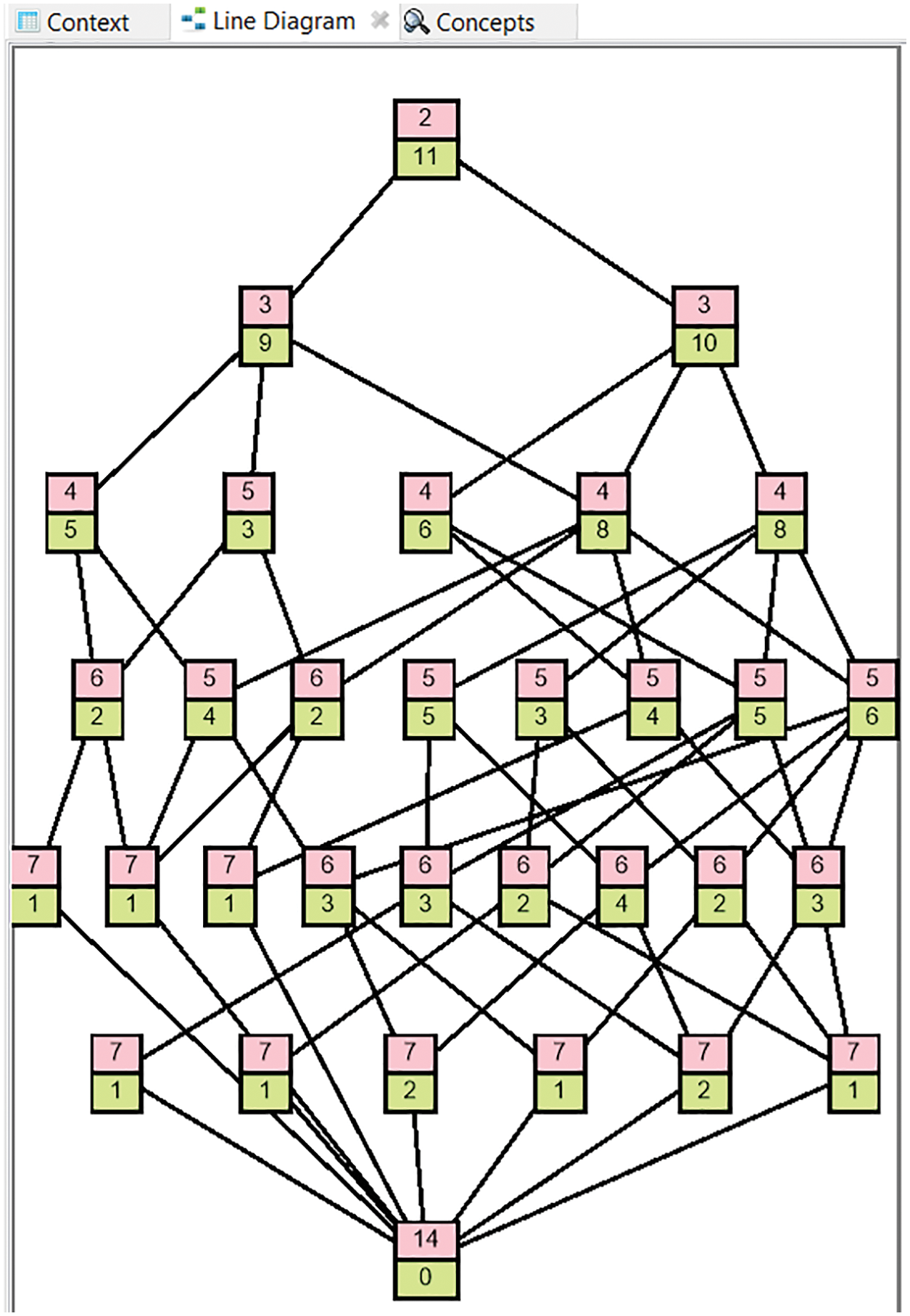
Figure 10: Concept lattice of automobile context through FCART tool
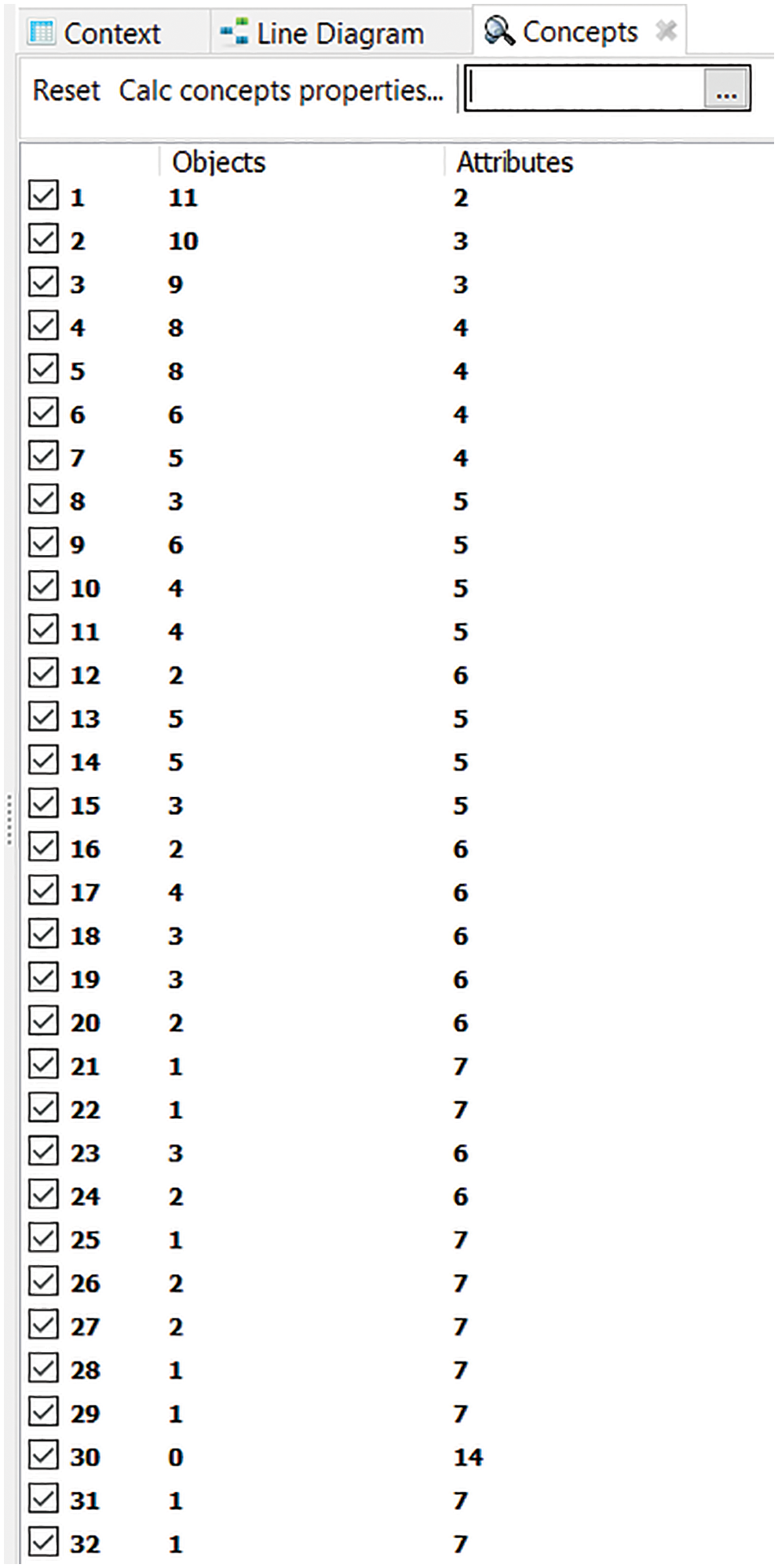
Figure 11: Maximal rectangles/formal concepts of automobile context generated through FCART tool
4.1.4 Formal Concepts Extracted from the Context
Following is the Formal concept narrations in the form of sets by using the symbolic representationsof attributes and objects. Concepts are depicted through C1, C2, C3…, C32.

4.1.5 Matching Input Data with Formal Concepts
Input Query
Test Input concept in Tab. 3, is compared with the retrieved formal concepts. Maximum matched formal concepts or maximal rectangles are identified in Tab. 4.


Now, these Formal Concepts are explained w.r.t the infimum of the formal concepts.
As for any two formal concepts

All other matched formal concepts comparisons generate C32 as an infimum that has a null object as an extent, so can’t be considered. So, here it is declared that the Infimum of all possibly matched concepts is C31, as shown in Fig. 12.
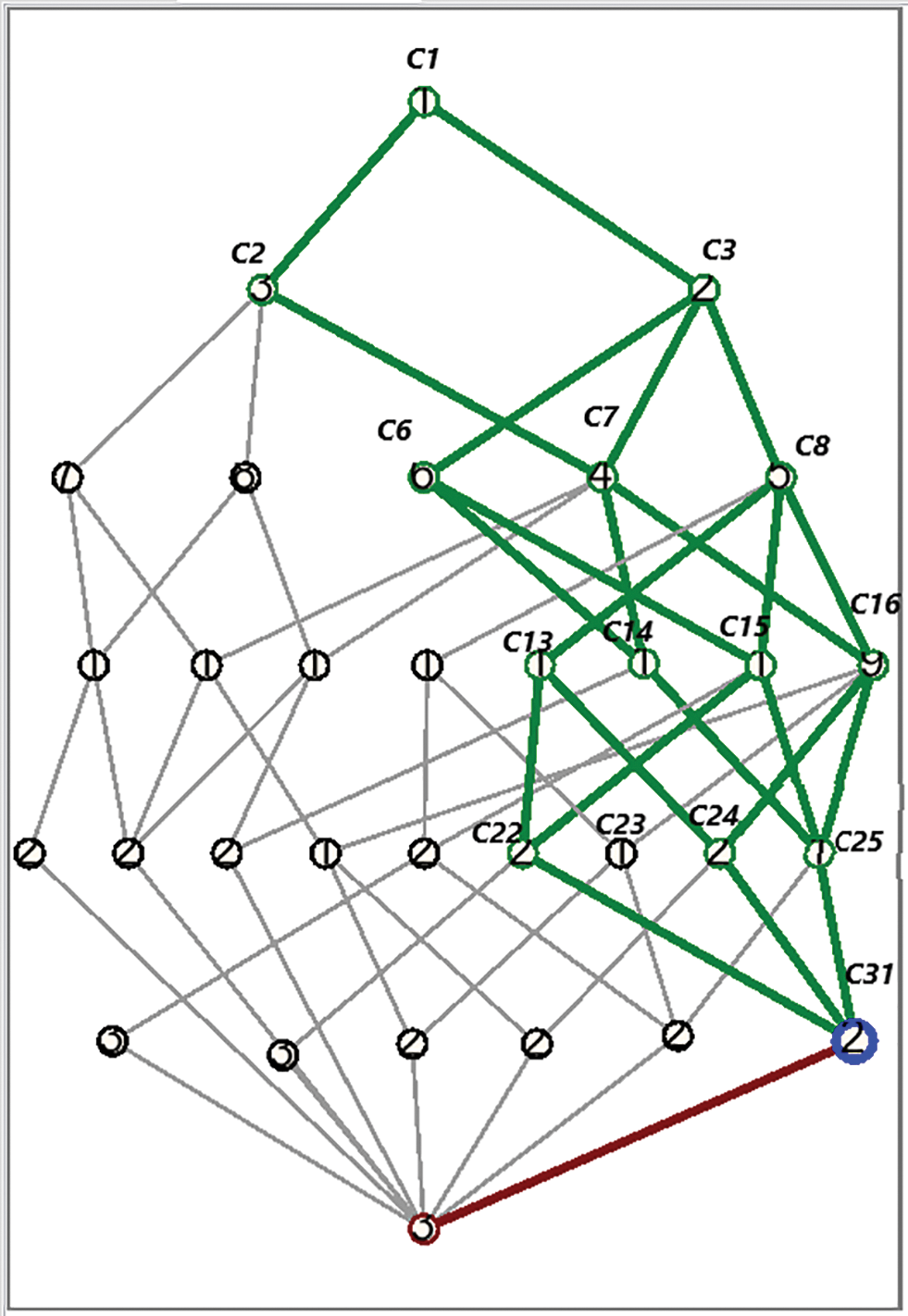
Figure 12: Final highlighted node C31 indicating INFIMUM of the formal concepts after step by step comparison of matched formal concepts
4.1.8 Explainable Recommendation to User
Finally, the infimum of formal concepts that is most appropriate for a recommendation, is retrieved. At this stage, it is explained to the user why a particular combination of objects and attributes i.e., infimum formal concept, is being recommended.
■ Explanations are given by considering the general to specific case relationship among all matched concepts through traversing concept lattice.
■ Traversing the concept lattice in descending order, it is found that if more specific the formal concept is, the more it is appropriate for recommendation to the user.
■ As maximum matched/common attributes are present in the most specific formal concept i.e., Infimum.
4.2 Qualitative Analysis and Explanation
After applying the trustworthiness metric i.e., Eq. (8), on matched formal concepts, trustworthiness score for each formal concept is calculated, as results are shown in Tab. 6.

Trustworthiness metric ranges from 0–1, if it is closer to 1 the more trustworthy it is. So concepts C22 and C31 are more trustworthy among all matched concepts because they are having highest trustworthiness score i.e., 0.71, which is closer to 1.
C22 and C31: 0.71 Trustworthiness score
From the trustworthy point of view, these two concepts can be recommended by giving explanation about their trustworthiness score. Both are equally able to satisfy the user requirements.
Here two results are generated i.e., final infimum formal concept and final trustworthy formal concept. Compare both the results and if they are same then it is the required combination of object and attributes to be recommended to user. At this stage, it is explained to user that why this object is being recommended. Trustworthiness emphasizes the user satisfaction, and infimum concept is explaining the most specific and relevant concept to be recommended.
4.3 Quantitative Evaluation and Comparative Analysis
In this part, IFCAER is quantitatively evaluated for an explainable recommendation system, on a real-world dataset. Benchmark dataset i.e., yelp dataset and its associated baselines are described first. After that, there is a comparative analysis of the proposed method with state-of-the-art methods, based on the performance and effectiveness of the system.
Baselines
Results are compared against previous state-of-the-art methods
NMF: Nonnegative Matrix Factorization [17], which is a widely applied latent factor model for the recommendation.
BPRMF: Bayesian Personalized Ranking on Matrix Factorization [18], which introduces BPR pairwise ranking constraint into factorization model learning
EFM: Explicit Factor Models [19]. A joint matrix factorization model for an explainable recommendation, which considers user-feature attention and item-feature quality
MTER: Multi-Task Explainable Recommendation [20].
Explainable Recommendation Performance Evaluation
All state-of-the-art models are compared using top-K recommendation measure, i.e., Normalized Discounted Cumulative Gain (NDCG). This measure is computed for top-k results of recommendation based on relevance ranking. Here, quantitative evaluation is done to check and compare the performance of the proposed Infimum-based FCA Explainable Recommendation method i.e., IFCAER for recommending objects/items to a user. The Automobile dataset is used to perform experiments for calculating Normalized Discounted Cumulative Gain (NDCG).
Steps of calculating NDCG of IFCAER:
• In response to input search query, all matched formal concepts are extracted, and their relevance score is given according to the matched attributes with the input concept. Relevance score is given on scale of 0–3,
where:
‘0’ shows no relevancy (no or very fewer attributes matched)
‘3’ shows the highest relevancy (maximum attributes matched)
‘2’ and ‘3’ lies in between brackets
• Now calculate the Cumulative Gain (CG) and Discounted Cumulative Gain (DCG) of this result by applying the formulas in Eqs. (9) and (10) respectively:
• For ideal ordering of the concepts i.e., from highly relevant towards less relevant, Normalized Discounted Cumulative Gain (NDCG) is calculated. NDCG is the ratio between DCG and Ideal DCG i.e., IDCG, that arrange the concepts in ideal manner as shown in Eq. (11). So, relevance score of the matched concepts list is ordered from high to low.
Following Tab. 7 shows the results of NDCG @ k of IFCAER and other state-of-the-art recommendation models. IFCAER’s performance is compared and better outcomes of the system is the result of good performance of proposed explainable recommendation framework i.e., IFCAER.
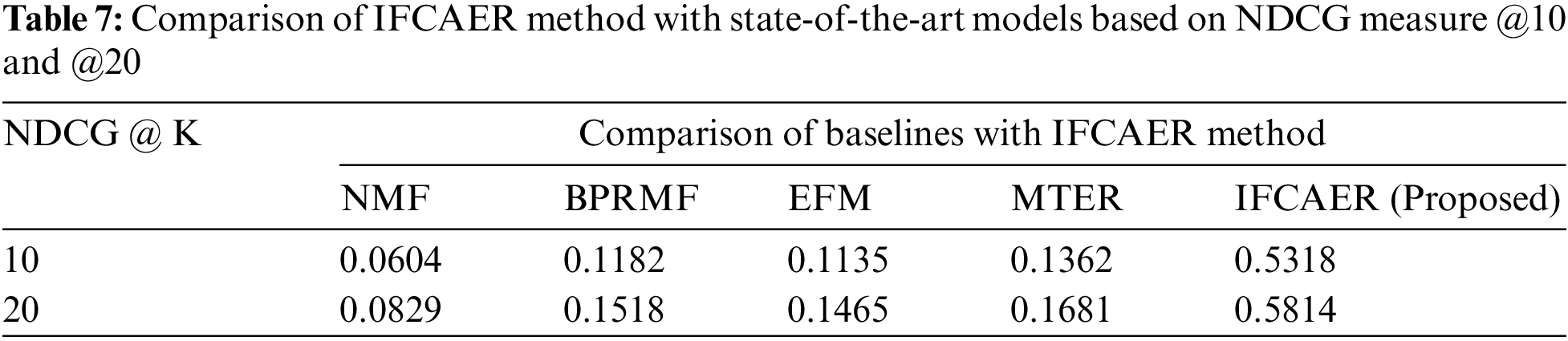
Fig. 13 shows the bar chart describing the improvement in the performance of the recommendation explanation of the proposed method compared with state-of-the-art methods.

Figure 13: Comparison of IFCAER method with state-of-the-art models based on NDCG measure @10 and @20
The proposed framework of explainable recommendation used the Infimum-based FCA (IFCAER) method, which is an addition in this field of research. Evaluations have been carried out on real-world automobile dataset. The input concept was compared with the formal concepts of available context i.e., dataset and FCA-based infimum formal concept was identified through different comparisons by following the proposed algorithm. A list of findings is as follows:
• The proposed algorithm produces a relevant priority array of matched formal concepts with the input concept
• The most specific formal concept is extracted that is maximum matched with user requirements
• It improves the quality of recommendation by explaining the specific-general relationships in formal concepts by traversing concept lattice
• Quantitative evaluation through NDCG has been done for comparative analysis with other methods
• Qualitative evaluation is done based on the trustworthiness metric i.e., satisfactory enough to confirm the better results of proposed framework
• Results of the data analysis satisfy the proposition
• Results prove that IFCAER is able to improve the accuracy of recommendation system by explaining the reason behind that with better outcomes
• IFCAER enhanced the trustworthiness of user about recommendation
• This work is applicable in different fields including health, education, and law domain
In the future, advanced research work on more methods related to explainable recommendations is required. This framework will also be applied to citation based datasets to test its effectiveness.
Acknowledgement: Thank you Iram Aziz for sharing your thoughts on my work.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. Shimizu, M. Matsutani and M. Goto, “An explainable recommendation framework based on an improved knowledge graph attention network with massive volumes of side information,” Knowledge-based Systems, vol. 239, pp. 107970, 2022. https://doi.org/10.1016/j.knosys.2021.107970. [Google Scholar]
2. M. H. Syed, T. Q. B. Huy and S. T. Chung, “Context-aware explainable recommendation based on domain knowledge graph,” Big Data and Cognitive Computing, vol. 6, no. 1, pp. 11, 2022. https://doi.org/10.3390/bdcc6010011. [Google Scholar]
3. R. Catherine, K. Mazaitis, M. Eskenazi and W. Cohen, “Explainable entity-based recommendations with knowledge graphs,” in 11th ACM Conf. on Recommender Systems (RecSys) Poster Proc., Como, Italy, August 27–31, 2017. [Google Scholar]
4. Y. Zhang, “Explainable recommendation theory and applications,” Ph.D. Dissertation, The state University of New Jersey, USA, 2017. [Google Scholar]
5. B. Abdollahi, “Accurate and justifiable: New algorithms for explainable recommendations,” Ph.D. Dissertations, University of Louisville, 2017. [Google Scholar]
6. A. Azizi, X. Chen and Y. Zhang, “Learning heterogeneous knowledge base embeddings for explainable recommendation.” Algorithms, vol. 11, no. 1, pp. 9, 2018. [Google Scholar]
7. Y. Zhang, K. Bi and W. B. Croft, “Explainable product search with a dynamic relation embedding model.” ACM Transactions on Information Systems, vol. 38, no. 1, pp. 1–29, 2019. [Google Scholar]
8. S. Andrews and C. Orphandies, “Analysis of large data sets using formal concept lattices,” in Proc. of the 7th Int. Conf. on Concept Lattices and their Applications, Seville, University of Seville, pp. 104–115, 2010. [Google Scholar]
9. B. D. Agudo and M. C. Martinez, “Explanation of recommenders using formal concept analysis,” in Int. Conf. on Case-Based Reasoning (ICCBRCase-Based Reasoning Research and Development, Springer, Salamanca, Spain, pp. 33–48, 2019. [Google Scholar]
10. N. Tintarev and J. Masthoff, “Designing and evaluating explanations for recommender systems,” in Recommender Systems Handbook, Boston: Springer, pp. 479–510, 2011. [Google Scholar]
11. A. J. Fernández-García, L. Iribarne, A. Corral, J. Criado and J. Z. Wang, “A recommender system for component-based applications using machine learning techniques,” Knowledge-Based Systems, vol. 164, pp. 68–84, 2019. [Google Scholar]
12. A. Formica, “Concept similarity in formal concept analysis: An information content approach,” Knowledge-Based Systems, vol. 21, no. 1, pp. 80–87, 2008. [Google Scholar]
13. B. Ganter and R. Wille, “Formal concept analysis, concept lattices of contexts,” Springer, vol. 21, pp. 17–61, 1999. [Google Scholar]
14. B. Ganter, “Formal concept analysis: Methods and applications in computer science,” Ph.D. Dissertation, Gerd Stumme Otto-von-Guericke University Magdeburg, 2002. [Google Scholar]
15. O. Sohaib, “Social networking services and social trust in social commerce: A PLS-SEM approach,” Journal of Global Information Management (JGIM), vol. 29, no. 2, pp. 23–44, 2021. [Google Scholar]
16. M. Helou and S. Kara, “Design, analysis and manufacturing of lattice structures: An overview,” International Journal of Computer Integrated Manufacturing, vol. 31, no. 3, pp. 243–261, 2018. [Google Scholar]
17. C. Ding, T. Li, W. Peng and H. Park, “Orthogonal nonnegative matrix tri-factorizations for clustering,” in KDD ‘06: Proc. of the 12th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Philadelphia PA, USA, pp. 126–135, 2006. [Google Scholar]
18. S. Rendle, C. Freudenthaler, Z. Gantner and T. Lars, “BPR: Bayesian personalized ranking from implicit feedback,” in UAI 2009, Proc. of the Twenty-Fifth Conf. on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, pp. 452–461, 2012. [Google Scholar]
19. Y. Zhang, G. Lai, M. Zhang, Y. Zhang, Y. Liu et al., “Explicit factor models for explainable recommendation based on phrase-level sentiment analysis,” in Proc. of the 37th ACM SIGIR, Gold Coast, Queensland, Australia, pp. 83–92, 2014. [Google Scholar]
20. N. Wang, H. Wang, Y. Jia and Y. Yin, “Explainable recommendation via multi-task learning,” in SIGIR’18: The 41st Int. ACM SIGIR Conf. on Research & Development in Information Retrieval, Ann Arbor MI, USA, pp. 165–174, 2018. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |