| Computers, Materials & Continua DOI:10.32604/cmc.2022.027974 |  |
| Article |
Truncation and Rounding-Based Scalable Approximate Multiplier Design for Computer Imaging Applications
1Department of Electronics and Communication Engineering, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, 522502, Andhra Pradesh, India
2Department of EECE, GITAM (Deemed to be University), Visakhapatnam, AP, India
3Department of Electronics and Communication Engineering, Francis Xavier Engineering College, Tirunelveli, 627003, Tamil Nadu, India
4Department of Computer Science and Engineering, Vardhaman College of Engineering, Shamshabad, Hyderabad, 501218, Telangana, India
*Corresponding Author: S. Rooban. Email: sroban123@gmail.com
Received: 30 January 2022; Accepted: 12 April 2022
Abstract: Advanced technology used for arithmetic computing application, comprises greater number of approximate multipliers and approximate adders. Truncation and Rounding-based Scalable Approximate Multiplier (TRSAM) distinguish a variety of modes based on height (h) and truncation (t) as TRSAM (h, t) in the architecture. This TRSAM operation produces higher absolute error in Least Significant Bit (LSB) data shift unit. A new scalable approximate multiplier approach that uses truncation and rounding TRSAM (3, 7) is proposed to increase the multiplier accuracy. With the help of foremost one bit architecture, the proposed scalable approximate multiplier approach reduces the partial products. The proposed approximate TRSAM multiplier architecture gives better results in terms of area, delay, and power. The accuracy of 95.2% and the energy utilization of 24.6 nJ is observed in the proposed multiplier design. The proposed approach shows 0.11%, 0.23%, and 0.24% less Mean Absolute Relative Error (MARE) when compared with the existing approach for the input of 8-bit, 16-bit, and 32-bit respectively. It also shows 0.13%, 0.19%, and 0.2% less Variance of Absolute Relative Error (VARE) when compared with the existing approach for the input of 8-bit, 16-bit, and 32-bit respectively. The proposed approach is implemented with Field-Programmable Gate Array (FPGA) and shows the delay of 3.640, 6.481, 12.505, 22.572, and 36.893 ns for the input of 8-bit, 16-bit, 32-bit, 64-bit, and 128-bit respectively. The proposed approach is applied in digital filters design which shows the Peak-Signal-to-Noise Ratio (PSNR) of 25.05 dB and Structural Similarity Index Measure (SSIM) of 0.98 with 393 pJ energy consumptions when used in image application. The proposed approach is simulated with Xilinx and MATLAB and implemented with FPGA.
Keywords: Truncation rounding based scalable approximate multiplier; foremost one detector; field programmable gate array; peak-signal-to-noise-ratio; structural similarity index measure
Digital system requires binary arithmetic operations to realize any boolean function. Adders are the key components in binary arithmetic, and they are used in all basic operations such as addition, subtraction, multiplication, and division. Adders are used to implement increment, decrement, and other similar operations in addition to arithmetic operations. As a result, at the micro-architecture level of abstraction, adders are considered as the fundamental building blocks in digital systems, particularly for data-intensive applications design. In computer arithmetic, addition and multiplication are the commonly used operations. For addition, full-adder cells are investigated for approximate computation. Approximate circuits are preferred over exact circuits because of their reliability, in most of the cases approximate circuits are energy efficient also occupying less Look-Up tables (LUT’s) [1]. In [2], compares various adders and provides several new measures for assessing approximate and probabilistic adders. When two numbers of equal bit size are multiplied, the size of the result is twice the bit size of the multiplicand or multiplier. Finite Impulse Response (FIR) filtering, Fast Fourier Transform (FFT), and Discrete Cosine Transform (DCT) are used in digital signal processing applications, and they are heavily relying on arithmetic operations. Arithmetic operations like multiplication and division on binary number system are computationally demanding reduced area, latency, and power. The fixed-point number system is suffered with overflow and scaling due to its lack of precision, but the floating-point number system offers superior precision and scalability. In [3], a method is proposed to derive an analytical correction term for reducing the error. A truncated multiplication approach is used in majority of these designs. Power consumption is one of the most significant qualities for any electronic equipment, particularly in battery-powered hand-held gadgets.
In [4], a static truncation-based technique that approximates the outcome by using the higher, medium, or lower portions of the inputs. These techniques are with the drawbacks that they are not easily scale to larger input widths, and their benefits are diminishing as the input size expands. Rounding of operands to the nearest exponent in both signed and unsigned multiplications are supported in [5], but hardware implementation is quite complex. In [6–8], to achieve high performance, the core operations of the arithmetic processor, such as addition, and multiplication are critical. For approximation computing, addition is intensively explored for power usage and latency reduction, these techniques can be used in image processing application. In [9], symmetric bit stacking approach multiplication is made easier by reducing the complexity of the wallace tree structure. A 4:2 compressor with a low supply voltage is proposed in [10–12], this design achieves lower delay with high energy efficiency, but worse normalized mean error.
In [13], Fin Field Effect Transistor (Fin-FET) is used to implement the ultra-efficient [14], approximate 4:2 compressor at the transistor level. Reduced number of transistors shows low power, low propagation delay and a shorter critical path avoids the capacitance effects. In [15], approximate booth multiplier models with radix-4 modified booth encoding technique is proposed. Compared with the existing approximate booth multipliers, shows significant increase in accuracy and hardware performance error rate when the approximation factor increased. For 8-Bit use, three new approximate 4:2 multiplier compressors are designed in [16]. In addition, an Error Correction Module (ECM) is included to improve the error performance in 4:2 compressors. The number of outputs of the approximate 4:2 compressor is reduced to one, and the energy efficiency is enhanced. In [17], new metrics including error distance (ED), mean error distance (MED) and Normalized Error Distance (NED) are proposed for evaluating the design of approximate adders.
In [18], a configurable architecture for implementing the FIR filter with low complexity is proposed by using Constant Shifts Method (CSM) and Programmable Shift Method (PSM). This approach is the combination of Shift and Add unit, Multiplexer unit, Final shifter unit, and Final adder unit. The proposed methodology in [19], round off the operands to the nearest power of two. This method works for both signed and unsigned augmentations and offer three approximate multiplier executions, one for unsigned tasks and two for marked tasks. The Truncation and Rounding based Scalable Approximate Multiplier (TOSAM) in [20], uses versatile approximated multiplier that reduce the number of partial products by truncating all the operands based on their leading one-bit location. In this structure, fixed-width result shows significant improvements in energy utilization and area when compared to other multipliers. The input operands are modified to the nearest odd number to improve the complete exactness. The method proposed in [21], relies on mathematical reasoning to separate the polynomial of the multiplier.
The above discussed methods determine the correctness by the values of t and h parameters, where the width of the input operands having no major impact. As a result, the proposed multiplier has a scalability characteristic. The following are the main contributions of the proposed work.
1. A new scalable approximate multiplier using truncation and rounding technique is proposed to increase the multiplier accuracy.
2. The combinations of different (h, t) parameters are examined in order to find a balance between accuracy, delay, and energy usage.
3. A hardware implementation of the truncation and rounding-based scalable approximate multiplier (TRSAM) for both signed and unsigned operations are presented.
The remainder of this work is organized as follows. Section 2 introduces the proposed approximate multiplier and its hardware implementation. Section 3 compares the results along with error analysis. The proposed approximate multiplier is used in image [6,7], processing applications, the parameters delay, area, and power are also analyzed in Section 4. Section 5 concludes this article.
2 Proposed Multiplier Approach
The proposed approach is an updated version of [20]. The proposed approximate multiplier performs the rounding and truncation at the inputs which reduces the error rate and the variation in MARE and VARE values to improve the overall circuit performance. In the proposed approach the LSB’s are modified in such a way, so that the approximate value is nearly equal to the accurate value. TRSAM modes based on height (h) and truncation (t) such as (h, t) in the architecture TRSAM (0, 2), TRSAM (0, 3), TRSAM (1, 5), TRSAM (2, 6), TRSAM (3, 7), TRSAM (4, 8) TRSAM (5, 9). Fig. 1 shows the proposed approximate multiplier for implementing various combinations of (h, t) along with bit lengths. There are few changes in the architecture and algorithm for different combinations of (h, t).
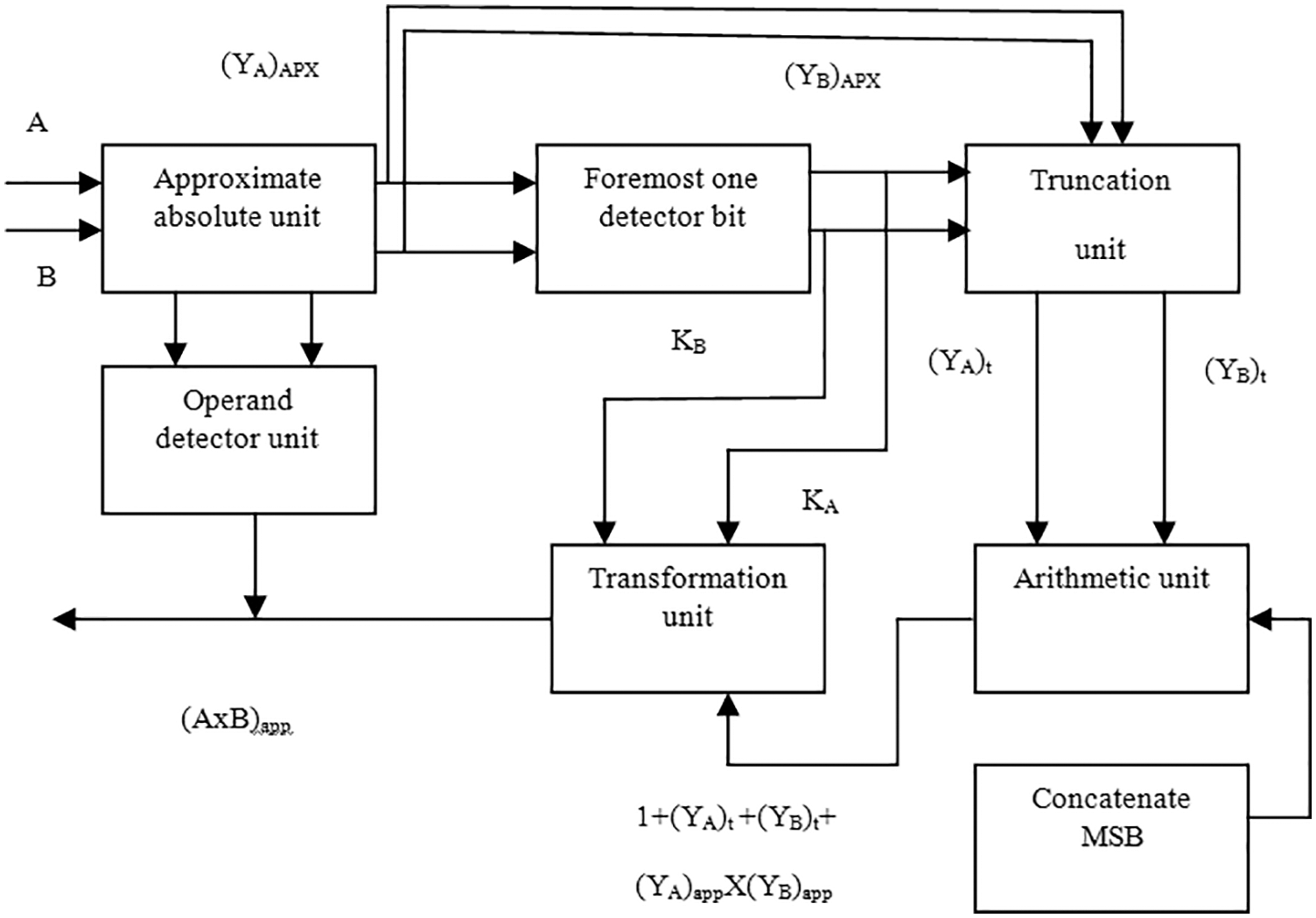
Figure 1: Block diagram of the proposed approximate multiplier
The proposed approximate multiplier consists of Approximate absolute unit (AAU), Foremost one Detector bit (FOD), Truncation Unit (TU), Arithmetic Unit (AU), Shift Unit (SU) and Operand Detector Unit (ODU). The AAU is applied with the inputs of A and B. If the input operand is negative, the results are inverted; if the input operand is positive, the results are unchanged. This AAU can be removed for unsigned multipliers. The operation in AAU is explained in detail through Fig. 2. The output of AAU is denoted as (YA)APX and (YB)APX. FOD unit takes the input (YA)APX and (YB)APX, values. By using these values, kA and kB are detected, which detects position of the bit value with ‘1’ from the MSB. These kA and kB are responsible for shifting operation. TU inputs are kA, kB, (YA)APX, and (YB)APX. The approximation inputs are trimmed and converted to a fixed width operands and they occupy the foremost position of the input operands. The output is obtained from the truncation unit (YA)t and (YB)t are given as inputs to the arithmetic unit. The terms (YA)t and (YB)t acquired from the truncated unit which is represented in Eq. (1).
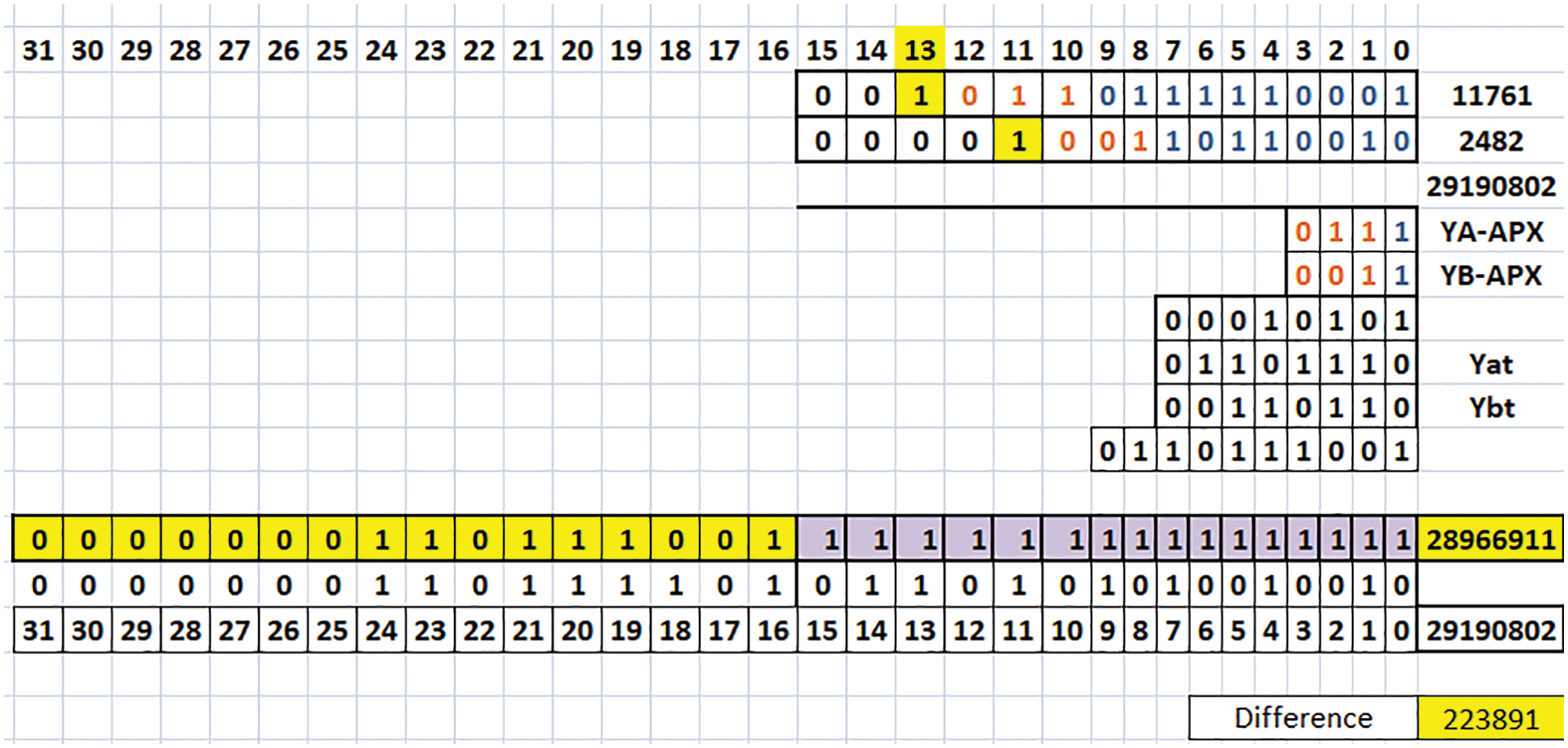
Figure 2: Example of 16-bit TRSAM (3, 7) (Case 1: A, B are positive)
The arithmetic unit performs addition on the truncated fixed width operands ((YA)t + (YB)t) and multiply the approximation inputs ((YA)APX (YB)APX), result is enlarged to one bit by concatenating ‘1’ at the MSB. The MSBs of (YA)APX and (YB)APX are identical to those of (YA)t and (YB)t. The adders and logic AND gates in the Arithmetic Unit use power gating, based on the operating mode. In TU, the arithmetic unit’s output is left shifted by kA + kB times (kA and kB are the leading one-bit values of A and B). The term (1000000000 + (YA)t + (YB)t + (YA)APX (YB)APX) is obtained by performing the shifting operation. The maximum possible truncation ‘t’ and rounding ‘h’ values are (5, 9) where h = 5 and t = 9.The output operand sign is determined by the sign of the input operands, and if at least one of the inputs is zero, the output is set to zero. The AAU is eliminated, by the unsigned input operands if ODU remains constant, in other words for unsigned operands this AAU is not producing any output, for signed operands. There are three cases for verifying the output they are i) both the inputs are positive, ii) both inputs are negative and iii) either one of the inputs is positive.
Fig. 2 is the example of 16-bit TRSAM approximate multiplier for the parameter (3, 7), the rounding value ‘h’ is 3 and truncation value ‘t’ is 7. Considering A and B both are positive inputs, assume A as 0010 1101 1111 0001 (binary of 11761) and B as 0000 1001 1011 0010 (binary of 2482). The Foremost one detector unit (FOD) represents KA and KB values are 13 and 11 respectively. The values of (YA)APX = 0111 and (YB)APX = 0011. These (YA)APX and (YB)APX are multiplied and gives the product value as 0001 0101. The values of (YA)tare seven places from the KA and the LSB bit is considered as 0, the (YA)t = 0110 1110 and in similar way (YB)t = 0011 0110. Next the product value of (YA)APX and (YB)APX are to be added with the terms (YA)t and (YB)t Eq. (1), represents the product value. The computed product value is 01 1011 1001. Here the shifting is based upon the addition of KA and KB values. The final output is 0000 0001 1011 1001 1111 1111 1111 1111 (binary of 28 966 911), so the value is (A × B)Proposed = 28 966 911, where the exact value is (A × B)Exact = 29 190 802, the difference value is 223 891.
Fig. 3 follows the above algorithm, considering A is positive, and B is negative inputs, assume the value of A as 0000 0001 1100 0000 (binary of 448) and B as 1100 0000 0000 0000 (binary of −16384). Here the KA and KB values are 8 and 15 respectively. The values (YA)APX = 1101 and (YB)APX = 1001. These (YA)APX and (YB)APX are multiplied and gives the product value as 0111 0101. The values of (YA)t = 1100 0000, similarly (YB)t = 1000 0000. The Eq. (1), represents the product value as 10 1011 0101. Base on shifting the final output is 1111 1111 0101 1010 1111 1111 1111 1111 (binary of −10 813 441), so the value is (A × B)Proposed = −10 813 441, where the exact value is (A × B)Exact = −7 340 032, the difference value is 3 473 409.
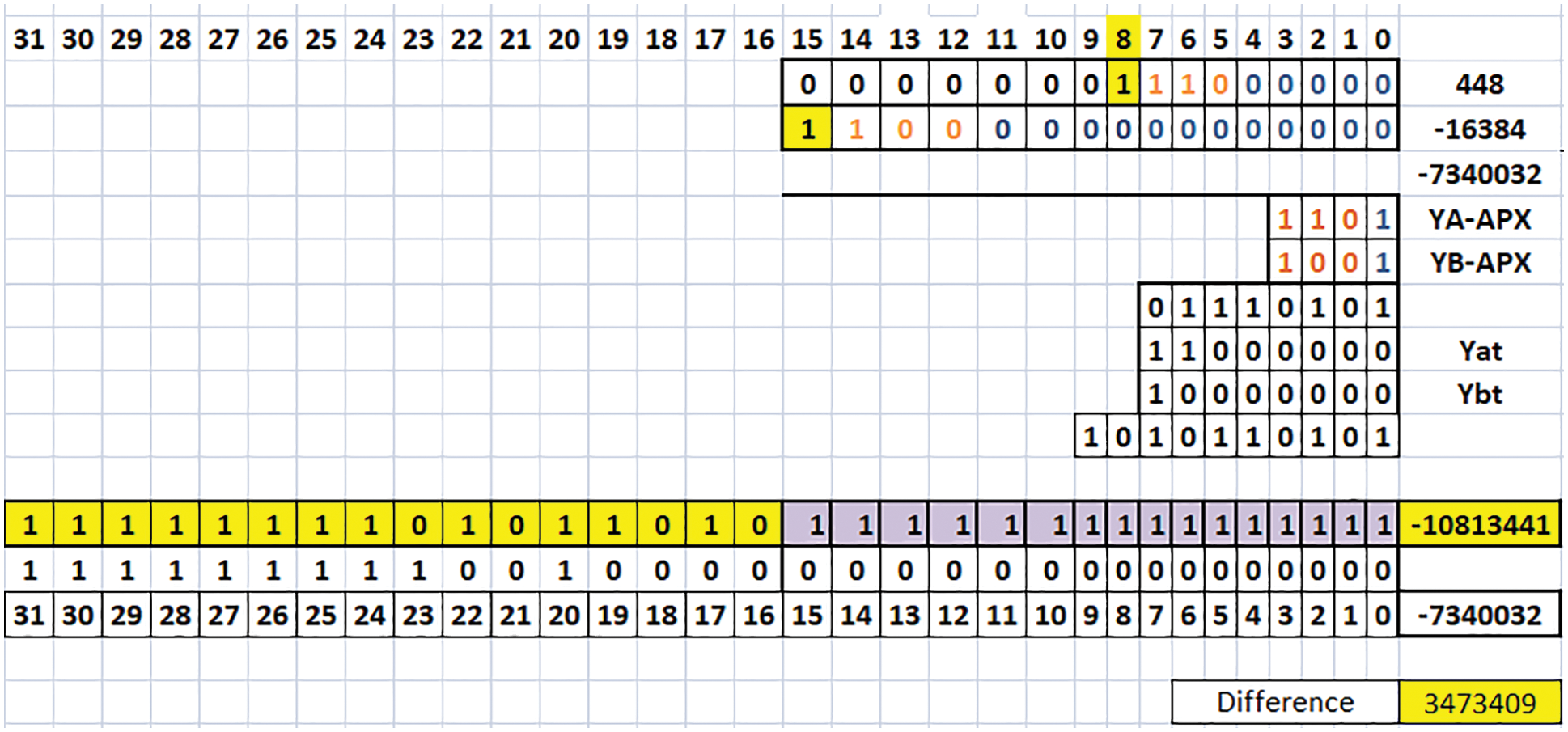
Figure 3: Example of 16-bit TRSAM (3, 7) (Case II: A is positive, and B is negative)
Fig. 4 is the example of 16-bit TRSAM approximate multiplier for the parameter (3, 7). Considering A and B are negative inputs, assume the value of A as 1111 1111 1100 0110 (binary of −58) and B as 1111 1111 1110 1010 (binary of −22). Here the KA and KB values 15 and 15 respectively. The values (YA)APX = 1111 and (YB)APX = 1111. These (YA)APX and (YB)APX are multiplied and gives the product value as 1110 0001. The values (YA)tis considered to be seven places from the KA and the LSB bit is considered as 0 in this case, so the (YA)t = 1111 1110 and in similar way (YB)t = 1111 1110. Next the product value of (YA)APX and (YB)APX are to be added with the terms (YA)t and (YB)t and the Eq. (1), represents the final product the final value is 10 0001 1101. The final output is 0000 0000 0000 0000 0000 0010 0001 1101 (binary of 541), so the value is (A × B)Proposed = 541, where the exact value is (A × B)Exact = 1276, the difference value is 735. The existed approach having more difference value also the error rate is more which is explained in [20]. We cannot say that the accuracy value is same or not for all the combinations, it depends on the parameters of (h, t).
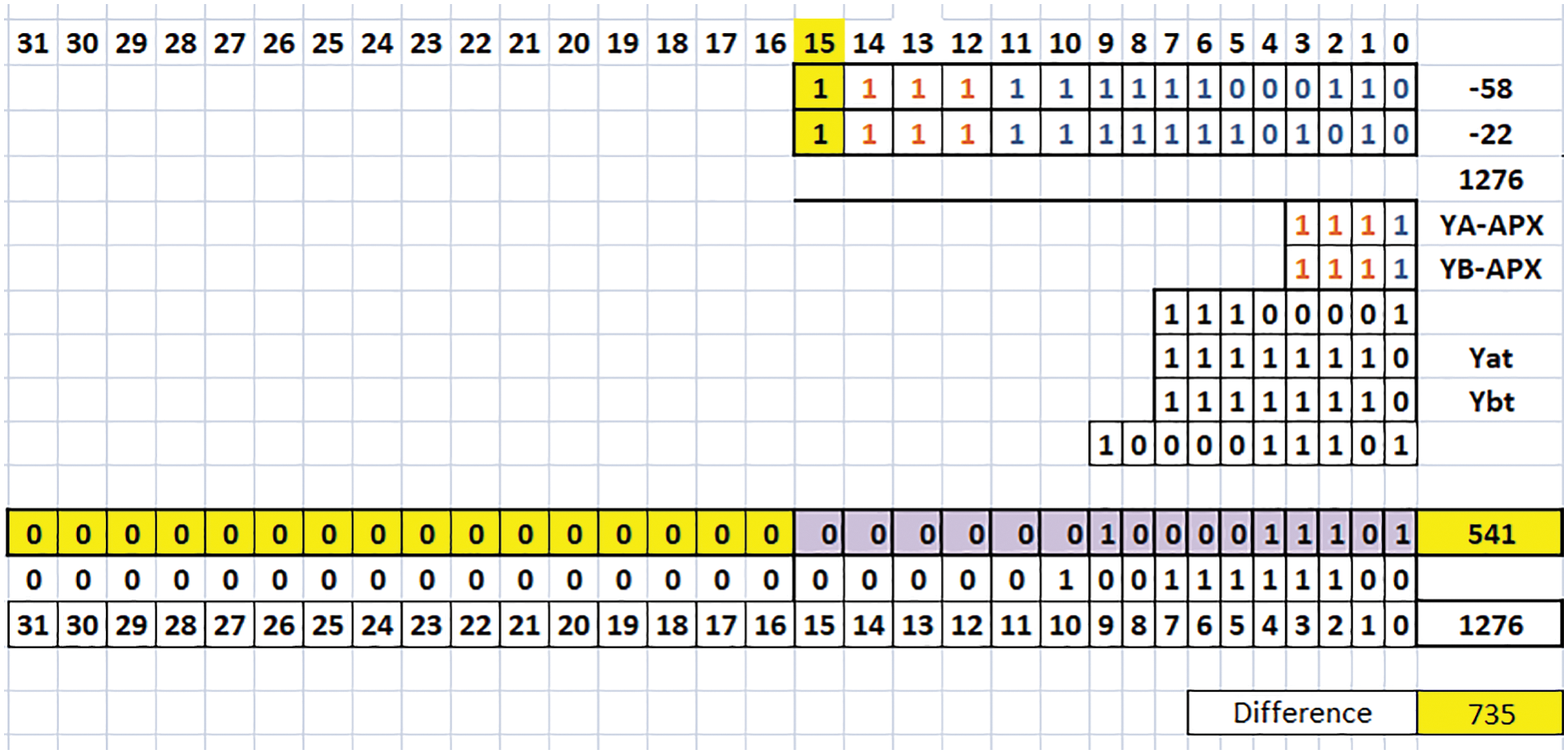
Figure 4: Example of 16-bit TRSAM (3, 7) (Case III: A, B are negative)
The proposed approximate multiplier is simulated in Xilinx Vivado. Several error metrics are used in approximate computing to quantify the errors and accuracy. Error Distance (ED) is defined as the arithmetic distance between a generated output and the correct one for every input. By considering the average impact of many inputs and the normalizing of multiple-bit adders, the mean error distance (MED) and the normalized error distance (NED) are determined. Because the NED is nearly invariant with the size of an implementation, it is used to examine the reliability of the design.
Error Rate (ER): The percentage of approximate outputs among all outputs.
Error Distance (ED): The arithmetic difference between the exact and approximate result.
Mean Error Distance (MED): The average of EDs for a set of outputs obtained by applying a set of inputs.
Relative Error Distance (RED): The ratio of ED to exact result.
Mean Relative Error Distance (MRED): The average value of all possible relative error distance (RED).
Normalized Mean Error Distance (NMED): The normalization of mean error distance (MED) by the maximum output of the accurate design. This metric is used for comparing circuit of different sizes.
maxARE is specified as maximum absolute relative error (considered from relative error RE)
MRE is specified as mean relative error
MARE is specified as mean absolute relative error
VARE is specified as variance of absolute relative error
NED is specified as normalized error distance
max_NED is specified as maximum normalized error distance
Tab. 1 shows the MARE and the variance of ARE (VARE) vs. the width of the unsigned multipliers to demonstrate the scalability of the existing and the proposed approach. From the results it is identified that the multiplier’s accuracy is greatly influenced by the h value (bit length of the multiplier). It is observed that increasing h by one, virtually halves the MARE value. The proposed approximation multiplier is implemented for 8-bit, 16-bit, 32-bit, 64-bit and 128-bits with the rounding and truncation values of (3, 7). The simulated results are shown in Figs. 5–9. From the results it is observed that the proposed approach gives better results than the earlier approaches.

Figure 5: Results of 8-bit TRSAM (3, 7)

Figure 6: Results of 16-bit TRSAM (3, 7)

Figure 7: Results of 32-bit proposed approach TRSAM (3, 7)
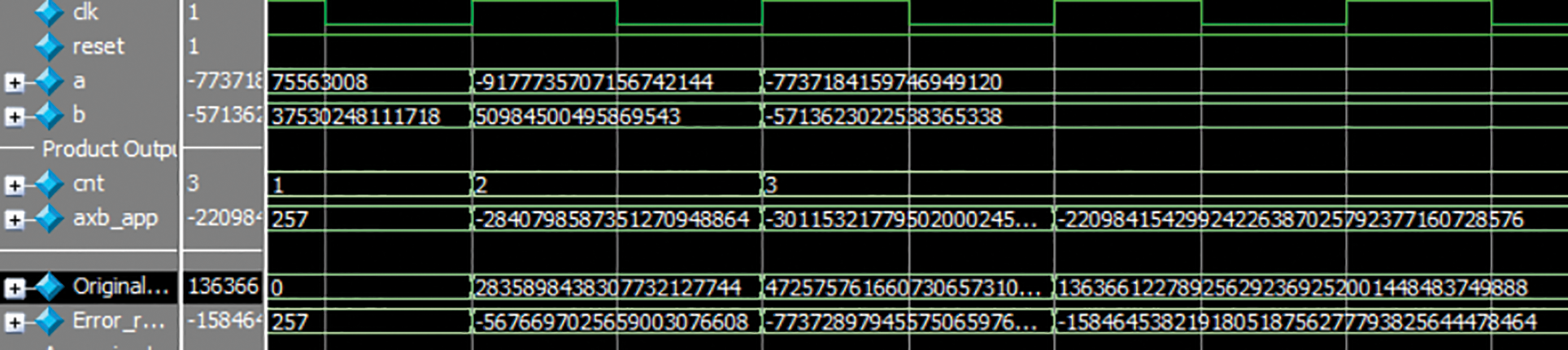
Figure 8: Results of 64-bit proposed approach TRSAM (3, 7) approximate multiplier

Figure 9: Results of 128-bit proposed approach TRSAM (3, 7) approximate multiplier
In Fig. 5 considering the value of A as 45 and B value as 27 the output is generated in the next cycle. The exact output (A × B)Exact = 1215, the output obtained from the previous approach [20], is (A × B)Existed = 714, and produce the error value of 501. For the same input case, the proposed approach produces the value for (A × B)Proposed = 715, the error value is 500. In other cases, for the same inputs the error value is gradually decreasing by using the proposed approach. Due to delay the first output value is shown in second cycle. In Fig. 6 considering A value is 11761 and B value is 2482. The exact output (A × B)Exact = 29 190 802, the output obtained from the previous approach [20], (A × B)Existed = 28 901 376, here the error value is 289 426. For the same input case using the proposed approach the value is (A × B)Proposed = 28 966 911 here the error value is 223 891. In other cases, for the same inputs the error value is gradually decreasing by using the proposed approach. Due to delay the first output value is shown in second cycle.
The Fig. 7 input A value is 75563008 and B value is 1795686 exact outputs (A × B)Exact = 135 687 435 583 488, the proposed approach value (A × B)Proposed = 138 263 587 192 832 the difference value is 2 576 151 609 344 is to be subtracted from the obtained output to get the exact value. Here in this 32-bit approximate multiplier approach for certain input values it is showing the same output value because we are considering kA and kB values and using those values in shifting, but the output value which is obtained from the proposed approach is so close to exact value, while the existing approach [20], is far from the exact value.
The results of 64-bit are shown in Fig. 8. To calculate the error rate a multiplier is used which shows the difference values in between proposed approach to exact value. For 128-bit the results are shown in Fig. 9. Three cases, A and B are positive, A is negative value and B is positive, A and B both are negative are considered for 64-bit and 128-bit simulations. The error rate is the difference value in between the original output and A × Bapp. The bit length goes on increasing, to find the exact output value it becomes so difficult, so for higher bit lengths original output block is used. The accuracy depends on the difference in between exact value and obtained value.
Fig. 10 is the RTL schematic of TRSAM approximate multiplier with parameter (3, 7). RTL schematic gives an overview of how the connections between one module to another module also, it explains the data path between the modules. The schematic is same for all the bit lengths and different combinations of (h, t).
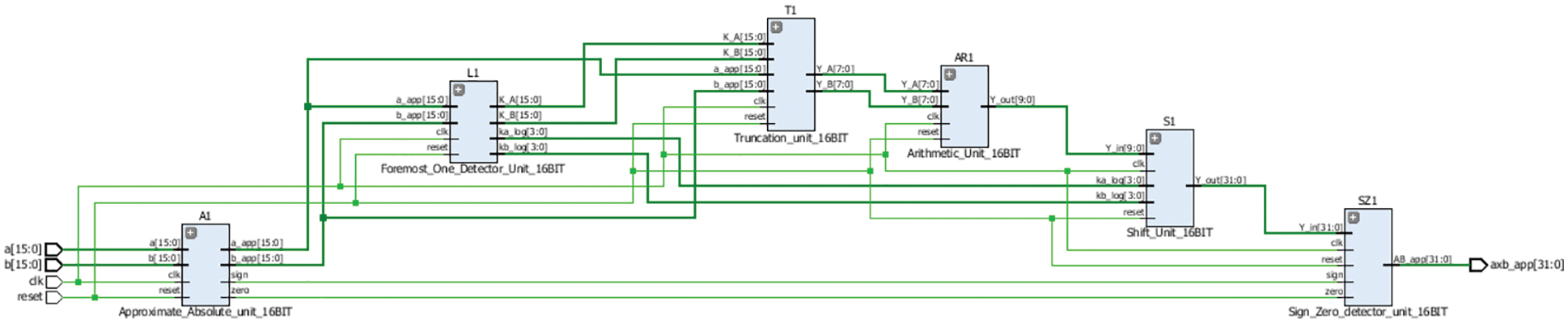
Figure 10: Schematic of proposed TRSAM (3, 7) for 16-bit approximate multiplier
In the Tab. 2, comparison consists of parameters like Slice register, Slice LUT, IOB, Fan-out, Power, Delay of 8-Bit, 16-Bit, 32-Bit, 64-Bit, and 128-Bit for the parameter (h, t) in FPGA family [22], of Vertex 7FPGA (XC7VX330T-2FFG1761). Fig. 11 shows how the parameters are varying against all the bit lengths. The proposed structure is energy efficient because it consumes the power from 12.8 to 84.5 for various bitlengths.
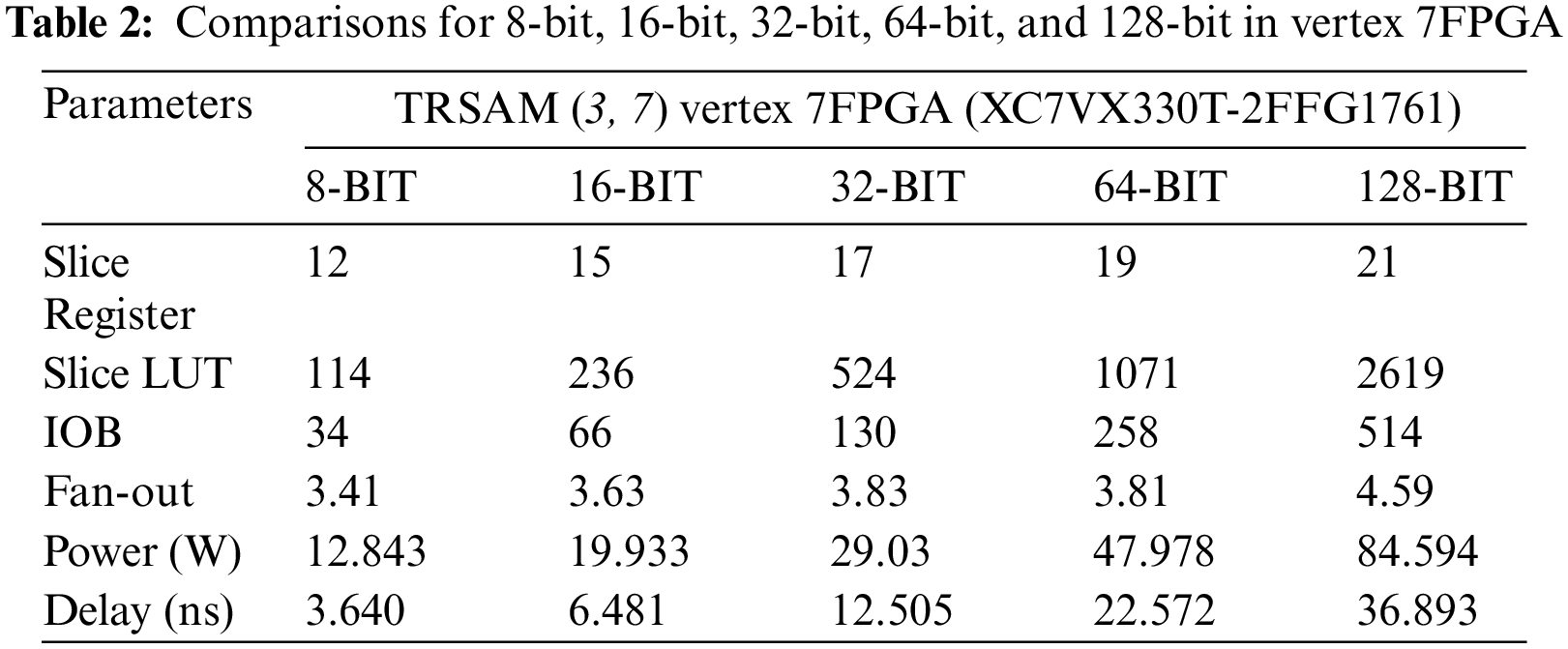
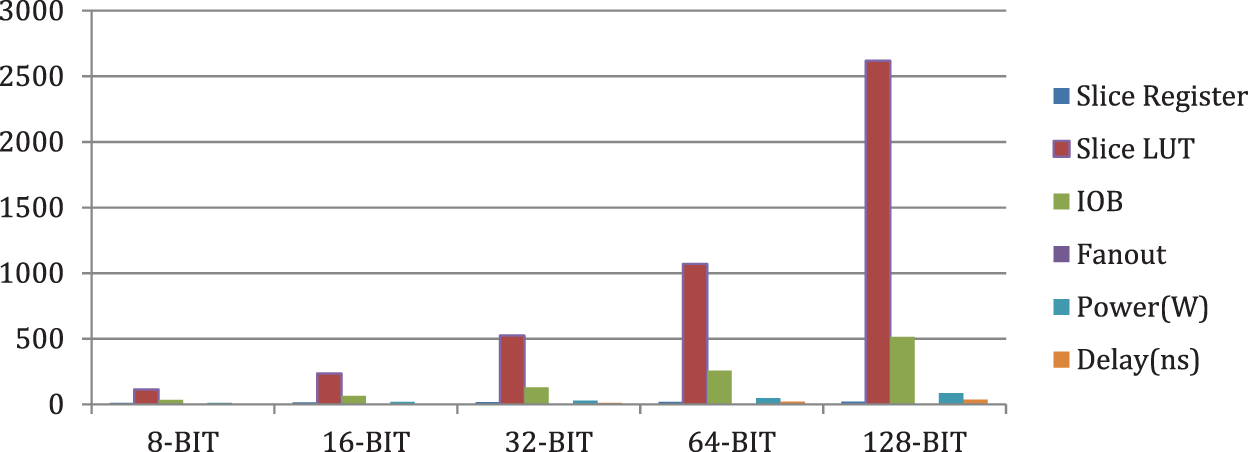
Figure 11: Graphical representation of parameters of TRSAM (3, 7) approximate multiplier
4 Image Processing Application
This section discusses the proposed approximation multipliers in image processing application. Gaussian filter in image processing uses the proposed multiplier to decrease the Gaussian noise. Convolution of the original image with the defined Gaussian mask is used for filtering [6]. Image multiplication is one of the most important operations in image processing which is used to evaluate the efficiency of the proposed approximate multipliers through real-world applications. Image processing with the proposed approximate multipliers is simulated with MATLAB. To analyze the precision of the output images, Peak Signal to Noise Ratio (PSNR) is calculated and is used as the metric for image quality assessment [23–26]. Convolution is performed through this approximate multiplier for an input picture of size 8 × 8 with 2D 3 × 3 Gaussian mask. Figure of merit PSNR is calculated using the mean-square error between the original and filtered images. The proposed truncated approximation multiplier is compared with various previous [22,27–30], multipliers to validate the quality through the errors. Testing of the proposed multipliers is performed with sharpening and JPEG compression image processing applications. The various benchmarks for sharpening and JPEG compression are Baboon and Lena. The PSNR block calculates the peak signal-to-noise ratio between two images in decibels. This ratio is used to compare the quality of the original and the compressed images. Higher PSNR shows the better quality of the compressed or reconstructed image.
The PSNR ratio and Structural Similarity Index Measurement (SSIM) of approximate outcomes are calculated in the sharpening application using MATLAB simulations and compared with the precise output images. Additionally, the Multiplier and Accumulator (MAC) module is included to construct a sharpening unit, and the MAC energy consumption with various multipliers are calculated. Image multiplication is performed through pixel-by-pixel, where the two input images are combined and produces the output of one image. Along with the PSNR, SSIM is also utilized to measure the structural similarity of the approximation and exact images. SSIM is considered as accuracy and consistent with image quality in human perception. It can be used to implement video applications and recent image applications techniques with few architecture changes. With some changes in the algorithm and inserting some new blocks there is possibility for usage in small object detection [31,32].
Tab. 3 compares the PSNR, SSIM and energy consumed by the various approximate multipliers which are obtained using MATLAB. Figs. 12–15 represents the exact and the output images which are produced by the proposed architecture. There is possibility for some modifications in the structure in case we want to use the Blocked RAM, as each multiplier can be associated with individual BRAM, or we can use alone based on the modifications which has to be done in the project.
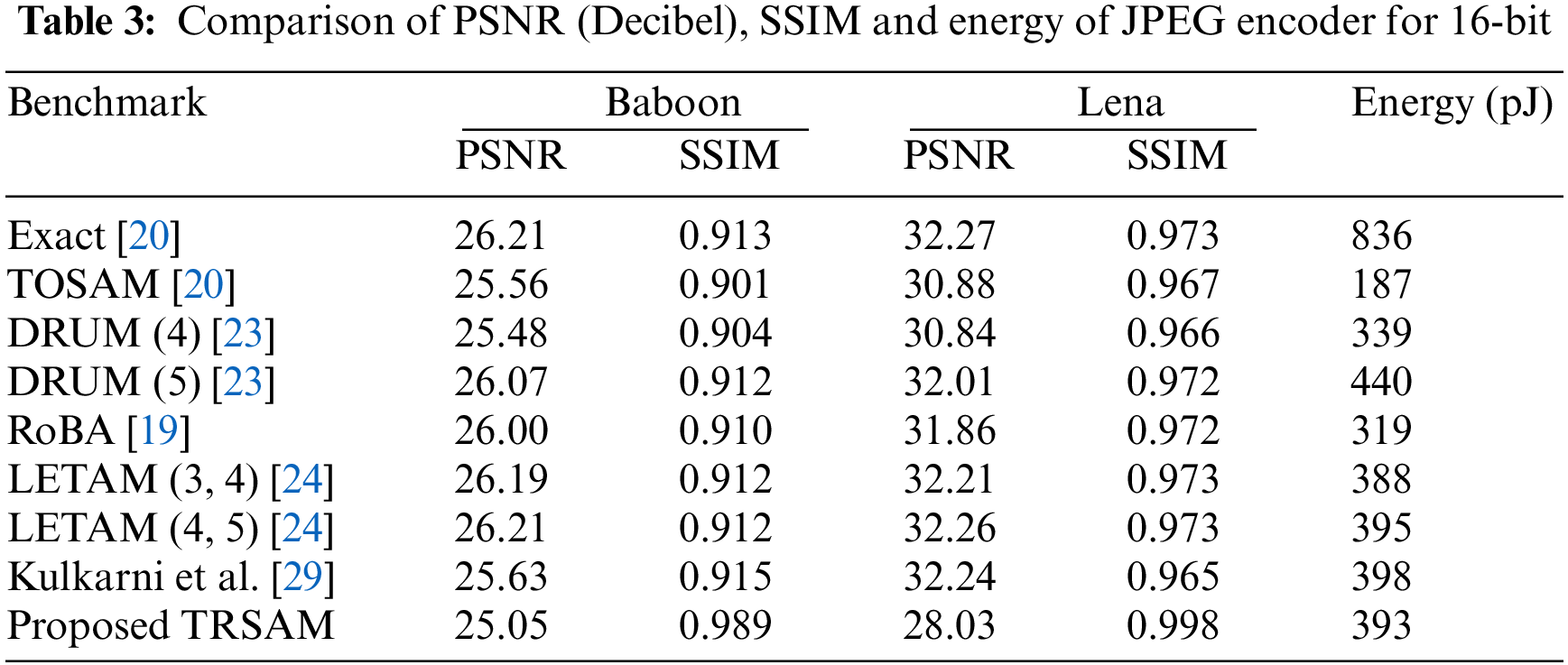
Figure 12: Baboon (a) exact image, (b) by using existed TOSAM, (c) by using proposed TRSAM

Figure 13: Lena (d) exact image, (e) by using existed TOSAM, (f) by using proposed TRSAM

Figure 14: Eyes (g) input image, (h) image by using the proposed approach
Figure 15: Voice (i) input image, (j) image by using the proposed approach
The PSNR is the expression for the ratio between the maximum power of a signal and the power consumed by the distorting noise which affects the quality. The SSIM ratio is calculated by measuring the quality between the original input image and the output image. Higher PSNR value gives the better quality of the compressed or reconstructed output image. By using SSIM quality of a digital television and pictures can be predicted. This is used for measuring the similarity between the two images. Generally, the SSIM values ranges from 0 to 1, 1 means perfect match of reconstructed image with original one. The values 0.97, 0.98, 0.99 are for a good quality reconstruction image. The PSNR and SSIM of different image values are tabulated in Tab. 4. The Accuracy for the respective architecture is tabulated in Tab. 5.
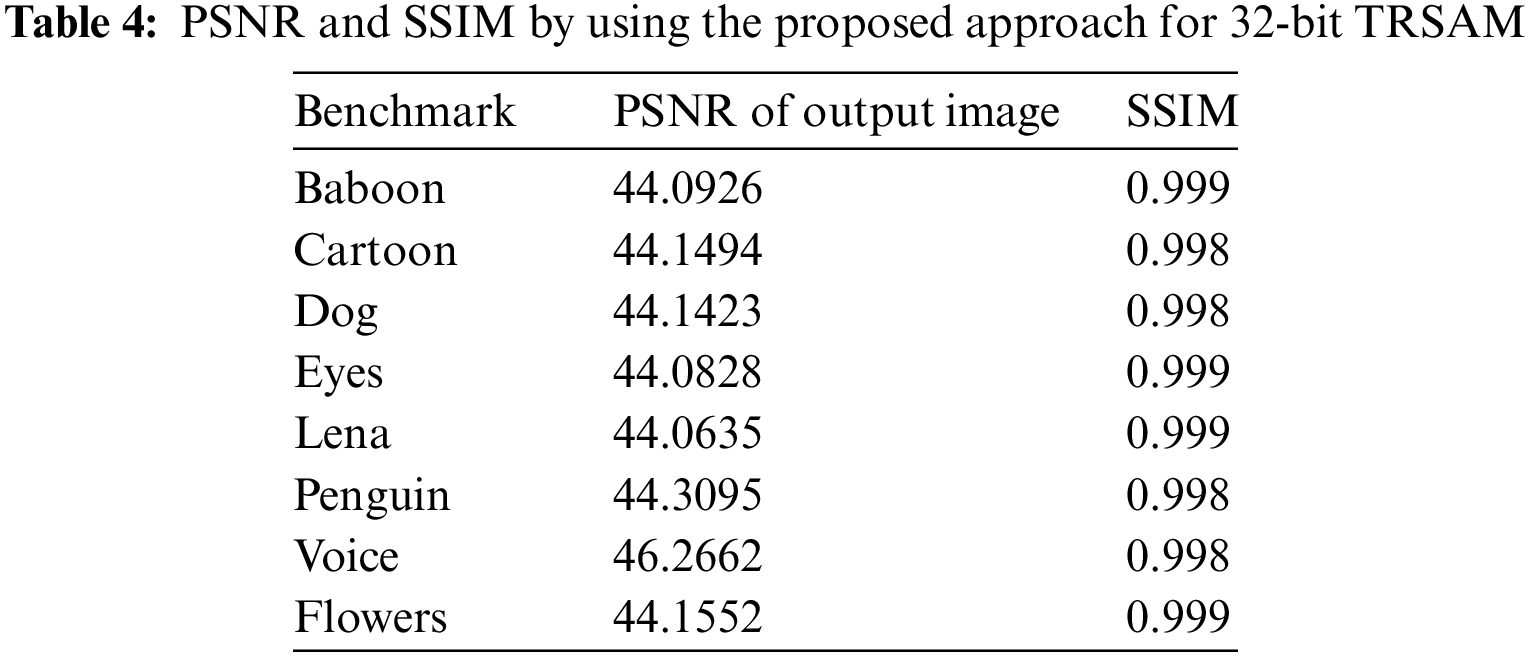
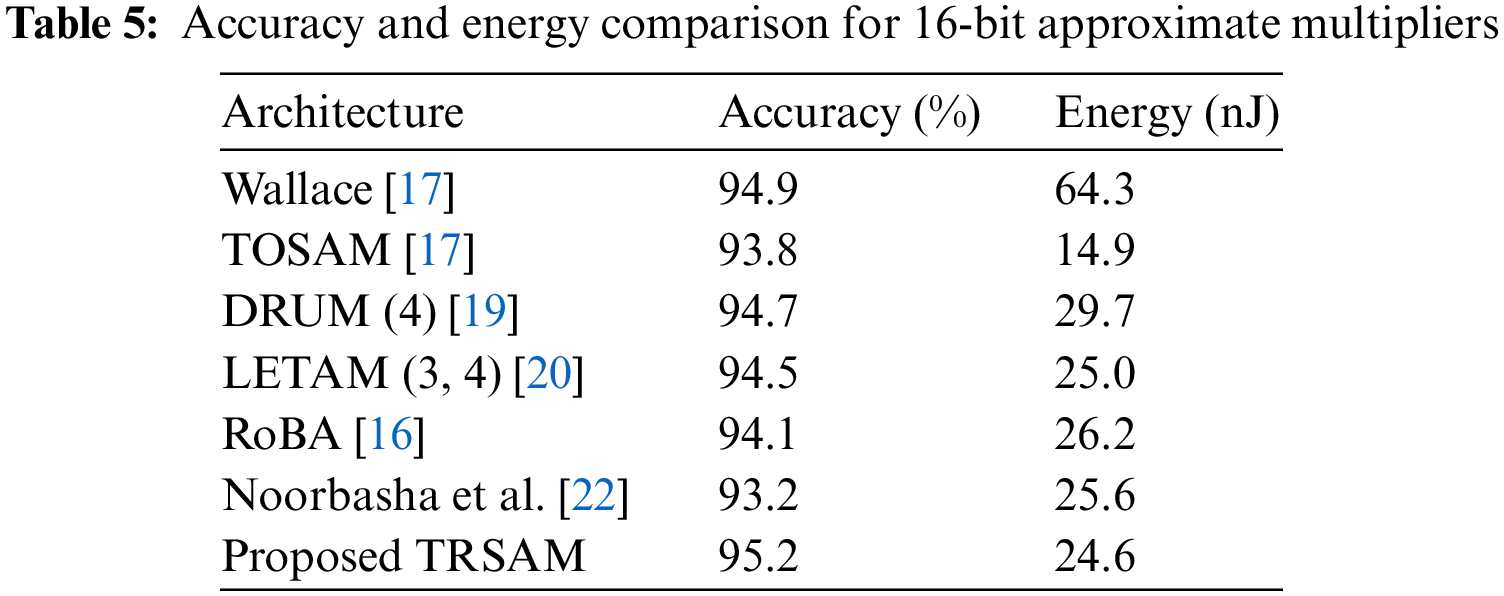
A novel method to reduce the error in approximation truncation multiplier is proposed. This proposed multiplier is scalable and outperformed when compared with other approximate multipliers in terms of area, delay, and power. The proposed 32-bit TRSAM multiplier improves the average energy utilization by 2% when compared to the exact ROBA, Wallace Tree, LETAM, DRUM, DSM, and DQ4:2C4 multipliers. This proposed approximation TRSAM (3, 7) multiplier shows an efficient result in three cases of inputs; they are i) both the inputs are positive, ii) one input is positive and another is negative and iii) both the inputs are negative. The accuracy for this approach is 95.2% and the energy utilized is 24.6 nJ. The proposed design shows 0.11%, 0.23%, and 0.24% less MARE for the input of 8-bit, 16-bit, and32-bit and also shows 0.13%, 0.19%, and 0.2% less VARE for the input of 8-bit, 16-bit, 32-bit respectively. This proposed method can be used in image processing, digital signal processing, and classification-based applications. Rounding of the patterns are optimized based on the level of precision required and the compression techniques used. The proposed approach in image applications shows better performance than the existing approaches in terms of PSNR and SSIM. The future scope of the proposed work is combining the approximation approach with high efficiency video coding to improve the efficiency. By incorporating few changes in the proposed techniques there is a possible way for acquiring high PSNR values and the SSIM values of closer to ‘1’. Modern-day computing with increasing power and sophistication, the concept of computation can be expanded beyond to approximate computation in future to reduce the power consumption and delay.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. I. Alouani, H. Ahangari, O. Ozturk and S. Niar, “A novel heterogeneous approximate multiplier for low power and high performance,” IEEE Embedded Systems Letters, vol. 10, no. 2, pp. 45–48, 2018. [Google Scholar]
2. Q. Xu, T. Mytkowicz and N. S. Kim, “Approximate computing: A survey,” IEEE Design & Test, vol. 33, no. 1, pp. 8–22, 2016. [Google Scholar]
3. J. Low and C. Jong, “Unified mitchell-based approximation for efficient logarithmic conversion circuit,” IEEE Transactions on Computers, vol. 64, no. 6, pp. 1783–1797, 2015. [Google Scholar]
4. S. Narayanamoorthy, H. Moghaddam, Z. Liu, T. Park and N. S. Kim, “Energy-efficient approximate multiplication for digital signal processing and classification applications,” IEEE Transactions on Very Large Scale Integration Systems, vol. 23, no. 6, pp. 1180–1184, 2015. [Google Scholar]
5. N. S. Arya and R. M. Nair, “Approximate computing: A new trend in VLSI based multipliers for error resilient DIP applications,” International Research Journal of Engineering and Technology (IRJET), vol. 5, no. 4, pp. 3866–3869, 2018. [Google Scholar]
6. O. S. Faragallah, A. I. Sallam and H. S. El-Sayed, “Utilization of HEVC chacha20-based selective encryption for secure telehealth video conferencing,” Computers, Materials & Continua, vol. 70, no. 1, pp. 831–845, 2022. [Google Scholar]
7. G. M. S. Latha and S. Rooban, “Quantum-dot cellular automata circuits using an efficient design and performance analysis,” Sustainable Energy Technologies and Assessments, vol. 48, no. 3, pp. 1–10, 2021. [Google Scholar]
8. W. Liu, L. Chen, C. Wang, M. O. Neill and F. Lombardi, “Design and analysis of inexact floating-point adders,” IEEE Transactions on Computers, vol. 65, no. 1, pp. 308–314, 2016. [Google Scholar]
9. S. Suguna and R. Kiruthika, “Low latency and power efficient approximate multipliers using compressors,” International Journal of Engineering Research & Technology (IJERT), vol. 8, no. 4, pp. 593–596, 2019. [Google Scholar]
10. R. Praveena, “Enhanced portable LUT multiplier with gated power optimization for biomedical therapeutic devices,” Computers, Materials & Continua, vol. 63, no. 1, pp. 85–95, 2020. [Google Scholar]
11. S. Rooban, N. Subbulakshmi and Y. P. Vamsi, “Low power circuit design for dynamic comparator,” International Journal of Performability Engineering, vol. 17, no. 5, pp. 444–4450, 2021. [Google Scholar]
12. C. H. Chang, J. Guand and M. Zhang, “Ultra low-voltage low-power CMOS 4-2 and 5-2 compressors for fast arithmetic circuits,” IEEE Transactions on Circuits and Systems-I, vol. 51, no. 10, pp. 1985–1997, 2004. [Google Scholar]
13. H. Jiang, J. Han, F. Qiao and F. Lombardi, “Approximate radix-8 booth multipliers for low-power and high-performance operation,” IEEE Transactions on Computers, vol. 65, no. 8, pp. 2638–2644, 2016. [Google Scholar]
14. S. Nour, S. A. Salem and S. M. Habashy, “A hybrid model for reliability aware and energy-efficient in multicore systems,” Computers, Materials & Continua, vol. 70, no. 3, pp. 4447–4466, 2022. [Google Scholar]
15. S. Venkatachalam, E. Adams, H. J. Lee and S. B. Ko, “Design and analysis of area and power efficient approximate booth multipliers,” IEEE Transactions on Computers, vol. 68, no. 11, pp. 1697–1703, 2019. [Google Scholar]
16. H. Pei, X. Yi, H. Zhou and Y. He, “Design of ultra-low power consumption approximate 4-2 compressors based on the compensation characteristic,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 68, no. 1, pp. 461–465, 2020. [Google Scholar]
17. M. Z. Rahman, P. Anupriya, C. Kavitha and P. Hithendra Sai Kumar, “Development of decision feedback equalizer using simplified adaptive algorithms,” Journal of Critical Reviews, vol. 7, no. 4, pp. 305–309, 2020. [Google Scholar]
18. G. Thumbur, N. B. Gayathri, P. V. Reddy, M. Z. U. Rahman and A. Lay-Ekuakille, “Efficient pairing-free identity-based ADS-B authentication scheme with batch verification,” IEEE Transactions on Aerospace and Electronic Systems, vol. 55, no. 5, pp. 2473–2486, 2019. [Google Scholar]
19. R. Zendegani, M. Kamal, M. Bahadori, A. Afzali-Kusha and M. Pedram, “RoBA multiplier: A rounding-based approximate multiplier for high-speed yet energy-efficient digital signal processing,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 25, no. 2, pp. 393–401, 2017. [Google Scholar]
20. S. Vahdat, M. Kamal, A. Afzali-Kusha and M. Pedram, “TOSAM: An energy-efficient truncation- and rounding based scalable approximate multiplier,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 27, no. 5, pp. 1161–1173, 2019. [Google Scholar]
21. S. Hsiao, J. Z. Jian and M. Chen, “Low-cost FIR filter designs based on faithfully rounded truncated multiple constant multiplication/accumulation,” IEEE Transactions on Circuits and Systems II: Express Briefs Very, vol. 60, no. 5, pp. 287–291, 2013. [Google Scholar]
22. F. Noorbasha, M. Manasa, R. Tulasi Gouthami, S. Sruthi, D. Hari Priya et al., “FPGA implementation of cryptographic systems for symmetric encryption,” Journal of Theoretical and Applied Information Technology, vol. 95, no. 9, pp. 2038–2045, 2017. [Google Scholar]
23. S. Hashemi, R. I. Bahar and S. Reda, “DRUM: A dynamic range unbiased multiplier for approximate multipliers,” in ICCAD’15: Proc. of the IEEE/ACM Int. Conf. on Computer-Aided Design, Austin, pp. 418–425, 2015. [Google Scholar]
24. S. Vahdat, M. Kamal, A. Afzali-Kusha and M. Pedram, “LETAM: A low energy truncation-based approximate multiplier,” Computers & Electrical Engineering, vol. 63, no. 4, pp. 1–17, 2017. [Google Scholar]
25. Z. Wang, A. C. Bovik, H. R. Sheikhand and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612, 2004. [Google Scholar]
26. M. Z. U. Rahman, S. Surekha, K. P. Satamraju, S. S. Mirza and A. Lay-Ekuakille, “A collateral sensor data sharing framework for decentralized healthcare systems,” IEEE Sensors Journal, vol. 21, no. 24, pp. 27848–27857, 2021. [Google Scholar]
27. G. J. Sullivan, J. Ohm, W. J. Hanand and T. Wiegand, “Overview of the high efficiency video coding (HEVC) standard,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 22, no. 12, pp. 1649–1668, 2012. [Google Scholar]
28. I. Almomani, A. Alkhayer and W. El-Shafai, “Novel ransomware hiding model using HEVC steganography approach,” Computers, Materials & Continua, vol. 70, no. 1, pp. 1209–1228, 2022. [Google Scholar]
29. P. Kulkarni, P. Gupta, and M. Ercegovac, “Trading accuracy for power with an underdesigned multiplier architecture,” Journal of low Power Electronics, vol. 7, no. 4, pp. 490–501, 2011. [Google Scholar]
30. M. Manasa, F. Noorbasha, C. L. Sudheshna, M. Santhosh, M. Rahman et al., “Comparative analysis of cordic algorithm and taylor series expansion,” Journal of Theoretical & Applied Information Technology, vol. 95, no. 9, pp. 2015–2022, 2017. [Google Scholar]
31. W. Sun, G. Z. Dai, X. R. Zhang, X. Z. He and X. Chen, “TBE-net: A three-branch embedding network with part-aware ability and feature complementary learning for vehicle re-identification,” IEEE Transactions on Intelligent Transportation Systems, vol. 99, pp. 1–13, 2021. [Google Scholar]
32. W. Sun, L. Dai, X. R. Zhang, P. S. Chang and X. Z. He, “RSOD: Real-time small object detection algorithm in UAV-based traffic monitoring,” Applied Intelligence, vol. 52, pp. 1–16, 2021. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |