DOI:10.32604/cmc.2022.030954

| Computers, Materials & Continua DOI:10.32604/cmc.2022.030954 |  |
| Article |
High Efficiency Crypto-Watermarking System Based on Clifford-Multiwavelet for 3D Meshes Security
1Department of Computer Engineering, College of Computer Engineering and Sciences, Prince Sattam bin Abdulaziz University, Al-Kharj, 11942, Saudi Arabia
2Department of Computer Engineering and Sciences, Higher School of Sciences and Technology of Hammam Sousse, University of Sousse, Sousse, 4011, Tunisia
3LATIS Laboratory of Advanced Technology and Intelligent Systems, University of Sousse, Sousse, 4023, Tunisie
4Control and Energy Management Laboratory (CEM Lab.), Ecole Nationale d Ingenieurs de Sfax (ENIS), Institut Superieur de Biotechnologie de Sfax (ISBS), University of Sfax, Sfax, 3038, Tunisia
*Corresponding Author: Wajdi Elhamzi. Email: wajdi.elhamzi@essths.rnu.tn
Received: 07 April 2022; Accepted: 18 May 2022
Abstract: Since 3D mesh security has become intellectual property, 3D watermarking algorithms have continued to appear to secure 3D meshes shared by remote users and saved in distant multimedia databases. The novelty of our approach is that it uses a new Clifford-multiwavelet transform to insert copyright data in a multiresolution domain, allowing us to greatly expand the size of the watermark. After that, our method does two rounds of insertion, each applying a different type of Clifford-wavelet transform. Before being placed into the Clifford-multiwavelet coefficients, the watermark, which is a mixture of the mesh description, source mesh signature (produced using SHA512), and a logo encrypted using the RSA (Ronald Shamir Adleman) technique, is encoded using Turbo-code. Using the Least Significant Bit method steps, data embedding involves modulation and insertion processes. Finally, the watermarked mesh is reconstructed using the inverse Clifford-multiwavelet transform. Due to the utilization of a hybrid insertion domain, our technique has demonstrated a very high insertion rate while retaining mesh quality. The mesh is watermarked, and the extracted data is acquired in real-time. Our approach is also resistant to the most common types of attacks. Our findings reveal that the current approach improves on previous efforts.
Keywords: Digital watermarking; Clifford-multiwavelet transform; Multiwavelet entropy; LSB method RSA algorithm; RSA algorithm; Turbocode; 3D multiresolution meshes
Three-dimensional imaging is a relatively new area; the utilization of 3D objects started with the introduction of personal computers in 1980. Since then, 3D imaging has grown in parallel with advances in computer power and internet connection speeds, allowing for the fast transmission of big data.
3D mesh is a novel data format that can model real-world things. Today, with the evolution of computing, this type of data has been mainly used for a variety of purposes since its inception, including medical image creation, computer-aided design, games, virtual reality, scientific simulation, and artificial intelligence.
3D objects have been progressively used in all domains during the previous decade. Because of the vast range of applications for 3D multiresolution meshes, their protection has become intellectual property. This sort of material is routinely shared between remote users and preserved in remote multimedia databases. Unfortunately, distributing 3D meshes among remote users has resulted in significant security issues. Digital copying, for example, results in no quality degradation. However, unlike counterfeit analog works, digital replication is inexpensive, and counterfeiters can operate anonymously without leaving a trace. All of these problems show that legal protection alone is not enough to make sure that works that are available to the public can be managed in peace.
In fact, one of the proposed solutions to these issues is digital watermarking. Watermarking 3D meshes, like watermarking photos, videos, and music, entails injecting data into the mesh without degrading the quality of the host mesh. Obviously, added data must not be erased, even if mesh treatments are used. Many new efforts have appeared in this context to safeguard mesh copyright, [1–5]. The main thing about 3D watermarking is where and how we can put information in.
Efforts to develop 3D watermarking algorithms have continued to exist until now in order to attain this goal. Using several approaches, researchers have been attempting to establish the optimal balance between insertion rate, invisibility, and robustness. Despite these advancements, the field of 3D watermarking is still far from mature.
Three types of insertion were chosen in the recently published works: spatial, frequency, and multi-resolution. On the one hand, these domains have been employed individually, and no hybrid 3D watermarking has been presented, despite the success of hybrid algorithms for other forms of data such as photos and videos. Watermarked data, on the other hand, is copyright information in the form of a binary sequence. There is no work that attempts to put an entire image into the 3D mesh.
The concept of multi-resolution is becoming increasingly relevant in the fields of geometric modeling and, in particular, object visualization. The original goal of multi-resolution was to make complex and dense meshes easier to work with, especially those made with subdivision techniques or 3D scanners. As a remedy, we present a new 3D crypto-watermarking approach that targets 3D multiresolution meshes in this work. Our method uses Clifford-multiwavelet to make the mesh more invisible while keeping the rate of insertion high. SHA512 is used to create the signature of the mesh source, and turbocode is used to make sure the mesh is strong.
The rest of this paper is organized as follows. Section 2 is dedicated to the state of the art by giving an overview of the recently published approaches aimed at securing 3D meshes as well as the different techniques. Section 3 explains the basic principles and mathematical basis of the Clifford multi-wavelet transform. After introducing the tools to be used, an overview of our approach, namely the insertion and extraction steps, is developed in Section 4. Next, Section 5 is devoted to metrics and evaluation, as its title indicates. It, therefore, aims to explain the metrics used during the experimentation of our algorithm. Section 6 is concerned with the experimental results, with eventual interpretations and discussion. The paper is concluded in Section 7.
Since the emergence of very high-speed computer networks, allowing the storage of 3D meshes in remote multimedia databases and their sharing between remote users, major security problems have appeared. Watermarking techniques may be divided into two basic categories: spatial and spectral. These approaches change the mesh’s shape or topology in order to embed the signature in the spatial domain in a more localized or global manner. In the second group of approaches, a spectral transform coefficient is changed by changing certain parts of the coefficients.
As a result, solutions such as watermarking [6,7], encryption [7], and steganographic [8–10] techniques have continued to emerge up to the present day. Several 3D watermarking technologies have arisen, especially to safeguard 3D meshes. The main goal of this paper is to use a variety of approaches and tools to find the best compromise between watermark requirements such as insertion rate, invisibility, and attack resistance. The insertion domain is used as a criterion for classifying these solutions. The first category includes approaches that operate in the spatial domain, such as Hitendra’s in [11], Tsai et al. in [12], and Wang et al. in [13]. Data is embedded in topological or geometric information in these methods. An altered domain is employed in the second category. A watermarking method based on computational ghost photography is proposed in the discrete wavelet transform domain in [14]. Then, an approach for protecting the integrity of 3D models expressed as a set of vertices and polygons is described in [15]. As an innovative and simpler flexible encryption scheme, Flexible Cryptosystem Based on Cellular Automata (FcCA) is suggested here by [16]. 3D objects and images of various sorts may be encrypted without any loss using FcCA’s simplified approaches for making cellular automata irreversible and a strong, adaptable cryptosystem. On the other hand, a statistical 3D watermarking approach is presented in [17] that stands out for the prominence of its points. It uses the invariance of salient points and their ability to be automatically detected to develop an automated region-wise and reversible watermark embedding strategy. In telemedicine applications, the user needs non-deformable medical data for diagnosis, and the watermark cannot make the original data unreadable. In this situation, [18] proposes an invisible 3D medical watermark based on the wavelet transform. This watermark embeds information about the watermark in the vertices of the relevant area of the 3D model to make sure that the 3D model is invisible.
The most commonly utilized domains are the frequency domain [2], Discrete Fourier Transform [1], and multiresolution domain [19]. Data is introduced in this example by altering the frequency and multiresolution coefficients. Despite the substantial advancements brought about by algorithms proposed over the last decade, the digital watermarking sector still has flaws. This is due, first and foremost, to the difficulty of finding the optimal compromise between watermark invisibility, large capacity, and resilience, all of which are mutually exclusive (the increase in capacity causes either a deterioration of the mesh quality or a reduction in the level of robustness). Second, as compared to other mesh types, processing 3D multiresolution meshes is a difficult task. Because of how 3D meshes look at different resolutions, these meshes are very sensitive when you work with them. This is because meshes look different at different resolutions. As a result, we present a new crypto-watermarking technique in this study that uses the Clifford-Multiwavelet transform to optimize the amount of information entered while retaining mesh quality. To improve the strength of our technique against the most common assaults, we use the RSA algorithm and turbocode.
To achieve the greatest balance between the amount of information to be inserted (which must be the maximum), the quality of the mesh (which must remain intact), and the robustness against attacks (the ability to correctly extract data despite attacks), we used the following techniques:
3.1 Clifford Wavelets/Multi-Wavelets and Entropy
The main tools to be used in our investigation, wavelets and their extensions to multiwavelets, are recalled in this section.
3.1.1 Clifford Wavelets/Multi-Wavelets
In the early 1980s, wavelet analysis emerged as a multidisciplinary technique that brought together engineers, mathematicians, and physicists. The mathematical synthesis produced fresh findings that broadened the scope of each original subject. The majority of scientists have heard of wavelets by this point.
When particular fields of research required frequency and temporal analysis at the same time, wavelets were born. Fourier analysis was the sole technique available in the nineteenth century for decomposing a signal/image into its frequency components [20]. Unfortunately, it only lets you do frequency analysis, not temporal localization, which is important for changes that happen quickly.
Multiwavelets have been around since the early 1990s as an alternative interpretation of wavelets that allows wavelet analysis to be rewritten in a vector form. The bulk of known multiwavelet formulations, especially in experimental contexts, start with a single wavelet or scaling function ψ/φ as illustrated by Eq. (1), and take the vector into account.
where N is the length of the matching filter for such functions. Although this perspective of wavelets has several advantages, such as short support, smoothness, precision, symmetry, and orthogonality, it also has significant disadvantages. However, due to the non-independence of the multiwavelet components, it invariably creates some connection between the components of the multiwavelet decomposition of signals/image, especially in non-orthogonal cases. Clifford multiwavelets will be used in the current paper. Multiwavelets, like Haar-Faber-Schauder multiwavelets, have been used in, [21–23] and have proven to be effective in estimating biological signals. In [23], the authors have developed an entropy-based procedure for approximating signals with such wavelets by considering a multiwavelet case whose components are exactly Haar and Faber-Schauder wavelets. Clifford wavelets, which were very recently invented, are responsible for this variation, [24,25]. By treating their Clifford components, such as the real parts, vector parts, bi-vector parts, and so on, as wavelets and merging them to generate a multiwavelet, such wavelets will be demonstrated to be able to induce a variation of multiwavelets in a natural fashion. Wavelet processing is done by using current families of multiwavelets that are made from single wavelets and have independent multi-scaling components and multiwavelet mother functions.
Denote next
The real Clifford algebra
In the real Clifford algebra, one of the concepts utilized to construct wavelets is the real Clifford algebra.
The structure of Clifford algebras, as well as its flexibility to encompass several forms of vector analysis at the same time, are the most demanding aspects of such notions. Clifford wavelets can be built in two ways, according to the literature. The first is based on spin groups and, as a result, includes the rotation factor in the wavelet analysis along with the translation and dilatation factors. See, [26,27]. Monogenic polynomials are used in the second problem. These are natural extensions of orthogonal polynomials in the context of Clifford algebras. As you may recall, orthogonal polynomials are commonly used in wavelet theory and signal/image processing. See for example, [21–22,26,28,29].
In this paper, we will apply the method presented in, [24,25] in which a class of Clifford-Hermite-Jacobi wavelet functions were formed by considering the Clifford-weight as indicated by Eq. (4).
This leads to a Clifford mother wavelet as
By fixing
where the
3.1.2 Clifford Multi-Wavelets Entropy
The goal of this section is to demonstrate that the entropy measure can be a useful processor for obtaining an optimal data approximation. The evaluation of wavelet entropy will allow for the accurate determination of the ideal reconstruction order. Remember that entropy, in its broadest sense, is a type of dimension from both a mathematical and scientific standpoint. As a result, it should be a global measure of invariance for the examined system in some way. As the multiresolution level rises, its value will tend to stabilize.
Shannon’s entropy is a metric for determining the randomness or order/disorder of information in a system. It also allows for the calculation of the smallest amount of data required to describe a system without sacrificing information, according to, [30,31]. Entropy-based techniques have been developed in, [32] to pick the appropriate basis for expressing the information from a wavelet packet library. In, [33, 34] the notion of entropy has been utilized in the same manner as before, to extract substantial information about turbulent flow fields from a discrete wavelet packet. Some experimental scenarios based on wavelet entropy for optimal scale search and coherent secondary flow characterization have been applied in, [35]. Rosso created a spectral entropy wavelet entropy approach in, [36] to quantify the complexity of a system by calculating the homogeneity of a signal’s spectral distribution from its discrete wavelet transform.
RSA (Ron Rivest, Adi Shamir, and Len Adleman), invented in 1977, is a symmetrical encryption algorithm that transforms a clear message (plain text) using a secret key K into an encrypted message (ciphertext), [37]. Since RSA is a symmetric algorithm, this same k key should be sent to the receiver to be able to decode the encrypted message. A public key is used to encrypt data, and a private key is used to decrypt it. The three phases of using the RSA algorithm are as follows:
– Key generations: Since RSA belongs to the category of asymmetric encryption algorithms, two keys must be used. The generation of these keys follows the following procedure:
a. Generate two large random primes, p and q. (In our case there are generated using a pseudo-random generator).
b. Compute
c. Choose an integer e such as
d. Compute the secret exponent d such as
The public key is then formed by the couple (n, e). As for the private key, it is formed by
– Encryption: The encryption phase is executed by the sender before the message is sent and it includes:
a. Getting the receiver’s public key (n, e).
b. Decomposition of the message into blocks of size m with
c. Encryption of each block by applying the formula:
d. Sending the Cipher Text Cipher to the Receiver
– Decryption: Once received, the message should be decrypted to be understandable. To do so, the receiver should apply the following steps:
a. Decompose the ciphertext into blocks of size m with
b. Decrypt each the bloc using formula:
The LSB (Least Significant Bit) approach is a stenographic technique that uses a sample of data’s least significant bit to represent another, as illustrated in Fig. 1. We employed the LSB approach in this paper to inject data into 3D meshes, particularly through its Clifford multi-wavelet coefficients. In fact, our watermarking technology is invisible because the low-weight bits of these coefficients are changed based on the information to be added.
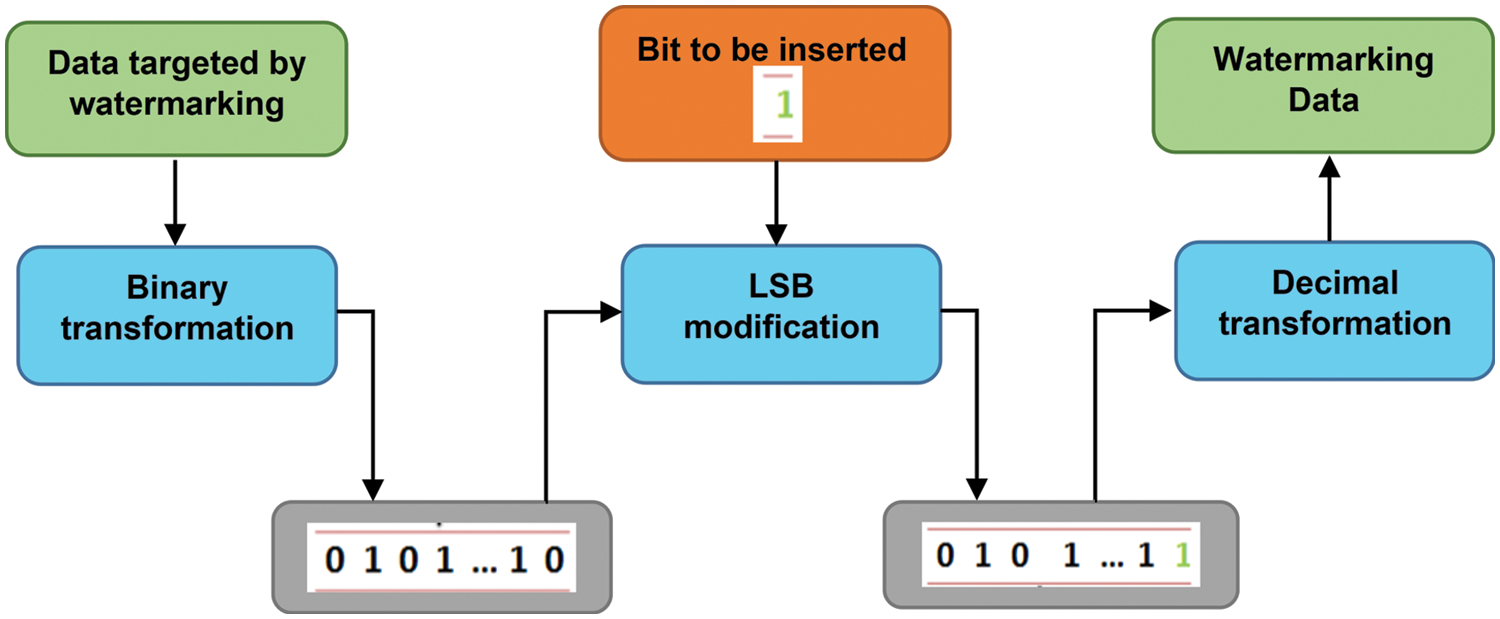
Figure 1: LSB method
The problem of reliability and robustness of the data transmitted through noisy channels has always been one of the concerns of those working in the field of telecommunications. Indeed, although countless domains require transmission without alteration, the problem of errors still persists. Error-correcting codes, though little known and widely used, can remedy this problem. The main purpose of a watermarking algorithm is the correct extraction of the watermark, especially if it concerns critical information. Watermarked meshes are often processed in order to exploit them. These treatments can readily change and even erase data that has already been input.
The efficacy of error-correcting codes in the telecommunications area has prompted us to consider using them to retrieve altered watermarks. We employ parallel turbo coding extensively in this paper. Because this new concept is the concatenation of two convolutional codes that are separated by an interleaving block, it is similar to concatenated error-correcting codes that are put together. Although this concatenation doubles the size of the output information, it significantly improves the model’s capacity to repair errors. We put a special emphasis on parallel concatenation in this paper.
Parallel turbo encoder: To add a control sequence to the original data, this step is performed before the dissemination stage. During the decoding step, these sequences enable error correction. The parallel turbo encoder uses two convolutional encoders to encode data at the same time. The result is in the form of three codewords, as shown in Fig. 2. The concatenation of these three becomes the final codeword (to be transmitted).
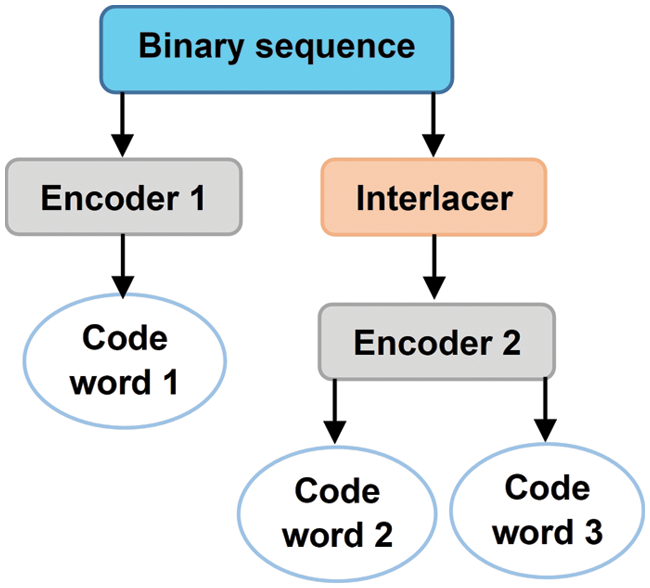
Figure 2: Parallel turbo encoder
Parallel turbo decoder: Its goal is to decode input data and repair any problems it finds. This decoder’s output data should be identical to that of the encoder’s input data. Fig. 3 shows the parallel turbo decoder architecture, which includes two convolutional decoders that use the Viterbi algorithm, two interleaves, and one deinterleave.
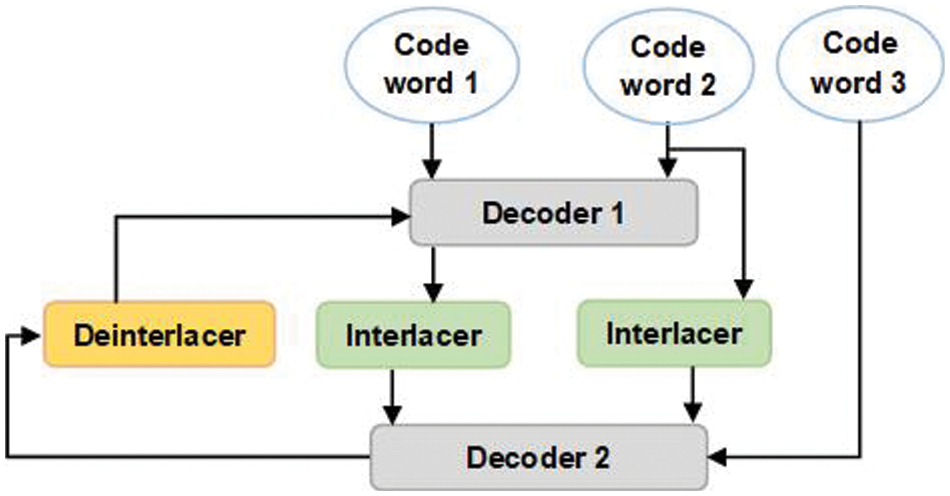
Figure 3: Parallel turbo decoder
Interleave block: It is a necessary component in the schematic of a turbo code, and its absence has a substantial impact on its power. Indeed, this block permits data to be swapped during their transition between the convolutional codes utilized, so that two symbols close to the origin are as far apart as possible, allowing direct action on the minimum Hamming distance of these codes. This enables, for example, the transformation of a grouped-bit error into an error scattered across the full sequence. Based on how the swap is done, the interleaving blocks can be put into three groups: transpose interleave, random interleave, and symmetrical interleave.
A digital watermarking scheme, as already mentioned, is an approach aimed at protecting digital data from unauthorized access. The data can be images, videos, sound signals, or 3D objects. In our case, we focus on protecting multi-resolution triangular meshes. Our algorithm is broken down into two phases, namely:
The watermarking diagram’s initial stage is this. Despite the high insertion rate, it seeks to put the data into the mesh without affecting its quality. Treatments or attacks on this mesh must not change the data that has been inserted. This phase includes preparing the watermark, host mesh, and two iterations of watermarking, as shown in Fig. 4.
The implementation of a Clifford-multiwavelet transform to derive two Clifford-wavelet coefficient vectors that will be adjusted according to the watermark is required for host mesh preparation. The fabrication of the watermark begins with the generation of the digital signature of the mesh’s source and the concatenation of that signature with a description. Second, the RSA technique will be used to encrypt a logo (which will reference copyright information). A turbo encoder will then encode the entire signal to generate the final codeword that will be placed into the mesh. Once the host mesh and watermark are complete, the LSB technique will be used for two iterations of insertion. Different modulation coefficients are used to avoid overlap between the inserted data.
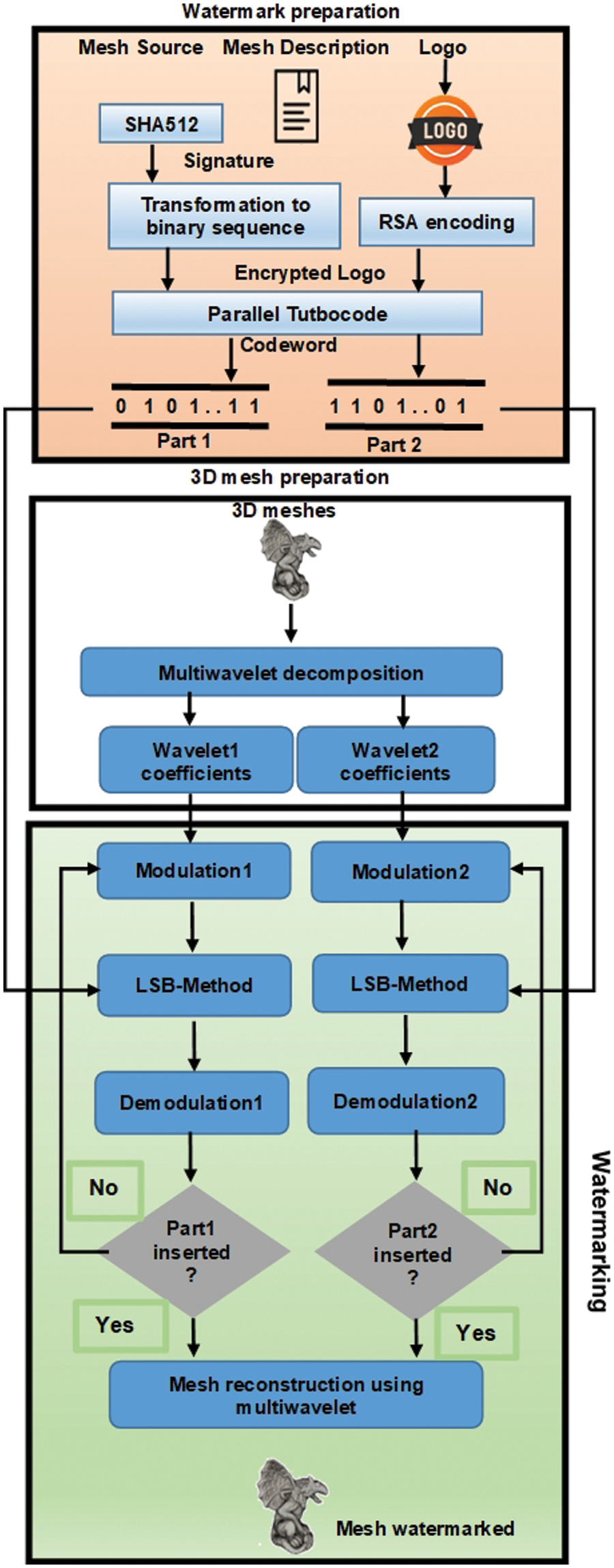
Figure 4: Insertion step
After a dissemination phase, the 3D watermarked mesh should be received, and the inserted data should be retrieved accurately despite any attacks. To do this, the watermarked mesh is decomposed into watermarked wavelet coefficients using a Clifford multiwavelet decomposition. Later, as shown in Fig. 5, these go through two rounds of extraction to get both parts of the data that had already been entered.
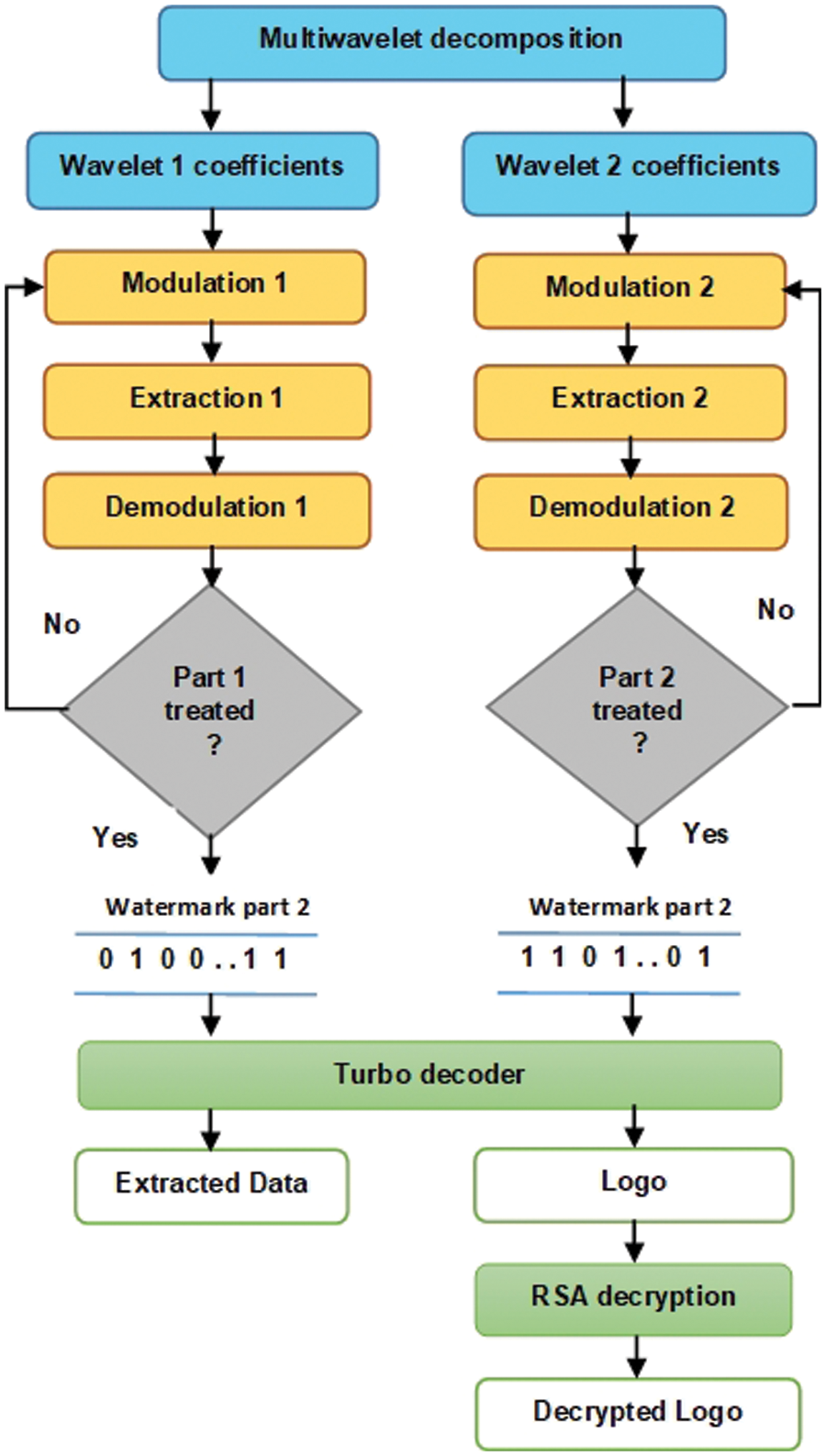
Figure 5: Extraction step
When the information is decoded with the parallel turbo decoder and the logo is decrypted, the integrity and copyright are checked.
The assessment of our approach must be made at two levels. The first is to study the effectiveness of the adopted encryption system, and this is done using PSNR and correlation. As for the second level, it is interested in evaluating the watermarking system. To do it, two essential points must be taken into account: the impact of the watermarking on the mesh quality and the robustness of the proposed algorithm (correct retrieval of inserted data).
5.1 Mean Square Quadratic Error
As shown in Eq. (6), to evaluate the invisibility criterion of a 3D watermarking algorithm, the Mean Square Quadratic Error (MSQE) can be used to find the distance between the watermarked and original meshes.
This distance is calculated between a point x from the first mesh and a surface from the second one.
The MSQE is then calculated using Eq. (7).
5.2 Peak Signal to Noise Ratio
Another tool of evaluation for the invisibility of digital watermarking algorithms is the Peak Signal to Noise Ratio (PSNR) [38]. It consists of finding the ratio between the original signals and those generated by watermarking. (See Eq. (8)).
To assess the influence of the application of attacks on the inserted watermark, the calculation of correlation can be used. The Eq. (9) [39,40] is used to calculate the correlation between the inserted information I1 and the extracted information I2:
As already mentioned, our approach is a link between cryptography and digital watermarking. The originality of this work is to transform the mesh in the multiresolution field using the clifford-multiwavelet transform. The joining of two wavelets allowed us to maximize the capacity of our watermarking algorithm while maintaining mesh quality. The RSA algorithm has the role of securing the inserted logo. Only unauthorized users have the right to extract it from the mesh and decrypt it. All tests were performed using a lenovo® core™i5 CPU 6300U @2.4 GHz with 12 GB Memory, running Windows 10 64-bit operating system and using MATLAB 8 and visual studio C++. The images used are grayscale images with size 512 × 512. To test our approach, we used the following triangular and multiresolution meshes: Feline (258046 vertex), Horse (112642 vertex), Venus (40962 vertex) and Rabbit (35329).
6.1.1 Encryption System Results
As already explained, a grayscale image, which can refer to a logo or image reflecting copyright information, is a part of the watermark. Before being inserted into the mesh, the image watermark is encrypted using the RSA algorithm. We show histograms of original and encrypted photos in Fig. 6. The histograms of encrypted photos are uniformly distributed, in contrast to those of original images, which have significant spikes. As a result, interpreting the appearance of the encrypted image is challenging.
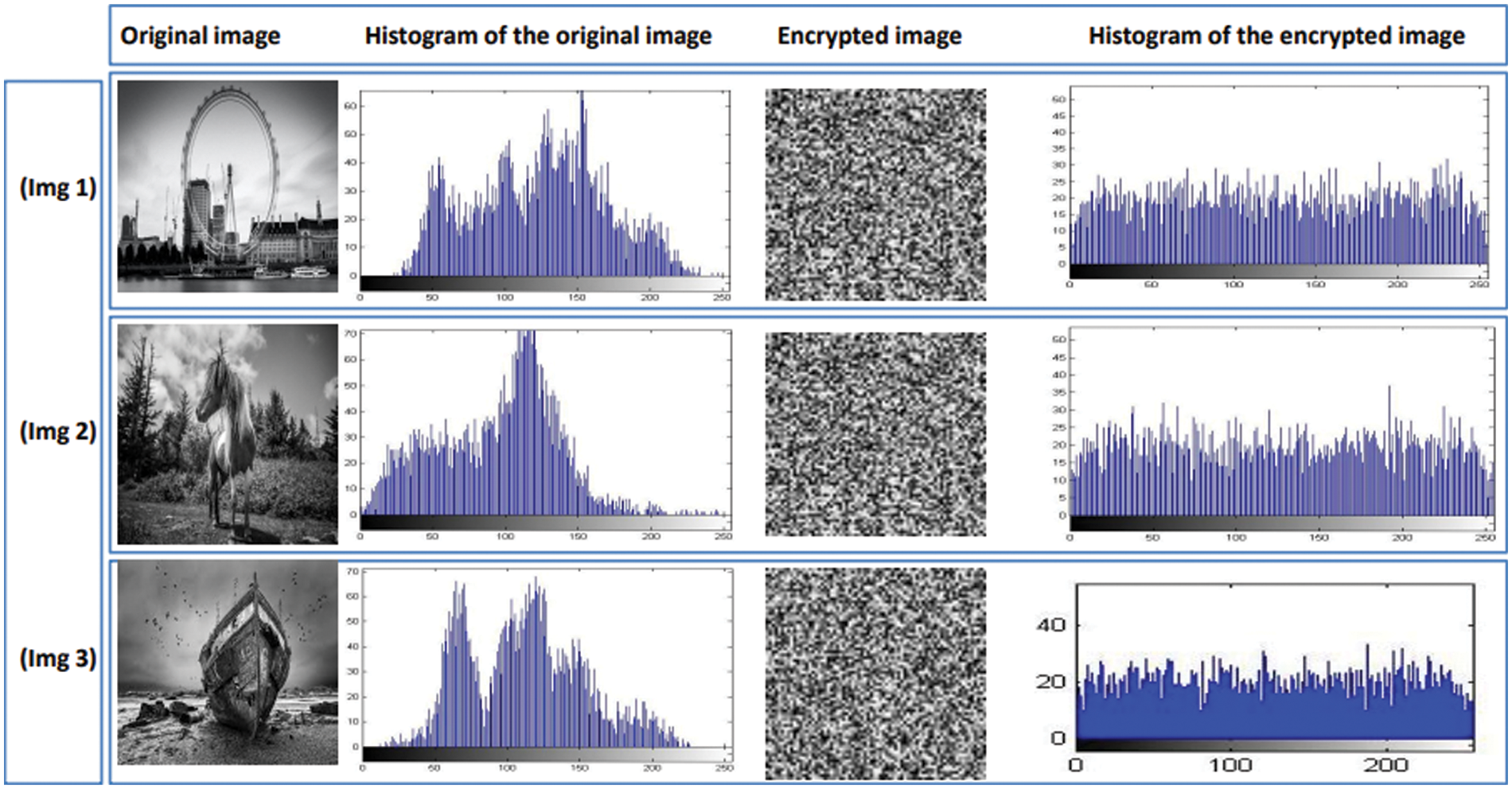
Figure 6: Histograms of original and encrypted images
Apart from histogram analysis, to conclude the efficiency of the encryption system, calculating entropy and PSNR is necessary. Results are presented in Tab. 1.
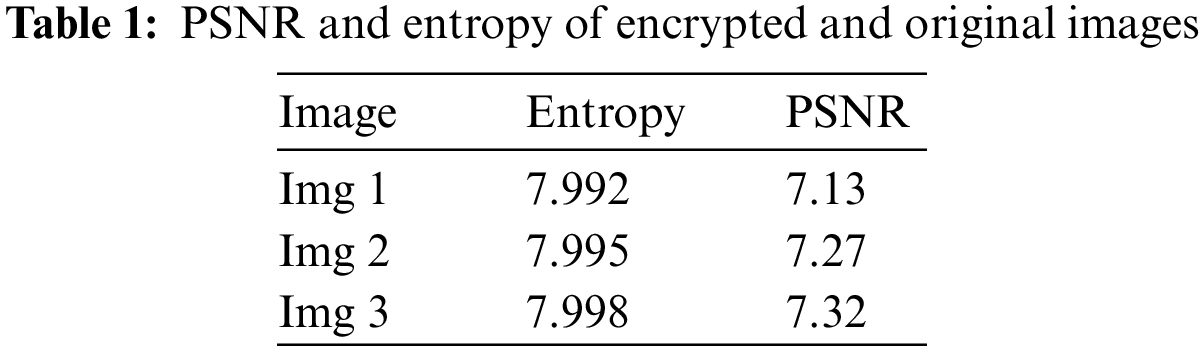
To ensure the effectiveness of an encryption algorithm [41] operating on an image, the entropy of an encrypted image should be very close to the ideal value of 8. The results in Tab. 1 show that the entropy values discovered are close to 8. As a result, we can conclude the efficiency of the used RSA algorithm, which has managed to equalize randomly the distribution of gray levels.
6.1.2 Watermarking System Results
• Invisibility and capacity criteria
It was necessary to investigate the invisibility and capacity of our technique in order to assess its efficacy. Tab. 2 shows that our approach has demonstrated a high insertion rate (on the order of 500000 bits) while retaining mesh quality (MSQE = 4.6 × 10 − 8 and PSNR = 134).
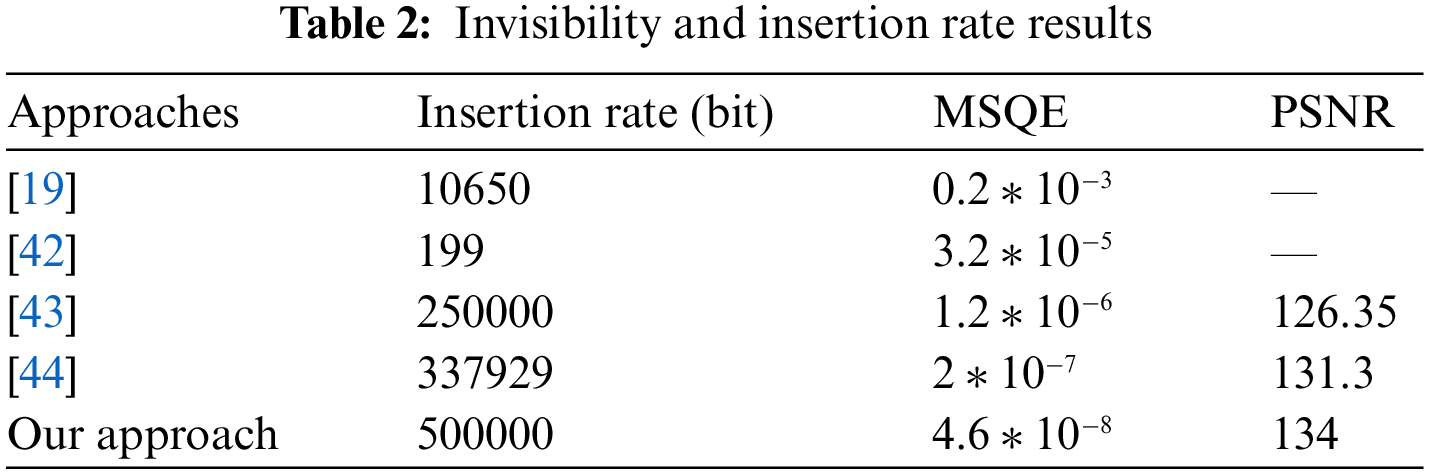
The high insertion rate (a grayscale image and a mesh description) is due to the employment of a Clifford-multiwavelet transform and a double round of insertion, which allows the quantity of information to be entered to be doubled. To evaluate the robustness of our algorithm we calculate the correlation between the extracted watermark and the original, data to evaluate the degree of watermark alteration. Of course, when the value of the correlation is near to 1, we can say that the watermark with stand attacks, [43].
In terms of MSQE value, it is in the 10 − 8 range. The transition of the mesh into the multiresolution domain (see Fig. 4) results in this low number, which reflects mesh quality conservation.
• Robustness against attacks criteria
Similarity transformation attack: Translation, rotation, and uniform scaling are all included. Watermarked meshes are routinely subjected to this process. Experiments, the results of which are shown in Tab. 3, show that, despite the attack, we can accurately extract input data. As a result, our method is resistant to such attacks.

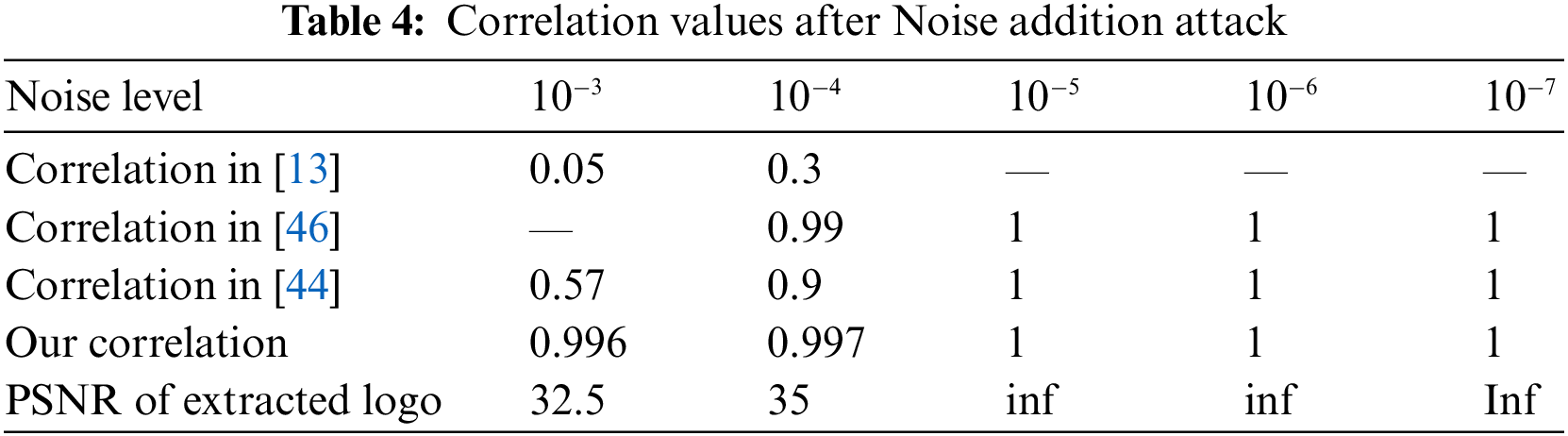
Noise addition attack: We applied noise addition to watermarked meshes and attempted to extract the inserted picture to test the resilience of our approach against this attack. We calculate the correlation between the original and extracted data for each noise level. The correlation values in Tab. 4 show that our watermarking system is resistant to this assault because they are greater than 0.95 (PSNR greater than 32) regardless of noise intensity. These results outperform those reported recently by, [13,44,45,46].
Smoothing attack: We varied the deformation factor and calculated the correlation between the injected and extracted data each time to test our approach’s robustness against smoothing attacks. As shown in Tab. 5, our system is capable of extracting the entire inserted data from a dfactor of 10 − 8. In comparison to recently published results in, [42,44,46–48], this outcome has improved.

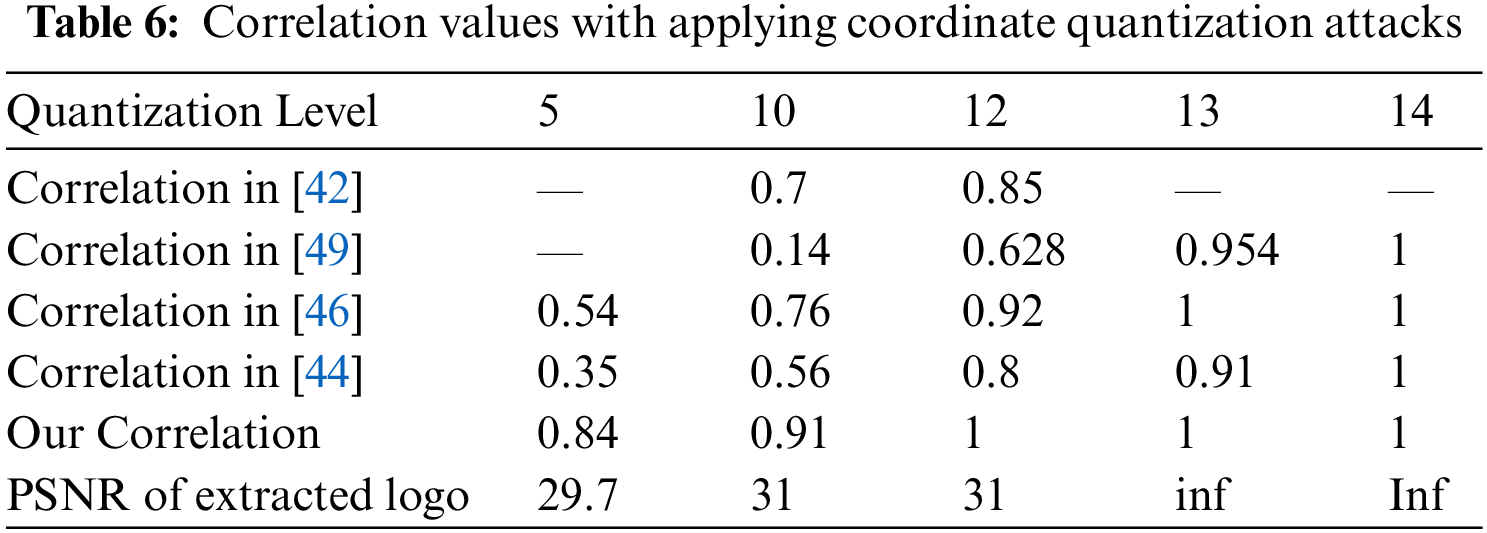
Coordinate quantization attack: To test our algorithm’s resistance to this attack, we changed the quantification level and calculated the correlation between the inserted and extracted data each time. For a level of quantification greater than 5, the obtained correlation (Tab. 6) is equivalent to 1. These results, which are supported by the application of convolutional codes to recover corrupted data, are far superior to those recently published, [42,44,46,49].
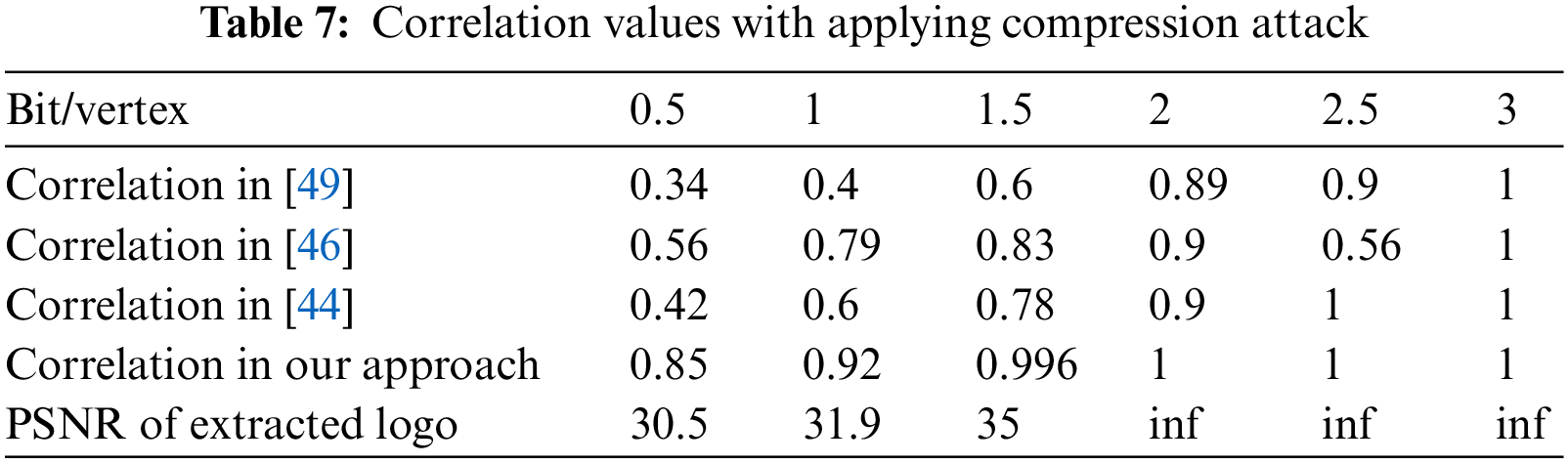
Compression attack: It is frequently used to reduce the size of watermarked meshes before transmission. The inserted image must not be altered or deteriorated by compression. The correlation values in Tab. 7 are close to or equal to 1 regardless of compression rate.
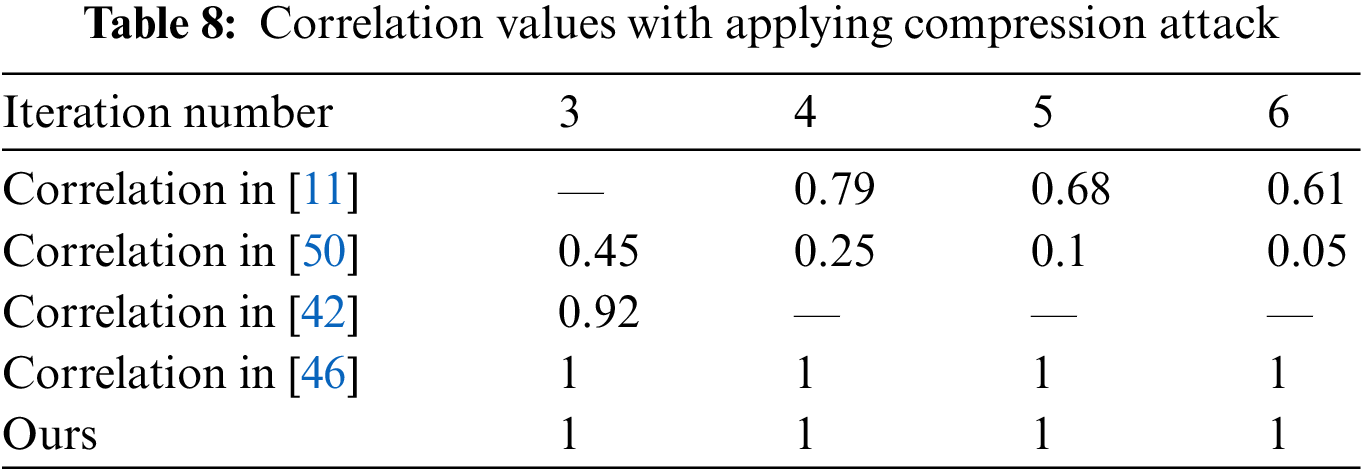
Robustness against Simplification attack: One of the most common attacks is simplification, which involves lowering the mesh resolution from one iteration to the next. We calculate the correlation between original and watermarked data in terms of iteration number to see how effective our solution is against this attack. The results in Tab. 8 show that our system is resistant to simplification attacks.
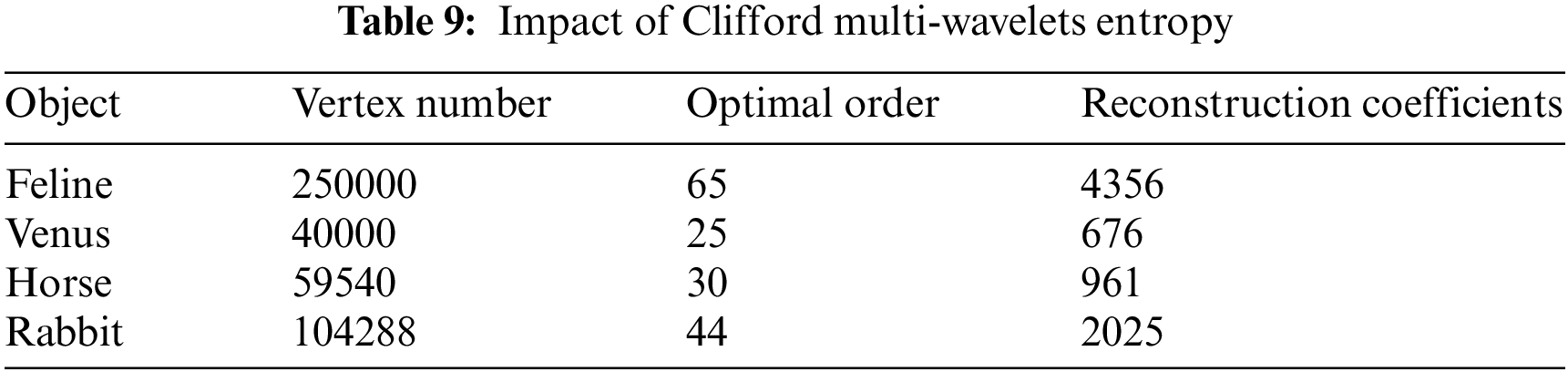
6.2 Clifford Multi-Wavelets Entropy Evaluation
A novel 3D multi-wavelet entropy was established in [22,23]. A link was made between multi-wavelet entropy and multi-wavelet modeling so that the optimal order of reconstruction could be found automatically and precisely without having to rebuild the model at each step of the modeling process. This makes it possible to find the optimal order of reconstruction without having to rebuild the 3D model at each step of the modeling process.
The results shown in Tab. 9 allow us to conclude that the multiwavelet entropy can be considered as a precise means to know in advance the optimal order of reconstruction.
In this paper, we describe a durable and high-capacity crypto-watermarking strategy for 3D multiresolution meshes based on the Clifford-multiwavelet transform, the RSA algorithm, and turbocode. The Clifford-multiwavelet transform is used to transform the host mesh into the multiresolution domain in our algorithm. Each coefficient resulting from this transformation passes through two iterations of insertion, with the message to be inserted using the LSB technique determining which iteration is used. A signature produced using the SHA512 algorithm, a mesh description, and a logo encrypted using the RSA algorithm make up the data to be put together. A parallel turbo encoder is used to encode all of the data. Mesh reconstruction begins after all of the data has been entered. After that, the watermarked mesh is obtained. Due to the usage of the Clifford-multiwavelet transform, the obtained results clearly illustrate that our technique protects mesh quality even when a huge quantity of information is inserted. The accurate retrieval of added information is not hampered by the use of various assaults (noise addition, coordinate quantization, smoothing, translation, rotation, uniform scaling, and compression) on a watermarked mesh. In comparison to recently published publications, the obtained findings are better. Furthermore, the efficacy of the given method has been demonstrated using a multiwavelet entropy on the same experimental examples of 3D objects. The Clifford multiwavelet was found to be effective in the experiments. Although, in many circumstances of information processing, this system has proven to be effective.
Acknowledgement: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IF-PSAU-2021/01/17567).
Funding Statement: This research work was funded by the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia through the project number (IF-PSAU-2021/01/17567).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. B. Geri, “A robust digital watermarking algorithm for three dimensional meshes,” in Int. Conf. on Information Engineering for Mechanics and Materials, Atlantis Press, pp. 1105–1110, 2015. [Google Scholar]
2. B. Lamiaa, H. I. Saleh and M. B. Abdelhalim, “Enhanced watermarking scheme for 3D mesh models,” in Int. Conf. on Information Technology, Amman, Jordan, pp. 612–619, 2015. [Google Scholar]
3. K. Yin, Z. Pan, J. Shi and D. Zhang, “Robust mesh watermarking based on multiresolution processing,” Computers & graphics, vol. 25, no. 3, pp. 409–420, 2001. [Google Scholar]
4. I. Sayahi, M. Jallouli, A. B. Mabrouk, C. B. Amar and M. A. Mahjoub, “A spherical harmonics-LSB-quantification adaptive watermarking approach for 3D multiresolution meshes security,” in Computer Analysis of Images and Patterns, vol. 13053, pp. 361–370, 2021. [Google Scholar]
5. M. Narendra, M. L. Valarmathi and L. J. Anbarasi, “Watermarking techniques for three-dimensional (3D) mesh models: A survey,” Multimedia Systems, vol. 28, no. 2, pp. 623–641, 2021. [Google Scholar]
6. W. Hao, L. Xiang, Y. Li, P. Yang and X. Shen, “Reversible natural language watermarking using synonym substitution and arithmetic coding,” Computers Materials & Continua, vol. 55, pp. 541–559, 2018. [Google Scholar]
7. M. Long, F. Peng and H. Y. Li, “Separable reversible data hiding and encryption for HEVC video,” Journal of Real-Time Image Processing, vol. 14, no. 1, pp. 171–182, 2018. [Google Scholar]
8. L. Y. Xiang, X. M. Sun, G. Luo and B. Xia, “Linguistic steganalysis using the features derived from synonym frequency,” Multimedia Tools and Applications, vol. 71, no. 3, pp. 1893–1911, 2014. [Google Scholar]
9. L. Y. Xiang, W. S. Wu, X. Li and C. F. Yang, “A linguistic steganography based on word indexing compression and candidate selection,” Multimedia Tools and Applications, vol. 77, no. 21, pp. 28969–28989, 2018. [Google Scholar]
10. L. Y. Xiang, X. H. Wang, C. F. Yang and P. Liu, “A novel linguistic steganography based on synonym run-length encoding,” IEICE Transactions on Information and Systems, vol. 100, no. 2, pp. 313–322, 2017. [Google Scholar]
11. G. Hitendra, K. K. Krishna, G. Manish and A. Suneeta, “Uniform selection of vertices for watermark embedding in 3-D polygon mesh using IEEE754 floating point representation,” in Int. Conf. on Communication Systems and Network Technologies, Bhopal, India, pp. 788–792, 2014. [Google Scholar]
12. Y. T. Yuan, “An efficient 3D information hiding algorithm based on sampling concepts,” Multimedia Tools and Applications, vol. 75, no. 13, pp. 7891–7907, 2016. [Google Scholar]
13. W. Jen-Tse, C. Yi-Ching, Y. Shyr-Shen and Y. Chun-Yuan, “Hamming code based watermarking scheme for 3D model verification,” in Int. Symposium on Computer, Consumer and Control, Taichung, Taiwan, pp. 1095–1098, 2014. [Google Scholar]
14. S. Yuan, D. A. Magayane, X. Liu, X. Zhou, G. Lu et al., “A blind watermarking scheme based on computational ghost imaging in wavelet domain,” Optics Communications, vol. 482, pp. 526–537, 2021. [Google Scholar]
15. M. Botta, D. Cavagnino, M. Gribaudo and P. Piazzolla, “Fragile watermarking of 3D models in a transformed domain,” Appl. Sci., vol. 10, no. 9, pp. 3244, 2020. [Google Scholar]
16. M. A. A. J. A. Mizher, R. Sulaiman, A. M. A. Abdalla and M. A. A. Mizher, “A simple flexible cryptosystem for meshed 3D objects and images,” Journal of King Saud University-Computer and Information Sciences, vol. 33, no. 6, pp. 629–646, 2021. [Google Scholar]
17. N. Medimegh, S. Belaid, M. Atri and N. Werghi, “3D mesh watermarking using salient points,” Multimedia Tools and Applications, vol. 77, no. 24, pp. 32287–32309, 2018. [Google Scholar]
18. X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]
19. A. O. Zaid, M. Hachani and W. Puech, “Wavelet-based high-capacity watermarking of 3-D irregular meshes,” Multimed Tools and Applications, vol. 74, no. 15, pp. 5897–5915, 2014. [Google Scholar]
20. H. Douzi, D. Mammass and F. Nouboud, “Faber-schauder wavelet transform, application to edge detection and image characterization,” Journal of Mathematical Imaging and Vision, vol. 14, no. 2, pp. 91–101, 2001. [Google Scholar]
21. M. Jallouli, M. Zemni, A. B. Mabrouk and M. A. Mahjoub, “Towards new multi-wavelets: Associated filters and algorithms. part l: Theoretical framework and investigation of biomedical signals, ECG and coronavirus cases,” Soft Computing, vol. 25, no. 22, pp. 14059–14079, 2021. [Google Scholar]
22. M. Jallouli, S. Arfaoui, A. B. Mabrouk and C. Cattani, “Clifford wavelet entropy for fetal ECG extraction,” Entropy, vol. 23, no. 7, pp. 844, 2021. [Google Scholar]
23. M. Zemni, M. Jallouli, A. B. Mabrouk and M. A. Mahjoub, “Explicit haar-schauder multiwavelet filters and algorithms. part II: Relative entropy-based estimation for optimal modeling of biomedical signals,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 17, no. 05, pp. 1950038, 2019. [Google Scholar]
24. S. Arfaoui, A. B. Mabrouk and C. Cattani, “New type of gegenbauer-hermite monogenic polynomials and associated clifford wavelets,” Journal of Mathematical Imaging and Vision, vol. 62, no. 1, pp. 73–97, 2020. [Google Scholar]
25. S. Arfaoui, A. B. Mabrouk and C. Cattani, “New type of gegenbauer-jacobi-hermite monogenic polynomials and associated continuous clifford wavelet transform,” Acta Applicandae Mathematicae, vol. 170, no. 1, pp. 1–35, 2020. [Google Scholar]
26. J. P. Antoine, R. Murenzi and P. Vandergheynst, “Directional wavelets revisited: Cauchy wavelets and symmetry detection in patterns,” Applied and Computational Harmonic Analysis, vol. 6, no. 3, pp. 314–345, 1999. [Google Scholar]
27. J. P. Antoine, P. Vandergheynst and R. Murenzi, “Two-dimensional directional wavelets in image processing,” Int. J. of Imaging Systems and Technology, vol. 7, no. 3, pp. 152–165, 1996. [Google Scholar]
28. M. Alvarez and G. Sansigre, “On polynomials with interlacing zeros,” in: C. Brezinski et al. (Eds.Polynomes orthogonaux et applications in Proceedings, Bar-le-Duc 1984, Berlin: Springer, pp. 255–258, 1985. [Google Scholar]
29. R. S. Stanković and B. J. Falkowski, “The haar wavelet transform: Its status and achievements,” Computers & Electrical Engineering, vol. 29, no. 1, pp. 25–44, 2003. [Google Scholar]
30. A. N. Kolmogorov, “On the shannon theory of information transmission in the case of continuous signals,” IRE Trans. Inf. Theory, vol. 2, no. 4, pp. 102–108, 1956. [Google Scholar]
31. C. Shannon, “A mathematical theory of communication,” The Bell System Technical Journal, vol. 27, no. 3, pp. 379–423, 1948. [Google Scholar]
32. R. R. Coifman and M. V. Wickerhauser, “Entropy-based algorithms for best basis selection,” IEEE Trans. Inf. Theory, vol. 38, no. 2, pp. 713–718, 1992. [Google Scholar]
33. F. Fischer, “Multiresolution analysis for 2D turbulence part 1: Wavelets vs cosince packets, a comparative study,” Discrete & Continuous Dynamical Systems-B, vol. 5, no. 3, pp. 659, 2005. [Google Scholar]
34. J. E. Ruppert-Felsot, O. Praud, E. Sharon and H. L. Swinney, “Extraction of coherent structures in a rotating turbulent flow experiment,” Physical Review E, vol. 72, no. 1, pp. 016311, 2005. [Google Scholar]
35. K. V. Bulusu and M. W. Plesniak, “Shannon entropy-based wavelet transform method for autonomous coherent structure identification in fluid flow field data,” Entropy, vol. 17, no. 10, pp. 6617–6642, 2015. [Google Scholar]
36. O. Rosso, S. Blanco, J. Yordanova, V. Kolev, A. Figliola et al., “Wavelet entropy: A new tool for analysis of short duration brain electrical signals,” Journal of Neuroscience Methods, vol. 105, no. 1, pp. 65–75, 2001. [Google Scholar]
37. Y. Guodong, J. Kaixin, W. Huishan, P. Chen and H. Xiaoling, “An asymmetric image encryption algorithm based on a fractional-order chaotic system and the RSA public-key cryptosystem,” International Journal of Bifurcation and Chao, vol. 30, no. 15, pp. 2050233, 2020. [Google Scholar]
38. K. A. Al-Afandy, O. S. Faragallah, E. S. M. EL-Rabaie, F. E. A. El-Samie and A. ELmhalawy, “Efficient color image watermarking using homomorphic based SVD in DWT domain,” in Fourth Int. Japan-Egypt Conf. on Electronics, Communications and Computers (JEC-ECC), Cairo, Egypt, IEEE, pp. 43–47, 2016. [Google Scholar]
39. K. A. Al-Afandy, O. S. Faragallah, E. S. M. EL-Rabaie, F. E. A. El-Samie and A. ELmhalawy, “A hybrid scheme for robust color image watermarking using DSWT in DCT domain,” in Fourth Int. Colloquium on Information Science and Technology (CiSt), Tangier, Morocco, IEEE, pp. 444–449, 2016. [Google Scholar]
40. M. Narendra, M. L. Valarmathi and L. J. Anbarasi, “Watermarking techniques for three-dimensional (3D) mesh models: A survey,” Multimedia Systems, vol. 28, no. 2, pp. 623–641, 2022. [Google Scholar]
41. S. Tjoa, C. Buttinger, K. Holzinger and P. Kieseberg, “Penetration testing artificial intelligence,” ERCIM News, vol. 123, pp. 36–37, 2020. [Google Scholar]
42. Y. Yang, R. Pintus, H. Rushmeier and I. Ivrissimtzis, “A 3D steganalytic algorithm and steganalysis-resistant watermarking,” IEEE Transactions on Visualization and Computer Graphics, vol. 23, no. 2, pp. 1002–1013, 2016. [Google Scholar]
43. I. Sayahi, A. Elkefi and C. B. Amar, “Blind watermarking algorithm for 3D multiresolution meshes based on spiral scanning method,” International Journal of Computer Science and Information Security, vol. 76, no. 15, pp. 16439–16462, 2016. [Google Scholar]
44. I. Sayahi, A. Elkefi and C. B. Amar, “Join cryptography and digital watermarking for 3D multiresolution meshes security,” in Int. Conf. on Image Analysis and Processing, Springer, Cham, pp. 637–647, 2017. [Google Scholar]
45. S. Hachicha, I. Sayahi, A. Elkefi and M. Zaied, “GPU-Based blind watermarking scheme for 3D multiresolution meshes using unlifted butterfly wavelet transformation,” Circuits System Signal Process, vol. 39, no. 3, pp. 1533–1560, 2020. [Google Scholar]
46. I. Sayahi, A. Elkefi and C. B. Amar, “Crypto-watermarking system for safe transmission of 3D multiresolution meshes,” International Journal of Multimedia Tools and Applications, vol. 78, no. 10, pp. 13877–13903, 2019. [Google Scholar]
47. M. Malipatil and D. C. Shubhangi, “An efficient 3D watermarking algorithm for 3D mesh models,” in Fourth Int. Conf. on I-SMAC (IoT in Social, Mobile, Analytics and Cloud)(I-SMAC), Palladam, India, IEEE, pp. 1–5, 2020. [Google Scholar]
48. I. Sayahi, A. Elkefi, M. Koubaa and C. B. Amar, “Robust watermarking algorithm for 3D multiresolution meshes,” in Int. Conf. on Computer Vision Theory and Applications, Berlin, Germany, pp. 150–157, 2015. [Google Scholar]
49. I. Sayahi, A. Elkefi and C. B. Amar, “A Multi-resolution approach for blind watermarking of 3D meshes using scanning spiral method,” in Int. Conf. on Computational Intelligence in Security for Information Systems, Wuxi, China, pp. 526–537, 2016. [Google Scholar]
50. D. J. Cho, “Watermarking scheme of mpeg-4 laser object for mobile device,” International Journal of Security and Its Applications, vol. 9, no. 1, pp. 305–312, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |