DOI:10.32604/cmc.2022.030698

| Computers, Materials & Continua DOI:10.32604/cmc.2022.030698 |  |
| Article |
Cartesian Product Based Transfer Learning Implementation for Brain Tumor Classification
1Electronic Engineering Department, Sir Syed University of Engineering & Technology, Karachi, 75300, Pakistan
2Department of Computer Science, Bahria University Karachi Campus, Karachi, 75260, Pakistan
3Christus Trinity Clinic, Texas, USA
*Corresponding Author: Irfan Ahmed Usmani. Email: iausmani@ssuet.edu.pk
Received: 31 March 2022; Accepted: 12 May 2022
Abstract: Knowledge-based transfer learning techniques have shown good performance for brain tumor classification, especially with small datasets. However, to obtain an optimized model for targeted brain tumor classification, it is challenging to select a pre-trained deep learning (DL) model, optimal values of hyperparameters, and optimization algorithm (solver). This paper first presents a brief review of recent literature related to brain tumor classification. Secondly, a robust framework for implementing the transfer learning technique is proposed. In the proposed framework, a Cartesian product matrix is generated to determine the optimal values of the two important hyperparameters: batch size and learning rate. An extensive exercise consisting of 435 simulations for 11 state-of-the-art pre-trained DL models was performed using 16 paired hyperparameters from the Cartesian product matrix to input the model with the three most popular solvers (stochastic gradient descent with momentum (SGDM), adaptive moment estimation (ADAM), and root mean squared propagation (RMSProp)). The 16 pairs were formed using individual hyperparameter values taken from literature, which generally addressed only one hyperparameter for optimization, rather than making a grid for a particular range. The proposed framework was assessed using a multi-class publicly available dataset consisting of glioma, meningioma, and pituitary tumors. Performance assessment shows that ResNet18 outperforms all other models in terms of accuracy, precision, specificity, and recall (sensitivity). The results are also compared with existing state-of-the-art research work that used the same dataset. The comparison was mainly based on performance metric “accuracy” with support of three other parameters “precision,” “recall,” and “specificity.” The comparison shows that the transfer learning technique, implemented through our proposed framework for brain tumor classification, outperformed all existing approaches. To the best of our knowledge, the proposed framework is an efficient framework that helped reduce the computational complexity and the time to attain optimal values of two important hyperparameters and consequently the optimized model with an accuracy of 99.56%.
Keywords: Deep transfer learning; Cartesian product; hyperparameter optimization; magnetic resonance imaging (MRI); brain tumor classification
One of the most widely known imperative causes for the increase in deaths among adults and children is brain tumors, which emerge as a group of anomalous cells developing inside or around the brain [1]. A precise and early brain tumor diagnosis plays a significant role in successful therapy. Among imaging modalities, MRI is the most extensively utilized non-invasive approach that succor radiologists and physicians in the discernment, diagnosis, and classification of brain tumors [2–4]. The radiologist approaches brain tumor classification in two ways: (i) categorizing the normal and anomalous magnetic resonance (MR) images and (ii) Scrutinize types and stages of the anomalous MR images [2].
Since brain tumors show a high-level of dissimilarities related to size, shape, and intensity [5], and tumors from various neurotic types might show comparatively similar appearances [6], therefore classification into different types and stages has become quite a wide research topic [7,8]. Manual classification of comparatively similar appearing brain tumor MR images is quite a challenging task, which relies upon the accessibility and capability of the radiologists. Despite the radiologist’s skills, the human visual system always bounds the analysis as the knowledge contained in an MR image surpasses the perception of the human visual system. Thus, the computer was used as the second eye to understand the MR images.
Computer vision-based image analysis methods usually encompass several sub-processes: preprocessing, segmentation, feature extraction, and classification. A low-level process, preprocessing consists of operations such as image sharpening, contrast enhancement, noise reduction, etc. [8]. Segmentation and classification are in the mid-level process domain. Image segmentation is the process used to extract the anomalous region from MR images, which helps to accurately locate the tumor and determine its size. The classification results depend upon suitable feature extraction from the delineated segmented region. Feature extraction is generally dependent on the knowledge of an expert in a particular domain, which makes it quite challenging for an unskilled person to use it in traditional image processing as well as in machine learning. One can eliminate the manual feature extraction problem by using DL approaches based on the self-learning hierarchical fashion principle.
Deep learning, especially convolutional neural networks (CNNs), outperforms many machine learning (ML) approaches in different areas, such as generating text [9], natural language processing [10], speech recognition [11], face verification [12], object detection [13], image description [14], machine translation [15], and the game of Go [16]. In particular, improved performance in computer vision boosted the utilization of DL methods for brain tumor MR image analysis [17,18]. For decades, CNN’s have been utilized but, they gained popularity when Krizhevsky [19] participated and won the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC) by developing a DL model “AlexNet” trained on ImageNet dataset [20], in 2012. Another similar but deeper visual geometry group (VGG) network, known as VGGNet, was presented by Zisserman and Simonyan [21] for classification in the 2014 ILSVRC. In fact, DL progressed with the availability of big data [20,22,23], advanced learning algorithms [24–28], and powerful graphical processing units (GPUs).
Algorithms based on deep learning for a certain classification task are difficult to effectively reuse and generalize. Therefore, a new algorithm from scratch has to be rebuilt even for a similar task that requires considerable computational power and time. At the same time, if sufficient data are not available for similar tasks, the developed algorithm may have difficulty in attaining the desired performance or might even fail to complete the tasks. In case of a shortage of data, for example, in brain tumor classification, the concept of knowledge-based transfer learning technique may be employed by using pre-trained DL models that are already trained for other classification problems. However, selection of a pre-trained DL model, hyperparameters' optimal values, and an optimization algorithm (solver) is challenging tasks to obtain an optimized model for targeted brain tumor classification. This research aims to provide a robust framework for implementing knowledge-based transfer learning techniques for brain tumor classification with a small-sized dataset. The research contributions of this study are as follows:
• A robust framework is proposed for brain tumor classification that describes complete approach to utilize the knowledge of a pre-trained DL model and re-train it for brain tumor classification with a small dataset.
• Following the framework, the knowledge transfer technique is deployed using 11 state-of-the-art pre-trained DL models to select an appropriate model for brain tumor classification.
• The concept of Cartesian Product Matrix is introduced to find the most suitable pair of two important hyperparameters, batch size and learning rate. The cartesian product matrix is formed from initialized set of hyperparameters vector. Each pre-trained DL model was evaluated for the three most popular solvers (SGDM, ADAM, RMSProp) to obtain the most appropriate set consisting of a solver, one batch size, and one learning rate.
• To investigate the model performance, a comprehensive comparative analysis of each model for brain tumor classification was conducted.
The rest of the paper is divided into five sections. Section 2 presents a comprehensive literature review related to brain tumor classification with the focus on their approaches. Section 3 describes the proposed framework to implement transfer learning technique with the used dataset, preprocessing, augmentation, pre-trained networks, fine-tuning and performance assessment. Section 4 discusses the results and analysis of the proposed frame work. At the end, conclusion and future work have been discussed in Section 5.
To classify brain tumors, many research efforts have contributed to different subfields of detection and classification processes. Different techniques have been presented for the segmentation of anomalous regions in MR images [29–32]. MRI(s) are classified into different types and grades after segmentation. In [33–35], binary classifiers were used for tumor classification into malignant and benign classes.
Abdolmaleki et al. [33] extracted 13 different features to differentiate malignant and benign tumors using a three-level neural network. The features were extracted with the help of the radiologists. The proposed methods were applied to a dataset of 165 patients’ MRIs, which helped to achieve accuracies of 94% and 91% for benign and malignant tumors, respectively. In [34], the author categorized brain tumors as malignant or benign by using a hybrid scheme consisting of a genetic algorithm (GA) and a support vector machine (SVM). Furthermore, Papageorgiou et al. [35] introduced fuzzy cognitive maps (FCM) to classify tumors into low-grade and high-grade gliomas. Papageorgiou’s FCM model used 100 cases and achieved 93.22% accuracy for high-grade gliomas and 90.26% accuracy for low-grade gliomas.
In addition to the binary classification of brain tumors, Zacharaki et al. [36] proposed a technique using SVM and K-nearest neighbor (KNN) for multi-classification of brain tumors into primary gliomas, meningiomas, metastases, and glioblastomas. This research encompasses sub-processes, such as segmentation and feature extraction, to perform multi-classification. Accuracies of 88% and 85% for binary classification and multi-classification, respectively, were achieved. Hsieh et al. [37] also proposed a technique based on extracted features from a dataset of 107 MR images, consisting of 73 and 34 low-grade and high-grade glioma MRIs respectively, to measure malignancy. The proposed technique produced accuracies of 83%, 76%, and 88% using local, global, and fused features, respectively. Sachdeva et al. [38] presented a technique that depends on optimal features, based on color and texture, extracted from segmented regions, and used GA in combination with SVM and artificial neural network (ANN). The technique achieved accuracies of 91.7% and 94.9% for GA-SVM and GA-ANN, respectively.
Cheng et al. [5] presented a framework based on the following approaches to extract features: intensity histogram, gray level co-occurrence matrix (GLCM), and bag-of-words (BoW). In the domain of classification, this research is considered as the first significant work towards brain tumor multi-classification using the challenging and largest publicly available dataset in figshare [39], consists of glioma, meningioma, and pituitary brain tumor types. The approach is dependent on a wide range of features extracted from a manually defined segmented region and applied as input to different classifiers. The author used sensitivity, specificity, and classification accuracy as measurement parameters and obtained the best results using SVM for a particular set of features. In [40], Ismael and Abdel Qadir worked on the same challenging publicly available dataset, as used in [5] and proposed an algorithm for brain tumor classification. The algorithm uses the Gabor filter and discrete wavelet transform (DWT) to extract the statistical features used to train the classifier. The authors randomly selected 70% and 30% of MR images for training and validation of the classifier, respectively. Feature extraction from a segmented region of interest (ROI) and its appropriate selection is significant in establishing the best learning of the classifier. These handcrafted features must be extracted by an expert with sound knowledge and skills to determine the most significant features. Furthermore, the feature extraction process requires a significant amount of time and is susceptible to errors when dealing with big data [41].
In contrast to ML, DL algorithms do not require handcrafted features. DL requires a preprocessed dataset and applies a self-learning approach to determine the significant features [42]. Eventually, many CNNs such as AlexNet [19], ResNet [43], and VGGNet [21] were deployed after being trained on a large ImageNet dataset in ILSVRC [20] for classification. These CNNs are recognized as state-of-the-art DL models [19,21,43]. Afshar et al. [44] proposed a method for the brain tumor classification based on the CapsNet model. The method relies on adopting CapsNets, capability of CapsNets, analysis of overfitting, and output visualization pattern setup. Furthermore, Zia et al. [45] presented a brain tumor classification technique that relied on rectangular window image cropping. The technique used DWT for feature extraction, principal component analysis for dimensionality reduction, and SVM for classification. Hossam et al. [46] presented a CNN-based DL model to classify different types of brain tumors using two datasets. They used one dataset for three-class brain tumor classification, while the other was used for glioma tumor classification into grades II, III, and IV. The proposed methodology proved to be useful for the multi-classification of brain tumors. Jia et al. [47] achieved an accuracy of 98.51% for normal and anomalous brain tissue classification while evaluating MR images. The author used a support vector machine to perform fully automatic heterogeneous segmentation of brain tumors based on the extreme learning machine (ELM) deep learning technique. They proposed a fully automatic algorithm with the support of structural, relaxometry, and morphological details to obtain optimum features.
The increase in deep CNN performance, owing to the concepts of feature extraction in a hierarchical fashion, motivated researchers to transfer the pre-trained network knowledge acquired during training with millions of images into new classification tasks with a small amount of data, to take advantage of their learned parameters, specifically, weights. Tab. 1 summarizes a review of research performed in the area of brain tumor classification based on knowledge-based transfer learning for the period 2017–2022. In [48], the author fine-tuned ResNet [49] and VGG [21], the pre-trained classification models, to distinguish between high-grade and low-grade brain tumors. They implemented the concept of transfer learning and achieved an accuracy of 97.19%. Talo et al. [50] presented a binary classifier based on the transfer learning concept for brain MR image classification into normal and anomalous brain images. The authors fine-tuned a pre-trained DL model, ResNet34, and claimed that this is the first work on brain MRI classification using the deep transfer learning approach. They used a dataset containing 613 images [51] and obtained better performance in comparison with other DL-based approaches using the same dataset. Sajjad et al. [52] used a pre-trained DL model and customized it for grading of brain tumors. The authors evaluated the proposed system on both original and segmented data. The results show a convincing performance in comparison with benchmark systems. Swati et al. [53] used VGG-19 [21], a pre-trained DL model, to transfer knowledge. The author performed a manual block-wise fine-tuning approach for the classification of a more challenging task of multi-class brain tumors. Following his work in [53], Swati proposed a method to develop similar brain tumor images based on content retrieval [54]. For similarity measurements, the author used the VGG-19 [21] features. Deepak et al. [55] utilized the knowledge of GoogleNet (ImageNet) [56] as a pre-trained DL model for brain tumor classification into different classes.
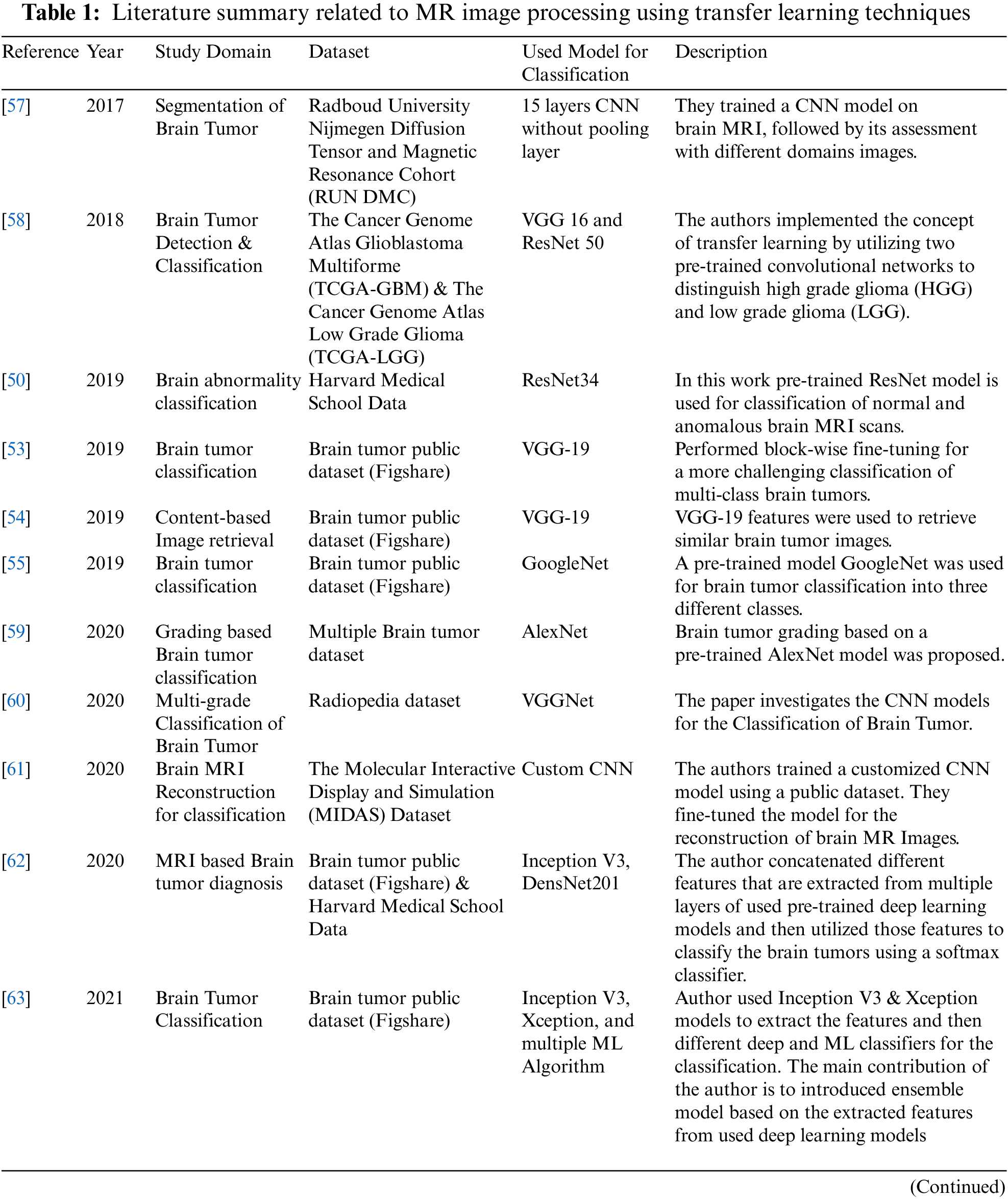
This section explains all the details related to the proposed framework, presented in Fig. 1, for implementing the transfer learning technique utilizing pre-trained DL models for the classification task. Any pre-trained classification model with its learned parameters can be used after customization. The proposed framework is based on a novel idea to input hyperparameters in the form of ordered pairs (batch size and learning rate). The ordered pair can be defined as a 2-tuple element of a matrix constructed using the concept of the Cartesian product of two initialized sets of batch size and learning rate. The following subsections discuss the step-by-step implementation of the transfer learning technique using the proposed framework.
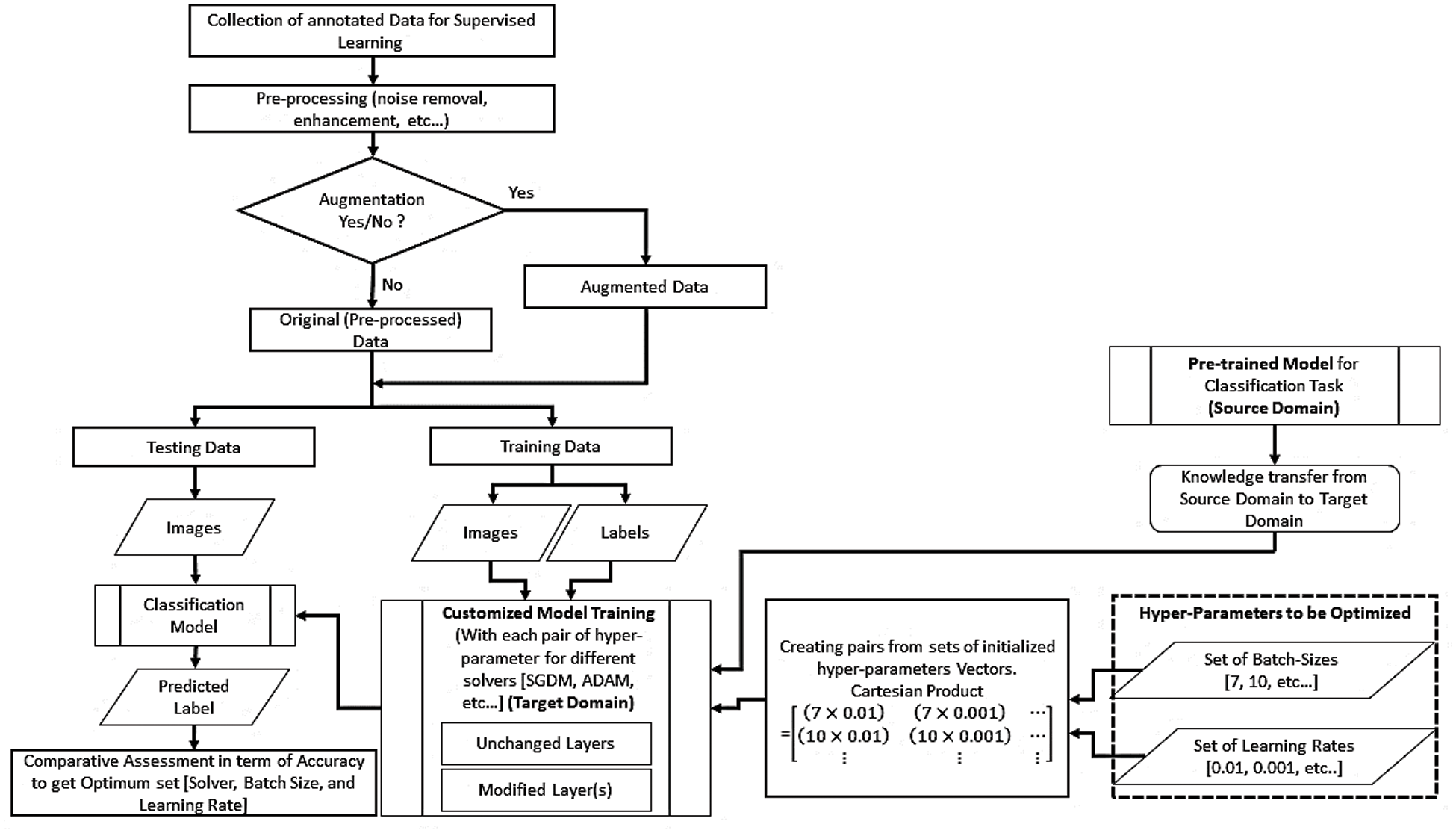
Figure 1: Proposed framework to implement transfer learning technique
A publicly accessible brain tumor dataset of 233 patients consisting of 3064 MR images [39], was used. Three types of brain tumor MR images comprising 1426 slices of gliomas, 708 slices of meningioma, and 930 slices of pituitary tumors are available in this dataset. Fig. 2 illustrates each type of tumor percentage in the dataset. The data is available in .mat file format (Matlab data format), contains a label for the image, patient ID, image in the form of a 512 × 512 matrix, a tumor mask, and discrete points coordinate on tumor border.
Dataset statistics clearly depicts that the classes in the dataset are imbalance. Imbalance dataset is itself a challenging issue in which predicting correctly smaller size class is more critical than larger size class. In this research, model-based approach, such as transfer learning technique, is used to tackle this issue. Experiments in previous research [50,53–55,57–64] have supported the use of model-based approach provided that the tuning parameters are chosen carefully. In fact, transfer learning technique takes advantage of the features extracted from source domain at different levels and compensates for the overall lack of samples in the training data or targeted domain, ending up with a good trained model for imbalanced small dataset.
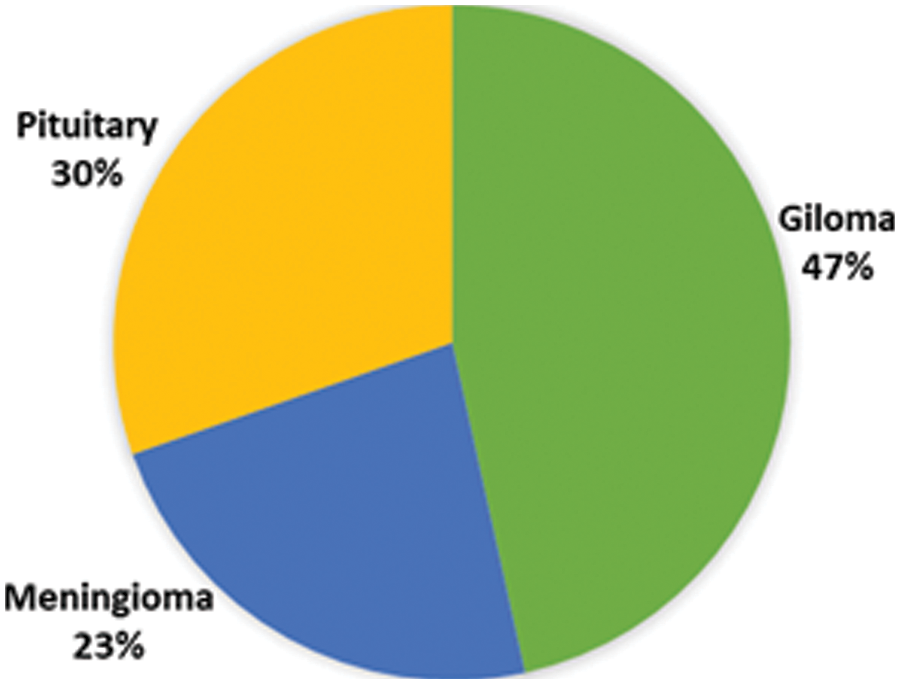
Figure 2: Percentage of different type of tumors in the dataset
Medical image analysis requires data preprocessing, which includes contrast enhancement and standardization. First, the dataset was normalized to the intensity values and then mapped to grayscale’s 256 levels using the relationship, as described in Eq. (1).
where
Figure 3: Original and enhanced image
The enhanced resultant images are resized and concatenated three times, as per the standard input image size of the pre-trained DL models, to create channels. Tab. 2 lists the models used in this research and their standard input sizes.

High-quality big data plays a significant role in the effective training of any DL model. It is undoubtedly expensive to collect sufficient medical data available for training to reconstruct the classifier. In general, data augmentation techniques are used to enlarge the data size to provide a larger input sample space to achieve the desired accuracy and to reduce overfitting.
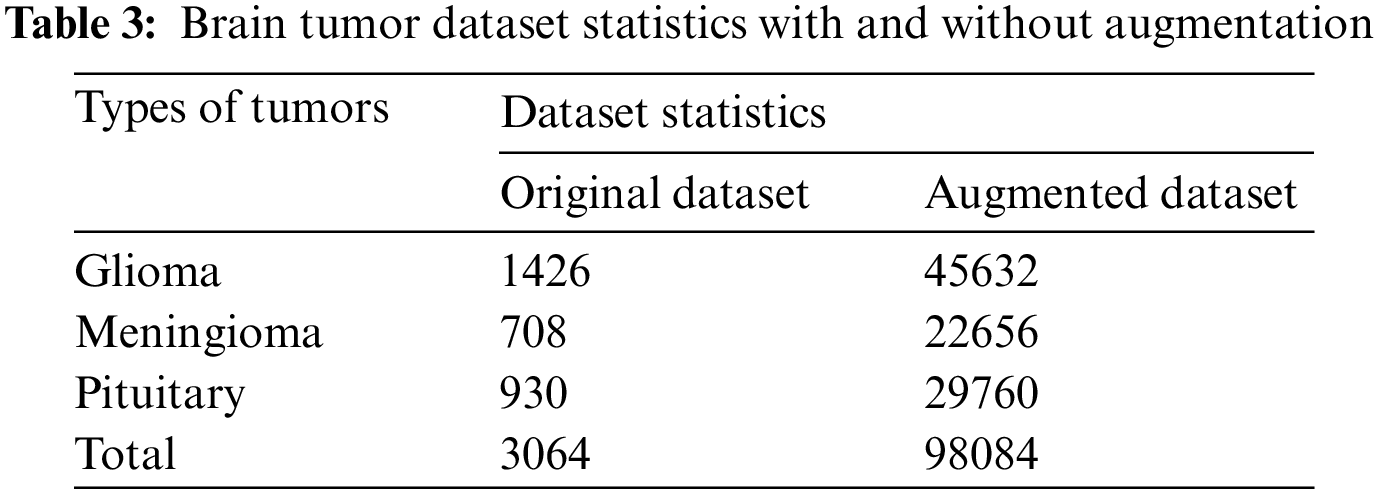
In this research, extensive data augmentation is performed not only to increase the data size but also to check the effectiveness of the knowledge-based transfer learning technique with and without data augmentation, particularly for our brain tumor classification task. A total of eight augmentation techniques with 32 different parameters were implemented to extend each data sample into 32 samples. Out of eight, four techniques–flipping, rotation, shears, and skewness–are for geometric transformation invariance, and the rest of the techniques, sharpening, Gaussian blur, emboss, and edge detection are used for noise invariance [52]. The details of the total dataset size and each class size before and after augmentation are listed in Tab. 3.
For the classification task, there were many pre-trained CNN models. In this research, the idea behind the proposed framework is domain adaptation, in which transfer learning allows us to utilize the network and knowledge in terms of network weights of pre-trained DL models, from a source domain, to re-train it using new training data for another classification task in the target domain. The data size and similarity between the target and source domain tasks are important parameters for pre-trained model selection. Because almost all pre-trained existing DL models are trained on millions of natural images, choosing one pre-trained model directly to implement the transfer learning technique for the classification of brain tumors is quite difficult. For this reason, we used 11 contemporary pre-trained DL models, as shown in Tab. 2, and fine-tuned them to find the optimum model for our classification task. All 11 models were selected based on their learned rich feature representation as they were trained on the ImageNet database, consisting of 1000 object categories except one GoogleNet variant that was trained on images from the places 365 database, consisting of 365 image categories. Other than the “similarity” between source and target domain, the selected model’s performance and efficiency differs because of many other characteristics such as nature of network architecture (sequential or Directed Acyclic Graph (DAG)), depth of the network (number of network layers), number of learned parameters (weights), etc. In this research, the selected models contain all types of networks, that is, sequential, DAG, and advanced compact CNN models.
In the proposed framework, all 11 selected pre-existing deep learning models were fine-tuned for brain tumor multi-classification. In general, deep learning models consist of different layers, including convolutional, max pooling, FC, softmax layer, and a last cross-entropy-based classification layer. Using the concept of transfer learning, we retained all the network layers with their learned parameters, particularly weights, except that the last FC layer was replaced with a new FC layer with output size three, and the network’s last cross-entropy-based classification layer is replaced with a new one. The retained layers help the network to use the low-level extracted features from the pre-trained model, while the replaced layers facilitate the network in high-level feature learning. The modified network is then fine-tuned to obtain an optimum model by training it with our brain tumor dataset. For training, the transfer learning technique uses two types of parameters: learned parameters (e.g., weights) from the original pre-existing deep learning model and hyperparameters, for example, batch size and learning rate, but the latter needs to be optimized. Because the choice of hyperparameters and their values depends on the targeted task, types in the dataset, and size of the dataset, it is quite difficult to select one specific hyper-parameter(s) optimal value that works for all pre-trained models.
In general, while training the CNN, a back-propagation algorithm is employed to minimize the cost function. Eq. (2) illustrates the cost function
where
where
We initialized two different sets
It can be generalized to
In our case, we transformed the Cartesian product vector into a matrix for a better understanding, as described in Eq. (8):
Each element of the Cartesian product matrix is applied as a pair of inputs for two hyperparameters to retrain the modified network architecture against each pre-trained deep learning model with our dataset for the brain tumor classification task. Each modified network architecture was evaluated for the three most popular solvers: SGDM, ADAM, and RMSProp. An extensive comparative assessment was conducted in terms of accuracy to obtain the optimal values of batch size and learning rate, along with the most appropriate solver.
The performance assessment of the proposed framework was carried out using the same performance metrics used in related references [5,40,52,53,55,62,64,70]. A classifier can be tested using four parameters: true positive (TP): an outcome where model predicts the positive class correctly, true negative (TN): an outcome where model predicts the negative class correctly, false positive (FP): an outcome where model predicts the positive class incorrectly, and false negative (FN): an outcome where model predicts the negative class incorrectly. These parameters can be extracted from the confusion matrix to compute the performance metrics: accuracy, precision, specificity, and sensitivity (recall).
Precision:
Precision represents the ratio of correctly predicted positive data samples (instances) to the total predicted positive instances. Mathematically,
Specificity:
Specificity measures the ratio of correctly predicted negative instances to the all instances in an actual class. Mathematically,
Sensitivity:
Sensitivity measures the ratio of correctly predicted positive instances to the all instances in an actual class. Mathematically,
Accuracy:
Accuracy measures the correctly classified instances with respect to the total number of instances.
4 Results and Analysis of Framework
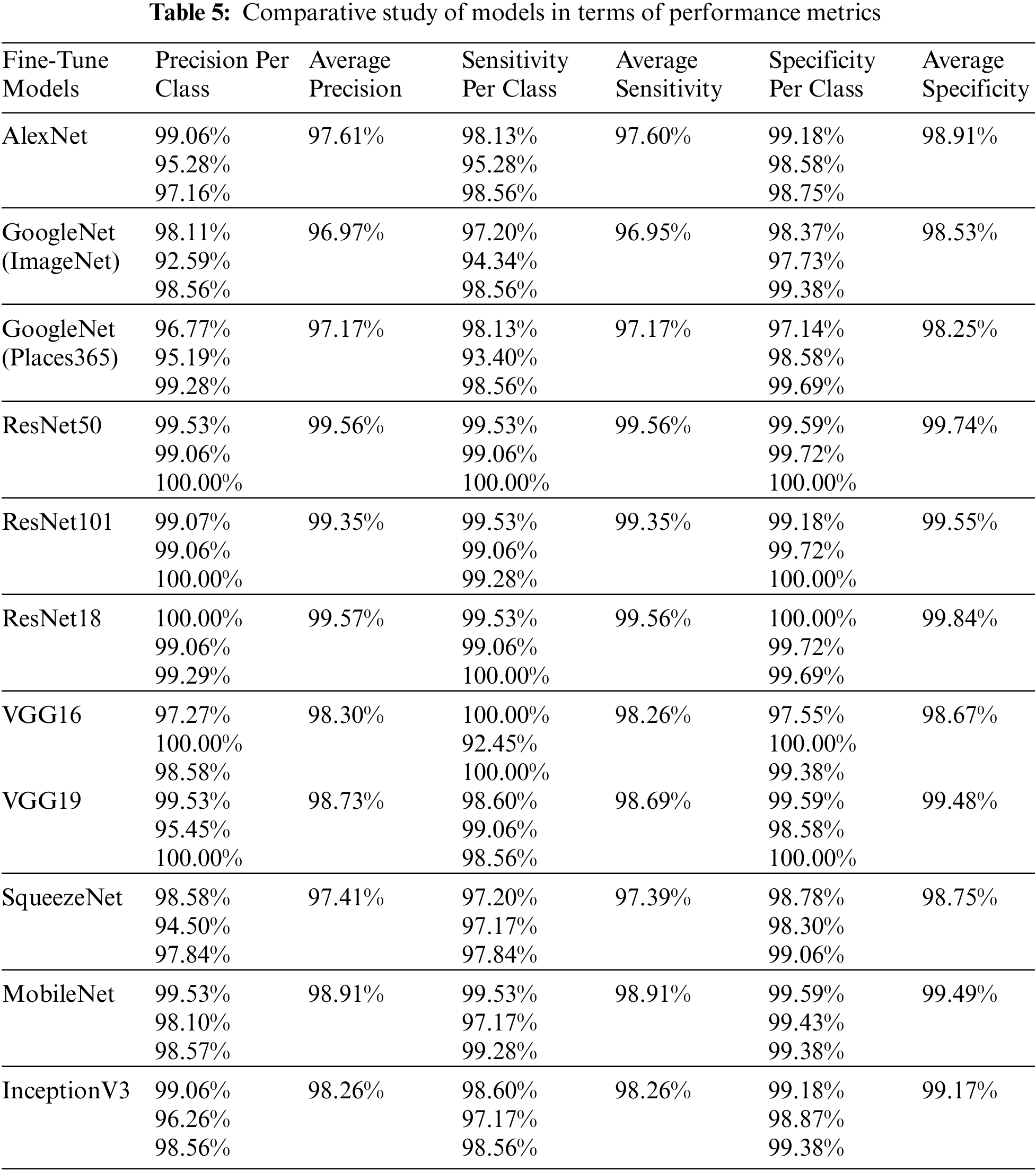
As discussed in Tab. 1, many researchers have explored transfer learning techniques for brain tumor classification by utilizing the knowledge of pre-trained DL models. The models were fine-tuned using different hyperparameters. However, the literature review reveals that pre-trained models have not been deeply investigated for brain tumor classification, particularly for multi-hyperparameters simultaneously. As discussed earlier, each hyperparameter has an impact on the model’s performance, depending on the targeted domain and task. To analyze the proposed framework, we performed an extensive comparative analysis to assess the optimal values of hyperparameters (Learning Rate and Batch Size) by applying their different values as 2-tuple input from a Cartesian product matrix, to 11 different deep learning models. The 11 models used for investigation were AlexNet, GoogleNet, GoogleNet (Places365) [71], ResNet18, ResNet50, ResNet101, VGG16, VGG19, SqueezeNet [72], MobileNet [73], and InceptionV3 [74]. The proposed framework was implemented and investigated for brain tumor classification using a system equipped with NVIDIA GEFORCE GTX 1080 – 8GB Graphics and MATLAB 2020. The dataset was divided into 70%, 15%, and 15% for training, validation, and testing of the model, respectively. After customizing the pre-trained deep learning model, a total of 435 experiments were performed with each pair of inputs from the Cartesian matrix of batch size and learning rate for the three most popular solvers. All the results in terms of accuracy are presented in Fig. 4.
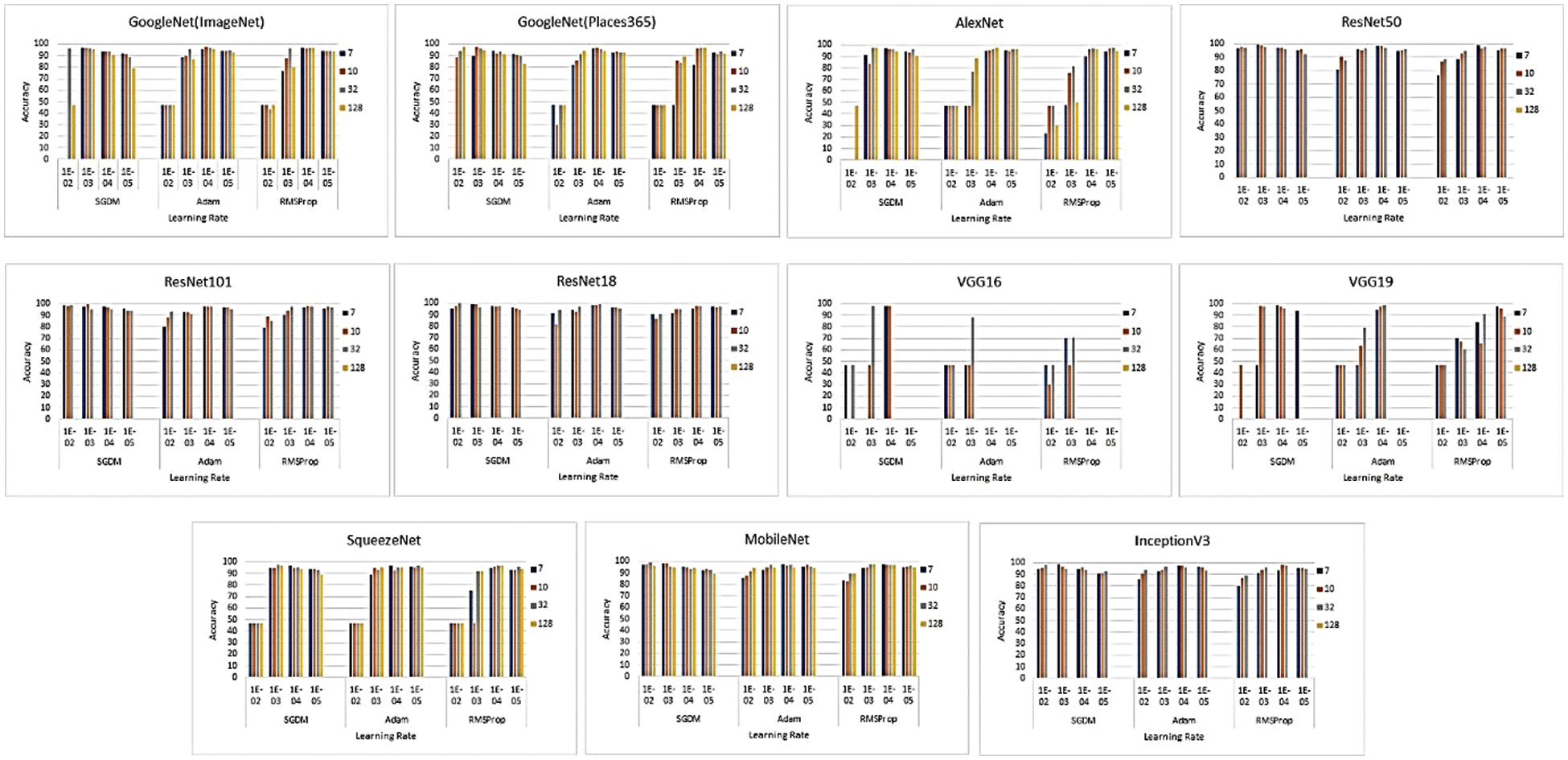
Figure 4: Performance evaluation in terms of accuracy for the pre-trained models using hyperparameters pair
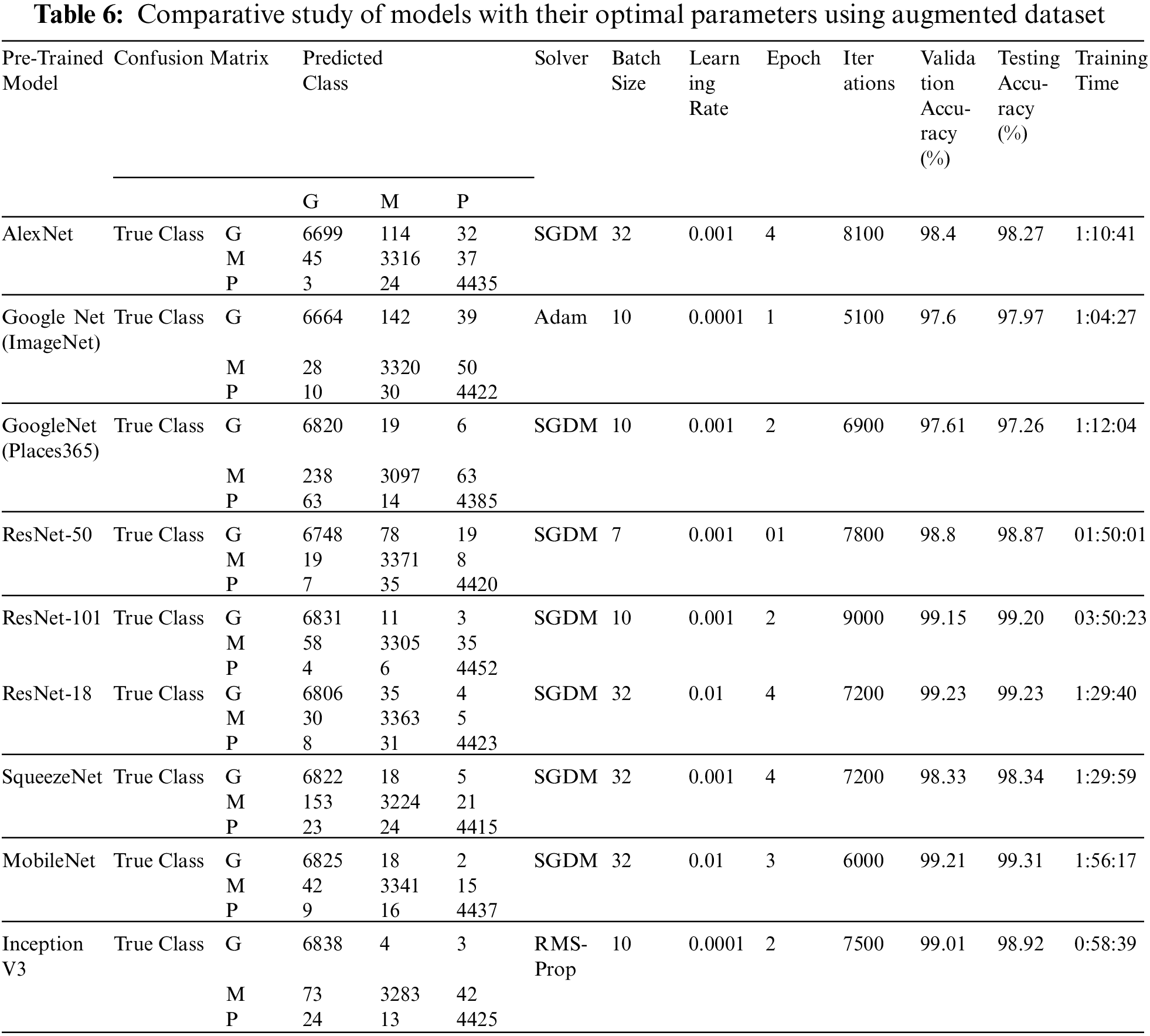
To determine the optimal parameters, we first separated the maximum accuracy result for each pre-trained model and summarized it in Tab. 4 with other parameters observed during the training processes. The other parameters are the number of epochs utilized in convergence, number of iterations, validation accuracy, training time, and confusion matrix. To determine the optimized model for our brain tumor classification problem, all experimental results were carefully investigated. Starting with AlexNet, out of 48 combinations of {Solver type, Batch Size, Learning Rate}, our proposed framework performed well for the combination {SGDM, 32, 0.001} with an accuracy of 97.6%. AlexNet showed good performance for another combination {Adam, 128, 0.0001} with an accuracy of 97.82%, but its training time was much higher than the previous one, and could not converge until forced stop on completing 100 epochs. It is quite obvious from the experimental results that the training time for AlexNet is considerably less than that for other pre-trained networks because of its sequential nature. The results of GoogleNet (ImageNet), GoogleNet (Places365), and SqueezeNet are almost the same as AlexNet, even though they have a complex architecture based on a DAG network. The modified models VGG16, VGG19, MobileNet, and InceptionV3 when re-trained using our proposed framework performed better than the models discussed earlier. All three variants of ResNet, especially ResNet18, outperformed all other networks with parameters {SGDM, 32, 0.01} by achieving 99.56% accuracy when using our proposed framework for brain tumor classification. This is due to the ResNet working principle of building a deeper network compared to other networks and its capability to solve the vanishing gradient problem simultaneously. Figs. 5(a) and 5(b) depict the training-validation accuracy and loss curve, and confusion matrix while training, validating, and testing ResNet18, the best-performing model. In addition to the ultimate accuracy measurement, utilizing three other measures: precision, recall, and specificity, the proposed framework was further evaluated. Tab. 5 summarizes the performance measures related to the above-mentioned measuring parameters for the average of all classes and each class separately as well for all deep learning networks presented in Tab. 4. The comparison shows that ResNet18 outperforms all the others in all the measuring fields. To the best of our knowledge, the strategy of our proposed framework has proven to be quite efficient, with an accuracy of 99.56%.
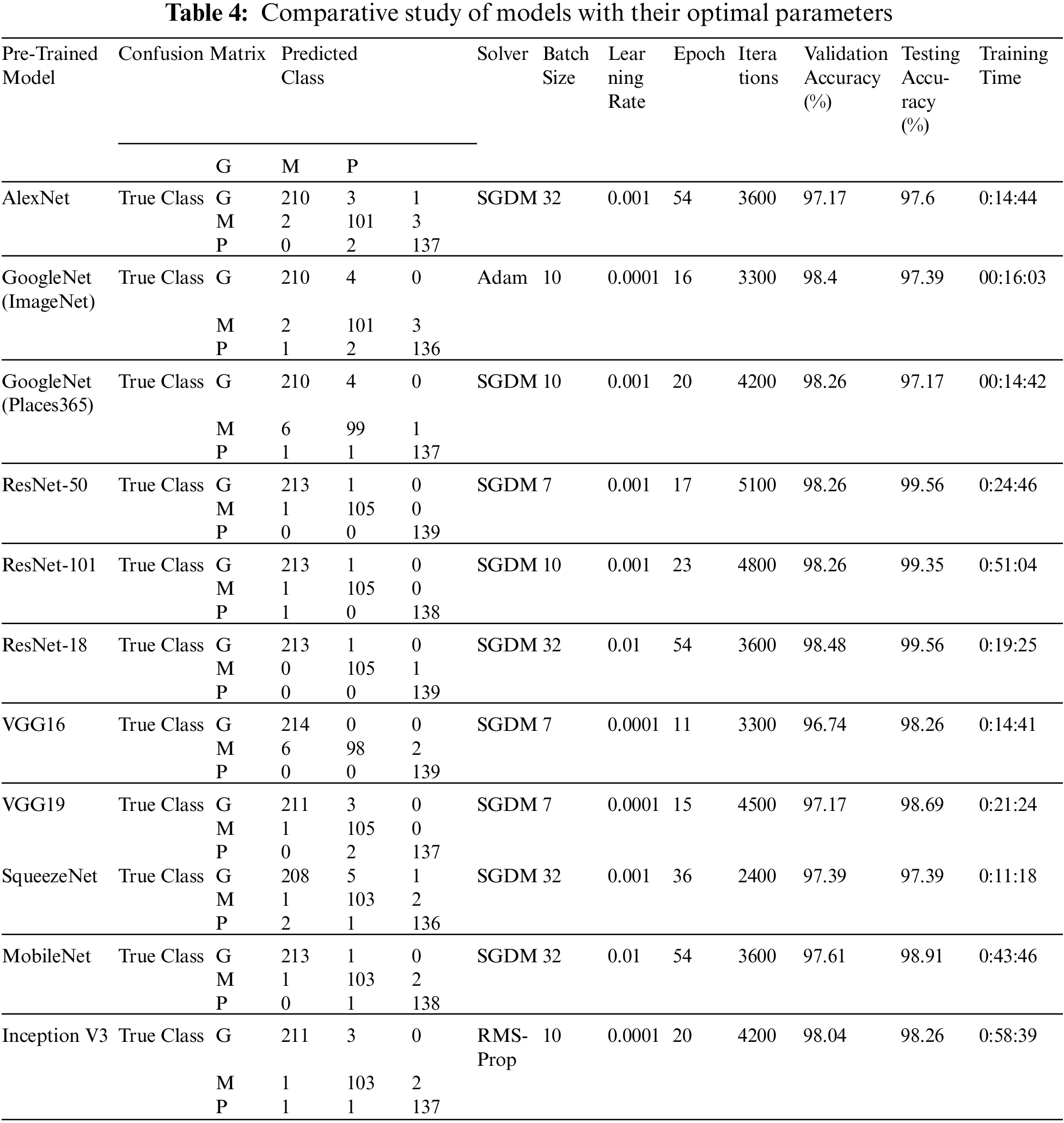
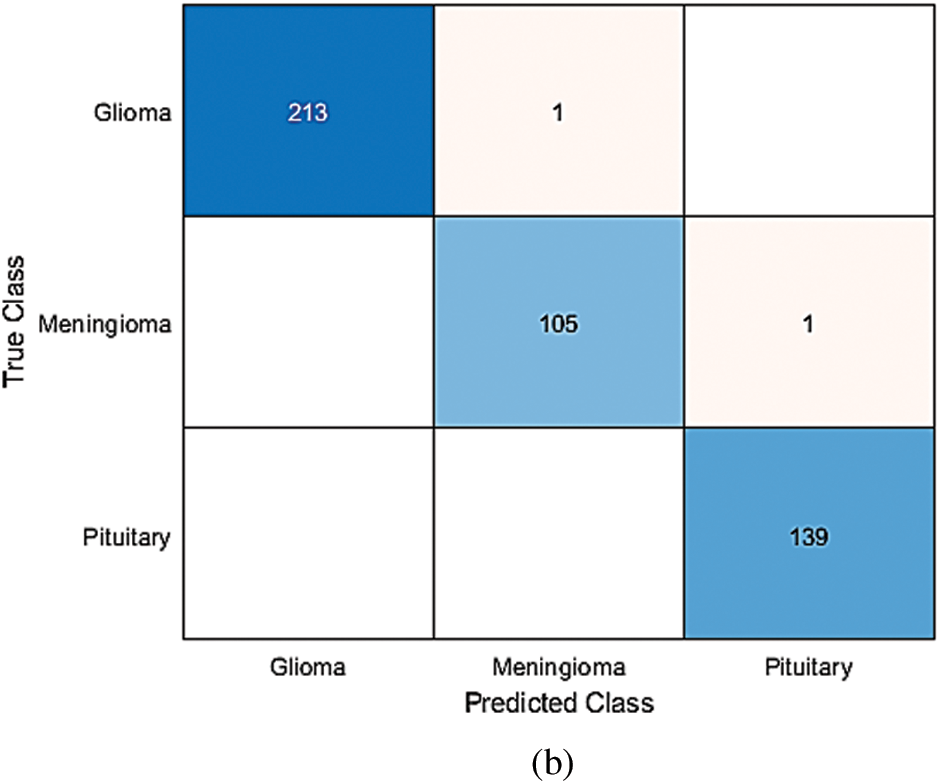
Figure 5: (a) Training-Validation accuracy and loss for best performing model, (b) Confusion matrix for best performing model
However, do we need an augmentation technique to increase the data size. In this research, as discussed above, to increase the data size, extensive data augmentation techniques are utilized, and the framework is evaluated only for the optimal hyperparameters that provide high accuracy for each pre-trained model without augmentation evaluation. Tab. 6 shows a minimum improvement of 0.09% using the GoogleNet (Places365) model and a maximum improvement of 0.95% using the SqueezeNet model, which shows quite similar results to the original data (without augmentation). This suggests that the transfer learning technique, if implemented with a proper framework for the selection of optimal hyperparameters, may not require data augmentation.
A performance comparison is presented in Tab. 7 between our work and other existing state-of-the-art research works that used the same brain tumor dataset for multi-type tumor classification. The comparison is mainly based on performance metric “accuracy” with support of three other parameters “precision,” “recall,” and “specificity.” The comparison shows that the transfer learning technique, implemented through our proposed framework for brain tumor classification, outperformed all existing approaches based on traditional image processing [5,40], CNN [44,70], and transfer learning [52,53,55,60,62,64,69].

This research presents a comprehensive literature review, along with a robust framework for implementing the transfer learning technique. The comprehensive review reveals that there is a need for a solution to select an appropriate pre-trained deep learning model and optimal hyperparameter(s) values for such an implementation. Our proposed model not only solves the model selection issue, but also helps in determining the optimal hyperparameter values. To determine the appropriate pre-trained deep learning model, 11 state-of-the-art pre-trained models were used. A Cartesian product matrix is created to obtain all possible pairs from initialized sets of hyperparameters (batch size and learning rate). All pairs were applied as input one-by-one to each pre-trained deep learning model and re-trained with our brain tumor dataset for the three most popular solvers for the evaluation of the performance of the proposed framework. The simulation work for the framework’s assessment reveals that the transfer learning technique is quite effective even with a small size imbalance dataset, and we may not need augmented data if it is implemented with a proper framework with an appropriate selection of hyperparameters and solvers. Further, the results reveal a tradeoff between batch size and learning rate, but it depends on the model architecture type and complexity. The assessment shows that the proposed framework is effective for radiologists and physicians in classifying diverse tumor types. The proposed framework can also be used for other classification issues.
The work can be broadened in the future to increase the dimensions of the Cartesian product matrix to obtain optimal values of other hyperparameters. Further, in-depth investigation is required for a few pre-trained DL models that failed to retrain on our dataset for selected pairs of the Cartesian product matrix.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. K. Selvanayaki and M. Karnan, “CAD system for automatic detection of brain tumor through magnetic resonance image—A review,” International Journal of Engineering Science and Technology, vol. 2, no. 10, pp. 5890–5901, 2010. [Google Scholar]
2. K. M. Brindle, J. L. Izquierdo-Garcia, D. Y. Lewis, R. J. Mair and A. J. Wright, “Brain tumor imaging,” Journal of Clinical Oncology, vol. 35, no. 21, pp. 2432–2438, 2017. [Google Scholar]
3. P. Y. Wen, D. R. Macdonald, D. A. Reardon, T. F. Cloughesy, A. G. Sorensen et al., “Updated response assessment criteria for high-grade gliomas: Response assessment in neuro-oncology working group,” Journal of Clinical Oncology, vol. 28, no. 11, pp. 1963–1972, 2010. [Google Scholar]
4. A. Drevelegas and N. Papanikolaou, “Imaging modalities in brain tumors,” in Imaging of Brain Tumors with Histological Correlations, 2nd ed., Berlin Heidelberg: Springer, pp. 13–33, 2011. [Google Scholar]
5. J. Cheng, W. Huang, S. Cao, R. Yang, W. Yang et al., “Enhanced performance of brain tumor classification via tumor region augmentation and partition,” PloS One, vol. 10, no. 12, pp. e0144479, 2015. [Google Scholar]
6. J. Cheng, W. Yang, M. Huang, W. Huang, J. Jiang et al., “Retrieval of brain tumors by adaptive spatial pooling and fisher vector representation,” PloS One, vol. 11, no. 6, pp. e0157112, 2016. [Google Scholar]
7. S. Kumar, C. Dabas and S. Godara, “Classification of brain MRI tumor images: A hybrid approach,” Procedia Computer Science, vol. 122, pp. 510–517, 2017. [Google Scholar]
8. G. Mohan and M. M. Subashini, “MRI based medical image analysis: Survey on brain tumor grade classification,” Biomedical Signal Processing and Control, vol. 39, pp. 139–161, 2018. [Google Scholar]
9. I. Sutskever, J. Martens and G. E. Hinton, “Generating text with recurrent neural networks,” in Proc. ICML, Bellevue, WA, USA, 2011. [Google Scholar]
10. R. Collobert and J. Weston, “A unified architecture for natural language processing: Deep neural networks with multitask learning,” in Proc. 25th Int. Conf. on Machine learning, Helsinki, Finland, pp. 160–167, 2008. [Google Scholar]
11. N. Jaitly and G. E. Hinton, “Vocal tract length perturbation (VTLP) improves speech recognition,” in Proc. ICML Workshop on Deep Learning for Audio, Speech and Language, vol. 117, Atlanta, Georgia, USA, pp. 21, 2013. [Google Scholar]
12. Y. Taigman, M. Yang, M. A. Ranzato and L. Wolf, “Deepface: Closing the gap to human-level performance in face verification,” in Proc. IEEE Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, pp. 1701–1708, 2014. [Google Scholar]
13. C. Szegedy, A. Toshev and D. Erhan, “Deep neural networks for object detection,” in Advances in Neural Information Processing Systems. Vol. 26, pp. 2553–2561, 2013. [Google Scholar]
14. A. Karpathy and L. Fei-Fei, “Deep visual-semantic alignments for generating image descriptions,” in Proc. IEEE Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 3128–3137, 2015. [Google Scholar]
15. J. Zhang and C. Zong, “Deep neural networks in machine translation: An overview,” IEEE Intelligent Systems, vol. 30, no. 5, pp. 16–25, 2015. [Google Scholar]
16. D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre et al., “Mastering the game of Go with deep neural networks and tree search,” Nature, vol. 529, no. 7587, pp. 484–489, 2016. [Google Scholar]
17. J. Kleesiek, G. Urban, A. Hubert, D. Schwarz, K. Maier-Hein et al., “Deep MRI brain extraction: A 3D convolutional neural network for skull stripping,” NeuroImage, vol. 129, no. 869–877, pp. 460–469, 2016. [Google Scholar]
18. N. Tajbakhsh, J. Y. Shin, S. R. Gurudu, R. T. Hurst, C. B. Kendall et al., “Convolutional neural networks for medical image analysis: Full training or fine tuning?,” IEEE Transactions on Medical Imaging, vol. 35, no. 5, pp. 1299–1312, 2016. [Google Scholar]
19. A. Krizhevsky, I. Sutskever and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” Communications of the ACM, vol. 60, no. 6, pp. 84–90, 2017. [Google Scholar]
20. O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh et al., “ImageNet large scale visual recognition challenge,” International Journal of Computer Vision, vol. 115, no. 3, pp. 211–252, 2015. [Google Scholar]
21. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Int. Conf. on Learning Representations (ICLR), 2015. https://arxiv.org/abs/1409.1556 [Google Scholar]
22. M. Everingham and J. Winn, “The pascal visual object classes challenge 2012 (voc2012) development kit,” Pattern Analysis, Statistical Modelling and Computational Learning, vol. 8, pp. 5, 2011. [Google Scholar]
23. L. Roux, “Mitosis Atypia 14 Grand Challenge,” 2014 [Online]. Available: https://mitos-atypia-14.grandcha. [Google Scholar]
24. G. E. Hinton, S. Osindero and Y. Teh, “A fast learning algorithm for deep belief nets,” Neural Computation, vol. 18, no. 7, pp. 1527–1554, 2006. [Google Scholar]
25. G. E. Hinton and R. R. Salakhutdinov, “Reducing the dimensionality of data with neural networks,” Science, vol. 313, no. 5786, pp. 504–507, 2006. [Google Scholar]
26. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. Int. Conf. on Machine Learning, Lille, France, 2015. [Google Scholar]
27. V. Nair and G. E. Hinton, “Rectified linear units improve restricted Boltzmann machines,” in Proc. ICML, Haifa, Israel, 2010. [Google Scholar]
28. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov, “Dropout: A simple way to prevent neural networks from overfitting,” The Journal of Machine Learning Research, vol. 15, no. 1, pp. 1929–1958, 2014. [Google Scholar]
29. T. Ateeq, M. N. Majeed, S. M. Anwar, M. Maqsood, Z. Rehman et al., “Ensemble-classifiers-assisted detection of cerebral microbleeds in brain MRI,” Computers & Electrical Engineering, vol. 69, pp. 768–781, 2018. [Google Scholar]
30. M. Havaei, A. Davy, D. Farley, A. Biard, A. Courville et al., “Brain tumor segmentation with deep neural networks,” Medical Image Analysis, vol. 35, no. 4, pp. 18–31, 2017. [Google Scholar]
31. B. H. Menze, A. Jakab, S. Bauer, J. Cramer, K. Farahni et al., “The multimodal brain tumor image segmentation benchmark (BraTS),” IEEE Transactions on Medical Imaging, vol. 34, no. 10, pp. 1993–2024, 2014. [Google Scholar]
32. M. Prastawa, E. Bullitt, N. Moon, K. V. Leemput and G. Gerig, “Automatic brain tumor segmentation by subject specific modification of atlas priors1,” Academic Radiology, vol. 10, no. 12, pp. 1341–1348, 2003. [Google Scholar]
33. P. Abdolmaleki, F. Mihara, K. Masuda and L. D. Buadu, “Neural networks analysis of astrocytic gliomas from MRI appearances,” Cancer Letters, vol. 118, no. 1, pp. 69–78, 1997. [Google Scholar]
34. A. Kharrat, K. Gasmi, M. B. Messaoud, N. Benamrane and M. Abid, “A hybrid approach for automatic classification of brain MRI using genetic algorithm and support vector machine,” Leonardo Journal of Sciences, vol. 17, no. 1, pp. 71–82, 2010. [Google Scholar]
35. E. I. Papageorgiou, P. P. Spyridonos, D. Glotsos, C. D. Stylios, P. Ravazoula et al., “Brain tumor characterization using the soft computing technique of fuzzy cognitive maps,” Applied Soft Computing, vol. 8, no. 1, pp. 820–828, 2008. [Google Scholar]
36. E. I. Zacharaki, S. Wang, S. Chawla, D. S. Yoo, R. Wolf et al., “Classification of brain tumor type and grade using MRI texture and shape in a machine learning scheme,” Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, vol. 62, no. 6, pp. 1609–1618, 2009. [Google Scholar]
37. K. L. Hsieh, C. Lo and C. Hsiao, “Computer-aided grading of gliomas based on local and global MRI features,” Computer Methods and Programs in Biomedicine, vol. 139, pp. 31–38, 2017. [Google Scholar]
38. J. Sachdeva, V. Kumar, I. Gupta, N. Khandelwal and C. K. Ahuja, “A package-SFERCB-Segmentation, feature extraction, reduction and classification analysis by both SVM and ANN for brain tumors,” Applied Soft Computing, vol. 47, no. 12B, pp. 151–167, 2016. [Google Scholar]
39. J. Cheng, “Brain magnetic resonance imaging tumor dataset,” in Figshare MRI Dataset Version 5, 2017. [Online]. Available: https://figshare.com/articles/dataset/brain_tumor_dataset/1512427/5 [Google Scholar]
40. M. R. Ismael and I. Abdel-Qader, “Brain tumor classification via statistical features and back-propagation neural network,” in Proc. IEEE Int. Conf. on Electro/Information Technology (EIT), Rochester, Michigan, USA, pp. 252–257, 2018. [Google Scholar]
41. S. Khalid, T. Khalil and S. Nasreen, “A survey of feature selection and feature extraction techniques in machine learning,” in Proc. Science and Information Conf., London, UK, pp. 372–378, 2014. [Google Scholar]
42. Y. LeCun, Y. Bengio and G. Hinton, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, 2015. [Google Scholar]
43. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]
44. P. Afshar, A. Mohammadi and K. N. Plataniotis, “Brain tumor type classification via capsule networks,” in Proc. IEEE Int. Conf. on Image Processing (ICIP), Athens, Greece, pp. 3129–3133, 2018. [Google Scholar]
45. R. Zia, P. Akhtar and A. Aziz, “A new rectangular window based image cropping method for generalization of brain neoplasm classification systems,” International Journal of Imaging Systems and Technology, vol. 28, no. 3, pp. 153–162, 2018. [Google Scholar]
46. H. H. Sultan, N. M. Salem and W. Al-Atabany, “Multi-classification of brain tumor images using deep neural network,” IEEE Access, vol. 7, pp. 69215–69225, 2019. [Google Scholar]
47. Z. Jia and D. Chen, “Brain tumor identification and classification of MRI images using deep learning techniques,” IEEE Access, pp. 1, 2020. https//org.10.1109/ACCESS.2020.3016319. [Google Scholar]
48. S. Banerjee, S. Mitra, F. Masulli and S. Rovetta, “Brain tumor detection and classification from multi-sequence MRI: Study using convnets,” in Proc. Int. MICCAI Brainlesion Workshop, Granada, Spain, pp. 170–179, 2018. [Google Scholar]
49. C. Szegedy, S. Ioffe, V. Vanhoucke and A. Alemi, “Inception-V4, inception-ResNet and the impact of residual connections on learning,” in Proc. AAAI Conf. on Artificial Intelligence, San Francisco, California, USA, 2017. [Google Scholar]
50. M. Talo, U. B. Baloglu, Ö. Yıldırım and U. R. Acharya, “Application of deep transfer learning for automated brain abnormality classification using MR images,” Cognitive Systems Research, vol. 54, pp. 176–188, 2019. [Google Scholar]
51. K. A. Johnson and J. A. Becker, “Braintumor datasets,” in Harvard Medical School Data [Online]. Available: http://www.med.harvard.edu/AANLIB/ [Google Scholar]
52. M. Sajjad, S. Khan, K. Muhammad, W. Wu, A. Ullah et al., “Multi-grade brain tumor classification using deep CNN with extensive data augmentation,” Journal of Computational Science, vol. 30, pp. 174–182, 2019. [Google Scholar]
53. Z. N. K. Swati, Q. Zhao, M. Kabir, F. Ali, Z. Ali et al., “Brain tumor classification for MR images using transfer learning and fine-tuning,” Computerized Medical Imaging and Graphics, vol. 75, pp. 34–46, 2019. [Google Scholar]
54. Z. N. K. Swati, Q. Zhao, M. Kabir, F. Ali, Z. Ali et al., “Content-based brain tumor retrieval for MR images using transfer learning,” IEEE Access, vol. 7, pp. 17809–17822, 2019. [Google Scholar]
55. S. Deepak and P. Ameer, “Brain tumor classification using deep CNN features via transfer learning,” Computers in Biology and Medicine, vol. 111, no. 3, pp. 103345, 2019. [Google Scholar]
56. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed et al., “Going deeper with convolutions,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 1–9, 2015. [Google Scholar]
57. M. Ghafoorian, A. Mehertash, T. Kapur, N. Karssemeijer, E. Marchiori et al., “Transfer learning for domain adaptation in MRI: Application in brain lesion segmentation,” in Proc. Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, Quebec, Canada, pp. 516–524, 2017. [Google Scholar]
58. C. Haarburger, P. Langenberg, D. Truhn, H. Schneider, J. Thuring et al., “Transfer learning for breast cancer malignancy classification based on dynamic contrast-enhanced MR images,” in Bildverarbeitung für die Medizin 2018. Berlin, Heidelberg, 216–221, 2018. [Google Scholar]
59. G. S. Tandel, A. Balestrieri, T. Jujaray, N. N. Khanna, L. Saba et al., “Multiclass magnetic resonance imaging brain tumor classification using artificial intelligence paradigm,” Computers in Biology and Medicine, vol. 122, no. 1, pp. 103804, 2020. [Google Scholar]
60. K. Muhammad, S. Khan, J. D. Ser and V. H. C. de Albuquerque, “Deep learning for multigrade brain tumor classification in smart healthcare systems: A prospective survey,” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 2, pp. 507–522, 2020. [Google Scholar]
61. S. U. H. Dar, M. Özbey, A. B. Çatlı and T. Çukur, “A transfer-learning approach for accelerated MRI using deep neural networks,” Magnetic Resonance in Medicine, vol. 84, no. 2, pp. 663–685, 2020. [Google Scholar]
62. N. Noreen, S. Palaniappan, A. Qayyum, I. Ahmad, M. Imran et al., “A deep learning model based on concatenation approach for the diagnosis of brain tumor,” IEEE Access, vol. 8, pp. 55135–55144, 2020. [Google Scholar]
63. N. Noreen, S. Palaniappan, A. Qayyum, I. Ahmad and M. O. Alassafi, “Brain tumor classification based on fine-tuned models and the ensemble method,” Computers Materials & Continua, vol. 67, no. 3, pp. 3967–3982, 2021. [Google Scholar]
64. A. Sekhar, S. Biswas, R. Hazra, A. K. Sunaniya, A. Mukherjee et al., “Brain tumor classification using fine-tuned GoogLeNet features and machine learning algorithms: IoMT enabled CAD system,” IEEE Journal of Biomedical and Health Informatics, vol. 26, no. 3, pp. 983, 2022. [Google Scholar]
65. A. B. T. Tahir, M. A. Khan, M. Alhaisoni, J. A. Khan, Y. Nam et al., “Deep learning and improved particle swarm optimization based multimodal brain tumor classification,” Computers, Materials & Continua, vol. 68, no. 1, pp. 1099–1116, 2021. [Google Scholar]
66. J. Kang, Z. Ullah and J. Gwak, “MRI-based brain tumor classification using ensemble of deep features and machine learning classifiers,” Sensors, vol. 21, no. 6, pp. 2222, 2021. [Google Scholar]
67. N. S. Shaik and T. K. Cherukuri, “Multi-level attention network: Application to brain tumor classification,” Signal, Image and Video Processing, vol. 16, no. 3, pp. 817–824, 2022. [Google Scholar]
68. M. Yaqub, J. Feng, M. S. Zia, K. Arshid, K. Jia et al., “State-of-the-art CNN optimizer for brain tumor segmentation in magnetic resonance images,” Brain Sciences, vol. 10, no. 7, pp. 427, 2020. [Google Scholar]
69. A. Rehman, S. Naz, M. I. Razzak, F. Akram and M. Imran, “A deep learning-based framework for automatic brain tumors classification using transfer learning,” Circuits, Systems, and Signal Processing, vol. 39, no. 2, pp. 757–775, 2020. [Google Scholar]
70. A. Pashaei, H. Sajedi and N. Jazayeri, “Brain tumor classification via convolutional neural network and extreme learning machines,” in Proc. Int. Conf. on Computer and Knowledge Engineering (ICCKE), Ferdowsi University of Mashhad, Iran, pp. 314–319, 2018. [Google Scholar]
71. B. Zhou, A. Khosla, A. Lapedriza, A. Torralba and A. Oliva, “Places: An image database for deep scene understanding,” Journal of Vision, vol. 17, no. 10, pp. 296, 2017. [Google Scholar]
72. F. N. Iandola, S. Han, M. W. Moskewicz, K. Ashraf, W. J. Dally et al., “SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and < 0.5 MB model size,” in Proc. Int. Conf. on Learning Representations, Toulon, France, 2017. [Google Scholar]
73. M. Sandler, A. Howard, M. Zhu, A. Zhmoginov and L. C. Chen, “MobilenetV2: Inverted residuals and linear bottlenecks,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 4510–4520, 2018. [Google Scholar]
74. C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens and Z. Wojna, “Rethinking the inception architecture for computer vision,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 2818–2826, 2016. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |