DOI:10.32604/cmc.2022.029432
| Computers, Materials & Continua DOI:10.32604/cmc.2022.029432 | |
| Article |
A Stochastic Study of the Fractional Order Model of Waste Plastic in Oceans
1Department of Mathematics and Statistics, College of Science, King Faisal University, P. O. Box 400, Al-Ahsa, 31982, Saudi Arabia
2Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
3Future Technology Research Center, National Yunlin University of Science and Technology, Douliou, Yunlin, 64002, Taiwan
*Corresponding Author: Muneerah Al Nuwairan. Email: msalnuwairan@kfu.edu.sa
Received: 03 March 2022; Accepted: 23 May 2022
Abstract: In this paper, a fractional order model based on the management of waste plastic in the ocean (FO-MWPO) is numerically investigated. The mathematical form of the FO-MWPO model is categorized into three components, waste plastic, Marine debris, and recycling. The stochastic numerical solvers using the Levenberg-Marquardt backpropagation neural networks (LMQBP-NNs) have been applied to present the numerical solutions of the FO-MWPO system. The competency of the method is tested by taking three variants of the FO-MWPO model based on the fractional order derivatives. The data ratio is provided for training, testing and authorization is 77%, 12%, and 11% respectively. The exactness of LMQBP-NNs is observed by using the comparative performances of the obtained and the Adams-Bashforth-Moulton method. To verify the competence, validity, capability, exactness, and consistency of LMQBP-NNs, the performances have been obtained using the regression, state transitions, error histograms, correlation and mean square error.
Keywords: Fractional order; ocean; Adams-Bashforth-Moulton; Levenberg-Marquardt backpropagation; numerical solutions
The plastics are a ubiquitous and versatile substantial in the global economy. The popularity of the plastic can be accredited in the field of polymers based on the durable, hydrophobic, light, bio-inert, and cheap to produce. The packaging and products of plastic have a significant role in the environmental productivity as well as economic global growth. The global manufacture of the plastics is massive, and Polyethylene is an important form of the plastic. The demand of European plastic in 2016 based on the polymer kind of high and low densities was reported 12.3%, and 17.5%, respectively. Plastic waste is affecting the environment sustainability in the developing the global economies. This can be attributed to the polymers that are low-cost in production, moldable, bioinert, hydrophobic and durable. Many reports [1,2] show that the global plastic production is vast. This large scale of plastic is resulting in discarded waste with the presence in the environment that can be measured through the ecological testation. The waste plastic is calculated to be approximately 150 million tons [3]. An assortment of waste plastic gets into the oceans [4], pausing a main risk to ocean systems and food chain management [5]. The wide-ranging plastic pollution is even present through the remote marine environments [6].
The plastic polymer can be organized by using the environment and plastic types [7–10]. As the massive populations placed in the atmosphere along with the absence of limited waste properties to progress the concept of “circular economy” [11]. The motivations of the natural ecosystems and reformatory models can make confidential environments using the condition of source abandoning as well as extraction of “waste” observation [12]. The major points of the circular economy are used in the technical and biological systems [13]. Numerous European strategies distress the plastic waste, which is implemented to the evolution of the circulatory economies [14,15]. In the circular budget, the recycling of plastic is important to the EU strategy [16]. The management task using the plastic waste in the economy of the EU is very important that is used to recycle in the developing countries except Europe. Hong Kong and China introduced mutually 70% of the waste plastic [17]. The collected post-consumer plastic waste is transported to EU about 46% [18]. The division of plastic is considered into three classes: plastics occupied, post-consumer and misuse of plastic waste [19]. The plastic waste management is liable by recycling, landfill, or incineration, whereas mistreated waste is disposed in the environment and merge in the oceans [20]. Mistreated waste can be used in the durable inverse association based on the economic sector.
The mathematical models are very famous due to the various disciplines of applications in the language as well as natural sciences (physics, statistics, earth science, biology, and chemistry), engineering and social science or non-physical networks. The present work aims to provide the realistic solutions for the nonlinear fractional order mathematical model using the management of waste plastic in ocean (FO-MWPO). The stochastic numerical solvers using the Levenberg-Marquardt backpropagation neural networks (LMQBP-NNs) have been applied to obtain the solutions of the FO-MWPO.
The organization of the paper is given as: Section 2 shows the design of the FO-MWPO. Section 3 presents the stochastic applications, while Section 4 describes the LMQBP-NNs structure. Section 5 provides the simulations of the FO-MWPO model, while the conclusions are drawn at the end.
2 The Construction of the FO-MWPO Model
In this section, the mathematical formulations of the waste plastic
The descriptions of each parameter is provided in Tab. 1.
The numerical investigations of the FO-MWPO have been provided through the artificial intelligence (AI) along with LMQBP-NNs. The FO-MWPO is given as:
where
3 Features of the Stochastic Solvers
In this section, the stochastic numerical operators using the LMQBP-NNs are provided to solve the FO-MWPO model. The use of stochastic computing solvers through the supervised/unsupervised learning have been explored to solve the complicated, stiff, and singular models [22,23]. In recent decades, the stochastic applications have been proposed to solve the food chain model [24], singular Lane-Emden systems [25], infectious disease considering its anatomical variables [26], functional order systems [27] and HIV dynamical models [28–31]. This study is related to design and present the numerical solutions of the fractional order derivative using the numerical computing procedures based on the LMQBP-NNs. Few novel topographies of the LMQBP-NNs to present the solutions of the FO-MWPO model are described as:
• The design of the nonlinear FO-MWPO model along with its numerical solutions is presented first time in this study.
• The numerical solutions of the designed FO-MWPO are presented using the stochastic paradigms based on the proposed LMQBP-NNs.
• The proposed LMQBP-NNs is tested to solve three variants of the FO-MWPO model by taking different values of FO derivatives.
• The brilliance and correctness of the computing stochastic LMQBP-NNs scheme is checked based on the comparison of the achieved and reference performances.
• The accuracy of the LMQBP-NNs approach is achieved using the absolute error (AE), which is accomplished in good measures to solve the FO-MWPO model.
• The STs, regression, MSE, correlation and EHs values approve the trustworthiness and dependability of the designed LMQBP-NNs for solving the nonlinear FO-MWPO model.
4 Proposed LMQBP-NNs Procedures
In this section, the designed LMQBP-NNs procedures are provided to solve the FO-MWPO model. The structure of the proposed LMQBP-NNs is given as:
• The essential performances based on the LMQBP-NNs are provided.
• The execution through the LMQBP-NNs is indicated to solve the FO-MWPO model.
Fig. 1 is drawn using the multi-layer optimization procedures based on the numerical stochastic paradigms of LMQBP-NNs. The stochastic procedures are given using a Matlab ‘nftool’ command with the data selection as 77% for training and 12% for testing and 11% for authorization.
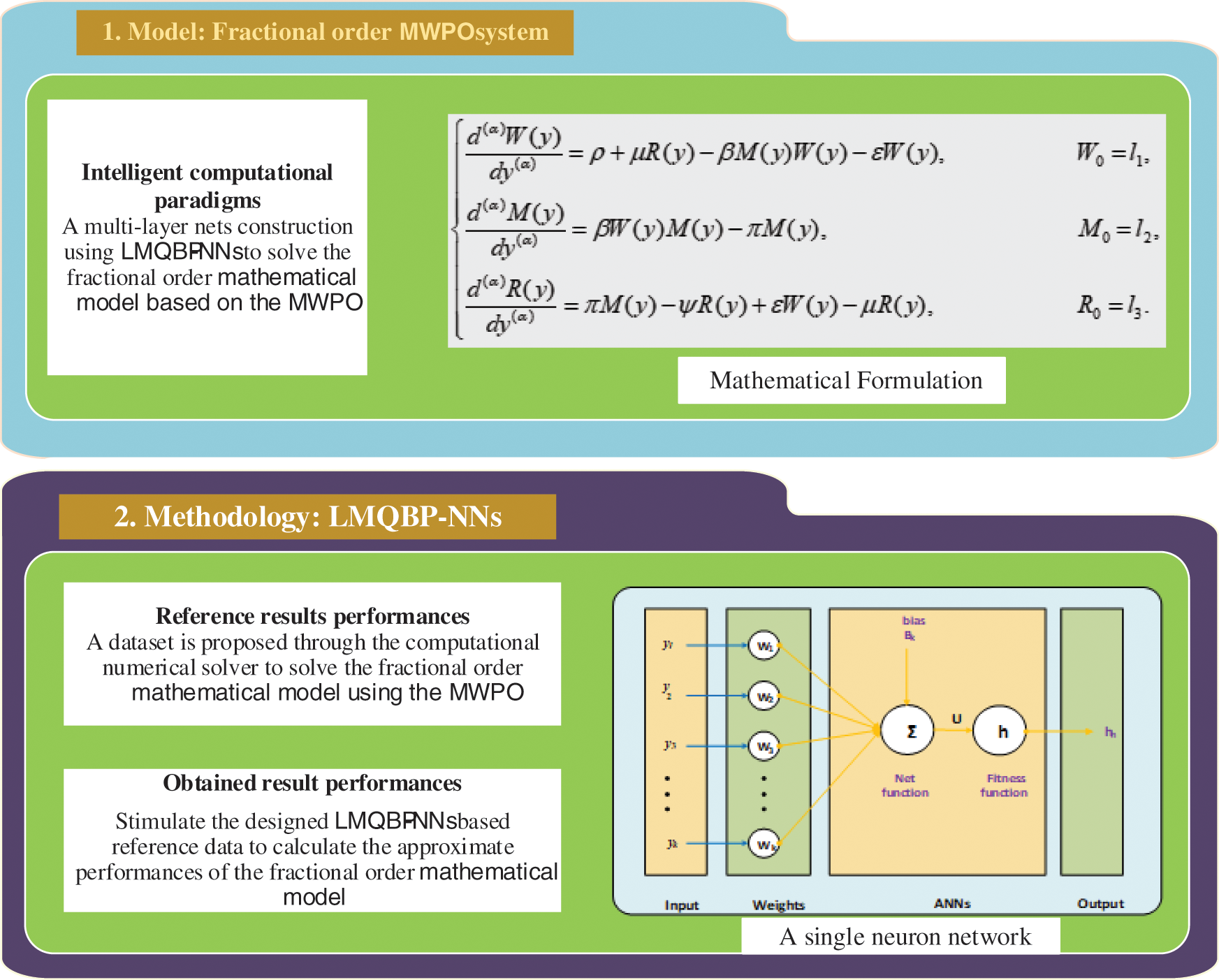
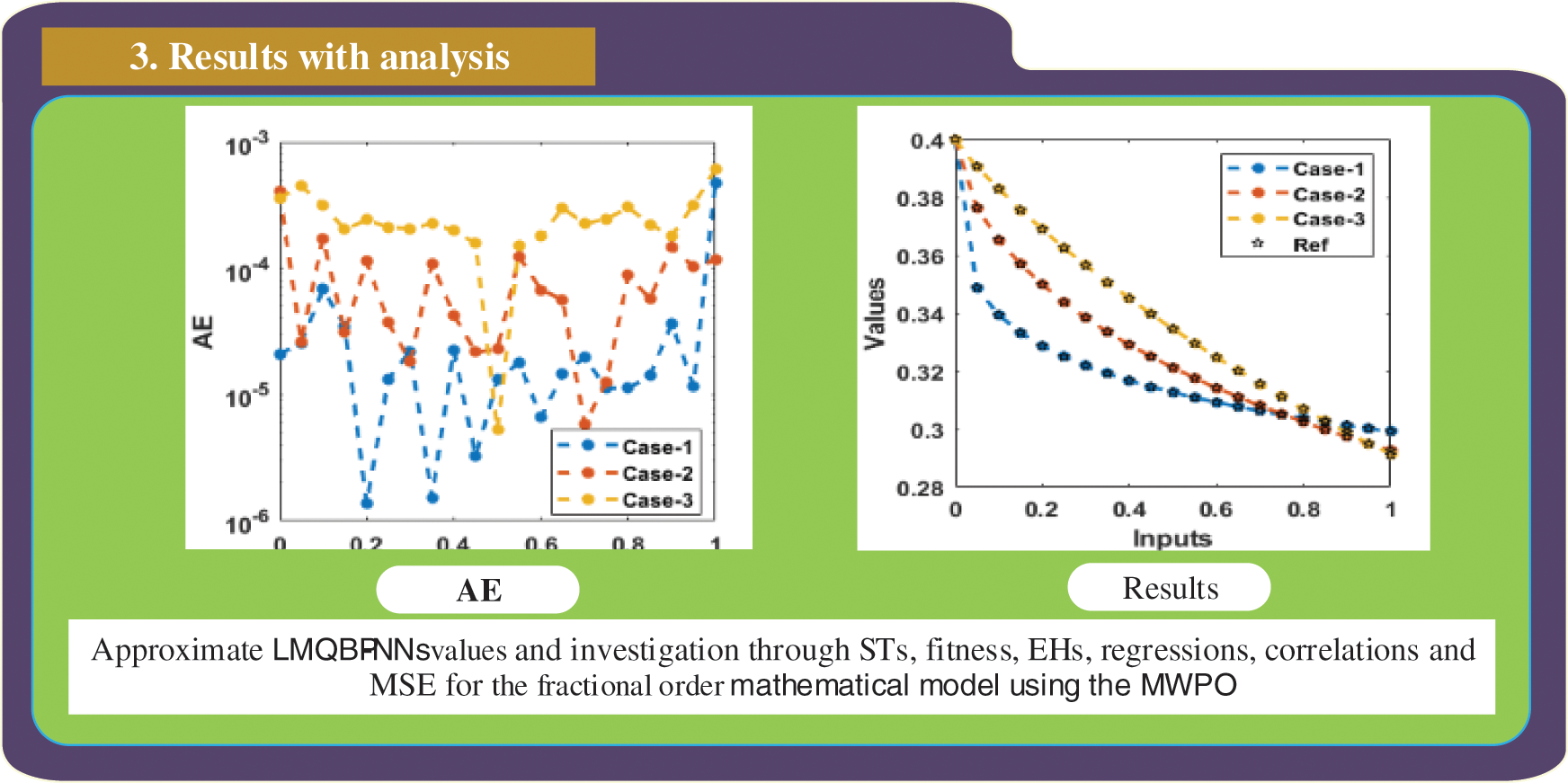
Figure 1: Workflow for the FO-MWPO model using the LMQBP-NNs
One may choose different values of these samples. If the training is selected greater than 77%, then the good results can be obtained due to the bias inputs. Additionally, the training samples are selected less than 77%, then the accuracy of the network LMQBP-NNs to solve the FO-MWPO degraded substantially. Therefore, the samples for bias and unbiased inputs should be set with care to avoid both premature convergence and divergence.
Three cases of the FO-MWPO model by taking different values of the FO derivatives using the designed LMQBP-NNs are presented in this Section
Case 1: Consider a FO-MWPO model is provided by taking
Case 2: Consider a FO-MWPO model is provided by taking
Case 3: Consider a FO-MWPO model is provided by taking
The numerical performances using the simulations of FO-MWPO model are described by using the computational LMQBP-NNs procedures with 13 numbers of neurons together with the data selection as 77% for training and 12% for testing and 11% for authorization. The neurons-based input, hidden and output structure are shown in Fig. 2.
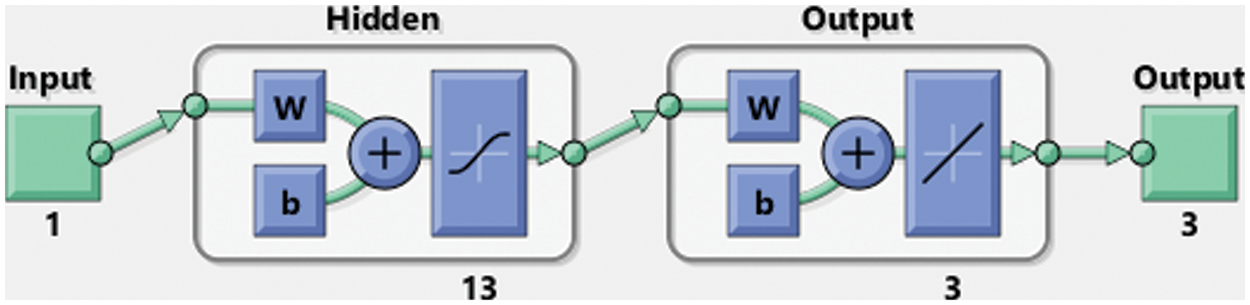
Figure 2: Designed LMQBP-NNs for the FO-MWPO model
Figs. 3 to 5 represent the FO-MWPO model using the designed LMQBP-NNs. The performances along with the EHs values representing the best curves, verifications and authentications are provided in Fig. 3 for the FO-MWPO model. The best achieved performances of the FO-MWPO model have been provided at epochs 63, 21 and 14, which are found as 1.5171 × 10−09, 1.0929 × 10−08 and 6.1108 × 10−08. The gradient values are calculated as 9.8428 × 10−08, 9.996 × 10−07 and 3.3348 × 10−06 for 1st, 2nd and 3rd case. These graphical measures represent the convergence of the designed LMQBP-NNs to solve the FO-MWPO model using the LMQBP-NNs. Fig. 4 represents the results valuations and EHs for the FO-MWPO model using the LMQBP-NNs. These result valuations indicate the comparative performances of the obtained and reference solutions. The result valuations based on the training, substantiation, and testing performances for the FO-MWPO model are provided. Figs. 4d–4f indicates the EHs values, which are calculated as 2.76 × 10−05, 5.65 × 10−05 and 5.15 × 10−05 for 1st, 2nd and 3rd case. Fig. 5 represents the correlation values for the FO-MWPO model using the designed LMQBP-NNs. The correlation values are found as 1 for the FO-MWPO model using the designed LMQBP-NNs. The training, substantiation and testing values label the exactness of the designed LMQBP-NNs procedure. The MSE convergence through the complexity, authentication, training, iterations, backpropagation, and testing is shown in Tab. 2 for the FO-MWPO model using the designed LMQBP-NNs.
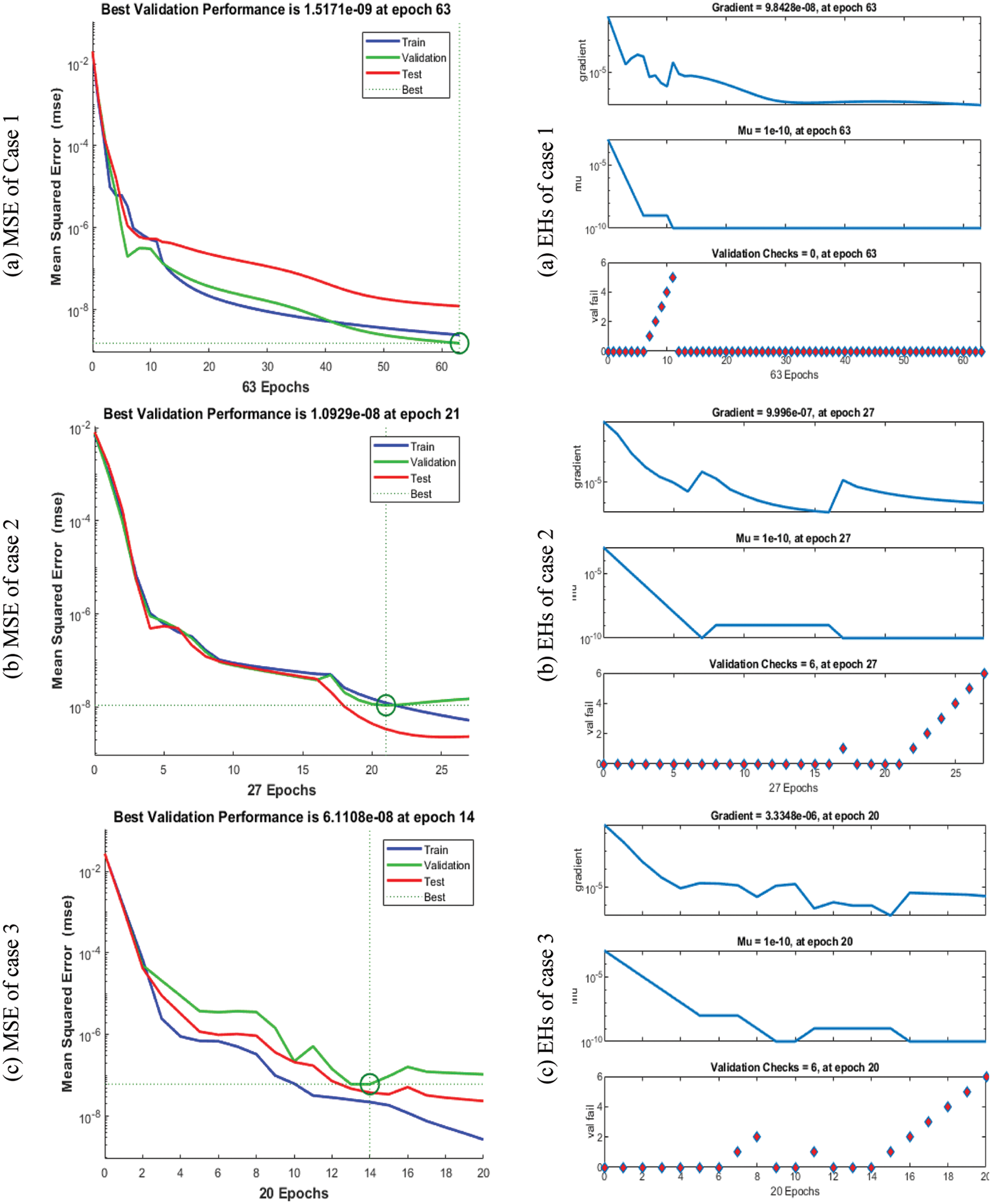
Figure 3: STs and MSE values for the FO-MWPO model
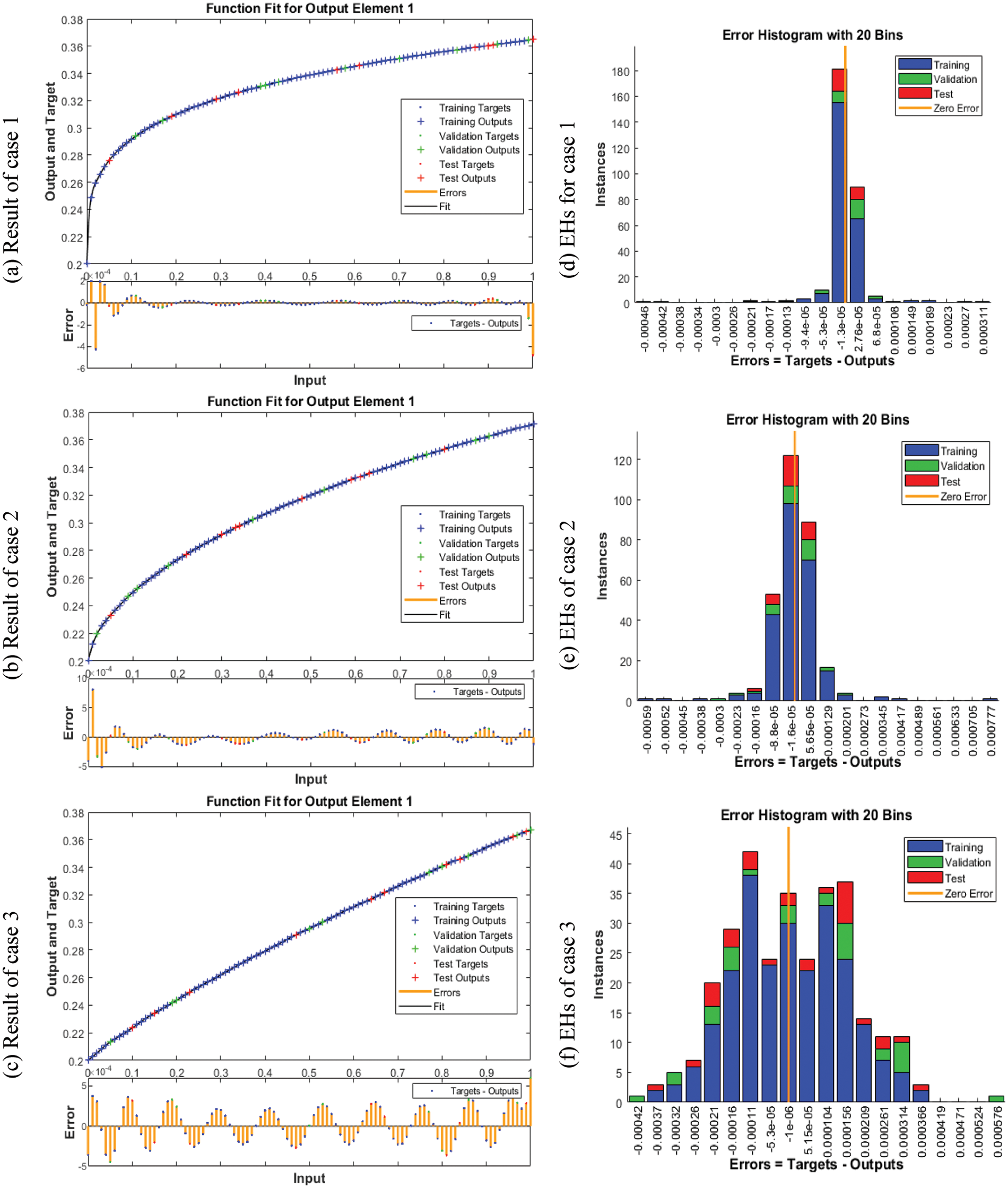
Figure 4: Results valuations and EHs for the FO-MWPO model
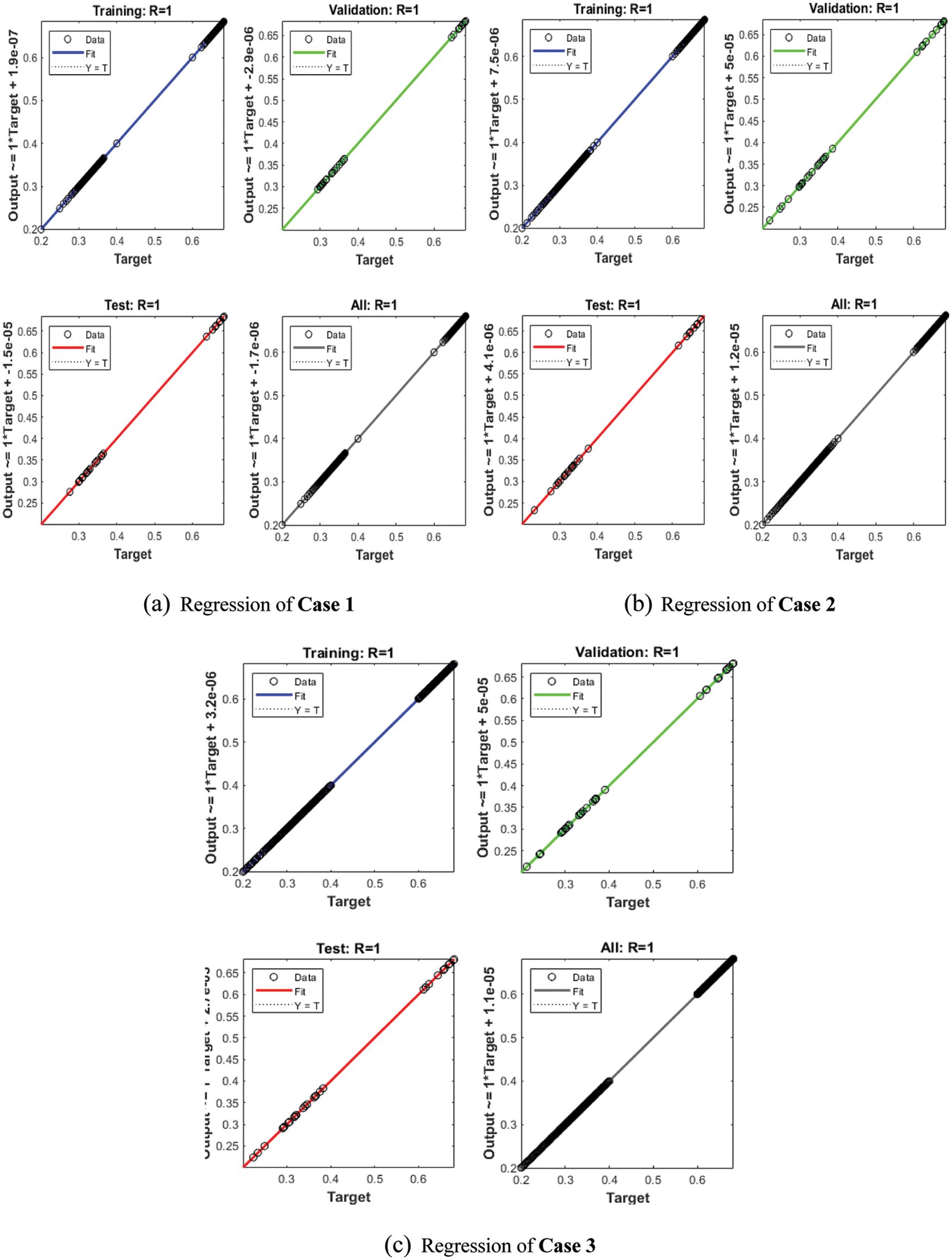
Figure 5: Regression values for the FO-MWPO model
The comparison plots and AE performances are shown in Figs. 6 and 7. The obtained numerical results have been provided to solve the nonlinear FO-MWPO model using the designed LMQBP-NNs. The overlapping of the obtained and reference solutions has been provided in Fig. 6. These overlapping of the results authenticates the correctness of the designed LMQBP-NNs to solve the nonlinear FO-MWPO model. The values of the AE have been performed to solve the nonlinear FO-MWPO model in Fig. 7. The AE for the waste plastic material
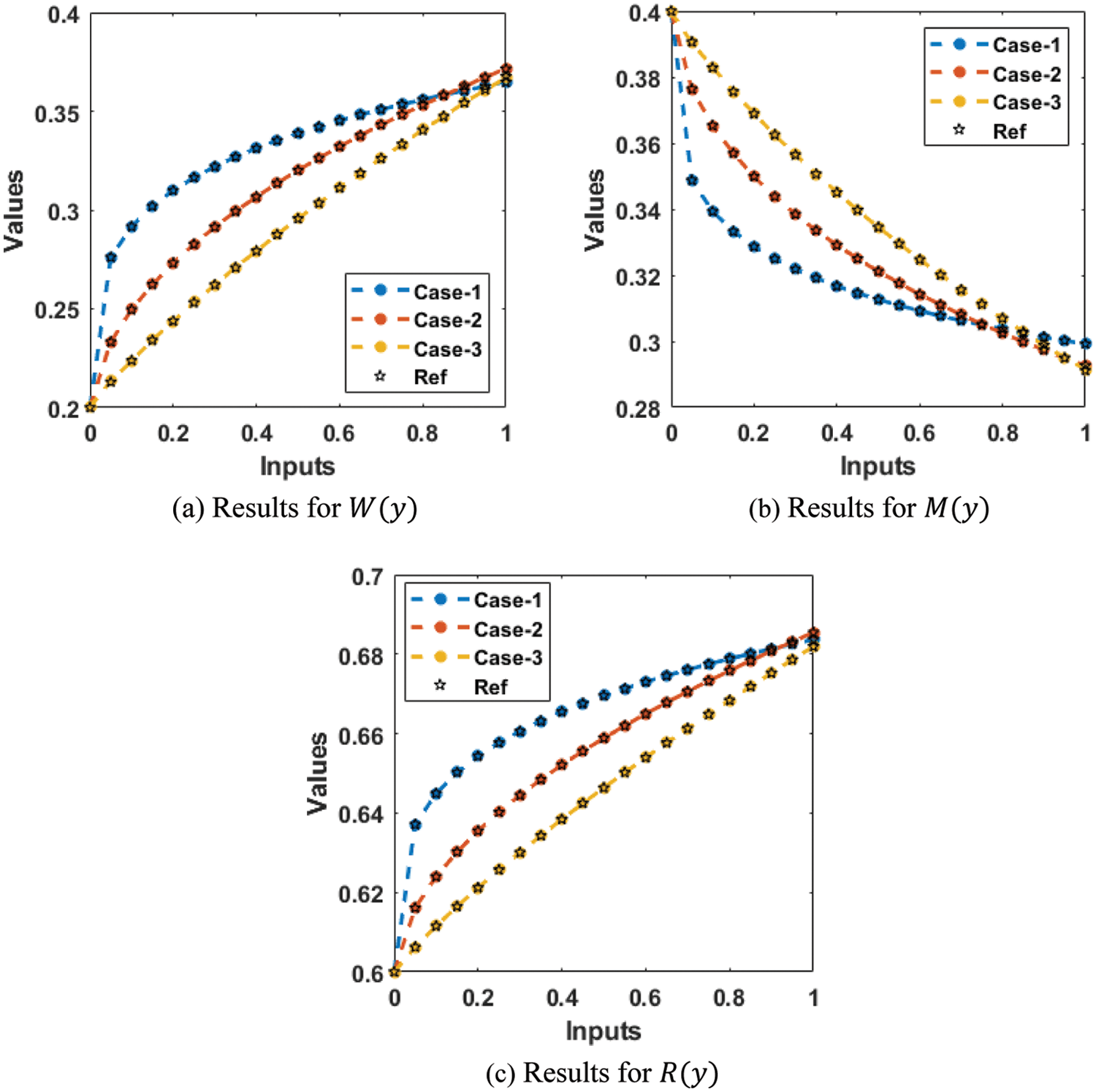
Figure 6: Comparison of the result for the FO-MWPO model
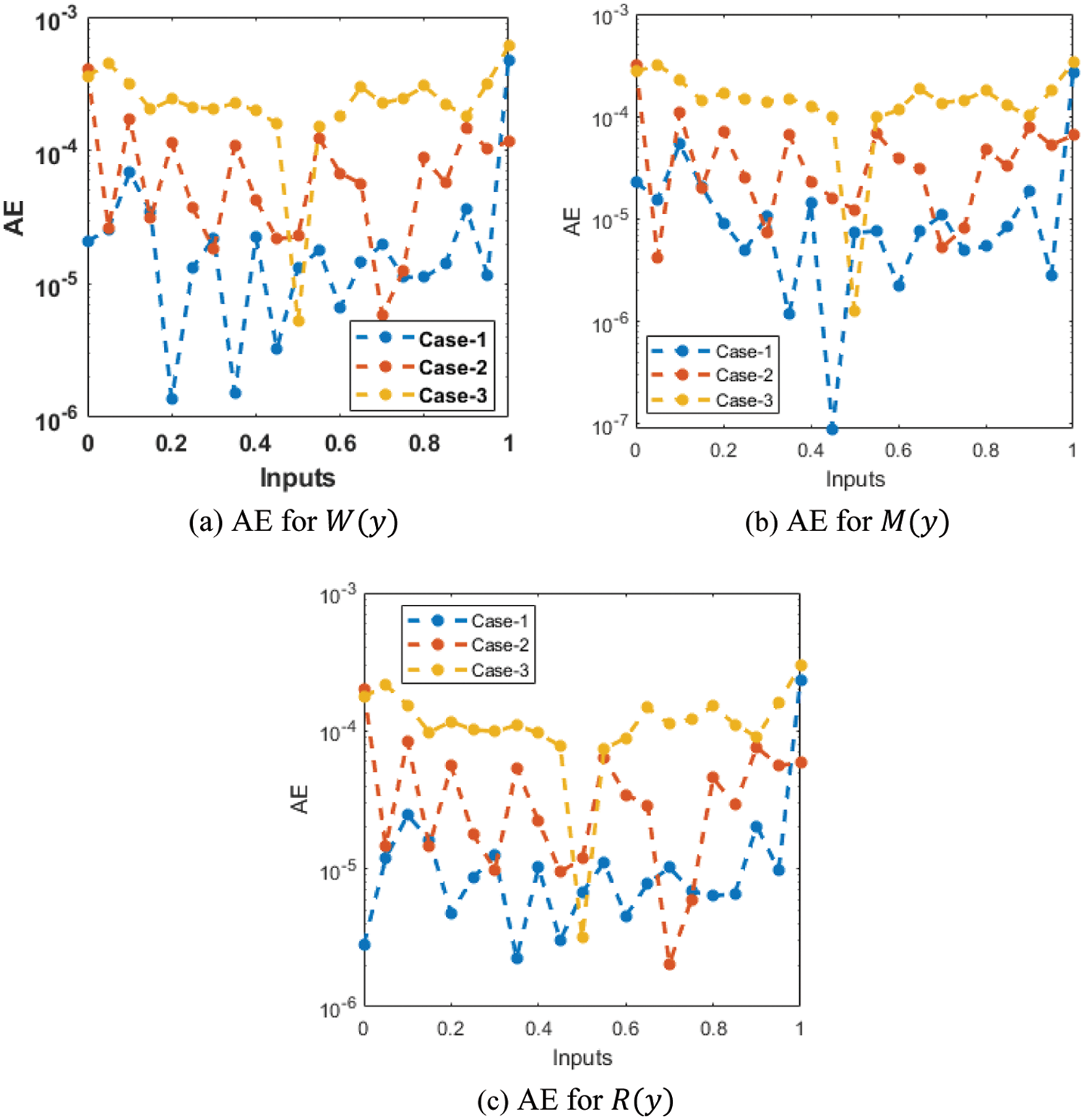
Figure 7: AE for the FO-MWPO model
The study shows the design of the fractional order mathematical model based on the MWPO. The investigations related to fractional order have been presented to get more realistic results of the ocean model. The designed system is divided into, waste plastic
In future study, the LMQBP-NNs will be applied to present the numerical outcomes of the fluid, fractional and lonngren-wave systems [32–49].
Acknowledgement: The authors acknowledge the Deanship of Scientific Research at King Faisal University, Saudi Arabia for their financial support under Project No. AN000128.
Data Availability Statement: The data that support the findings of this study are available from the corresponding author upon reasonable request.
Funding Statement: This work was supported through the Annual Funding track by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [Project No. AN000128].
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. R. Geyer, J. R. Jambeck and K. L. Law, “Production, use, and fate of all plastics ever made,” Science Advances, vol. 3, no. 7, pp. 1207–1221, 2017. [Google Scholar]
2. N. Ottman, L. Ruokolainen, A. Suomalainen, H. Sinkko, P. Karisola et al., “Soil exposure modifies the gut microbiota and supports immune tolerance in a mouse model,” The Journal of Allergy and Clinical Immunology, vol. 143, no. 3, pp. 1198–1206, 2019. [Google Scholar]
3. J. Payne and M. D. Jones, “The chemical recycling of polyesters for a circular plastics economy: Challenges and emerging opportunities,” ChemSusChem, vol. 14, no. 19, pp. 4041–4070, 2021. [Google Scholar]
4. H. S. Auta, C. U. Emenike and S. H. Fauziah, “Distribution and importance of microplastics in the marine environment: A review of the sources, fate, effects, and potential solutions,” Environment International, vol. 102, pp. 165–176, 2017. [Google Scholar]
5. C. Wilcox, E. Van Sebille and B. D. Hardesty, “Threat of plastic pollution to seabirds is global, pervasive, and increasing,” Proceedings of the National Academy of Sciences, vol. 112, no. 38, pp. 11899–11904, 2015. [Google Scholar]
6. S. Chiba, H. Saito, R. Fletcher, T. Yogi, M. Kayo et al., “Human footprint in the abyss: 30 year records of deep-sea plastic debris,” Marine Policy, vol. 96, pp. 204–212, 2018. [Google Scholar]
7. E. C. Snell-Rood, M. E. Kobiela, K. L. Sikkink and A. M. Shephard, “Mechanisms of plastic rescue in novel environments,” Annual Review of Ecology, Evolution, and Systematics, vol. 49, pp. 331–354, 2018. [Google Scholar]
8. D. Xanthos and T. R. Walker, “International policies to reduce plastic marine pollution from single-use plastics (plastic bags and microbeadsA review,” Marine Pollution Bulletin, vol. 118, no. 1–2, pp. 17–26, 2017. [Google Scholar]
9. R. Verma, K. S. Vinoda, M. Papireddy and A. N. S. Gowda, “Toxic pollutants from plastic waste-A review,” Procedia Environmental Sciences, vol. 35, pp. 701–708, 2016. [Google Scholar]
10. A. L. Lusher, G. Hernandez-Milian, J. O’Brien, S. Berrow, I. O’Connor et al., “Microplastic and macroplastic ingestion by a deep diving, oceanic cetacean: The true’s beaked whale mesoplodon mirus,” Environmental Pollution, vol. 199, pp. 185–191, 2015. [Google Scholar]
11. W. McDonough and M. Braungart, Cradle to Cradle: Remaking the Way We Make Things, NY, USA: North Point Press, 2010. [Google Scholar]
12. M. Geissdoerfer, P. Savaget, N. M. P. Bocken and E. J. Hultink, “The circular economy–A new sustainability paradigm,” Journal of Cleaner Production, vol. 143, pp. 757–768, 2017. [Google Scholar]
13. P. T. Anastas, J. B. Zimmerman, W. McDonough and M. Braungart, “Applying the principles of green engineering to cradle-to-cradle design,” Environ. Sci. Technol., vol. 37, no. 23, pp. 434A–441A, 2003. [Google Scholar]
14. B. Mrowiec, “Plastics in the circular economy (CE),” Environmental Protection and Natural Resources, vol. 29, no. 4, pp. 16–19, 2018. [Google Scholar]
15. M. V. van Beek, “Proposal for a directive of the european parliament and of the council on improving the gender balance among non-executive directors of companies listed on stock exchanges and related measures. Is it courageous and visionary or is it,” R.R.D.E, pp. 109, 2015. [Google Scholar]
16. D. Lazarevic, E. Aoustin, N. Buclet and N. Brandt, “Plastic waste management in the context of a European recycling society: Comparing results and uncertainties in a life cycle perspective,” Resources, Conservation and Recycling, vol. 55, no. 2, pp. 246–259, 2010. [Google Scholar]
17. A. L. Brooks, S. Wang and J. R. Jambeck, “The Chinese import ban and its impact on global plastic waste trade,” Science Advances, vol. 4, no. 6, pp. eaat0131, 2018. [Google Scholar]
18. D. C. Wilson, L. Rodic, P. Modak, R. Soos, A. Carpintero et al., “Global waste management outlook,” UNEP, 2015. [Google Scholar]
19. L. Lebreton and A. Andrady, “Future scenarios of global plastic waste generation and disposal,” Palgrave Commun, vol. 5, no. 6, pp. 1–11, 2019. [Google Scholar]
20. T. Van Emmerik, M. Loozen, K. Van Oeveren, F. Buschman and G. Prinsen, “Riverine plastic emission from Jakarta into the ocean,” Environmental Research Letters, vol. 14, no. 8, pp. 084033, 2019. [Google Scholar]
21. M. Al Nuwairan, Z. Sabir, M. A. Z. Raja and A. Aldhafeeri, “An advance artificial neural network scheme to examine the waste plastic management in the ocean,” AIP Advances, vol. 12, pp. 045211, 2022. [Google Scholar]
22. Z. Sabir, M. A. Z. Raja, S. R. Mahmoud, M. Balubaid, A. Algarni et al., “A novel design of morlet wavelet to solve the dynamics of nervous stomach nonlinear model,” International Journal of Computational Intelligence Systems, vol. 15, no. 1, pp. 1–15, 2022. [Google Scholar]
23. Z. Sabir, M. A. Z. Raja, T. Botmart and W. Weera, “A neuro-evolution heuristic using active-set techniques to solve a novel nonlinear singular prediction differential model,” Fractal and Fractional, vol. 6, no. 29, pp. 1–14, 2022. [Google Scholar]
24. Z. Sabir, “Stochastic numerical investigations for nonlinear three-species food chain system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250005, 2021. [Google Scholar]
25. Z. Sabir, M. A. Z. Raja, M. Umar, M. Shoaib and D. Baleanu, “FMNSICS: Fractional Meyer neuro-swarm intelligent computing solver for nonlinear fractional Lane–Emden systems,” Neural Computing and Applications, vol. 34, pp. 4193–4206, 2021. [Google Scholar]
26. Z. Sabir, M. A. Z. Raja and Y. Guerrero Sánchez, “Solving an infectious disease model considering its anatomical variables with stochastic numerical procedures,” Journal of Healthcare Engineering, vol. 2022, no. 3774123, pp. 1–12, 2022. [Google Scholar]
27. M. A. Abdelkawy, Z. Sabir, J. L. Guirao and T. Saeed, “Numerical investigations of a new singular second-order nonlinear coupled functional Lane–Emden model,” Open Physics, vol. 18, no. 1, pp. 770–778, 2020. [Google Scholar]
28. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, no. 104235, pp. 1–13, 2021. [Google Scholar]
29. Y. Guerrero–Sánchez, M. Umar, Z. Sabir, J. L. Guirao and M. A. Z. Raja, “Solving a class of biological HIV infection model of latently infected cells using heuristic approach,” Discrete & Continuous Dynamical Systems-S, vol. 14, no. 10, pp. 3611–3628, 2021. [Google Scholar]
30. M. Umar, Z. Sabir, M. A. Z. Raja, J. G. Aguilar, F. Amin et al., “Neuro-swarm intelligent computing paradigm for nonlinear HIV infection model with CD4+T-cells,” Mathematics and Computers in Simulation, vol. 188, pp. 241–253, 2021. [Google Scholar]
31. Z. Sabir, M. Umar, M. A. Z. Raja, H. M. Baskonus and W. Gao, “Designing of Morlet wavelet as a neural network for a novel prevention category in the HIV system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250012, 2021. [Google Scholar]
32. K. Vajravelu, S. Sreenadh, and R. Saravana, “Influence of velocity slip and temperature jump conditions on the peristaltic flow of a Jeffrey fluid in contact with a Newtonian fluid,” Applied Mathematics and Nonlinear Sciences, vol. 2, no. 2, pp. 429–442, 2017. [Google Scholar]
33. Z. Sabir, A. A. A. Ibrahim, M. A. Z. Raja, K. Nisar, M. Umar, J. J. Rodrigues and S. R. Mahmoud, “Soft Computing Paradigms to Find the Numerical Solutions of a Nonlinear Influenza Disease Model,” Applied Sciences, vol. 11, no. 18, pp. 8549, 2021. [Google Scholar]
34. M. S. M. Selvi and L. Rajendran, “Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 351–364, 2019. [Google Scholar]
35. E. İlhan and İ. O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]
36. H. Durur, O. Tasbozan and A. Kurt, “New analytical solutions of conformable time fractional bad and good modified Boussinesq equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 447–454, 2020. [Google Scholar]
37. A. O. Akdemir, E. Deniz and E. Yüksel, “On some integral inequalities via conformable fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 489–498, 2021. [Google Scholar]
38. M. Gürbüz and Ç. Yıldız, “Some new inequalities for convex functions via Riemann-Liouville fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 5 37–544, 2021. [Google Scholar]
39. I. Khan, A. M. Alqahtani, A. KHAN, D. Khan, A. H. Ganie et al., “New results of fractal fractional model of drilling nanoliquids with clay nanoparticles,” Fractals, vol. 30, no. 1, pp. 2250024, 2022. [Google Scholar]
40. G. Bary, W. Ahmed, R. Ahmad, A. H. Ganie, F. Alotaibi et al., “A novel approach to analyze pion fem toscopy for the particle emitting source with Bose-Einstein condensation,” Results in Physics, vol. 32, pp. 105075, 2022. [Google Scholar]
41. P. A. Naik, K. M. Owolabi, J. Zu and M. U. D. NaiK, “Modeling the transmission dynamics of COVID-19 pandemic in caputo type fractional derivative,” Journal of Multiscale Modelling, vol. 12, no. 3, pp. 2150006, 2021. [Google Scholar]
42. P. A. Naik, J. Zu, and K. M. Owolabi, “Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order,” Physica A: Statistical Mechanics and its Applications, vol. 545, pp. 123816, 2020. [Google Scholar]
43. A. H. Ganie, A. A. Memon, M. A. Memon, A. M. Al-Bugami, K. Bhatti et al., “Numerical analysis of laminar flow and heat transfer through a rectangular channel containing perforated plate at different angles,” Energy Reports, vol. 8, pp. 539–550, 2022. [Google Scholar]
44. G. Ali, F. Ali, A. Khan, A. H. Ganie and I. Khan, “A generalized magnetohydrodynamic two-phase free convection flow of dusty Casson fluid between parallel plates,” Case Studies in Thermal Engineering, vol. 29, pp. 101657, 2022. [Google Scholar]
45. H. Ahmad, A. R. Seadawy, A. H. Ganie, S. Rashid, T. A. Khan et al., “Approximate numerical solutions for the nonlinear dispersive shallow water waves as the Fornberg–Whitham model equations,” Results in Physics, vol. 22, pp. 103907, 2021. [Google Scholar]
46. M. Khan, S. A. Lone, A. Rasheed and M. N. Alam, “Computational simulation of Scott-Blair model to fractional hybrid nanofluid with Darcy medium,” International Communications in Heat and Mass Transfer, vol. 130, pp. 105784, 2022. [Google Scholar]
47. X. R. Zhang, J. Zhou, W. Sun, and S. K. Jha, “A lightweight CNN based on transfer learning for COVID-19 diagnosis,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]
48. L. Chen, B. Wang, W. Yu and X. Fan, “CNN-based fast hevc quantization parameter mode decision,” Journal of New Media, vol. 1, no. 3, pp. 115–126, 2019. [Google Scholar]
49. H. M. Baskonus, H. Bulut, “On the numerical solutions of some fractional ordinary differential equations by fractional Adams-Bashforth-Moulton method,” Open Mathematics, vol. 13, no. 1, pp. 547–556, 2015. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |