Computers, Materials & Continua DOI:10.32604/cmc.2022.029385
Article

Optimal Kernel Extreme Learning Machine for COVID-19 Classification on Epidemiology Dataset

Saud S. Alotaibi1, Amal Al-Rasheed2, Sami Althahabi3, Manar Ahmed Hamza4,*, Abdullah Mohamed5, Abu Sarwar Zamani4, Abdelwahed Motwakel4 and Mohamed I. Eldesouki6

1Department of Information Systems, College of Computing and Information System, Umm Al-Qura University,Saudi Arabia
2Department of Information Systems, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, P. O. Box 84428, Riyadh, 11671, Saudi Arabia
3Department of Computer Science, College of Science & Art at Mahayil, King Khalid University, Saudi Arabia
4Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
5Research Centre, Future University in Egypt, New Cairo, 11745, Egypt
6Department of Information System, College of Computer Engineering and Sciences, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
*Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 03 March 2022; Accepted: 26 April 2022

Abstract: Artificial Intelligence (AI) encompasses various domains such as Machine Learning (ML), Deep Learning (DL), and other cognitive technologies which have been widely applied in healthcare sector. AI models are utilized in healthcare sector in which the machines are used to investigate and make decisions based on prediction and classification of input data. With this motivation, the current study involves the design of Metaheuristic Optimization with Kernel Extreme Learning Machine for COVID-19 Prediction Model on Epidemiology Dataset, named MOKELM-CPED technique. The primary aim of the presented MOKELM-CPED model is to accomplish effectual COVID-19 classification outcomes using epidemiology dataset. In the proposed MOKELM-CPED model, the data first undergoes pre-processing to transform the medical data into useful format. Followed by, data classification process is performed by following Kernel Extreme Learning Machine (KELM) model. Finally, Symbiotic Organism Search (SOS) optimization algorithm is utilized to fine tune the KELM parameters which consequently helps in achieving high detection efficiency. In order to investigate the improved classifier outcomes of MOKELM-CPED model in an effectual manner, a comprehensive experimental analysis was conducted and the results were inspected under diverse aspects. The outcome of the experiments infer the enhanced performance of the proposed method over recent approaches under distinct measures.

Keywords: COVID-19; epidemiology dataset; machine learning; artificial intelligence; metaheuristics; healthcare

1  Introduction

Healthcare is one of the major sectors that produce big data in its day-to-day’s tasks with a wide range of perspectives and healthcare data experience huge privacy and security issues. The application of Artificial Intelligence (AI) upon health care information occur from life to death of an individual. AI helps nurses, doctors, diagnostic professionals, and other health care staff in their day-to-day work [1]. It has the potential to improve quality of life whereas preventive care is an important concept in healthcare since it produces precise diagnosis and treatment plans which result in better patient outcomes [2]. Artificial Intelligence can predict and track the spread of infectious diseases by investigating information from healthcare, government, and other sources. Consequently, AI plays a critical part in global public health as a tool that can combat pandemics and epidemics. The outbreak of COVID-19, a type of Severe Acute Respiratory Infection (SARI), was first diagnosed in December 2019 at Wuhan, China [3]. Asymptomatic cases and lack of diagnoses kit for COVID-19 resulted in missed or delayed diagnoses and exposed the visitors, patients, and health care workers to 2019- nCoV infection [4]. This posed a significant risk to both healthcare infrastructure and economic development of countries. Thus, it is obvious that non-clinical methods namely, data mining, expert system, machine learning, and other artificial intelligence approaches should play a major role in containment and diagnoses of COVID19 pandemic. Non-therapeutic methods can minimize the massive problems faced by healthcare system since it can offer the optimum predictable and diagnostic approach for 2019-nCoV [5].

Machine Learning (ML) is the newest concept of AI and offers a strategic method to develop automatic, objective algorithmic, and complex techniques for analyzing the dimensional biomedical and mathematical data or to conduct multimodal analysis [6]. ML algorithm is capable of reading and modifying its architecture, according to the group of information, while it can adapt by augmenting the objective or a cost function [7]. ML has demonstrated the possibility to diagnose, detect, contain, and monitor the disease therapeutically. ML method starts by gathering information distinctly viz., from different resources [8]. Next, it fixes the preprocessed information to data interrelated problems and minimize space size by removing invalid information so as to select the stimulating information [9]. Sometimes, the dataset value could be the same for a scheme to take decision. Thus, the ML algorithm is developed by other concepts namely, theory control, probability statistics, and so on to examine information and extract novel and useful knowledge or hidden pattern or information based on previous experience [10]. Then, the effectiveness of the model is assessed and the model is optimized at last through new rules and dataset. ML technique is utilized in different fields namely, engineering, medicine, education, forecast, traffic management, manufacturing, and production.

The current study introduces a new Metaheuristic Optimization with Kernel Extreme Learning Machine for COVID-19 Prediction Model on Epidemiology Dataset, named MOKELM-CPED technique. The presented MOKELM-CPED model undergoes data pre-processing to transform the medical data into useful format. In addition, data classification process is performed based on Kernel Extreme Learning Machine (KELM) model. Moreover, Symbiotic Organism Search (SOS) optimization algorithm is utilized to fine tune the KELM parameters. This consequently results in achieving high detection efficiency. In order to investigate the improved classifier outcomes of MOKELM-CPED model in an effective manenr, a comprehensive experimental analysis was conducted and the results were inspected under different aspects.

Rest of the paper is organized as follows. Section 2 provides a review of literature, Section 3 discusses the proposed model, Section 4 validates the performance of the proposed model, and Section 5 draws conclusion for the study.

2  Related Works

Yuan et al. [11] proposed a two-stage multi-feature selection technique utilizing GA and PSO techniques with NN classification method. The presented method was effectual in predicting CKD. It enhanced the accuracy on other typical approaches. Two-stage Feature Selection (FS) was followed with the help of PSO and GA techniques in a layer-by-layer format so as to optimize irrelevant features in the dataset. Chen et al. [12] presented a confidence-based and cost effectual FS technique utilizing binary PSO and CCFS. The objective of CCFS is to enhance the search efficiency by developing a novel upgrade method, whereas the confidence of all the features is explicitly regarded since it comprises of correlation between the feature and types and historically-chosen frequency of all the features. Dong et al. [13] proposed Backpropagation Network (BPN) as a classifier since it is flexible, less difficult, and implements optimum output with noise-free data. The experimental analysis was executed by collecting the data set from UCI repository. Popular datasets such as diabetes, liver, cancer, and heart were selected for the study. High classification efficacy was demonstrated and minimum RMSE value was detected with superior accuracy upon other factors.

In literature [14], a new healthcare observing structure was proposed based on cloud environment and big data analytics engine. This structure was proposed to store and analyze the healthcare data in a precise format and to improve the accuracy of the classifier. The presented big data analytics engine was dependent upon data mining approaches, ontologies, and Bi-LSTM. The data mining approaches effectually pre-process the healthcare data and decrease its dimensionality. The authors in the study conducted earlier [15] concentrated on referring to imbalanced class distribution in a manner such that the performance of the classifier technique is not compromised. The technique was presented based on Adjusting Kernel Scaling (AKS) approach to deal with multi-class imbalanced data set. The chosen kernel function was estimated with the help of weighing conditions and chi-square test. Nagarajan et al. [16] established a hybrid GA-ABC that signifies a genetic-based ABC approach for FS and classification using ensemble approaches. Ensemble classifier has four approaches such as SVM, RF, NB, and DT.

3  MOKELM-CPED Model

In this study, a new MOKELM-CPED technique is developed to accomplish effectual COVID-19 classification outcomes using epidemiology dataset. In the initial stage of MOKELM-CPED model, the data undergoes pre-processing so as to transform the medical data into useful format. Then, KELM-based data classification is executed and SOS algorithm is utilized for fine-tuning the KELM parameters which consequently helps in achieving high detection efficiency. Fig. 1 illustrates the block diagram of the proposed MOKELM-CPED model.

Figure 1: Block diagram of MOKELM-CPED model

3.1 Data Pre-processing

At first, data pre-processing is performed to transform epidemiology data into useful format. Z-score calculation is a normalized and standardized method that describes the count of Standard Deviations (SD); a raw datapoint is below/above the population mean. It preferably lies in the range of −3 and +3. It standardizes the dataset to the aforementioned scale so as to alter the data with distinct scales to default scale. In order to standardize the data with z-score, subtract the mean of population in raw datapoint and divide it by SD, which offers a score that ideally differs amongst −3 and +3,⋅ Therefore, it reflects several SDs at a point below/above the mean as follows. But, x represents the value of specific sample, μ refers to mean and σ depicts SD.

z−score =(x−μ)σ(1)

3.2 KELM-Based Classification

In skin lesion classification process, KELM model receives the skin lesion images for effective identification of class labels. In the structural method of SLFNs, Huang et al. presented ELM to improve the network’s training speed. Then, the theory of ELM is expanded from one neuron hidden node to another hidden node. Fig. 2 depicts the framework of ELM. The trained instances are demonstrated as follows {xi,tj}i=1n, whereas n is the number of trained instances, xj refers to the input of ith model with m-dimension and tj is the outcome of ith model. Next, the input vector x is provided, whilethe resultant of SLFNs with L hidden node is expressed as [17]:

f(x)=∑i=1Lβihi(x)=hT(x)β(2)

In which h(x)=[h1(x)⋯hL(x)]T represents the hidden outcome, and β=[β1⋯βL]T implies the resultant weights. Considering that the output of these n trained instances is estimated with zero errors, the compact equation is written as follows.

Hβ=t(3)

Here, H=[h(x1)⋯h(xn)]T is termed as hidden resultant matrix. The solution of resultant weight β contains only an easy linear formula while the solution corresponds to minimum training error i.e., min‖Hβ−t‖. The optimum evaluation of the resultant weights is demonstrated as Moore-Penrose generalized inverse H† which is given below.

β^=H†t(4)

Usually, the orthogonal projection is utilized to resolve the generalized inverse H†. When HTH is non-singular, H†=(HTH)−1HT, or if HHT is non-singular, H†=HT(HHT)−1. KELM is established in ELM with the help of kernel transformation technology so as to have optimum generalized performance than ELM, because of the kernel transformation in input to kernel spaces. The trained errors and resultant weights are minimized simultaneously while KELM is the resultant of the subsequent constrained optimized method.

minβ12‖β‖22+C2∑i=1nεi2(5)

s.t.φT(xi)β=ti−εi′i=1,2,⋯n

Figure 2: Structure of ELM model

In which, φ(⋅) demonstrates the kernel transformation in input to kernel spaces, εi refers to the ith trained error, the stated parameter C is utilized to represent the trade-off between β and ε. In line with Karush-Kuhn-Tucker (KKT) theorem and after presenting the Lagrange multiplier αi, the subsequent dual optimization problem is employed for solving the resultant weight, β.

minβ,α,ε{L=12‖β‖22+C2∑i=1nεi2−∑i=1nαi(φT(xi)β−ti+εi)}(6)

Proceeds with the partial derivative and create them as zero while the KKT conditions are expressed as follows

∂L∂βj=0,j=1,⋯L′→β=ΦTα

∂L∂εi=0,i=1,⋯n→α=Cε(7)

∂L∂αi=0,i=1,⋯,n→Φβ−t+ε=0

Here, Φ=[ϕ(x1)⋯ϕ(xn)]T implies the kernel resultant function. Through easy substitution and derivation, the resultant function is altered as subsequent expression.

f(x)=ϕT(x)ΦTα=ϕT(x)ΦT(In/C+ΦΦT)−1t(8)

Here, In represents the identity matrix with n-dimension, and depending upon ridge regression model, the improvement of regulation item In/C is capable of improving the generalized performance. For the convenience of computation, kernel transformation is uniformly expressed as inner product while kernel matrix is demonstrated as follows.

K=ΦΦT:Ki,j=ϕ(xi)⋅ϕ(xj)=k(xi,xj)(9)

The network infrastructure of new KELM technique comprises of input feature layer, kernel mapping layer, and output layer. During kernel mapping layer, every trained instance is utilized as an hidden node. Therefore, the resultant function is demonstrated as follows.

f(x)=[k(x,x1)⋯k(x,xn)]α(10)

whereas α=(In/C+K)−1t represents the resultant weight with respect to kernel mapping.

3.3 SOS Based Parameter Optimization

In order to determine the KELM parameters in an efficient manner and improve the detection performance, SOS algorithm is applied. SOS approach imitates a symbiotic relationship amongst different species in the ecosystem and was proposed in the study conducted earlier [18]. Here, the generation of solutions can be directed by mimicking the biological interactions between both species in the ecosystem. This method consists of Commensalism, Parasitism, and Mutualism, where all the species interact with another species randomly, until the end conditions are satisfied. The position of the organism, during iteration phase, gets upgraded by mimicking the three stages of symbiotic relations (parasitism, mutualism, and commensalism).

Definition 1. Assumed a function f:U→RfindX′∈u:∀X∈uf(X′)≤or≥f(X). ≤(≥) minimization (maximization) in which f denotes objective function that needs to be enhanced and U indicates the searching space with an element of U as the feasible solution. x represents the vector of optimization variable with value X={x1,x2,x3,…,xn}. Optimum solution is a possible solution X′ which enhances f. SOS process is defined herewith. It is possible to create the ecosystem initialized population along with other control parameters like ecosystem size and maximum number of iterations. The real number is utilized for indicating the position of organism in solution space. The following stage is used to select the organism with a better-fitting objective function.

In Mutualism, organism Ri, and organism Rj, using j≠i, are arbitrarily selected from the population so as to interact with each other. These two organisms benefit from mutualistic symbiotic relations. The new candidate solution for Ri and Rj organisms are estimated as follows.

Ri′=Ri+γ′∗[Rbest−(Mv∗BF−1)](11)

Rj′=Rj+γ′′∗[Rbesi−(Mv∗BP−2)](12)

In which γ′ and γ′′ denote arbitrary values between 0 and 1. The joint relational vector between the organisms Ri and Rj is represented by Mv while the benefit factors BP−1 and BF−2 are estimated using the following equations.

Mv=Ri+Rj2(13)

BF−1=1+round(γ′)(14)

BP−2=1+round(γ′′)(15)

The new Ri′ and Rj′ species are created by modeling the structure from Mv whereas BP corresponds to the optimal organism Rbesi of the existing population. Here, Mv denotes the mutual relations between different organisms while on the other hand BF, indicates the benefit level accomplished by species from the interaction. γ′ and γ′′ denote the function of arbitrarily-created values between 0 and 1 which follows a uniform distribution. The fitness values of new species f(Ri′) and f(Rj′) are compared and evaluated to all the predecessors so as to select the fittest one among the population. For example, f(Ri′) and f(Rj′) fitness functions are estimated, Ri is upgraded to Ri′ when f(Ri′) is higher than f() and Rj is similarly upgraded to Rj′, when f(Rj′) is higher than f(Rj). It is to be noted that the worst fitness value is substituted. During ith iteration, the organism Rj is arbitrarily designated from the ecosystem to interact with Ri, while i≠j. Now Rj is impartially affected in the relation, Ri gains the benefit. The commensalism interaction is modeled based on the following equation.

Ri′=Ri+γ′∗(Rbest)(16)

where γ′ denotes an arbitrary value between −1 and 1. Thus, the fitness function f(Ri′) is estimated and Ri is upgraded to Ri′, when f(Ri′) is higher than f(Ri). During ith iteration, a parasite vector RP is formed by adapting Ri with arbitrarily-created numbers in the range of the decision variable, and the organism Rj is selected arbitrarily using i≠j from the population to perform as host to the parasite, RP. When the fitness value f(Rp) is higher than the fitness value f, RP replaces Rj, or else, RP gets rejected. Steps 2–5 are executed, until the ending condition is satisfied. During final step, stopping or termination condition is fixed.

4  Experimental Validation

In this section, the experimental validation of the proposed MOKELM-CPED model is performed using the benchmark epidemiology dataset sourced from Kaggle repository (available at https://www.kaggle.com/marianarfranklin/mexico-covid19-clinical-data/metadata). In this study, the researchers considered 5,000 samples under positive class and 5,000 samples under negative classes.

Fig. 3 demonstrates a pair of confusion matrices generated by the proposed MOKELM-CPED model on training and testing datasets. On the applied 70% of training dataset, MOKELM-CPED model classified 3,186 images under positive class and 3,261 images under negative class. Similarly, with 30% of testing dataset, the proposed MOKELM-CPED model categorized 1,413 images under positive class and 1,395 images under negative class.

Figure 3: Confusion matrix of MOKELM-CPED model (a) 70% training data, (b) 30% testing data

Tab. 1 provides a brief outline of COVID-19 classification results, accomplished by MOKELM-CPED model with 70% training dataset and 30% testing dataset.

Fig. 4 reports the overall classifier results achieved by the proposed MOKELM-CPED model on 70% training dataset. The proposed MOKELM-CPED model classified positive classes with accuy, precn, recal, specy, and Fscore values being 92.10%, 92.64%, 91.39%, 92.80%, and 92.01% respectively. Besides, MOKELM-CPED model recognized negative classes with accuy, precn, recal, specy, and Fscore values such as 92.10%, 91.58%, 92.80%, 91.39%, and 92.18% respectively. Moreover, MOKELM-CPED model classified the images with average accuy, precn, recal, specy, and Fscore values namely, 92.10%, 92.11%, 92.10%, 92.10%, and 92.10%.

Figure 4: Result analysis of MOKELM-CPED technique under 70% of training dataset

Fig. 5 provides the detailed overall classifier results accomplished by the proposed MOKELM-CPED model on 30% testing dataset. MOKELM-CPED model categorized positive classes with accuy, precn, recal, specy, and Fscore values such as 93.60%, 93.95%, 93.33%, 93.88%, and 93.64% respectively. Also, the proposed MOKELM-CPED model acknowledged the negative classes with accuy, precn, recal, specy, and Fscore values such as 93.60%, 93.25%, 93.88%, 93.33%, and 93.56% respectively. Furthermore, MOKELM-CPED model categorized the images with average accuy, precn, recal, specy, and Fscore values such as 93.60%, 93.60%, 93.60%, 93.60%, and 93.60% respectively.

Figure 5: Result analysis of MOKELM-CPED technique under 30% of testing dataset

The accuracy investigation of the proposed MOKELM-CPED approach was conducted on test data and the results are portrayed in Fig. 6. The results exposed that MOKELM-CPED technique can enhance validation accuracy related to training accuracy. Further, it can be observed that the accuracy value got saturated with the count of epochs.

Figure 6: Accuracy graph analysis of MOKELM-CPED technique

The loss study was conducted for the proposed MOKELM-CPED system on test data and the results are shown in Fig. 7. The figure demonstrates that the proposed MOKELM-CPED approach significantly reduced the validation loss than the training loss. It can be moreover observed that the loss value got saturated with the count of epochs.

Figure 7: Loss graph analysis of MOKELM-CPED technique

Fig. 8 portrays a clear ROC curve generated from the results achieved by MOKELM-CPED model on test dataset. The figure portrays that MOKELM-CPED model produced proficient results with maximum ROC values under distinct class labels.

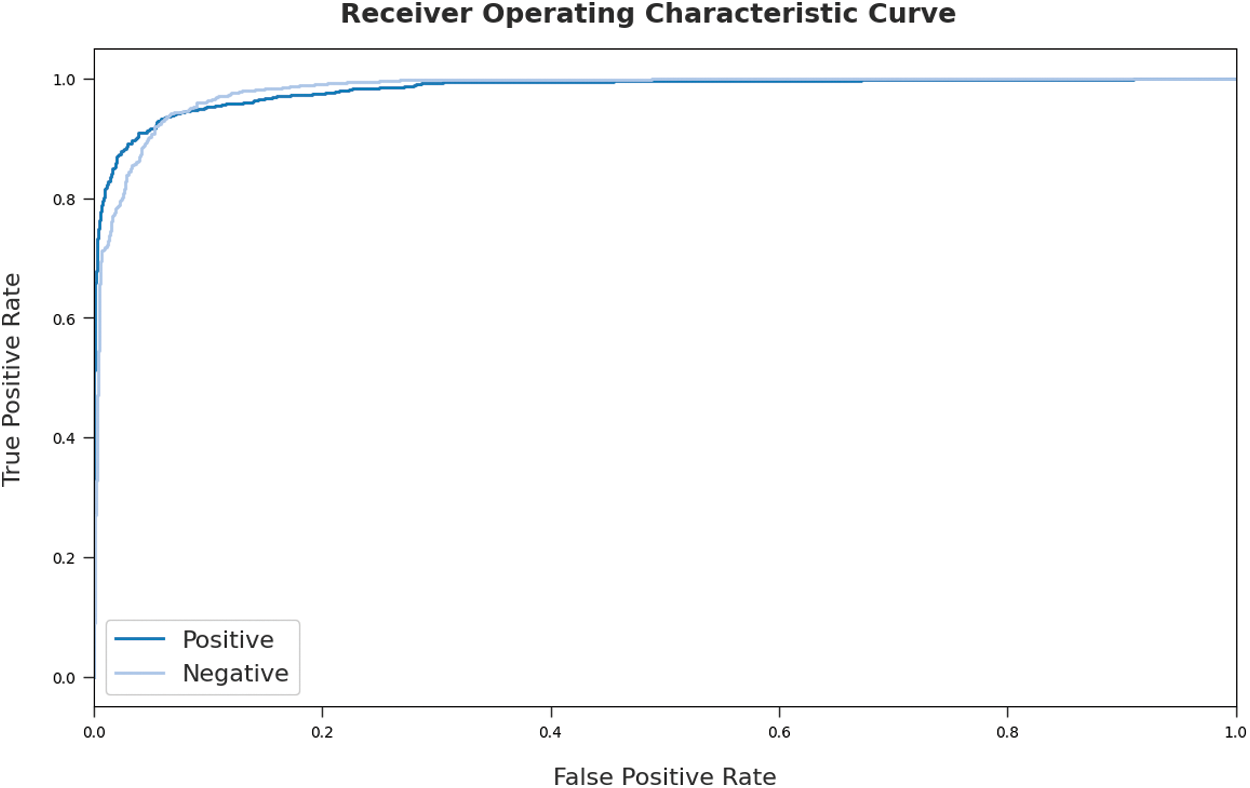
Figure 8: ROC analysis of MOKELM-CPED technique

Tab. 2 reports the results of an overall comparison study of MOKELM-CPED model against recent methods [19]. Fig. 9 offers the brief results of comparative analysis between MOKELM-CPED system and existing systems with respect to accuy. The figure indicates that Artificial Neural Network (ANN) produced the least accuy of 0.8973. Followed by, SVM technique attained a slightly increased performance with an accuy of 0.9280. Further, DT, LOR, NB, and SVM models reached reasonable outcomes with accuy values such as 0.9301, 0.9316, and 0.9322 respectively. However, the proposed MOKELM-CPED model produced high accuy i.e., 0.9360.

Figure 9: Accy analysis of MOKELM-CPED technique with existing methods

Fig. 10 provides the results of detailed comparison analysis, achieved by MOKELM-CPED approach against existing systems in terms of sensy. The figure indicates that NB system achieved the least sensy of 0.8428. Followed by, DT and LOR models attained slightly increased performance with sensy values such as 0.8923 and 0.8631 respectively. SVM and ANN models, on the other hand, reached reasonable outcomes with sensy values such as 0.9320 and 0.9293 respectively. However, the proposed MOKELM-CPED model resulted in increased sensy of 0.9360.

Figure 10: Sency analysis results of MOKELM-CPED technique against existing methods

Fig. 11 provides a brief overview on comparative analysis results accomplished by the proposed MOKELM-CPED system against existing systems with respect to specy. The figure indicates that SVM system achieved the least specy of 0.7676. Followed by, ANN system attained a slightly increased performance with a specy of 0.8358. Afterwards, DT, LOR, and NB models reached reasonable outcomes with specy values being 0.9242, 0.8716, and 0.9316 respectively. However, the proposed MOKELM-CPED model achieved an enhanced specy of 0.9360. The above-mentioned results and discussion infer the enhanced performance of MOKELM-CPED methodology over other methods.

Figure 11: Specy analysis results of MOKELM-CPED technique against existing algorithms

5  Conclusion

In this study, a new MOKELM-CPED model has been developed to accomplish effectual COVID-19 classification outcome using epidemiology dataset. In the initial stage of MOKELM-CPED model, the data undergoes pre-processing to transform the medical data into useful format. Then, KELM-based data classification process is executed whereas SOS algorithm is utilized for fine-tuning the KELM parameters which consequently helps in achieving high detection efficiency. To investigate the improved classifier outcomes of the proposed MOKELM-CPED model in an effective manner, a comprehensive experimental analysis was conducted and the results were inspected under diverse aspects. The outcome of the experiments pointed out the enhanced performance of the proposed model over recent approaches under distinct measures. In future, advanced DL-based detection models can be developed to boost classifier outcomes.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under grant number (RGP 1/322/42). Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R235), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4210118DSR01).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  T. Davenport and R. Kalakota, “The potential for artificial intelligence in healthcare,” Future Healthcare Journal, vol. 6, no. 2, pp. 94–98, 2019. [Google Scholar]

 2.  S. Secinaro, D. Calandra, A. Secinaro, V. Muthurangu and P. Biancone, “The role of artificial intelligence in healthcare: A structured literature review,” BMC Medical Informatics and Decision Making, vol. 21, no. 1, pp. 125, 2021. [Google Scholar]

 3.  A. İ. Tekkeşin, “Artificial Intelligence in Healthcare: Past, Present and Future,” Anatolian Journal of Cardiology, vol. 22, pp. 8–9, 2019. [Google Scholar]

 4.  J. Amann, A. Blasimme, E. Vayena, D. Frey and V. I. Madai, “Explainability for artificial intelligence in healthcare: A multidisciplinary perspective,” BMC Medical Informatics and Decision Making, vol. 20, no. 1, pp. 310, 2020. [Google Scholar]

 5.  H. Swapnarekha, H. S. Behera, J. Nayak and B. Naik, “Role of intelligent computing in COVID-19 prognosis: A state-of-the-art review,” Chaos, Solitons & Fractals, vol. 138, no. 12, pp. 109947, 2020. [Google Scholar]

 6.  J. Shuja, E. Alanazi, W. Alasmary and A. Alashaikh, “COVID-19 open source data sets: A comprehensive survey,” Applied Intelligence, vol. 51, no. 3, pp. 1296–1325, 2021. [Google Scholar]

 7.  J. She, L. Liu and W. Liu, “COVID-19 epidemic: Disease characteristics in children,” Journal of Medical Virology, vol. 92, no. 7, pp. 747–754, 2020. [Google Scholar]

 8.  J. Chen, K. Li, Z. Zhang, K. Li and P. S. Yu, “A survey on applications of artificial intelligence in fighting against COVID-19,” ACM Computing Surveys, vol. 54, no. 8, pp. 1–32, 2022. [Google Scholar]

 9.  N. E. Rashidy, S. E. Sappagh, S. M. R. Islam, H. M. E. Bakry and S. Abdelrazek, “End-to-end deep learning framework for coronavirus (covid-19) detection and monitoring,” Electronics, vol. 9, no. 9, pp. 1439, 2020. [Google Scholar]

10. H. B. Syeda, M. Syed, K. W. Sexton, S. Syed, S. Begum et al., “Role of machine learning techniques to tackle the covid-19 crisis: Systematic review,” JMIR Medical Informatics, vol. 9, no. 1, pp. e23811, 2021. [Google Scholar]

11. M. Yuan, Z. Yang, G. Huang and G. Ji, “A novel feature selection method to predict protein structural class,” Computational Biology and Chemistry, vol. 76, pp. 118–129, 2018. [Google Scholar]

12. Y. Chen, Y. Wang, L. Cao and Q. Jin, “An effective feature selection scheme for healthcare data classification using binary particle swarm optimization,” in 2018 9th Int. Conf. on Information Technology in Medicine and Education (ITME), Hangzhou, China, pp. 703–707, 2018. [Google Scholar]

13. B. Dong, Y. Liu, B. Guo and X. Zhang, “Generalization threshold optimization of fuzzy rough set algorithm in healthcare data classification,” International Journal of Database Theory and Application, vol. 9, no. 3, pp. 229–238, 2016. [Google Scholar]

14. F. Ali, S. E. Sappagh, S. M. R. Islam, A. Ali, M. Attique et al., “An intelligent healthcare monitoring framework using wearable sensors and social networking data,” Future Generation Computer Systems, vol. 114, pp. 23–43, 2021. [Google Scholar]

15. S. Ketu and P. K. Mishra, “Scalable kernel-based SVM classification algorithm on imbalance air quality data for proficient healthcare,” Complex & Intelligent Systems, vol. 7, no. 5, pp. 2597–2615, 2021. [Google Scholar]

16. S. M. Nagarajan, V. Muthukumaran, R. Murugesan, R. B. Joseph and M. Munirathanam, “Feature selection model for healthcare analysis and classification using classifier ensemble technique,” International Journal of System Assurance Engineering, vol. 13, no. 5, pp. 971, 2021. [Google Scholar]

17. J. Lu, J. Huang and F. Lu, “Distributed kernel extreme learning machines for aircraft engine failure diagnostics,” Applied Sciences, vol. 9, no. 8, pp. 1707, 2019. [Google Scholar]

18. M. Abdullahi, M. A. Ngadi and S. M. Abdulhamid, “Symbiotic organism search optimization based task scheduling in cloud computing environment,” Future Generation Computer Systems, vol. 56, no. 3, pp. 640–650, 2016. [Google Scholar]

19. L. J. Muhammad, E. A. Algehyne, S. S. Usman, A. Ahmad, C. Chakraborty et al., “Supervised machine learning models for prediction of covid-19 infection using epidemiology dataset,” SN Computer Science, vol. 2, no. 1, pp. 11, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.