Computers, Materials & Continua DOI:10.32604/cmc.2022.029166
Article

A Novel Stochastic Framework for the MHD Generator in Ocean

Sakda Noinang1, Zulqurnain Sabir2, Shumaila Javeed3, Muhammad Asif Zahoor Raja4, Dostdar Ali3, Wajaree Weera5,* and Thongchai Botmart5

1Department of Mathematics Statistics and Computer, Faculty of Science, Ubon Ratchathani University, Ubon Ratchathani 34190, Thailand
2Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
3Department of Mathematics, Comsats University Islamabad, 45550 Islamabad Campus, Islamabad, Pakistan
4Future Technology Research Center, National Yunlin University of Science and Technology, Yunlin 64002, Taiwan
5Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
*Corresponding Author: Wajaree Weera. Email: wajawe@kku.ac.th
Received: 26 February 2022; Accepted: 06 May 2022

Abstract: This work aims to study the nonlinear ordinary differential equations (ODEs) system of magnetohydrodynamic (MHD) past over an inclined plate using Levenberg-Marquardt backpropagation neural networks (LMBNNs). The stochastic procedures LMBNNs are provided with three categories of sample statistics, testing, training, and verification. The nonlinear MHD system past over an inclined plate is divided into three profiles, dimensionless momentum, species (salinity), and energy (heat) conservations. The data is applied 15%, 10%, and 75% for validation, testing, and training to solve the nonlinear system of MHD past over an inclined plate. A reference data set is designed to compare the obtained and proposed solutions for the MHD system. The plots of the absolute error (AE) are provided to check the accuracy and precision of the considered nonlinear system of MHD. The obtained numerical solutions of the nonlinear magnetohydrodynamic system have been considered to reduce the mean square error (MSE). For the capability, dependability, and aptitude of the stochastic LMBNNs procedure, the numerical performances are provided to authenticate the relative arrangements of MSE, error histograms (EHs), state transitions (STs), correlation, and regression.

Keywords: MHD energy; salinity; levenberg-marquardt backpropagation; Soret number; nonlinear

1  Introduction

Ocean energy is considered one of the significant sources of renewable energy globally. Due to the necessity of long-term hydropower systems, various electrical power systems have existed and been installed based on demand and energy usage. For example, the improved and low-cost system is photovoltaic panels [1], which recharged the solar collectors through geothermal energy reservoirs, biomass gasification [2], and turbines [3]. In order to obtain an energy system, the interest in power production marine energy can be included (especially in Asian regions) along with the advanced systems that have been established in the ocean thermal energy conversion [4], wave energy conversion devices [5], and tidal powerhouse [6]. Although several alternative oceanic renewable designs have been proposed, the magnetohydrodynamic (MHD) saltwater generator [7]. These types of converters interchange the kinetic energy of source energy into electrical energy in the process of MHD [8]. The experimental magnetic field is an important aspect in optimizing both efficiency and performance parameters in MHD ocean generators, as it is in the traditional land-based MHD generators. Rotating disk and channels, Hall current along with the helicoid [9–12], are well-known systems that have been researched in the present decade. To perform better, the complicated features of heat, mass, and momentum are used to improve operational efficiency, which has sparked a lot of interest in mathematical and computer modeling. The physical parameters of sea wave motion are determined by salinity, temperature, and pressure, posing significant seawater properties. The presence of tiny, suspended particles in seawater significantly impacts the generation of marine waterpower [13].

In recent years, the mass and heat flows have achieved significant attention with inclined MHD. Such studies of different physical parameters affect the energy production systems and how porous inclined plate affects magnetized nanofluid flow [14]. In a stretching plate, magnetic number and heat effects are studied on hydromagnetic flow with an inclined plane [15,16]. Palani et al. investigated a hydromagnetic solution using a numerical technique named finite-difference to find the natural convection with the help of ohmic impacts [17]. Chamkha et al. obtained the numerical solutions of buoyancy-driven magneto-convection by the blotter-difference method [18]. Masthanrao et al. investigated the chemical reaction impacts on the stable 2-D hydromagnetic natural process of convection in a porous phase [19]. Hossain et al. examined the inclined plate and their convection together with the effects of the weak-magnetic line by using the finite-difference method and local similarity [20]. Ramadan et al. obtained a computational solution of two-phase convection (natural) in an inclined surface considering the variable characteristics and effect on the magnetized boundary-layer flow [21]. Wang et al. proposed the implicit method of inverse direction cubic spline to replicate the mixed convection flow (magneto-hydrodynamic) from an inclined wavy plate [22]. Along with that, they observed that the leading-edge flow depends on the force of increasing magnetic body, whereas decelerates the flow when the wavy surface is far from downstream. Chen studied the characteristics (mass transfer, heat, and momentum) of non-isothermal flow in joule and viscous dissipation from a porous slope surface [23].

The above studies discussed the rate of heat flow and generally ignored mass transfer, which is simultaneous species in the process of diffusion. However, as noted previously, the combined impacts of heat as well as mass transfer is important in systems devices. In the ocean, MHD generators have serious issues with salinity. The diffusion of mass and mixed convection flow investigations show that mass transfer obeys the Frckian-law [24] and complex properties of the mixed-convection flow. Ferdows et al. found the double-diffusive convection effects on wall slip [25]. Rashidi et al. solved the transport phenomena due to the reactive boundary-layer convection [26]. Zueco et al. applied numerical-network simulation on thermophoretic magneto-convection to get the effect by thermophysical variable [27,28]. However, these findings have been excluded from the diffuse-thermal (Dufour) or thermal–diffusion (Soret) effects. Bég et al. used boundary layer theory and local non-similarity processes to find the Dufour effects [29]. Bég et al. simulated the effects of Soret based on thermo-diffusion considering the peristaltic pumping and described the relationship among wave amplitude buoyancy force [30]. Few more studies related to Soret have been presented in the references [31,32]. Vasu et al. investigated the Dufour effect and Soret effect on hydromagnetic transportation from a circular body in porous channels [33]. In recent years, Vasu et al. interrogated advanced solutions employing finite-difference scheme considering the effects of Dufour-Soret cross-diffusion [33]. Soret/Dufour impacts are substantial. The energy flux generates the difference of concertation and produces diffusion-Thermo or Dufour effects. While the mass flux is induced via temperature difference is the thermo-diffusion or Soret effect.

The present literature has not studied the MHD ocean system flows from the inclined plate with heat generation and Soret effects. Therefore, we focused on that and examined the MHD ocean-generator, the transport phenomena of thermo-diffusion, and heat-generation effects from an inclined surface. Saltwater liquid transportation phenomena have a Soret effect. The laminar steady-state edge leading system is studied for MHD double-diffusive flow in ocean water convection besides heat generation with the inclined insulated (non-conducting) plate. The velocity, concentration (salinity), and temperature are also a wide range of self-control parameters along with surface-heat transfer, skin-friction coefficient, and mass transfer.

1.1 Mathematical Form of the Transport System

The ocean-generator MHD approach is one of the feasible capabilities of mankind. Numerous Russian, Japanese, American, and French engineers studied renewable energy. In Japan, the floating installation system represents the construction of MHD floating ocean-energy along with the basic MHD ocean-energy production. Here α is the slope of the inclined plate. The initial assumption is that the same temperature, T for both plate and fluid, and gets the same salinity level, S at every point. Also, assumed that both are at rest, the generator plate (channel wall) and the fluid. When the wall moves forward along X-axis with a constant velocity then the temperature of species salinity and the wall becomes SW(>S∞) and TW(>T∞). Here, SW is the rest species salinity, TW is the temperature at rest, while SW and TW are far away from the wall respectively, and as a result, a low magnetic field B0. The magnetic field is every time normal to the wall and never alters due to the change of wall. The force (Lorentz) is always directed and relative to the plate (wall). To study the boundary-layer approximation, the governing equations of energy conservation, momentum, salinity, mass, incorporating heat-generation and Soret effects are as follows:

Continuity equation:

∂U∂x+∂V∂y=0.(1)

Momentum Conservation:

(U∂U∂x+V∂V∂y)=v (∂2U∂y2)+gβ(T−T∞)sin⁡α − σβ02ρU.(2)

Species (Salinity) Conservation.

(U∂S∂x+V∂S∂y)=Ks (∂2S∂y2)+Fs(∂2T∂y2). (3)

Energy (heat) conservation:

(U∂T∂x+V∂T∂y)=KT (∂2T∂y2)+Fs(QTρCP). (4)

The specified boundary-conditions are given below:

U=0a   Y=0 V=0  T= Tw=T∞=+sinα As Y→∞:U→0:V→0:T→ T∞,  S→S∞,       (5)

where, U is the uniform velocity, V is the kinematic viscosity, g is the acceleration (gravity), β is the expansion coefficient of the volumetric thermal process, β* is the expansion coefficient of mass, σ is the conductivity of the fluid, ρ is the density of fluid. QT is the heat generation, CP is the constant pressure of specific heat. Moreover, Ks, KT are thermal diffusive due to temperature, and salinity (salt species) respectively and Fs is the molecular diffusivity. The second last factor in Eq. (3) represents the Soret effect term. The key point to be noted in Eq. (5), the thermal and solutal boundary-conditions show the inclusion plate’s place under the temperature field and solutal [34]. In this study, the isothermal and non-solutal effects are ignored. Thermal and concentration impacts at the plate cannot be fully measured, particularly in the MHD domain of the ocean generator. It is impossible to minimize completely the time or spatial difference of such phenomena. Gebhart et al. followed boundary-layer theory and founded a robust boundary-value problem, which helped the logical and validated supposition for engineers [34]. This supports a reasonable estimation for close wall transfer phenomena. Eqs. (1)–(4) define boundary-value problems that cannot solve analytically under the considered boundary-conditions (c.f. Eq. (5)). In primitive variables, the primitive boundary-value problem using numerical methods cannot yield explanations in terms of significant dimensionless measures. To overcome this, the similarity transformation makes the problem dimensionless and converts the partial differential equations to the system of ordinary differential equations. This is an easy method that is helpful to observe several physical parameters of the transport phenomena.

1.2 Transformation of Model

Proceeding for transformation and defining dimensionless variables as follows:

η=yUo2vX,ψ=2xUoXf(η),θ=θ(η)=T−T∞Tw−T∞, ϕ=ϕ(η)=S−S∞Sw−S∞=∂ψ∂Y,…v=−∂ψ∂X(6)

These parameters introduced in the systems (c.f. Eqs. (1)–(4)) as the non-dimensional ODEs are

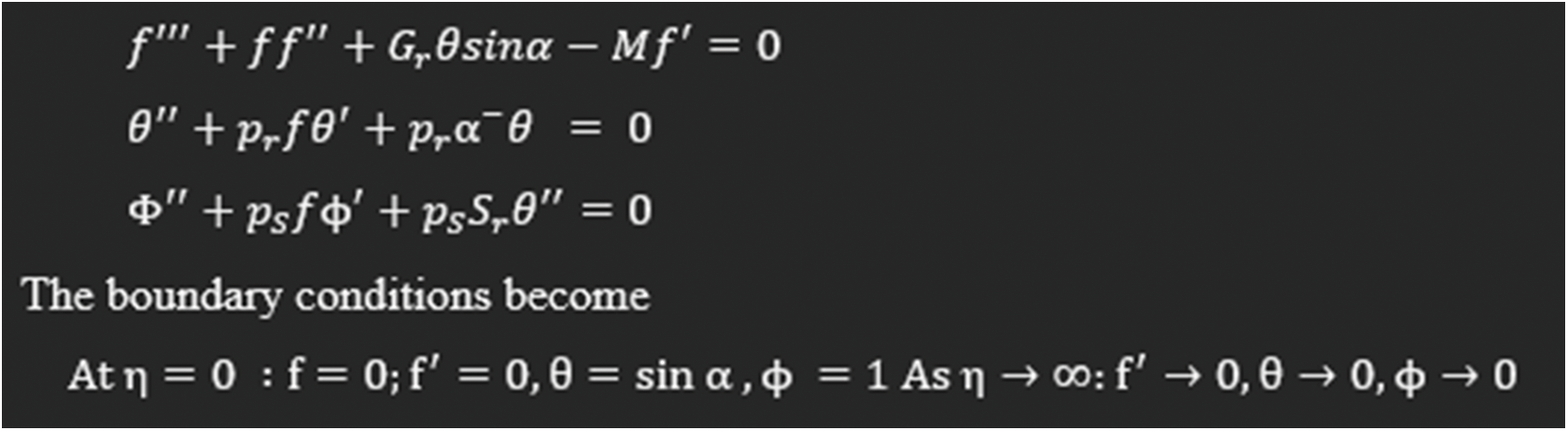
The energy systems in which the coefficient of skin-friction along with the rate of heat and salinity transfer is computed by the below expressions:

Cj(Re)−12=−f′′(0) Nu(Re)−12=−θ′(0) Sh(Re)−12=−ϕ′(0) .

Here Re is the Reynolds-number.

The purpose of this investigation is to design a robust computational artificial neural network (ANN) technique using the novel characteristics of the Levenberg-Marquardt backpropagation (LBMBP), i.e., ANN-LBMBP for solving the MHD generators in the ocean system. The nonlinear mathematical form of the boundary-layer wall in the ocean system is in three groups, heat transfer, mass transfer and momentum. The obtained solutions through the proposed ANN-LBMBP procedure for solving the MHD ocean energy generating system are related to the reference work out solutions. The stochastic-based numerical processes have been applied to solve various evolutionary/swarming schemes [35–37]. Additionally, the stochastic methods have been applied to solve the fractional order singular nonlinear model [38,39], SITR model based on coronavirus [40,41], functional order singular system [42], HIV nonlinear model [43–45], delayed form of the models [46], dengue fever systems [47] and periodic differential models [48,49]. The general novel features of the ANN-LBMBP for solving the MHD in the ocean system are provided as follows:

•   A novel stochastic ANN-LBMBP procedure is presented for solving the energy generating in the ocean system.

•   The obtained numerical results through the stochastic ANN-LBMBP procedures have been compared with the reference solutions for boundary-layer approximation in the ocean system.

•   The results correspond with performance, which indicates the exactness of the designed stochastic NN-LBMBP for solving energy generation in the ocean system.

The absolute error (AE) performances are found in good ranges to solve the waste energy in the ocean system. The rest of the paper’s parts are summarized: The procedure for the MHD in the ocean’s nonlinear ODEs system past over an inclined plate is provided in Section 2. The numerical results are given in Section 3. The concluding remarks and future work directions are provided in Section 4.

2  Methodology: Stochastic LMBNNs

In this section, the designed stochastic LMBNNs procedures are provided in two steps for solving the MHD nonlinear ODEs system past over an inclined plate. Firstly, the necessary details of the stochastic process for the ODEs are explained, whereas the execution actions of the stochastic procedures are provided in the second phase.

An appropriate optimization LMBNNs procedure is provided in Fig. 1 based on the multi-layer processes. The LMBNNs procedures are executed with ‘nftool’ command, which is build-in MATLAB procedure using the statistics, 10%, 15% and 75% for testing, validation and training are provided to solve the MHD nonlinear ODEs system past over an inclined plate.

Figure 1: Workflow illustrations of the proposed LMBNNs for solving the nonlinear ODEs system past over an inclined plate

3  Numerical Simulations

Case-1: Consider the nonlinear MHD past over an inclined plate with Gr=4, M=0.4, α=90°, Pr=0.5, Ps =0.3, α−=0.5, Sr=0.4. The mathematical representations of non-linear, non-dimensional ODEs system (7) using these values are provided as:

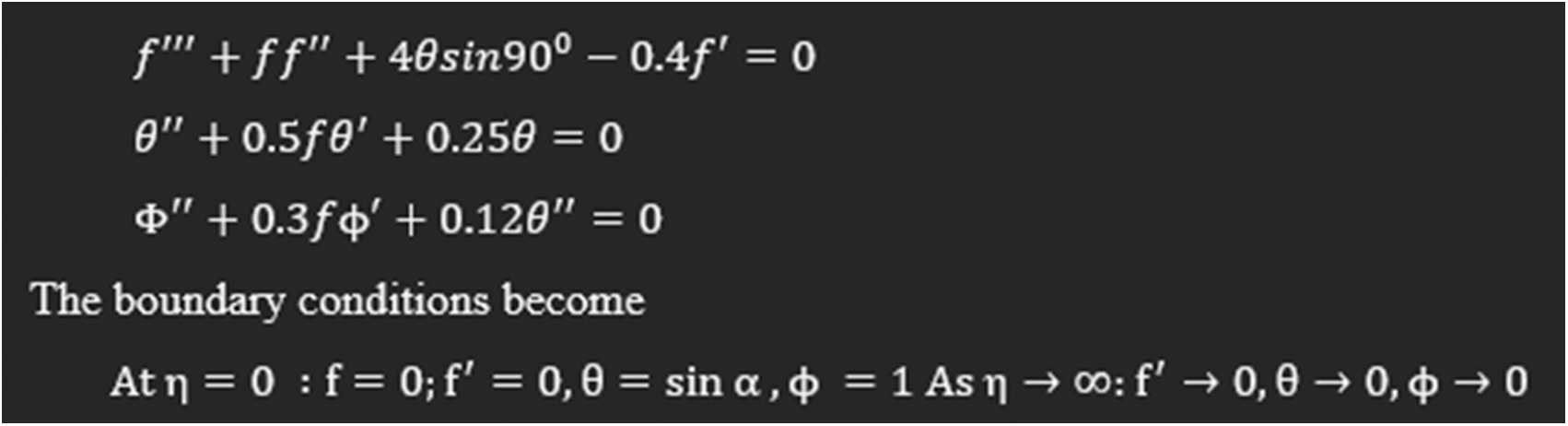
Case-2: Consider the nonlinear MHD past over an inclined plate with Gr=4, M=0.4, α=90°, Pr=0.8, Ps =0.3, α−=0.5, Sr=0.4. The mathematical representations of non-linear, non-dimensional ODEs system (7) using these values are provided as:

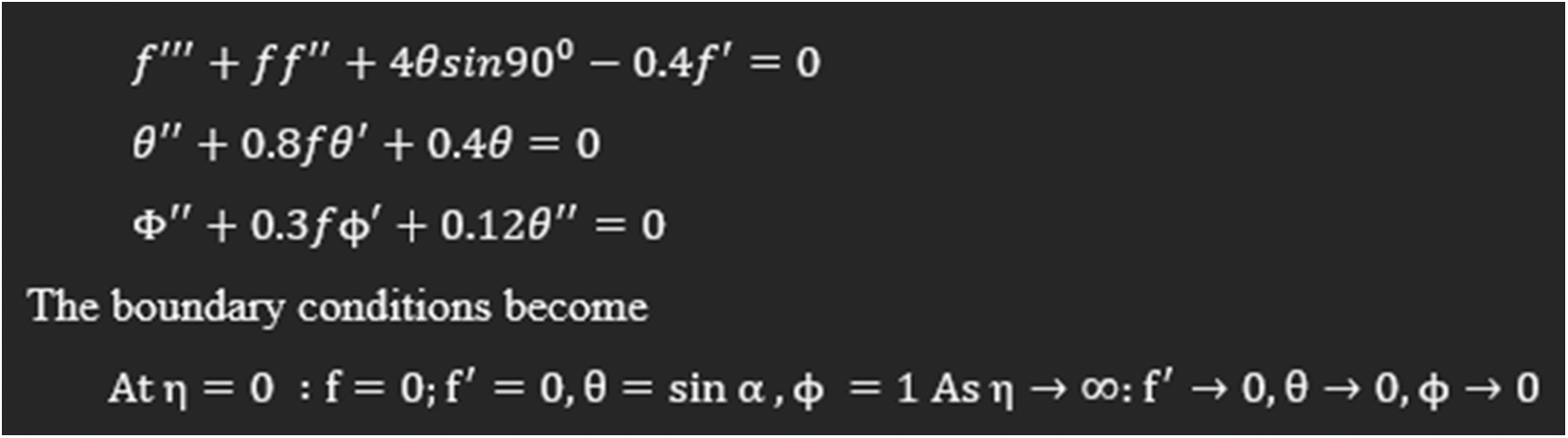
Case-3: Consider the nonlinear MHD past over an inclined plate with Gr=4, M=0.4, α=90°, Pr=1.3, Ps =0.3, α−=0.5, Sr=0.4. The mathematical representations of non-linear, non-dimensional ODEs system (7) using these values are provided as:

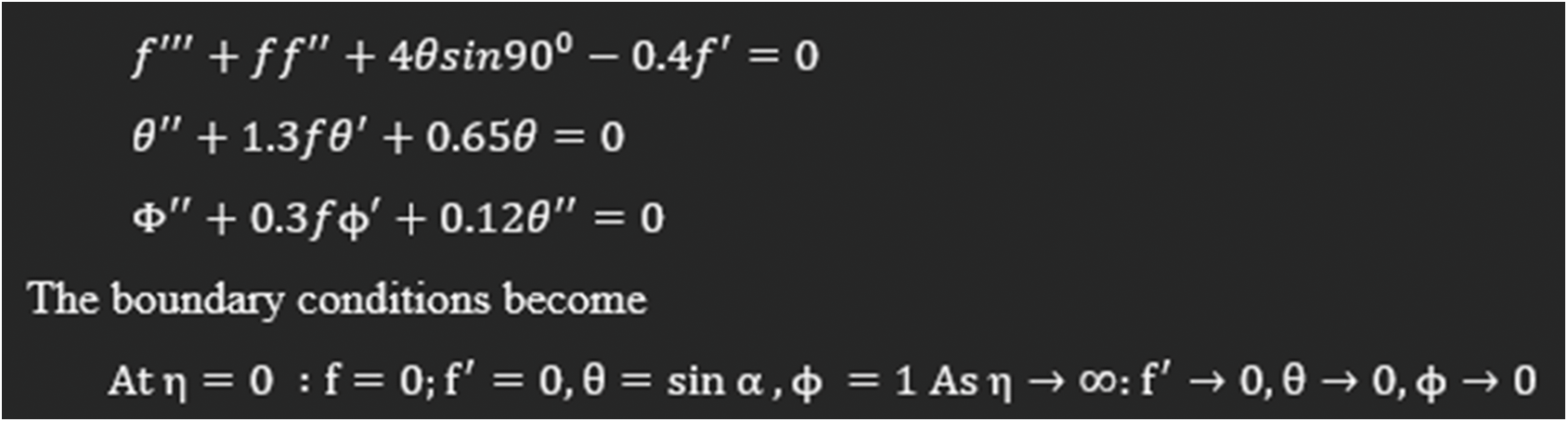
The numerical results based on stochastic LMBNNs procedures for solving the MHD system past over an inclined plate are provided in the input [0, 1]. The ‘nftool’ command is built-in MATLAB procedure using the statistics, 15%, 10% and 75% for testing, validation, and training to solve the MHD past over an inclined plate. Seven numbers of neurons have been used throughout this numerical study. The obtained numerical representations of the stochastic procedures for the nonlinear MHD past over an inclined plate are illustrated in Fig. 2.

Figure 2: Stochastic LMBNNs procedure to solve the nonlinear MHD system past over an inclined plate

The numerical representations to solve the nonlinear MHD system past over an inclined plate are drawn in Figs. 3–11 using the stochastic LMBNNs procedures. The proficient numerical performances are given in Figs. 3–5 based on the STs and performances. The obtained performances using the MSE for training, STs, best curve, testing states and authentication are plotted in Fig. 3. The best routines for the ODEs model are calculated at epochs 116, 116 and 122 around 2.96 × 10−10, 1.13 × 10−11 and 6.16 × 10−12, respectively. Fig. 4 represents the gradient performances of the stochastic procedures for the MHD past over an inclined plate, which lie around 9.79 × 10−08, 9.98 × 10−08 and 9.81× 10−08. These illustrations designate the accuracy and precision of the proposed stochastic procedures for the MHD past over an inclined plate. The fitting curve representations are illustrated in Figs. 5–7, which are drawn on the basis of the comparison of the obtained results through LMBNNs and the database results. The error plots are shown based on the performances of training, testing and authentication through the proposed stochastic procedures for the nonlinear ODEs system of MHD past over an inclined plate. The plots of EHs are drawn in Figs. 8a–8c based on the regression, which are calculated around 4.51 × 10−08, 4.93 × 10−07 and 3.83 × 10−07 for cases 1, 2 and 3. The correlation performances are observed in Figs. 9–11 for cases 1, 2 and 3 to solve the nonlinear ODEs system of MHD past over an inclined plate. One can observe that the values of correlation are calculated around 1 to solve the nonlinear ODEs system of MHD past over an inclined plate, which indicates the perfect system. The testing, verification and training illustrations indicate the correctness of the proposed stochastic scheme for the system of MHD past over an inclined plate. Furthermore, the MSE convergence is accomplished for authentication, training, epochs and testing in Tab. 1 for the system of MHD past over an inclined plate.

Figure 3: MSE performance using the stochastic procedures for the system of MHD past over an inclined plate

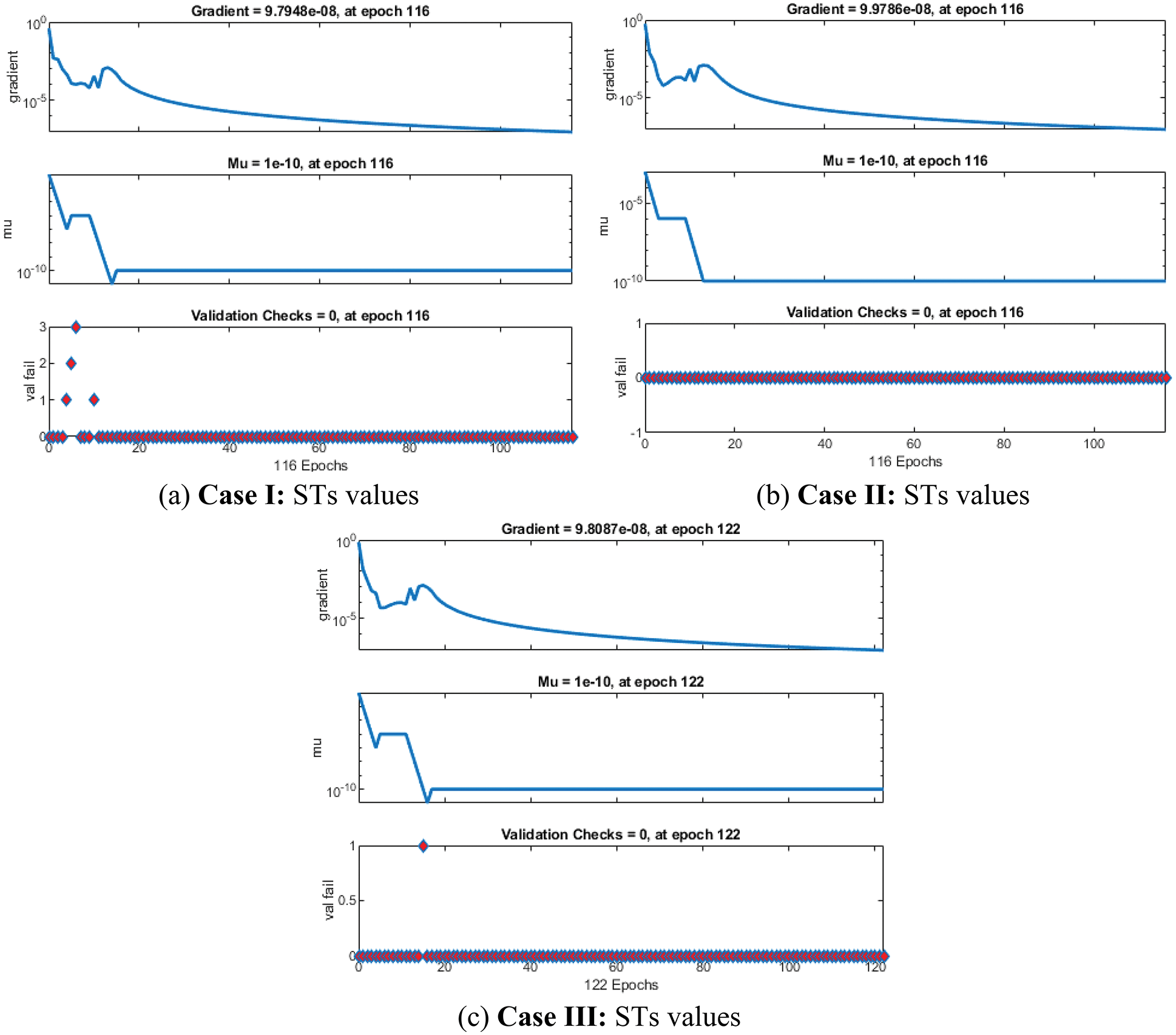
Figure 4: STs values using the stochastic procedures for the system of MHD past over an inclined plate

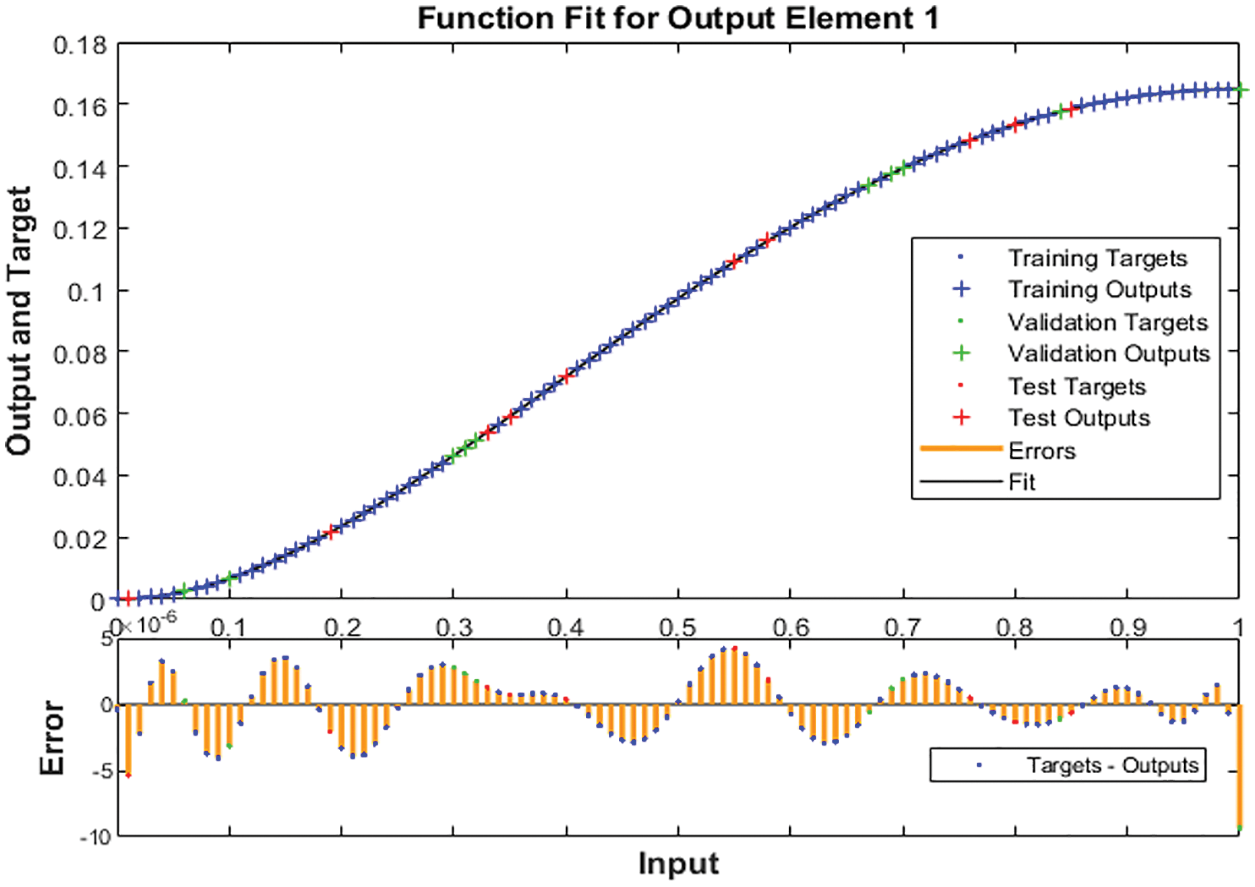
Figure 5: Case 1: Results using the stochastic procedures for the system of MHD past over an inclined plate

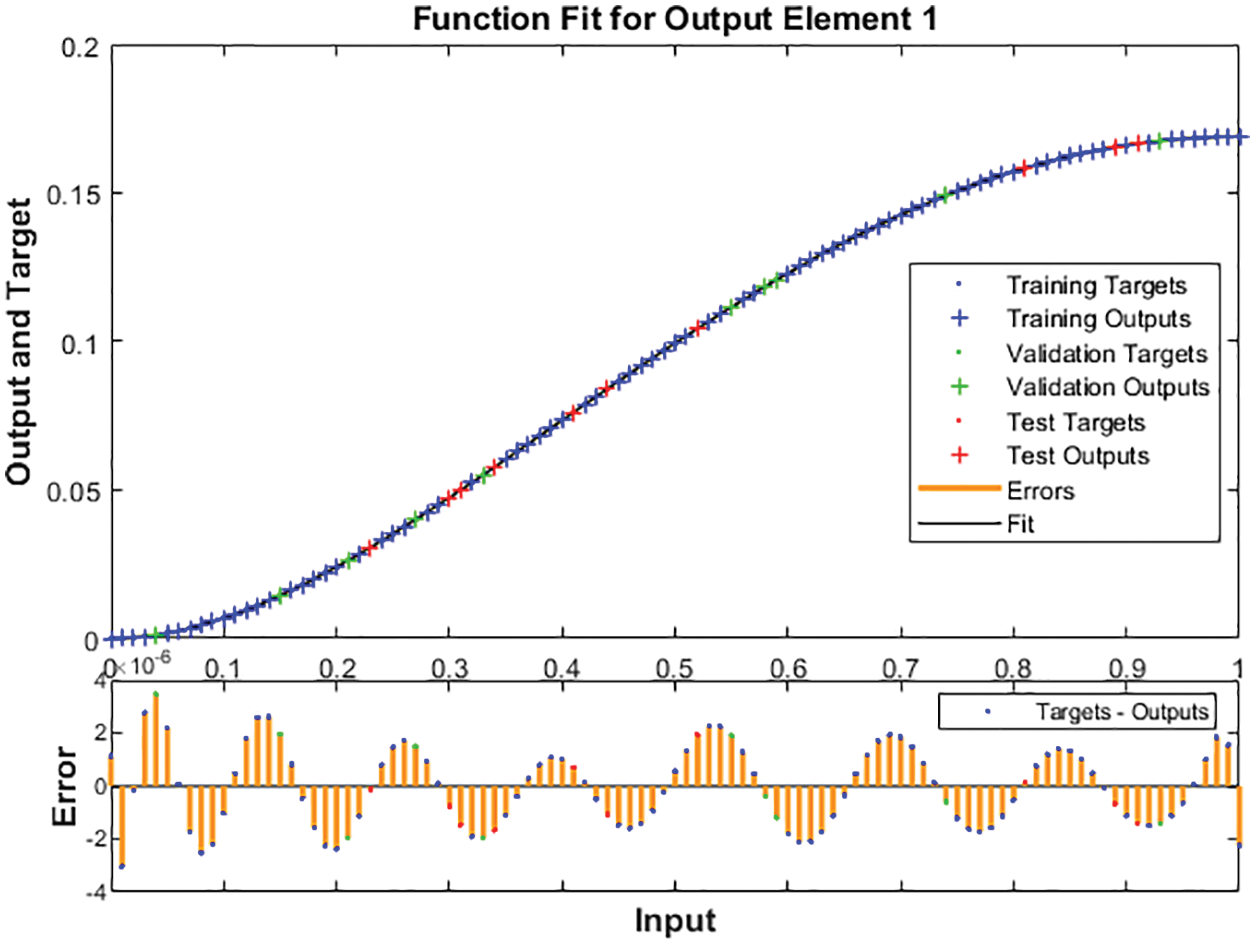
Figure 6: Case 2: Results using the stochastic procedures for the system of MHD past over an inclined plate

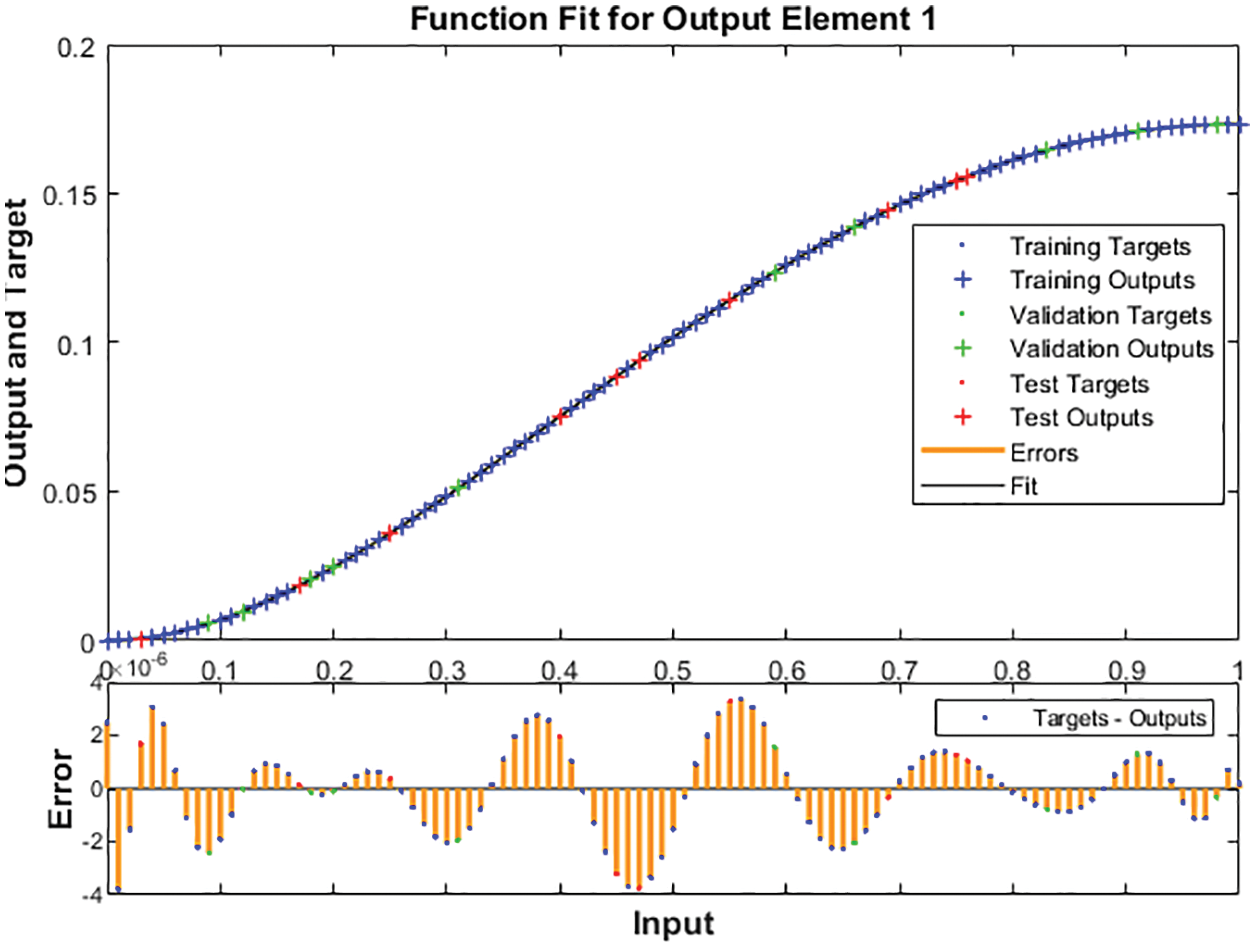
Figure 7: Case 3: Results using the stochastic procedures for the system of MHD past over an inclined plate

Figure 8: EHs based on the stochastic procedures for the system of MHD past over an inclined plate

Figure 9: Regression plots for case 1

Figure 10: Regression plots for case 2

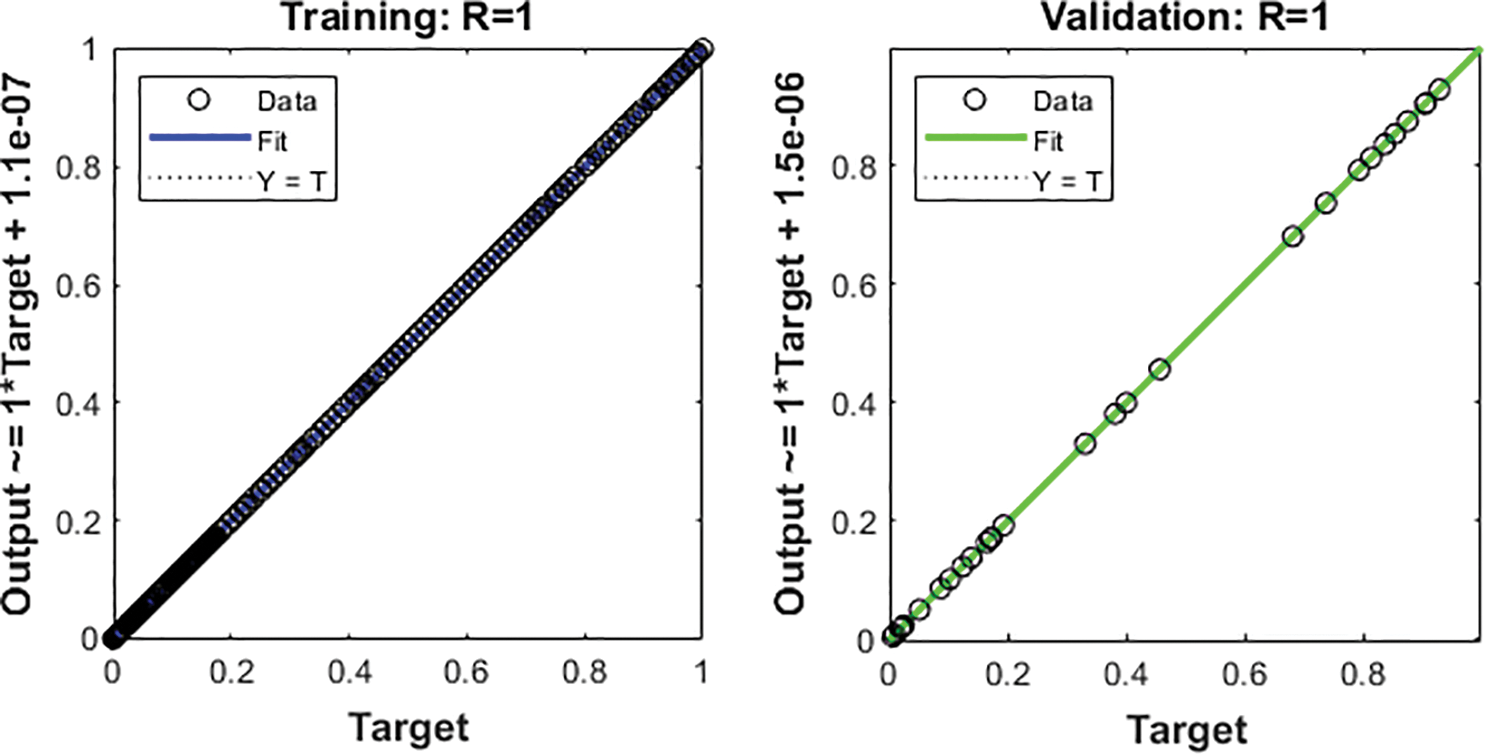
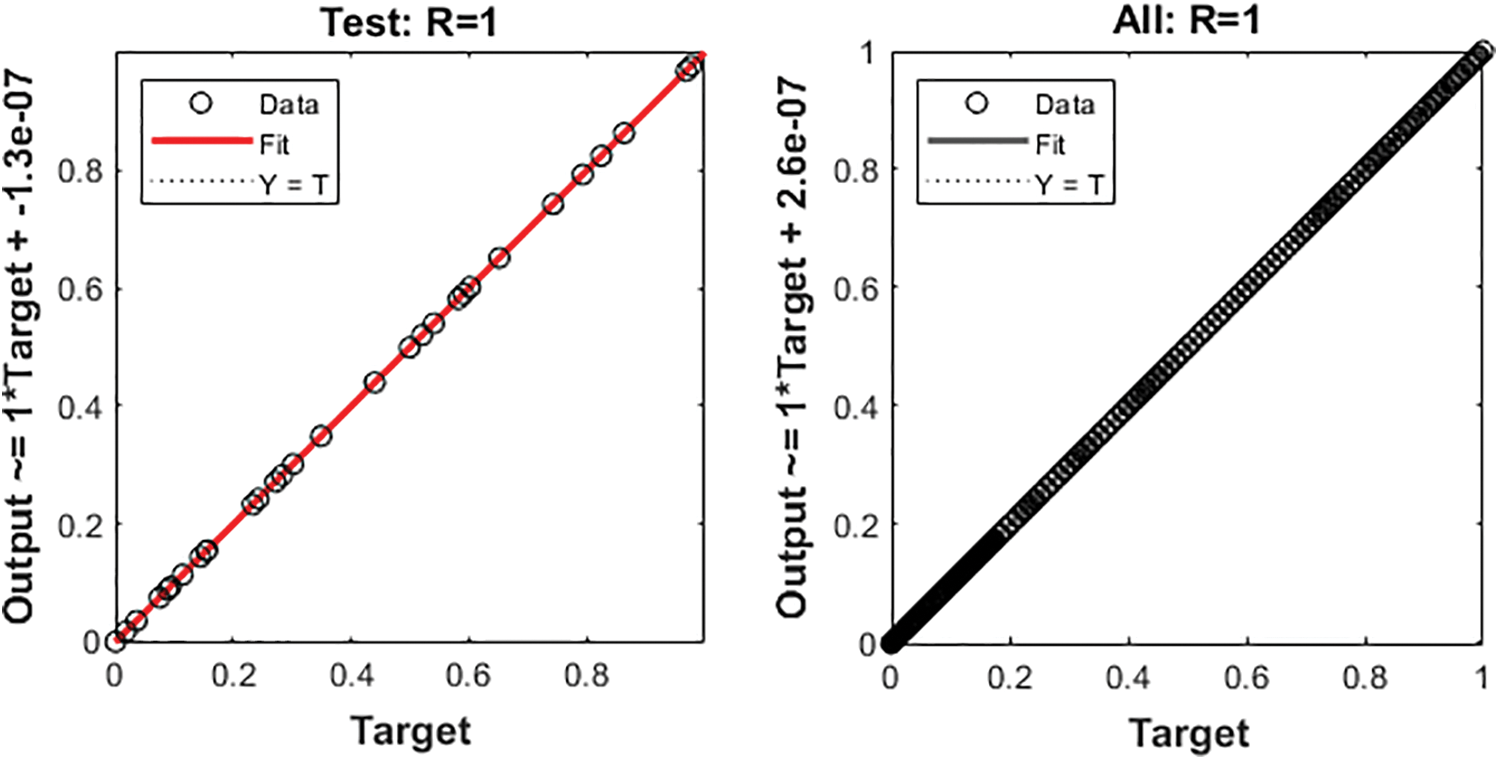
Figure 11: Regression plots for case 3

The comparison plots are drawn in Figs. 12 and 13 to solve the nonlinear ODEs system of MHD past over an inclined plate. The parameters f(η), θ(η) and ϕ(η) plots are provided in Figs. 12a–12c based on stochastic procedures for the system of MHD past over an inclined plate. The overlapping results are performed to check the precision and accuracy of the designed stochastic procedures. The AE values are illustrated in Fig. 13 to solve the nonlinear ODEs system of MHD past over an inclined plate. The parameters f(η), θ(η) and ϕ(η) plots are illustrated in Figs. 13a–13c for the nonlinear ODEs system of MHD past over an inclined plate. One can observe in Fig. 13a, that the values of the AE for f(η) lie around 10−05 to 10−08 for case 1, 10−05 to 10−07 for case 2 and 10−05 to 10−06 for case 3. Fig. 13b authenticates the AE for θ(η) calculated around 10−05 to 10−08 for case 1, 10−05 to 10−07 for case 2 and 10−04 to 10−06 for case 3, respectively. Likewise, the AE values for ϕ(η) is observed in Fig. 13c, which is calculated 10−05 to 10−07 for case 1, 10−04 to 10−06 for case 2 and 10−05 to 10−06 for case 3, respectively. These closely overlapped results of the AE values designate the correctness and exactness of the nonlinear MHTWF past over a stretched surface.

Figure 12: Comparison routine using the stochastic procedures for the system of MHD past over an inclined plate

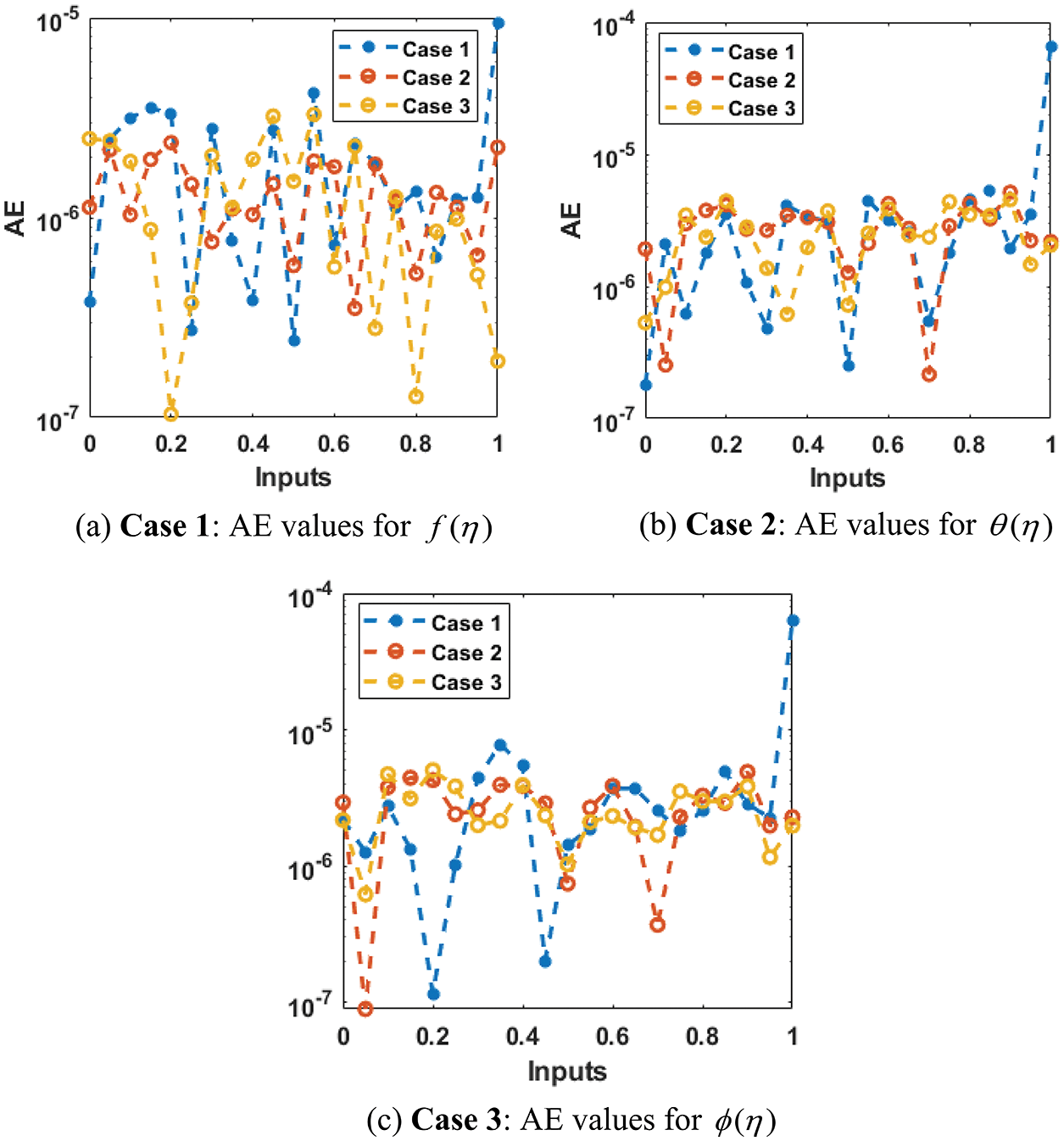
Figure 13: AE values using the designed stochastic procedures for the system of MHD past over an inclined plate

4  Concluding Remarks

The purpose of this study was to perform the numerical simulations based on the ANNs along with the novel stochastic procedures of the LMB for solving the system of MHD past over an inclined plate. The nonlinear system of MHD past over an inclined plate was categorized into three profiles, Momentum Conservation, Species (Salinity) Conservation, and Energy (heat) conservation. The procedures based on the stochastic paradigms were provided with three different categories of sample statistics, testing, training, and validation. The statistics 10%, 15% and 75% for testing, validation and training were given to solve the MHD past over an inclined plate. Seven numbers of neurons have used in this numerical study for solving the nonlinear transport model. A reference dataset was proposed for the comparison of the obtained and proposed solutions for the MHD system in the ocean. One can observe the overlying of the solutions, which demonstrates the correctness of the LMBNNs. The absolute error plots were provided in good measures that validated the accuracy and precision of the nonlinear ODEs system of MHD past over an inclined plate. The obtained numerical solutions of the nonlinear above mention system using the LMBNNs performances have calculated to reduce the MSE. For the capability, dependability and aptitude of the stochastic procedure, the numerical performances were provided to authenticate the proportional arrangements of MSE, error histograms (EHs), state transitions (STs), correlation and regression. The MSE convergence presentations were applied to the best curve, training, validation and testing for each variation of the nonlinear transfer model. The correlation representations were capable to confirm the regression actions. The gradient measures were also provided for the nonlinear transfer model. Furthermore, the precision was pragmatic using the numerical conformations as well as graphical procedures through the STs, MSE, EHs, regression and convergence measures, respectively.

In future work, the designed LMBNNs procedures can be applied to solve the biological, fluid, singular, fractional, and lonngren-wave models [50–58].

Funding Statement: This research is supported by Department of Mathematics, Faculty of Science, Khon Kaen University, Fiscal Year 2022.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. R. Hughes, N. P. S. Cherisa and O. Beg, “Computational study of improving the efficiency of photovoltaic panels in the UAE,” World Academy of Science, Engineering and Technology, vol. 73, pp. 278–287, 2011. [Google Scholar]

 2.  M. Puig-Arnavat, J. C. Bruno and A. Coronas, “Review and analysis of biomass gasification models,” Renewable and Sustainable Energy Reviews, vol. 14, no. 9, pp. 2841–2851, 2010. [Google Scholar]

 3.  R. W. Whittlesey, S. C. Liska and J. O. Dabiri, “Fish schooling as a basis for vertical-axis wind turbine farm design,” Bioinspiration & Biomimetics, vol. 5, no. 3, pp. 035005, 2010. [Google Scholar]

 4.  X. He, W. He, Y. Liu, Y. Wang, G. Li et al., “Robust adaptive control of an offshore ocean thermal energy conversion system,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 50, no. 12, pp. 5285–5295, 2018. [Google Scholar]

 5.  S. Behrens, J. Hayward, M. Hemer and P. Osman, “Assessing the wave energy converter potential for Australian coastal regions,” Renewable Energy, vol. 43, pp. 210–217, 2012. [Google Scholar]

 6.  M. Grabbe, “Marine current energy conversion: Resource and technology,” Ph.D. Dissertation, Uppsala University, Sweden, 2009. [Google Scholar]

 7.  S. O. Mathew, O. C. Dike, E. U. Akabuogu and J. N. Ogwo, “Magneto hydrodynamics power generation using salt water,” Asian J. Natural Appl. Sci., vol. 1, no. 4, pp. 66–69, 2012. [Google Scholar]

 8.  T. F. Lin and J. B. Gilbert, “Studies of helical magnetohydrodynamic seawater flow in fields up to twelve teslas,” Journal of Propulsion and Power, vol. 11, no. 6, pp. 1349–1355, 1995. [Google Scholar]

 9.  M. Takeda, Y. Okuji, T. Akazawa, X. Liu and T. Kiyoshi, “Fundamental studies of helical-type seawater MHD generation system,” IEEE Transactions on Applied Superconductivity, vol. 15, no. 2, pp. 2170–2173, 2005. [Google Scholar]

10. T. Terasawa, “Hall current effect on tearing mode instability,” Geophysical Research Letters, vol. 10, no. 6, pp. 475–478, 1983. [Google Scholar]

11. S. K. Ghosh, O. A. Bég, J. Zueco and V. R. Prasad, “Transient hydromagnetic flow in a rotating channel permeated by an inclined magnetic field with magnetic induction and Maxwell displacement current effects,” ZAMP: Journal of Applied Mathematics and Physics, vol. 61, no. 1, pp. 147–169, 2010. [Google Scholar]

12. E. D. Ross and G. D. Roy, “Flow development and analysis of MHD generators and seawater thrusters,” ASME Journal of Fluids Engineering, vol. 114, pp. 68–72, 1992. [Google Scholar]

13. M. Takeda, N. Tomomori, T. Akazawa, K. Nishigaki and A. Iwata, “Flow control of seawater with a diverging duct by MHD separation method,” IEEE Transactions on Applied Superconductivity, vol. 14, no. 2, pp. 1543–1546, 2004. [Google Scholar]

14. G. V. P. N. Srikanth, G. Srinivas and B. R. K. Reddy, “MHD convective heat transfer of a nanofluid flow past an inclined permeable plate with heat source and radiation,” International Journal of Physics and Mathematical Sciences, vol. 3, no. 1, pp. 89–95, 2013. [Google Scholar]

15. G. K. Ramesh, B. J. Gireesha and C. S. Bagewadi, “Heat transfer in MHD dusty boundary layer flow over an inclined stretching sheet with non-uniform heat source/sink,” Advances in Mathematical Physics, vol. 2012, pp. 1–13, 2012. [Google Scholar]

16. M. A. Kabir and M. A. Al Mahbub, “Effects of thermophoresis on unsteady MHD free convective heat and mass transfer along an inclined porous plate with heat generation in presence of magnetic field,” Scientific Research, vol. 2, no. 4, pp. 120–129, 2012. [Google Scholar]

17. G. Palani and K. Y. Kim, “Joule heating and viscous dissipation effects on MHD flow past a semi-infinite inclined plate with variable surface temperature,” Journal of Engineering Thermophysics, vol. 20, no. 4, pp. 501–517, 2011. [Google Scholar]

18. A. J. Chamkha, C. Issa and K. Khanafer, “Natural convection from an inclined plate embedded in a variable porosity porous medium due to solar radiation,” International Journal of Thermal Sciences, vol. 41, no. 1, pp. 73–81, 2002. [Google Scholar]

19. S. Masthanrao, K. Balamurugan and S. Varma, “Chemical reaction effects on mhd free convection flow through a porous medium bounded by an inclined surface,” International Journal of Mathematics, vol. 3, no. 3, pp. 13–22, 2013. [Google Scholar]

20. M. A. Hossain, I. Pop and M. Ahamad, “MHD free convection flow from an isothermal plate inclined at a small angle to the horizontal,” Journal of Applied Fluid Mechanics, vol. 1, pp. 194–207, 1996. [Google Scholar]

21. H. M. Ramadan and A. J. Chamkha, “Hydromagnetic free convection of a particulate suspension from a permeable inclined plate with heat absorption for non-uniform particle-phase density,” Heat and Mass Transfer, vol. 39, pp. 367–374, 2003. [Google Scholar]

22. C. C. Wang and C. K. Chen, “Mixed convection boundary layer flow on inclined wavy plates including the magnetic field effect,” International Journal of Thermal Sciences, vol. 44, no. 6, pp. 577–586, 2005. [Google Scholar]

23. C. H. Chen, “Heat and mass transfer in MHD flow by natural convection from a permeable inclined surface with variable wall temperature and concentration,” Acta Mechanica, vol. 172, no. 3, pp. 219–235, 2004. [Google Scholar]

24. Y. Fan, J. Guo, X. Wang, Y. Xia, P. Han et al., “Comparative Failure Study of Different Bonded Basalt Fiber-Reinforced Polymer (BFRP)-AL Joints in a Humid and Hot Environment,” Polymers, vol. 13, no. 16, p. 2593, 2021. [Google Scholar]

25. M. Ferdows, M. J. Uddin and T. S. Khaleque, “Double diffusion, slips and variable diffusivity effects on combined heat mass transfer with variable viscosity via a point transformation,” Progress in Computational Fluid Dynamics, vol. 13, no. 1, pp. 54–64, 2013. [Google Scholar]

26. M. M. Rashidi, N. Rahimzadeh, M. Ferdows, M. J. Uddin and O. Anwar Bég, “Group theory and differential transform analysis of mixed convective heat and mass transfer from a horizontal surface with chemical reaction effects,” Chemical Engineering Communications, vol. 199, no. 8, pp. 1012–1043, 2012. [Google Scholar]

27. J. Zueco, O. A. Bég, H. S. Takhar and V. R. Prasad, “Thermophoretic hydromagnetic dissipative heat and mass transfer with lateral mass flux, heat source, ohmic heating and thermal conductivity effects: Network simulation numerical study,” Applied Thermal Engineering, vol. 29, no. 14–15, pp. 2808–2815, 2009. [Google Scholar]

28. O. D. Makinde, K. Zimba and O. A. Bég, “Numerical study of chemically-reacting hydromagnetic boundary layer flow with Soret/Dufour effects and a convective surface boundary condition,” International Journal of Thermal & Environmental Engineering, vol. 4, no. 1, pp. 89–98, 2012. [Google Scholar]

29. O. A. Bég, A. Bakier, R. Prasad and S. K. Ghosh, “Numerical modelling of non-similar mixed convection heat and species transfer along an inclined solar energy collector surface with cross diffusion effects,” World Journal of Mechanics, vol. 1, pp. 185–196, 2011. [Google Scholar]

30. O. A. Bég and D. Tripathi, “Mathematica simulation of peristaltic pumping with double-diffusive convection in nanofluids: A bio-nano-engineering model,” Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials, Nanoengineering and Nanosystems, vol. 225, no. 3, pp. 99–114, 2011. [Google Scholar]

31. O. A. Bég, A. Y. Bakier and V. R. Prasad, “Numerical study of free convection magnetohydrodynamic heat and mass transfer from a stretching surface to a saturated porous medium with Soret and Dufour effects,” Computational Materials Science, vol. 46, no. 1, pp. 57–65, 2009. [Google Scholar]

32. O. A. Bég, R. Bhargava, S. Rawat and E. Kahya, “Numerical study of micropolar convective heat and mass transfer in a non-darcy porous regime with Soret and Dufour diffusion effects,” Emirates Journal for Engineering Research, vol. 13, no. 2, pp. 51–66, 2008. [Google Scholar]

33. V. R. Prasad, B. Vasu and O. A. Bég, “Thermo-diffusion and diffusion-thermo effects on MHD free convection flow past a vertical porous plate embedded in a non-darcian porous medium,” Chemical Engineering Journal, vol. 173, no. 2, pp. 598–606, 2011. [Google Scholar]

34. B. Gebhart and L. Pera, “The nature of vertical natural convection flows resulting from the combined buoyancy effects of thermal and mass diffusion,” International journal of heat and mass transfer, vol. 14, no. (12), pp. 2025–2050, 1971. [Google Scholar]

35. Z. Sabir, M. A. Z. Raja, A. S. Alnahdi, M. B. Jeelani and M. A. Abdelkawy, “Numerical investigations of the nonlinear smoke model using the Gudermannian neural networks,” Mathematical Biosciences and Engineering, vol. 19, pp. 351–370, 2021. [Google Scholar]

36. Z. Sabir, H. A. Wahab, S. Javeed and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 1–14, 2021. [Google Scholar]

37. Z. Sabir, M. A. Z. Raja, J. L. G. Guirao and T. Saeed, “Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations,” Alexandria Engineering Journal, vol. 60, no. 6, pp. 5935–5947, 2021. [Google Scholar]

38. Z. Sabir, M. A. Z. Raja, J. L. G. Guirao and T. Saeed, “Solution of novel multi-fractional multi-singular Lane–Emden model using the designed FMNEICS,” Neural Computing and Applications, vol. 33, no. 24, pp. 17287–17302, 2021. [Google Scholar]

39. J. L. G. Guirao, Z. Sabir, M. A. Z. Raja and D. Baleanu, “Design of neuro-swarming computational solver for the fractional bagley–Torvik mathematical model,” The European Physical Journal Plus, vol. 137, pp. 1–15, 2022. [Google Scholar]

40. M. Umar, Z. Sabir, M. A. Z. Raja, M. Shoaib, M. Gupta et al., “A stochastic intelligent computing with neuro-evolution heuristics for nonlinear SITR system of novel COVID-19 dynamics,” Symmetry, vol. 12, no. 10, pp. 1–17, 2020. [Google Scholar]

41. M. Umar, Z. Sabir, M. A. Z. Raja, F. Amin, T. Saeed et al., “Integrated neuro-swarm heuristic with interior-point for nonlinear SITR model for dynamics of novel COVID-19,” Alexandria Engineering Journal, vol. 60, no. 3, pp. 2811–2824, 2021. [Google Scholar]

42. J. L. Guirao, Z. Sabir and T. Saeed, “Design and numerical solutions of a novel third-order nonlinear Emden–Fowler delay differential model,” Mathematical Problems in Engineering, vol. 2020, pp. 1–9, 2020. [Google Scholar]

43. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “Neuro-swarm intelligent computing paradigm for nonlinear HIV infection model with CD4+ T-cells,” Mathematics and Computers in Simulation, vol. 188, pp. 241–253, 2021. [Google Scholar]

44. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, pp. 1–13, 2021. [Google Scholar]

45. J. Z. Sabir, J. L. G. Guirao and T. Saeed, “Solving a novel designed second order nonlinear Lane–Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, pp. 1–12, 2021. [Google Scholar]

46. M. Umar, Z. Sabir, M. A. Z. Raja and Y. G. Sánchezand, “A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever,” Results in Physics, vol. 19, pp. 1–9, 2020. [Google Scholar]

47. M. Umar, Z. Sabir, M. A. Z. Raja, K. S. Al-Basyouni, S. R. Mahmoud et al., “An advance computing numerical Heuristic of nonlinear SIR dengue fever system using the Morlet wavelet kernel,” Journal of Healthcare Engineering, vol. 2020, pp. 1–14, 2022. [Google Scholar]

48. Z. Sabir, M. A. Z. Raja, J. L. Guirao and M. Shoaib, “A Neuro-swarming intelligence-based computing for second order singular periodic non-linear boundary value problems,” Frontiers in Physics, vol. 8, pp. 1–12, 2020. [Google Scholar]

49. S. Javeed, A. Ahmed, M. S. Khan and M. A. Javed, “Stability analysis and solutions of dynamical models for dengue,” Punjab University Journal of Mathematics, vol. 50, no. 2, pp. 45–67, 2018. [Google Scholar]

50. S. Ahmad, S. Javeed, H. Ahmad, J. Khushi, S. K. Elagan et al., “Analysis and numerical solution of novel fractional model for dengue,” Results in Physics, vol. 28, pp. 1–9, 2021. [Google Scholar]

51. T. D. Leta, W. Liu, H. Rezazadeh, J. Ding and A. E. Achab, “Analytical traveling wave and soliton solutions of the (2+ 1) dimensional generalized Burgers–Huxley equation,” Qualitative Theory of Dynamical Systems, vol. 20, no. 3, pp. 1–23, 2021. [Google Scholar]

52. H. M. Baskonus, H. Bulut and T. A. Sulaiman, “New complex hyperbolic structures to the Lonngren-wave equation by using Sine-Gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 129–138, 2019. [Google Scholar]

53. A. Yokuş and S. Gülbahar, “Numerical solutions with linearization techniques of the fractional Harry Dym equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 35–42, 2019. [Google Scholar]

54. A. Imran, A. Waheed, S. Javeed, D. Baleanu, M. Zeb et al., “Investigation of electroosmosis flow of copper nanoparticles with heat transfer due to metachronal rhythm,” Thermal Science, vol. 25, no. 2, pp. 193–198, 2021. [Google Scholar]

55. M. Dewasurendra and K. Vajravelu, “On the method of inverse mapping for solutions of coupled systems of nonlinear differential equations arising in nanofluid flow, heat and mass transfer,” Applied Mathematics and Nonlinear Sciences, vol. 3, no. 1, pp. 1–14, 2018. [Google Scholar]

56. E. Tala-Tebue, A. Korkmaz, H. Rezazadeh and N. Raza, “New auxiliary equation approach to derive solutions of fractional resonant Schrödinger equation,” Analysis and Mathematical Physics, vol. 11, no. 4, pp. 1–13, 2021. [Google Scholar]

57. M. S. Hashemi, H. Rezazadeh, H. Almusawa, H. Ahmad and I. Bonab, “A lie group integrator to solve the hydromagnetic stagnation point flow of a second grade fluid over a stretching sheet,” AIMS Mathematics, vol. 6, no. 12, pp. 13392–13406, 2021. [Google Scholar]

58. A. Waheed, A. Imran, S. Javeed, D. Baleanu, M. Zeb et al., “Study of electro-osmotic nanofluid transport for scraped surface heat exchanger with heat transfer phenomenon,” Thermal Science, vol. 25, no. 2, pp. 213–218, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.