Computers, Materials & Continua DOI:10.32604/cmc.2022.028765
Article

Mordell Elliptic Curve Based Design of Nonlinear Component of Block Cipher

Hafeez ur Rehman1,*, Tariq Shah1, Mohammad Mazyad Hazzazi2, Ali Alshehri3 and Bassfar Zaid4

1Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
2Department of Mathematics, College of Science, King Khalid University, Abha, Saudi Arabia
3Department of Computer Science, University of Tabuk, Tabuk, 71491, Saudi Arabia
4Department of Information Technology, University of Tabuk, Tabuk, 71491, Saudi Arabia
*Corresponding Author: Hafeez ur Rehman. Email: hrehman@math.qau.edu.pk
Received: 16 February 2022; Accepted: 14 April 2022

Abstract: Elliptic curves (ECs) are deemed one of the most solid structures against modern computational attacks because of their small key size and high security. In many well-known cryptosystems, the substitution box (S-box) is used as the only nonlinear portion of a security system. Recently, it has been shown that using dynamic S-boxes rather than static S-boxes increases the security of a cryptosystem. The conferred study also extends the practical application of ECs in designing the nonlinear components of block ciphers in symmetric key cryptography. In this study, instead of the Mordell elliptic curve (MEC) over the prime field, the Galois field has been engaged in constructing the S-boxes, the main nonlinear component of the block ciphers. Also, the proposed scheme uses the coordinates of MEC and the operation of the Galois field to generate a higher number of S-boxes with optimal nonlinearity, which increases the security of cryptosystems. The proposed S-boxes resilience against prominent algebraic and statistical attacks is evaluated to determine its potential to induce confusion and produce acceptable results compared to other schemes. Also, the majority logic criteria (MLC) are used to assess the new S-boxes usage in the image encryption application, and the outcomes indicate that they have significant cryptographic strength.

Keywords: Galois field; Mordell elliptic curve; nonlinearity; substitution box

1  Introduction

When it comes to electronic data transfer, digital technology and network communications have had a significant impact during the past few decades. Various issues about the privacy of sensitive data transmissions through open communication networks arise, as most of these networks are exposed to the public. Cryptography, steganography, and watermarking are the most common methods for securing information. The robust watermarking algorithm is presented in [1,2] to assure the safe transmission and storage of medical data and to prevent the leakage of patient information in telemedicine. Consequently, the security of sensitive data has been a significant focus of cryptography in recent decades. The researchers have proposed various information security strategies to counter the most recent security threats. S-box is a nonlinear component in numerous famous algorithms, especially in advanced encryption standards (AES) [3]. The security of all such cryptosystems is thus reliant on the cryptographic aspects of these S-boxes. Because of this, many researchers have expressed an interest in developing new and more effective S-boxes. The S-box is predicated on algebraic systems, which are impervious to linear and differential cryptanalysis; they have received a lot of interest because of their solid cryptographic properties. Thus, secure transmission based on various classes of S-boxes is always promoted. Like the AES, the affine power affine (APA) S-box is presented to increase algebraic complexity while maintaining accessible encryption features [4]. In [5], the action of the symmetric group S8 over AES is utilized to generate S-boxes. The Gray S-box is generated by adding an extra transformation based on binary gray codes to the basic AES S-box by employing a polynomial of 255 terms instead of a polynomial having 8 terms, which retains all the features and strengthens AES security [6]. Also, the chaotic map-based generators produced secure S-boxes that were impenetrable to the linear, differential, and algebraic attacks. In [7], a sturdy S-Box design is proposed by using a continuous-time Lorenz system as the chaotic system. By effectively exploiting the characteristics of a chaotic map and the evolution process, a method of S-boxes is presented in [8]. However, a parallel and more uncomplicated technique for constructing a block cipher nonlinear component is still required.

1.1 Related Work

ECs have recently gained a lot of interest in the cryptography sector. The techniques based on ECs are the most extensively used for enhancing information security. We will concentrate on EC-based cryptography and the various methods presented by numeral experts in this domain. Cheon et al. [9] characterized S-boxes by offering the relation between nonlinearity of rational functions over F2n and the points are lying on the corresponding hyper EC. Hayat et al. [10] designed an algorithm for constructing an 8×8 S-box using an x-coordinate of ordered EC over a prime field. Reference [11] is a refinement of the previous work; Hayat et al. use the x-coordinate of an EC over prime field followed by modulo operation to construct a different number of S-boxes. An algorithm for designing 8×8 S-boxes has been developed by Azam et al. [12] by using specific orderings on a class of Mordell elliptic curves (MEC). A search method is used rather than more configuration group rules to build EC points, which is computationally expensive. These techniques can be used to make a various number of 8×8 S-boxes. However, their conclusion is unpredictable because they are independent of any specific EC that may or may not produce an S-box for any input variables. Farwa et al. [13] offered an exceptional and new way for developing a 4 × 4 S-box by applying an EC over the Galois field GF(24). In this paper, the authors constructed a bijective Boolean function by applying the structure of a group to the elements of EC having the same order as the order of the Galois field. Recently, Rehman et al. [14] designed an algorithm for the construction of a higher number of different 8×8 S-boxes by deploying MEC over the Galois field GF(2n) where n=8 or an odd n≥9.

1.2 Motivation

The following are the key motives for this scheme to boost the performance of ECs based S-boxes and their effectiveness in numerous cryptographic algorithms.

1.    S-boxes are typically constructed by considering ECs over prime fields. Yet, the outcomes of these studies remain uncertain. i.e., the algorithms do not invariably output an S-box to every set of specified parameters.

2.    Furthermore, the prime field-based S-boxes do not encompass all the S-box possibilities.

3.    In [11], the authors design an algorithm by choosing a particular EC over the Galois field GF(24) and they are constructing a single 4 × 4 S-box.

4.    In [12], they considered MEC over Galois field GF(2n), where n=8 or an odd n≥9 and develop a practical scheme for the generation of 8×8 S-boxes but did not attain the optimal results, also they generate a single 8×8 S-box while utilizing MEC over the Galois field of order 256. However, in this study, we bring a comprehensive approach to design an algorithm by employing MEC over the Galois field GF(2n), where n≥8 and generate 8×8 S-boxes having outstanding results.

1.3 Our Contribution

To overcome the shortcomings of current schemes, we have developed a new one. To summarize a lengthy piece of writing, follow these steps:

1.    We implemented a simple technique rather than rigorous S-boxes algorithms with exceptional outcomes to construct 8×8 S-boxes in the proposed work.

2.    We utilized MEC over the Galois fields GF(2n) with n=8,9,10 and higher with different numbers of primitive irreducible polynomials (PIPs) to generate points of EC.

3.    Following the current approach, we used the EC points, prime numbers characteristics that rely on an EC x and y-coordinates, and an Inverse function under a predefined Galois field and PIP.

4.    S-box figures can be changed by varying the MEC variable b or by amending the PIP of a degree equivalent to the Galois field GF(2n).

The following documents still need to be executed: Some introductory details are given in Section 2. The proposed algorithm can be found in Section 3. In Section 4, we compared our newly developed S-boxes to other S-boxes already in use. Section 4 also deals with S-boxes in the image encryption technique and the majority logic criterion (MLC). Towards the end of Section 5, there are several compelling arguments.

2  Preliminaries

In this part, several fundamental and crucial notions like ECs, Galois fields, Euler’s phi function, and primitive polynomials are presented.

2.1 Galois Fields

A mathematical concept is known as finite field, or Galois field is considered the cornerstone of all cryptography theory. The representation of Galois field is GF(pn), where p signifies any prime number and n∈Z+. Galois fields can be roughly divided into two categories: prime fields, which have p=1, and extension fields, which have p>1.

2.2 Euler’s Phi Function

Euler’s phi function offers the coprime numbers to an integer m, denoted as φ(m), [15]. To put it another way, when the number m is greater than one, φ(m) is the number of elements in Um.

2.3 Primitive Irreducible Polynomials (PIPs) and Galois Fields

Galois field and PIPs over the Galois field are explained below in [16]. If it isn’t explicitly stated, the base field GF(2) is used in this section.

2.3.1 Definition

For each prime number p and positive integer m with order pm, there is one finite field. The elements of these finite fields under multiplication form a cyclic group excluding zero. Consequently, there is a generator α that generates finite field apart from zero and αpm−1=1.

2.3.2 Definition

An irreducible polynomial in GF(p)[X] cannot be reduced into a pair of lower-degree polynomials in GF(p)[X]. For example, the polynomial x3+x+1 is irreducible in GF(23) and x3+1 is reducible.

2.3.3 Definition

A polynomial h(x)∈GF(pm)[X] is known as a primitive polynomial of degree m if all its roots are also primitive elements in the corresponding Galois field. Irreducible polynomials of degree m that are binary primitives are φ(2m−1)m, where φ represents Euler’s phi function. For example, if p=2 and n=4, then φ(24−1)4=2.

2.3.4 Lemma

An EC of the form Ep,b:y2=x3+b is known as MEC, where p is used for prime field. The specialty of this curve is that it has precisely p+1 points for the prime number of forms p≡2(mod3). Also, y-coordinates of this specified MEC are random, Washington [17](6.6(c),p.188).

2.3.5 Addition, Subtraction, and Multiplication in GF(2n)

The addition and subtraction operations are identical because we are operating in characteristic 2. Adding polynomials in Galois Field [18] is relatively easy. In multiplication let h∗(x) is PIP of order m and f∗(x),g∗(x) are polynomials in GF(2n), then

m∗(x)=(f∗(x)⋅g∗(x))mod h∗(x)(1)

where m∗(x) is the resultant polynomial.

And k∗(x) provides the multiplicative inverse of g∗(x), i.e.,

(g∗(x)⋅k∗(x))mod h∗(x)=1(2)

Multiplying two polynomials and finding the multiplicative inverse of a polynomial need’s modulo 2 for coefficients and modulo h∗(x) for polynomials.

3  S-boxes Design by MEC over GF(2n), for n≥8

Here, the proposed S-box algorithm is described using two different approaches. In the first technique, we used MEC over Galois field GF(28) to generate EC points and design an algorithm involving the x and y coordinates of the specified EC points. In the second technique, rather than selecting a particular Galois field GF(28), we created a comprehensive algorithm for the construction of S-boxes by employing MEC over GF(2n) where n≥9.

3.1 Construction of S-box Using MEC over Galois Field GF(28)

1. Take PIP of degree 8

f(x)=x8+x4+x3+x2+1(3)

over the binary field.

2. Choose MEC

Eb:y2=x3+b(4)

where b∈GF(28)/{0}.

3. Generate an EC points by utilizing that MEC over the Galois field GF(28).

4. Calculate how many primes there are between the beginning and current parameter b and take an inverse of the parameter b under the Galois field GF(28).

5. Instead of choosing b, the inverse of b under Galois field GF(28) and the sum of primes there are between the beginning value of b and the current value of parameter b, we replace them with the y-coordinates at that place.

6. Adjust the x-coordinates of EC points based on the resulting y-coordinates and parameter b, as shown in Fig. 1.

7. Take an inverse under the Galois field GF(28) of that x-coordinates except zero using specified PIP and generate 8×8 S-boxes.

To build a different number of S-boxes, one can adjust the parameters of MEC or the PIP. As the number of PIPs over Galois field GF(28) is 16. Through this technique, we can generate a different number of 16×255 S-boxes in which every S-box has nonlinearity between 110 to 112. The S-box having nonlinearity 111.25 is presented in Tab. 1. A diagram of the proposed algorithm is shown in Fig. 1.

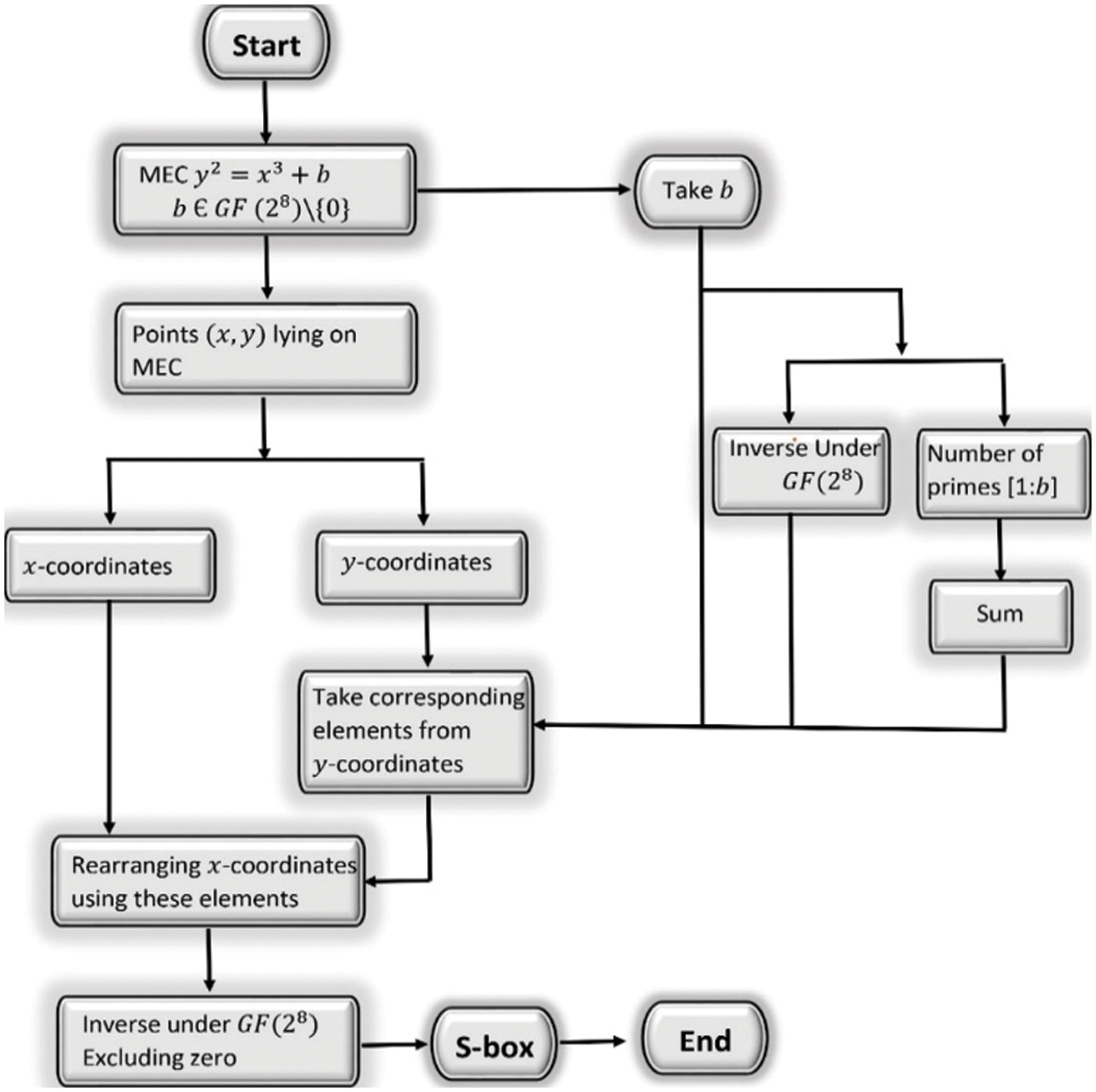
Figure 1: Proposed algorithm using MEC over GF(28)

3.2 Construction of S-box Using MEC over Galois Field GF(2n)

The Galois fields GF(2n) where n≥9 is applied in this study to establish a more comprehensive and effective approach for the designing of a large number of distinct 8 × 8 S-boxes. A diagram of the proposed algorithm is shown in Fig. 2.

Figure 2: Proposed algorithm using MEC over GF(2n)

3.2.1 Construction of S-box Using MEC over Galois field GF(29)

1. Choose PIP of order degree 9

f(x)=x9+x4+1(5)

Also, an independently one can take any other PIP of degree 9 over the binary field.

2. Consider MEC

Eb:y2=x3+b(6)

where b be the element of Galois field GF(29) excluding zero.

3. Utilize MEC over the Galois field GF(29) and generate EC points.

4. Compute the inverse of the parameter b under the Galois field GF(29), find the number of primes between the smallest possible value of parameter b and the value b used forspecified MEC.

5. Calculate the position of b, its inverse under the Galois field GF(29), the number obtainedby summing the number of primes and taking the corresponding y-coordinates from ECpoints at that place.

6. Managing parameter b and the resultant y-coordinates, re-adjust the x-coordinates ofcorresponding EC points.

7. Taking the inverse of each x-coordinate except zero under the Galois field GF(29) withcorresponding PIP.

8. Finally, randomly take those elements less than 256 to construct an S-box.

The number of S-boxes can be varied by modifying the MEC parameter b or the PIP. The total number of PIPs over Galois field GF(29) is calculated by φ(29−1)9, where phi represents the Euler totient function. This technique allows one to construct a different number of 48×511 S-boxes. The S-box created using this technique is given in Tab. 2.

3.2.2 Construction of S-box Using MEC over Galois Field GF(210)

1. Choose PIP of order degree 10 over the binary field.

2. Consider MEC

Eb:y2=x3+b(7)

where b be the element of Galois field GF(210)/{0}.

3. Utilize MEC over the Galois field GF(210) and generate EC points.

4. Compute the inverse of the parameter b under the Galois field GF(210), find the number of primes between the smallest possible value of parameter b and the value b used forspecified MEC.

5. Calculate the position of b, its inverse under the Galois field GF(210), the number obtainedby summing the number of primes and taking the corresponding y-coordinates from ECpoints at that place.

6. Managing parameter b and the resultant y-coordinates, re-adjust the x-coordinates ofcorresponding EC points.

7. Taking the inverse of each x-coordinate except zero under the Galois field GF(210)with corresponding PIP.

8. Finally, randomly take those elements less than 256 to get an S-box.

The number of S-boxes can be varied by modifying the MEC parameter b or the PIP. The total number of PIPs over Galois field GF(210) is calculated by φ(210−1)/10, where phi represents the Euler totient function. This technique allows one to generate 62×1023 different S-boxes. The S-box created using this technique is given in Tab. 3.

4  Security Analysis

The cryptographic integrity of the proposed scheme is obtained using several conventional tests. This section will briefly review these security tests and the offered method’s results compared to other methods.

4.1 Nonlinearity (NL)

An S-box must confuse the data to a certain amount to keep the data safe from an attacker. The NL security test is a measure that computes the ability of an S-box to confuse the data, as represented in the following

N∗(S)=minμ,β,η⁡{α∈GF(2n)|μ.S(α)=β⋅α⊗η}(8)

where μ∈GF(2n), β∈GF(2n)∖{0}, η∈GF(2), and “·” denotes the dot product over GF(2).

An S-box with considerable NL can inflict a lot of data confusion. The optimal value of an 8×8 S-box is 120, which is calculated as 2n−1−2n2−1, [19]. In Tab. 4, the NL of newly designed S-boxes and some existent S-boxes are given comparatively. One can notice clearly that the newly formed S-boxes have more significant NL when compared to the EC-based S-boxes in [10,12].

4.2 Strict Avalanche Criterion (SAC)

Webster and Tavares [28] were the first to introduce SAC in 1985. The SAC is built on the principles of avalanche and completion. The requirement of SAC is fulfilled when a single bit of information is updated; half of the matching output bits must change. The offered S-boxes meet the SAC criteria according to the calculated performance indexes. In Tab. 5, the proposed S-boxes SAC values are compared to the existing S-boxes, which shows that our S-boxes have an optimal SAC value.

4.3 Bit Independent Criterion (BIC)

The other vital test to study any cryptographic technique is BIC [29], which is operated to evaluate the independence of pair of output bits when the input bit is changed. Tab. 5 displays the outcomes of BIC analysis of the proposed S-boxes, and in the significance of encryption stability, the BIC of the proposed S-boxes is satisfactory. Performance Indexes of S-boxes given in Tab. 5 reveal that the rank of our proposed S-box is comparable with S-boxes from literature, and we marked that the offered S-boxes satisfied BIC close to the satisfactorily probable value.

4.4 Linear Approximation Probability (LP)

Linear approximation attacks on S-boxes can be approximated by determining the maximum number of coincidental input and output bit pairs. If an S-box has a lower LP, it is extremely resistant to linear attacks [29]. According to Tab. 6, the LP values of the new S-boxes are significantly lower than those of other S-boxes.

4.5 Differential Approximation Probability (DP)

A differential approximation probability is offered in [33] to find the probability impact of a particular disparity in the input bit on the variance of the resulting output bits. The DAP of an S-box S is shown below in the mathematical phrase: g∗,h∗∈GF(28),

DP(S)=maxg∗.h∗{#{g∈GF(28)|S(g+g∗)−S(g)=h∗}}(9)

The S-box has more potential against differential attacks if it has a lower value of DP. The experimental outcomes of DP of the newly spawned S-boxes are presented in Tab. 6, which indicates that the newly designed S-boxes have high resistance against differential attacks.

4.6 NPCR and UACI Analysis

It’s common for hackers to make minor adjustments to an image before using the recommended method. You can compare the original with the substituted image. Using this method, they discovered the relationship between the original and encrypted images. A one-pixel change in the original image considerably impacts the image following substitution. This section combines two key tests, the unified average change intensity (UACI) and the several pixels changing rate (NPCR), to determine the design’s resistance to differential attacks. NPCR can be summed up as

NPCR=∑g∗,h∗F(g∗,h∗)M∗×N∗×100%(10)

And UACI is defined as

UACI=1M∗×N∗[∑g∗,h∗abs(F1∗(g∗,h∗)−F2∗(g∗,h∗))255]×100%(11)

where M∗ and N∗ denotes the image height. Tab. 7 depicts the proposed scheme NPCR and UACI values, indicating that our system is more resistant to various attacks.

4.7 Statistical Analysis

When evaluating statistical analyses, one uses the majority logic criteria (MLC) [44]. Also, an S-box is used to encrypt a test image by swapping pixel values in this standard. Even though this isn’t an encryption technology, the actual and encrypted data are analyzed statistically using this criterion. Multiple statistical analyses, including as homogeneity, correlation, contrast, energy, and entropy, can be evaluated using the MLC as a standard. This evaluation determines whether the S-box can be used to encrypt an image or not. Lena's image of 256×256 is operated for the MLC study, and the outcomes of the presented scheme are given in Tab. 8. The MLC analysis showed that the diffusion level of the newly developed S-boxes is up to the mark. All of this can be seen in Fig. 3.

Figure 3: (1) Original Lena Image (2,3,4) Encrypted Lena image using S-box 1, S-box 2, and S-box 3

4.8 Comparative Analysis

Various cryptographic tests assess the proposed algorithm to examine its potential against different cryptographic attacks. The comparison of the proposed technique with other algorithms is discussed briefly in the following point-by-point discussion.

1.    In Tab. 4, different algorithms are listed based on Chaos, group, Galois field, and EC. By using MEC over a 256-order Galois field, one can see that we generate 4080 S-boxes having nonlinearity between 110 to 112.The algorithms in [10,12,22] were constructed using EC over the prime field but did not achieve outstanding results compared to our proposed technique.

2.    The proposed S-boxes BIC and SAC values are more satisfactory than the algorithms in [10,12,30–32] mentioned in Tab. 5. Furthermore, our BIC and SAC values are optimal, indicating that the offered S-boxes can cause enough diffusion in the data.

3.    The proposed S-boxes LP values are also acceptable compared to the different algorithms in Tab. 6. Similarly, the lower value of the DP of the proposed scheme shows that our method is more invulnerable to various attacks.

4.    The NPCR and UACI values of the proposed S-boxes are comparatively better than the cited algorithms in Tab. 7. Furthermore, the MLC analysis in Tab. 8 shows that the offered algorithm is more significant for image encryption.

5.    The number of S-boxes creation ability of the proposed algorithm is very high compared to other EC-based algorithms noted in Tab. 9, proclaiming that the presented scheme is novel and more significant.

The above analysis shows that the proposed scheme has good resistance against various cryptographic attacks compared to existing algorithms. The results of the MLC tests reveal that the proposed algorithm has good image encryption features.

5  Conclusion

In this article, we considered MEC over the binary extension field GF(2n), where n≥8 and developed a comprehensive algorithm for the construction of S-boxes. Generally, EC-based algorithms are considered over prime fields where the possibilities of generating distinct S-boxes are not as great as the binary extension field. The outputs of different tests imply that the proposed algorithm is also resilient to various cryptographic attacks. Also, the presented S-boxes are assessed by a substitution process to study the importance of the proposed algorithm in image encryption applications. In the future, the various types of ECs over the binary extension field can also be utilized to construct different cryptographic algorithms.

Funding Statement: The authors extend their gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through the research groups program under grant number R. G. P. 2/109/43.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

 2.  X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

 3.  C. E. Shannon, “Communication theory of secrecy systems,” The Bell System Technical Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]

 4.  L. Cui and Y. Cao, “A new S-box structure named affine-power-affine,” International Journal of Innovative Computing, Information and Control, vol. 3, no. 3, pp. 751–759, 2007. [Google Scholar]

 5.  I. Hussain, T. Shah and H. Mahmood, “A new algorithm to construct secure keys for AES,” International Journal of Contemporary Mathematical Sciences, vol. 5, no. 26, pp. 1263–1270, 2010. [Google Scholar]

 6.  M. T. Tran, D. K. Bui and A. D. Duong, “Gray S-box for advanced encryption standard,” Int. Conf. on Computational Intelligence and Security, IEEE, vol. 1, pp. 253–258, 2008. [Google Scholar]

 7.  F. Özkaynak and A. B. Özer, “A method for designing strong S-Boxes based on chaotic Lorenz system,” Physics Letters A, vol. 374, no. 36, pp. 3733–3738, 2010. [Google Scholar]

 8.  Y. Wang, K. W. Wong, C. Li and Y. Li, “A novel method to design S-box based on chaotic map and genetic algorithm,” Physics Letters A, vol. 376, no. 6, pp. 827–833, 2012. [Google Scholar]

 9.  J. H. Cheon, S. Chee and C. Park, “S-boxes with controllable nonlinearity,” in Int. Conf. on the Theory and Applications of Cryptographic Techniques, Berlin, Heidelberg, Springer, pp. 286–294, 1999. [Google Scholar]

10. U. Hayat, N. A. Azam and M. Asif, “A method of generating 8 × 8 substitution boxes based on elliptic curves,” Wireless Personal Communications, vol. 101, no. 1, pp. 439–451, 2018. [Google Scholar]

11. U. Hayat and N. A. Azam, “A novel image encryption scheme based on an elliptic curve,” Signal Processing, vol. 155, no. 2–3, pp. 391–402, 2019. [Google Scholar]

12. N. A. Azam, U. Hayat and I. Ullah, “Efficient construction of a substitution box based on a Mordell elliptic curve over a finite field,” Frontiers of Information Technology, Electronic Engineering, vol. 20, no. 10, pp. 1378–1389, 2019. [Google Scholar]

13. S. Farwa, A. Sohail and N. Muhammad, “A novel application of elliptic curves in the dynamical components of block ciphers,” Wireless Personal Communications, vol. 115, no. 2, pp. 1309–1316, 2020. [Google Scholar]

14. H. U. Rehman, T. Shah, A. Aljaedi, M. M. Hazzazi and A. R. Alharbi, “Design of nonlinear components over a mordell elliptic curve on galois fields,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1313–1329, 2022. [Google Scholar]

15. E. W. Weisstein, “Totient function,” 2003. [Online]. Available: https://Mathworld.Wolfram.Com/. [Google Scholar]

16. S. Maitra, K. C. Gupta and A. Venkateswarlu, “Results on multiples of primitive polynomials and their products over GF (2),” Theoretical Computer Science, vol. 341, no. 1–3, pp. 311–343, 2005. [Google Scholar]

17. L. C. Washington, “Elliptic curves,” in Number Theory and Cryptography, CRC press, 2008. [Google Scholar]

18. C. J. Benvenuto, “Galois field in cryptography,” University of Washington, vol. 1, no. 1, pp. 1–11, 2012. [Google Scholar]

19. W. Meier and O. Staffelbach, “Nonlinearity criteria for cryptographic functions,” in Workshop on the Theory and Application of Cryptographic Techniques, Berlin, Heidelberg, Springer, pp. 549–562, 1989. [Google Scholar]

20. A. Belazi and A. A. Abd El-Latif, “A simple yet efficient S-box method based on chaotic sine map,” Optik, vol. 130, no. August 3, pp. 1438–1444, 2017. [Google Scholar]

21. M. Khan and T. Shah, “An efficient construction of substitution box with fractional chaotic system,” Signal, Image and Video Processing, vol. 9, no. 6, pp. 1335–1338, 2015. [Google Scholar]

22. N. A. Azam, U. Hayat and I. Ullah, “An injective S-box design scheme over an ordered isomorphic elliptic curve and its characterization,” Security and Communication Networks, vol. 18, no. 2, pp. 9, 2018. [Google Scholar]

23. M. A. Gondal, A. Raheem and I. Hussain, “A scheme for obtaining secure S-boxes based on chaotic Baker’s map,” 3D Research, vol. 5, no. 3, pp. 17, 2014. [Google Scholar]

24. U. Cavusoglu, A. Zengin, I. Pehlivan and S. Kacar, “A novel approach for strong S-box generation algorithm design based on chaotic scaled Zhongtang system,” Nonlinear Dynamics, vol. 87, no. 2, pp. 1081–1094, 2017. [Google Scholar]

25. K. Kazlauskas, G. Vaicekauskas and R. Smaliukas, “An algorithm for key-dependent S-box generation in block cipher system,” Informatica, vol. 26, no. 1, pp. 5165, 2015. [Google Scholar]

26. F. U. Islam and G. Liu, “Designing S-box based on 4D-4wing hyperchaotic system,” 3D Research, vol. 8, no. 1, pp. 9, 2017. [Google Scholar]

27. G. Liu, W. Yang, W. Liu and Y. Dai, “Designing S-boxes based on 3-D four-wing autonomous chaotic system,” Nonlinear Dynamics, vol. 82, no. 4, pp. 1867–1877, 2015. [Google Scholar]

28. A. F. Webster and S. E. Tavares, “On the design of S-boxes,” in Conf. on the Theory and Application of Cryptographic Techniques, Berlin, Heidelberg, Springer, pp. 523–534, 1985. [Google Scholar]

29. C. Adams and S. Tavares, “The structured design of cryptographically good S-boxes,” Journal of Cryptology, vol. 3, no. 1, pp. 27–41, 1990. [Google Scholar]

30. G. Jakimoski and L. Kocarev, “Chaos and cryptography: Block encryption ciphers based on chaotic maps,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 48, no. 2, pp. 163–169, 2001. [Google Scholar]

31. F. Özkaynak, V. Çelik and A. B. Özer, “A new S-box construction method based on the fractional-order chaotic Chen system,” Signal, Image and Video Processing, vol. 4, no. 11, pp. 659–664, 2016. [Google Scholar]

32. A. Belazi, A. A. Abd El-Latif, A. V. Diaconu, R. Rhouma and S. Belghith, “Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms,” Optics and Lasers in Engineering, vol. 88, no. 11–12, pp. pp 37–50, 2017. [Google Scholar]

33. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of Cryptology, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]

34. S. Farwa, T. Shah and L. Idrees, “A highly nonlinear S-box based on a fractional linear transformation,” Springer Plus, vol. 5, no. 1, pp. 1–12, 2016. [Google Scholar]

35. F. Özkaynak, “Construction of robust substitution boxes based on chaotic systems,” Neural Computing and Applications, vol. 31, no. 8, pp. 3317–3326, 2019. [Google Scholar]

36. A. Razaq, A. Yousaf, U. Shuaib, N. Siddiqui, A. Ullah et al., “A novel construction of substitution box involving coset diagram and a bijective map,” Security and Communication Networks, vol. 2017, no. 48, pp. 1–16, 2017. [Google Scholar]

37. I. Hussain, T. Shah, M. A. Gondal, W. A. Khan and H. Mahmood, “A group theoretic approach to construct cryptographically strong substitution boxes,” Neural Computing and Applications, vol. 23, no. 1, pp. 97–104, 2013. [Google Scholar]

38. K. Loukhaoukha, J. Y. Chouinard and A. Berdai, “A secure image encryption algorithm based on Rubik’s cube principle,” Journal of Electrical and Computer Engineering, vol. 12, no. 7, pp. 7–13, 2012. [Google Scholar]

39. G. A. Sathishkumar and D. N. Sriraam, “Image encryption based on diffusion and multiple chaotic maps,” 2011. [Online]. Available: https://arxiv.org/abs/1103.3792. [Google Scholar]

40. C. K. Huang and H. H. Nien, “Multi chaotic systems-based pixel shuffle for image encryption,” Optics Communications, vol. 282, no. 11, pp. 2123–2127, 2009. [Google Scholar]

41. C. K. Huang, C. W. Liao, S. L. Hsu and Y. C. Jeng, “Implementation of gray image encryption with pixel shuffling and gray-level encryption by single chaotic system,” Telecommunication Systems, vol. 52, no. 2, pp. 563–571, 2013. [Google Scholar]

42. S. Hussain, S. S. Jamal, T. Shah and I. Hussain, “A power associative loop structure for the construction of non-linear components of block cipher,” IEEE Access, vol. 8, pp. 123492–123506, 2020. [Google Scholar]

43. X. Wang, X. Zhu and Y. Zhang, “An image encryption algorithm based on Josephus traversing and mixed chaotic map,” IEEE Access, vol. 6, no. 17, pp. 23733–23746, 2018. [Google Scholar]

44. A. K. Farhan, N. M. Al-Saidi, A. T. Maolood, F. Nazarimehr and I. Hussain, “Entropy analysis and image encryption application based on a new chaotic system crossing a cylinder,” Entropy, vol. 21, no. 10, pp. 958, 2019. [Google Scholar]

45. Y. Naseer, T. Shah, S. Hussain and A. Ali, “Steps towards redesigning cryptosystems by a non-associative algebra of IP-loops,” Wireless Personal Communications, vol. 108, no. 3, pp. 1379–1392, 2019. [Google Scholar]

46. F. Ali Khan, J. Ahmed, J. S. Khan, and J. Ahmad “A new technique for designing 8 × 8 substitution box for image encryption applications,” in 2017 9th Computer Science and Electronic Engineering (CEEC), IEEE, pp. 7–12, 2017. [Google Scholar]

47. Y. Naseer, T. Shah, D. Shah and S. Hussain, “A novel algorithm of constructing highly nonlinear Sp-boxes,” Cryptography, vol. 3, no. 1, pp. 6, 2019. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.