DOI:10.32604/cmc.2022.027655

| Computers, Materials & Continua DOI:10.32604/cmc.2022.027655 |  |
| Article |
Construction and Optimization of TRNG Based Substitution Boxes for Block Encryption Algorithms
1Quaid e Azam University, Islamabad, 45320, Pakistan
2Foundation University Islamabad, Islamabad, 44000, Pakistan
3College of Business Administration, University of Tabuk, Tabuk, 71491, Saudi Arabia
4Department of Mathematics, College of Science, King Khalid University, Abha, 61413, Saudi Arabia
5Department of Mathematics and Sciences, Dhofar University, Salalah, 211, Oman
*Corresponding Author: Muhammad Fahad Khan. Email: mfkhan@cs.qau.edu.pk
Received: 22 January 2022; Accepted: 30 March 2022
Abstract: Internet of Things is an ecosystem of interconnected devices that are accessible through the internet. The recent research focuses on adding more smartness and intelligence to these edge devices. This makes them susceptible to various kinds of security threats. These edge devices rely on cryptographic techniques to encrypt the pre-processed data collected from the sensors deployed in the field. In this regard, block cipher has been one of the most reliable options through which data security is accomplished. The strength of block encryption algorithms against different attacks is dependent on its nonlinear primitive which is called Substitution Boxes. For the design of S-boxes mainly algebraic and chaos-based techniques are used but researchers also found various weaknesses in these techniques. On the other side, literature endorse the true random numbers for information security due to the reason that, true random numbers are purely non-deterministic. In this paper firstly a natural dynamical phenomenon is utilized for the generation of true random numbers based S-boxes. Secondly, a systematic literature review was conducted to know which metaheuristic optimization technique is highly adopted in the current decade for the optimization of S-boxes. Based on the outcome of Systematic Literature Review (SLR), genetic algorithm is chosen for the optimization of s-boxes. The results of our method validate that the proposed dynamic S-boxes are effective for the block ciphers. Moreover, our results showed that the proposed substitution boxes achieve better cryptographic strength as compared with state-of-the-art techniques.
Keywords: IoT security; sensors data encryption; substitution box generation; True Random Number Generators (TRNG); heuristic optimization; genetic algorithm
IoT created a new paradime by connecting various devices and everyday objects to the network but now days IoT devices have facing serious security issues to protect the confidentiality of transmitted data. Block ciphers are most reliable option for ensuring the data confidentiality. The strength of block ciphers against different attacks depends on their substitution boxes which provides confusion in the cryptosystem. S-box is a mapping of n-bits inputs to m-bits output and it can be seen as a Boolean function and this can be viewed as
On the other side, randomness is a fundamental aspect of many processes in nature and an indubitably valuable resource for cryptography. Researchers endorse the true random numbers in cryptography due to the fact that true random numbers are irreversible, unpredictable, and unreproducible even if their internal structure and response history is known to the adversaries. We are using the lightning strike phenomenon as an entropy source to generate true random numbers. In this research first of all, we intake the locations of lightning strikes in the row data format from the standard repository of National Aeronautics and Space Administration(NASA) which name is Lightning Detection and Ranging System (LDAR) [38]. Secondly, a novel technique is proposed for the generation of TRNG based substitution boxes. Thirdly genetic algorithm applied for the optimization of newly generated S-boxes but before this phase, a systematic literature review was conducted to know which metaheuristic optimization technique is highly adopted in the last 10 years. Based on the outcome of SLR, a genetic algorithm is chosen. The remaining paper is structured as follows; Sections 2 and 3 present our contribution and the proposed methodology respectively, Section 4 explains the results and evaluation section, Section 5 shows the conclusion section.
The main contributions of this research are follows:
• A novel method is proposed for the generation of substitution boxes of symmetric encryption algorithms based on true random numbers.
• Multi population genetic algorithm is applied for optimization of substitution boxes.
• A systematic literature review was conducted to know which metaheuristic optimization technique is highly adopted in the last 10 years for the optimization of cryptographic substitution boxes.
• A novel technique proposed for the true random numbers generation.
The proposed technique has three phase’s first phase is true random bits extraction, second phase is construction of substitution boxes and the third phase is optimization of substitution boxes. These three phases are explained in the following and the proposed system architecture is depicted in Fig. 1.

Figure 1: Proposed system architecture

3.1 True Random Bits Extraction
To calculate the difference between each location of the lightning strike with other lightning strike locations, firstly we acquire the lightning strike locations (in the row data format) from the standard repository of NASA [38]. Lightning detection and the ranging system is a volumetric lightning mapping system, which stores the real-time location of the striking point. The format of the row data is dd,hh,mm,ss,ll,xx,yy, zz, where dd represents the day of the month, hh represents the hour, mm represents the minute, ss represents second, ll represents microsecond. xx and yy represent the distance in meters from site-1 to the east direction and north direction respectively where zz represents the distance in meters above the surface of the earth. Secondly, each location of the 1st lightning strike is subtracted from the other locations of the lightning strikes. For the experiment, data of the randomly picked 9613227 lightning strikes are processed from the proposed algorithm and then resultant binary stream enhanced through the Von Neumann extractor, after this, these random bits are tested through the National Institute of Standards and Technology (NIST) statistical test suite. Results of the NIST statistical test (shown in Appendix A) proved that lightning strikes are useful entropy source for the generation of true random numbers.
3.2 Construction of Substitution Boxes
In the first step of dynamic substitution boxes construction, an algorithm proposed which name is SboxConstruction(). This algorithm takes, true random bits from the last phase and a total number of required S-boxes from the user as parameters. In the second step SboxConstruction() algorithm, further calls the RandomWalk() algorithm by passing the two-dimensional N * N space of truly random bits. On every run RandomWalk() algorithm generates a single dynamic s-box by using the 8 states random walk rule ( left = 0, left up = 1, up word = 2, right up = 3, right = 4, right down = 5, down = 6, left down = 7). SboxConstruction() algorithm is presented in the above. Randomly we plotted the two RandomWalk() runs as sample in the Figs. 2a and 2b and their resultant S-boxes in the Tabs. 1a and 1b. For the results, the total number of ten thousand S-boxes are constructed, where the nonlinearity score of 1674 S-boxes are ≤ 99, nonlinearity score of 3277 S-boxes are between 100 to 102, nonlinearity score of 4126 S-boxes are between 103 to 104, nonlinearity score of 923 S-boxes are between 105 to 106. The nonlinearity score of our sample S-boxes 2a, 2b is 105 and 104 respectively. As sample TRNG based S-box is shown in the Appendix B.




Figure 2: Plotted S-boxes (a) 8-steps random walk of Sbox-1 (b) 8-steps random walk of Sbox-2
3.3 Optimization of Substitution Box
The most important strength of true random-based construction of S-boxes is that, these S-boxes are immune against the attacks which are mentioned in the introduction section. This is our first goal which is achieved in the above Sections 3.2 by using the true randomness. The 2nd goal of this research is to find out, which metaheuristic optimization technique is effective (highly adopted) in existing literature for the optimization of S-boxes (which are not based on true randomness). To discover the answer to this question, a SLR was conducted over the last 10 years. Query wise search results of SLR is mentioned in the Tab. 2 and based on the SLR recommendation, a technique is presented in the following for the optimization of newly constructed S-boxes using the genetic algorithm. Reverse S-box algorithm for the TRNG and GA based S-boxes is shown in the Appendix C.

GA is based on the Charles Darwin’s theory of natural selection and survival of the fittest In the standard genetic algorithm, selection, crossover, and mutation are the common processes. In our problem for the selection process, all the substitution boxes whose nonlinearity score lies in the range of 100 to 106 are acquired as the initial population. For the crossover process, we used the one-point crossover strategy in which pair of parents exchange the half part of each parent to each other and generate new offspring. Complete crossover process is represented with yellow color in the flowchart which is depicted in Fig. 1. Widely in the literature [39–44], the nonlinearity score is the highly desirable property that’s why we also chose the nonlinearity score as the fitness value. In the conventional genetic algorithm, crossover and mutation are the two independent processes but here for the substitution box generation, we combine the crossover and mutation process together. The reason is that, the substitution boxes generated by the crossover operation usually do not satisfy the bijective property due to repeated elements. So, repetition must be removed from the new offspring to achieve the bijective property and for that purpose, a simple strategy is adopted in the mutation process. In the mutation process we flipped the one bit from right side to the left side, and after flipping each bit, the corresponding number is checked within the s-box. If the corresponding number is unique, then we stop the flipping process, otherwise we flip the next bit and so on. In the numerous cases, we achieved the bijective property but in the few cases after flipping the eight bits, we did not get the unique element of the s-box and in those cases, we simply add one to the original element from where we start the flipping process. The mutation process is represented with green color in the flowchart of Fig. 1. From the results, we observed that numerous S-boxes and their subsets are repeated therefore we used SHA-3 based searching for removal and this process is shown with blue color in the flowchart. Here, for the experiment hundred thousand S-boxes are optimized and to examine the performance, we compared the highest quality ten thousand optimized S-boxes with the ten thousand S-boxes which are already constructed through the TRNG based technique. After optimization, it can be clearly seen from Fig. 3 that GA improves the overall quality of the S-Boxes. After optimization process, there are no S-box having non-linearity of less than and equal to 99 where TRNG based S-box construction technique 1674 S-boxes in that range. Similarly, GA produce more S-boxes in the range of 105 and 106 as compared to TRNG construction method. Furthermore, GA produce 616 new S-boxes having non-linearity of 107 and 108 and these S-Boxes were not discovered in TRNG based approach.

Figure 3: Nonlinearity score of TRNG and GA based S-box construction
In this section sample S-boxes of Section 3.2 are evaluated through the S-box evaluation criteria which are shown in the following 4.1 to 4.5.
Out of all cryptographic properties, nonlinearity is said to be the most significant. For a strong encryption scheme, the mapping between input and output in an S-box must be nonlinear. Nonlinearity can be defined as the smallest distance of Boolean function to the set of affine functions. To get the closet affine function in the Boolean truth table, the total number of bits altered needs to be determined by the nonlinearity score. In the above Fig. 3 we saw that six hundred sixteen S-boxes attains a 108 nonlinearity score and from these S-boxes, we picked randomly one S-box as a sample which is shown in Tab. 1c. The Nonlinearity scores of proposed S-boxes are better or equal to the state-of-the-art. S-boxes which are shown in Tab. 3. By using Walsh spectrum, the nonlinearity of Boolean function is determined as:
where

4.2 Strict Avalanche Criteria (SAC)
SAC computes the number of output bits altered caused by inverting a single bit of input. To make the system more reliable, we need to deviate output vector with half probability when one input bit is inverted. To evaluate the SAC property, dependency matrix are used. For an S-box that can satisfy SAC property, all values need to be close to ideal value of 0.5 in its dependence matrix. The SAC value of our randomly picked optimized S-box is 0.501465 which satisfies the avalanche criteria. The offsets of the dependence matrix can be determined by:
4.3 BIT Independent Criterion (BIC)
BIC is another cryptographic metric used to measure the efficiency of S-boxes. For an S-box to satisfy the BIC property, all avalanche variables should be independent pair wise for a number of avalanche vectors created by modifying a single bit of plaintext. BIC states that reversing the input bit i modifies the output bits j and k in such a way that the no dependency lies between output bits. This would tend to improve the confusion function’s effectiveness. To satisfy the BIC property, the output bits must exhibits independent behavior. Therefore, efforts are being made to decrease the dependency of output bits. The correlation coefficient is used to calculate the degree of independence among avalanche variable pairs. The bit independence of the jth and kth bits of Bei is:
S-box function (h) is defined as: h: {0, 1}n →{0, 1}n .BIC parameter for the S-box function is expressed as follows:
Average SAC-BIC score of our optimized S-box is 0.49937. Which is almost optimal and indicates that proposed S-box fulfills the required criteria.
4.4 Linear Approximation Probability (LP)
LP is used to evaluate the security of S-box against linear cryptanalysis. S-box provides diffusion and confusion of bits through linear mapping between input and output. Maximum imbalance of an event is determined by LP. The input bit’s parity given by the mask
where the input mask is represented by
4.5 Differential Approximation Probability (DP)
Differential approximation probability means that output shall have a difference of
where X represents the set of all possible input values, 2n is a total number of all the elements in the S-box, Δx and Δy are the input and output differentials. S-boxes with small differentials values are strong and good at resisting differential cryptanalysis. The DP results of Sbox1 are following in the Tab. 4, and we can see that our proposed S-box fulfils the DP criteria.

4.6 Substitution Permutation based Image Encryption
In this section simple Substitution Permutation Network (SPN) used for the image encryption. Detailed steps of the SPN are mentioned bellow. Here for the substitution step optimize S-boxes of the Section 3.3 used, we used the P-boxes and keys from the [57].
Step-1: Extract the Red, Green and Blue channel values from the color image frames and repeat the following steps-2 to step-4 for every channel(R or G or B).
Step-2: Perform the bitwise XOR between the plain pixel values and sub keyi to obtain the key additive pixel values.
Step-3: Replace each value of step-2 with entries of the optimized (Sboxi) values.
Step 4: Diffuse the each value of step-3 by using (P-boxi) values.
Step 5: Repeat step-2 to step-4 for i<16.
Step 6: Combine the individual R, G, B encrypted pixel values into a single frame.
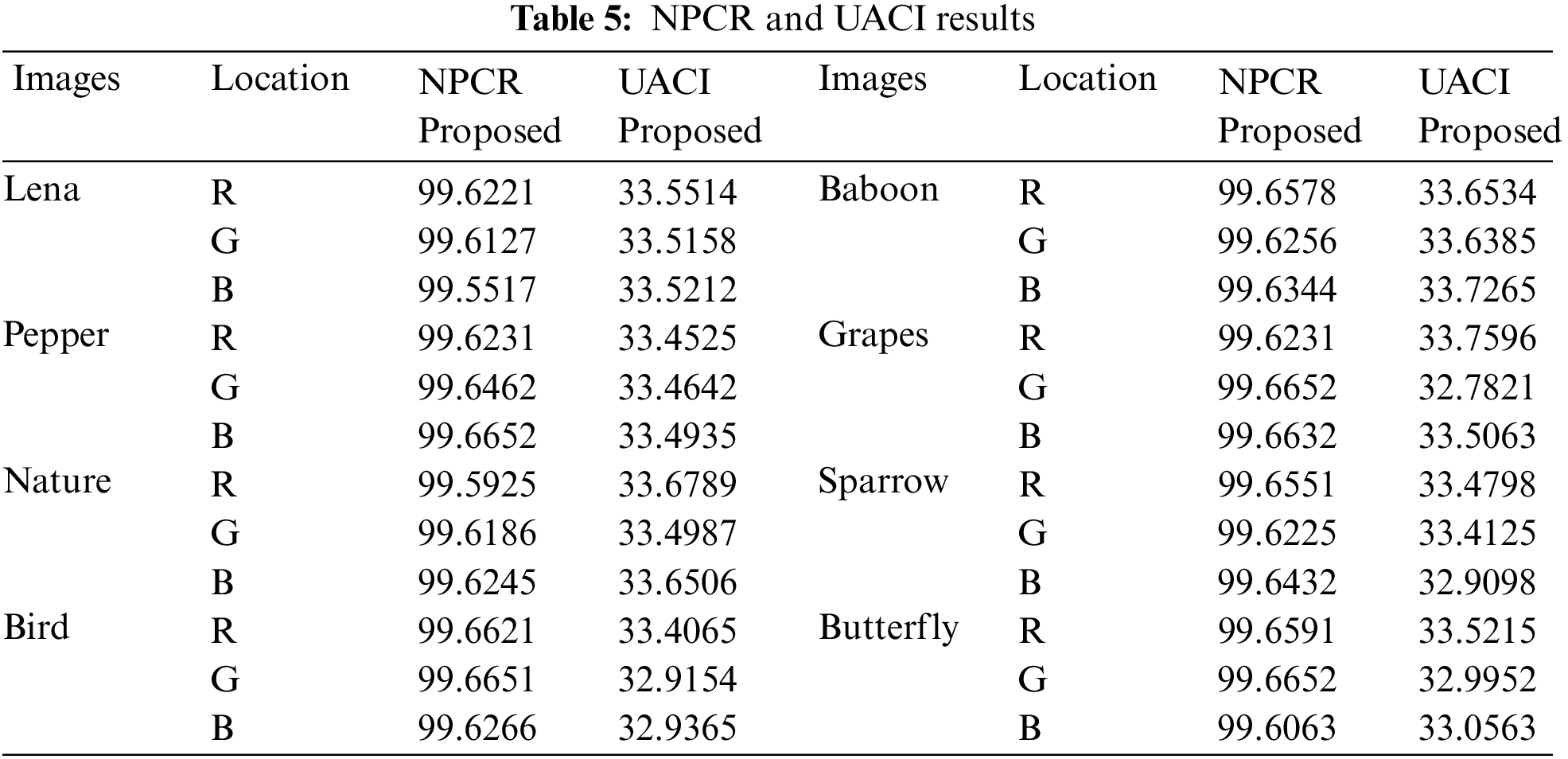
The NPCR and UACI are the two frequently used tests of the image cipher to check the strength against various attacks. NPCR, UACI are used to evaluate a large number of plain images to measure the impact of pixel change on the encrypted images. We examined the image encryption results on various standard color images (Lena, pepper, nature, bird, baboon, grapes, sparrow, butterfly). Ideal image encryption algorithm must produce different results when a pixel of the image is slightly varied. NCPR is the rate of change in the number of pixels between two encrypted images obtained from two slightly different images. To achieve maximum sensitivity in an algorithm the value of NCPR should close to 100%. UAIC measure the mean variation of pixel intensity of two encrypted images at same location. Following Tab. 5 indicates the values of NPCR and UACI. Constantly our NPCR values are around to 99.63 which is the very good value. Similarly the UACI values are around 33.5 which is also the good value.
The IoT-based computationally intelligent schemes are expanding due to the growing concerns of privacy leakage and security attacks in connected systems. It has added a new potential to the internet by enabling communications between objects and humans, making a smarter and more intelligent ecosystem. In this regard, block encryption algorithms have been a standout amongst the most reliable option by which data security is accomplished. The strength of block encryption algorithms against different attacks is dependent on its nonlinear primitive which is called S-boxes. The objective of this research is dynamic generation and optimization of highly secure S-boxes for the block encryption algorithms. For this purpose we used the true random numbers as the entropy source of the proposed method because true random numbers are irreversible, unpredictable, and unreproducible. The proposed method passes all the security evaluation criteria including nonlinearity, linear approximation probability, differential approximation probability, strict avalanche criterion, bit independence criterion, differential analysis, histogram analysis, correlation coefficient tests, NPCR, and UACI tests. The results of our method validate that the proposed dynamic s-boxes are effective for the block encryption algorithms. In the future, we will extend this research to the design of cryptographic key generation technique for the IoT systems.
Acknowledgement: We thank the R. G. P. 2/132/42, NASA Global Hydrology Resource Center DAAC DOI: http://dx.doi.org/10.5067/LIS/LDAR/DATA101. Accessed on Dec 04, 2021.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. M. F. Khan, A. Ahmed and K. Saleem, “A novel cryptographic substitution box design using gaussian distribution,” IEEE Access, vol. 7, no. 4, pp. 15999–16007, 2019. [Google Scholar]
2. M. F. Khan, A. Ahmed, K. Saleem and T. Shah, “A novel design of cryptographic SP-network based on gold sequences and chaotic logistic tent system,” IEEE Access, vol. 7, no. 1, pp. 84980–84991, 2019. [Google Scholar]
3. X. Wu, D. Wang, J. Kurths and H. Kan, “A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system,” Information Sciences, vol. 349, no. 10, pp. 137–153, 2016. [Google Scholar]
4. E. Y. Xie, C. Li, S. Yu and J. Lü, “On the cryptanalysis of Fridrich’s chaotic image encryption scheme,” Signal Processing, vol. 132, no. 2, pp. 150–154, 2017. [Google Scholar]
5. R. Zahmoul, R. Ejbali and M. Zaied, “Image encryption based on new beta chaotic maps,” Optics and Lasers in Engineering, vol. 96, no. 3, pp. 39–49, 2017. [Google Scholar]
6. Z. Hua, F. Jin, B. Xu and H. Huang, “2D LogisticSine-coupling map for image encryption,” Signal Processing, vol. 149, no. 3, pp. 148–161, 2018. [Google Scholar]
7. R. Lan, J. He, S. Wang, T. Gu and X. Luo, “Integrated chaotic systems for image encryption,” Signal Processing, vol. 147, no. 2, pp. 133–145, 2018. [Google Scholar]
8. Y. Zhou, Z. Hua, C. M. Pun and C. L. Philip Chen, “Cascade chaotic system with applications,” IEEE Transaction in Cybernetics, vol. 45, no. 9, pp. 2001–2012, 2015. [Google Scholar]
9. M. Alawida, J. S. Teh, A. Samsudin and W. H. Alshoura, “An image encryption scheme based on hybridizing digital chaos and finite state machine,” Signal Processing, vol. 164, no. 1, pp. 249–266, 2019. [Google Scholar]
10. Y. Liu, Y. Luo, S. Song, L. Cao, J. Liu et al., “Counteracting dynamical degradation of digital chaotic chebyshev map via perturbation,” International Journal of Bifurcation and Chaos, vol. 27, no. 3, pp. 1750033, 2017. [Google Scholar]
11. C. Pak and L. Huang, “A new color image encryption using combination of the 1D chaotic map,” Signal Processing, vol. 138, no. 2, pp. 129–137, 2017. [Google Scholar]
12. R. Parvaz and M. Zarebnia, “A combination chaotic system and application in color image encryption,” Optical Laser Technology, vol. 101, pp. 30–41, 2018. [Google Scholar]
13. Y. Zhou, L. Bao and C. L. P. Chen, “A new 1D chaotic system for image encryption,” Signal Processing, vol. 97, no. 11, pp. 172–182, 2014. [Google Scholar]
14. Y. Deng, H. Hu, N. Xiong, W. Xiong and L. Liu, “A general hybrid model for chaos robust synchronization and degradation reduction,” Information Sciences, vol. 305, pp. 146–164, 2015. [Google Scholar]
15. C. Li, “Cracking a hierarchical chaotic image encryption algorithm based on permutation,” Signal Processing, vol. 118, no. 3, pp. 203–210, 2016. [Google Scholar]
16. C. Li, B. Feng, S. Li, J. Kurths and G. Chen, “Dynamic analysis of digital chaotic maps via state-mapping networks,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 6, pp. 2322–2335, 2019. [Google Scholar]
17. W. Zhang and E. Pasalic, “Highly nonlinear balanced S-boxes with good differential properties,” IEEE Transaction in Information Theory, vol. 60, no. 12, pp. 7970–7979, 2014. [Google Scholar]
18. D. Arroyo, J. Diaz and F. B. Rodriguez, “Cryptanalysis of a one round chaos-based substitution permutation network,” Signal Processing, vol. 93, no. 5, pp. 1358–1364, 2013. [Google Scholar]
19. G. Chen, Y. Chen and X. Liao, “An extended method for obtaining S-boxes based on three-dimensional chaotic Baker maps,” Chaos Solitons and Fractals, vol. 31, no. 3, pp. 571–579, 2007. [Google Scholar]
20. M. Alawida, A. Samsudin, J. Sen Teh and R. S. Alkhawaldeh, “A new hybrid digital chaotic system with applications in image encryption,” Signal Processing, vol. 160, no. 8, pp. 45–58, 2019. [Google Scholar]
21. L. Y. Zhang, X. Hu, Y. Liu, K. W. Wong and J. Gan, “A chaotic image encryption scheme owning temp-value feedback,” Communication in Nonlinear Science and Numerical Simulation, vol. 19, no. 10, pp. 3653–3659, 2014. [Google Scholar]
22. Z. Hua and Y. Zhou, “Design of image cipher using block-based scrambling and image filtering,” Information Science, vol. 396, no. 4, pp. 97–113, 2017. [Google Scholar]
23. Y. Q. Zhang and X. Y. Wang, “A symmetric image encryption algorithm based on mixed linear-nonlinear coupled map lattice,” Information Science, vol. 273, no. 15, pp. 329–351, 2014. [Google Scholar]
24. F. Özkaynak, V. Çelik and A. B. Özer, “A new Sbox construction method based on the fractional-order chaotic Chen system,” Signal Image Video Process, vol. 11, no. 4, pp. 659–664, 2017. [Google Scholar]
25. K. Majid, T. Shah and S. I. Batool, “Construction of S-box based on chaotic Boolean functions and its application in image encryption,” Neural Computing and Applications, vol. 27, no. 3, pp. 677–685, 2016. [Google Scholar]
26. K. Majid, T. Shah, H. Mahmood, M. A. Gondal and I. Hussain, “A novel technique for the construction of strong S-boxes based on chaotic Lorenz systems,” Nonlinear Dynamics, vol. 70, no. 3, pp. 2303–2311, 2012. [Google Scholar]
27. K. Majid and T. Shah, “An efficient construction of substitution box with fractional chaotic system”,” Signal, Image and Video Processing, vol. 9, no. 6, pp. 1335–1338, 2015. [Google Scholar]
28. M. A. Gondal, “A projective general linear group based algorithm for the construction of substitution box for block ciphers,” Neural Computing and Applications, vol. 22, no. 6, pp. 1085–1093, 2013. [Google Scholar]
29. I. Hussain and T. Shah, “A novel approach for designing substitution-boxes based on nonlinear chaotic algorithm,” Nonlinear Dynamics, vol. 70, no. 3, pp. 1791–1794, 2012. [Google Scholar]
30. F. Özkaynak and S. Yavuz, “Designing chaotic S-boxes based on time-delay chaotic system,” Nonlinear Dynamics, vol. 74, no. 3, pp. 551–557, 2013. [Google Scholar]
31. A. Ullah, S. S. Jamal and T. Shah, “A novel scheme for image encryption using substitution box and chaotic system,” Nonlinear Dynamics, vol. 91, no. 1, pp. 359–370, 2018. [Google Scholar]
32. A. Belazi, M. Khan, A. A. Abd and E. S. Belghith, “Efficient cryptosystem approaches : S-boxes and permutation-substitution-based encryption,” Nonlinear Dynamics, vol. 87, no. 1, pp. 337–361, 2017. [Google Scholar]
33. A. A. A. El-latif, B. Abd-el-atty and M. Amin, “Quantum-inspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic applications,” Scientific Report, vol. 10, no. 1, pp. 1–16, 2020. [Google Scholar]
34. M. Khan, T. Shah and H. Mahmood, “An efficient method for the construction of block cipher with multi-chaotic systems,” Nonlinear Dynamics, vol. 71, no. 3, pp. 489–492, 2013. [Google Scholar]
35. F. Özkaynak and A. Bedri, “A method for designing strong S-Boxes based on chaotic Lorenz system,” Physics Letter A, vol. 374, no. 36, pp. 3733–3738, 2010. [Google Scholar]
36. Ü. Çavu and A. Zengin, “A novel approach for strong S-Box generation algorithm design based on chaotic scaled Zhongtang system,” Nonlinear Dynamics, vol. 87, no. 2, pp. 1081–1094, 2016. [Google Scholar]
37. I. Hussain, T. Shah and M. Asif, “A group theoretic approach to construct cryptographically strong substitution boxes,” Neural Computing and Applications, vol. 23, no. 1, pp. 97–104, 2013. [Google Scholar]
38. B. Richard J, M. Bateman and D. Mach, “Lightning detection and ranging (LDAR) raw data,” https://cmr.earthdata.nasa.gov/search/concepts/C1979878937-GHRC_DAAC.html Accessed on Dec 04, 2021. [Google Scholar]
39. Y. Wang and K. W. Wong, “A method for constructing bijective S-box with high nonlinearity based on chaos and optimization,” International Journal of Bifurcation and Chaos, vol. 25, no. 10, pp. 127–155, 2015. [Google Scholar]
40. W. Yung, Z. Zhang, L. Zhang, Y. Feng, J. Gao et al., “A genetic algorithm for constructing bijective substitution boxes with high nonlinearity,” Information Sciences, vol. 23, no. 1, pp. 152–166, 2020. [Google Scholar]
41. F. Artuğer and F. Özkaynak, “An effective method to improve nonlinearity value of substitution boxes based on random selection,” Information Sciences, vol. 576, no. 1, pp. 577–588, 2021. [Google Scholar]
42. M. Ahmad, I. A. Khaja, A. Baz, A. Alhakami and W. Alhakami, “Particle swarm optimization based highly nonlinear substitution-boxes generation for security applications,” IEEE Access, vol. 8, pp. 116132–116147, 2020. [Google Scholar]
43. I. Ullah, N. A. Azam and U. Hayat, “Efficient and secure substitution box and random number generators over Mordell elliptic curves,” Journal of Information Security and Applications, vol. 56, no. 3, pp. 102–619, 2021. [Google Scholar]
44. N. Siddiqui, F. Yousaf, F. Murtaza, M. Ehatisham-ul-Haq, M. U. Ashraf et al., “A highly nonlinear substitution-box (S-box) design using action of modular group on a projective line over a finite field,” PLOS ONE, vol. 15, no. 11, pp. 024–189, 2021. [Google Scholar]
45. F. Özkaynak, “On the effect of chaotic system in performance characteristics of chaos-based S-box designs,” Physical A: Statistical Mechanics and its Applications, vol. 20, no. 10, pp. 48–57, 2020. [Google Scholar]
46. A. A. A. El-Latif, B. Abd-El-Atty, W. Mazurczyk, C. Fung and S. E. Venegas-Andraca, “Secure data encryption based on quantum walks for 5G Internet of Things scenario,” IEEE Transactions on Network and Service Management, vol. 17, no. 1, pp. 118–131, 2020. [Google Scholar]
47. Z. M. Zahir and F. Özkaynak, “A cryptographic confusion primitive based on Lotka–Volterra chaotic system and its practical applications in image encryption,” in PROC. TCSET, Slavske Ukraine, vol. 11, pp. 694–698, 2020. [Google Scholar]
48. A. A. A. El-Latif, B. Abd-El-Atty, M. Amin and A. M. Iliyasu, “Quantuminspired cascaded discrete-time quantum walks with induced chaotic dynamics and cryptographic application,” Sci. Rep., vol. 10, no. 1, pp. 116--132, 2020. [Google Scholar]
49. B. Faheem, A. Ali, M. A. Khan, M. E. Ul-Haq and W. Ahmad, “Highly dispersive substitution box (S-box) design using chaos,” ETRI Journal, vol. 42, no. 4, pp. 619–632, 2020. [Google Scholar]
50. G. Liu and T. Guangjie, “Designing S-box based on 4D-4wing hyperchaotic system,” 3D Research, vol. 1, no. 9, pp. 1–9, 2017. [Google Scholar]
51. B. Akram, M. Khan, A. El-Latif and S. Belghith, “Efficient cryptosystem approaches: S-boxes and permutation-substitution-based encryption,” Nonlinear Dynamics, vol. 87, no. 1, pp. 337–361, 2017. [Google Scholar]
52. F. Özkaynak, “Construction of robust substitution boxes based on chaotic systems,” Neural Computing and Applications, vol. 29, no. 8, pp. 317–329, 2019. [Google Scholar]
53. Ç. Ünal, A. Zengin, I. Pehlivan and S. Kaçar, “A novel approach for strong S-Box generation algorithm design based on chaotic scaled Zhongtang system,” Nonlinear Dynamics 87, vol. 2, pp. 1081–1094, 2017. [Google Scholar]
54. E. A. Solami, M. Ahmad, C. Volos, M. Doja and M. Beg, “A new hyper chaotic system-based design for efficient bijective substitution-boxes,” Entropy, vol. 20, no. 7, pp. 525, 2018. [Google Scholar]
55. D. Lambić, “A novel method of S-box design based on discrete chaotic map,” Nonlinear Dynamics, vol. 87, no. 4, pp. 2407–2413, 2017. [Google Scholar]
56. D. Lambić, “A new discrete-space chaotic map based on the multiplication of integer numbers and its application in S-box design,” Nonlinear Dynamics, vol. 100, no. 1, pp. 699–711, 2020. [Google Scholar]
57. M. F. Khan, A. Ahmed, K. Saleem and T. Shah, “A novel design of cryptographic SP-Network based on gold sequences and chaotic logistic tent system,” IEEE Access, vol. 7, no. 1, pp. 84980–84991, 2019. [Google Scholar]



 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |