DOI:10.32604/cmc.2022.029563

| Computers, Materials & Continua DOI:10.32604/cmc.2022.029563 |  |
| Article |
A Novel Peak-to-Average Power Ratio Reduction for 5G Advanced Waveforms
1Department of Computer Science & Engineering, JECRC University, Jaipur, 303905, India
2Centre for Nonlinear Systems, Chennai Institute of Technology, Chennai, India
3Department of Electronics and Communication, JECRC University, Jaipur, 303905, India
4Department of Computer Science, College of Science & Art at Mahayil, King Khalid University, Abha, Saudi Arabia
5Department of Information Systems, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, 11671, Saudi Arabia
6Electrical Engineering Department, Faculty of Engineering and Technology, Future University in Egypt, New Cairo, 11845, Egypt
7Department of Computer and Self Development, Preparatory Year Deanship, Prince Sattam bin Abdulaziz University, AlKharj, Saudi Arabia
*Corresponding Author: Manar Ahmed Hamza. Email: ma.hamza@psau.edu.sa
Received: 06 March 2022; Accepted: 12 April 2022
Abstract: Multi and single carrier waveforms are utilized in cellular systems for high-speed data transmission. In The Fifth Generation (5G) system, several waveform techniques based on multi carrier waveforms are proposed. However, the Peak to Average Power Ratio (PAPR) is seen as one of the significant concerns in advanced waveforms as it degrades the efficiency of the framework. The proposed article documents the study, progress, and implementation of PAPR reduction algorithms for the 5G radio framework. We compare the PAPR algorithm performance for advanced and conventional waveforms. The simulation results reveal that the advanced Partial Transmission Sequence (PTS) and Selective Mapping (SLM) methods enhanced the throughput and gain of the 5G waveforms. Furthermore, we have also analyzed the performance of Orthogonal Time Frequency Space Modulation (OTFSM) based on a single carrier system and found that PAPR is significantly low and is best suited to fading environments. It is seen that the conventional algorithms lower the PAPR but increase the complexity. The proposed PTS and SLM have shown good performance with low computational complexity.
Keywords: PAPR; 5G; OFDM; NOMA; OTFSM; PTS; SLM
Orthogonal Frequency Division Multiplexing (OFDM) is the latest high-end technology in the field of wireless and wire-line communications. OFDM is compatible with a variety of technologies, including Long Term Evolution (LTE), Worldwide Interoperability for Microwave Access (Wi-Max), optical networks, and digital audio and video broadcasting [1]. Because of those subcarriers [2], OFDM has higher spectrum efficiency than Frequency Division Multiplexing (FDM). In spite of having many advantages, such as high spectral efficiency and immunity towards frequency-selective fading, another drawback in OFDM is interference, which is the biggest challenge in wireless communication. It is not completely eliminated; however, it can be mitigated to a permissible level. The Wavelet transform turns out to be a significant method to mitigate the problem Of Inter-Symbol Interference (ISI) [3]. Hence, it is not considered a suitable candidate for 5G. Filter Bank Multi-Carrier (FBMC) is another candidate proposed by researchers to meet the requirements of 5G. It is seen that FBMC provides better spectral efficiency than OFDM as it divides the bandwidth into groups of subcarriers and then filters them on a subcarrier basis [4]. This will reduce Out of Band (OOB) radiation and Inter-Carrier Interference (ICI) by using the spread spectrum technique. The filtering of the sub-carrier also enables the FBMC to reduce Adjacent Channel Leakage (ACL) [5]. However, filtering cannot avoid the ICI in between the symbols. The major drawback of FBMC is the length of its symbol duration. Since the length of the symbol duration is very long, it requires a large filter to provide reasonable filtration with a very narrow band of single sub-carrier. In 5G, small bursts of data are generated through devices. These devices will not be able to find compatibility with long duration symbols [6]. NOMA applications in downlink transmission were tested in the Third Generation Partnership Project (3GPP). In the same project, the NOMA uplink transmission was also tested. However, NOMA uplink transmission in the power domain has performance degradation in major regions. That's why it is not considered a possible technique in 3GPP. If the channel gains of the users are the same, then the spectral efficiency performance of NOMA is not better than OMA [7]. Superposition Coding (SC) and Successive Interference Cancellation (SIC) are also the mechanisms used in NOMA to associate the users with their particular resource block. At the transmitter, a composite signal is formed by the base station's having information about all the users using SC. For the careful detection of transmitting signals, SIC is performed at the receiver to decode the information of users. Here, user 1 will perform the SIC to first decode its own signal, considering all the other information as noise, and the same mechanism is performed by all the users on the composite signal transmitted by the transmitter [8]. Orthogonal Time Frequency Space Modulation (OTFSM) is an advanced waveform based on a single carrier system. The performance of OTSM is better than that of OFDM in multipath propagation. OTSM transmits in Doppler mode due to the way it holds the channel structure that designs the cellular terminals and reflectors in large fading scenarios. It modulates the symbols, integrating the IFFT with Doppler and latency, which helps to achieve an efficient performance in a multipath environment. The characteristics of OFTSM, such as low PAPR, alternate multiplexing method for uplink, high gain, utilisation of simple equalizers, and multiple ways of OFTSM design, make it a suitable alternate waveform for the advanced radio framework. Mathematically, PAPR is expressed as the ratio of peak power to average power of signals. It significantly reduces the performance of the power amplifier used in the user device, as a result of which the cost is also increased. In any multicarrier technique, we use PAPR reduction techniques just after the IFFT block. In this work, the author suggested a Selective Mapping Circular Transformation hybrid (SLMCT) method to reduce the PAPR in FBMC and NOMA systems. The experimental work reveals that the performance of hybrid methods is significantly better than the existing technology and enhances the system's overall execution [9]. Researchers proposed a novel finite impulse response (FIR) filter based on the Hadamard transform pre-coded uplink multi-carrier NOMA technique to reduce PAPR to a higher degree. Simulation results demonstrate that the above-mentioned technique outperforms the pre-coded uplink multicarrier scheme without any filtration process and side information requirements [10]. The Discrete Sine Transform (DST) matrix pre-coding based uplink NOMA technique is suggested by the authors to reduce PAPR. Computer simulations demonstrate that the proposed method provides better results than the Walsh Hadamard transform matrix in the uplink NOMA scheme [11]. In this paper, clipping and windowing techniques for additive white Gaussian noise as a channel are proposed to eliminate the PAPR problem. The simulation results indicate that for a threshold level of 0.7, there is a drop of 8 dB in PAPR for clipping and an 11 dB reduction when considering Kaiser Window [12]. The author suggested a discrete cosine transform matrix for uplink NOMA for the reduction of PAPR. Along with that, this technique has the superiority of information spreading for the whole system bandwidth [13]. In this work, the authors gave thorough insights into comparing various techniques in orthogonal multiple access. The performance of different parameters, such as system efficiency, bit error rate, and energy spectrum capacity, is analyzed. The comparison results indicated that NOMA may achieve the targets for advanced waveforms in terms of system efficiency, user experience, and interference management [14]. In this work, researchers proposed a pre-coding technique to reduce Carrier Frequency Offset (CFO) with a simple receiver system. Banded Matrix Implementation (BMI) is suggested as a solution for low complexity joint equalization. The outcomes of the study reveal that the proposed method works very well for low-complexity systems; however, for high-complexity systems, it requires more bandwidth at a high Signal-to-Noise Ratio (SNR) [15]. For better analysis of the fractional frequency used in NOMA signals, a block of wavelet transform is proposed as a substitute to the fast Fourier transform (FFT). To investigate the performance of a WT-based NOMA system, methods like selective mapping and Genetic Algorithms (GA) are used. Simulation results demonstrate that the WT-SLM technique obtains the best results among various techniques used [16]. In [17], the authors presented a thorough comparison between non-orthogonal and orthogonal multiple access techniques. The comparison specifically emphasizes information theory. In the same work classification of NOMA, such as power and code-domain NOMA, various key factors like system efficiency, receiver's design, and performance of the spectrum are discussed in detail. The challenges in the path of NOMA, with its design and spreading sequence, were highlighted. Finally, after a long comparison, the author supports NOMA as a contender for 5G in low latency and higher connectivity [18]. The achievable sum rate was critically analyzed in the optical domain with the effect of clipping noise and polarity divided DC-Biased optical OFDM. A comparative study was carried out by considering factors like transmitted power and DC bias. The simulation results reveal that for a two-user scenario, polarity divided DC-OFDM provides better results than DC-biased OFDM systems [19]. In this work, the integration of NOMA with single frequency-frequency division multiple access systems is suggested. To achieve low PAPR, SC-FDMA needs continuous resource allocation. In the presented work, the authors demonstrate the main factors in the uplink-NOMA technique. Important factors like fractional frequency reuse and scheduling granularity are investigated in up-link NOMA. The outcomes of the study support NOMA for radio access technology for 5G networks [20]. The researchers proposed a Hartley transformed pre-coding technique along with filtering and clipping techniques. The simulation done by Matlab reveals that pre-coded signals have a lower PAPR than that of non-pre-coded signals [21]. For the reduction of PAPR, the vector-based low-complexity dispersive Selection Mapping (C-DSLM) is proposed. In this technique, sequences of conversion vectors are designed for the FBMC signal, and candidate signals are produced by the product of the original signal and the shift of conversion vectors with non-zero circular elements. The evaluation results show that this technique has the same efficiency as the DSLM scheme while having only 10% of the computational complexity [22]. Different versions of FBMC are used to further reduce the PAPR. DFT and IDFT are only mentioned once. The evaluation methods indicate that the proposed technique achieves better PAPR than the traditional SC-FDMA method. Additionally, the side information requirement is not needed in the suggested method [23]. In this work, a new hybrid processing algorithm is introduced to reduce PAPR in FBMC-OQAM systems. A double-layer search algorithm is proposed to find the optimal phase factor. Evaluation results indicate that the proposed H-PTS method achieves better performance as well as good computational complexity than the conventional PTS [24]. Direct application of tone reservation has no effect due to the overlapping structure of the FBMC and OQAM systems. Thus, the sliding window tone reservation (SW-TR) technique promised a solution to the problem of PAPR. The proposed scheme uses several data blocks of PRT's (Peak Reduction Tone) to eliminate the highs of the FBMC-OQAM signal [25]. Simulation results reveal that the suggested hybrid PTS-TR technique proves to be better than the conventional PTS. The contribution of the article is given below:
• By changing their structure, we propose a novel PAPR algorithm by applying it to the advanced waveforms.
• To the best of our knowledge, the waveform scheme performance of OTFSM is compared to that of NOMA, FBMC, and OFDM.
• The power saving of a power amplifier is enhanced by 83% after applying an advanced PTS algorithm.
SC is a technique of concurrently transmitting information to several users from a single source. To do that, the transmitter is required to encode information for each user. Let us consider a two-user scenario. The transmitter must have two point-to-point encoders that can map their corresponding data to complex valued sequences [26]. Assume that user 1 has high transmitter power and user 2 has low transmitting power. In superposition encoding, two encoders
E1:{0,1}|2TU1|=>(1)
Map the inputs to two outputs, such as
Here,
2.2 Successive Interference Cancellation (SIC)
The common idea behind SIC is that signals from different users are decoded successively [27]. Firstly, when the user successfully decodes its signals, their signals are subtracted from the composite signal.
• User 1 will decode its signals using single user decoder
• User 2 will perform a three step method to receive its signal:
o Decode the signal of user 1
o Subtract decoded signal from received signal
o Decode user 2 signal by performing another decoding on the remaining signal.
• In first step, the original information is encoded by the users. The encoded information is modulated using Quadrature Amplitude Modulation (QAM), given as:
• In the second step, each transmitted symbols (M) are assigned to the N sub-carriers, given as:
where W is the Vandermonde matrix. Element of this matrix is defined as:
(
• The symbols transmitted over sub-carrier is given as:
• An IFFT is applied on the modulated symbols (
The Eq. (4) can be also written as:
where time duration of NOMA symbols is estimated as:
• Mathematically, PAPR is defined by:
• The PAPR of the NOMA is given as:
Considering equal amount of power assigned to both users:
where
The structure of SLM is given in Fig. 1. It is one of the best methods for PAPR reduction in multicarrier waveforms. In this method, the input signals are divided into V-sub-blocks and multiplied with phase vectors (Pv). An IFFT is applied to each sub-block, and the signal with the lowest PAPR value is selected for transmission. However, the presence of side information and high complexity are seen as constraints in SLM [28].
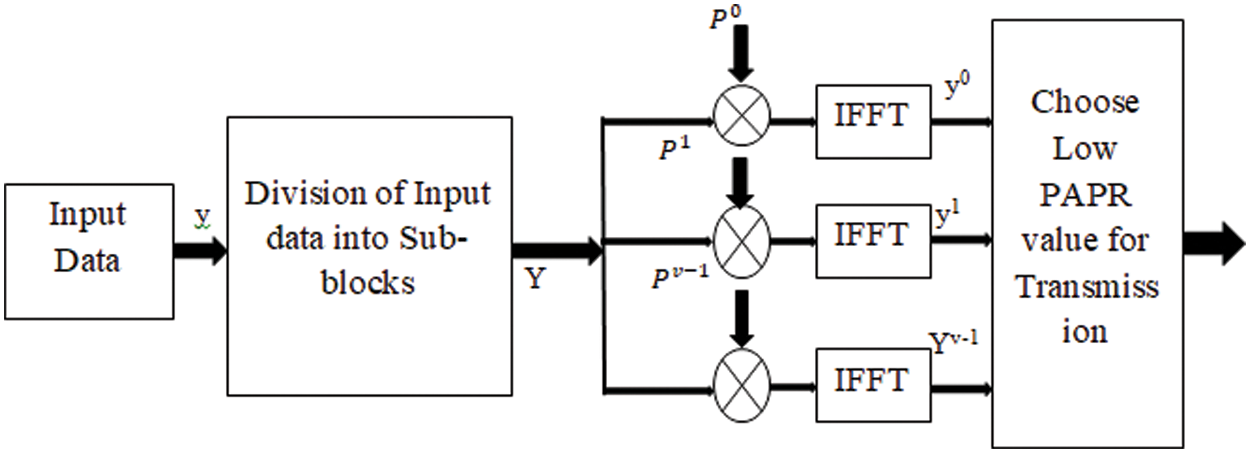
Figure 1: Advanced SLM
The input signal can be written as:
The Phase vector can be written as:
An IFFT is applied to the input signal (Y) and phase vector (
where
3.2 Partial Transmission Sequence (PTS)
PTS is considered as an efficient PAPR reduction method with low computational intricacy, shown in Fig. 2. In this method, the input signal of M-sequence is mapped into N-sub-blocks. An IFFT is applied to each sub-blocks and multiplied by Phase vector to decrease the PAPR of the combined transmitted signal [29].
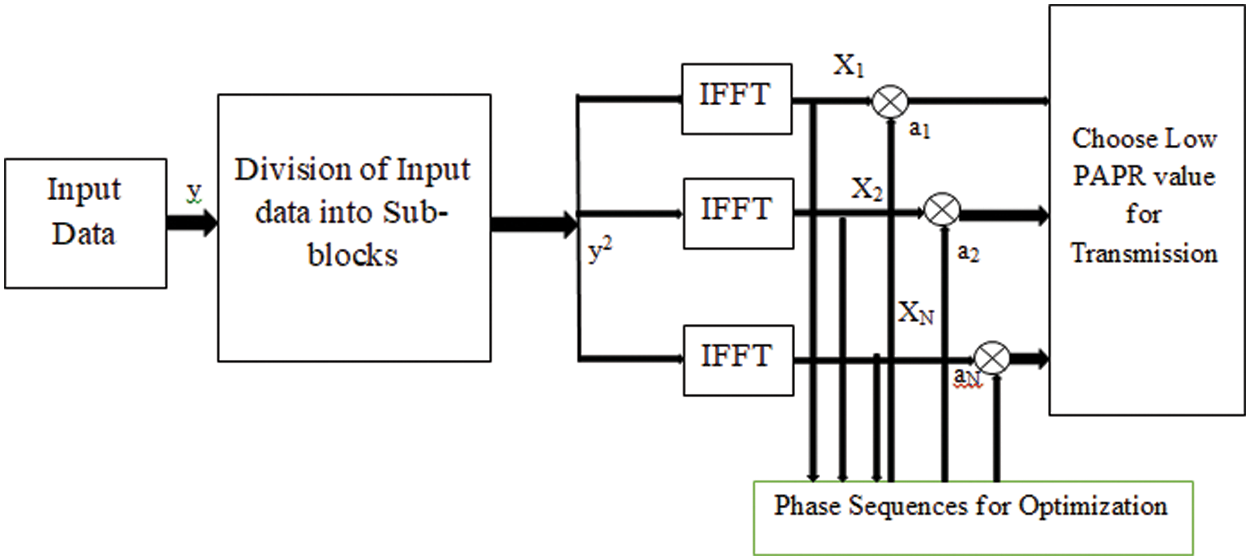
Figure 2: Advanced PTS
Let us consider an input signal given by:
Applying IFFT to Eq. (18) and multiplying with phase factors (
The phase sequences are selected to lower down the PAPR, can be written as:
It is one of the suitable approaches to overcome the PAPR problem in multicarrier waveforms. It reduces the PAPR by clipping the PAPR beyond a certain threshold [30]. However, this technique also degrades the throughput and enhances the spectrum leakage of the framework.
The basic difference among the techniques like SLM, PTS, and the companding technique is that in the latter technique the signals are transformed after the multicarrier modulation stage, whereas the former techniques change the formation of the signals before the multicarrier modulation stage. In the schematic, companding is used just after the IFFT block, and a random variable is used to denote the amplitude of the signals after the compression scheme. At the receiver, the inverse process is performed to obtain the signal with the least PAPR. In [31], a thorough analysis of the companding technique is presented in a systematic manner.
Through a reduction in PAPR levels, power saving can be achieved in wireless communication. It is a very important point as in the uplink scenario; the battery of the device is used by the inbuilt antenna/transmitter, so power saving becomes more important in that case. Generally, class-A amplifiers are considered high power amplifiers because of their good sound fidelity and less distortion. However, the maximum efficiency is only 50%. The efficiency of the system model can be represented as [32].
In the proposed work, we have used Matlab-2014 to evaluate the performance of the 5G waveforms. The simulation parameters used in the proposed work are given in Tab. 1.

Fig. 5 illustrates the PAPR responses for various waveforms implemented in 5G cellular communication systems. As seen from Fig. 3, OTFSM outclasses all the existing waveforms by a significant difference of 9.1, 7.1, and 5.1 dB more than OFDM, FBMC, and NOMA, respectively.
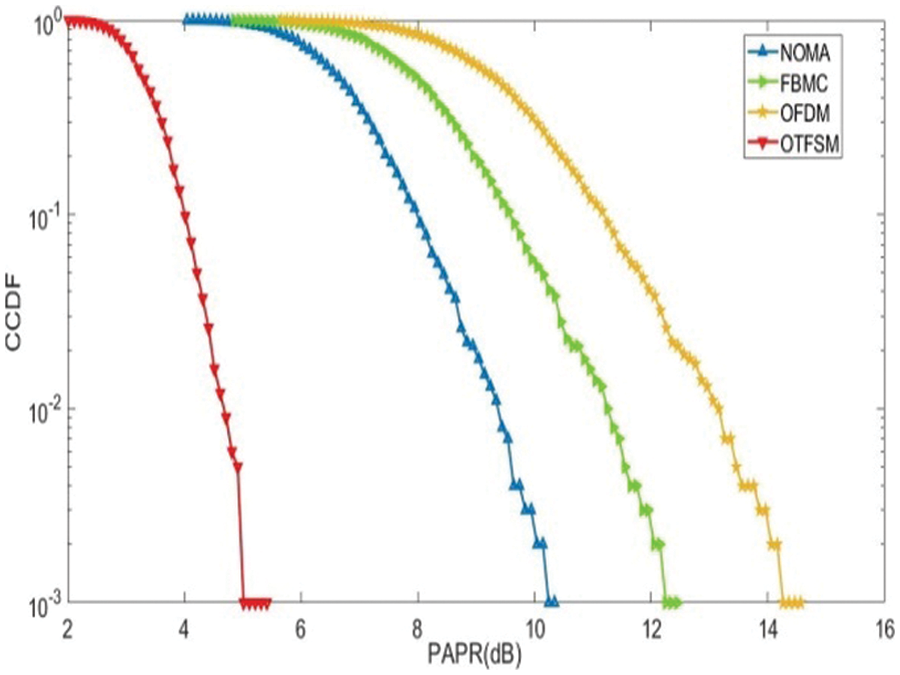
Figure 3: Original PAPR
Fig. 4 depicts the CCDF of FBMC systems using numerous techniques like Companding, clipping & filtering, SLM, and PTS. We can see that PTS in FBMC systems performs significantly better than all other shown techniques at a CCDF of 10−3. The PAPR of the PTS-FBMC technique is 3.3 dB, whereas the different techniques such as SLM, Clipping & Filtering, and Companding have values of PAPR of 4.1, 7, and 8.4 dB, respectively.

Figure 4: PAPR analysis of FBMC
Fig. 5 depicts the CCDFs of NOMA systems using numerous techniques like Companding, clipping & filtering, SLM, and PTS. We can see that PTS in NOMA systems performs significantly better than all other shown techniques at the CCDF of 10−3. The PAPR of the PTS-NOMA technique is 2.0 dB, whereas the different techniques such as SLM, Clipping & Filtering, and Companding have values of PAPR of 2.9, 5.3, and 7.8 dB, respectively.

Figure 5: PAPR analysis of NOMA
Fig. 6 depicts the CCDFs of OTFSM systems using numerous techniques like Companding, clipping & filtering, SLM, and PTS. We can see that PTS in OTFSM systems performs significantly better than all other shown techniques at a CCDF of 10−3. The PAPR of the PTS-OTFSM technique is 2 dB, whereas the different techniques such as SLM, Clipping & Filtering, and Companding have values of PAPR as 3.1, 3.6, and 4.3 dB, respectively. Tab. 2 shows the impact of power saving by various techniques used under different systems such as OFDM, FBMC, NOMA, and OTFSM.

Figure 6: PAPR analysis of OTFSM
The work proposed novel PAPR reduction techniques for advanced waveforms. The PAPR algorithms are applied to improve the power efficiency of an amplifier. It is seen that OTFSM gives a good PAPR performance as compared to other waveforms and is considered as one of the potential contenders for 5G and beyond. However, NOMA also gives better performance and can be used by reducing its receiver complexity. The PAPR algorithms, namely companding, Clipping and Filtering, SLM, and PTS, are analysed in this work, and it is seen that PTS outperforms the other PAPR algorithms. The utilization of PTS enhanced the power savings by up to 83% for NOMA and OTFSM. The proposed article indicates that the High Power Amplifier (HPA) works efficiently under OTFSM systems when used with PAPR algorithms.
Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R237), Princess Nourah bint Abdulrahman University, Riyadh,Saudi Arabia.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work under Grant Number (RGP 1/322/42).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. A. Kumar, “PAPR reduction of FBMC using hybrid and k-hybrid techniques,” Radio Electronics and Communications System, vol. 62, pp. 501–509, 2019. [Google Scholar]
2. Y. Acar and T. Cooklev, “High performance OFDM with index modulation,” Phyical Communication, vol. 32, pp. 192–199, 2019. [Google Scholar]
3. M. Chafii, E. Basar and S. Member, “Index modulation aided uplink noma for massive machine type communications,” IEEE Wireless Communications, vol. 2337, no. c, pp. 10–13, 2020. [Google Scholar]
4. X. Chen, M. Wen and S. Dang, “On the performance of cooperative OFDM-NOMA system with index modulation,” IEEE Wireless Communications, vol. 9, no. 10, pp. 1346–1350, 2020. [Google Scholar]
5. Y. Lai, Y. Ciou and J. Wu, “Index modulation multiple access,” in 2018 IEEE 29th Annual Int. Symp. on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, pp. 1–5, 2018. [Google Scholar]
6. X. Chen, M. Wen, S. Member, T. Mao and S. Dang, “Spectrum resource allocation based on cooperative noma with index modulation,” IEEE Transactions on Cognitive Communications and Networking, vol. 6, no. 3, pp. 946–958, 2020. [Google Scholar]
7. A. Tusha, “NOMA with index modulation for uplink urllc through grant-free access,” IEEE Journal of Selected Topics in Signal Processing, vol. 13, no. 6, pp. 1249–1257, 2019. [Google Scholar]
8. K. D. Choe, S. C. Kim and S. K. Park, “Pre-scrambling method for papr reduction in ofdm communication systems,” in IEEE Transactions on Consumer Electronics, vol. 50, no. 4, pp. 1044–1048, Nov. 2004. [Google Scholar]
9. A. Kumar, M. K. Sharma, K. Sengar and S. Kumar, “NOMA based cr for qam-64 and qam-256,” Egyptian Informatics Journal, vol. 21, no. 2, pp. 67–71, 2020. [Google Scholar]
10. S. Zhang, S. Member and B. Shahrrava, “A hybrid papr reduction scheme for ofdm systems using perfect sequences,” IEEE Transactions on Broadcasting, vol. PP, pp. 1–10, 2019. [Google Scholar]
11. S. Gokceli, T. Levanen, T. Riihonen, M. Renfors and M. Valkama, “Frequency-selective papr reduction for ofdm,” in IEEE Transactions on Vehicular Technology, vol. 68, no. 6, pp. 6167–6171, 2019. [Google Scholar]
12. K. Liu, W. Deng and Y. Liu, “Theoretical analysis of the peak-to-average power ratio and optimal pulse shaping filter design for gfdm systems,” IEEE Transactions on Signal Processing, vol. 67, no. 13, pp. 3455–3470, 2019. [Google Scholar]
13. S. Lv, J. Zhao, L. Yang and Q. Li, “Genetic algorithm based bilayer pts scheme for peak-to-average power ratio reduction of fbmc/oqam signal,” in IEEE Access, vol. 8, pp. 17945–17955, 2020. [Google Scholar]
14. D. Kong, X. Zheng, Y. Yang, Y. Zhang and T. Jiang, “A novel DFT-based scheme for PAPR reduction in FBMC/OQAM systems,” in IEEE Wireless Communications Letters, vol. 10, no. 1, pp. 161–165, 2021. [Google Scholar]
15. M. Laabidi, R. Zayani, D. Roviras and R. Bouallegue, “PAPR reduction in fbmc/oqam systems using active constellation extension and tone reservation approaches,” in 2015 IEEE Symp. on Computers and Communication (ISCC), Larnaca, Cyprus, pp. 657–662, 2015. [Google Scholar]
16. M. A. Aboul-dahab, M. M. Fouad and R. A. Roshdy, “Generalized discrete Fourier transform for fbmc peak to average power ratio reduction,” IEEE Access, vol. 7, pp. 81730–81740, 2019. [Google Scholar]
17. S. S. Al-samahi, B. K. Khoo, C. C. Tsimenidis and B. S. Sharif, “Selected mapping without side information for PAPR reduction in OFDM,” in IEEE Transactions on Wireless Communications, vol. 8, no. 7, pp. 3320–3325, 2009. [Google Scholar]
18. H. A. N. Wang, X. Wang, L. Xu and W. Du, “Hybrid papr reduction scheme for fbmc/oqam systems based on multi data block pts and tr methods,” in IEEE Access, vol. 4, pp. 4761–4768, 2016. [Google Scholar]
19. S. Lu, D. Qu, Y. He and S. Member, “Sliding window tone reservation technique for the peak-to-average power ratio reduction of fbmc-oqam signals,” in IEEE Wireless Communications Letters, vol. 1, no. 4, pp. 268–271, 2012. [Google Scholar]
20. Z. He, L. Zhou, Y. Chen and X. Lin, “Low-complexity pts scheme for papr reduction in fbmc-oqam systems,” IEEE Communication Letter, vol. PP, no. c, pp. 1, 2018. [Google Scholar]
21. D. Na, K. Choi and S. Member, “Low PAPR FBMC,” in IEEE Transactions on Wireless Communications, vol. 1276, no. c, pp. 1–12, 2017. [Google Scholar]
22. X. Cheng, D. Liu, W. Shi, Y. Zhao, Y. Li et al., “A novel conversion vector-based low-complexity SLM scheme for PAPR reduction, ” IEEE Transactions on Broadcasting, vol. 66, no. 3, pp. 656–666, 2020. [Google Scholar]
23. A. Li, A. Benjebbour, X. Chen, H. Jiang and H. Kayama “Uplink non-orthogonal multiple access ( noma ) with single-carrier frequency division multiple access (sc-fdma ) for 5g systems,” IEICE Transactions on Communication, vol. E98, no. 8, pp. 1426–1435, 2015. [Google Scholar]
24. K. Chandekar and V. Nithya, “Hybrid papr reduction using hartley transform precoding with clipping and filtering technique in ofdm-noma,” International Journal of Electrical Engineering and Technology, vol. 11, no. 4, pp. 341–348, 2020. [Google Scholar]
25. Z. H. Gebeyehu, “Heliyon impact of clipping noise on the sum rate of noma with pd-dco-ofdm and conventional dco-ofdm,” Heliyon, vol. 6, no. 2019, pp. e03363, 2020. [Google Scholar]
26. L. Dai, B. Wang, Z. Ding, Z. Wang, S. Chen et al., “A survey of non-orthogonal multiple access for 5g,” in IEEE Communications Surveys & Tutorials, vol. 20, no. 3, pp. 2294–2323, 2018. [Google Scholar]
27. C. Qian, Q. Xiong, B. Yu and C. Sun, “Low complexity detection algorithm for low papr interleaving based noma schemes,” in 2017 IEEE 86th Vehicular Technology Conf. (VTC-Fall), Toronto, ON, Canada, pp. 1–5, 2017. [Google Scholar]
28. A. Kumar and M. Gupta, “A review on activities of fifth-generation mobile communication system,” Alexandria Engineering Journal, vol. 57, no. 2, pp. 1125–1135, 2018. [Google Scholar]
29. A. Ghassemi and T. A. Gulliver, “PAPR reduction of OFDM using PTS and error-correcting code subblocking,” in IEEE Transactions on Wireless Communications, vol. 9, no. 3, pp. 980–989, 2010. [Google Scholar]
30. M. Hu, Y. Li, W. Wang and H. Zhang, “A piecewise linear companding transform for papr reduction of ofdm signals with companding distortion mitigation,” in IEEE Transactions on Broadcasting, vol. 60, no. 3, pp. 532–539, 2014. [Google Scholar]
31. T. Jiang, C. Li and C. Ni, “Effect of papr reduction on spectrum and energy efficiencies in ofdm systems with class-a hpa over awgn channel,” in IEEE Transactions on Broadcasting, vol. 59, no. 3, pp. 513–519, 2013. [Google Scholar]
32. A. Kumar, S. Gupta, H. Sharma and M. Masud, “PAPR reduction of noma using vandermonde matrix-particle transmission sequence,” Computer Systems Science and Engineering, vol. 43, no. 1, pp. 193–201, 2022. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |