Computers, Materials & Continua DOI:10.32604/cmc.2022.029009
Article

Analysis of Eigenvalues for Molecular Structures

Muhammad Haroon Aftab1, Kamel Jebreen2,*, Mohammad Issa Sowaity3 and Muhammad Hussain4

1Department of Mathematics and Statistics, The University of Lahore, Lahore, 54000, Pakistan
2Department of Mathematics, An-Najah National University, Nablus, P400, Palestine
3Department of Mathematics, Palestince Polytechnic University, Hebron, P766, Palestine
4Department of Mathematics, Comsats University Islamabad, Lahore Campus, Lahore, 54000, Pakistan
*Corresponding Author: Kamel Jebreen. Email: Jebreen20@yahoo.com
Received: 22 February 2022; Accepted: 30 March 2022

Abstract: In this article, we study different molecular structures such as Polythiophene network, PLY(n) for n = 1, 2,  and  3, Orthosilicate (Nesosilicate) SiO4, Pyrosilicates (Sorosilicates)  Si2O7, Chain silicates (Pyroxenes) (SiO3)n, and Cyclic silicates (Ring Silicates) Si3O9 for their cardinalities, chromatic numbers, graph variations, eigenvalues obtained from the adjacency matrices which are square matrices in order and their corresponding characteristics polynomials. We convert the general structures of these chemical networks in to mathematical graphical structures. We transform the molecular structures of these chemical networks which are mentioned above, into a simple and undirected planar graph and sketch them with various techniques of mathematics. The matrices obtained from these simple undirected graphs are symmetric. We also label the molecular structures by assigning different colors. Their graphs have also been studied for analysis. For a connected graph, the eigenvalue that shows its peak point (largest value) obtained from the adjacency matrix has multiplicity 1. Therefore, the gap between the largest and its smallest eigenvalues is interlinked with some form of “connectivity measurement of the structural graph”. We also note that the chemical structures, Orthosilicate (Nesosilicate) SiO4, Pyrosilicates (Sorosilicates)  Si2O7, Chain silicates (Pyroxenes)  (SiO3)n, and Cyclic silicates (Ring Silicates)  Si3O9  generally have two same eigenvalues. Adjacency matrices have great importance in the field of computer science.

Keywords: Vertex degree; edges; eigenvalues; characteristics polynomials; adjacency matrices; graphical model; genetics; polythiophene; silicates

1  Introduction

Combinatorics is also known as combinatorial mathematics. The study of eigenvalues of networks or diagrams plays a vital role in combinatorics. In 1957, Von Collatz et al. [1] presented the eigenvalues obtained from the adjacency matrix of the given graph.

Let’ s suppose M is a p×p matrix with real numbers entries. Eigenvector of M is defined in such a way that vector Mx is parallel to x or simply it can be defined as Mx=λx,   λ∈R. Whereas λ is known as the eigenvalue of M and belongs to the eigenvector  V. We can find the eigenvalue λ if and only if the matrix obtained from [M−λI] is singular that is determinant of [M−λI]=0. The algebraic equation obtained is of degree p has number of p roots. The eigenvalues of any network are in fact the eigenvalues of the given matrix known as adjacency matrix. The maximum absolute eigenvalue of a graph is called as its spectral radius. Eigenvalues has its extreme importance in the field of frequency analysis, differential equations, physics, computer graphics and in many more subjects [2,3].

2  Material and Methods

To understand the eigenvalues of a molecular structure, firstly, we construct a mathematical graph of the molecular structure by converting it into a planar graph. And then we label its vertices in two different ways, by numbering and coloring. After that we construct its adjacency matrix to get the eigenvalues. Suppose τ is a simple, finite, and undirected graph having vertex set  V(τ)= {1, 2, 3, …, n}. Then its adjacency matrix can be computed as the  n × n  matrix  Mτ=Mij  for that

Mij={1,  if  i and j are adjacent0,  otherwise                         

The adjacency matrix cannot be written uniquely as we can construct the matrix in several different ways i.e., by changing the position of rows or columns and then by relabeling them, by changing the names of vertices of the graph etc.

2.1 Pholythiophene Network PLYn=1, 2, 3 

Polythiophenes are the polymers having five structural components and play a vital role in industrial part because of its better thermal permanency and high ecological consistency. They are being used in many microelectronic devices [4,5]. Let’s consider the molecular structures of Polythiophene networks for n = 1, 2  and  3 as displayed in Figs. 1–3, respectively. Characteristics polynomials, eigenvalues, number of vertices and edges, and chromatic numbers are computed in Tabs. 1–3. We have displayed below two molecular graphs, one is for the construction of its adjacency matrix and while the other one in which we have labeled different colors in such a way that no edge has two same colors at its end nodes, is for its chromatic number.

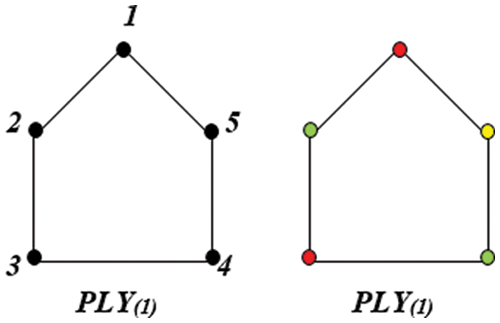
Figure 1: Polythiophene at n = 1

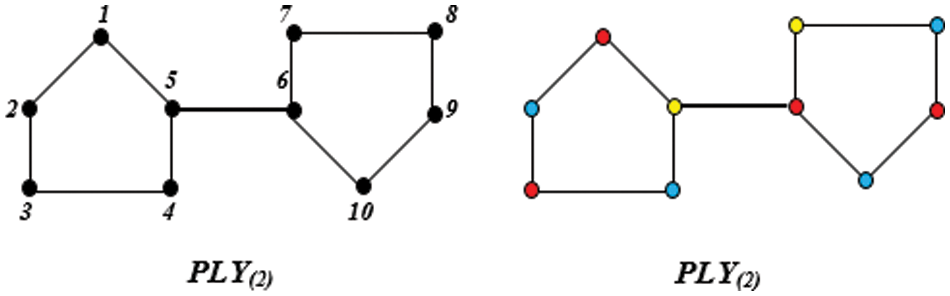
Figure 2: Polythiophene at n = 2

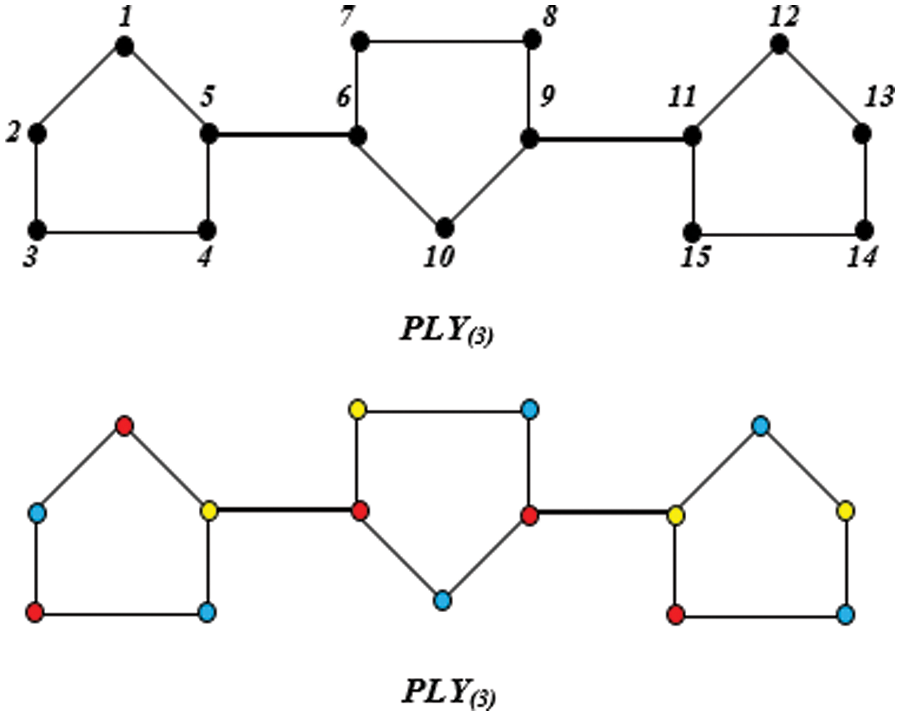
Figure 3: Polythiophene at n = 3

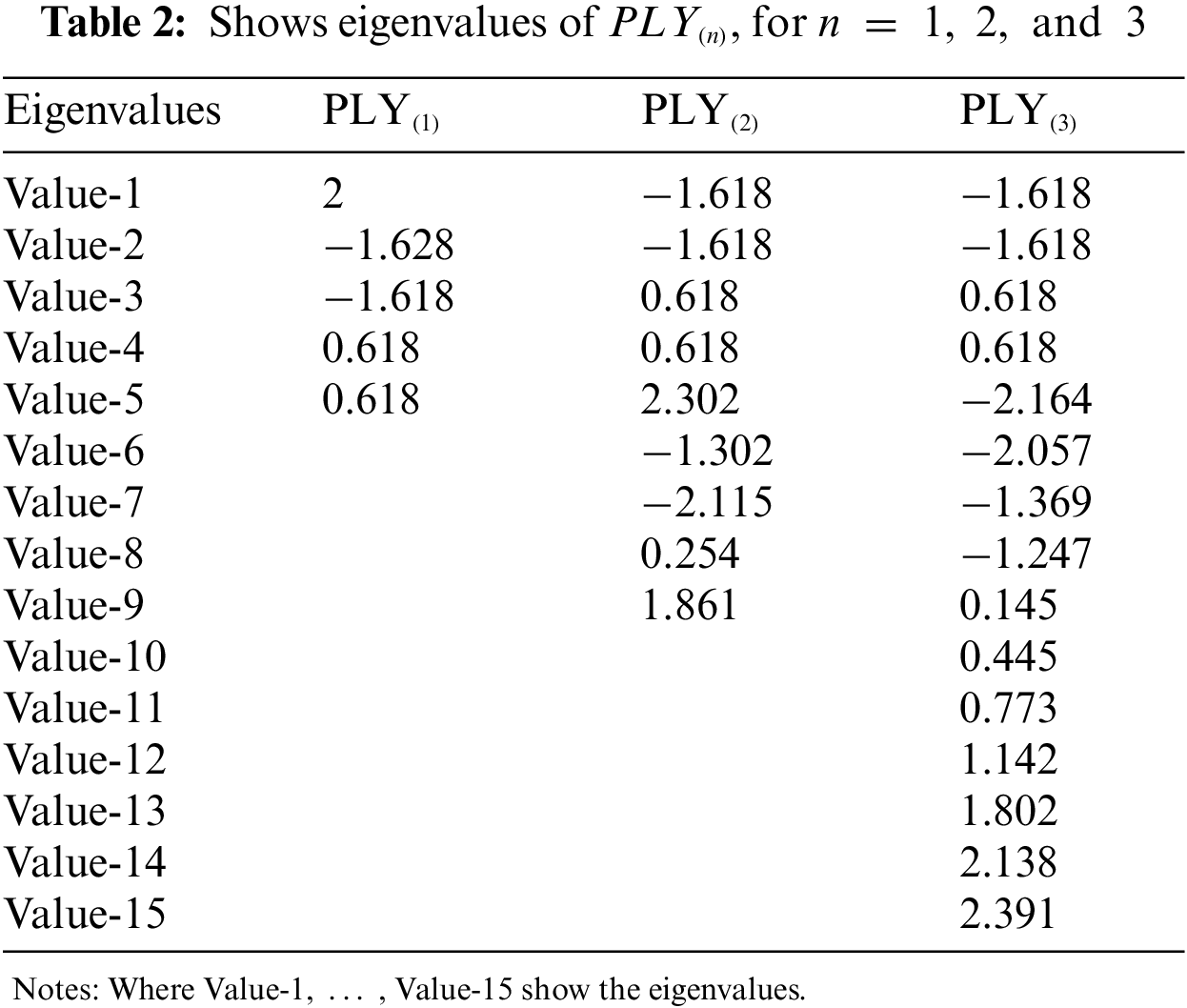
Adjacency matrices of PLY(n) for n = 1, 2, & 3 are given by:

MPLY(1)=(0100110100010100010110010)

MPLY(2)=(0100100000101000000001010000000010100000100101000000001010010000010100000000101000000001010000010010)

MPLY(3)=(010010000000000101000000000000010100000000000001010000000000100101000000000000010100100000000001010000000000000101000000000000010110000000001001000000000000001001001000000000010100000000000001010000000000000101000000000010010)

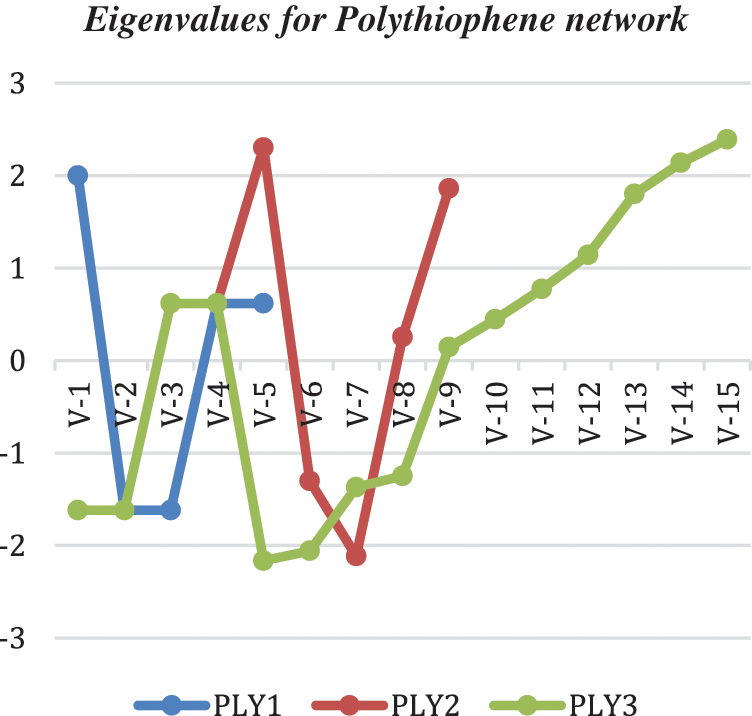
Graph 1: Eigenvalues for polythiophene network

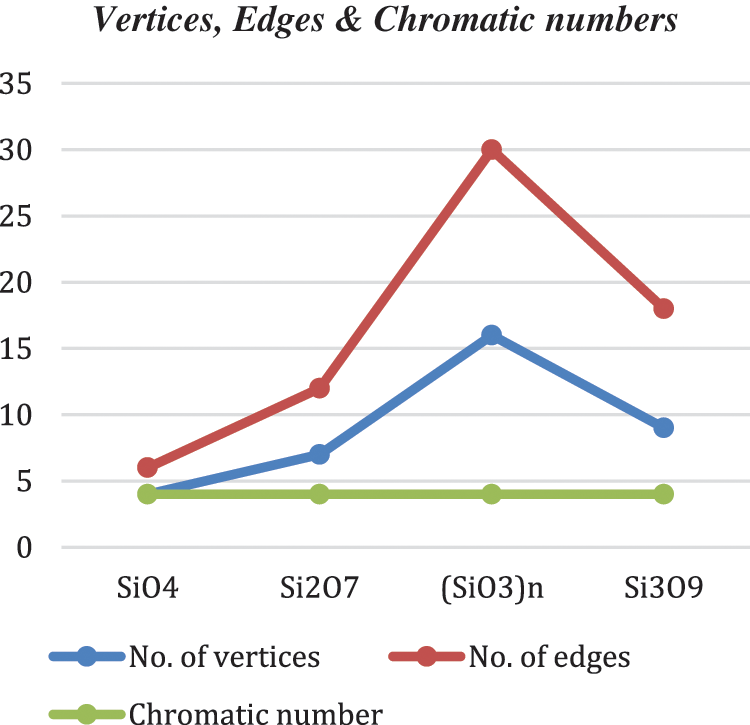
Graph 2: Vertices, edges & chromatic numbers

2.2 Different Silicates Networks

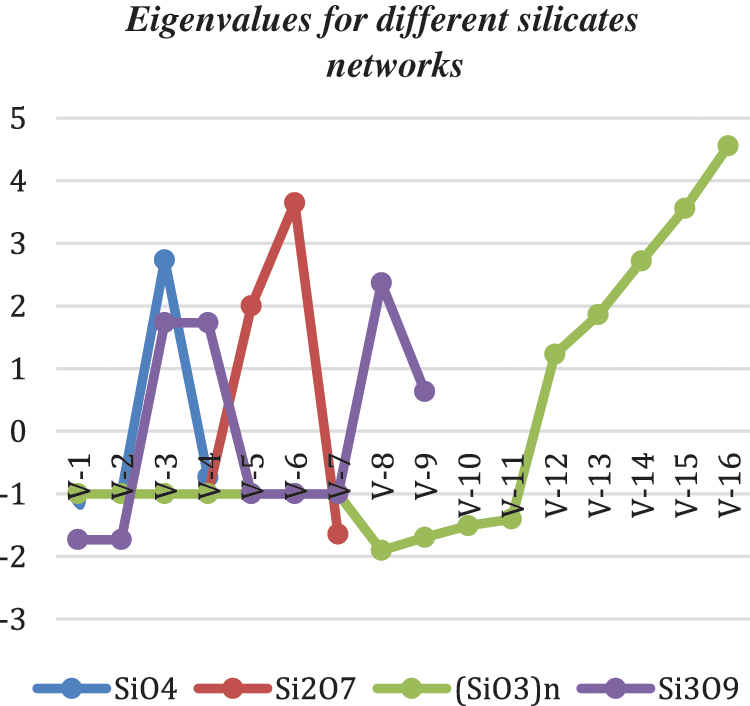
A silicate sheet is a ring of tetrahedrons which are joined by oxygen to other rings. A single and basic unit of silicate sheet is represented by SiO4 which is tetrahedron in shape just like a pyramid that has a base triangular in shape. It has one silicon atom surrounded by four oxygen atoms [6,7]. The topological structures of different silicates are studied and then identified equilateral properties of these different silicates. We consider the molecular structures of different silicates networks such as Orthosilicate (Nesosilicate) SiO4, Pyrosilicates (Sorosilicates)  Si2O7, Chain silicates (Pyroxenes)  (SiO3)n, and Cyclic silicates (Ring Silicates)  Si3O9 are shown in Figs. 4–7, respectively. We have shown below two types of graphs, one is used in the formation of its adjacency matrix and while other one of which different colors are labeled adopting the way that no two same colors are adjacent through edges, is constructed for the investigation of its chromatic number. We have computed characteristics polynomials, eigenvalues, number of vertices and edges, chromatics numbers, largest and smallest eigenvalues in Tabs. 4–7.

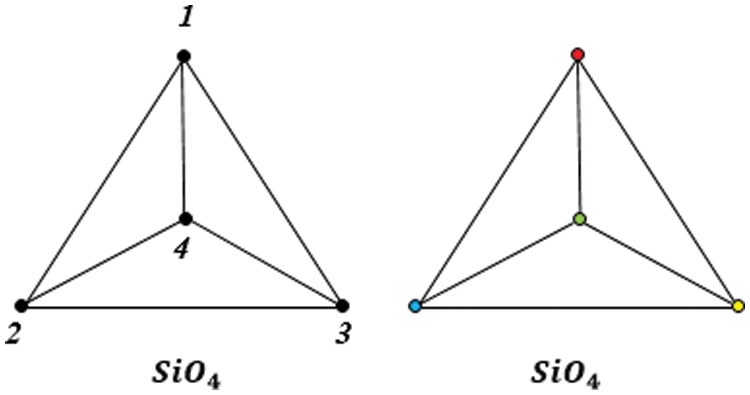
Figure 4: Orthosilicate

Figure 5: Pyrosilicates

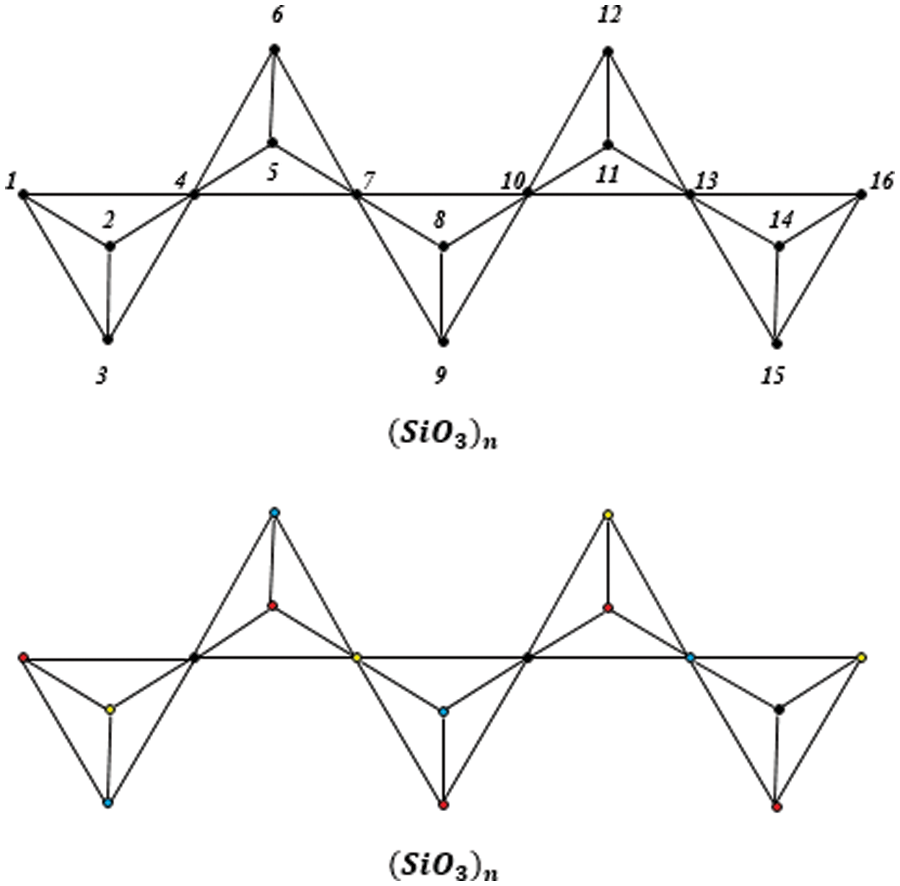
Figure 6: Pyroxenes

Figure 7: Ring silicates

Adjacency matrices of Orthosilicate (Nesosilicate) SiO4, Pyrosilicates (Sorosilicates)  Si2O7, Chain silicates (Pyroxenes)  (SiO3)n, and Cyclic silicates (Ring Silicates)  Si3O9 are given below:

MSiO4=(0111100111011110)

MSi2O7=(0111000101100011011111110000001001100101010010110)

MSi3O9=(010001100101101110010100010011011011000101001110110101110001000011100000000111000)

M(SiO3)n=(0111000000000000101100000000000011010000000000001110111000000000000101100000000000011010000000000001110111000000000000101100000000000011010000000000001110111000000000000101100000000000011010000000000001110111000000000000101100000000000011010000000000001110)

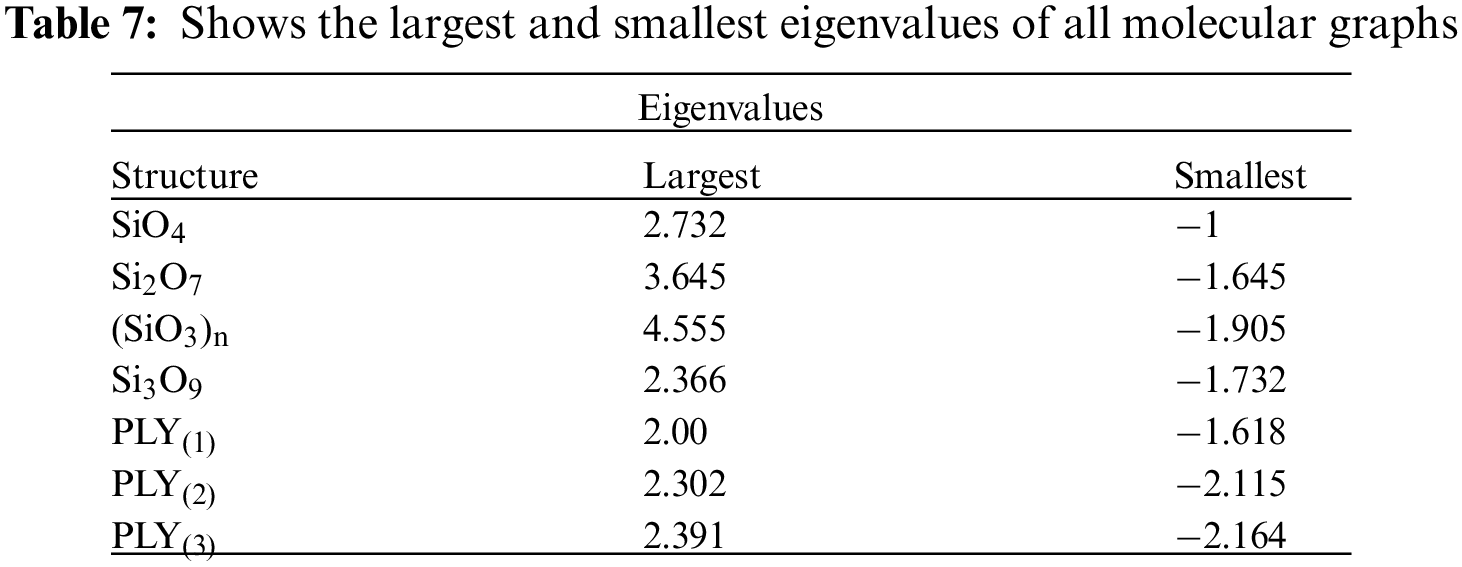
Graph 3: Eigenvalues for different silicates networks

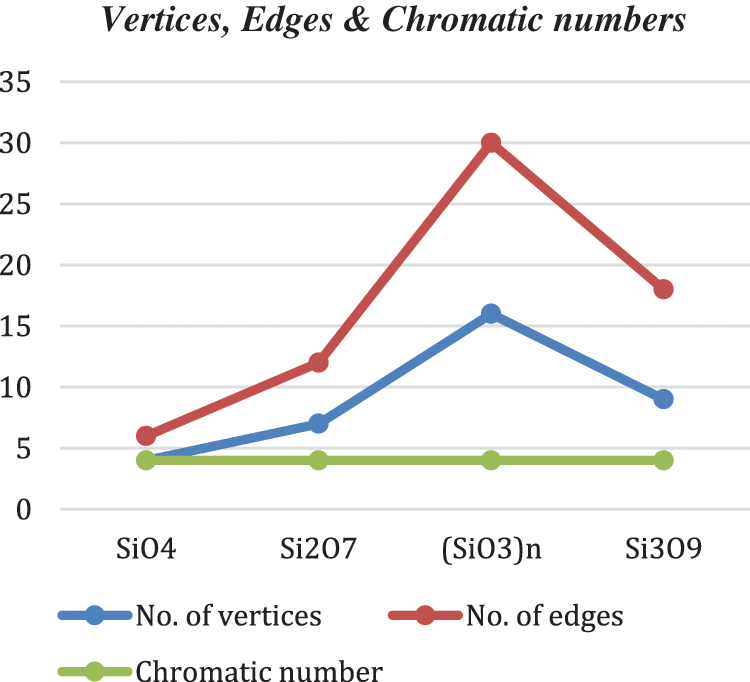
Graph 4: Vertices, edges & chromatic numbers

3  Discussion and Results

We have plotted different graphs based upon the computations of various molecular networks [8,9] such as Polythiophene network PLY(n) for n = 1, 2,  and  3, Orthosilicate (Nesosilicate) SiO4, Pyrosilicates (Sorosilicates) Si2O7, Chain silicates (Pyroxenes)  (SiO3)n, and Cyclic silicates (Ring Silicates)  Si3O9 to show some relations between the structure of a graph and its spectrum, whereas the collective degree obtained from the characteristics polynomial depicts the cardinality of its vertex set. The space between the first and the second eigenvalues has extreme importance in numerous fields of mathematics [10,11]. If a connected graph is seen in the diagram, then the largest eigenvalue of the calculated adjacency matrix has multiplicity 1. Consequently, the space between the maximum and its minimum eigenvalues is associated with a type of “connectivity measure of the graph”. It has also been observed that all four silicates graphs generally have two same eigenvalues. The largest and smallest eigenvalues in all the above calculated networks are given below.

Whereas eigenvalue tells us about the measurement of variance in a data and spread out of data on a line.

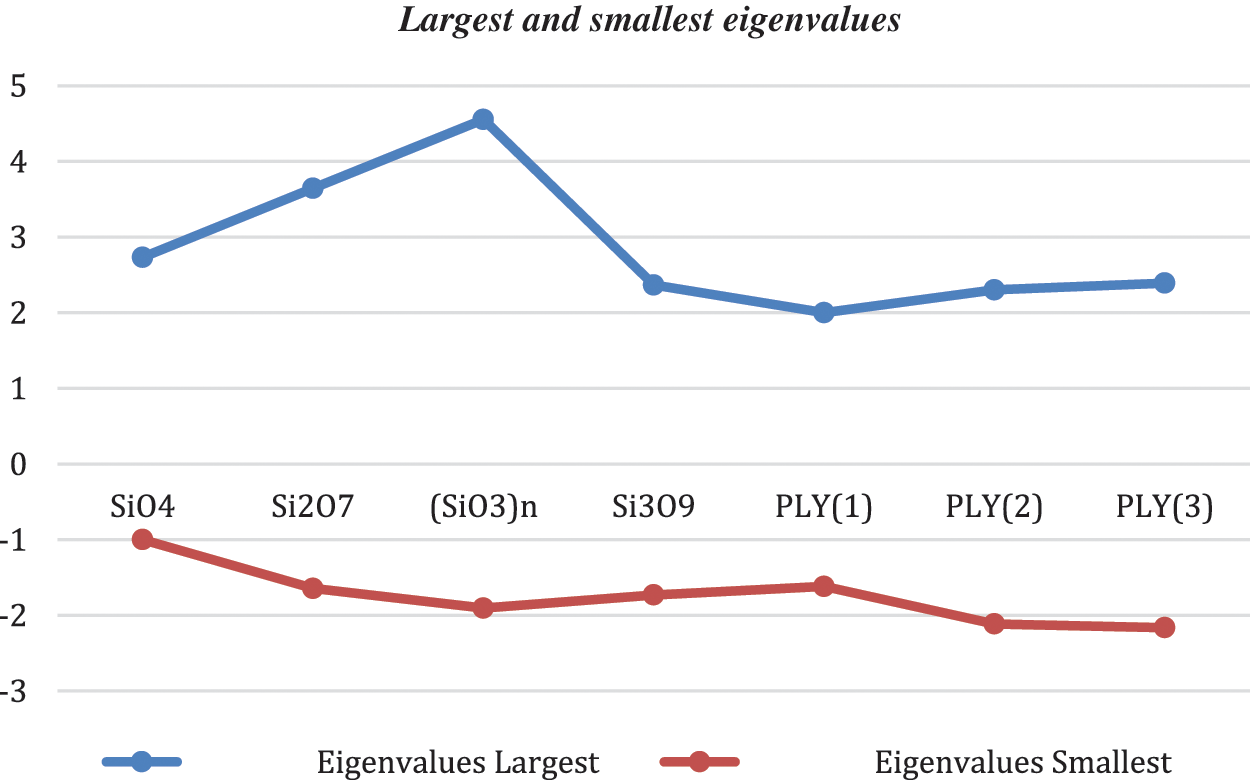
Graph 5: Largest and smallest eigenvalues for all networks

4  Conclusion

The eigenvector having largest eigenvalue is also known as a principal component. The eigenvalue which is less than 1 indicates that the principal component has a single original variable. The original variable had better value than new one. It will fit with factor rotation constructing a second factor which is associated with a single variable. The results obtained can be used for “discrete analogues of Cheeger’s inequality in differential geometry” [12]. The eigenvalue that is chosen as the smallest value is diligently associated to the categorization of graphs. The chromatic numbers (CN) [13,14] have also been utilized for a proper coloring of a graph.

Acknowledgement: The authors like to show their gratitude to the concerned persons for sharing their pearls of wisdom with us during this research work. Authors should thank those who contributed to the article but cannot include themselves.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  L. Von Collatz and U. Sinogowitz, “Spektren endlicher grafen,” in Abhandlungen Mathematical Seminar, Der Universitat Hamburg, Germany, pp. 63–77, 1957. [Google Scholar]

 2.  S. Hoory, N. Linial and A. Wigderson, “Expander graphs and their applications,” Bulletin of American Mathematical Society, vol. 43, no. 4, pp. 439–561, 2006. [Google Scholar]

 3.  M. Krivelevich and B. Sudakov, “Pseudo-random graphs,” Bolyai Society Mathematical Studies, vol. 15, pp. 199–262, 2006. [Google Scholar]

 4.  M. H. Aftab, M. Rafaqat, M. Hussain and T. Zia, “On the computation of some topological descriptors to find closed formulas for certain chemical graphs,” Journal of Chemistry, vol. 2021, pp. 1–16, 2021. [Google Scholar]

 5.  Y. Kongyang, C. Xiaosong, J. Zhepeng, Z. Cong, W. Dacheng et al., “Two-dimensional cross-linked polythiophene network,” Journal of Materials Chemistry C, vol. 7, pp. 9362–9368, 2019. [Google Scholar]

 6.  P. Manuel and I. Rajasingh, “Topological properties of silicate networks,” in 5th IEEE GCC Conf. and Exhibition, Kuwait, March, pp. 16–19, 2009. [Google Scholar]

 7.  F. Simonraj and A. George, “Topological properties of few poly oxide, poly silicate, dox and dsl networks,” International Journal of Future Computer and Communication, vol. 2, no. 2, pp. 90–95, 2013. [Google Scholar]

 8.  M. H. Aftab, M. Rafaqat and M. Hussain, “On the computation of topological indices for molecular structures of subdivided aztec diamonds,” Computational Journal of Combinatorial Mathematics, vol. 2021, no. 2, pp. 13–20, 2021. [Google Scholar]

 9.  M. H. Aftab, M. Rafaqat and M. Hussain, “Topological invariants for the general structure of grape seed proanthocyanidins,” Punjab University Journal of Mathematics, vol. 54, no. 1, pp. 45–53, 2022. [Google Scholar]

10. N. Alon, “Eigenvalues and expanders,” Combinatorica, vol. 6, no. 2, pp. 83–96, 1986. [Google Scholar]

11. N. Alon and V. D. Milman, “λ1, isoperimetric inequalities for graphs and superconcentrators,” Journal of Combinatorial Theory B, vol. 38, no. 1, pp. 73–88, 1985. [Google Scholar]

12. B. Colbois and A. M. Matei, “On the optimality of J. cheeger and P. buser inequalities,” Differential Geometry and its Applications, vol. 19, no. 3, pp. 281–293, 2003. [Google Scholar]

13. L. A. Sz´ekely, “Measurable chromatic number of geometric graphs and sets without some distances in Euclidean space,” Combinatorica, vol. 4, pp. 213–218, 1984. [Google Scholar]

14. A. Ali, G. Chartrand and P. Zhang, “Irregularity in graphs,” Springer Briefs in Mathematics, 1st edition, vol. 2021, pp. 1–109, 2021. [Google Scholar]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.